3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification †
Abstract
1. Introduction
- We examine earthquake magnitude categorization as a multi-label classification task by evaluating the features extracted through log-Mel spectrograms and analyzing the relationships among different earthquake classes.
- We present a 3D-CNN-RNN based architecture to evaluate the multi-label earthquake classification task. It encapsulates a 3D-CNN to extract features from an input spectrogram, and recurrent layers are employed on each kernel of the final CNN layer to model the similarities among different earthquake signals.
- We develop a new multi-label earthquake dataset and reorganize an existing dataset [29] for the earthquake categorization task.
2. Our Approach
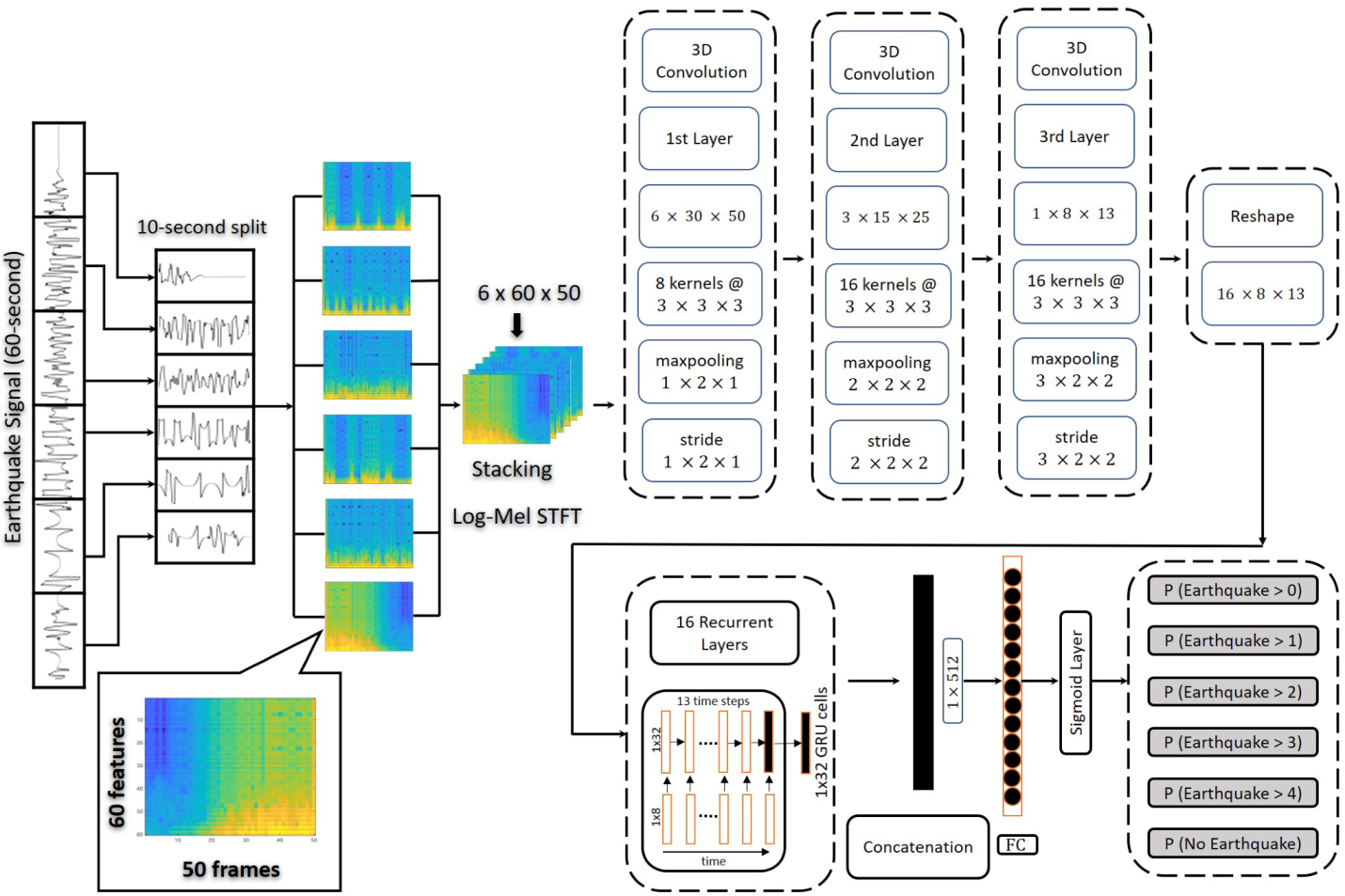
2.1. 3D Convolutional Neural Networks
2.2. Recurrent Neural Network (RNN)
2.3. 3-Dimensional Convolutional Recurrent Architecture
3. Data and Methods
3.1. Properties of Dataset
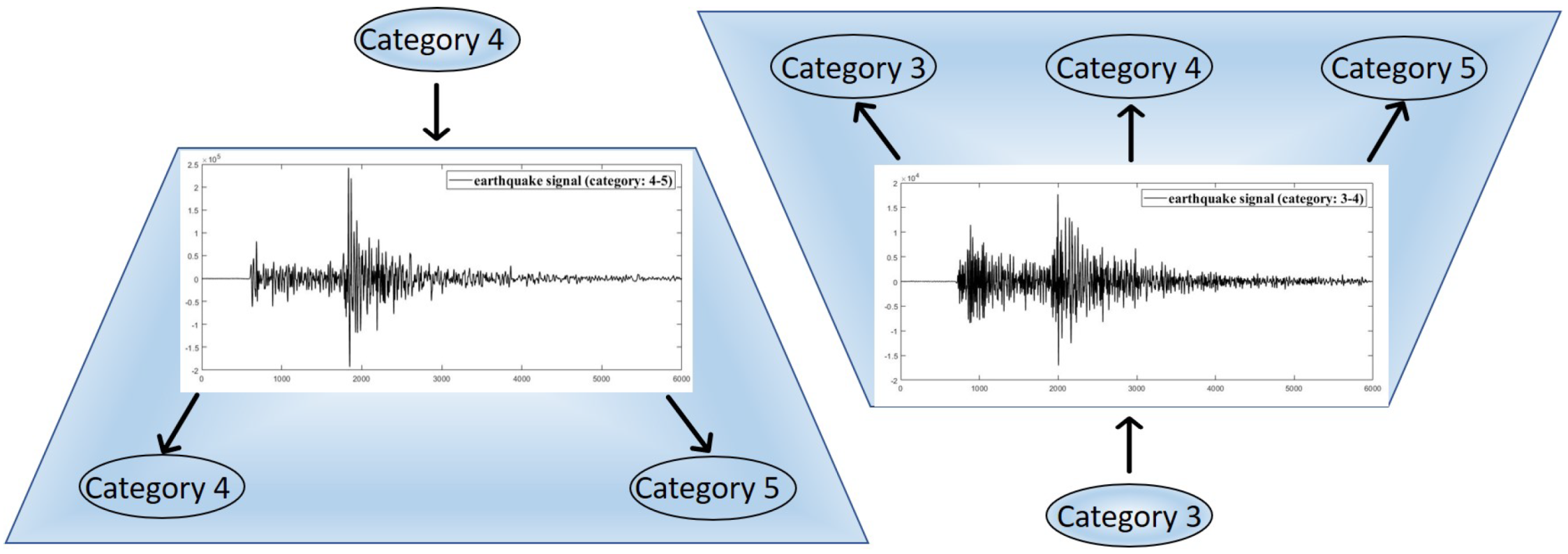
3.2. Transforming Multi-Class to Multi-Label Dataset
4. Experiments
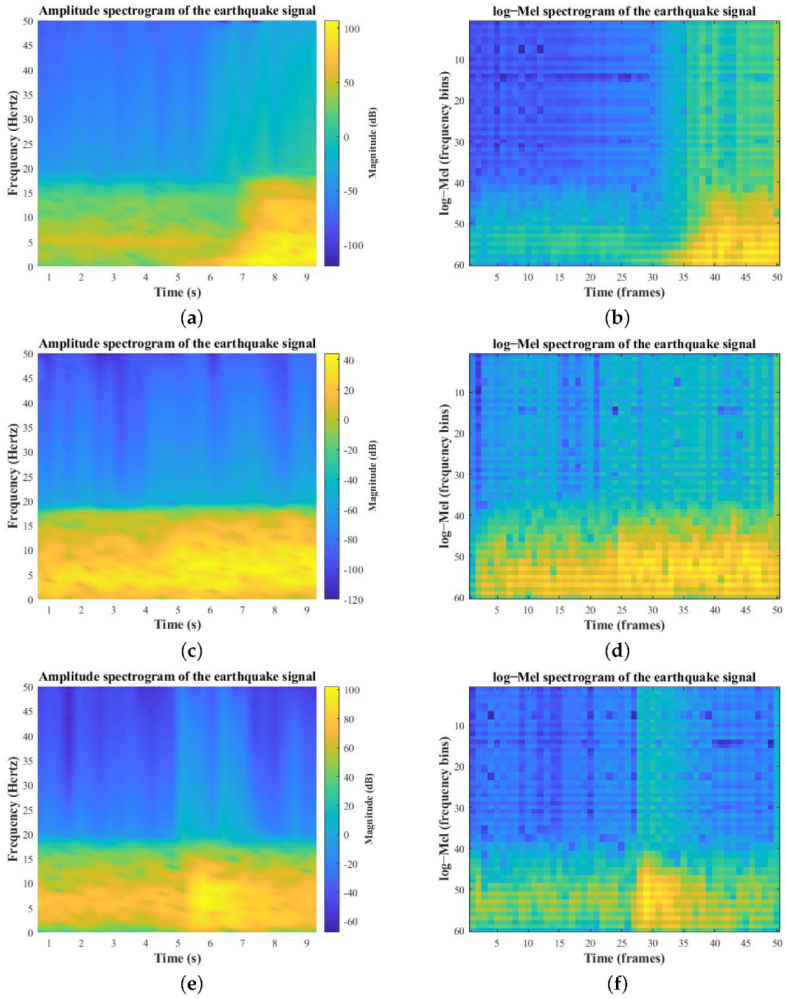
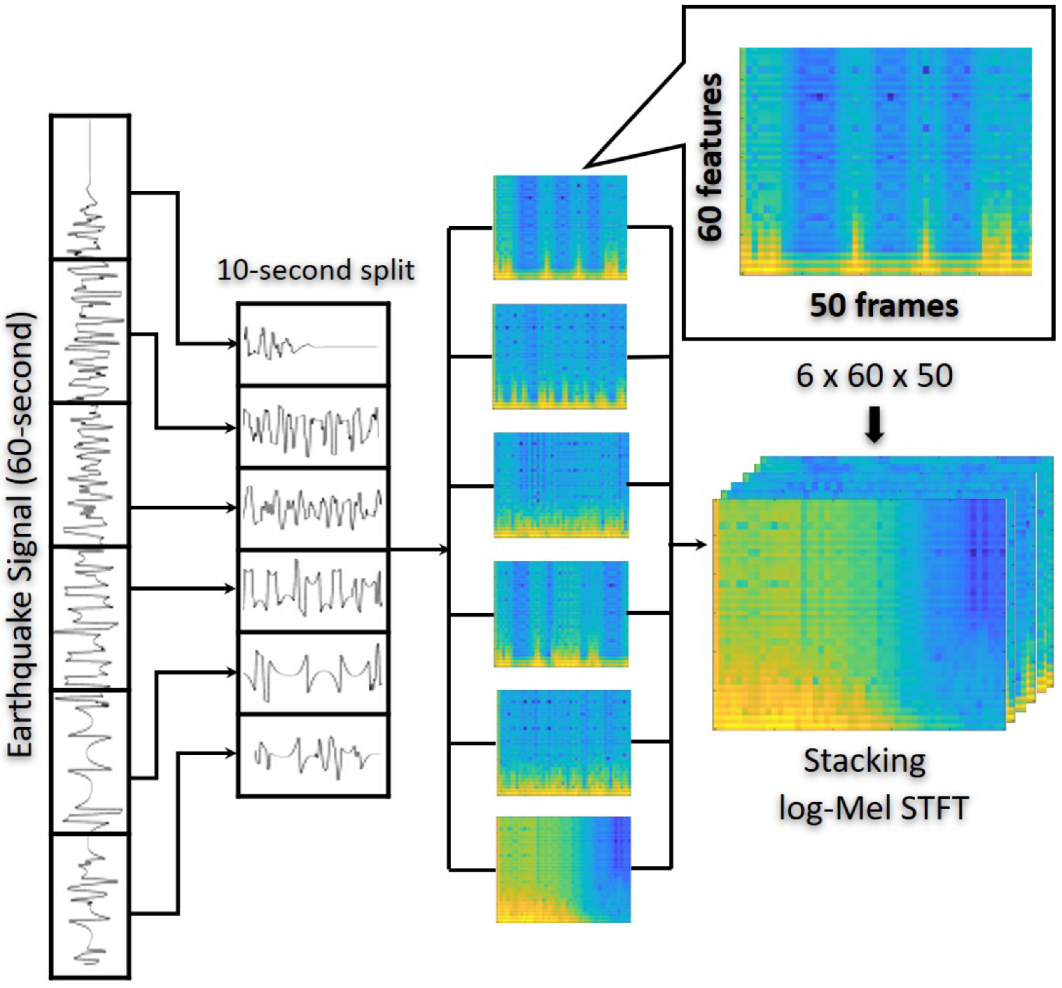
Data Representation: Feature Extraction
5. Evaluation
5.1. Evaluation Metrics
5.2. Training
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.-L.; Zhou, Z.-H. A Review on Multi-Label Learning Algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Xu, D.; Shi, Y.; Tsang, I.W.; Ong, Y.-S.; Gong, C.; Shen, X. Survey on Multi-Output Learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 2409–2429. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, W.; Wang, H.; Shen, X.; Tsang, I. The Emerging Trends of Multi-Label Learning. arXiv 2020, arXiv:2011.11197. [Google Scholar] [CrossRef] [PubMed]
- Adeli, J.E.; Zhang, A.; Taflanidis, A. Convolutional generative adversarial imputation networks for spatio-temporal missing data in storm surge simulations. arXiv 2014, arXiv:2111.02823. [Google Scholar]
- Zhang, M.-L.; Zhou, Z.-H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 2038–2048. [Google Scholar] [CrossRef][Green Version]
- Hsu, D.J.; Sham, M.; Kakade, J.L.; Tong, Z. Multi-Label Prediction via Compressed Sensing. In Proceedings of the 22nd International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 7–10 December 2009; pp. 772–780. [Google Scholar] [CrossRef]
- Gong, Y.; Jia, Y.; Leung, T.; Toshev, A.; Ioffe, S. Deep Convolutional Ranking for Multilabel Image Annotation. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Wei, Y.; Xia, W.; Lin, M.; Huang, J.; Ni, B.; Dong, J.; Zhao, Y.; Yan, S. HCP: A Flexible CNN Framework for Multi-Label Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1901–1907. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Yang, Y.; Mao, J.; Huang, Z.; Huang, C.; Xu, W. CNN-RNN: A unified framework for multi-label image classification. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2285–2294. [Google Scholar]
- Briggs, F.; Lakshminarayanan, B.; Neal, L.; Fern, X.Z.; Raich, R.; Hadley, S.J.K.; Hadley, A.; Betts, M.G. Acoustic classification of multiple simultaneous bird species: A multi-instance multi-label approach. J. Acoust. Soc. Am. 2012, 131, 4640–4650. [Google Scholar] [CrossRef][Green Version]
- Bucak, S.S.; Jin, R.; Jain, A.K. Multi-label learning with incomplete class assignments. CVPR 2011, 2011, 2801–2808. [Google Scholar] [CrossRef][Green Version]
- Johnson, T. Effective Use of Word Order for Text Categorization with Convolutional Neural Networks. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, CO, USA, 15 June 2015; pp. 103–112. [Google Scholar]
- Joulin, T. Bag of Tricks for Efficient Text Classification. In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics, Valencia, Spain, 19–23 April 2017; Volume 2, pp. 427–431. Available online: https://aclanthology.org/E17-2068 (accessed on 17 February 2022).
- Prabhu, Y.; Varma, M. FastXML. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 263–272. [Google Scholar]
- Mousavi, S.M.; Zhu, W.; Sheng, Y.; Beroza, G.C. CRED: A Deep Residual Network of Convolutional and Recurrent Units for Earthquake Signal Detection. Sci. Rep. 2019, 9, 10267. [Google Scholar] [CrossRef]
- Perol, T.; Gharbi, M.; Denolle, M. Convolutional neural network for earthquake detection and location. Sci. Adv. 2018, 4, e1700578. [Google Scholar] [CrossRef][Green Version]
- Shakeel, M.; Itoyama, K.; Nishida, K.; Nakadai, K. Detecting earthquakes: A novel deep learning-based approach for effective disaster response. Appl. Intell. 2021, 51, 8305–8315. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bormann, P.; Saul, J. Earthquake Magnitude. In Encyclopedia of Complexity and Systems Science; Meyers, R., Ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Jung, M.; Chi, S. Human activity classification based on sound recognition and residual convolutional neural network. Autom. Constr. 2020, 114, 103177. [Google Scholar] [CrossRef]
- Li, G.; Zhang, M.; Li, J.; Lv, F.; Tong, G. Efficient densely connected convolutional neural networks. Pattern Recognit. 2021, 109, 107610. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhang, X.; Zou, J.; He, K.; Sun, J. Accelerating Very Deep Convolutional Networks for Classification and Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1943–1955. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving Deep Convolutional Neural Networks for Image Classification. IEEE Trans. Evol. Comput. 2020, 24, 394–407. [Google Scholar] [CrossRef][Green Version]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef][Green Version]
- Scarpiniti, M.; Comminiello, D.; Uncini, A.; Lee, Y.-C. Deep Recurrent Neural Networks for Audio Classification in Construction Sites. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 24–28 August 2020; pp. 810–814. [Google Scholar]
- Deng, Y.; Wang, L.; Jia, H.; Tong, X.; Li, F. A Sequence-to-Sequence Deep Learning Architecture Based on Bidirectional GRU for Type Recognition and Time Location of Combined Power Quality Disturbance. IEEE Trans. Ind. Inform. 2019, 15, 4481–4493. [Google Scholar] [CrossRef]
- Ravanelli, M.; Brakel, P.; Omologo, M.; Bengio, Y. Light Gated Recurrent Units for Speech Recognition. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 2, 92–102. [Google Scholar] [CrossRef][Green Version]
- Mousavi, S.M.; Sheng, Y.; Zhu, W.; Beroza, G.C. STanford EArthquake Dataset (STEAD): A Global Data Set of Seismic Signals for AI. IEEE Access 2019, 7, 179464–179476. [Google Scholar] [CrossRef]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D Convolutional Neural Networks for Human Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chung, J.; Çaglar, G.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Glorot, X.; Yoshua, B. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Shakeel, M.; Itoyama, K.; Nishida, K.; Nakadai, K. EMC: Earthquake Magnitudes Classification on Seismic Signals via Convolutional Recurrent Networks. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Virtual, 11–14 January 2021; pp. 388–393. [Google Scholar]
- Davis, S.; Mermelstein, P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 357–366. [Google Scholar] [CrossRef][Green Version]
- O’Shaughnessy, D. Speech Communications: Human and Machine (Addison-Wesley Series in Electrical Engineering); Addison-Wesley: Boston, MA, USA, 1987. [Google Scholar]
- Diaz, J.; Schimmel, M.; Ruiz, M.; Carbonell, R. Seismometers Within Cities: A Tool to Connect Earth Sciences and Society. Front. Earth Sci. 2020, 8, 9. [Google Scholar] [CrossRef][Green Version]

| Earthquake Categories | Earthquake Waveforms (Training Set) | Earthquake Waveforms (Test Set) |
|---|---|---|
| Magnitudes (0–1) | 10,868 | 4656 |
| Magnitudes (1–2) | 10,868 | 4656 |
| Magnitudes (2–3) | 10,868 | 4656 |
| Magnitudes (3–4) | 10,868 | 4656 |
| Magnitudes (4–8) | 10,868 | 4656 |
| Non-earthquake | 10,868 | 4656 |
| Total | 65,208 | 27,936 |
| Earthquake Categories | Precision | Recall | F1-Score |
|---|---|---|---|
| Magnitudes (0–1) | 0.72 | 0.60 | 0.65 |
| Magnitudes (1–2) | 0.52 | 0.52 | 0.52 |
| Magnitudes (2–3) | 0.50 | 0.34 | 0.40 |
| Magnitudes (3–4) | 0.46 | 0.58 | 0.52 |
| Magnitudes (4–8) | 0.61 | 0.75 | 0.67 |
| Earthquake Categories | Precision | Recall | F1-Score |
|---|---|---|---|
| Magnitudes (0–1) | 0.97 | 0.50 | 0.66 |
| Magnitudes (1–2) | 0.98 | 0.69 | 0.81 |
| Magnitudes (2–3) | 0.83 | 0.51 | 0.63 |
| Magnitudes (3–4) | 0.93 | 0.90 | 0.91 |
| Magnitudes (4–8) | 0.84 | 0.81 | 0.82 |
| Non-earthquake | 0.99 | 0.87 | 0.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakeel, M.; Nishida, K.; Itoyama, K.; Nakadai, K. 3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification. Appl. Sci. 2022, 12, 2195. https://doi.org/10.3390/app12042195
Shakeel M, Nishida K, Itoyama K, Nakadai K. 3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification. Applied Sciences. 2022; 12(4):2195. https://doi.org/10.3390/app12042195
Chicago/Turabian StyleShakeel, Muhammad, Kenji Nishida, Katsutoshi Itoyama, and Kazuhiro Nakadai. 2022. "3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification" Applied Sciences 12, no. 4: 2195. https://doi.org/10.3390/app12042195
APA StyleShakeel, M., Nishida, K., Itoyama, K., & Nakadai, K. (2022). 3D Convolution Recurrent Neural Networks for Multi-Label Earthquake Magnitude Classification. Applied Sciences, 12(4), 2195. https://doi.org/10.3390/app12042195






