A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
3.1. Sequential Pattern Mining
3.2. Noise Graph Addition
3.3. Differential Privacy
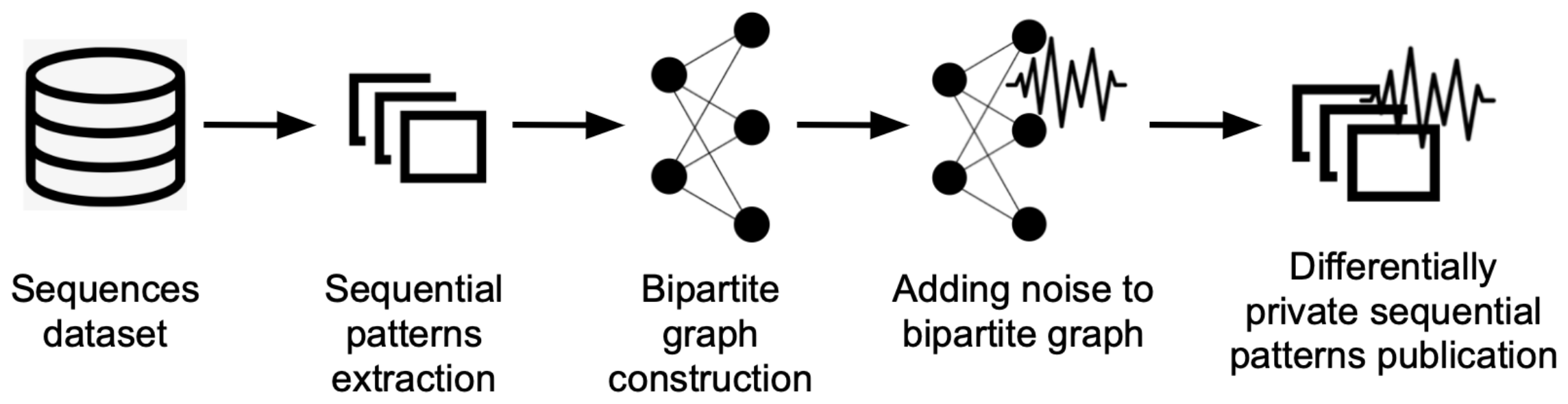
3.4. Graph-Based Differential Privacy for Frequent Sequential Patterns
- 1
- Frequent sequential pattern mining (pre-processing);
- 2
- Graph representation of frequent patterns;
- 3
- Adding noise to the client-pattern graph;
- 4
- Publishing the frequent sequential patterns with noise.
3.5. Measures
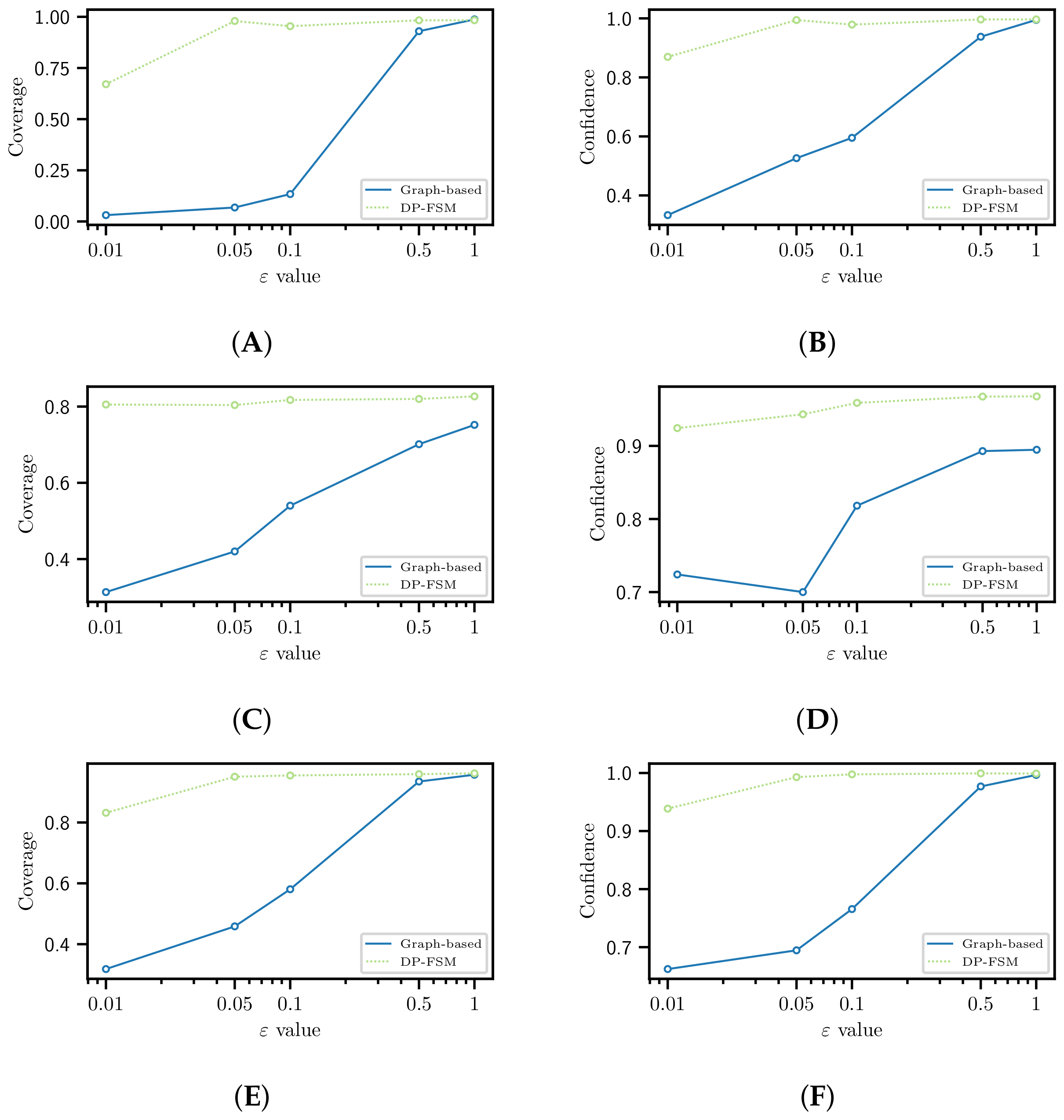
4. Experiments and Results
- 1
- Statlog or German Credit Data: This dataset was provided by Prof. Hofmann. It contains categorical attributes to clients having good or bad credit risk (German Credit Data: https://archive.ics.uci.edu/ml/datasets/statlog+(german+credit+data), accessed on 13 February 2022). In this work, the characteristics of each client having credit are represented as a sequence. For instance, A40 represents if the client has a new car, and A71 represents if the client is unemployed;
- 2
- Bank Transactions: this private dataset contains credit and debit card transactions in monetary units, grouped by the Classification of Individual Consumption by Purpose (COICOP), the international reference classification of household expenditure (COICOPs https://unstats.un.org/unsd/class/revisions/coicop_revision.asp, accessed on 13 February 2022). Each bank user is represented by a sequence of COICOPs (C1 to C12). For instance, C1 represents food and non-alcoholic beverages, and C3 groups clothing and footwear;
- 3
- NYC and Tokyo Check-in: this dataset contains 801131 check-ins in NYC and Tokyo collected from April 2012 to February 2013. Each check-in is associated with its timestamp, GPS coordinates, and venue categories (NYC and Tokyo Check-in: https://sites.google.com/site/yangdingqi/home/foursquare-dataset#h.p_ID_46, accessed on 13 February 2022). To build the sequences, the venue categories (represented by letters) of the visited place were grouped for each user. For example, A represents a pet store, and B represents a beauty store.
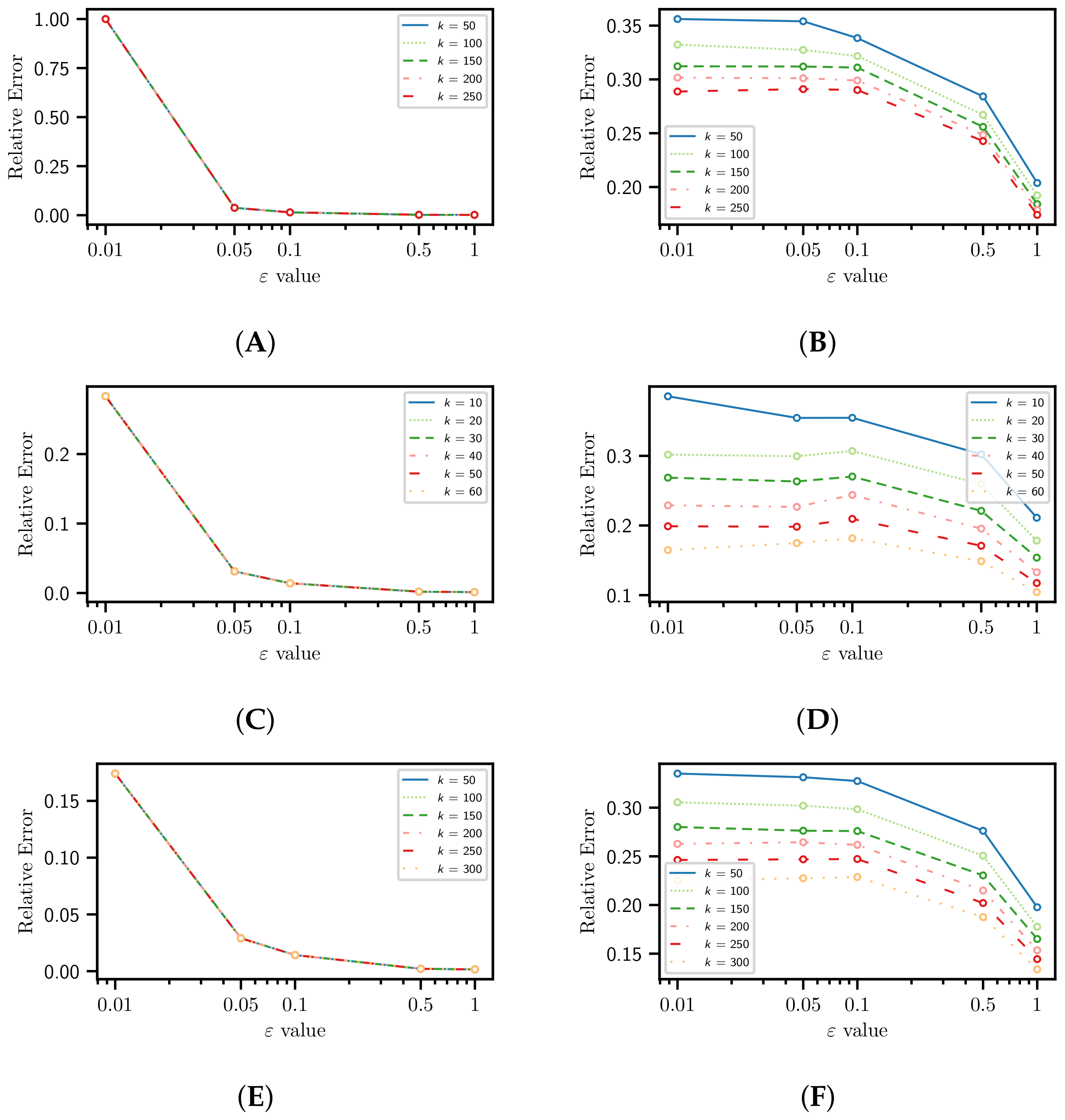
4.1. Information Loss
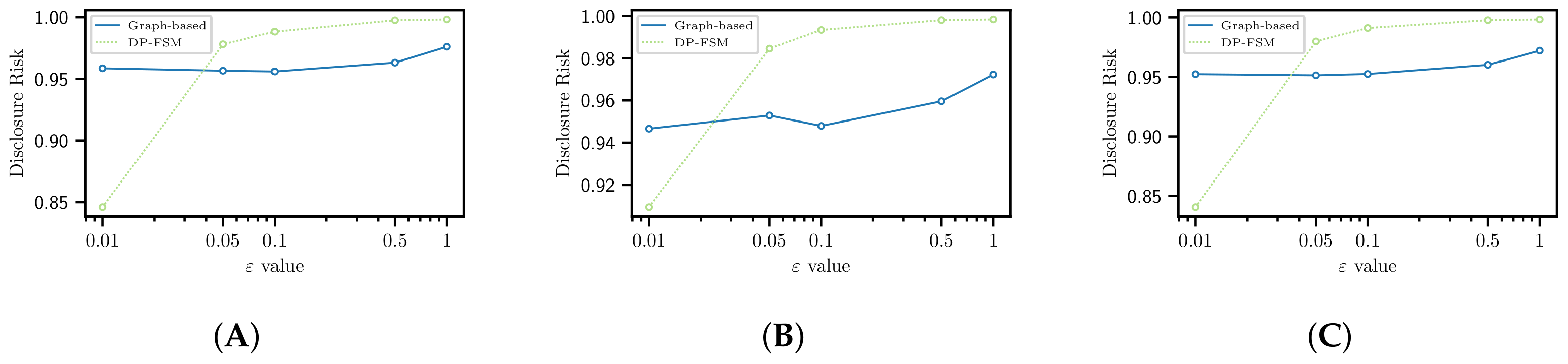
4.2. Disclosure Risk
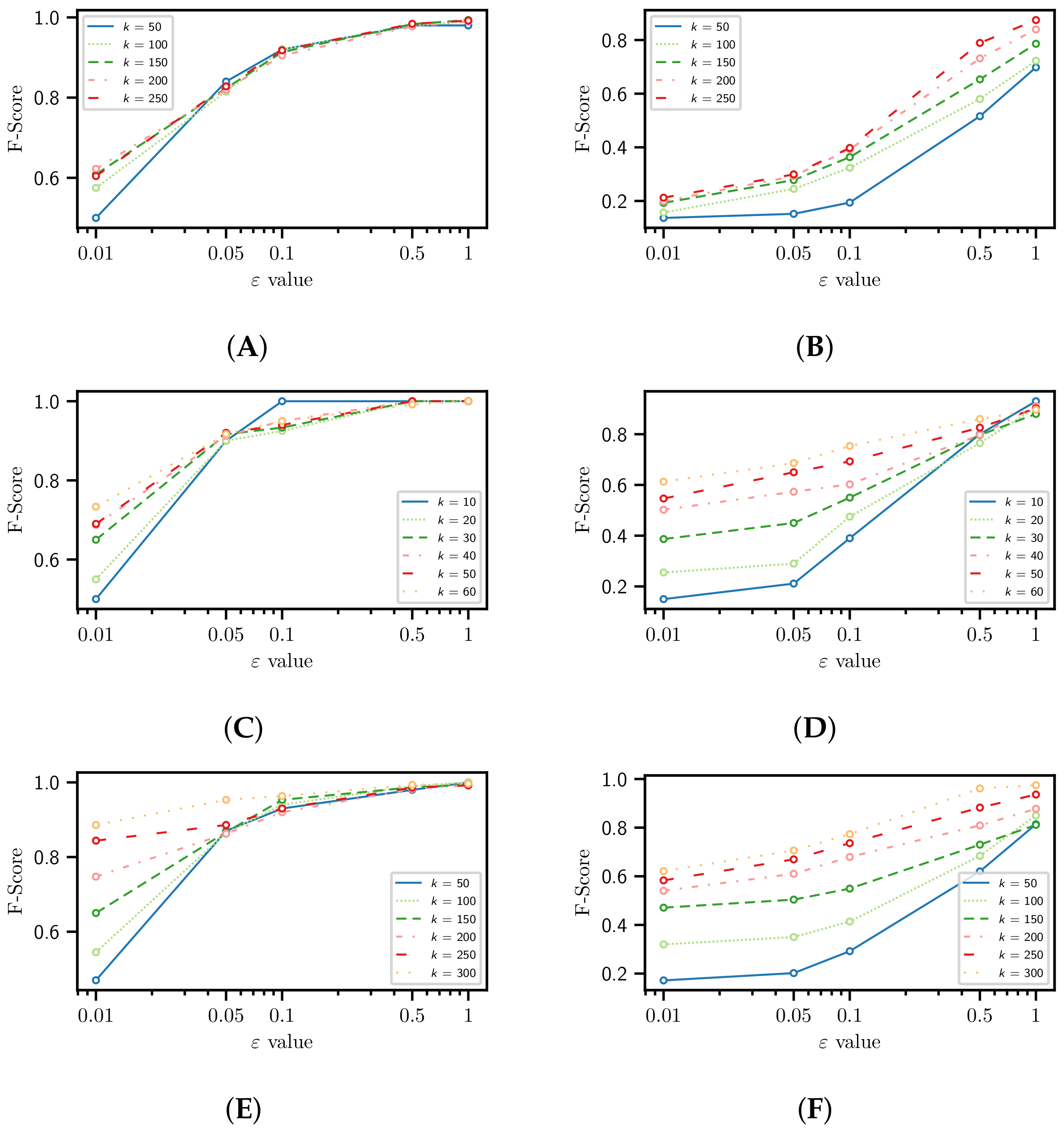
4.3. Utility
4.4. Utility for Recommendation Tasks
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Alatrista-Salas, H.; Azé, J.; Bringay, S.; Cernesson, F.; Selmaoui-Folcher, N.; Teisseire, M. A knowledge discovery process for spatiotemporal data: Application to river water quality monitoring. Ecol. Inform. 2015, 26, 127–139. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.; Yang, G.; Li, X. Mining sequential patterns of PM2.5 pollution between 338 cities in China. J. Environ. Manag. 2020, 262, 110341. [Google Scholar] [CrossRef] [PubMed]
- Pinaire, J.; Chabert, E.; Azé, J.; Bringay, S.; Poncelet, P.; Landais, P. Prediction of In-Hospital Mortality from Administrative Data: A Sequential Pattern Mining Approach. Stud. Health Technol. Inform. 2021, 281, 293–297. [Google Scholar] [PubMed]
- Tandan, M.; Acharya, Y.; Pokharel, S.; Timilsina, M. Discovering symptom patterns of COVID-19 patients using association rule mining. Comput. Biol. Med. 2021, 131, 104249. [Google Scholar] [CrossRef] [PubMed]
- Nunez-del Prado, M.; Salas, J.; Alatrista-Salas, H.; Maehara-Aliaga, Y.; Megías, D. Are Sequential Patterns Shareable? Ensuring Individuals’ Privacy. In International Conference on Modeling Decisions for Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2021; pp. 28–39. [Google Scholar]
- Torra, V.; Salas, J. Graph Perturbation as Noise Graph Addition: A New Perspective for Graph Anonymization. In Data Privacy Management, Cryptocurrencies and Blockchain Technology; Springer International Publishing: Cham, Switzerland, 2019; pp. 121–137. [Google Scholar]
- Salas, J.; Torra, V. Differentially Private Graph Publishing and Randomized Response for Collaborative Filtering. In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications, ICETE 2020-V2: SECRYPT, Lieusaint, Paris, France, 8–10 July 2020; ScitePress: Setúbal, Portugal, 2020; pp. 415–422. [Google Scholar]
- Chen, R.; Acs, G.; Castelluccia, C. Differentially private sequential data publication via variable-length n-grams. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh, NC, USA, 16–18 October 2012; pp. 638–649. [Google Scholar]
- Xu, S.; Cheng, X.; Su, S.; Xiao, K.; Xiong, L. Differentially private frequent sequence mining. IEEE Trans. Knowl. Data Eng. 2016, 28, 2910–2926. [Google Scholar] [CrossRef]
- Xu, S.; Su, S.; Cheng, X.; Li, Z.; Xiong, L. Differentially private frequent sequence mining via sampling-based candidate pruning. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea, 13–17 April 2015; pp. 1035–1046. [Google Scholar]
- Zhou, F.; Lin, X. Frequent sequence pattern mining with differential privacy. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2018; pp. 454–466. [Google Scholar]
- Chen, R.; Fung, B.C.; Desai, B.C.; Sossou, N.M. Differentially private transit data publication: A case study on the montreal transportation system. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 213–221. [Google Scholar]
- Bonomi, L.; Xiong, L. A two-phase algorithm for mining sequential patterns with differential privacy. In Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 269–278. [Google Scholar]
- Bonomi, L.; Xiong, L. Mining frequent patterns with differential privacy. Proc. VLDB Endow. 2013, 6, 1422–1427. [Google Scholar] [CrossRef]
- Lee, E.W.; Xiong, L.; Hertzberg, V.S.; Simpson, R.L.; Ho, J.C. Privacy-preserving Sequential Pattern Mining in distributed EHRs for Predicting Cardiovascular Disease. AMIA Jt. Summits Transl. Sci. Proc. 2021, 2021, 384–393. [Google Scholar] [PubMed]
- Pei, J.; Han, J.; Mortazavi-Asl, B.; Wang, J.; Pinto, H.; Chen, Q.; Dayal, U.; Hsu, M.C. Mining sequential patterns by pattern-growth: The prefixspan approach. IEEE Trans. Knowl. Data Eng. 2004, 16, 1424–1440. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast algorithms for mining association rules. In Proceedings of the 20th VLDB Conference, Santiago, Chile, 12 September 1994; Volume 1215, pp. 487–499. [Google Scholar]
- Alatrista-Salas, H.; Guevara-Cogorno, A.; Maehara, Y.; Nunez-del Prado, M. Efficiently Mining Gapped and Window Constraint Frequent Sequential Patterns. In International Conference on Modeling Decisions for Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 240–251. [Google Scholar]
- Dwork, C. Differential Privacy. In Proceedings of the 33rd International Conference on Automata, Languages and Programming-Volume Part II (ICALP’06), Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Hay, M.; Li, C.; Miklau, G.; Jensen, D. Accurate Estimation of the Degree Distribution of Private Networks. In Proceedings of the 2009 Ninth IEEE International Conference on Data Mining, Miami Beach, FL, USA, 6–9 December 2009; pp. 169–178. [Google Scholar]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback–Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
- Zeng, C.; Naughton, J.F.; Cai, J.Y. On differentially private frequent itemset mining. Proc. VLDB Endow. 2012, 6, 25–36. [Google Scholar] [CrossRef]
- Suneetha, K.; Rani, M.U. Web Page Recommendation Approach Using Weighted Sequential Patterns and Markov Model. Glob. J. Comput. Sci. Technol. 2012, 1–12. Available online: https://computerresearch.org/index.php/computer/article/view/493 (accessed on 13 February 2022).
| Metrics | German | Bank | NYC |
|---|---|---|---|
| Sequences | 1000 | 548,263 | 1083 |
| Different items | 90 | 12 | 14 |
| Max size | 21 | 4028 | 2697 |
| Min size | 21 | 1 | 100 |
| Avg size | 21 | 111 | 210 |
| Freq. Patterns | 75 | 22 | 14,494 |
| Rel. Support | 0.5 | 0.8 | 0.9 |
| License | Public | Private | Public |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunez-del-Prado, M.; Maehara-Aliaga, Y.; Salas, J.; Alatrista-Salas, H.; Megías, D. A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns. Appl. Sci. 2022, 12, 2131. https://doi.org/10.3390/app12042131
Nunez-del-Prado M, Maehara-Aliaga Y, Salas J, Alatrista-Salas H, Megías D. A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns. Applied Sciences. 2022; 12(4):2131. https://doi.org/10.3390/app12042131
Chicago/Turabian StyleNunez-del-Prado, Miguel, Yoshitomi Maehara-Aliaga, Julián Salas, Hugo Alatrista-Salas, and David Megías. 2022. "A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns" Applied Sciences 12, no. 4: 2131. https://doi.org/10.3390/app12042131
APA StyleNunez-del-Prado, M., Maehara-Aliaga, Y., Salas, J., Alatrista-Salas, H., & Megías, D. (2022). A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns. Applied Sciences, 12(4), 2131. https://doi.org/10.3390/app12042131







