Abstract
Topological mechanics is rapidly emerging as an attractive field of research where mechanical waveguides can be designed and controlled via topological methods. With the development of topological phases of matter, recent advances have shown that topological states have been realized in the elastic media exploiting analogue quantum Hall effect, analogue quantum spin Hall effect, analogue quantum valley Hall effect, higher-order topological physics, topological pump, topological lattice defects and so on. This review aims to introduce the experimental and theoretical achievements with defect-immune protected elastic waves in mechanical systems based on the abovementioned methods, respectively. From these discussions, we predict the possible perspective of topological mechanics.
1. Introduction
Over the last decade, topological mechanics has rapidly attracted extensive research. This field mainly investigates topological wave propagation, which is immune to defects and backscattering in mechanical systems, originally discovered in quantum systems. In this review, we aim to cover the main achievements of topological mechanics, including the fundamental concepts of topological phases of matter, theories and experimental realizations.
Over the past 40 years, topological phases of matter appeared as a leading field of research. This field of research originated from the discovery of the quantum Hall effect (QHE). In 1980, Klitzing et al. found that the Hall conductance equal to integer multiples of the fundamental constant with a two-dimensional electron gas sample in a low temperature and strong magnetic environment [1]. In 1982, Thouless et al. explored the mechanism of the integer quantum Hall effect and elucidated the relationship between the integer in the Hall conductance and a topological invariant in the QHE system [2]. Importantly, they proposed the TKNN (Thouless–Kohmoto–Nightingale–den Nijs) theory to define the integer, namely the Chern number. The Chern number characterizes the topological phases of matter in momentum space over the Brillouin zone. Specifically, combining the bulk-boundary correspondence [3], there exist edge states in the system with a non-zero Chern number, while the ordinary insulators and vacuum with a zero Chern number are trivial. However, realizing QHE requires breaking time-reversal symmetry, which is not beneficial to practical application.
About 20 years later, in 2005, the quantum spin Hall effect (QSHE) or topological insulators(TIs) were proposed in graphene [4], conventional semiconductors with a strain gradient [5] and HgTe quantum wells [6]. Realizing QSHE exploits the spin-orbit interactions and time-reversal symmetry. In these systems, a Chern number of zero arose from the existence of conjugate electronic spins, hence the topological nature is characterized by a topological invariant or the spin Chern number [7,8]. Phenomenologically, TIs have gapless edge or surface states when the spin Chern numbers are non-zero.
Shortly afterwards, the quantum valley Hall effect (QVHE) was discovered in 2007 [9,10]. Valleys refer to the extrema of the band structure in momentum space, and the sign of the valley Chern number at and is opposite. Of note is the fact that the total Chern number remains zero. In addition, the edge or surface states protected by the time-reversal symmetry could be observed at the interface between the two lattices with opposite valley Chern numbers.
Over the past five years, a new type of topological phase called higher-order topological insulators (HOTIs) has attracted rapidly growing attention, a phase which does not apply the bulk-boundary correspondence [11,12,13]. Phenomenologically, a d-dimensions n-th order HOTI hosts gapped (d − 1)-, (d − 2)-, …, (d − n + 1)-dimensional gapped boundaries and (d − n)-dimensional gapless modes [14]. For example, a two-dimensional (2D) HOTI has gapped one-dimensional (1D) boundaries and zero-dimensional (0D) corner states. A three-dimensional (3D) HOTI has 2D gapped surface states and 1D gapless hinge states, or 2D gapped surface states, 1D gapped hinge states and 0D corner states. The topological phases of HOTIs are characterized by new topological invariants [15]. Specifically, the topological invariants for the quantized multipole insulators are quantized multipole moments, which can be calculated by the nested Wilson loop approach [11,12] or the many-body multipole operators [16,17]. Specifically, for the nested Wilson loop approach, the gapped Wannier bands carrying their own topological invariants can be evaluated by this approach. One could start by constructing Wilson loop operators and in the x and y directions, and is the starting point of the loop. Here , and is a similar form, where , are the occupied Bloch functions. For the many-body multipole operators, the bulk multipoles in crystalline systems could be expressed in terms of ground-state expectation values of many-body operators, and this approach has a wider range of applications that could be used in interacting quantum many-body systems. The topological invariants for the Cn-symmetric HOTIs are the dipole polarizations (extended Zak phase), which are defined as an integration of the Berry phase vector potential A over the first Brillouin zone(BZ): [18,19].
An interesting exploration direction, topological pump, was firstly proposed in 1983 by Thouless [20]. This work showed the relationship between the 1D quantization of particle transport and 2D QHE. Recently, a topological pump was connected to 6D QHE [21,22] via synthetic dimensions. More recently, a topological pump has been observed in higher-order topological systems [23]. The topological phases of 2D QHE are characterized by the first Chern number, which is defined as the integration of the Berry curvature over the generalized 2D Brillouin zone, and 4D QHE, characterized by the second Chern number, which is defined as the integration of the Berry curvature over the generalized 4D Brillouin zone [24].
As we all know, topological crystalline insulators can be identified by the robust spectral features and quantized fractional charges on boundaries or corners in experiments. Moreover, topological lattice defects could serve as a bulk probe to characterize the topological crystalline insulators [25]. Topological lattice defects, such as dislocations and disclinations, break the local crystal symmetry, which can be constructed by a Volterra process [25,26,27,28]. In general, topological defects are characterized by their holonomy [25] or the Burgers vector [19,29], and the topological nature is characterized by the topological index (the polarizations) [19].
The abovementioned distinct topological states could also be realized in classical systems, such as photonics, acoustics, mechanics, electric circuits and so on since the topological nature is unrelated to the quantum characteristics and depends on the wave characteristics [30]. In this context, there are extensive efforts to realize topological states in various elastic systems, leading to the emerging research field of topological mechanics. Elastic solids support both longitudinal and transverse waves, which are highly hybridized, bringing a great challenge to realize topological waveguides. However, elastic materials are still a good platform for implementing topological band structures because their large scale makes the control of fabrication and the experimental process more flexible. Moreover, elastic systems are not restricted by the Fermi levels therefore spectrum signature can be measured directly at any region. Furthermore, there are a lot of potential applications containing sensors, low loss devices, actuation, signal processing and so on [31].
The framework of this review is as follows. In Section 2, we introduce the main achievements of elastic topological edge states. In Section 3, we present the main studies of elastic HOTIs. In Section 4, we show the main researches of elastic topological pumps. In Section 5, we discuss the main realization of elastic topological defect states. Finally, some of the future perspectives in topological mechanical systems are outlined in Section 6.
2. Mechanical Topological Edge Sates
The discovery of the integer quantum Hall effect opened a new research field in condensed-matter physics [1]. It was later discovered that the existence of the topological invariant (non-zero Chern number) is the root cause of quantization, which is independent of symmetry breaking [2]. If the Chern number is zero, the phase of the structure is ordinary; otherwise, it is topological. The Chern number in 2D systems [32] is given by:
where the Berry connection , is the Bloch state on the nth energy band. It has been proven that achieving the QHE requires an externally reinforced magnetic field to break the time-reversal symmetry. However, it is difficult to apply a magnetic field in a real environment.
Soon after that, Kane and Zhang et al. proposed the QSHE around 2005 [4,6]. This new state of matter exhibits two topologically protected spin-up and spin-down edge states. The implementation of the QSHE is different from QHE in that it does not need to break the time-reversal symmetry and depends on spin–orbit interactions. The topological states can be classified by a topological invariant or the spin Chern number. The spin Chern number [32] is given by:
With the development of TIs, QVHE was proposed in 2007 [10]. Compared to the QHE and QSHE, realizing the QVHE is simpler and only needs to break the space symmetry, such as inverse symmetry or mirror symmetry, which leads to the Dirac degeneracies being opened in momentum space. The integral over the full Brillouin zone is zero because the Berry curvature is opposite at two valleys. The integral for each valley is a half-integer. The QVHE is characterized by valley Chern number , m is the effective mass.
Although implementing QHE, QSHE and QVHE require structures to satisfy different conditions, they have the common feature that the gapless edge states span the band gap when the topological material is nontrivial. With the rapid development of topological phases in quantum systems, they were quickly transferred to photonics [33,34,35,36,37,38,39,40,41], acoustics [42,43,44,45,46,47,48,49,50,51,52,53] and mechanical metamaterials [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80]. Next, we will introduce the achievements of elastic topological edge states in three categories which include QHE, QSHE and QVHE.
2.1. Analogue Hall Insulators
As we all know, realizing the QHE must break time-reversal symmetry. QHE analogs have been realized in photonics using gyromagnetic material in a magnetic field [33] and acoustics by introducing moving airflow [43]. Elastic waves, such as sound waves, hardly couple with the magnetic field, and therefore the interaction between elastic materials and magnetic fields cannot be exploited to break time-reversal symmetry. Hence, breaking time-reversal symmetry is quite challenging for mechanical systems. So far, the analogs of QHE have been verified for elastic waves by using Coriolis force [54,55,80] in the non-inertial reference frame or inducing gyroscopic inertial effects [56,57].
In 2015, Yao-Ting Wang et al. designed a mechanical system (see Figure 1a) that exhibits topologically nontrivial one-way edge states, numerically demonstrating the topological nature [54]. Specifically, the structure consists of a mass-spring honeycomb lattice, whose time-reversal symmetry is broken by placing it in a rotating frame, as shown in Figure 1b. Here, the objects only have Coriolis force since the centrifugal force can be neglected for enough small angular frequencies. The nontrivial topological orders can be confirmed by calculating the Chern numbers for each band. The Chern numbers from the first band to the fourth band are when the constant angular velocity (z direction) , while the Chern numbers are when reaches .
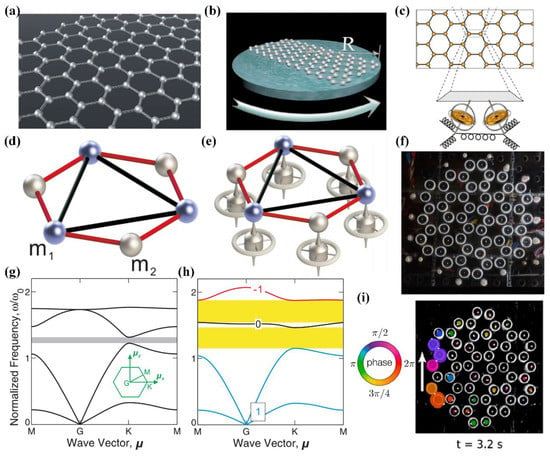
Figure 1.
Analogue Hall insulators. (a) The mass-spring system is arranged in honeycomb lattices [54]. (b) The non-inertial system [54]. (c)The hexagonal gyroscopic lattice [57]. (d) The ordinary (nongyroscopic) unit cell [56]. (e) The gyroscopic unit cell [56]. (f) The experimental system [57]. (g) The dispersion of the ordinary (nongyroscopic) phononic crystal [56]. (h) The dispersion of the gyroscopic phononic crystal with the Chern numbers labeled on the bulk bands [56]. (i) One period of the unidirectional waveguide mode at , the ellipses denote the shape of each orbit, and the colors denote the phase at a fixed time [57].
In 2015, Pai Wang et al. constructed a new type of elastic phononic crystal by inducing the gyroscopic inertial effects [56]. The ordinary unit cell with equal masses () connected by linear springs is shown in Figure 1d. The corresponding band structure of the ordinary phononic crystal is shown in Figure 1g. The gap between the second and third bands is topologically trivial. To acquire the nontrivial band gaps, how to break the time-reversal symmetry needs to be solved. Consequently, the topological unit cell for the gyroscopic phononic crystal is designed with each mass attached to the tip of the rotational axis of a gyroscope, as shown in Figure 1e. The time-reversal symmetry is broken by modulating gyroscopic coupling. The corresponding band structure of the gyroscopic phononic crystal with the spinner constants of the gyroscopes is shown in Figure 1h. The two band gaps are nontrivial according to the non-zero Chern numbers labeled on the bands. There are gapless one-way edge states in the two topologically nontrivial gap frequency ranges. In these frequency ranges, the edge modes can unidirectionally propagate without any reflection under topological protection even in the presence of the sharp corner and the line defect.
In the same year, Nash et al. experimentally and theoretically demonstrated that a coupled system of gyroscopes could generate topological states [57]. The honeycomb lattices consisting of gyroscope–spring networks are shown in Figure 1c, and the experimental system is shown in Figure 1f. The experimental system consists of 54 coupling gyroscopes on a honeycomb lattice; the gyroscopes are composed of small dc motors spinning cylindrical masses, which are coupled by placing a small neodymium magnet in each mass with its moment aligned vertically. The time-reversal symmetry could be broken by controlling the spinning gyroscopes and the geometry of the lattice. As expected, robust and topologically protected one-way waveguides were observed in the experiment, as shown in Figure 1i.
2.2. Analogue Spin Hall Insulators
QSHE was firstly proposed in electronic systems based on spin-orbital coupling effects [4,6]. Although the bosons do not have half-integer spin as electrons, the QSHE is also demonstrated in photonics [35,36,37,81] and acoustics [47,48,51,82] by constructing pseudo spins. In addition, the QSHE has been verified in elastic materials theoretically and experimentally [58,59,60,61,62,63,64,65,66,67,68]. We note that there are three main methods used to construct mechanical structures via QSHE, which include designing coupled pendula mimicking spin-orbital coupling effects [58,59], using the elastic plates with distinct polarizations and coupled deformation mechanisms to produce accidental fourfold degeneracy [60,61], and a zone-folding method with honeycomb lattices [62,63,64,65,66,67,68].
In 2015, Mousavi et al. numerically demonstrated elastic-wave analogs of the QSHE with a dual-scale phononic slab [60]. Inspired by this work, Miniaci et al. experimentally investigated the topologically protected helical edge modes via elastic plates, e.g., the sample in Ref. [60] in 2018 [61]. The patterned plate (PP) which resemblesthe twisted Kagome lattice geometrically [83] and the unit cell, are shown in Figure 2a. The perspective and cross-sectional view of the unit cells are shown in Figure 2b. By introducing circular through holes (THs) in the PP, the accidental fourfold degeneracy of two Dirac cones emerges at the K point. Furthermore, replacing THs with blind holes (BHs), the through-the-thickness symmetry is broken, which resembles spin orbital coupling and lifts the degeneracy at K point, as shown in Figure 2c The manufacturing pattern plate used for the experiment is divided into two parts by a Z-shaped interface with BHs drilled on the opposite (top or bottom) surfaces. As expected, the topologically protected Z-shaped interface supports helical edge modes.
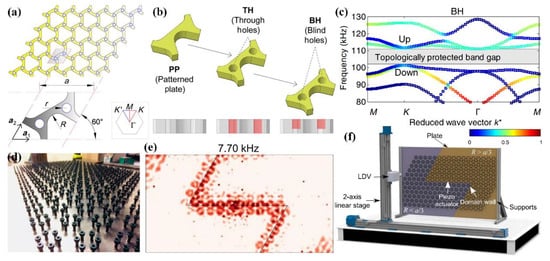
Figure 2.
Analogue spin Hall insulators. (a) The elastic plate and the zoomed-in view of the unit cell. The inset presents the high-symmetry points of the first irreducible Brillouin zone. [61]. (b) The schematic of three types of unit cell with distinct holes [61]. (c) Dispersion curve for the plate with blind holes. The colors ranging from blue to red suggest that from pure in-plane modes to pure out-of-plane modes [61]. (d) The experimental configuration [63]. (e) The edge-state transmission along the domain wall at 7.70 kHz frequency [63]. The color represents the power spectral density, which is calculated from the measured out-of-plane velocity of the plate. (f) The experimental setup, in which a piezoelectric actuator is positioned at the center to excite the plate, and out-of-plane velocity is measured point-by-point by an LDV (Polytec OFV 534 laser Doppler vibrometer) mounted on a two-axis linear stage [63].
In 2018, Chaunsali et al. numerically [62] and experimentally [63] demonstrated the pseudospin Hall effect via a zone-folding technique, respectively [81]. The actual system, with bolts mounted on the thin plate and arranged in hexagonal lattices, is shown in Figure 2d. The advent of double Dirac cones at and the energy band reversal are controlled by modulating the circumferential radius R of the bolts. The emergence of the low-frequency edge states at the domain wall created between two topologically distinct lattice patterns are controlled by the local resonance of bolts as shown in Figure 2e, and the experimental setup is shown in Figure 2f. In the same year, Cha et al. designed an on-chip topological elastic material that can generate high-frequency waves [64]. These on-chip devices could produce steady-state transmission and might have potential applications in on-chip acoustic devices.
2.3. Analogue Valley Hall Insulators
A new degree of freedom, valley, has been introduced into the classical wave systems. The QVHE has been theoretically and experimentally demonstrated in photonic crystals [38,39,40,41,84,85], sonic crystals [42,49,50,53] and mechanical structures [55,69,70,71,72,73,74,75,76,77,78,79,86,87]. In particular, topologically valley-polarized states in elastic systems have been proposed via bi-layered lattices [69,74], hexagonal lattices [55,70,73,75,76,77,78,79,88,89,90] and triangular lattices [71,72,86]. The key to realizing the QVHE is breaking mirror symmetries or inversion symmetries. Now we will discuss some iconic achievements regarding QVHE in mechanical systems.
In 2017, Vila et al. constructed a continuous elastic plate that consists of hexagonal lattices with magnetic cylinders attached to the sublattice sites, as shown in Figure 3a [76]. The magnetic cylinders act as the localized masses at the nodes used to break the mirror symmetry. Particularly, it refers to reducing the original symmetry to symmetry in a unit cell. The number of cylinders (masses) is controlled by the parameter . The masses of the two sites a, b in a unit cell are and respectively, as shown in Figure 3b. The value represents no additional masses, and the Dirac cones appear at the K and points in this case. The value refers to additional masses at site a; on the contrary, the value refers to additional masses at site b. The degeneracy would be lifted when . The band structure with the valley Chern numbers labelled at the K and points is shown in Figure 3c. In this context, the topological boundary state emerges at a line interface of the elastic plate by setting the value or on the left or right side of the interface, as shown in Figure 3d.
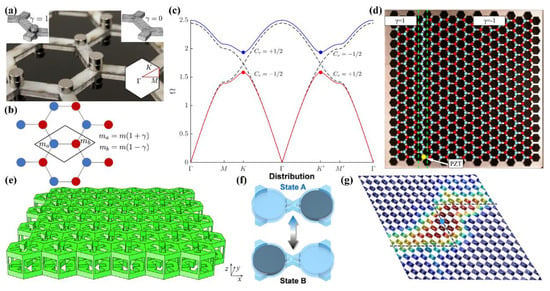
Figure 3.
Analogue valley Hall insulators. (a) The experimental continuous elastic plate [76]. (b) The hexagonal mass-spring lattices [76]. (c) The energy spectrum with (dashed black line) and (solid red and blue lines). The valley Chern numbers are marked at the corresponding energy extrema in momentum space [76]. (d)The elastic plate with line interface consists of the left strip ( ) and right strip ( ). The red (cyan) dots represent two(zero) cylinders attached to the plate [76]. (e) The bilayer phononic crystal slabs of a hexagonal lattice [74]. (f) The magnetic fluid distribution in a unit cell [79]. (g) The measured displacement field for the Z-shaped interface structure [79].
In 2019, Jiao et al. observed the topological valley transport of elastic waves in numerical simulations based on the bi-layered lattices [74]. The structure is constructed by two layers of snowflake plates connected by a honeycomb array of cylinders, as shown in Figure 3e. In the same year, Zhang et al. proposed a programmable elastic valley Hall insulator whose edge states could propagate along arbitrary interface routes by a programmable magnet lifting array [79]. The unit cell consists of two cylindrical cavities with a small arched channel connecting them. It is obvious that to gap the K-point (Dirac cone), the inversion symmetry should first be broken. Hence, magnetic fluid with equal volume as one cavity is injected into the unit cell, and the inversion symmetry is broken by independently adjusting the magnetic fluid distribution in each unit cell (see Figure 3f). The measured displacement field for the Z-shaped interface configurations is shown in Figure 3g.
3. Mechanical Higher-Order Topological Insulators
The discovery of HOTIs provides a new platform for wave regulation in metamaterials. The HOTIs have topologically protected corner states and/or hinge states and form a new class of topological phases where the bulk-boundary correspondence does not apply. In 2017, Benalcazar et al. [11,12] solved a long-standing puzzle and firstly described higher electric multipole moments of crystals in detail, such as the quadrupole and octupole moments. In 2018, Schindler et al. [13] proposed the notion of HOTIs. So far, the HOTIs have been realized experimentally in photonics [91,92,93,94,95,96,97,98], acoustics [99,100,101,102,103,104], mechanical systems [105,106,107,108,109,110,111,112] and other classical waves systems [113,114,115] owing to their advantages in manufacturing, spectral analysis and local signal detection [15]. Next, we try to summarize the achievements in elastic systems from two categories of quantized multipole insulators and -symmetric HOTIs without quantized multipole moments.
3.1. Quantized Multipole Insulators
Benalcazar et al. proposed quantized multipole insulators (QMIs) with generalized berry phases in 2017 and mainly discussed the quantized quadrupole moment in a 2D crystal and the quantized octupole moment in a 3D crystal (see Figure 4a,b) [11,12]. Specifically, a 2D quadrupole TI has gapped first-order edge states and second-order corner states in the gap; a 3D octupole TI has gapped first-order surface states, second-order hinge states and third-order corner states in the gap. Importantly, there must be reflection and inversion symmetries to realize QMIs, and there must be at least two or four occupied bands to make the dipole moments or quadrupole moments vanish. In the following, we will clearly illustrate the advances of QMIs in elastic wave systems.
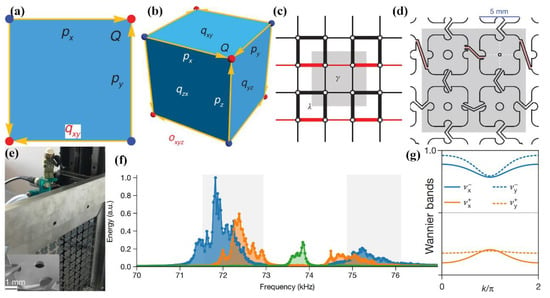
Figure 4.
Quantized multipole insulators. (a) Bulk quadrupole moment , edge dipole moments and corner charges Q [11]. (b) Bulk octupole moment , surface quadrupole moments , hinge dipole moments , and corner charges Q [11]. (c) A 2D tight-binding model of quadrupole insulators. Red (black) lines represent negative (positive) hopping terms. Thin (thick) lines indicate intracell (intercell) hopping terms [105]. (d) Metamaterial structure. Dashed white lines represent the two nodal lines of the out-of-plane modes which are coupled based on the bent beams [105]. (e) Photo of the experimental sample [105]. (f) The spectrum for the quadrupole insulator [105]. (g) The schematic of the Wannier bands [105].
In 2018, Serra-Garcia et al. proposed a mechanical configuration to realize a quadrupole topological insulator [105]. A tight-binding model with positive and negative couplings is shown in Figure 4c. The unit cell and experimental photo of the setup are, respectively, shown in Figure 4d,e. The quantized quadrupole TIs can be realized by manipulating the positive or negative couplings and the amplitudes of the intracell or intercell couplings. Specifically, the amplitudes of the intracell hoppings or intercell hoppings are controlled by the distance between the given beam and the nodal line, and the positive or negative hoppings depend on which sides of the nodal lines are connected by the beams. The amplitudes of the intracell or intercell hoppings controlling the emergence of the bandgap between two pairs of degenerate bands. The positive or negative couplings emulate a magnetic flux per plaquette. The gapped edge states and in-gap corner states appear at the single plate for . The corresponding spectrum is shown in Figure 4f. Here, two pivotal features of the quantized quadrupole phase should be focused on. The first feature is that the response is located at around 72.92 kHz and 74.89 kHz, which represents the gapped edge modes. The second feature is that there are strong corner resonances in the middle of the gap, which is indicative of the in-gap corner states. To further confirm the TIs is quadrupole, the Wannier bands are calculated as shown in Figure 4g. The bulk-induced edge polarization could be calculated using the eigenvectors of the Wilson loops since the Wannier bands and are gapped. The value of the polarizations are , which suggest the existence of in-gap states.
3.2. -Symmetric HOTIs
Realizing that QMIs requires the aforementioned structure to satisfy noncommutative reflection symmetries brings some difficulties to the structural design. Hence, numerous researchers are exploring simpler methods to implement HOTIs. In 2018, Ezawa theoretically proposed HOTIs via breathing Kagome lattices and Pyrochlore lattices [116]. In 2019, Benalcazar et al. systematically investigated the 2D second-order topological crystalline insulators (TCIs) in class AI protected by symmetry and proposed the topological indices which could characterize the topological nature of the TCIs with corner or defect-bound fractional charges [19]. Moreover, they analyzed the relationship between the locations of the Wannier centers of the electrons and the topological nature of the TCIs on the premise of the insulators that admit a Wannier representation. Specifically, the phase is trivial when Wannier centers are located at the center of the unit cell, while the phase is nontrivial when Wannier centers are located at the corners or edges of the unit cell. Then, we will summarize the experimental achievements of -symmetric HOTIs in elastic wave systems [105,106,107,108,109,110,111,112].
In 2019, Fan et al. constructed a HOTI with a 2D continuous elastic system via SSH models [106]. The composite unit cell with six magnets attached to each side is shown in Figure 5a, and the schematic of the honeycomb lattices is shown in Figure 5e. The intracell and intercell couplings could be changed by turning the lengths of acrylic beams and . Then we fabricated three large experimental honeycomb-shaped samples with 37 expanded unit cells (), shrunken unit cells () and shrunken unit cells with defects, respectively, as shown in Figure 5b–d. The numerically evaluated eigenfrequencies shown in Figure 5f–h correspond to Figure 5b–d, respectively. As we can see, Figure 5f show that there are only bulk states outside the forbidden band, the Figure 5g show that there are gapped edge states and in-gap corner states in the topological band gap, since the honeycomb-shaped sample with shrunken unit cells in Figure 5c is a topological structure. However, one type of corner states (marked by red in Figure 5g) in the band gap is topological, and the other is trivial (marked by blue in Figure 5g) in the topological structure. Figure 5h show that the eigenfrequencies of the trivial corner states are changed, inducing the defects. The simulated displacement field distributions of the topological structure are shown in Figure 5i–l. One of the simulated edge states (marked by green in Figure 5g) is shown in Figure 5l; the displacement field is almost completely localized along the boundaries of the sample except for the six corners. One of the topological corner states is shown in Figure 5j, which has immunity to defects. One of the trivial corner states is shown in Figure 5k, which is sensitive to defects and disorders. One of the bulk states (marked by black in Figure 5g) is shown in Figure 5i, and the displacement field is almost localized at the center of the sample. Combined with these diagrams, we observed the gapped edge states and two kinds of corner states, one kind of corner state is nontrivial whose partial vibration is located at the sharpest corner, while another kind of corner state whose vibration does not locate at the sharpest corner is trivial. In order to verify the relationship between corner states and corner points, we constructed a large triangular-shaped model and found that there are no topologically protected corner states in the regular triangle elastic phononic crystal plate, but only trivial corner states. Then we induced a topological index ( and represent topological charges +1 and −1, respectively) to explain this phenomenon. Consequently, the trivial corner states locate at the acute-angled corners of in the case of , while the nontrivial corner states locate at the obtuse-angled corners of in the case of .
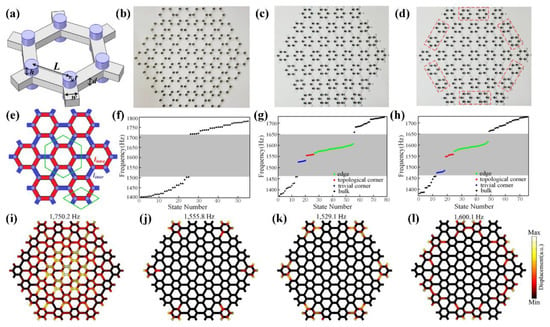
Figure 5.
Elastic hexagon-shaped Tis [106]. (a) A composite unit cell of the hexagonal lattice. (b–d) Hexagon-shaped structures consisting of expanded unit cells (b), shrunken unit cells (c) and shrunken unit cells with defects (d), respectively. The defects are realized through adding a magnet on six nodes, respectively, at the upper side of 12 composite unit cells (marked by the red dashed box). (e) The schematic of the honeycomb lattice model. The red (blue) beams whose lengths are denoted by representing the intracell (intercell) hoppings. (f–h) The schematics of the simulated state number responding to (b–d), respectively. (i–l) The simulated modes of bulk state at 1750.2 Hz (i), topological corner state at 1555.8 Hz (j), trivial corner state at 1529.1 Hz (k) and gapped edge state at 1600.1 Hz (l).
In 2020, Fan et al. proposed a pseudospin-valley-coupled HOTI and observed topological higher-states [109]. The topological higher-states are induced by combining the coupling of lattice deformation and reflection symmetry breaking. The lattice deformation can be induced by expanding or shrinking the composite unit cell, which will lead to the pseudospin Hall effect. The reflection symmetry can be broken by varying the adjacent additional masses in a composite unit cell, which will lead to the valley Hall effect. The two perturbative composite unit cells are shown in Figure 6a. Here, the additional masses on the A and B nodes are obtained by the formulas and . The length of the intracell and intercell beam is and respectively. The elastic phononic crystal sample with the two kinds of structural perturbations is shown in Figure 6b. Specifically, a valley-polarized edge state will emerge when the value is , and a pseudospin-dependent edge state will emerge when the value . The edge states and corner states will appear at domain walls and the central position, respectively, arising from the topological phases transition. The diagram of the corner state is shown in Figure 6c.
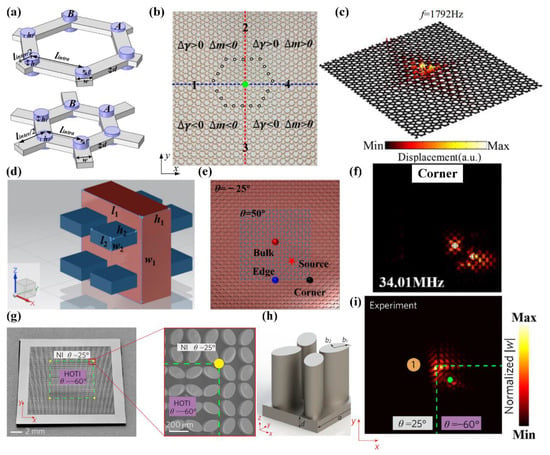
Figure 6.
Other experimental realizations of -symmetric HOTIs. (a) Composite unit cells with , (top) and , (bottom) [109]. (b) The square elastic phononic crystal sample. The black circles signal the locations of defects [109]. (c) The corner mode at 1792 Hz [109]. (d) A composite unit cell consists of stainless-steel prisms(blue) and an aluminum plate(red) [110]. (e) The squared metamaterial formed by the two phononic crystals and , respectively. (f) The corner state at 34.01 MHz [110]. (g) The photo of the fabricated sample chip [111]. (h) The unit cell of the square lattice photonic crystal [111]. (i) One corner mode in the experiment system [111].
In the same year, Wang et al. designed a HOTI with 2D elastic phononic plates protected by symmetry [110]. The unit cell consists of stainless steel prisms (blue), and a squared aluminum plate (red), as shown in Figure 6d. This structure could generate much stronger scattering because of the different acoustic impedance between stainless steel and aluminum. The key to realizing higher-order states is to produce gapped edge states, and the emergence of the bandgap is controlled by the rotation angle of atoms arising from the glide and time-reversal symmetries. In this context, they designed a squared structure formed by two parts of phononic crystals with and , respectively, as shown in Figure 6e. As expected, the 0D corner states and 1D edge states appeared at the interface because the glide symmetry is broken at the interface. The diagram of the corner state is shown in Figure 6f.
In 2021, there are also a few achievements on implementing higher-order states in mechanics [107,111,112,117]. Recently, Wu et al. experimentally demonstrated that higher-order topological states for elastic waves at MHz could emerge in an on-chip micromechanical metastructure [111]. The sample chip is constructed with two partial structures referring to a HOTI surrounded by a normal insulator (NI), as shown in Figure 6g. The unit cell with four elliptic pillars in a square lattice is shown in Figure 6h. Manipulating the rotation angle of the pillars could open the crystal bandgap and induce band inversion at the Brillouin zone corners. Specifically, the topological nature can be characterized by the topological index which can be calculated from the symmetry eigenvalues at high-symmetry momenta of the bands below the bandgap and corner charges. The topological index is and the corner charge is when , while the topological index is and the corner charge is when . Hence, the rotation angle of the pillars in the HOTI is , the rotation angle of the pillars in the NI is . The topological corner mode localized at one corner of the central square region is shown in Figure 6i.
4. Topological Pump
In parallel with the development of the QHE, a new perspective, a topological pump, has been proposed to investigate topologically protected modes [20,118,119,120,121,122,123]. The topological pump exploits synthetic dimensions mapped to time [123,124,125,126,127] or space [24,119,120,128,129,130,131], controlling the generation and transition of topological states. The synthetic dimensions refer to exploring higher-dimensional physics with virtual dimensions in lower-dimensional systems. Up to now, the synthetic dimensions has been used to relate the 2D, 4D and 6D QHE with 1D pump, 2D pump and 3D pump via 1D [119,120,125,127,128,132], 2D [24,129,133] and 3D [21,22] lattices respectively. The topological nature of the 2D (4D) quantum Hall systems are characterized by the first Chern number (the second Chern number) [129,134]. The Chern number dictates a quantization of particle transport in (meta)material during one cycle of an adiabatical pump.
Recently, the topological pump in elastic systems has been demonstrated theoretically and experimentally [124,126,128,130,135,136,137]. In 2019, Rosa et al. firstly theoretically demonstrated the topological pump in spatially modulated elastic lattices [128]. The 1D elastic lattices connected by springs whose constant are defined by the sampling of a 2D surface at , where (p and q are co-prime) denotes q masses in a unit cell, denotes the pump parameter. The schematics of the 1D elastic lattices and the 2D surface is shown in Figure 7a,b. The value of controls the generation of the nonzero gap. The dispersion surfaces as a function of (the nondimensional wave number) and , and the band structure as the variation of about a finite chain of 60 masses are shown in Figure 7c,d. Of note is the fact that the topological nature is characterized by the Chern number:
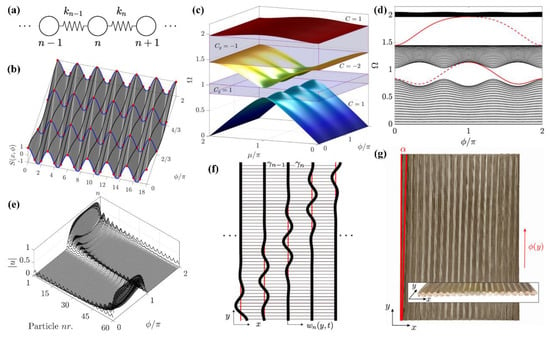
Figure 7.
Spatially modulated elastic lattices. (a) 1D lattices model with modulated spring stiffness [128]. (b) 2D surface . The black lines denote stiffness variation with at a lattice node, and the blue lines denote cross-sections at [128]. (c) The dispersion surfaces with Chern numbers labeled on the gaps [128]. (d) The energy spectrum as a function of . The red lines signals the edge modes [128]. (e) The transition of the edge wave across the system from left to right as the variation of in he second gap. [128]. (f) The array of continuous beams: the thick black lines signal the notional deformed beams, the thick red lines signal the undeformed beams, and the thin black horizontal lines correspond to the distributed springs with coupling constant [128]. (g) The square wave modulated continuous elastic plate employed in experiments [130].
Here, signals the Bloch eigenmodes, space, , . In this context, the topological edge modes will emerge when the Chern number . Specifically, denotes a right-to-left transition for increasing in the first band gap, while denotes an opposite transition in the second bandgap. The schematic of the topological mode in the second gap is shown in Figure 7e. Figure 7f display an elastic structure designed based on the 1D elastic lattices model with the adiabatic topological pump. Inspired by this work, Riva et al. firstly experimentally realized the topological pump in a continuous elastic plate, as shown in Figure 7g. The edge-to-edge transitions could be modulated by smoothly altering the phase along a second spatial dimension [130].
In 2021, Xia et al. proposed an experimental demonstration of the adiabatic temporal pump in an electromechanical system [135]. Specifically, the one-dimensional elastic beam is modulated spatiotemporally by an array of piezoelectric patches glued on the upper and lower surfaces and shunted through negative capacitance (NC) circuits, as shown in Figure 8a. The boundary states depend on the spatial stiffness modulation with a fixed phase , and the wave motion along the waveguide depends on the temporal modulation of the phase . The left-to-right temporal pumping with the phase parameter varying from to is shown in Figure 8b,c. Figure 8d show the edge-to-edge transitions that could be realized with tunable phase modulation speeds, which has potential applications for the controlled transmission of information across the waveguide.
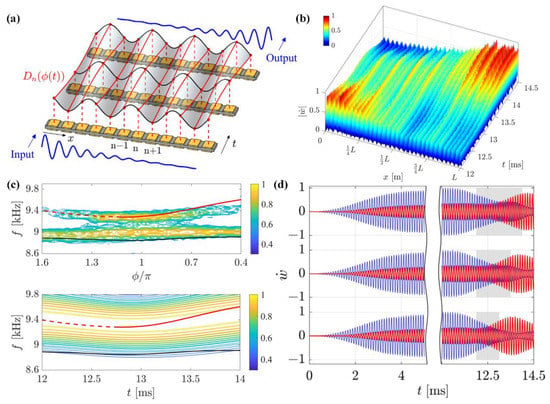
Figure 8.
Temporal pump in electromechanical waveguides [135]. (a) The electromechanical elastic beam with modulated bending stiffness . (b) The schematic of the transient pump. (c) The dispersion diagram in quasistatic conditions (top) or in the time domain (bottom). (d) The influence of different phase modulation durations (top, 2 ms; middle, 1.5 ms; bottom, 1 ms) on edge-to-edge transitions.
5. Topological Defect States
Topological lattice defects [27] have been extensively studied in electronic systems [138,139,140] and classical systems [141,142,143,144,145,146,147,148] over the past decade. The classification of topological lattice defects depends on the holonomy along a closed path around the defect core [25,149]. At present, the common achievements of topological defects are dislocations [138,149,150,151,152] and disclinations [25,139,153]. The dislocations and disclinations are defined as a gauge flux for translational symmetry and rotational symmetry, respectively [28]. Dislocations and disclinations are mainly investigated on honeycomb lattices and square lattices [149], and it has been demonstrated that they can serve as a bulk probe to detect the topological nature which exhibits topological states [139,140,141,142,143,146,147,148,154,155,156] and/or fractional charges [144,145,157,158] in TCIs protected by crystal symmetries. More recently, topological defect states have been proposed in elastic materials [87,159,160,161], and then we will discuss the related papers.
In 2021, Xia et al. experimentally realized valley-polarized edge states by introducing disclinations into elastic phononic plates [160]. The original honeycomb lattices elastic plate with two same cylindrical magnets attached to the top and bottom nodes of sublattices A and B is protected by symmetry, as shown in Figure 9a. Hence, the band could degenerate at the K point of the Brillouin zone and produce a Dirac cone state. Then changing the masses of sublattices A and B, the mirror symmetry of the unit cell will be broken, and a gap will appear to arise from the lifting of the Dirac cone. In addition, the modes at K point are inversed with each other. Furthermore, cutting a sector and gluing two boundary beams, a pentagonal elastic plate is shown in Figure 9b. Of note is the fact that the masses of the sublattices A and B above or below the interface is inversed. The tight-binding Hamiltonians [141] of this pentagonal elastic plate are , where v is the Dirac velocity, and signal valley Pauli matrices and sublattice Pauli matrices, respectively, m is the sublattice detuning and denote the sublattice distortion. Consequently, a topological edge state will be accessed at the interface attributed to the opposite valley polarizations of the two types of unit cells as shown in Figure 9c. Moreover, we constructed a more complex structure with a straight waveguide by inducing a disclination dipole on honeycomb lattices, as shown in Figure 9d. As such, a topological edge state could be observed in this phononic plate, as shown in Figure 9e.
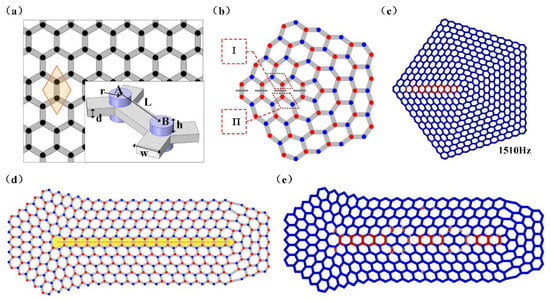
Figure 9.
Valley-polarized structure with disclinations. (a) The hexagonal lattices with a rhombic (orange) unit cell. (b) The pentagonal elastic phononic plate with a pentagonal core and a new interface (gray dashes). The red and blue circles signal two categories of magnets with different heights ( and ). The unit cell I and II are displayed by the red parallelogram region. (c) One of the eigenmodes of the pentagonal elastic plate at 1510 Hz. (d) The composite elastic structure with a disclination dipole (a disclination connecting a pentagonal and heptagonal core) waveguide. (e) One of the eigenmodes of the composite elastic system at 1550 Hz.
In the same year, Xia et al. experimentally demonstrated the topological bound states in elastic phononic plates by inducing disclinations [161]. The pentagonal plate is designed by cutting a sector and reattaching the remaining boundary sides; the deformation process is shown in Figure 10a–c. The topological features can be presented by modulating the intensity of the intracell and intercell couplings. It was revealed that the pentagonal plate with shrunken unit cells has topological nontrivial states, as shown in Figure 10d. The distribution of the Wannier centers around the TCIs depend on the tight-binding models and crystal symmetries [19]. The schematics of the distribution of Wannier centers in topological nontrivial or trivial (expanded unit cells) plates are shown in Figure 10e,f. Moreover, 1/2 fractional charge is trapped at the pentagonal core in topological nontrivial elastic phononic plates. As expected, the localized states immunize against the finite sizes and the moderate structural defects.
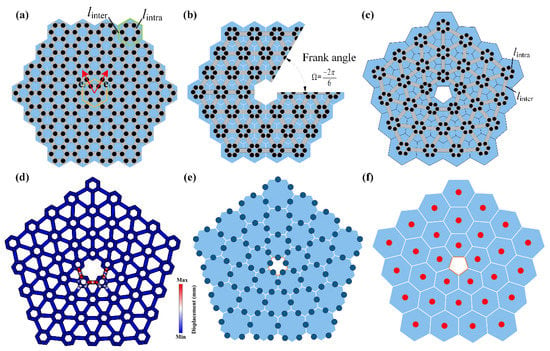
Figure 10.
Bulk–disclination correspondence in elastic phononic plates. (a) The hexagonal lattices. The lengths of the intercell (intracell) beams are denoted by linter and lintra. (b) The topological nontrivial structure with a missing crystalline wedge. (c) The topological nontrivial structure with a pentagonal core. (d) One of the eigenmodes of the elastic system with 30 unit cells. (e) The distributions of Wannier centers (blue solid circles) of the topological nontrivial structure. (f) The distributions of Wannier centers (red solid circles) of the topological trivial structure.
6. Conclusions and Future Directions
In the previous sections, we have shown the breakthroughs in this research field made in recent years. Now, we can regulate the elastic waves in different topological protection methods. However, the development of topological physics in mechanical systems still lag behind the electronic, photonic and acoustic systems. As a result, we will outline those future developments of topological mechanics as follows:
- (1)
- 3D higher-order topological insulators
Strikingly, 3D HOTIs have gapped surface and hinge states and corner states in the gap. Even though implementing 3D HOTIs is a big challenge, it has been observed in acoustics [100,102,162,163,164,165] and electric circuits [166,167] via the 3D tight-binding model of octupole TIs or the generalization SSH models [15]. We can refer to these advances to design 3D HOTIs in mechanics.
- (2)
- Higher-order topological pump
More recently, the topological pump, the second central, has been observed in photonics [23,129] and acoustics [133] in higher-order topological band theory. Phenomenologically, a higher-order topological pump could produce edge-to-edge and/or corner-to-corner transport in certain metamaterial platforms. Physically, the higher-order topological pump could be characterized by the second Chern numbers or the position of the Wannier centers versus the centers of their assigned unit cells. Consequently, we can investigate how to realize a higher-order topological pump in mechanics based on this discovery.
- (3)
- Fractional charges
Fractional charges have been an important feature to recognize the topological crystalline insulators (TCIs), which offer another experimental identification when TCIs lack robust spectral features [144]. Recently, fractional charges have been observed at corners [168] and disclinations [144,145] of the TCIs. Generally, fractional charges could be found exploiting the real-space localized Wannier representation of TCIs [19]. In addition, we can attempt to design elastic structures to trap fractional charges.
- (4)
- Non-Hermitian topological states
The abovementioned achievements are investigated based on the hypothesis of the Hermiticity of a Hamiltonian. Recently, topological phases of non-Hermitian systems have attracted extensive research, whose exceptional points and complex-valued spectra can produce many notable properties, including the non-Hermitian skin effects [169,170], bulk Fermi arcs [171] and Weyl exceptional rings [172], to name a few. At present, HOTIs of non-Hermitian systems have been realized in sonic crystals [173,174]. As such, we can study how to connect the higher-order topological physics with non-Hermitian systems in mechanics by inducing friction.
- (5)
- Application implementation
Even though there are plenty of achievements about undulation control using TIs in mechanics, the actual devices still have not appeared. We could explore how to apply these advances in practice, such as shrinking the mechanical structures to a micro-scale, designing low loss devices, manufacturing vibration sensors, signal processing, microparticle manipulations and so on.
Author Contributions
Writing—original draft preparation, S.Z. and G.D.; writing—outline of the paper, review and editing, supervision, funding acquisition, B.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 12072108, and the postgraduate Scientific Research Innovation Project of Hunan Province, grant number CX20210392.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data were created in this review.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klitzing, K.V.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 1980, 45, 494. [Google Scholar] [CrossRef] [Green Version]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef] [Green Version]
- Kane, C.L.; Mele, E.J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernevig, B.A.; Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 2006, 96, 106802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [Green Version]
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [Green Version]
- Sheng, L.; Sheng, D.; Ting, C.; Haldane, F. Nondissipative spin Hall effect via quantized edge transport. Phys. Rev. Lett. 2005, 95, 136602. [Google Scholar] [CrossRef] [Green Version]
- Rycerz, A.; Tworzydło, J.; Beenakker, C. Valley filter and valley valve in graphene. Nature Phys. 2007, 3, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Yao, W.; Niu, Q. Valley-contrasting physics in graphene: Magnetic moment and topological transport. Phys. Rev. Lett. 2007, 99, 236809. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef] [Green Version]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Jacob, Z.; Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci. Appl. 2020, 9, 1–30. [Google Scholar] [CrossRef]
- Xie, B.; Wang, H.-X.; Zhang, X.; Zhan, P.; Jiang, J.-H.; Lu, M.; Chen, Y. Higher-order band topology. Nat. Rev. Phys. 2021, 1–13. [Google Scholar] [CrossRef]
- Kang, B.; Shiozaki, K.; Cho, G.Y. Many-body order parameters for multipoles in solids. Phys. Rev. B 2019, 100, 245134. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, W.A.; Wagner, L.K.; Hughes, T.L. Many-body electric multipole operators in extended systems. Phys. Rev. B 2019, 100, 245135. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Wakabayashi, K. Novel topological phase with a zero berry curvature. Phys. Rev. Lett. 2017, 118, 076803. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Li, T.; Hughes, T.L. Quantization of fractional corner charge in C n-symmetric higher-order topological crystalline insulators. Phys. Rev. B 2019, 99, 245151. [Google Scholar] [CrossRef] [Green Version]
- Thouless, D. Quantization of particle transport. Phys. Rev. B 1983, 27, 6083. [Google Scholar] [CrossRef]
- Lee, C.H.; Wang, Y.; Chen, Y.; Zhang, X. Electromagnetic response of quantum Hall systems in dimensions five and six and beyond. Phys. Rev. B 2018, 98, 094434. [Google Scholar] [CrossRef] [Green Version]
- Petrides, I.; Price, H.M.; Zilberberg, O. Six-dimensional quantum Hall effect and three-dimensional topological pumps. Phys. Rev. B 2018, 98, 125431. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Noh, J.; Wang, M.; Huang, S.; Chen, K.P.; Rechtsman, M.C. Higher-order topological pumping. arXiv 2020, arXiv:2006.13242. [Google Scholar]
- Lohse, M.; Schweizer, C.; Price, H.M.; Zilberberg, O.; Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 2018, 553, 55–58. [Google Scholar] [CrossRef]
- Geier, M.; Fulga, I.C.; Lau, A. Bulk-boundary-defect correspondence at disclinations in rotation-symmetric topological insulators and superconductors. SciPost Phys. 2021, 10, 092. [Google Scholar] [CrossRef]
- Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. In Annales Scientifiques de l’École Normale Supérieure; Société Mathématique de France: France, 1907; pp. 401–517. [Google Scholar] [CrossRef] [Green Version]
- Kleman, M.; Friedel, J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, 80, 61. [Google Scholar] [CrossRef] [Green Version]
- Thorngren, R.; Else, D.V. Gauging spatial symmetries and the classification of topological crystalline phases. Phys. Rev. X 2018, 8, 011040. [Google Scholar] [CrossRef] [Green Version]
- Teo, J.C.; Kane, C.L. Topological defects and gapless modes in insulators and superconductors. Phys. Rev. B 2010, 82, 115120. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, Q.; Zhang, Y.-F.; Xia, B.-Z.; Liu, X.-N.; Zhou, X.-M.; Chen, C.-Q.; Hu, G.-K. Research progress of elastic topological materials. Adv. Mech. 2021, 51, 189–256. [Google Scholar]
- Miniaci, M.; Pal, R. Design of topological elastic waveguides. J. Appl. Phys. 2021, 130, 141101. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, M.; Cheng, Y.; Lu, M.-H.; Christensen, J. Topological sound. Commun. Phys. 2018, 1, 97. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef] [Green Version]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.-K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Khanikaev, A.B.; Mousavi, S.H.; Shvets, G. Guiding electromagnetic waves around sharp corners: Topologically protected photonic transport in metawaveguides. Phys. Rev. Lett. 2015, 114, 127401. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Sun, X.-C.; Liu, X.-P.; Lu, M.-H.; Chen, Y.; Feng, L.; Chen, Y.-F. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl. Acad. Sci. USA 2016, 113, 4924–4928. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X. Observing Zitterbewegung for photons near the Dirac point of a two-dimensional photonic crystal. Phys. Rev. Lett. 2008, 100, 113903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sepkhanov, R.; Nilsson, J.; Beenakker, C. Proposed method for detection of the pseudospin-1/2 Berry phase in a photonic crystal with a Dirac spectrum. Phys. Rev. B 2008, 78, 045122. [Google Scholar] [CrossRef] [Green Version]
- Weick, G.; Woollacott, C.; Barnes, W.L.; Hess, O.; Mariani, E. Dirac-like plasmons in honeycomb lattices of metallic nanoparticles. Phys. Rev. Lett. 2013, 110, 106801. [Google Scholar] [CrossRef]
- Zhang, F. Brought to light. Nat. Phys. 2018, 14, 111–113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, Z. Extremal transmission and beating effect of acoustic waves in two-dimensional sonic crystals. Phys. Rev. Lett. 2008, 101, 264303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleury, R.; Sounas, D.L.; Sieck, C.F.; Haberman, M.R.; Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 2014, 343, 516–519. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, F.; Shi, X.; Lin, X.; Gao, Z.; Chong, Y.; Zhang, B. Topological acoustics. Phys. Rev. Lett. 2015, 114, 114301. [Google Scholar] [CrossRef] [PubMed]
- Khanikaev, A.B.; Fleury, R.; Mousavi, S.H.; Alu, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 2015, 6, 8260. [Google Scholar] [CrossRef]
- Ni, X.; He, C.; Sun, X.-C.; Liu, X.-p.; Lu, M.-H.; Feng, L.; Chen, Y.-F. Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow. New J. Phys. 2015, 17, 053016. [Google Scholar] [CrossRef]
- Peng, Y.-G.; Qin, C.-Z.; Zhao, D.-G.; Shen, Y.-X.; Xu, X.-Y.; Bao, M.; Jia, H.; Zhu, X.-F. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 2016, 7, 13368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, C.; Li, Z.; Ni, X.; Sun, X.-C.; Yu, S.-Y.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Topological phononic states of underwater sound based on coupled ring resonators. Appl. Phys. Lett. 2016, 108, 031904. [Google Scholar] [CrossRef]
- Lu, J.; Qiu, C.; Ke, M.; Liu, Z. Valley vortex states in sonic crystals. Phys. Rev. Lett. 2016, 116, 093901. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2017, 13, 369–374. [Google Scholar] [CrossRef] [Green Version]
- Xia, B.-Z.; Liu, T.-T.; Huang, G.-L.; Dai, H.-Q.; Jiao, J.-R.; Zang, X.-G.; Yu, D.-J.; Zheng, S.-J.; Liu, J. Topological phononic insulator with robust pseudospin-dependent transport. Phys. Rev. B 2017, 96, 094106. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Peng, Y.; Zhu, Y.; Fan, X.; Yang, J.; Liang, B.; Zhu, X.; Wan, X.; Cheng, J. Experimental demonstration of acoustic Chern insulators. Phys. Rev. Lett. 2019, 122, 014302. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Duan, G.; Xia, B. Underwater acoustic positioning based on valley-chirality locked beam of sonic system. Int. J. Mech. Sci. 2020, 174, 105463. [Google Scholar] [CrossRef]
- Wang, Y.-T.; Luan, P.-G.; Zhang, S. Coriolis force induced topological order for classical mechanical vibrations. New J. Phys. 2015, 17, 073031. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Hu, G. Topological phase transition in mechanical honeycomb lattice. J. Mech. Phys. Solids 2019, 122, 54–68. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef] [PubMed]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Süsstrunk, R.; Huber, S.D. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef] [Green Version]
- Salerno, G.; Berardo, A.; Ozawa, T.; Price, H.M.; Taxis, L.; Pugno, N.M.; Carusotto, I. Spin–orbit coupling in a hexagonal ring of pendula. New J. Phys. 2017, 19, 055001. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Miniaci, M.; Pal, R.; Morvan, B.; Ruzzene, M. Experimental observation of topologically protected helical edge modes in patterned elastic plates. Phys. Rev. X 2018, 8, 031074. [Google Scholar] [CrossRef] [Green Version]
- Chaunsali, R.; Chen, C.-W.; Yang, J. Subwavelength and directional control of flexural waves in zone-folding induced topological plates. Phys. Rev. B 2018, 97, 054307. [Google Scholar] [CrossRef] [Green Version]
- Chaunsali, R.; Chen, C.-W.; Yang, J. Experimental demonstration of topological waveguiding in elastic plates with local resonators. New J. Phys. 2018, 20, 113036. [Google Scholar] [CrossRef]
- Cha, J.; Kim, K.W.; Daraio, C. Experimental realization of on-chip topological nanoelectromechanical metamaterials. Nature 2018, 564, 229–233. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Nassar, H.; Norris, A.N.; Hu, G.; Huang, G. Elastic quantum spin Hall effect in kagome lattices. Phys. Rev. B 2018, 98, 094302. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.-Y.; He, C.; Wang, Z.; Liu, F.-K.; Sun, X.-C.; Li, Z.; Lu, H.-Z.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Elastic pseudospin transport for integratable topological phononic circuits. Nat. Commun. 2018, 9, 3072. [Google Scholar] [CrossRef]
- Zheng, L.-Y.; Theocharis, G.; Tournat, V.; Gusev, V. Quasitopological rotational waves in mechanical granular graphene. Phys. Rev. B 2018, 97, 060101. [Google Scholar] [CrossRef]
- Li, G.-H.; Ma, T.-X.; Wang, Y.-Z.; Wang, Y.-S. Active control on topological immunity of elastic wave metamaterials. Sci. Rep. 2020, 10, 9376. [Google Scholar] [CrossRef]
- Pal, R.K.; Schaeffer, M.; Ruzzene, M. Helical edge states and topological phase transitions in phononic systems using bi-layered lattices. J. Appl. Phys. 2016, 119, 084305. [Google Scholar] [CrossRef] [Green Version]
- Pal, R.K.; Ruzzene, M. Edge waves in plates with resonators: An elastic analogue of the quantum valley Hall effect. New J. Phys. 2017, 19, 025001. [Google Scholar] [CrossRef]
- Wang, J.; Mei, J. Topological valley-chiral edge states of Lamb waves in elastic thin plates. Appl. Phys. Express 2018, 11, 057302. [Google Scholar] [CrossRef]
- Gao, N.; Qu, S.; Si, L.; Wang, J.; Chen, W. Broadband topological valley transport of elastic wave in reconfigurable phononic crystal plate. Appl. Phys. Lett. 2021, 118, 063502. [Google Scholar] [CrossRef]
- Liu, T.-W.; Semperlotti, F. Tunable acoustic valley–hall edge states in reconfigurable phononic elastic waveguides. Phys. Rev. Appl. 2018, 9, 014001. [Google Scholar] [CrossRef] [Green Version]
- Jiao, J.; Chen, T.; Dai, H.; Yu, D. Observation of topological valley transport of elastic waves in bilayer phononic crystal slabs. Phys. Lett. A 2019, 383, 125988. [Google Scholar] [CrossRef]
- Yao, L.; Zhang, D.; Xu, K.; Dong, L.; Chen, X. Topological phononic crystal plates with locally resonant elastic wave systems. Appl. Acoust. 2021, 177, 107931. [Google Scholar] [CrossRef]
- Vila, J.; Pal, R.K.; Ruzzene, M. Observation of topological valley modes in an elastic hexagonal lattice. Phys. Rev. B 2017, 96, 134307. [Google Scholar] [CrossRef] [Green Version]
- Yan, M.; Lu, J.; Li, F.; Deng, W.; Huang, X.; Ma, J.; Liu, Z. On-chip valley topological materials for elastic wave manipulation. Nat. Mater. 2018, 17, 993–998. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, T.-W.; Semperlotti, F. Design and experimental observation of valley-Hall edge states in diatomic-graphene-like elastic waveguides. Phys. Rev. B 2018, 97, 174301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Chen, Y.; Zhang, K.; Hu, G. Programmable elastic valley Hall insulator with tunable interface propagation routes. Extrem. Mech. Lett. 2019, 28, 76–80. [Google Scholar] [CrossRef]
- Kariyado, T.; Hatsugai, Y. Manipulation of dirac cones in mechanical graphene. Sci. Rep. 2015, 5, 18107. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.-H.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- He, C.; Ni, X.; Ge, H.; Sun, X.-C.; Chen, Y.-B.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 2016, 12, 1124–1129. [Google Scholar] [CrossRef]
- Lubensky, T.; Kane, C.; Mao, X.; Souslov, A.; Sun, K. Phonons and elasticity in critically coordinated lattices. Rep. Prog. Phys. 2015, 78, 073901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, J.-W.; Chen, X.-D.; Zhu, H.; Wang, Y.; Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 2017, 16, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Xue, H.; Yang, Z.; Lai, K.; Yu, Y.; Lin, X.; Chong, Y.; Shvets, G.; Zhang, B. Topologically protected refraction of robust kink states in valley photonic crystals. Nat. Phys. 2018, 14, 140–144. [Google Scholar] [CrossRef]
- Huang, H.; Huo, S.; Chen, J. Subwavelength elastic topological negative refraction in ternary locally resonant phononic crystals. Int. J. Mech. Sci. 2021, 198, 106391. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, B.-Z. Topological interface propagation characteristics of valleypolarized three-dimensional elastic phononic crystals induced by lattice defects. Chin. Sci. Bull. 2021, 1–10. [Google Scholar]
- Huo, S.-y.; Chen, J.-j.; Huang, H.-b.; Huang, G.-l. Simultaneous multi-band valley-protected topological edge states of shear vertical wave in two-dimensional phononic crystals with veins. Sci. Rep. 2017, 7, 10335. [Google Scholar] [CrossRef] [Green Version]
- Tong, L.; Fan, H.; Xia, B. Elastic phononic plates with first-order and second-order topological phases. J. Phys. D Appl. Phys. 2020, 53, 115303. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Y.; Zhang, K.; Hu, G. Dirac degeneracy and elastic topological valley modes induced by local resonant states. Phys. Rev. B 2020, 101, 014101. [Google Scholar] [CrossRef]
- Noh, J.; Benalcazar, W.A.; Huang, S.; Collins, M.J.; Chen, K.P.; Hughes, T.L.; Rechtsman, M.C. Topological protection of photonic mid-gap defect modes. Nat. Photonics 2018, 12, 408–415. [Google Scholar] [CrossRef] [Green Version]
- Mittal, S.; Orre, V.V.; Zhu, G.; Gorlach, M.A.; Poddubny, A.; Hafezi, M. Photonic quadrupole topological phases. Nat. Photonics 2019, 13, 692–696. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.-D.; Deng, W.-M.; Shi, F.-L.; Zhao, F.-L.; Chen, M.; Dong, J.-W. Direct observation of corner states in second-order topological photonic crystal slabs. Phys. Rev. Lett. 2019, 122, 233902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, M.; Rho, J. Topological edge and corner states in a two-dimensional photonic Su-Schrieffer-Heeger lattice. Nanophotonics 2020, 9, 3227–3234. [Google Scholar] [CrossRef]
- Xie, B.; Su, G.; Wang, H.-F.; Liu, F.; Hu, L.; Yu, S.-Y.; Zhan, P.; Lu, M.-H.; Wang, Z.; Chen, Y.-F. Higher-order quantum spin Hall effect in a photonic crystal. Nat. Commun. 2020, 11, 3768. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Lin, Z.K.; Lu, W.; Lai, Y.; Hou, B.; Jiang, J.H. Twisted quadrupole topological photonic crystals. Laser Photonics Rev. 2020, 14, 2000010. [Google Scholar] [CrossRef]
- El Hassan, A.; Kunst, F.K.; Moritz, A.; Andler, G.; Bergholtz, E.J.; Bourennane, M. Corner states of light in photonic waveguides. Nat. Photonics 2019, 13, 697–700. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Xie, B.-Y.; Lu, Y.-H.; Chang, Y.-J.; Wang, H.-F.; Gao, J.; Jiao, Z.-Q.; Feng, Z.; Xu, X.-Y.; Mei, F. Quantum superposition demonstrated higher-order topological bound states in the continuum. Light Sci. Appl. 2021, 10, 173. [Google Scholar] [CrossRef]
- Xue, H.; Yang, Y.; Gao, F.; Chong, Y.; Zhang, B. Acoustic higher-order topological insulator on a kagome lattice. Nat. Mater. 2019, 18, 108–112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Xie, B.-Y.; Wang, H.-F.; Xu, X.; Tian, Y.; Jiang, J.-H.; Lu, M.-H.; Chen, Y.-F. Dimensional hierarchy of higher-order topology in three-dimensional sonic crystals. Nat. Commun. 2019, 10, 5331. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wang, H.-X.; Lin, Z.-K.; Tian, Y.; Xie, B.; Lu, M.-H.; Chen, Y.-F.; Jiang, J.-H. Second-order topology and multidimensional topological transitions in sonic crystals. Nat. Phys. 2019, 15, 582–588. [Google Scholar] [CrossRef] [Green Version]
- Xue, H.; Yang, Y.; Liu, G.; Gao, F.; Chong, Y.; Zhang, B. Realization of an acoustic third-order topological insulator. Phys. Rev. Lett. 2019, 122, 244301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; López, M.R.; Cheng, Y.; Liu, X.; Christensen, J. Non-hermitian sonic second-order topological insulator. Phys. Rev. Lett. 2019, 122, 195501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Liu, L.; Lu, M.-H.; Chen, Y.-F. Valley-selective topological corner states in sonic crystals. Phys. Rev. Lett. 2021, 126, 156401. [Google Scholar] [CrossRef]
- Serra-Garcia, M.; Peri, V.; Süsstrunk, R.; Bilal, O.R.; Larsen, T.; Villanueva, L.G.; Huber, S.D. Observation of a phononic quadrupole topological insulator. Nature 2018, 555, 342–345. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Xia, B.; Tong, L.; Zheng, S.; Yu, D. Elastic higher-order topological insulator with topologically protected corner states. Phys. Rev. Lett. 2019, 122, 204301. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-W.; Chaunsali, R.; Christensen, J.; Theocharis, G.; Yang, J. Corner states in a second-order mechanical topological insulator. Commun. Mater. 2021, 2, 62. [Google Scholar] [CrossRef]
- Gao, P.; Torrent, D.; Cervera, F.; San-Jose, P.; Sánchez-Dehesa, J.; Christensen, J. Majorana-like zero modes in Kekulé distorted sonic lattices. Phys. Rev. Lett. 2019, 123, 196601. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Xia, B.; Zheng, S.; Tong, L. Elastic phononic topological plate with edge and corner sates based on pseudospin-valley-coupling. J. Phys. D Appl. Phys. 2020, 53, 395304. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Q.; Xu, H.-Y.; Wu, D.-J. A higher-order topological insulator with wide bandgaps in Lamb-wave systems. J. Appl. Phys. 2020, 127, 075105. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, M.; Lin, Z.-K.; Wang, H.-X.; Li, F.; Jiang, J.-H. On-chip higher-order topological micromechanical metamaterials. Sci. Bull. 2021, 66, 1959–1966. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Q. An elastic higher-order topological insulator based on kagome phononic crystals. J. Appl. Phys. 2021, 129, 035102. [Google Scholar] [CrossRef]
- Imhof, S.; Berger, C.; Bayer, F.; Brehm, J.; Molenkamp, L.W.; Kiessling, T.; Schindler, F.; Lee, C.H.; Greiter, M.; Neupert, T. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 2018, 14, 925–929. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, C.-C.; Lu, Y.-M.; Zhang, F. High-temperature majorana corner states. Phys. Rev. Lett. 2018, 121, 186801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, B.; Chen, R.; Li, R.; Guan, C.; Zhou, B.; Dong, G.; Zhao, C.; Li, Y.; Wang, Y.; Tao, H. Realization of quasicrystalline quadrupole topological insulators in electrical circuits. Commun. Phys. 2021, 4, 108. [Google Scholar] [CrossRef]
- Ezawa, M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices. Phys. Rev. Lett. 2018, 120, 026801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Li, J.; Zhu, J. Topology optimization of quantum spin Hall effect-based second-order phononic topological insulator. Mech. Syst. Signal Process. 2022, 164, 108243. [Google Scholar] [CrossRef]
- Geerligs, L.; Anderegg, V.; Holweg, P.; Mooij, J.; Pothier, H.; Esteve, D.; Urbina, C.; Devoret, M. Frequency-locked turnstile device for single electrons. Phys. Rev. Lett. 1990, 64, 2691. [Google Scholar] [CrossRef] [Green Version]
- Kraus, Y.E.; Lahini, Y.; Ringel, Z.; Verbin, M.; Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 2012, 109, 106402. [Google Scholar] [CrossRef] [Green Version]
- Verbin, M.; Zilberberg, O.; Lahini, Y.; Kraus, Y.E.; Silberberg, Y. Topological pumping over a photonic Fibonacci quasicrystal. Phys. Rev. B 2015, 91, 064201. [Google Scholar] [CrossRef] [Green Version]
- Kraus, Y.E.; Ringel, Z.; Zilberberg, O. Four-dimensional quantum Hall effect in a two-dimensional quasicrystal. Phys. Rev. Lett. 2013, 111, 226401. [Google Scholar] [CrossRef] [PubMed]
- Kraus, Y.E.; Zilberberg, O. Quasiperiodicity and topology transcend dimensions. Nat. Phys. 2016, 12, 624–626. [Google Scholar] [CrossRef]
- Lohse, M.; Schweizer, C.; Zilberberg, O.; Aidelsburger, M.; Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 2016, 12, 350–354. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Yao, L.; Nassar, H.; Huang, G. Mechanical quantum hall effect in time-modulated elastic materials. Phys. Rev. Appl. 2019, 11, 044029. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, S.; Tomita, T.; Taie, S.; Ichinose, T.; Ozawa, H.; Wang, L.; Troyer, M.; Takahashi, Y. Topological Thouless pumping of ultracold fermions. Nat. Phys. 2016, 12, 296–300. [Google Scholar] [CrossRef] [Green Version]
- Riva, E.; Casieri, V.; Resta, F.; Braghin, F. Adiabatic pumping via avoided crossings in stiffness-modulated quasiperiodic beams. Phys. Rev. B 2020, 102, 014305. [Google Scholar] [CrossRef]
- Grinberg, I.H.; Lin, M.; Harris, C.; Benalcazar, W.A.; Peterson, C.W.; Hughes, T.L.; Bahl, G. Robust temporal pumping in a magneto-mechanical topological insulator. Nat. Commun. 2020, 11, 974. [Google Scholar] [CrossRef] [Green Version]
- Rosa, M.I.; Pal, R.K.; Arruda, J.R.; Ruzzene, M. Edge states and topological pumping in spatially modulated elastic lattices. Phys. Rev. Lett. 2019, 123, 034301. [Google Scholar] [CrossRef] [Green Version]
- Zilberberg, O.; Huang, S.; Guglielmon, J.; Wang, M.; Chen, K.P.; Kraus, Y.E.; Rechtsman, M.C. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 2018, 553, 59–62. [Google Scholar] [CrossRef]
- Riva, E.; Rosa, M.I.; Ruzzene, M. Edge states and topological pumping in stiffness-modulated elastic plates. Phys. Rev. B 2020, 101, 094307. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.-G.; Tang, W.; Zhang, R.-Y.; Chen, Z.; Ma, G. Landau-Zener Transition in the Dynamic Transfer of Acoustic Topological States. Phys. Rev. Lett. 2021, 126, 054301. [Google Scholar] [CrossRef]
- Zeng, L.-S.; Shen, Y.-X.; Peng, Y.-G.; Zhao, D.-G.; Zhu, X.-F. Selective Topological Pumping for Robust, Efficient, and Asymmetric Sound Energy Transfer in a Dynamically Coupled Cavity Chain. Phys. Rev. Appl. 2021, 15, 064018. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Wu, Q.; Huang, Y.; Nguyen, H.; Prodan, E.; Zhou, X.; Huang, G. Physical rendering of synthetic spaces for topological sound transport. arXiv 2020, arXiv:2012.11828. [Google Scholar]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Riva, E.; Rosa, M.I.; Cazzulani, G.; Erturk, A.; Braghin, F.; Ruzzene, M. Experimental observation of temporal pumping in electromechanical waveguides. Phys. Rev. Lett. 2021, 126, 095501. [Google Scholar] [CrossRef] [PubMed]
- Nassar, H.; Chen, H.; Norris, A.; Huang, G. Quantization of band tilting in modulated phononic crystals. Phys. Rev. B 2018, 97, 014305. [Google Scholar] [CrossRef] [Green Version]
- Riva, E.; Castaldini, G.; Braghin, F. Adiabatic edge-to-edge transformations in time-modulated elastic lattices and non-Hermitian shortcuts. arXiv 2021, arXiv:2105.02196. [Google Scholar] [CrossRef]
- Ran, Y.; Zhang, Y.; Vishwanath, A. One-dimensional topologically protected modes in topological insulators with lattice dislocations. Nat. Phys. 2009, 5, 298–303. [Google Scholar] [CrossRef] [Green Version]
- Teo, J.C.; Hughes, T.L. Existence of Majorana-fermion bound states on disclinations and the classification of topological crystalline superconductors in two dimensions. Phys. Rev. Lett. 2013, 111, 047006. [Google Scholar] [CrossRef] [PubMed]
- Tuegel, T.I.; Chua, V.; Hughes, T.L. Embedded topological insulators. Phys. Rev. B 2019, 100, 115126. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Xue, H.; Zhang, B.; Chong, Y. Observation of protected photonic edge states induced by real-space topological lattice defects. Phys. Rev. Lett. 2020, 124, 243602. [Google Scholar] [CrossRef]
- Li, F.-F.; Wang, H.-X.; Xiong, Z.; Lou, Q.; Chen, P.; Wu, R.-X.; Poo, Y.; Jiang, J.-H.; John, S. Topological light-trapping on a dislocation. Nat. Commun. 2018, 9, 2462. [Google Scholar] [CrossRef] [PubMed]
- Grinberg, I.H.; Lin, M.; Benalcazar, W.A.; Hughes, T.L.; Bahl, G. Trapped state at a dislocation in a weak magnetomechanical topological insulator. Phys. Rev. Appl. 2020, 14, 064042. [Google Scholar] [CrossRef]
- Peterson, C.W.; Li, T.; Jiang, W.; Hughes, T.L.; Bahl, G. Trapped fractional charges at bulk defects in topological insulators. Nature 2021, 589, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Leung, S.; Li, F.-F.; Lin, Z.-K.; Tao, X.; Poo, Y.; Jiang, J.-H. Bulk–disclination correspondence in topological crystalline insulators. Nature 2021, 589, 381–385. [Google Scholar] [CrossRef]
- Xue, H.; Jia, D.; Ge, Y.; Guan, Y.-J.; Wang, Q.; Yuan, S.-Q.; Sun, H.-X.; Chong, Y.; Zhang, B. Observation of dislocation-induced topological modes in a three-dimensional acoustic topological insulator. arXiv 2021, arXiv:2104.13161. [Google Scholar] [CrossRef] [PubMed]
- Ye, L.; Qiu, C.; Xiao, M.; Li, T.; Du, J.; Ke, M.; Liu, Z. Topological dislocation modes in three-dimensional acoustic topological insulators. arXiv 2021, arXiv:2104.04172. [Google Scholar] [CrossRef]
- Wang, Q.; Ge, Y.; Sun, H.-x.; Xue, H.; Jia, D.; Guan, Y.-j.; Yuan, S.-q.; Zhang, B.; Chong, Y. Vortex states in an acoustic Weyl crystal with a topological lattice defect. Nat. Commun. 2021, 12, 3654. [Google Scholar] [CrossRef]
- Teo, J.C.; Hughes, T.L. Topological defects in symmetry-protected topological phases. Annu. Rev. Condens. Matter Phys. 2017, 8, 211–237. [Google Scholar] [CrossRef]
- Barkeshli, M.; Qi, X.-L. Topological nematic states and non-abelian lattice dislocations. Phys. Rev. X 2012, 2, 031013. [Google Scholar] [CrossRef] [Green Version]
- Juričić, V.; Mesaros, A.; Slager, R.-J.; Zaanen, J. Universal probes of two-dimensional topological insulators: Dislocation and π flux. Phys. Rev. Lett. 2012, 108, 106403. [Google Scholar] [CrossRef] [Green Version]
- Mesaros, A.; Kim, Y.B.; Ran, Y. Changing topology by topological defects in three-dimensional topologically ordered phases. Phys. Rev. B 2013, 88, 035141. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Teo, J.C.; Hughes, T.L. Classification of two-dimensional topological crystalline superconductors and majorana bound states at disclinations. Phys. Rev. B 2014, 89, 224503. [Google Scholar] [CrossRef] [Green Version]
- Queiroz, R.; Fulga, I.C.; Avraham, N.; Beidenkopf, H.; Cano, J. Partial lattice defects in higher-order topological insulators. Phys. Rev. Lett. 2019, 123, 266802. [Google Scholar] [CrossRef] [Green Version]
- Roy, B.; Juričić, V. Dislocation as a bulk probe of higher-order topological insulators. Phys. Rev. Res. 2021, 3, 033107. [Google Scholar] [CrossRef]
- Yamada, S.S.; Li, T.; Lin, M.; Peterson, C.W.; Hughes, T.L.; Bahl, G. Bound states at partial dislocation defects in multipole higher-order topological insulators. arXiv 2021, arXiv:2105.01050. [Google Scholar]
- Van Miert, G.; Ortix, C. Dislocation charges reveal two-dimensional topological crystalline invariants. Phys. Rev. B 2018, 97, 201111. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Zhu, P.; Benalcazar, W.A.; Hughes, T.L. Fractional disclination charge in two-dimensional C n-symmetric topological crystalline insulators. Phys. Rev. B 2020, 101, 115115. [Google Scholar] [CrossRef] [Green Version]
- Paulose, J.; Chen, B.G.-g.; Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 2015, 11, 153–156. [Google Scholar] [CrossRef] [Green Version]
- Xia, B.; Zhang, J.; Tong, L.; Zheng, S.; Man, X. Topologically valley-polarized edge states in elastic phononic plates yielded by lattice defects. Int. J. Solids Struct. 2022, 239–240, 111413. [Google Scholar] [CrossRef]
- Xia, B.; Jiang, Z.; Tong, L.; Zheng, S.; Man, X. Topological bound states in elastic phononic plates induced by disclinations. Acta Mech. Sin. 2021, 1. [Google Scholar]
- Ni, X.; Li, M.; Weiner, M.; Alù, A.; Khanikaev, A.B. Demonstration of a quantized acoustic octupole topological insulator. Nat. Commun. 2020, 11, 2108. [Google Scholar] [CrossRef]
- Weiner, M.; Ni, X.; Li, M.; Alù, A.; Khanikaev, A.B. Demonstration of a third-order hierarchy of topological states in a three-dimensional acoustic metamaterial. Sci. Adv. 2020, 6, eaay4166. [Google Scholar] [CrossRef] [Green Version]
- Xue, H.; Ge, Y.; Sun, H.-X.; Wang, Q.; Jia, D.; Guan, Y.-J.; Yuan, S.-Q.; Chong, Y.; Zhang, B. Observation of an acoustic octupole topological insulator. Nat. Commun. 2020, 11, 2442. [Google Scholar] [CrossRef]
- Zheng, S.; Xia, B.; Man, X.; Tong, L.; Jiao, J.; Duan, G.; Yu, D. Three-dimensional higher-order topological acoustic system with multidimensional topological states. Phys. Rev. B 2020, 102, 104113. [Google Scholar] [CrossRef]
- Bao, J.; Zou, D.; Zhang, W.; He, W.; Sun, H.; Zhang, X. Topoelectrical circuit octupole insulator with topologically protected corner states. Phys. Rev. B 2019, 100, 201406. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Ma, S.; Zhang, Q.; Zhang, L.; Yang, C.; You, O.; Gao, W.; Xiang, Y.; Cui, T.J.; Zhang, S. Octupole corner state in a three-dimensional topological circuit. Light Sci. Appl. 2020, 9, 145. [Google Scholar] [CrossRef]
- Peterson, C.W.; Li, T.; Benalcazar, W.A.; Hughes, T.L.; Bahl, G. A fractional corner anomaly reveals higher-order topology. Science 2020, 368, 1114–1118. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, H.; Gupta, S.K.; Zhang, H.; Xie, B.; Lu, M.; Chen, Y. Photonic non-Hermitian skin effect and non-Bloch bulk-boundary correspondence. Phys. Rev. Res. 2020, 2, 013280. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhou, Q.; Chen, S. Localization transition, spectrum structure, and winding numbers for one-dimensional non-Hermitian quasicrystals. Phys. Rev. B 2021, 104, 024201. [Google Scholar] [CrossRef]
- Zhou, H.; Peng, C.; Yoon, Y.; Hsu, C.W.; Nelson, K.A.; Fu, L.; Joannopoulos, J.D.; Soljačić, M.; Zhen, B. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science 2018, 359, 1009–1012. [Google Scholar] [CrossRef] [Green Version]
- Cerjan, A.; Huang, S.; Wang, M.; Chen, K.P.; Chong, Y.; Rechtsman, M.C. Experimental realization of a Weyl exceptional ring. Nat. Photonics 2019, 13, 623–628. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Xue, H.; Gu, Z.; Liu, T.; Zhu, J.; Zhang, B. Non-Hermitian route to higher-order topology in an acoustic crystal. Nat. Commun. 2021, 12, 1888. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Tian, Y.; Jiang, J.-H.; Lu, M.-H.; Chen, Y.-F. Observation of higher-order non-Hermitian skin effect. arXiv 2021, arXiv:2102.09825. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).