GRASP Optimization for the Strip Packing Problem with Flags, Waste Functions, and an Improved Restricted Candidate List
Abstract
:1. Introduction
1.1. Literature That Allows Object Rotation
1.2. Literature That Does Not Allow Object Rotation
2. Strip Packing Problem (SPP)
3. GRASP Algorithm for SPP
| Algorithm 1 GRASP General Procedure |
|
| Output: best |
3.1. GRASP Construction
| Algorithm 2 GRASP Construction Part 1 |
Input:k
|
| Algorithm 3 GRASP Construction Part 2 |
|
3.2. Roulette Procedure
| Algorithm 4 General Roulette Procedure |
Input:,
|
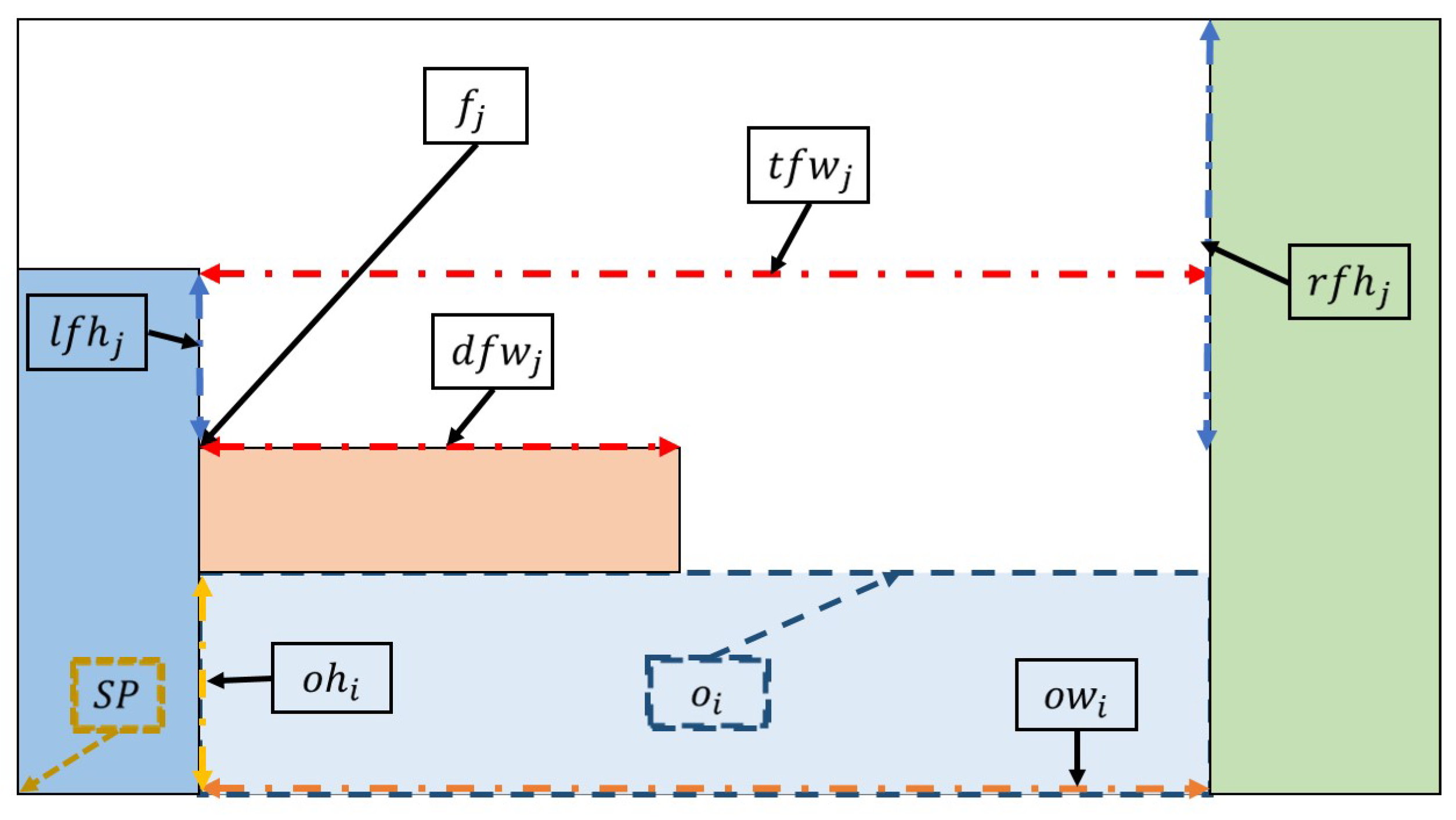
3.3. Object Arrangement
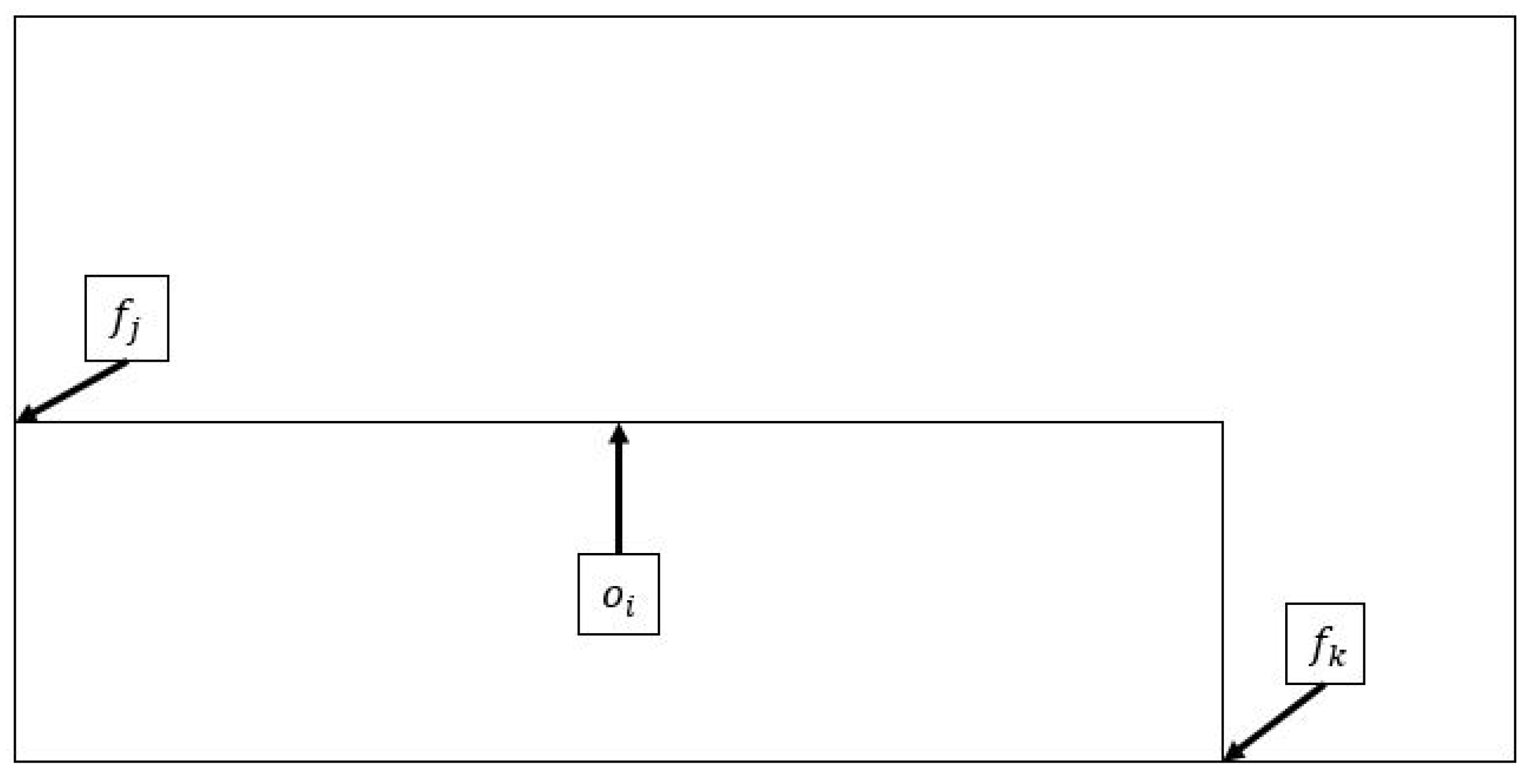
3.4. Overlapping among Objects
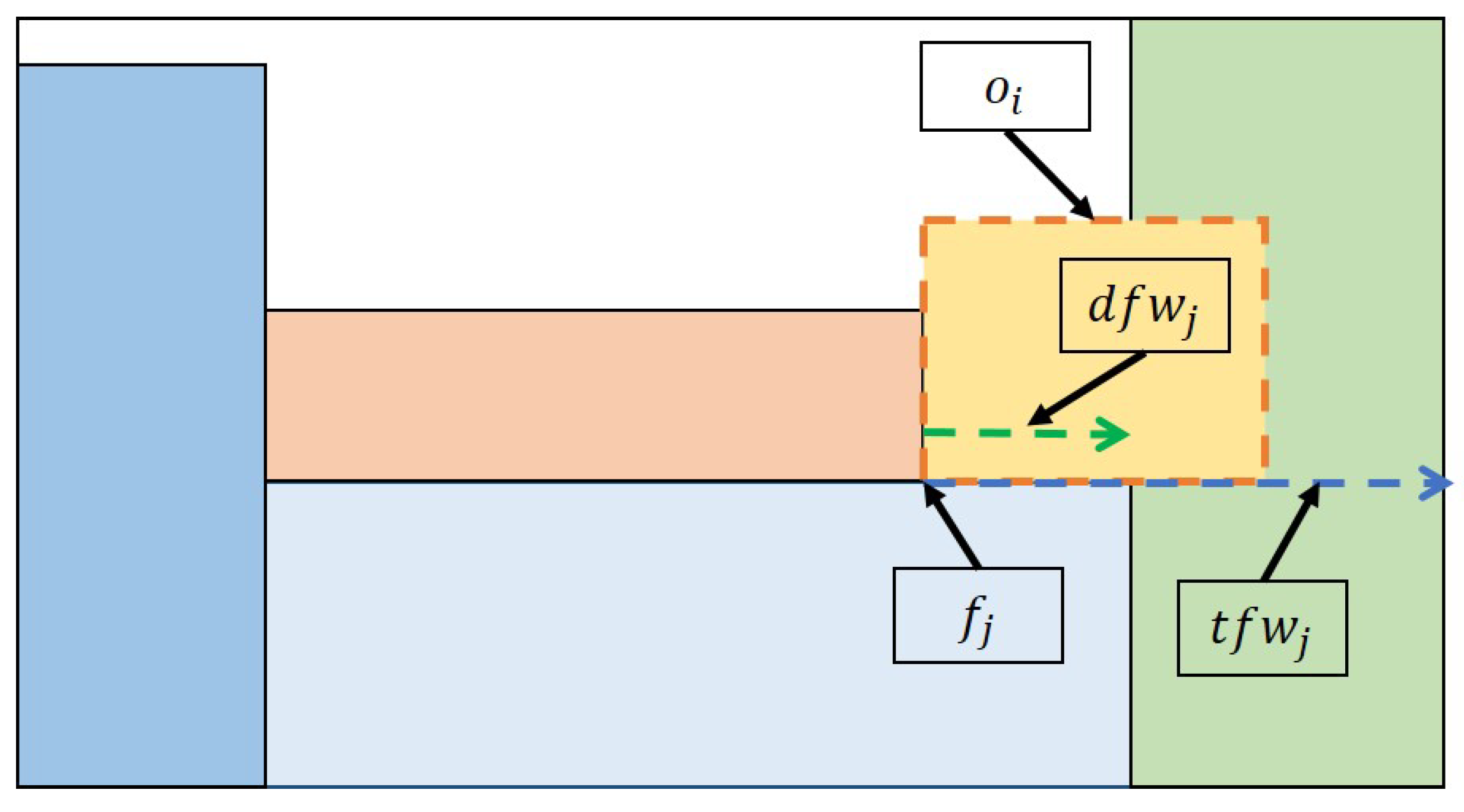
3.5. Overlaps between Rectangles and Flags
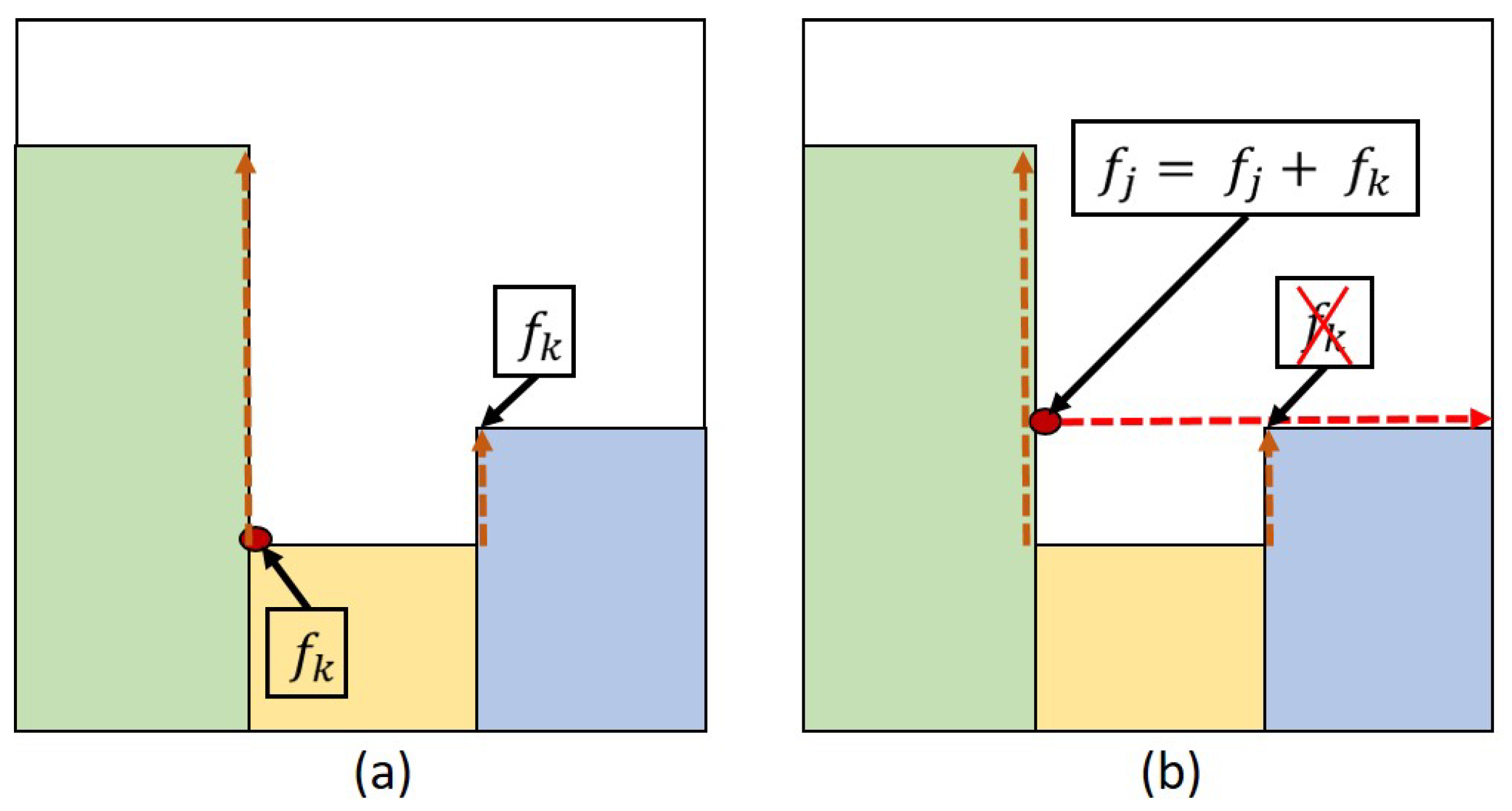
3.6. Rise Flag
4. Experimental Results
4.1. Configuration and Instances
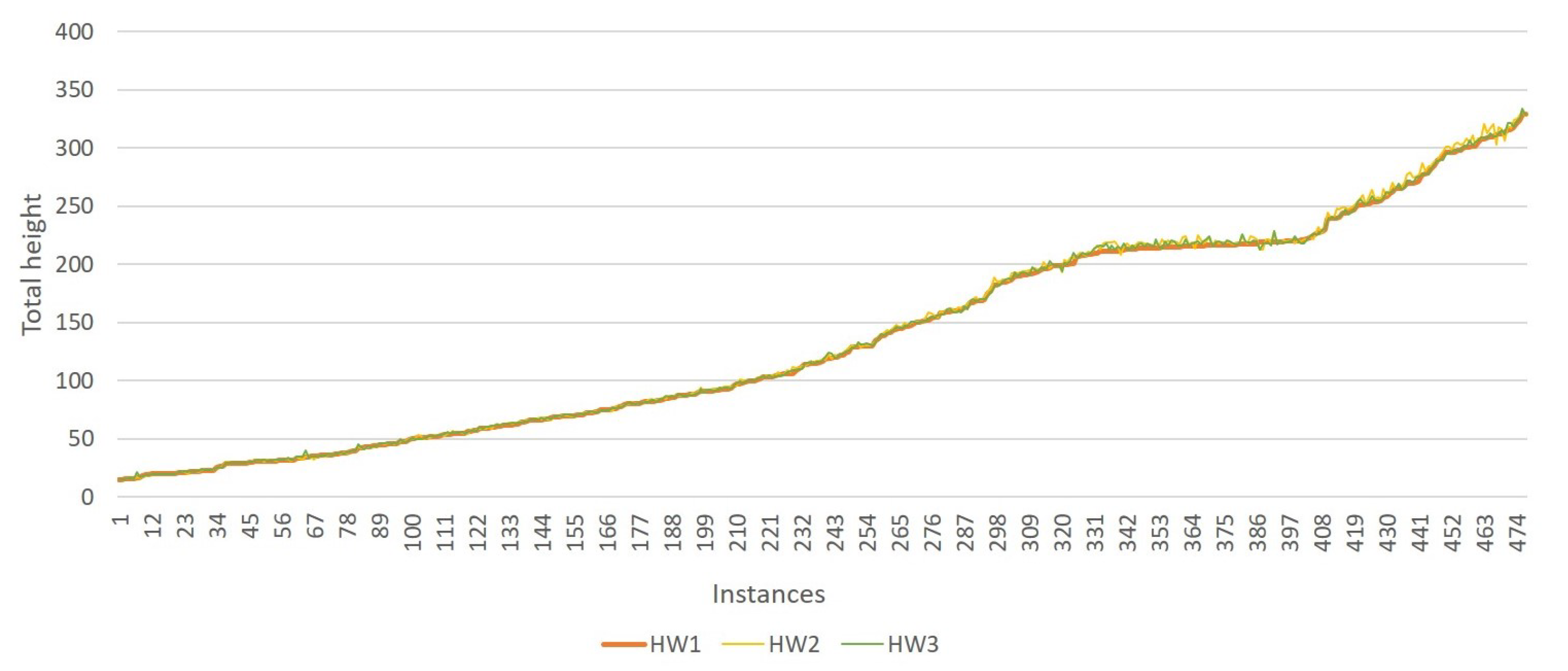
4.2. Waste Comparison
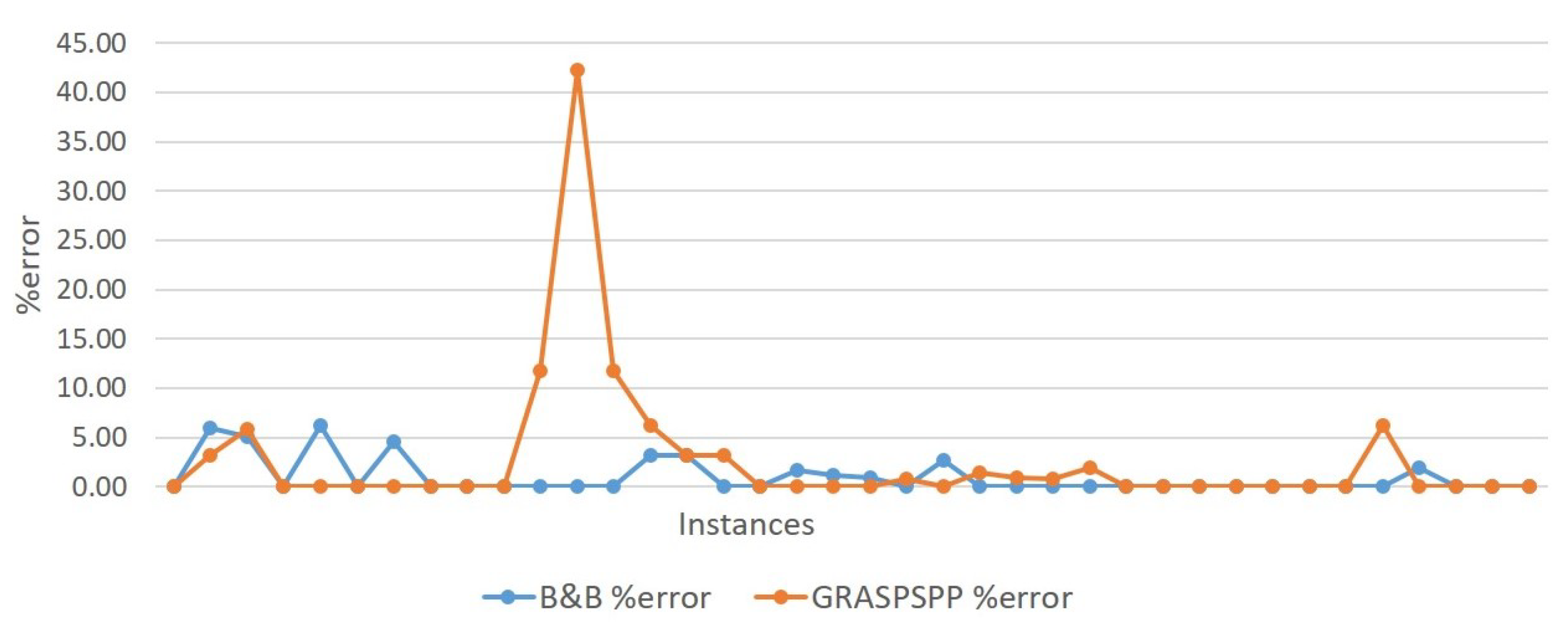
4.3. Comparison between GRASPSPP and Iterative Search Algorithm
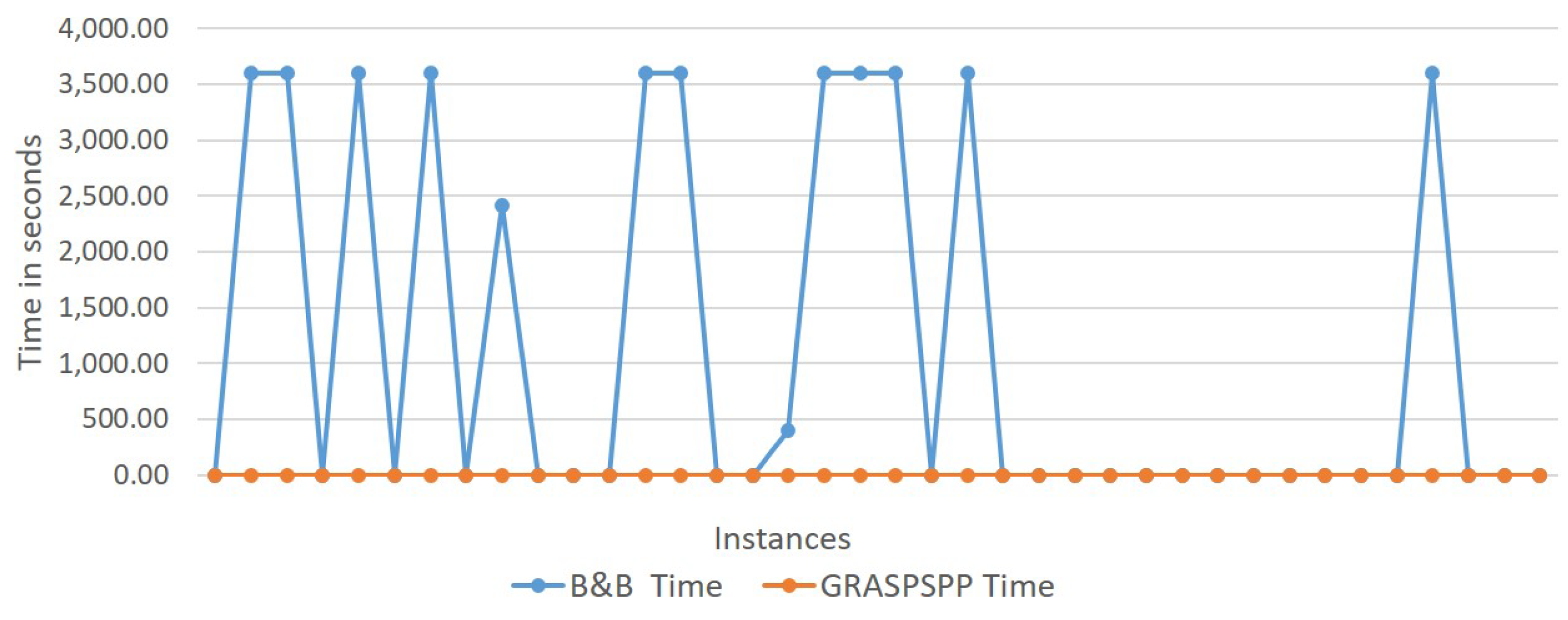
4.4. Comparison between GRASPSPP and Branch and Bound Algorithm
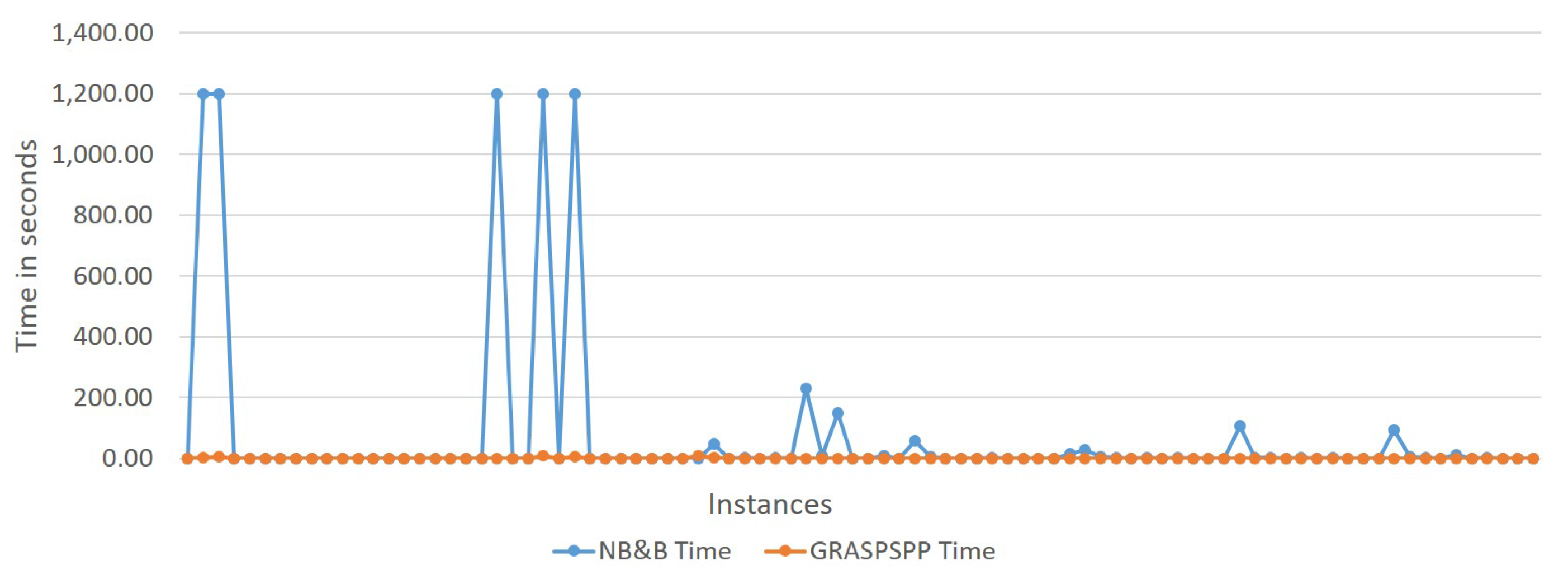
4.5. Comparison beteween GRASPSPP and a New Branch & Bound Algorithm
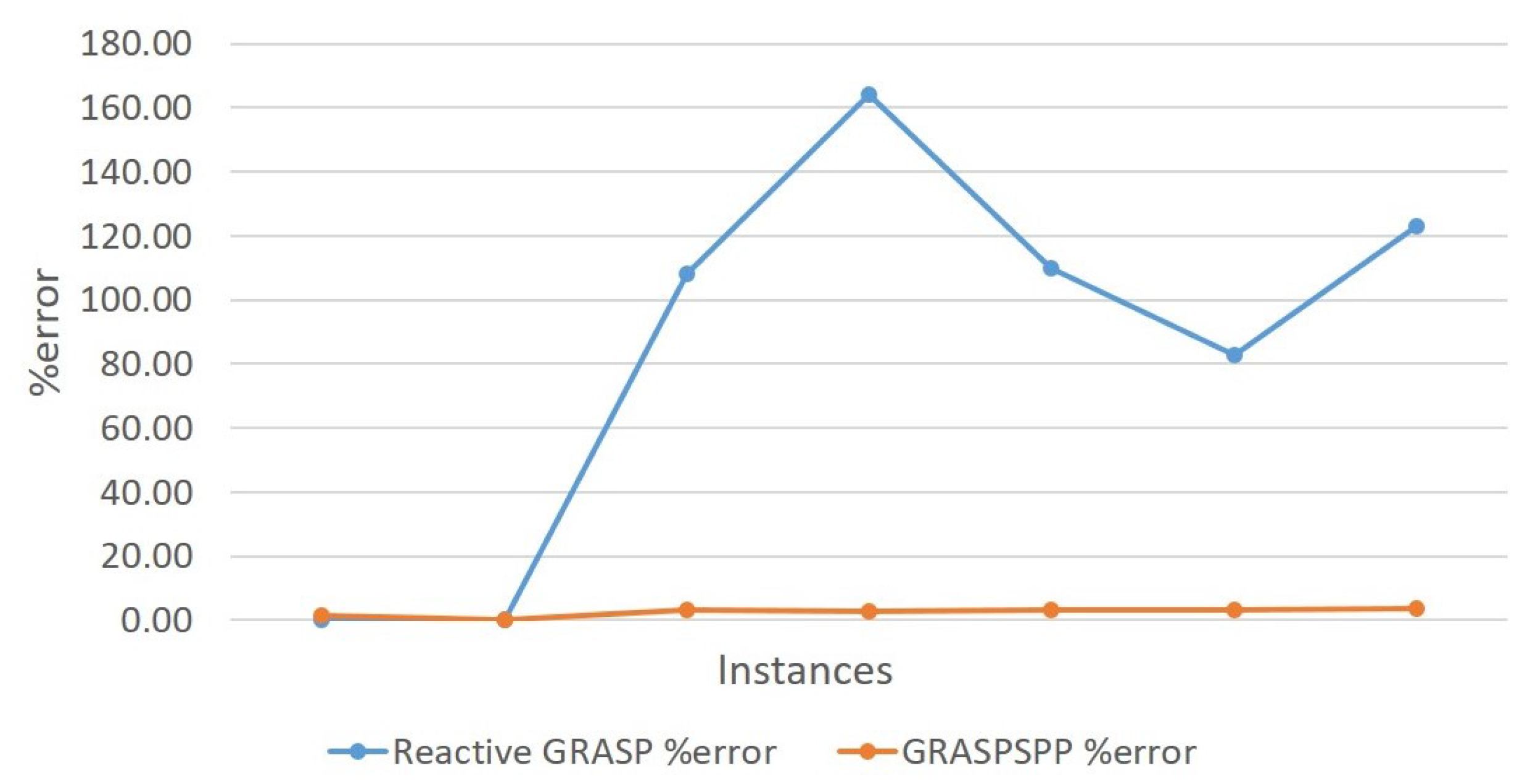
4.6. Comparison between GRASPSPP and Reactive GRASP Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Egeblad, J.; Pisinger, D. Heuristic approaches for the two- and three-dimensional knapsack packing problem. Comput. Oper. Res. 2009, 36, 1026–1049. [Google Scholar] [CrossRef]
- Fadda, E.; Fedorov, S.; Perboli, G.; Barbosa, I.D.C. Mixing machine learning and optimization for the tactical capacity planning in last-mile delivery. In Proceedings of the 2021 IEEE 45th Annual Computers, Software, and Applications Conference, COMPSAC, Madrid, Spain, 12–16 July 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 1291–1296. [Google Scholar] [CrossRef]
- Martello, S.; Pisinger, D.; Vigo, D. The Three-Dimensional Bin Packing Problem. Oper. Res. 2000, 48, 256–267. [Google Scholar] [CrossRef] [Green Version]
- Baker, B.S.; Coffman, E.G., Jr.; Rivest, R.L. Orthogonal Packings in Two Dimensions. SIAM J. Comput. 1980, 9, 846–855. [Google Scholar] [CrossRef]
- Routledge. Optimization in Industry: Volume 2, Industrial Applications, 2nd ed.; Routledge: Philadelphia, PA, USA, 2017; p. 270. [Google Scholar]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Rajkumar, M.; Asokan, P.; Anilkumar, N.; Page, T. A GRASP algorithm for flexible job-shop scheduling problem with limited resource constraints. Int. J. Prod. Res. 2011, 49, 2409–2423. [Google Scholar] [CrossRef]
- Sohrabi, S.; Ziarati, K.; Keshtkaran, M. A Greedy Randomized Adaptive Search Procedure for the Orienteering Problem with Hotel Selection. Eur. J. Oper. Res. 2020, 283, 426–440. [Google Scholar] [CrossRef]
- Gokalp, O. DNA Sequence Motif Discovery Using Greedy Construction Algorithm Based Techniques. In Proceedings of the 2020 5th International Conference on Computer Science and Engineering (UBMK), Diyarbakir, Turkey, 9–11 September 2020; pp. 176–180. [Google Scholar] [CrossRef]
- Bruni, M.; Beraldi, P.; Khodaparasti, S. A hybrid reactive GRASP heuristic for the risk-averse k-traveling repairman problem with profits. Comput. Oper. Res. 2020, 115, 104854. [Google Scholar] [CrossRef]
- Santiago, A.; Terán-Villanueva, J.D.; Martínez, S.I.; Rocha, J.A.C.; Menchaca, J.L.; Berrones, M.G.T.; Ponce-Flores, M. GRASP and Iterated Local Search-Based Cellular Processing algorithm for Precedence-Constraint Task List Scheduling on Heterogeneous Systems. Appl. Sci. 2020, 10, 7500. [Google Scholar] [CrossRef]
- Saad, A.; Kafafy, A.; El Raouf, O.A.; El-Hefnawy, N. A GRASP-Simulated Annealing approach applied to solve Multi-Processor Task Scheduling problems. In Proceedings of the 2019 14th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 17–18 December 2019; pp. 310–315. [Google Scholar] [CrossRef]
- Khamlichi, H.; Oufaska, K.; Zouadi, T.; Dkiouak, R. A Hybrid GRASP Algorithm for an Integrated Production Planning and a Group Layout Design in a Dynamic Cellular Manufacturing System. IEEE Access 2020, 8, 162809–162818. [Google Scholar] [CrossRef]
- Beltran, J.D.; Calderon, J.E.; Cabrera, R.J.; Perez, J.A.M.; Moreno-Vega, J.M. GRASP/VNS hybrid for the strip packing problem. In Proceedings of the First International Workshop on Hybrid Meta-Heuristics (HM04), Valencia, Spain, 22–23 August 2004. [Google Scholar]
- Da Silveira, J.L.; Miyazawa, F.K.; Xavier, E.C. Heuristics for the strip packing problem with unloading constraints. Comput. Oper. Res. 2013, 40, 991–1003. [Google Scholar] [CrossRef] [Green Version]
- Gaticia, G.; Reyes, P.; Contreras-Bolton, C.; Linfati, R.; Escobar, J.W. Un algoritmo para el Strip Packing Problem obtenido mediante la extracción de habilidades de expertos usando minería de datos. Ing. Investig. Tecnol. 2016, 17, 179–190. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Wu, C.; Tang, X.; Peng, X.; Zeng, Z.; Liu, S. An efficient deterministic heuristic algorithm for the rectangular packing problem. Comput. Ind. Eng. 2019, 137, 106097. [Google Scholar] [CrossRef]
- Martin, M.; Morabito, R.; Munari, P. A bottom-up packing approach for modeling the constrained two-dimensional guillotine placement problem. Comput. Oper. Res. 2020, 115, 104851. [Google Scholar] [CrossRef]
- Martello, S.; Monaci, M.; Vigo, D. An Exact Approach to the Strip-Packing Problem. Informs J. Comput. 2003, 15, 310–319. [Google Scholar] [CrossRef]
- Alvarez-Valdes, R.; Parreño, F.; Tamarit, J.M. Reactive GRASP for the strip-packing problem. Comput. Oper. Res. 2008, 35, 1065–1083. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Valdes, R.; Parreño, F.; Tamarit, J.M. A branch and bound algorithm for the strip packing problem. OR Spectr. 2009, 31, 431–459. [Google Scholar] [CrossRef]
- Leung, S.C.; Zhang, D.; Sim, K.M. A two-stage intelligent search algorithm for the two-dimensional strip packing problem. Eur. J. Oper. Res. 2011, 215, 57–69. [Google Scholar] [CrossRef]
- Zhang, D.; Che, Y.; Ye, F.; Si, Y.W.; Leung, S.C. A hybrid algorithm based on variable neighbourhood for the strip packing problem. J. Comb. Optim. 2016, 32, 513–530. [Google Scholar] [CrossRef]
- Wei, L.; Wang, Y.; Cheng, H.; Huang, J. An open space based heuristic for the 2D strip packing problem with unloading constraints. Appl. Math. Model. 2019, 70, 67–81. [Google Scholar] [CrossRef]
- Rakotonirainy, R.G.; van Vuuren, J.H. Improved metaheuristics for the two-dimensional strip packing problem. Appl. Soft Comput. J. 2020, 92, 106268. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. A probabilistic heuristic for a computationally difficult set covering problem. Oper. Res. Lett. 1989, 8, 67–71. [Google Scholar] [CrossRef]
- Feo, T.A.; Resende, M.G. Greedy Randomized Adaptive Search Procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef] [Green Version]
- An, N.T.; Dong, P.D.; Qin, X. Robust feature selection via nonconvex sparsity-based methods. J. Nonlinear Var. Anal. 2021, 5, 59–77. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y. Integrated Methods for Optimization, 2nd ed.; Springer: New York, NY, USA, 2012; Volume 146, p. 648. [Google Scholar] [CrossRef]
- Gendreau, M.; Iori, M.; Laporte, G.; Martello, S. A Tabu Search heuristic for the vehicle routing problem with two-dimensional loading constraints. Networks 2008, 51, 4–18. [Google Scholar] [CrossRef] [Green Version]
- Christofides, N.; Whitlock, C. An Algorithm for Two-Dimensional Cutting Problems. Oper. Res. 1977, 25, 30–44. [Google Scholar] [CrossRef] [Green Version]
- Burke, E.K.; Kendall, G.; Whitwell, G. A New Placement Heuristic for the Orthogonal Stock-Cutting Problem. Oper. Res. 2004, 52, 655–671. [Google Scholar] [CrossRef] [Green Version]
- Bengtsson, B.E. Packing rectangular pieces—A heuristic approach. Comput. J. 1982, 25, 353–357. [Google Scholar] [CrossRef] [Green Version]
- Hopper, E.; Turton, B.C. A review of the application of meta-heuristic algorithms to 2D strip packing problems. Artif. Intell. Rev. 2001, 16, 257–300. [Google Scholar] [CrossRef]
- Hopper, E.; Turton, B.C.H. Problem Generators for Rectangular packing problems. Stud. Inform. Univ. 2002, 2, 123–136. [Google Scholar]
- Beasley, J.E. An Exact Two-Dimensional Non-Guillotine Cutting Tree Search Procedure. Oper. Res. 1985, 33, 49–64. [Google Scholar] [CrossRef]
- Beasley, J.E. Algorithms for unconstrained two-dimensional guillotine cutting. J. Oper. Res. Soc. 1985, 36, 297–306. [Google Scholar] [CrossRef]
- Berkey, J.O.; Wang, P.Y. Two-Dimensional Finite Bin-Packing Algorithms. J. Oper. Res. Soc. 1987, 38, 423–429. [Google Scholar] [CrossRef]
- Ferreira, E.; Oliveira, J. Algorithm based on graphs for the non-guillotinable two-dimensional packing problem. In Proceedings of the Second ESICUP Meeting, Southampton, UK, 1 January 2005. [Google Scholar]
- Babu, A.R.; Babu, N.R. Effective nesting of rectangular parts in multiple rectangular sheets using genetic and heuristic algorithms. Int. J. Prod. Res. 1999, 37, 1625–1643. [Google Scholar] [CrossRef]







| Differences between Approaches | |
|---|---|
| GRASPSPP (Our proposal) | Reactive GRASP [20] |
| Simple GRASP | Use of reactive GRASP |
| Use of flags | Use of best fit (BF) |
| Overlap functions | Evaluate and rearrange the solution |
| Height and width measurement functions | Use of floating accommodations |
| Avoid floating objects | - |
| New Branch and Bound [21] | Iterative Search [24] |
| Use of Branch and Bound | Use of first-fit |
| GRASP for improvements | Arrangement in open space |
| Evaluate and rearrange the solution | Change solutions |
| Floating objects | Use of random local search |
| Waste space validation | Combination of 2D-SPP and CVRP |
| Branch and Bound [19] | Two-stage ISA [22] |
| Use of Branch and Bound | Use of search algorithm |
| Available space by two points | GRASP makes improvements |
| Arrangements by constraints | Accommodations in six dynamic spaces |
| Height and width evaluation | Width measurement |
| Branches reduction by selection | - |
| Name | Autor | Total | n |
|---|---|---|---|
| 2lcvrp | Gendreau [30] | 180 | 15–255 |
| Chr/cgcut | Christofides & Whitlock [31] | 3 | 10–70 |
| Brk/N1-13 | Burke [32] | 13 | 10–500 |
| Ben/beng | Bengtsson [33] | 10 | 20–200 |
| Htu/ht | Hopper and Turton [34] | 114 | 16–28 |
| Hop | Hopper and Turton [35] | 350 | 17–199 |
| Bea/gcut-ngcut | Beasley [36,37] | 25 | 10–22 |
| Class 1–4 | Martello and Vigo [19] | 200 | 20–100 |
| Class 5–10 | Berkey and Wang [38] | 300 | 20–100 |
| 50cx–15,000cx | Pinto and Oliveira [39] | 6 | 50–15,000 |
| P1 | Ramesh Babu [40] | 1 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oviedo-Salas, E.; Terán-Villanueva, J.D.; Ibarra-Martínez, S.; Santiago-Pineda, A.; Ponce-Flores, M.P.; Laria-Menchaca, J.; Castán-Rocha, J.A.; Treviño-Berrones, M.G. GRASP Optimization for the Strip Packing Problem with Flags, Waste Functions, and an Improved Restricted Candidate List. Appl. Sci. 2022, 12, 1965. https://doi.org/10.3390/app12041965
Oviedo-Salas E, Terán-Villanueva JD, Ibarra-Martínez S, Santiago-Pineda A, Ponce-Flores MP, Laria-Menchaca J, Castán-Rocha JA, Treviño-Berrones MG. GRASP Optimization for the Strip Packing Problem with Flags, Waste Functions, and an Improved Restricted Candidate List. Applied Sciences. 2022; 12(4):1965. https://doi.org/10.3390/app12041965
Chicago/Turabian StyleOviedo-Salas, Edgar, Jesús David Terán-Villanueva, Salvador Ibarra-Martínez, Alejandro Santiago-Pineda, Mirna Patricia Ponce-Flores, Julio Laria-Menchaca, José Antonio Castán-Rocha, and Mayra Guadalupe Treviño-Berrones. 2022. "GRASP Optimization for the Strip Packing Problem with Flags, Waste Functions, and an Improved Restricted Candidate List" Applied Sciences 12, no. 4: 1965. https://doi.org/10.3390/app12041965
APA StyleOviedo-Salas, E., Terán-Villanueva, J. D., Ibarra-Martínez, S., Santiago-Pineda, A., Ponce-Flores, M. P., Laria-Menchaca, J., Castán-Rocha, J. A., & Treviño-Berrones, M. G. (2022). GRASP Optimization for the Strip Packing Problem with Flags, Waste Functions, and an Improved Restricted Candidate List. Applied Sciences, 12(4), 1965. https://doi.org/10.3390/app12041965







