Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method
Abstract
Featured Application
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
1.3. Organization
2. Problem Formulation
2.1. Notation
2.2. UAV Dynamics Model
2.3. Problem Statement
- 1.
- The UAV and obstacle are seen as spheres with radii , respectively;
- 2.
- The obstacle mentioned in this article is assumed to be a moving but non-maneuvering obstacle;
- 3.
- Suppose sensors mounted on the UAV can accurately provide measurements, such as locations , velocities and radii of the UAV itself and obstacles;
- 4.
- The control system cycle is consistent with the detection system cycle;
- 5.
- The influence of wind is ignored during the flight of the UAV to simplify the problem.
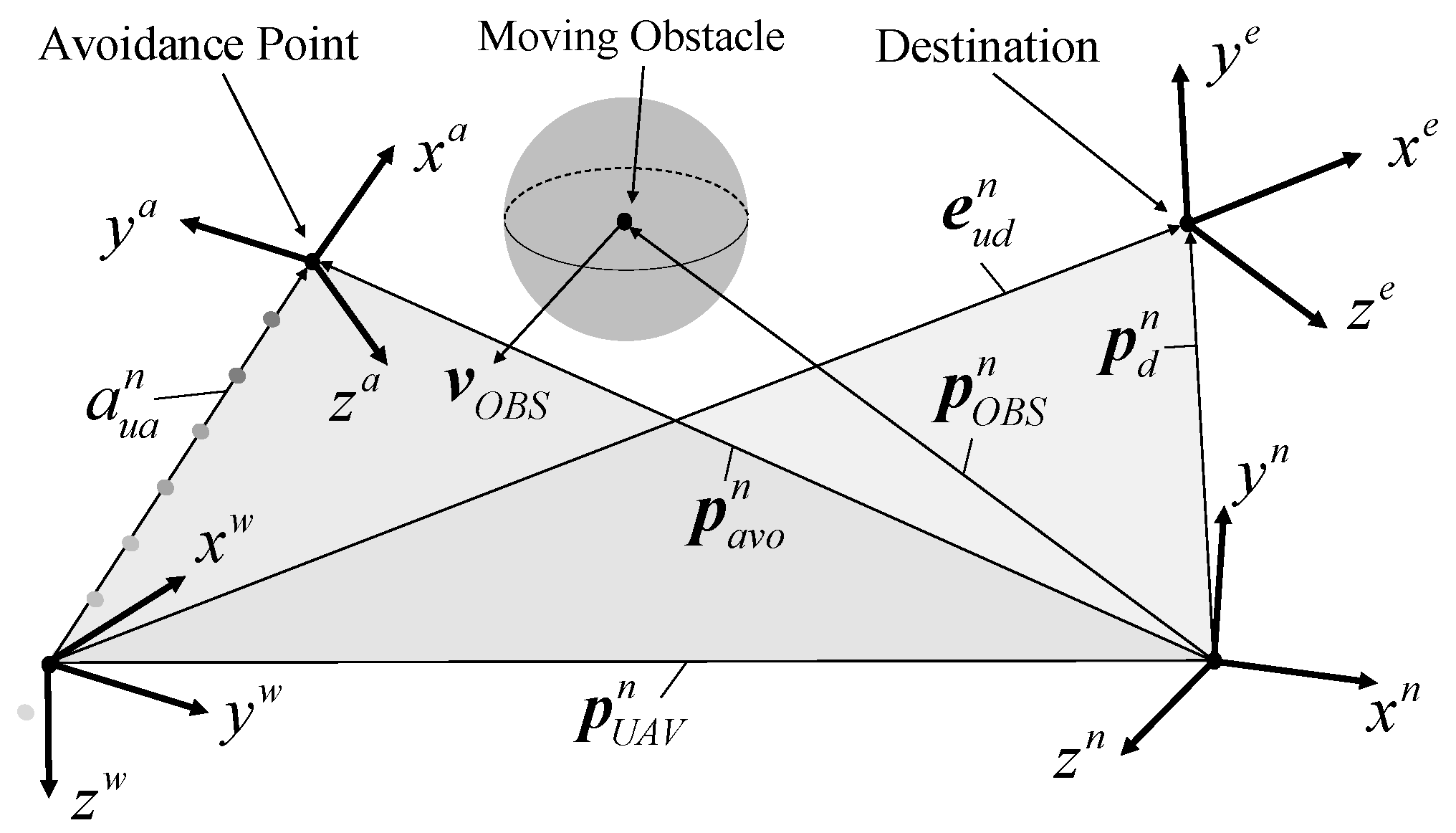
3. Improved 3D-VO Method for UAV Collision Avoidance
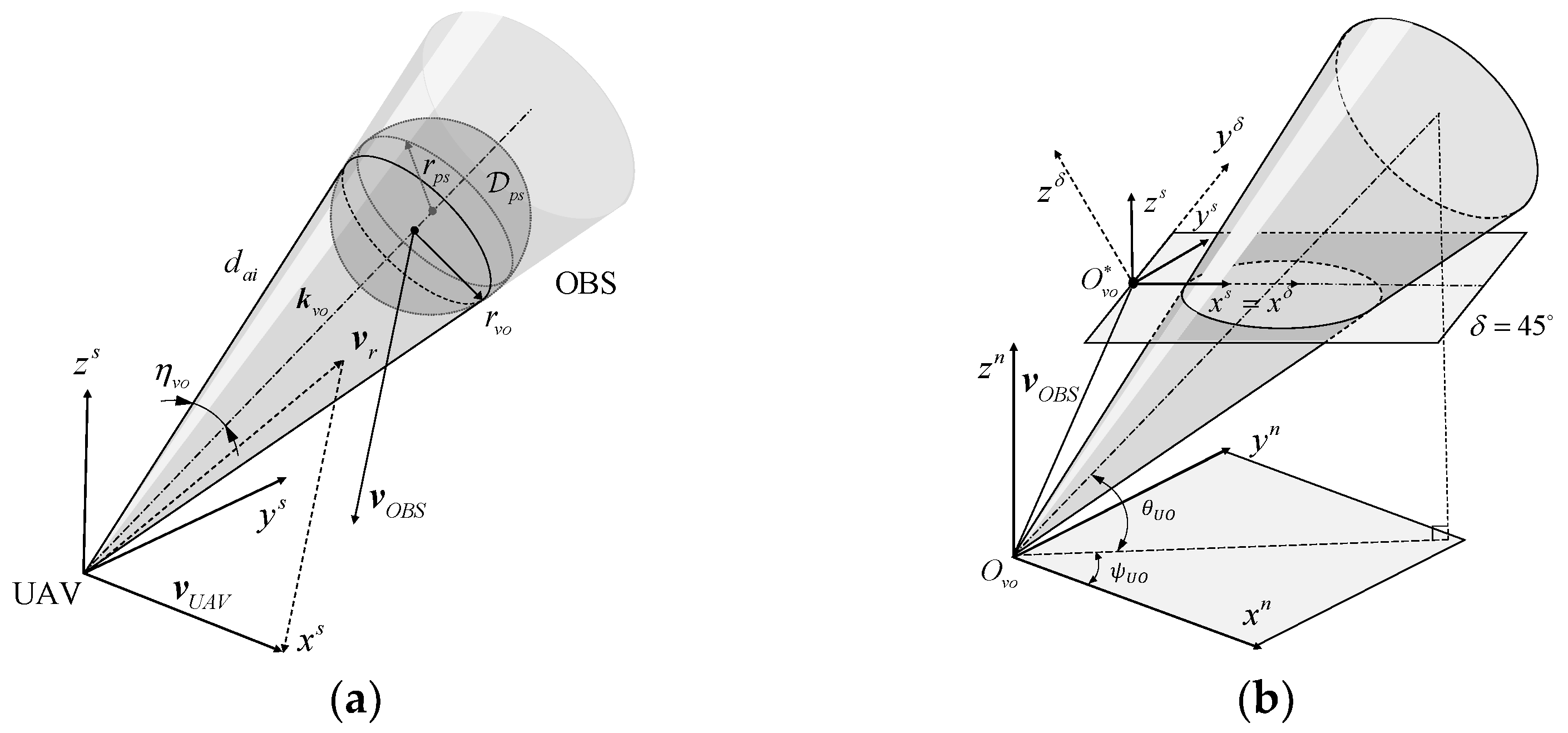
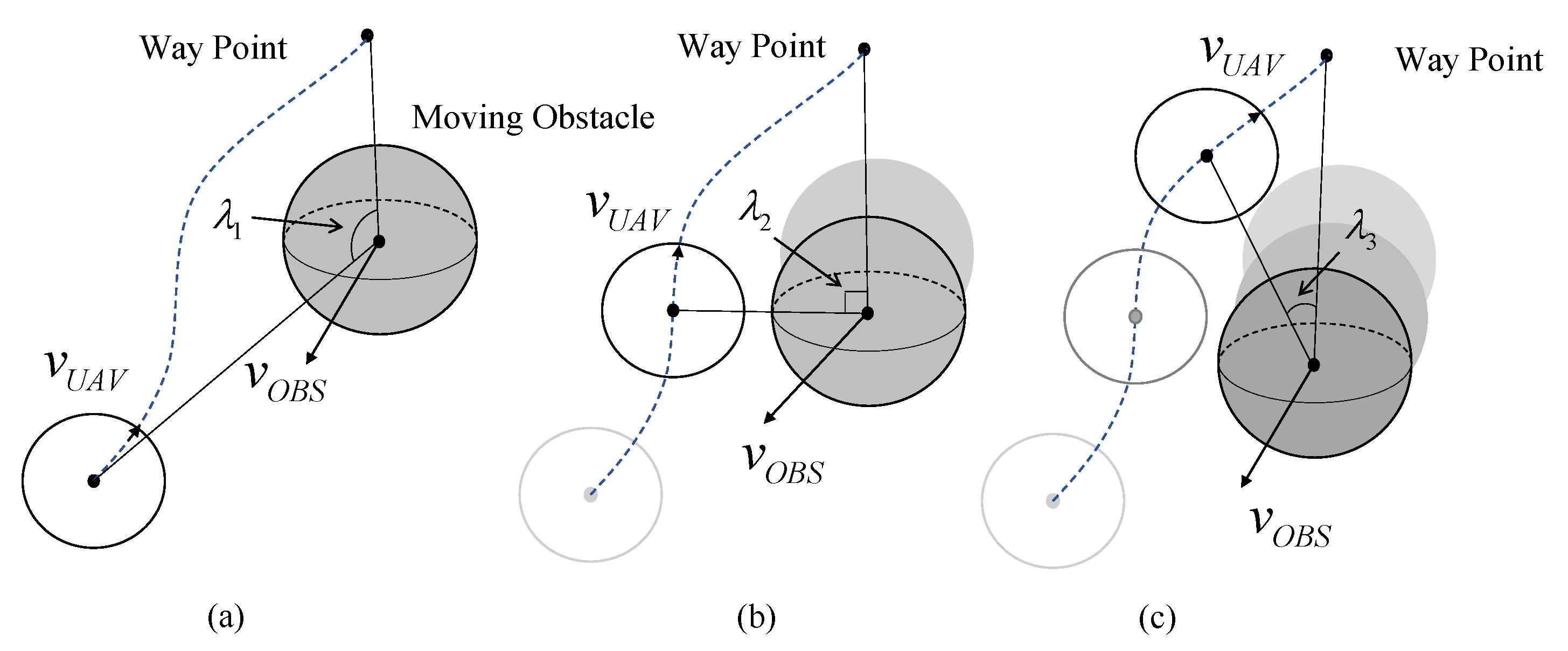
3.1. Formation of 3D-Velocity Obstacle Set
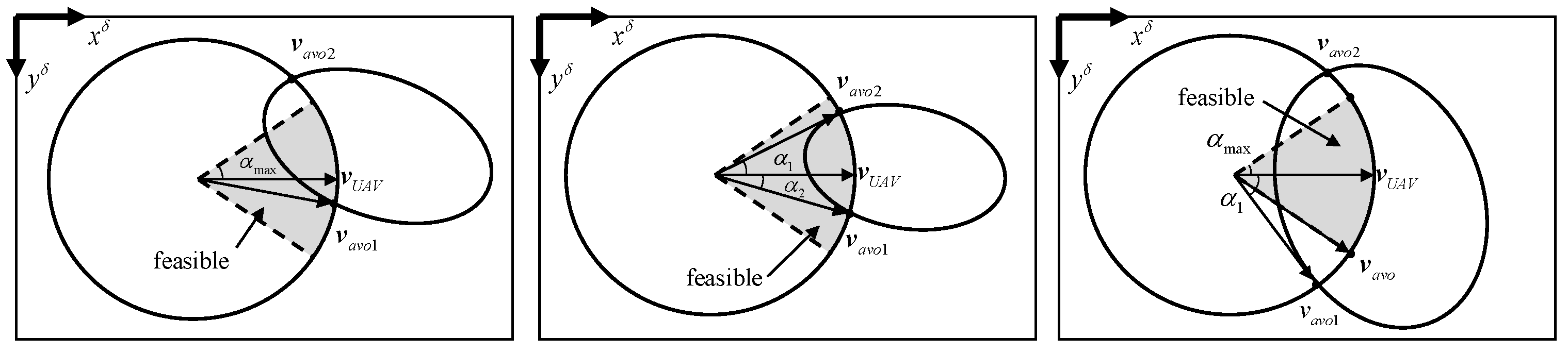
3.2. Avoidance Planes
3.3. Avoidance Velocity
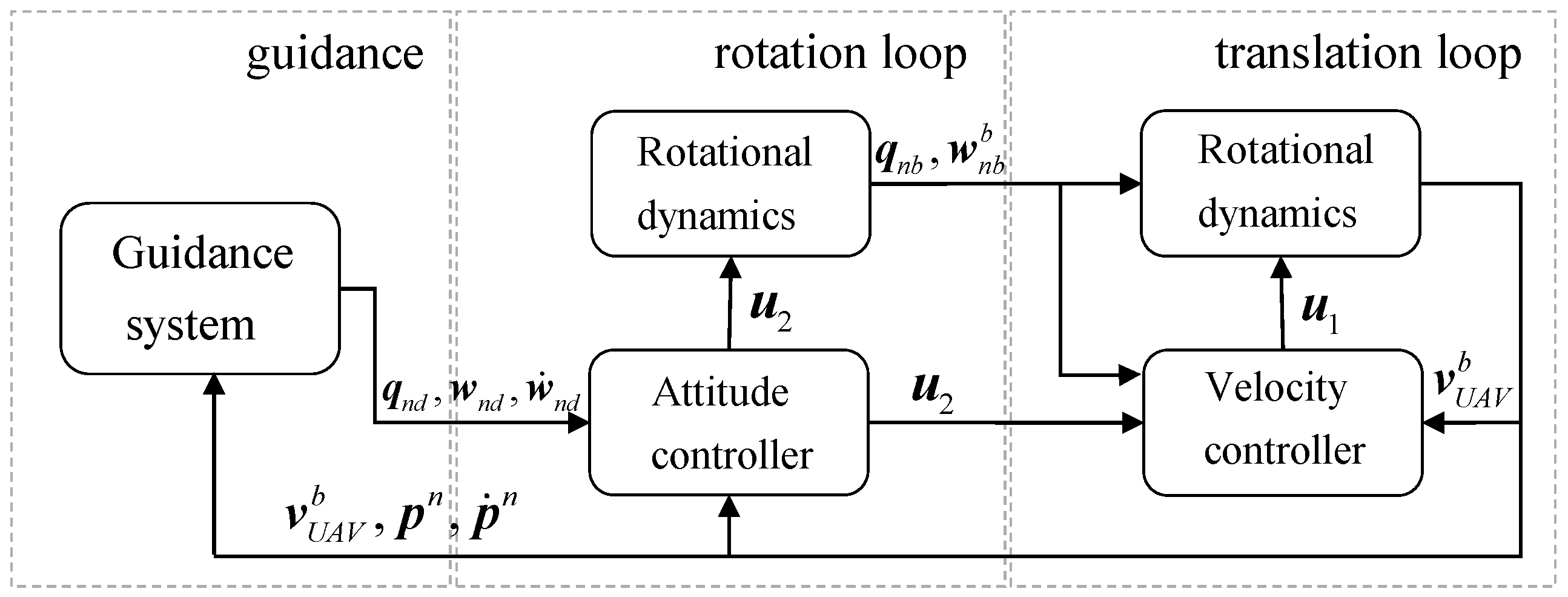
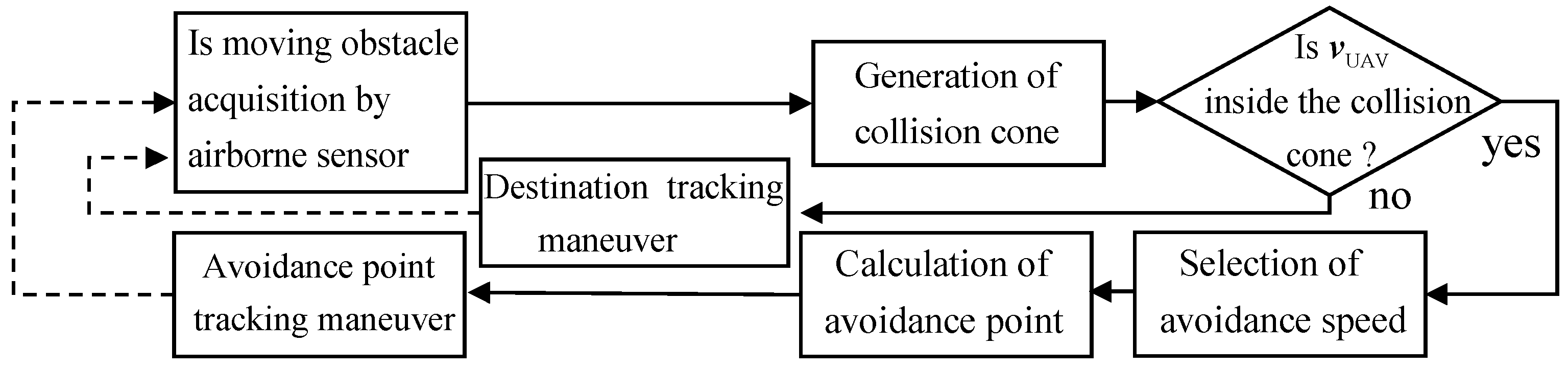
4. Multiple Task Implementation Using a Hierarchical Architecture
4.1. Task Quaternion 1: Destination Point Tracking
4.2. Task Quaternion 2: Collision Avoidance
5. Attitude and Velocity Control Commands
5.1. Velocity Controller
5.2. Attitude Controller
| Algorithm 1. Attidude and Velocity Commands at the K-th Step |
| 1. design parameter: |
| 2. Input: |
| 3. Output: |
| 4. begin |
| 5. obtain by substituting into Equations (26)–(33) |
| 6. if and meet the conditions: Equation (15) then |
| 7. for each δ in , do |
| 8. Solution of quadratic Equation (23) with constrain Equation (22) |
| 9. if feasible Section(δ) = ’Ture’ |
| 10. |
| 11. end if |
| 12. end for |
| 13. if then |
| 14. select with the smallest rotation angle α |
| 15. return |
| 16. // If , the needs to be extended |
| 17. end |
| 18. Map to following Equation (25), Equations (34)–(38) |
| ←Equation (39) |
| 19. else |
| 20. Equation (39) |
| 21. end if |
| 22. Compute velocity command following Equations (40)–(44) |
| 23. Compute Attitude command following Equations (46)–(51) |
| 24. Apply controls |
| 25. end |
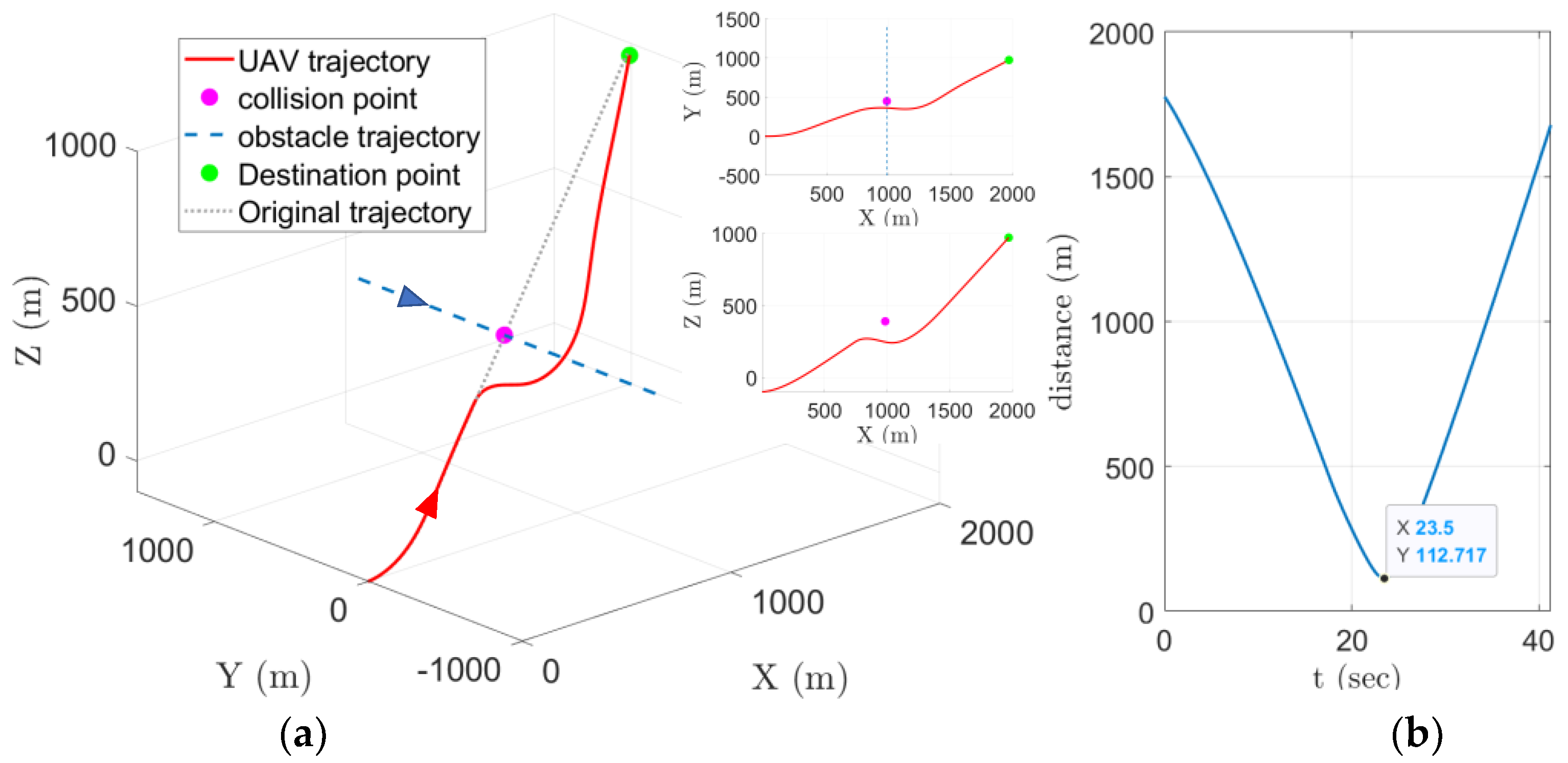
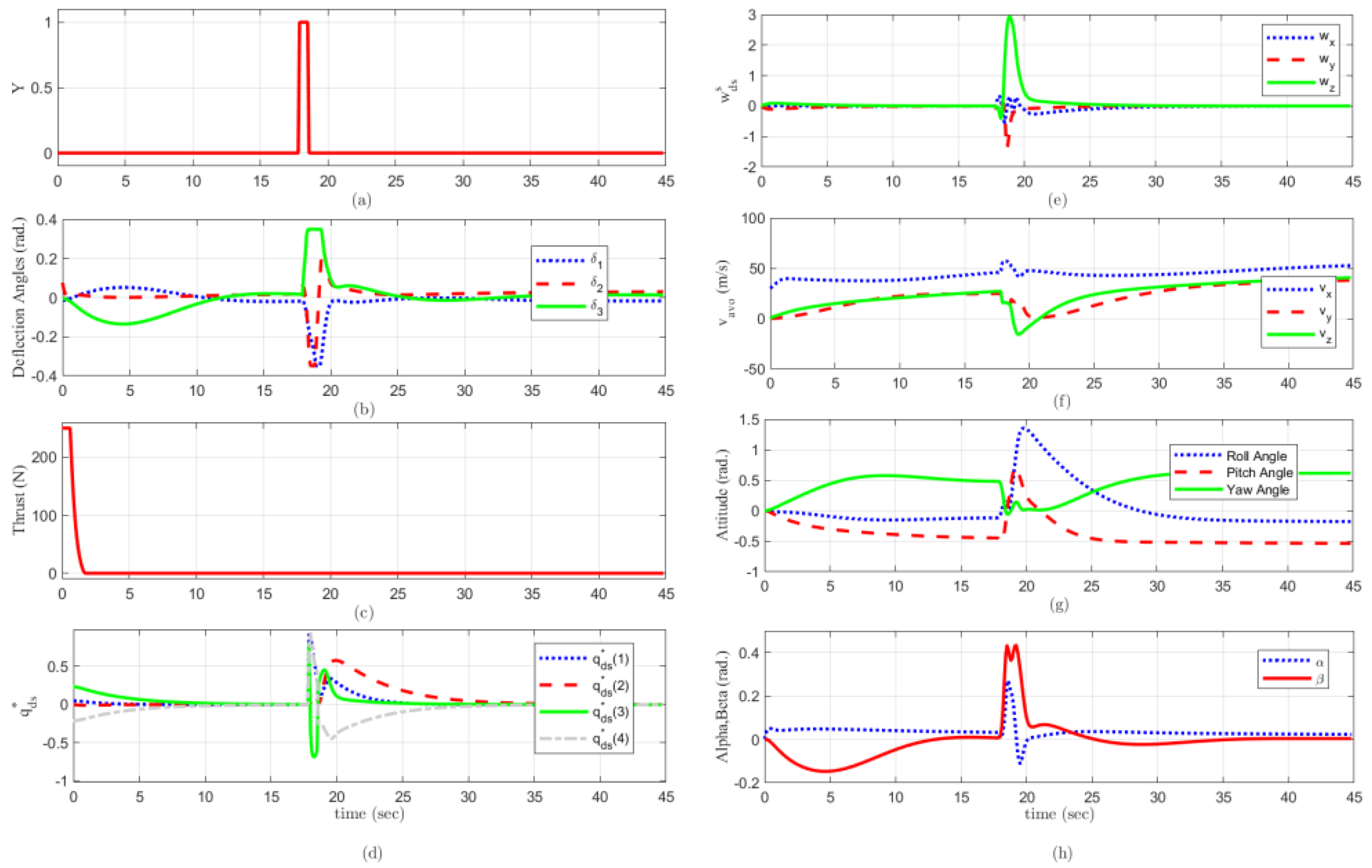
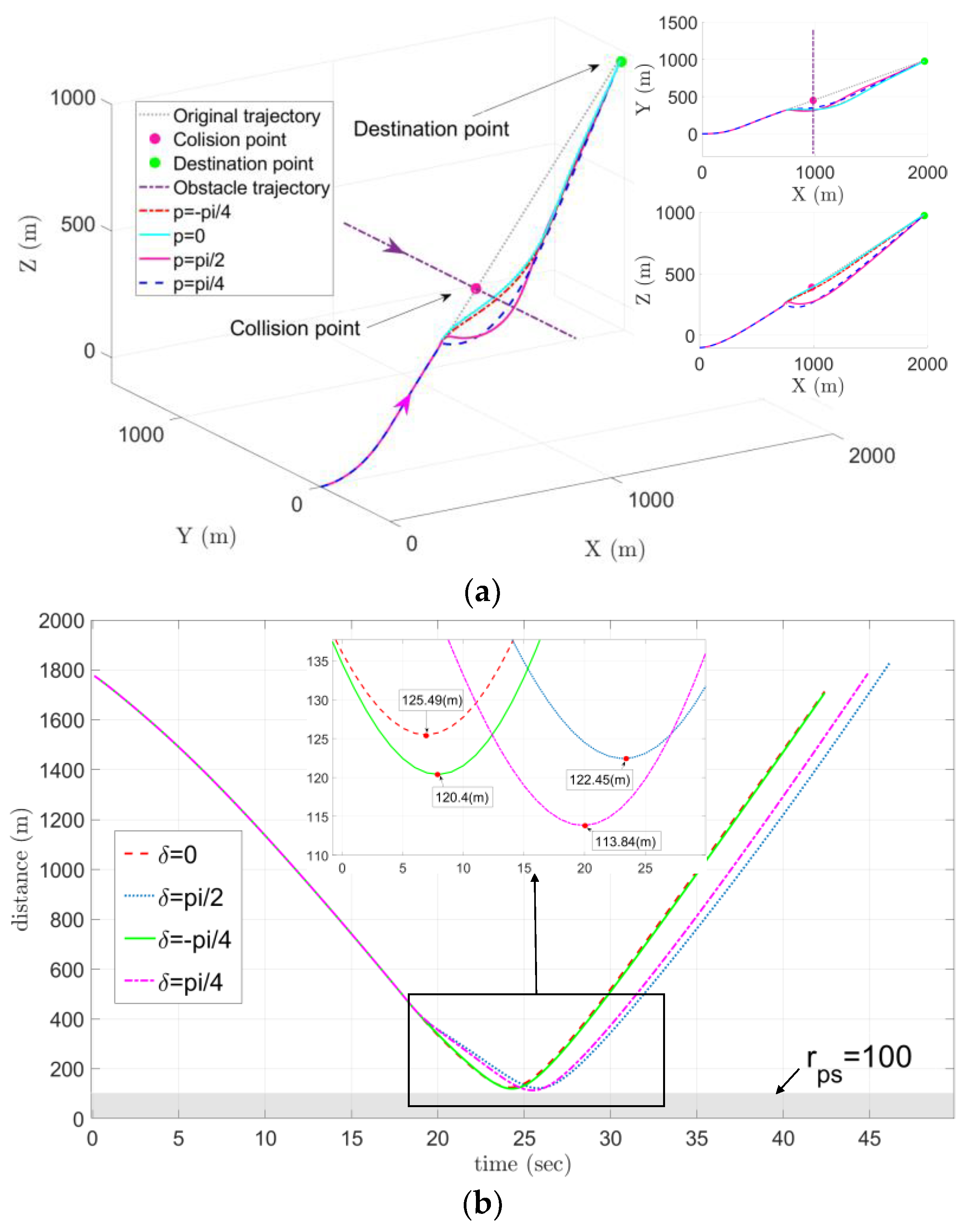
6. Simulation
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Yan, B.; Yue, Y. Path planning and collision avoidance in unknown environments for usvs based on an improved d* Lite. Appl. Sci. 2021, 11, 7863. [Google Scholar] [CrossRef]
- Oland, E.; Andersen, T.S.; Kristiansen, R. Subsumption architecture applied to flight control using composite rotations. Automatica 2016, 69, 195–200. [Google Scholar] [CrossRef][Green Version]
- Moe, S.; Antonelli, G.; Pettersen, K.Y.; Schrimpf, J. Experimental results for set-based control within the singularity-robust multiple task-priority inverse kinematics framework. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics, Zhuhai, China, 6–9 December 2015; pp. 1233–1239. [Google Scholar]
- Moe, S.; Teel, A.R.; Antonelli, G.; Pettersen, K.Y. Stability analysis for set-based control within the singularity-robust multiple task-priority inverse kinematics framework. In Proceedings of the 2015 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 171–178. [Google Scholar]
- Lin, Y.; Saripalli, S. Sampling-Based Path Planning for UAV Collision Avoidance. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3179–3192. [Google Scholar] [CrossRef]
- Fan, Y.; Sun, X.; Wang, G.; Mu, D. Collision Avoidance Controller for Unmanned Surface Vehicle Based on Improved Cuckoo Search Algorithm. Appl. Sci. 2021, 11, 9741. [Google Scholar] [CrossRef]
- Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles. Int. J. Robot. Res. 1998, 17, 760–772. [Google Scholar] [CrossRef]
- Park, S.O.; Lee, M.C.; Kim, J. Trajectory Planning with Collision Avoidance for Redundant Robots Using Jacobian and Artificial Potential Field-based Real-time Inverse Kinematics. Int. J. Control Autom. Syst. 2020, 18, 2095–2107. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Zhang, P. Fixed-wing UAV formation control design with collision avoidance based on an improved artificial potential field. IEEE Access 2018, 6, 78342–78351. [Google Scholar] [CrossRef]
- Choi, D.; Kim, D.; Lee, K. Enhanced potential field-based collision avoidance in cluttered three-dimensional urban environments. Appl. Sci. 2021, 11, 11003. [Google Scholar] [CrossRef]
- Jenie, Y.I.; Van Kampen, E.J.; De Visser, C.C.; Ellerbroek, J.; Hoekstra, J.M. Selective velocity obstacle method for deconflicting maneuvers applied to unmanned aerial vehicles. J. Guid. Control Dyn. 2015, 38, 1140–1145. [Google Scholar] [CrossRef]
- Bareiss, D.; Van Den Berg, J. Generalized reciprocal collision avoidance. Int. J. Robot. Res. 2015, 34, 1501–1514. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Beardsley, P.; Siegwart, R. Cooperative Collision Avoidance for Nonholonomic Robots. IEEE Trans. Robot. 2018, 34, 404–420. [Google Scholar] [CrossRef]
- Wilkie, D.; Van Den Berg, J.; Manocha, D. Generalized velocity obstacles. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 5573–5578. [Google Scholar]
- Alonso-mora, J.; Breitenmoser, A.; Rufli, M.; Beardsley, P.; Siegwart, R. Optimal Reciprocal Collision Avoidance for Multiple Non-Holonomic Robots; Springer: Berlin/Heidelberg, Germany, 2013; Volume 83, pp. 203–216. [Google Scholar]
- Chakravarthy, A.; Ghose, D. Generalization of the collision cone approach for motion safety in 3-D environments. Auton. Robots 2012, 32, 243–266. [Google Scholar] [CrossRef]
- Jenie, Y.I.; Van Kampen, E.J.; De Visser, C.C.; Ellerbroek, J.; Hoekstra, J.M. Three-dimensional velocity obstacle method for uncoordinated avoidance maneuvers of unmanned aerial vehicles. J. Guid. Control Dyn. 2016, 39, 2312–2323. [Google Scholar] [CrossRef]
- Tan, C.Y.; Huang, S.; Tan, K.K.; Teo, R.S.H. Three Dimensional Collision Avoidance for Multi Unmanned Aerial Vehicles Using Velocity Obstacle. J. Intell. Robot. Syst. Theory Appl. 2020, 97, 227–248. [Google Scholar] [CrossRef]
- Van Den Berg, J.; Snape, J.; Guy, S.J.; Manocha, D. Reciprocal collision avoidance with acceleration-velocity obstacles. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3475–3482. [Google Scholar]
- Rufli, M.; Alonso-Mora, J.; Siegwart, R. Recipro collision avoidance with motion continuity constraints. IEEE Trans. Robot. 2013, 29, 899–912. [Google Scholar] [CrossRef]
- Ma, Y.; Manocha, D.; Wang, W. AutoRVO: Local Navigation with Dynamic Constraints in Dense Heterogeneous Traffic. arXiv 2018, arXiv:1804.02915. [Google Scholar]
- Park, J.; Baek, H. Stereo vision based obstacle collision avoidance for a quadrotor using ellipsoidal bounding box and hierarchical clustering. Aerosp. Sci. Technol. 2020, 103, 105882. [Google Scholar] [CrossRef]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints. IEEE Trans. Veh. Technol. 2017, 66, 952–964. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef]
- Arrichiello, F.; Chiaverini, S.; Indiveri, G.; Pedone, P. The null-space-based behavioral control for mobile robots with velocity actuator saturations. Int. J. Robot. Res. 2010, 29, 1317–1337. [Google Scholar] [CrossRef]
- Egeland, O.; Gravdahl, J.T. Modeling and Simulation for Automatic Control; Marine Cybernetics: Trondheim, Norway, 2002; ISBN 9788292356012. [Google Scholar]
- Xiao, S. Multiplication of Quaternion Matrix and Its Feasibility. ACTA Mech. Sin. 1984, 16, 159–166. [Google Scholar]
- Ellerbroek, J.; Brantegem, K.C.R.; Rene Van Paassen, M.M.; Mulder, M. Design of a coplanar airborne separation display. IEEE Trans. Hum.-Mach. Syst. 2013, 43, 277–289. [Google Scholar] [CrossRef][Green Version]
- Oland, E.; Schlanbusch, R.; Kristiansen, R. Underactuated Waypoint Tracking of a Fixed-Wing UAV; IFAC: Compiegne, France, 2013; Volume 2, ISBN 9783902823571. [Google Scholar]
- Guan, J.; Yi, W.J.; Chang, S.J.; Liang, Z.D.; Lyu, Y.P. Study of flight path tracking and control of an UAV in 3D sp7ace. Binggong Xuebao/Acta Armamentarii 2016, 37, 64–70. [Google Scholar]
- Oland, E.; Kristiansen, R. Trajectory tracking of an underactuated fixed-wing UAV. AIP Conf. Proc. 2014, 1637, 1345–1354. [Google Scholar]


| Fixed-Wing UAV | 3D-VO Collision Avoidance | Control System | |||
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, Y.; Yi, W. Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method. Appl. Sci. 2022, 12, 955. https://doi.org/10.3390/app12030955
Qu Y, Yi W. Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method. Applied Sciences. 2022; 12(3):955. https://doi.org/10.3390/app12030955
Chicago/Turabian StyleQu, Yue, and Wenjun Yi. 2022. "Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method" Applied Sciences 12, no. 3: 955. https://doi.org/10.3390/app12030955
APA StyleQu, Y., & Yi, W. (2022). Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method. Applied Sciences, 12(3), 955. https://doi.org/10.3390/app12030955





