Three-Dimensional Obstacle Avoidance Strategy for Fixed-Wing UAVs Based on Quaternion Method

Featured Application

This work provides a generalization of the velocity obstacle (VO) collision avoidance strategy to nonlinear second-order underactuated systems in three-dimensional dynamic uncertain environments.

Abstract

This work provides a generalization of the three-dimensional velocity obstacle (VO) collision avoidance strategy for nonlinear second-order underactuated systems in three-dimensional dynamic uncertain environments. A hierarchical architecture is exploited to deal with conflicting multiple subtasks, which are defined as several rotations and are parameterized by quaternions. An improved VO method considering the kinodynamic constraints of a class of fixed-wing unmanned aerial vehicles (UAV) is proposed to implement the motion planning. The position error and velocity error can be mapped onto one desired axis so that, only relying on an engine, UAVs can achieve the goal of point tracking without collision. Additionally, the performance of the closed-loop system is demonstrated through a series of simulations performed in a three-dimensional manner.

1. Introduction

In recent years, fixed-wing UAVs have gained growing applications in the civilian field as well as military fields, such as search, mapping, rescue, surveillance, and patrol. These applications commonly require the UAV to autonomously track predefined waypoints or prescribed trajectories. In addition, the autonomous detection of potential threats and an online obstacle avoidance algorithm are necessary for UAVs to ensure adequate security [1]. Accordingly, the control problem of UAVs is a multi-objective issue, which indicates that it is extremely important to introduce an integrated approach, taking into account global navigation as well as the local potential obstacle avoidance simultaneously. However, fixed-wing UAVs are typical underactuated systems with nonholonomic constraints, and it is still a challenging problem to develop a guidance framework when facing such a system.

Another important case is that UAVs need to perform multiple tasks, especially as there exist conflicts in sub-tasks, which motivates us to carry out our research. To this end, we introduce a hierarchical architecture [2,3,4] to cope with an arbitrary number of subtasks.

1.1. Related Works

Substantial research on motion planning for UAVs has been conducted, including sampling-based methods [5] and search-based methods [6]. For UAVs, the methods mentioned above are not directly applicable since they heavily rely on target prior information and large-scale iteration.

In view of the aforementioned considerations, reactive collision avoidance methods have been utilized to tackle the motion planning problem of systems with limited computing resources. The VO method was first proposed in [7], and it was originally developed for moving obstacles, considering the velocity of each obstacle in the environment. Since the VO method computes the avoidance velocity reactively based on the instantaneous geometric relationship of collisions, target prior information becomes needless. Compared with other reactive collision avoidance methods, such as artificial potential field (APF) methods [8,9,10], the VO method guarantees a lower computational cost and is less prone to problems with local minimums. Refs. [11,12,13] extend VO methods to heterogeneous agents. Ref. [11] relies on specific implicit coordination, Ref. [12] assumes that agents have the same type of control input, and Ref. [13] depends on an abstraction kinodynamic model of the robot; the latter makes the VO algorithm truly independent of the model. VO methods were further extended to the system with non-holonomic constraints by testing the optimality of sampling control [14], by mapping between the holonomic speed and the nonholonomic control input [15]. The latter guarantees a lower computational cost. Following the concept proposed in Ref. [15], we map the avoidance velocity to the nonholonomic control input. Thanks to the contributions of Refs. [16,17] on the three-dimensional velocity obstacle (3D-VO) method, the range of feasible solutions (obstacle avoidance velocity or acceleration) has been significantly expanded. Our method builds on the concept proposed in [17] which was successfully verified by experiments for collision avoidance with static obstacles [18] and extended to the dynamic system with nonholonomic constraints. The approaches mentioned above directly update velocities to avoid moving obstacles, and thus, it is summarized as the first-order method. Actually, compared with the quadcopter, the fixed-wing UAV cannot instantly change the direction of the velocity vector. Instead of computing an avoidance velocity command, it is possible to produce an avoidance acceleration that ensures that the collision avoidance can always be maintained.

A systematical extension of VO methods to second-order or higher-order systems has been conducted [12,13,19,20,21]. However, the aforementioned approaches contain some assumptions that limit their application to UAVs, such as only considering the simplified linear robot model, calculating the solution in a two-dimensional plane, and supposing that the robot can implement omni-directional acceleration. In [22], a 3D collision cone was utilized to examine collision condition and rigid quadrotor dynamics were considered. However, the obstacle avoidance only considers static obstacles in the environment. The fixed-wing UAV involved in our research has more complex dynamics. To the best of our knowledge, the extension of the 3D-VO method to a second-order nonlinear dynamic system of an underactuated fixed-wing UAV cannot be found in the literature. Mainly, there are the following difficulties: (1) a fixed-wing UAV is not only a nonholonomic system, but also a kinodynamic constrained nonholonomic system. It must take explicitly into account this nature of UAVs in planning strategies. However, collision avoidance may then no longer be guaranteed. (2) The dynamics of a fixed-wing UAV is represented as a second-order nonlinear differential equation with variable coefficients, which make it extremely difficult to directly derive a feasible velocity set or acceleration set, as described in [12,19,20].

1.2. Contributions

(1) Inspired by the work [19], we incorporate second-order kinodynamic constraints into the velocity by limiting the set of feasible velocities to those that can be achieved with position error below a predefined value. A reference trajectory resulting from the 3D-VO approach can be retained as formulated in [20]. We derive the control input of the velocity loop as well as the attitude loop to enable the UAV to converge to the reference trajectory, such that the motion planning problem can be transformed into a trajectory tracking problem, which has been extensively studied [23,24]. Since the derivation of the reference trajectory does not directly depend on the kinodynamic model of the UAV, complex derivation of control obstacles (CO) [20] or acceleration–velocity obstacles (AVO) [19] can be avoided.

(2) The additional tasks add to the overall flexibility of the UAV. Inspired by the concept of behavior-based control [2,25], we establish a guidance framework, where multi-tasks are arranged according to a hierarchy plan and conducted in a desired priority. The subtasks can be defined as velocity vectors as presented in [25]. In line with the conventional behavior-based approaches and similar to the approach proposed in [2], we decompose the overall mission into several rotations, which are parameterized by quaternions.

1.3. Organization

The rest of the paper is organized as follows. In Section 2, we give some important definitions, the dynamic model of a fixed-wing UAV, and the problem statement. In Section 3, we introduce an improved 3D-VO method for the UAV collision avoidance. In Section 4, a hierarchical architecture to deal with the multiple task is represented. In Section 5, we describe in detail the design of the translation loop and attitude loop controllers. The results presented in this paper are illustrated by a series of simulations in Section 6. The paper ends with conclusion in Section 7.

2. Problem Formulation

2.1. Notation

Matrices are in capital $M$, vectors are in bold $\mathit{x}$, sets are in mathcal $\mathscr{H}$, and the Minkowski sum of two sets is expressed as $\mathscr{H}\oplus ℱ$. The Euclidean norm of vector $\mathit{x}$ is expressed as $\Vert \mathit{x}\Vert$. The superscript indicates the coordinate, and the coordinate systems involved in this article include the inertial coordinate system [26], n; body coordinate system, b; velocity coordinate system, s; error coordinate, e; avoidance coordinate system, a; and desired coordinate system, d.

The conversion between coordinate systems commonly relies on rotation matrixes or quaternions. A velocity vector $v$ in b-frame $v^b={\left[\begin{array}{ccc}{v}_{\mathit{x}}^b& v_y^b& v_z^b\end{array}\right]}^{\mathrm{{\rm T}}}\in {ℝ}^3$ coincides with the x-axis of the s-frame. Then, the velocity vector $v$ in the s-frame is expressed as $v^s={\left[\begin{array}{ccc}\Vert v^b\Vert & 0& 0\end{array}\right]}^{\mathrm{{\rm T}}}=R_b^s{v}^b$, where the rotation matrix

$$R_b^s\in S{O}^3=\left\{R\in {ℝ}^3:R^{\mathrm{{\rm T}}}R={\rm I},\det \left(R\right)=1\right\}$$

(${\rm I}$ is an identity matrix) represents the rotation from frame-b to frame-s. The quaternion is represented by a column matrix:

$$q_{sb}={\left[\begin{array}{cccc}{q}_0& q_1& q_2& q_3\end{array}\right]}^{\mathrm{{\rm T}}}={\left[\begin{array}{cc}{\eta }_{sb}& {\epsilon }_{sb}{}^{\mathrm{{\rm T}}}\end{array}\right]}^{\mathrm{{\rm T}}}={\left[\begin{array}{cc}\cos (\frac{{\theta }_{sb}}{2})& k_{sb}{}^{\mathrm{{\rm T}}}\sin (\frac{{\theta }_{sb}}{2})\end{array}\right]}^{\mathrm{{\rm T}}}$$

where ${\eta }_{sb}$ is a scalar, ${\epsilon }_{sb}\in {ℝ}^3$ is a vector, ${\theta }_{sb}={\cos }^{-1}\left(\frac{v^b·v^s}{{\Vert v^s\Vert }^2}\right)$ represents the rotation angle, and $k_{sb}\in {ℝ}^3=\frac{v^b\times v^s}{\Vert v^b\times v^s\Vert }$ represents the rotation axis. The quaternion and the rotation matrix can be transformed through the equation:

$$R_b^s=I+2{\eta }_{sb}S\left({\epsilon }_{sb}\right)+2S^2\left({\epsilon }_{sb}\right),S\left(v\right)=\left[\begin{array}{ccc}0& -v_3& v_2\\ v_3& 0& -v_1\\ -v_2& v_1& 0\end{array}\right]$$

(1)

Taking the derivative of the rotation matrix, we get ${\dot{R}}_b^s=R_b^{s}S\left(w_{sb}^b\right)$, where is the projection of the rotation of vector b relative to vector c on b.

Quaternion multiplication can deal with the problem of combing finite time rotations of the rigid body. Supposing there are two consecutive rotation quaternions, then they can be combined into an equivalent quaternion through quaternion multiplication: $q\otimes \mathit{p}=M\left(q\right)\mathit{p}$, where $M(·)$ is the quaternion multiplication operator: $M\left(q\right)=\left[\begin{array}{cccc}{q}_0& -q_1& -q_2& -q_3\\ q_1& q_0& q_3& -q_2\\ q_2& -q_3& q_0& q_1\\ q_3& q_2& -q_1& q_0\end{array}\right]$.

Theorem 1.

([27]).If a rigid body makes a finite number of consecutive rotations around the axes that pass the same fixed point, then the size of the composite rotation angle has nothing to do with the order of each continuous rotation, but the direction of the composite rotation is related to the order of each continuous rotation.

That is to say, the final attitude of the rigid body is related to the sequence of continuous rotation, and the position of the composite rotation axis changes with the sequence of continuous rotation.

The rotation of the UAV between two coordinate systems can be disassembled into multiple continuous rotations: $q_{na}=q_{ne}\otimes q_{ea}$, where the formula represents the rotation from frame-a to frame-e, and then to frame-n. According to Theorem 1, defining the current quaternion $q_{ea}$ relative to the previous quaternion $q_{ne}$.guarantees the direction that a vector rotated by $q_{na}$ is pointing in is determine by the last quaternion $q_{ea}$. This inspires us to define each rotation as a subtask and arrange subtasks according to their importance, then combine subtasks into a total task. For example, the task represented by quaternion $q_{ea}$ takes precedence over the task represented by $q_{ne}$. After the high-level task $q_{ea}$ is completed, it will degenerate into a unit quaternion ${\left[\begin{array}{cc}1& {\mathbf{0}}^{\mathrm{{\rm T}}}\end{array}\right]}^{\mathrm{{\rm T}}}$, and its effect on the composite rotation will reduce to zero. Then, the system will proceed to the next task defined as $q_{ne}$.

2.2. UAV Dynamics Model

The dynamic of a fixed-wing UAV is represented by the following equations of motion:

$${\dot{\mathit{p}}}_{UAV}^n=R_b^n{v}_{UAV}^b$$

(2)

$$m{\dot{v}}_{UAV}^b=F_{ag}^b\left(v_{UAV}^b\right)-mS\left(w_{nb}^b\right)v_{UAV}^b+m{\mathit{u}}_1$$

(3)

$$J{\dot{w}}_{nb}^b=M_{at}^b\left(w_{nb}^b,v_{UAV}^b\right)-S\left(w_{nb}^b\right)J{w}_{nb}^b+A{\mathit{u}}_2$$

(4)

In the Equation (2), ${\mathit{p}}_{UAV}^n$ represents the position of the UAV relative to the n-frame, and $v_{UAV}^b={\left[\begin{array}{ccc}{v}_{\mathit{x}}^b& v_y^b& v_z^b\end{array}\right]}^{\mathrm{{\rm T}}}$ is the velocity of the UAV in b-frame. In the Equation (3), m is the quality of the UAV, $F_{ag}^b$ is the combined force of the aerodynamic and gravity forces of the UAV in b-frame, which is a nonlinear function of $v_{UAV}^b$. ${\mathit{u}}_1={\left[\begin{array}{ccc}{T}_{\mathit{x}}^b& 0& 0\end{array}\right]}^{\mathrm{{\rm T}}}$ is the control input of the translation loop, and only includes a thrust of the body. In the Equation (4), J is the inertia matrix, $M_{at}^b$ is the resultant moment of the aerodynamic and thrust moments of the UAV, which is a nonlinear function of $w_{nb}^b,v_{UAV}^b$, and ${\mathit{u}}_2={\left[\begin{array}{ccc}{\varpi }_a& {\varpi }_e& {\varpi }_r\end{array}\right]}^{\mathrm{{\rm T}}}$ is the control input of the rotation loop, denoting the rudder angle.

The guidance system computes a desired quaternion, a desired angular velocity, and a desired angular acceleration. The translation loop and rotation loop solve the control inputs ${\mathit{u}}_1,{\mathit{u}}_2$ to track the desired speed and attitude, respectively. The structure of the UAV controller is shown in Figure 1.

2.3. Problem Statement

Assumption:

1.

The UAV and obstacle are seen as spheres with radii $r_{UAV},r_{OBS}$, respectively;

2.

The obstacle mentioned in this article is assumed to be a moving but non-maneuvering obstacle;

3.

Suppose sensors mounted on the UAV can accurately provide measurements, such as locations ${\mathit{p}}_{UAV},{\mathit{p}}_{OBS}\in {ℝ}^3$, velocities $v_{UAV},v_{OBS}\in {ℝ}^3$ and radii $r_{UAV},r_{OBS}$ of the UAV itself and obstacles;

4.

The control system cycle is consistent with the detection system cycle;

5.

The influence of wind is ignored during the flight of the UAV to simplify the problem.

The UAV and the obstacle are moving in a three-dimensional space $\mathcal{W}={ℝ}^3$. $\mathcal{X}\subset {ℝ}^{m1}$ represents the set of states of the UAV, m1 denotes the dimension of the state space, $\mathcal{U}\subset {ℝ}^{m2}$ represents the set of control input of the UAV, and m2 denotes the dimension of the control input

$$\dot{\mathit{x}}\left(t\right)=f_1\left(\mathit{x}\left(t\right)\right)+f_2\left(\mathit{x}\left(t\right)\right)\mathit{u}\left(t\right)$$

(5)

where $\mathit{x}\in \mathcal{X},\mathit{u}\in \mathcal{U}$, $f_1(\cdot )$ and $f_2(\cdot )$ are nonlinear functions of the state $\mathit{x}$. Given an initial $\mathit{x}\left(t_0\right)$ and a control input $\mathit{u}\left(t\right)$, the state of the robot at time $t\ge t_0$ can be solved. If $\mathrm{rank}\left[f_2\left(\mathit{x}\left(t\right)\right)\right]<\dim \left[\mathit{x}\left(t\right)\right]$, the system described in Equation (5) is said to be underactuated. The position of the UAV ${\mathit{p}}_{\mathrm{UAV}}$ can be derived from $\mathit{x}\left(t_0\right)$ and $\mathit{u}\left(t\right)$:

$${\mathit{p}}_{UAV}\left(t\right)=f_3\left(\mathit{x}\left(t_0\right),\mathit{u}\left(t\right)\right)$$

(6)

where $f_3(\cdot )\in \mathcal{X}\times \mathcal{U}\to {ℝ}^3$. $D\left(\mathit{p},r\right)=\left\{l|\Vert l-\mathit{p}\Vert \le r\right\}$ denotes the area occupied by a sphere, centered at p with radius $r$. Similarly, the airspace occupied by the UAV can be expressed as $O\left({\mathit{p}}_{\mathrm{UAV}}\right)=D\left({\mathit{p}}_{UAV},r_{UAV}\right)\in {ℝ}^3$, where $r_{UAV}$ is the radius of the UAV. This also applies to obstacles $O\left({\mathit{p}}_{OBS}\right)=D\left({\mathit{p}}_{OBS},r_{OBS}\right)\in {ℝ}^3$.

Definition 1.

The UAV will remain collision-free with the obstacle in period$\tau$.

$$O\left({\mathit{p}}_{UAV}\left(t\right)\right)\cap O\left({\mathit{p}}_{OBS}\left(t\right)\right)=\mathrm{\varnothing },\forall t\in \left[\begin{array}{cc}{t}_0& t_0+\tau \end{array}\right)$$

(7)

Definition 2.

The UAV arrives at the destination${\mathit{p}}_{pre}$.

$$e:={\mathit{p}}_{UAV}-{\mathit{p}}_{pre},\Vert e\left(t_0\right)\Vert >\epsilon >0,\exists t>0,\epsilon \le e\left(t\right)\le \mathrm{\Lambda }$$

(8)

When $\Vert e\left(t\right)\Vert \le \mathrm{\Lambda }$, we conclude that the UAV has arrived at the destination point. To achieve Definitions 1 and 2, we define a desired frame-d and make the frame-s align with the desired frame-d by controlling the attitude and speed of the UAV. Quaternions $q_{ea}$ and $q_{ne}$ are used to represent the obstacle avoidance and target tracking sub-task, respectively, and then the quaternion multiplication $q_{na}=q_{ne}\otimes q_{ea}$ is utilized to combine these sub-tasks into a total task, which is defined as the desired quaternion, $q_{nd}\text{:}:=q_{na}$. The purpose of this work can be defined as follows: given the initial state $\mathit{x}\left(t_0\right)$ and the information of the obstacle, computing a control input $\mathit{u}\left(t\right)$ for the UAV, such that

$$q_{nd}\to {\left[\begin{array}{cc}1& {\mathbf{0}}^{\mathrm{{\rm T}}}\end{array}\right]}^{\mathrm{{\rm T}}}$$

(9)

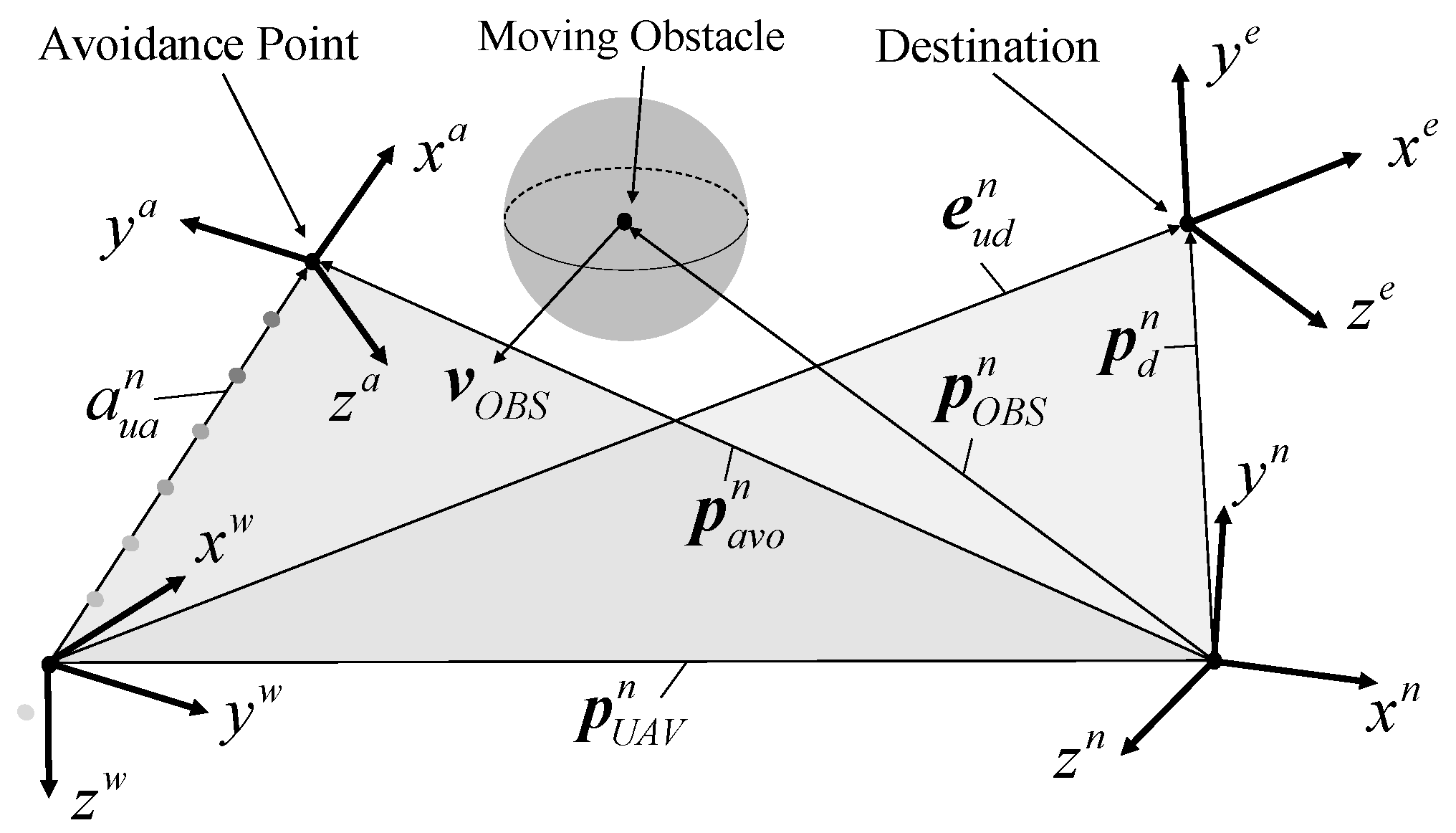
3. Improved 3D-VO Method for UAV Collision Avoidance

Under the guidance framework proposed in this work, all subtasks are described by position vectors in the n-frame. In this section, we introduce obstacle avoidance points resulting from the improved 3D-VO algorithm.

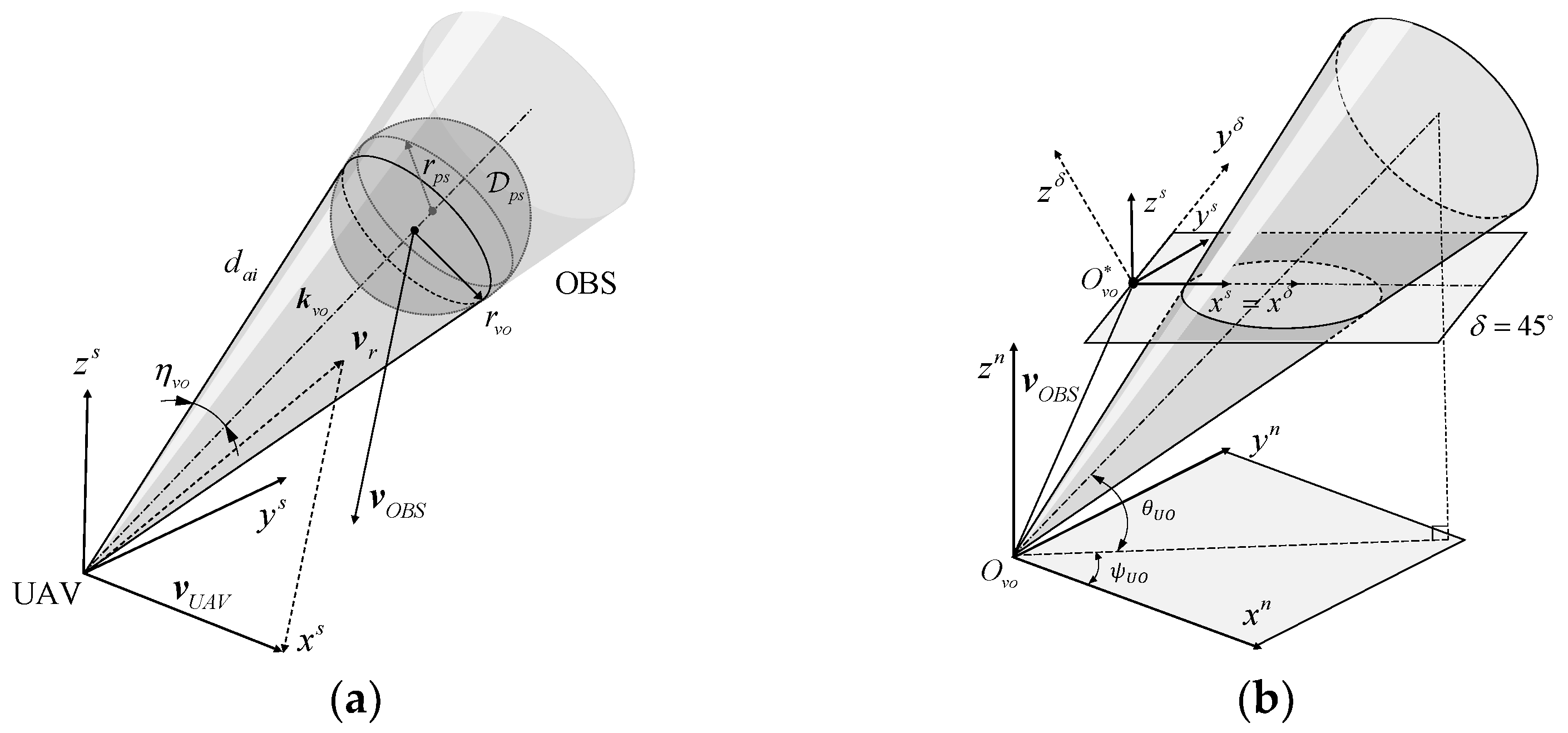
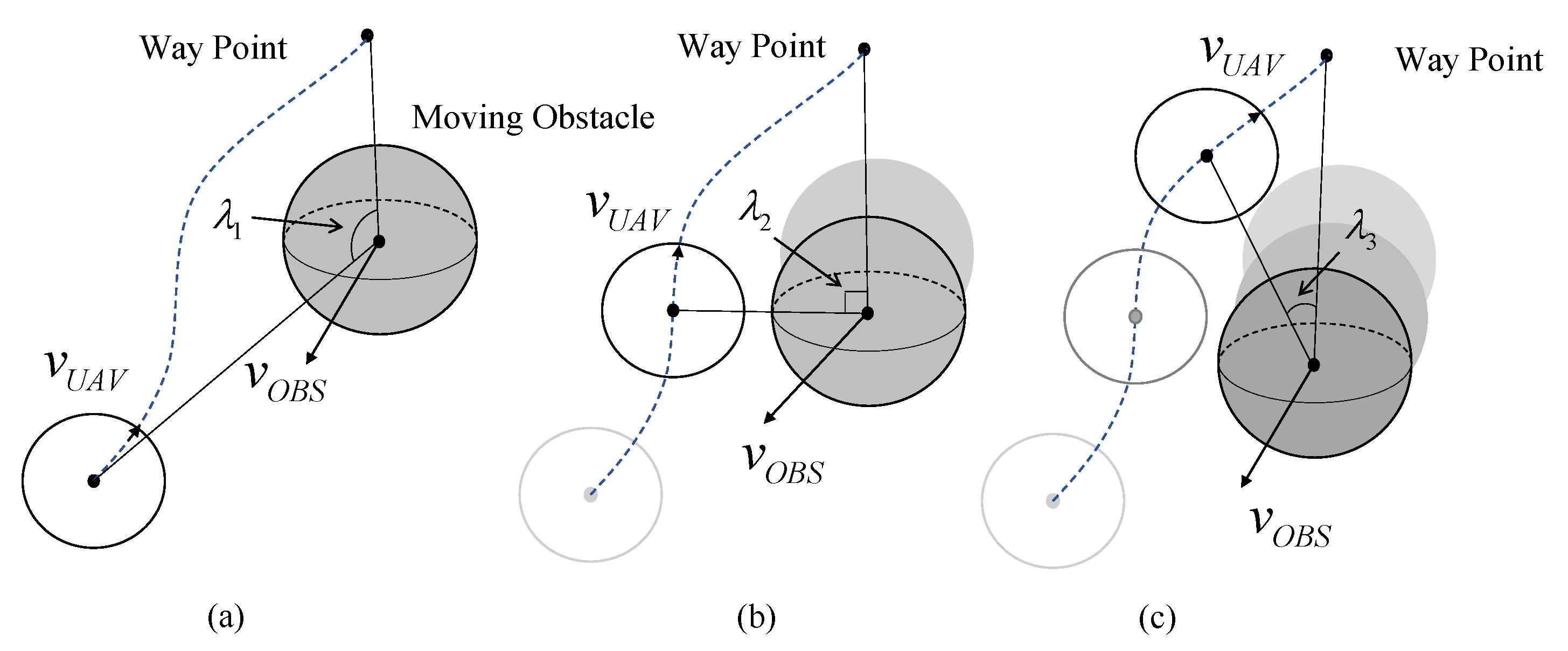
3.1. Formation of 3D-Velocity Obstacle Set

For UAVs, 3D-VO [17] methods define the set of velocities that will collide with moving obstacles within the time horizon $\tau$. The set is denoted by $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$:

$$\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)=\left\{v_{UAV}|\mathcal{R}\left({\mathit{p}}_{UAV},v_{UAV}-v_{OBS}\right)\cap \left(\mathcal{D}\left({\mathit{p}}_{UAV},r_{UAV}\right)\oplus \mathcal{D}\left({\mathit{p}}_{OBS},r_{OBS}\right)\right)\ne \varnothing \right\}$$

(10)

where $\mathcal{R}\left(\mathit{p},v\right)=\left\{\mathit{p}+tv|t>0\right\}$ includes the rays with the starting point $\mathit{p}$ and the direction $v$. The UAV will not collide with the moving obstacle with velocity $v_{OBS}$ when $v_{UAV}$ lies outside $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$. The geometry of $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$ is a cone. Related parameters are shown in Equation (11).

$$\{\begin{array}{c}{O}_{vo}=v_{OBS},d_{ai}=\sqrt{d_{uo}^2-r_{ps}^2}\\ d_{vo}=\frac{d_{ai}^2}{d_{uo}},r_{vo}=r_{ps}\frac{d_{ai}^{}}{d_{uo}}\\ {\eta }_{vo}=\arcsin \left(\frac{r_{vo}}{d_{ai}}\right)\\ k_{vo}=\left[\begin{array}{l}\cos {\theta }_{uo}\cos {\psi }_{uo}\\ \cos {\theta }_{uo}\sin {\psi }_{uo}\\ \hfill \sin {\theta }_{uo}\hfill \end{array}\right]d_{vo}\end{array}$$

(11)

where $d_{uo}$ is the distance between the UAV and the moving obstacle, $k_{vo}$ and ${\eta }_{VO}$ represent the axis and the half angle of the cone, respectively, as shown in Figure 2a. The position of the obstacle is described by the spherical coordinates relative to frame-n. The vertex $O_{VO}$ of the cone is translated from the position $O_{vo}^{\ast }$ of the UAV along $v_{OBS}$, as shown in Figure 2b.

A standard cone parametric equation is illustrated in Equation (12)

$$\left[\begin{array}{c}{x}_c^{}\\ y_c^{}\\ z_c^{}\end{array}\right]=\left[\begin{array}{c}q\\ q\tan {\eta }_{vo}\cos \phi \\ q\tan {\eta }_{vo}\sin \phi \end{array}\right]$$

(12)

where $q\in \left[0,d_{VO}\right]$, $\phi \in \left[0,2\pi \right]$. Further, it is necessary to rotate the above cone twice to align its cone axis with $k_{vo}$ and translate along $v_{OBS}$ until the vertex coincides with $O_{vo}$. Finally, we obtain the geometry of $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$, which is called the VO cone. This process is represented by Equation (13).

When the distance $d_{uo}$ between the UAV and the obstacle below the safety threshold distance $d_{safe}$($d_{safe}>r_{UAV}+r_{OBS}$), $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$ is updated in real time to determine whether the collision will happen in the future. This is mainly based on whether the positive extension of $v_{UAV}$ is inside the VO cone.

$$\left[\begin{array}{c}{x}_{VO}^{}\\ y_{VO}^{}\\ z_{VO}^{}\end{array}\right]=\left[\begin{array}{ccc}\cos {\psi }_{UO}& \sin {\psi }_{UO}& 0\\ -\sin {\psi }_{UO}& \cos {\psi }_{UO}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos {\theta }_{UO}& 0& -\sin {\theta }_{UO}\\ 0& 1& 0\\ \sin {\theta }_{UO}& 0& \cos {\theta }_{UO}\end{array}\right]\left[\begin{array}{c}{x}_c^{}\\ y_c^{}\\ z_c^{}\end{array}\right]+O_{vo}$$

(13)

$$\{\begin{array}{c}{d}_{UO}\le d_{safe}\\ [v_{UAV}-O_{vo}]’k_{vo}>\cos {\eta }_{vo}\Vert v_{UAV}-O_{vo}\Vert \end{array}$$

(14)

If the condition in Equation (14) is satisfied, the positive extension of $v_{UAV}$ is inside the VO cone, then the set of avoidance velocities further generate $\mathcal{A}{\mathcal{V}}_{UAV|OBS}=W\text{}\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$. When the avoidance velocity $v_{avo}$ of the UAV in the next time horizon belongs to $\mathcal{A}{\mathcal{V}}_{UAV|OBS}$, the collision can be avoided. The solution of $v_{avo}$ is introduced in Section 4.2. The termination of obstacle avoidance mode cannot be judged by $v_{UAV}\notin \mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$ alone. When the obstacle avoidance mode is nearing the end, it is often the moment that the distance is close to the minimum, which can easily distort the VO cone, resulting in failing to find the correct obstacle avoidance velocity and even causing the control commands of the UAV chattering. Consequently, we introduce a $\lambda$ angle, which is the angle between two vectors. The stage shown in Figure 3a is the initial stage of obstacle avoidance ${\lambda }_1>{\lambda }^{\ast }$, where ${\lambda }^{\ast }$ is a design parameter. Figure 3c shows ${\lambda }_3<{\lambda }^{\ast }$, indicating that the avoidance mode has ended. The UAV is between the obstacle and the destination point. The stage shown in Figure 3b is the critical stage and ${\lambda }_2={\lambda }^{\ast }$. Hence, the judgment basis of the avoidance mode is redefined as

$$\{\begin{array}{cc}\hfill d_{UO}\le & d_{safe}\hfill \\ \hfill [v_{UAV}-O_{vo}]’k_{vo}>& \cos {\eta }_{vo}\Vert v_{UAV}-O_{vo}\Vert \hfill \\ \hfill \lambda >& {\lambda }^{\ast }\hfill \end{array}$$

(15)

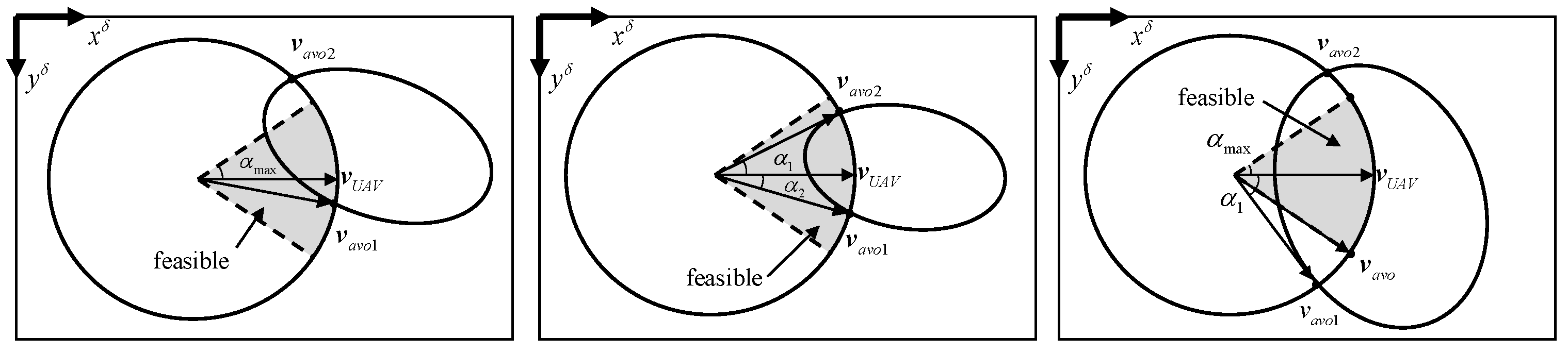
3.2. Avoidance Planes

Similar to two-dimensional velocity obstacle (2D-VO) methods, the UAV needs to independently find the avoidance velocity in the set $\mathcal{A}{\mathcal{V}}_{UAV|OBS}$ that is constantly being updated in real time. However, compared with the 2D-VO method, the topological dimension of the configuration space is expanded to three, and the difficulty of solving the avoidance velocity also increases. Hence, we follow the concept on the avoidance planes mentioned in Refs. [17,28]. Avoidance planes help transform the 3D problems into a series of 2D setups. $\mathcal{S}$ is defined as a series of discrete planes that rotate around the x-axis of the s-frame at certain angles. The plane of rotation angle $\delta$ is denoted as $S^{\delta }\in \mathcal{S}$, shown in Figure 2b.

The cross section obtained by the intersection of $\mathcal{V}{\mathcal{O}}_{UAV|OBS}\left(v_{OBS}\right)$ and the plane $S^{\delta }={ℝ}^2$ is denoted as $S_{UAV|OBS}^{\delta }\left(v_B\right)$. If there is a collision in the $S^{\delta }$ plane, then selecting the avoidance velocity $v_{avo}\in S^{\delta }\backslash S_{UAV|OBS}^{\delta }\left(v_B\right)$ outside the area $S_{UAV|OBS}^{\delta }\left(v_B\right)$ can avoid the collision.

To obtain expressions of conic sections in any obstacle avoidance plane, we implement a rotation-plane coordinate system $\left\{{\mathit{x}}_{}^{\delta },y_{}^{\delta },z_{}^{\delta }\right\}$ by rotating the s-frame around the ${\mathit{x}}^s$ axis at an angle of $\delta$ and then projecting the VO cone under the rotation-plane coordinate system:

$$\left[\begin{array}{c}{\mathit{x}}_{}^{\delta }\\ y_{}^{\delta }\\ z_{}^{\delta }\end{array}\right]=R_s^{\delta }\left[\begin{array}{c}{x}_{}^s\\ y_{}^s\\ z_{}^s\end{array}\right],R_s^{\delta }=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \delta & \sin \delta \\ 0& -\sin \delta & \cos \delta \end{array}\right]$$

(16)

We set the $z^{\delta }-\mathrm{axis}$ coordinate of the VO cone to zero and obtain the coordinate points set $\mathcal{F}==\left\{\left(x_{vo}^{\delta },y_{vo}^{\delta }\right)|\begin{array}{c}\\ z_{vo}^{\delta }=0\end{array}\right\}$, which is the coordinates of the conic section on the avoidance plane $S^{\delta }$. When $z_{}^{\delta }=0$, for each $\phi$, there exists a unique $q$ corresponding to it. The mapping relationship is described as

$$q_{|z_{}^{\delta }=0}=\frac{O_{v{o}_y}\sin \delta -O_{v{o}_z}\cos \delta }{\sin {\psi }_{uo}\cos {\theta }_{uo}\sin \delta -\tan {\eta }_{vo}\cos \phi \cos {\psi }_{uo}\sin \delta -\tan {\eta }_{vo}\sin \phi \sin {\psi }_{uo}\sin {\theta }_{uo}\sin \delta +\sin {\theta }_{uo}\cos \delta +\tan {\eta }_{vo}\sin \phi \cos {\theta }_{uo}\cos \delta }$$

(17)

When $\delta$ takes different values, the shape of the conic section is different, roughly divided into ellipse, hyperbola, and triangle. Generally, there is a strong correlation between the shape of the conic section and collision risk for the UAV. The shapes of the collision risk from high to low are the triangle, hyperbola, and ellipse. Therefore, we would better find an appropriate $v_{avo}^{}$ in the elliptical conic section, which can be selected by judging the relationship between ${\zeta }_{\delta }$ and ${\eta }_{VO}$:

$${\zeta }_{\delta }=\arccos \left(\frac{k_{vo}^{’}}{d_{vo}}\left[\begin{array}{l}0\\ \sin \delta \\ \cos \delta \end{array}\right]\right)$$

(18)

When

$${\zeta }_{\delta }<\frac{\pi }{2}-{\eta }_{VO}$$

(19)

the conic section shape is an ellipse; otherwise it is a hyperbola or triangle.

3.3. Avoidance Velocity

We rely on the concept of the VO cone and the avoidance plane introduced in the previous sections to solve the avoidance velocity, mainly referring to Ref. [17], additionally taking into account the kinematic and dynamic constraints of the fixed-wing UAV. The original VO methods usually update the avoidance velocity to a point on the boundary of the VO cone. There are many ways to solve such a velocity, for example: by changing the magnitude without changing the direction, changing the direction without changing the magnitude, or a combination the two strategies, according to a certain optimization index. For fixed-wing UAVs, its velocity magnitude must be greater than the stall speed. At the same time, the top speed is limited, due to physical limitations. Therefore, the velocity control range seems to be narrow. Moreover, due to the inertia of the UAV, the thrust is less sensitive for controlling the velocity. Consequently, relying on rudders to change the direction of the velocity is considered to be the best way in this work.

Constraints 1 (dynamic constraints): We introduce the concept of the maximum deflection angle $\alpha$, which is the maximum change of the velocity in the direction, in order to characterize the dynamic constraints of the UAV, similar to the motion primitives proposed in Ref. [13]. In this work, $v_{avo}$ is a continuous control parameter $v_{avo}\mapsto \mathit{u}\left(v_{avo}\right)$, indicating the magnitude and direction of the velocity of the UAV, defining the reference trajectory from the moment the UAV avoidance mode starts.

$${\mathit{p}}_{ref}\left(t\right)=\mathit{p}\left(t_0\right)+\left(t-t_0\right)v_{avo},t\ge t_0$$

Meanwhile, the trajectory ${\mathit{p}}_{UAV}\left(t\right)$ is the bijective function of the initial state $\mathit{x}\left(t_0\right)$ and the control input $\mathit{u}\left(t\right)$. The control input needs to meet the dynamic constraints of the UAV:

$$\mathcal{U}=\left\{\mathit{u}\in {ℝ}^3,\mathrm{respect}\mathrm{all}\mathrm{dynamic}\mathrm{constrains}\right\}$$

(20)

The trajectory of the UAV gradually converges to the reference trajectory under the control force. The maximum error between the trajectory and the reference trajectory $\chi \left(t\right)=\max \left(\Vert p_{UAV}\left(t\right)-p_{ref}\left(t\right)\Vert \right)$ shows a significant difference under different initial states and control input. The influence of the control parameter $v_{avo}$ on $\chi$ is what we are concerned about. As shown in Figure 4b, the UAV can track the reference trajectory of the original direction with a small error, and the maximum error value increases almost linearly with the increase in $\alpha$ Figure 4a. We can quickly query the maximum error corresponding to a different value of $\alpha$, which is constant relative to a given initial value. Given the initial state $x\left(t_0\right)$, the set of control parameters that limit the maximum error below ${\chi }^{\ast }$ is defined as follows:

$$\mathcal{A}:=\left\{v_{avo}|\max \left(\Vert {\mathit{p}}_{UAV}\left(t\right)-{\mathit{p}}_{ref}\left(t\right)\Vert \right)\le {\chi }^{\ast }\mathit{u}\in \mathcal{U}\right\}$$

(21)

where $v_{avo}^{\ast }$ refers to the boundary of the set $\mathcal{A}$, corresponding to the maximum deflection angle ${\alpha }_{\max }$. In the avoidance plane $S^{\delta }={ℝ}^2$, the relationship between the original velocity of the UAV and the avoidance velocity is expressed as follows:

$$\{\begin{array}{l}{v}_{avo}^{\delta }=K\left(\alpha \right)\cdot v_{UAV}^{\delta }\\ K\left(\alpha \right)=\left[\begin{array}{cc}\cos \left(\alpha \right)& -\sin \left(\alpha \right)\\ \sin \left(\alpha \right)& \cos \left(\alpha \right)\end{array}\right]\end{array}\begin{array}{c}\\ \left(\Vert \alpha \Vert \le {\alpha }_{\max }\right)\\ \end{array}$$

(22)

Constraints 2 (collision avoidance and kinematic constraints): In addition to the magnitude constraint, $v_{avo}^{}$ must satisfy the obstacle avoidance constraint as well, that is, the end of the vector, which we call the velocity point, should be on the conic section $\mathcal{F}$.

$$\left(v_{av{o}_x}^{\delta },v_{av{o}_y}^{\delta }\right)\in \left\{\left(x_{vo}^{\delta },y_{vo}^{\delta }\right)|\begin{array}{c}\\ z_{vo}^{\delta }=0\end{array}\right\}\cap \left\{\left(x_{}^{\delta },y_{}^{\delta }\right)|{\left(x_{}^{\delta }\right)}^2+{\left(y_{}^{\delta }\right)}^2={\Vert v_{UAV}\Vert }^2\right\}$$

(23)

In Equation (23), the velocity point in the avoidance plane $S^{\delta }$ is defined as the intersection of the conic section $\mathcal{F}$ and circular curve $\left\{\left(x_{}^{\delta },y_{}^{\delta }\right)|{\left(x_{}^{\delta }\right)}^2+{\left(y_{}^{\delta }\right)}^2={\Vert v_{UAV}\Vert }^2\right\}$. As shown in Figure 5, three situations need to be considered: (a) $\mathcal{F}$ and the circular curve only have one intersection, $v_{av{o}_1}^{}$, in the feasible region (gray). Then this point is defined as the velocity point. (b) There are two intersection points of $\mathcal{F}$ and the circular curve in the feasible region. Then the vector with the smallest $\alpha$ is chosen as the avoidance velocity. (c) There is no intersection point of $\mathcal{F}$ and the circular curve in the feasible region. Then the vector corresponding to ${\alpha }_{\max }$ is the avoidance velocity. In this case, a reasonable selection of $d_{\mathrm{safe}}$ [11] can ensure that the UAV avoids collision in the worst scenario (the UAV flying toward the obstacle):

$$\{\begin{array}{cc}\hfill d_{\min }=& \sqrt{{\left(2\sqrt{\frac{\Vert v_{UAV}\Vert r_{\mathit{p}z}\tau }{{\alpha }_{\max }}}+\Vert v_{OBS}\Vert T\right)}^2+r_{\mathit{p}z}^2}\hfill \\ \hfill T=& \frac{\tau }{{\alpha }_{\max }}\arctan \left(\frac{2\sqrt{\Vert v_{UAV}\Vert r_{\mathit{p}z}\tau {\alpha }_{\max }}}{\Vert v_{UAV}\Vert \tau -{\alpha }_{\max }{r}_{\mathit{p}z}}\right)\hfill \\ \hfill d_{\mathrm{safe}}\ge & d_{\min }\hfill \end{array}$$

(24)

where $\tau$ is the control system cycle. The smaller ${\alpha }_{\max }$ is, the larger $d_{\mathrm{safe}}$ is needed. Nevertheless, the selection of $d_{\mathrm{safe}}$ needs to meet the requirements of ${\alpha }_{\max }$ and consider the detection range of the sensor.

When Equation (15) is satisfied, $v_{avo}^{\delta }$ is calculated in each avoidance plane $S^{\delta }\left(\delta ={\delta }_1,\delta ={\delta }_2\cdot \cdot \cdot \delta ={\delta }_n\right)$. Among these solutions, the avoidance velocity with the smallest angle $\alpha$ will be selected and mapped to the inertial coordinate system to generate the avoidance points:

$${\mathit{p}}_{avo}^n\left(t\right)={\mathit{p}}_{UAV}^n\left(t_0\right)+{\displaystyle {\int }_{t_0}^t{v}_{avo}^n\left(t\right)dt}$$

(25)

where $t_0$ is the initial time of the avoidance mode, $v_{avo}^n\left(t\right)$ is constantly updated, and ${\mathit{p}}_{avo}^n\left(t\right)$ will be used in the next chapter to construct the avoidance coordinate system and be mapped onto the control input.

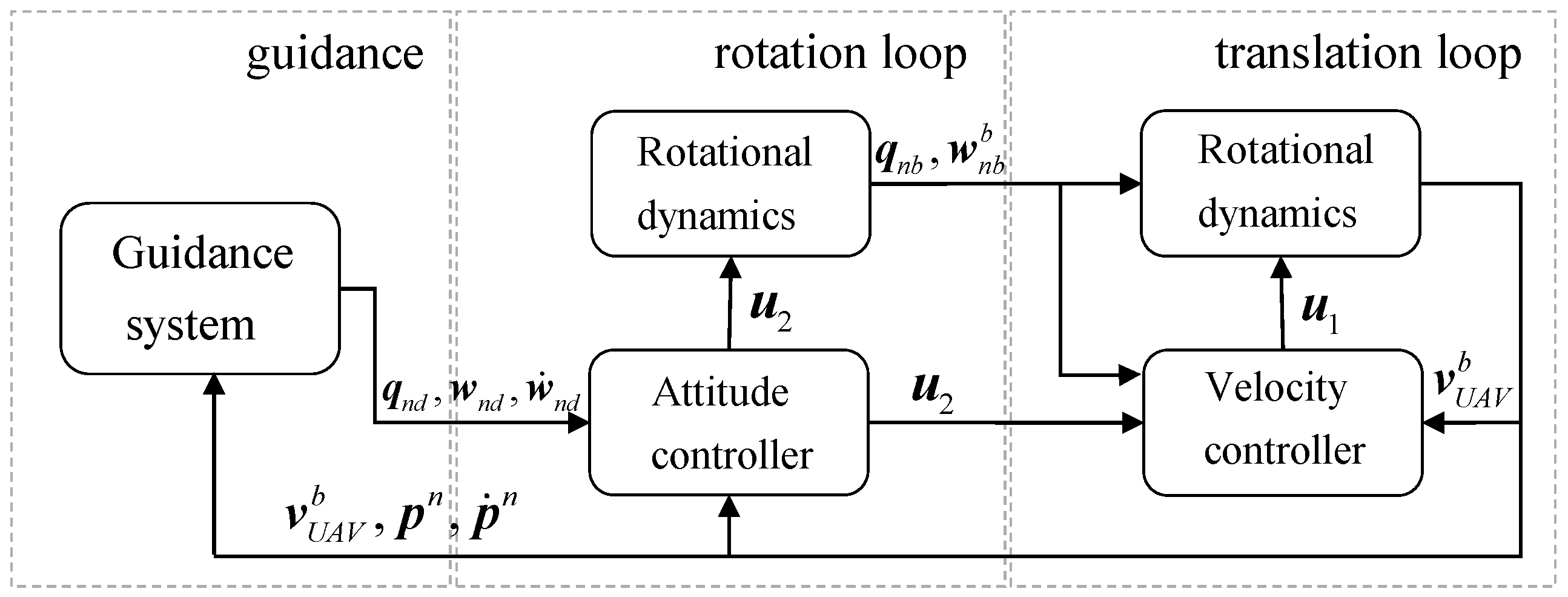
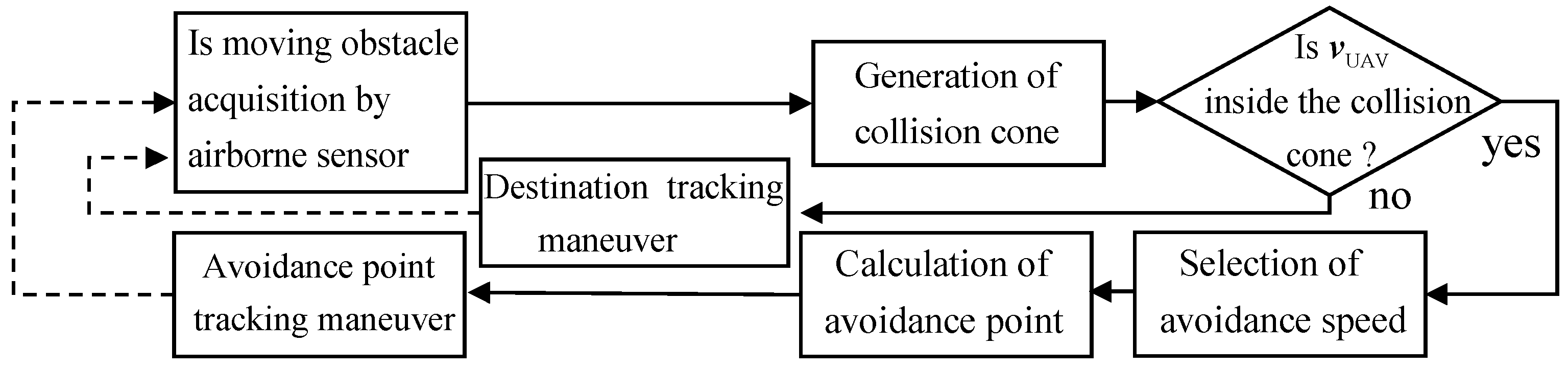
4. Multiple Task Implementation Using a Hierarchical Architecture

Dealing with conflicting tasks is considered the key to behavior control, the difference of which is reflected in the way they arrange conflicting tasks and the way they construct subtasks into a total task. The hierarchical architecture used in this work is a form of behavior control. It arranges conflicting tasks in order of their importance. High-level tasks always subsume low-level tasks. The construction structure is shown in Figure 6. Ref. [29] utilized quaternion to describe the desired attitude of the UAV and applied it to the waypoint tracking problem. Our approach extends this previous work, defines the outputs of each subtask module as a task quaternion and calculates the total task quaternion by the quaternion multiplication. We assume that the UAV is flying under the effect of two behaviors.

Behavior 1: destination point tracking, task quaternion $q_{ne}$.

Behavior 2: obstacle avoiding, task quaternion $q_{ec}$.

The task quaternion of obstacle avoiding is established relative to the task quaternion of destination point tracking, so $q_{ec}$ always subsumes $q_{ne}$, which coincides with the concept of hierarchical architecture. Each task is defined by describing the error between the current position and the desired position. As shown in Figure 7, ${\mathit{p}}_{UAV}^n,{\mathit{p}}_{avo}^n,{\mathit{p}}_{OBS}^n,{\mathit{p}}_d^n$ respect the position of the UAV, avoidance point, obstacle, and destination point, respectively.

4.1. Task Quaternion 1: Destination Point Tracking

To guide the UAV to the destination point, the position error of the UAV is projected onto the ${\mathit{x}}^e$ axis of the error coordinate system. Then, the UAV translates along with ${\mathit{x}}^e$ under the action of the attitude controller until the destination point is reached. As in Figure 7, $e_{\mathit{u}d}^n$ denotes the position error between ${\mathit{p}}_d^n$ and ${\mathit{p}}_{UAV}^n$ in the n-frame. The positive direction of the x-axis of the e-frame is aligned with $e_{\mathit{u}d}^n$, so the e-frame can be defined through the rotation:

$$e_{\mathit{u}d}^e={\left[\begin{array}{ccc}\Vert e_{\mathit{u}d}^n\Vert & 0& 0\end{array}\right]}^{\mathrm{{\rm T}}}=R_n^e\left({\mathit{p}}_d^n-{\mathit{p}}_{UAV}^n\right)=R_n^e{e}_{\mathit{u}d}^n$$

(26)

The control objective is to make $e^e\to {\left[{\mathbf{0}}^{\mathrm{{\rm T}}}\right]}^{\mathrm{{\rm T}}}$. The rotation quaternion between the n-frame and the e-frame and the rotation matrix can be defined as

$${\theta }_{ne}={\cos }^{-1}\left(\frac{e_{\mathit{u}d}^e·e_{\mathit{u}d}^n}{{\Vert e_{\mathit{u}d}^n\Vert }^2}\right)k_{ne}=\frac{e_{\mathit{u}d}^e\times e_{\mathit{u}d}^n}{\Vert e_{\mathit{u}d}^e\times e_{\mathit{u}d}^n\Vert }$$

(27)

$$q_{ne}={\left[\begin{array}{cc}{\eta }_{ne}& {\epsilon }_{ne}^{\mathrm{{\rm T}}}\end{array}\right]}^{\mathrm{{\rm T}}}={\left[\begin{array}{cc}\cos (\frac{{\theta }_{ne}}{2})& k_{ne}{}^{\mathrm{{\rm T}}}\sin (\frac{{\theta }_{ne}}{2})\end{array}\right]}^{\mathrm{{\rm T}}}$$

(28)

$$R_e^n={\rm I}+2{\eta }_{ne}S\left({\epsilon }_{ne}\right)+2S^2\left({\epsilon }_{ne}\right)$$

(29)

To obtain the desired angular velocity, we first take the derivative of Equation (26), which gives

$${\dot{e}}^e=-S\left(w_{ne}^e\right)e^e-R_b^e{v}_{UAV}^b$$

(30)

Then, substituting equation $-S\left(w_{ne}^e\right)e^e=S\left(e^e\right)w_{ne}^e$ into Equation (30), gives

$$\left[\begin{array}{c}\Vert {\dot{e}}_{\mathit{u}d}^n\Vert \\ 0\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ \Vert e_{\mathit{u}d}^n\Vert w_{ne}^e\left(2\right)\\ \Vert e_{\mathit{u}d}^n\Vert w_{ne}^e\left(3\right)\end{array}\right]-R_b^e{v}_{UAV}^b$$

(31)

It can be seen from Equation (31) that $w_{ne}^e$ only contains the second and third terms. Therefore, rewriting Equation (30) as Equation (32) will not affect the final calculation result of $w_{ne}^e$.

$$S\left(e_{\mathit{u}d}^e\right)w_{ne}^e=R_b^e{v}_{UAV}^b$$

(32)

$$w_{ne}^e=S^{†}\left(e_{ud}^e\right)R_b^n{R}_n^e{v}_{UAV}^b$$

(33)

Equation (28) defines the rotation between two coordinate systems. When the task quaternion in Equation (28) degenerates into a unit quaternion, we think that two coordinate systems have reached a coincidence and the task is completed. At the same time, the desired angular velocity in Equation (33) converges to zero.

4.2. Task Quaternion 2: Collision Avoidance

What remains is establishing the avoidance coordinate system denoted as an a-frame. Ideally, the a-frame should be aligned with $v_{avo}$; however, this cannot be achieved since the acceleration of obstacles is difficult to measure in practice. Therefore, we build the a-frame based on the avoidance points mentioned in Section 2. As shown in Figure 7, $a_{ua}^n$ denotes the error between ${\mathit{p}}_{UAV}^n$ and ${\mathit{p}}_{avo}^n$, and the positive x-axis direction of the a-frame is aligned with $a_{ua}^n$.

$$a^a={\left[\begin{array}{ccc}\Vert a^e\Vert & 0& 0\end{array}\right]}^{\mathrm{{\rm T}}}=R_e^a{R}_n^e\left({\mathit{p}}_{avo}^n-{\mathit{p}}_{UAV}^n\right)=R_e^a{R}_n^e{a}^n$$

(34)

where $a^n$ rotates from n-frame to e-frame, and then generates the quaternion to rotate from $a^e$ to $a^a$. That is to say, $a^n$ first rotates to align with the e-frame, and then to align with the a-frame. The obstacle avoidance task quaternion, the rotation matrix between the e-frame and the a-frame, and the obstacle avoidance angular velocity are expressed by the following Equations (35)–(38).

$${\theta }_{ea}={\cos }^{-1}\left(\frac{{\mathit{a}}^a·{\mathit{a}}^e}{{\Vert {\mathit{a}}^e\Vert }^2}\right)k_{ea}=\frac{{\mathit{a}}^a\times {\mathit{a}}^e}{\Vert {\mathit{a}}^a\times {\mathit{a}}^e\Vert }$$

(35)

$$q_{ea}={\left[\begin{array}{cc}{\eta }_{ea}& {\mathit{\epsilon }}_{ea}^{\mathrm{{\rm T}}}\end{array}\right]}^{\mathrm{{\rm T}}}={\left[\begin{array}{cc}\cos \left(\frac{{\theta }_{ea}}{2}\right)& k_{ea}^{\mathrm{{\rm T}}}\sin \left(\frac{{\theta }_{ea}}{2}\right)\end{array}\right]}^{\mathrm{{\rm T}}}$$

(36)

$$R_a^e=I+2{\eta }_{ea}S\left({\epsilon }_{ea}\right)+2S^2\left({\epsilon }_{ea}\right)$$

(37)

$${\omega }_{ea}^a=S^{†}\left(a^a\right)\left(R_e^{a}S\left({\omega }_{ne}^e\right)R_n^e{a}^n-R_n^e{R}_e^a\left(v_{OBS}^n-v_{UAV}^n\right)\right)$$

(38)

Finally, two subtask quaternions are combined into a total task quaternion, which is defined as the desired quaternion. The desired angular velocity is also derived:

$$\{\begin{array}{l}{q}_{nd}\text{:}=q_{na}=q_{ne}\otimes q_{ea}\\ w_{nd}^d\text{:}=w_{na}^a=R_e^a{w}_{ne}^e+w_{ea}^a\end{array}$$

(39)

5. Attitude and Velocity Control Commands

The desired quaternion and the desired angular velocity are derived in the previous section. What remains is deriving the attitude and velocity control commands to track the desired attitude and velocity, respectively. For underactuated UAVs, Ref. [29] designed a sliding mode attitude controller, Ref. [30] proposed a velocity controller based on the backstepping technique, and Ref. [31] utilized a virtual saturated controller guaranteed the attitude error and the velocity error converge to zero. The controller designed in this chapter is mainly based on Refs. [29,30].

5.1. Velocity Controller

Given the Equation (3), we know the UAV is underactuated since ${\mathit{u}}_1$ contains only a thrust $T_{\mathit{x}}^b$ along ${\mathit{x}}^b$. Hence, our approach introduces a velocity scalar and then utilizes the backstepping method to design a velocity controller to make the velocity scalar converge to a desired value ${\mathit{v}}_d$. The speed scalar of the UAV is defined as

$$v_{UAV}=\sqrt{{\left({\mathit{v}}_{UAV}^b\right)}^{\mathrm{{\rm T}}}{\mathit{v}}_{UAV}^b}$$

(40)

Taking the derivative of Equation (40), we obtain

$${\dot{\mathit{v}}}_{UAV}=\frac{1}{{\mathit{v}}_{UAV}}{\left({\mathit{v}}_{UAV}^b\right)}^{\mathrm{{\rm T}}}{\dot{v}}_{UAV}^b=\frac{{\left(v_{UAV}^b\right)}^{\mathrm{{\rm T}}}{F}_{ag}^b\left(v_{UAV}^b\right)}{m{v}_{UAV}}+\frac{{\mathit{v}}_{UA{V}_x}^b{T}_x^b}{m{v}_{UAV}}$$

(41)

where we use the fact, $v_1^{\mathrm{{\rm T}}}S\left(v_2\right)v_1=0$. The desired velocity scalar is a constant $v_d>0$, and the velocity error is defined as $\widehat{v}:=v_{UAV}-v_d$. Given Equation (41) and the introduced variables $x_1={\displaystyle {\int }_0^t\widehat{v}d\tau }\mathrm{and}{x}_2=\widehat{v}$, we find

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\frac{{\left(v_{UAV}^b\right)}^{\mathrm{{\rm T}}}{F}_{ag}^b\left(v_{UAV}^b\right)}{m{v}_{UAV}}+\frac{{\mathit{v}}_{UA{V}_x}^b{T}_x^b}{m{v}_{UAV}}\end{array}$$

(42)

We further introduce a Lyapunov function $V_1=\frac{1}{2}{x}_1^2$, then take the derivative of it, giving ${\dot{V}}_1=x_1{x}_2$. Another Lyapunov function is constructed as $V_2=V_1+\frac{1}{2}{z}^2$, where $z=x_2+k_1{x}_1$. Taking the derivative of $V_2$ gives

$${\dot{V}}_2={\dot{V}}_1+z\dot{z}=x_{1}z-k_1{x}_1^2+z\left({\dot{x}}_2+k_1{x}_2\right)=x_{1}z-k_1{x}_1^2+z\left(\frac{{\left(v_{UAV}^b\right)}^{\mathrm{{\rm T}}}{F}_{ag}^b\left(v_{UAV}^b\right)}{m{v}_{UAV}}+\frac{{\mathit{v}}_{UA{V}_x}^b{T}_x^b}{m{v}_{UAV}}+k_1{x}_2\right)$$

(43)

Above, a control input of the thrust is designed as

$$T_x^b=\frac{m{v}_{UAV}}{v_{UA{V}_x}^b}\left(-\frac{{\left(v_{UAV}^b\right)}^{\mathrm{{\rm T}}}{F}_{ag}^b\left(v_{UAV}^b\right)}{m{v}_{UAV}}-k_1{x}_2-x_1-k_{2}z\right)$$

(44)

where parameters $k_1,k_2>0$. Substituting Equation (44) into Equation (43), we find

$${\dot{V}}_2=-k_1{x}_1^2-k_2{z}^2\le -k_1{x}_1^2-k_2{x}_2{}^2$$

(45)

According to the Lyapunov stability theory, when $\left(x_1,x_2\right)\to \left(0,0\right)$, the velocity error $\widehat{v}$ will go to zero.

5.2. Attitude Controller

In this section, we implement a sliding mode attitude controller to align the s-frame of the UAV with the d-frame. We do so firstly by defining the rotational quaternion between the s-frame and the d-frame: $q_{ds}=q_{dn}\otimes q_{nb}\otimes q_{bs}$. When $q_{ds}\to {\left[\begin{array}{cc}1& \mathbf{0}\end{array}\right]}^{\mathrm{{\rm T}}}$ under the effect of the control input, we think that the s-frame coincides with the d-frame. However, from a control point of view, we are more accustomed to the control variable converging to the relative origin. Therefore, we introduce a virtual variable $q_{ds}^{\ast }:={\left[\begin{array}{cc}1& \mathbf{0}\end{array}\right]}^{\mathrm{{\rm T}}}-q_{ds}$ such that $q_{ds}^{\ast }\to {\left[\mathbf{0}\right]}^{\mathrm{{\rm T}}}$ is equivalent to $q_{ds}\to {\left[\begin{array}{cc}1& \mathbf{0}\end{array}\right]}^{\mathrm{{\rm T}}}$. Then, taking the derivative of $q_{ds}^{\ast }$ gives ${\dot{q}}_{ds}^{\ast }=D_q\left(q_{ds}^{\ast }\right)w_{ds}^s$, where $D_q\left(q_{ds}^{\ast }\right):=\frac{1}{2}\left[\begin{array}{c}{\epsilon }_{ds}^{\mathrm{{\rm T}}}\\ {\eta }_{ds}I+S\left({\epsilon }_{ds}\right)\end{array}\right]$. Finally, we define the sliding variable [29,30]:

$$s=w_{nb}^b-w_{ref}^b$$

(46)

$$w_{ref}^b=w_{nd}^b-w_{bs}^b-{\kappa }_1{R}_s^b{D}_q^{\mathrm{{\rm T}}}{\mathit{q}}_{ds}^{\ast }$$

(47)

where $w_{ref}^b$ is the projection of the reference angular velocity relative to n-frame on the b-frame.

$$\dot{s}=\frac{1}{J}\left(M_{at}^b\left(w_{nb}^b,v_{UAV}^b\right)-S\left(w_{nb}^b\right)J{w}_{nb}^b+A{\mathit{u}}_2\right)-{\dot{w}}_{ref}^b$$

(48)

We introduce a Lyapunov function $V_3=\frac{1}{2}{\kappa }_2{\left(q_{ds}^{\ast }\right)}^{\mathrm{{\rm T}}}{q}_{ds}+\frac{1}{2}{s}^{\mathrm{{\rm T}}}Js$ and take the derivative of $V_3$, giving

$${\dot{V}}_3={\kappa }_2{\left(q_{ds}^{\ast }\right)}^{\mathrm{{\rm T}}}{D}_q{w}_{ds}^s+s^{\mathrm{{\rm T}}}\left(M_{at}^b\left(w_{nb}^b,v_{UAV}^b\right)-S\left(w_{nb}^b\right)J{w}_{nb}^b+A{\mathit{u}}_2-J{\dot{w}}_{ref}^b\right)$$

(49)

where ${\kappa }_2>0$, and since $w_{ds}^s=R_b^s\left(s-{\kappa }_1{R}_s^b{D}_q^{\mathrm{{\rm T}}}{q}_{ds}^{\ast }\right)$, ${\dot{V}}_3$ can be rewritten as

$${\dot{V}}_3=-{\kappa }_1{\kappa }_2{\left(q_{ds}^{\ast }\right)}^{\mathrm{{\rm T}}}{D}_q{D}_q^{\mathrm{{\rm T}}}{q}_{ds}^{\ast }+s^{\mathrm{{\rm T}}}\left(M_{at}^b\left(w_{nb}^b,v_{UAV}^b\right)-S\left(w_{nb}^b\right)J{w}_{nb}^b+A{\mathit{u}}_2-J{\dot{w}}_{ref}^b+{\kappa }_2{R}_s^b{D}_q^{\mathrm{{\rm T}}}{q}_{ds}^{\ast }\right)$$

(50)

The control input ${\mathit{u}}_2$ can be given similar to before as

$${\mathit{u}}_2=A^{-1}\left(S\left(w_{nb}^b\right)J{w}_{nb}^b-M_{at}^b\left(w_{nb}^b,v_{UAV}^b\right)+J{\dot{w}}_{ref}^b-{\kappa }_2{R}_s^b{D}_q^{\mathrm{{\rm T}}}{q}_{ds}^{\ast }-K_{s}s\right)$$

(51)

where $K_s$ is a positive-definite matrix. Substituting Equation (51) into Equation (50) gives

$${\dot{V}}_3=-{\kappa }_1{\kappa }_2{\left(q_{ds}^{\ast }\right)}^{\mathrm{{\rm T}}}{D}_q{D}_q^{\mathrm{{\rm T}}}{q}_{ds}^{\ast }-s^{\mathrm{{\rm T}}}{K}_{s}s\le \frac{-{\kappa }_1{\kappa }_2}{8}{\Vert q_{ds}^{\ast }\Vert }^2-{\lambda }_{\min }\left(K_s\right){\Vert s\Vert }^2$$

(52)

where ${\lambda }_{\min }$ is the minimal eigenvalue of the matrix $K_s$. According to the Lyapunov stability theory and Equation (52), we find $\left(q_{ds}^{\ast },s\right)\to \left(0,0\right)$; then, as a consequence, the s-frame coincides with the d-frame.

A flowchart of the overall method is shown in Figure 8. Algorithm 1 summarizes the collision avoidance guidance frame, where ${\mathcal{V}}_k$ is the set of the avoidance velocity at the K-th step, and the function $\mathrm{feasible}\mathrm{Section}\left(\delta \right)$ checks if the shape of the conic section is expected, given a rotation angle $\delta$ in Equation (18). If Equation (19) satisfied, then return ‘true’; else ‘false’. We assumed that the control system as well as the detection system operate at the same rate and uniformly set the cycle as the time constant $\tau$.

Algorithm 1. Attidude and Velocity Commands at the K-th Step

1.   design parameter: $r_{\mathit{ps}},d_{safe},{\alpha }_{\max },{\mathit{p}}_d^n,\tau ,\mathcal{A}\mathcal{G}=[0°,\pm \frac{\pi }{4},\frac{\pi }{2}]$

2.   Input: ${\mathit{p}}_{UAV}^n,{\mathit{p}}_{OBS}^n,{\mathit{v}}_{UAV},{\mathit{v}}_{OBS},r_{OBS}$

3.   Output: ${\mathit{u}}_2,T_x^b$

4.    begin

5.     obtain ${\mathit{q}}_{ne}\left(k\right),{\mathit{w}}_{ne}^e\left(k\right)$ by substituting ${\mathit{p}}_{UAV}^n\left(k\right),{\mathit{p}}_d^n$ into Equations (26)–(33)

6.       if $\Vert {\mathit{p}}_{UAV}^n-{\mathit{p}}_{OBS}^n{\Vert }_2<d_{safe}$ and meet the conditions: Equation (15) then

7.           for each δ in $\mathcal{A}\mathcal{G}$, do

8.             ${\mathit{v}}_{avo}^{\delta }\leftarrow$ Solution of quadratic Equation (23) with constrain Equation (22)

9.                if feasible Section(δ) = ’Ture’

10.                   ${\mathcal{V}}_k\leftarrow {\mathcal{V}}_k\cup v_{avo}^{\delta }$

11.              end if

12.          end for

13.          if ${\mathcal{V}}_k\ne \varnothing$ then

14.            select ${\mathit{v}}_{avo}\left(k\right)\in {\mathcal{V}}_k$ with the smallest rotation angle α

15.            return ${\mathit{v}}_{avo}\left(k\right)$

16.            // If ${\mathcal{V}}_k=\varnothing$, the $\mathcal{A}\mathcal{G}$ needs to be extended

17.          end

18.         Map ${\mathit{v}}_{avo}\left(k\right)$ to ${\mathit{q}}_{ea}\left(k\right),{\mathit{w}}_{ea}^a\left(k\right)$ following Equation (25), Equations (34)–(38)

${\mathit{q}}_{nd}\left(k\right)$←Equation (39)

19.     else

20.          ${\mathit{q}}_{ea}\left(k\right)\leftarrow {\left[\begin{array}{cc}1& \mathbf{0}\end{array}\right]}^{\mathrm{{\rm T}}};{\mathit{w}}_{ea}^a\left(k\right)\leftarrow {\left[\mathbf{0}\right]}^{\mathrm{{\rm T}}};{\mathit{q}}_{nd}\left(k\right)\leftarrow$ Equation (39)

21.     end if

22.     Compute velocity command $T_x^b\left(k\right)$ following Equations (40)–(44)

23.     Compute Attitude command ${\mathit{u}}_2\left(k\right)$ following Equations (46)–(51)

24.     Apply controls

25.  end

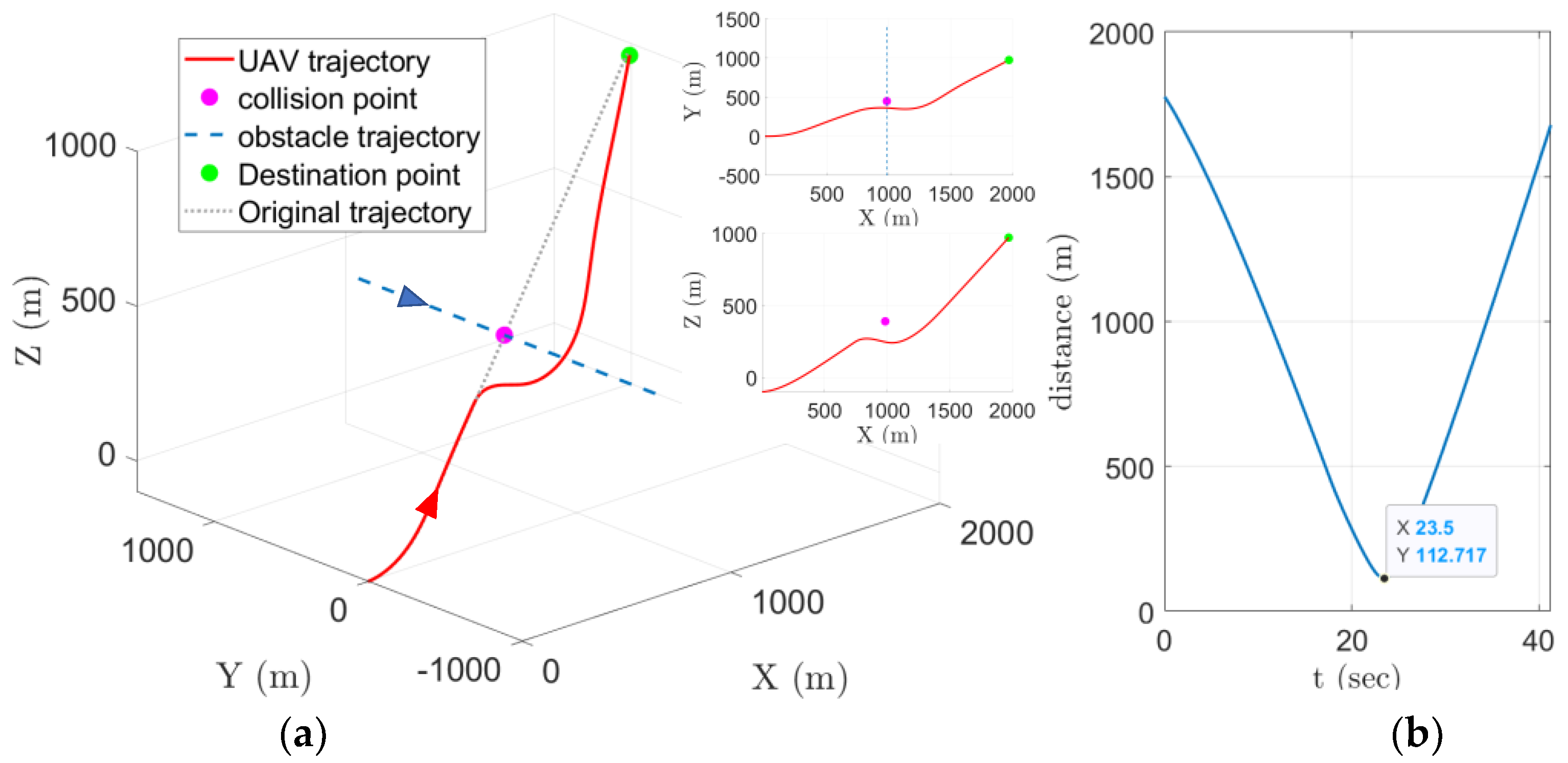
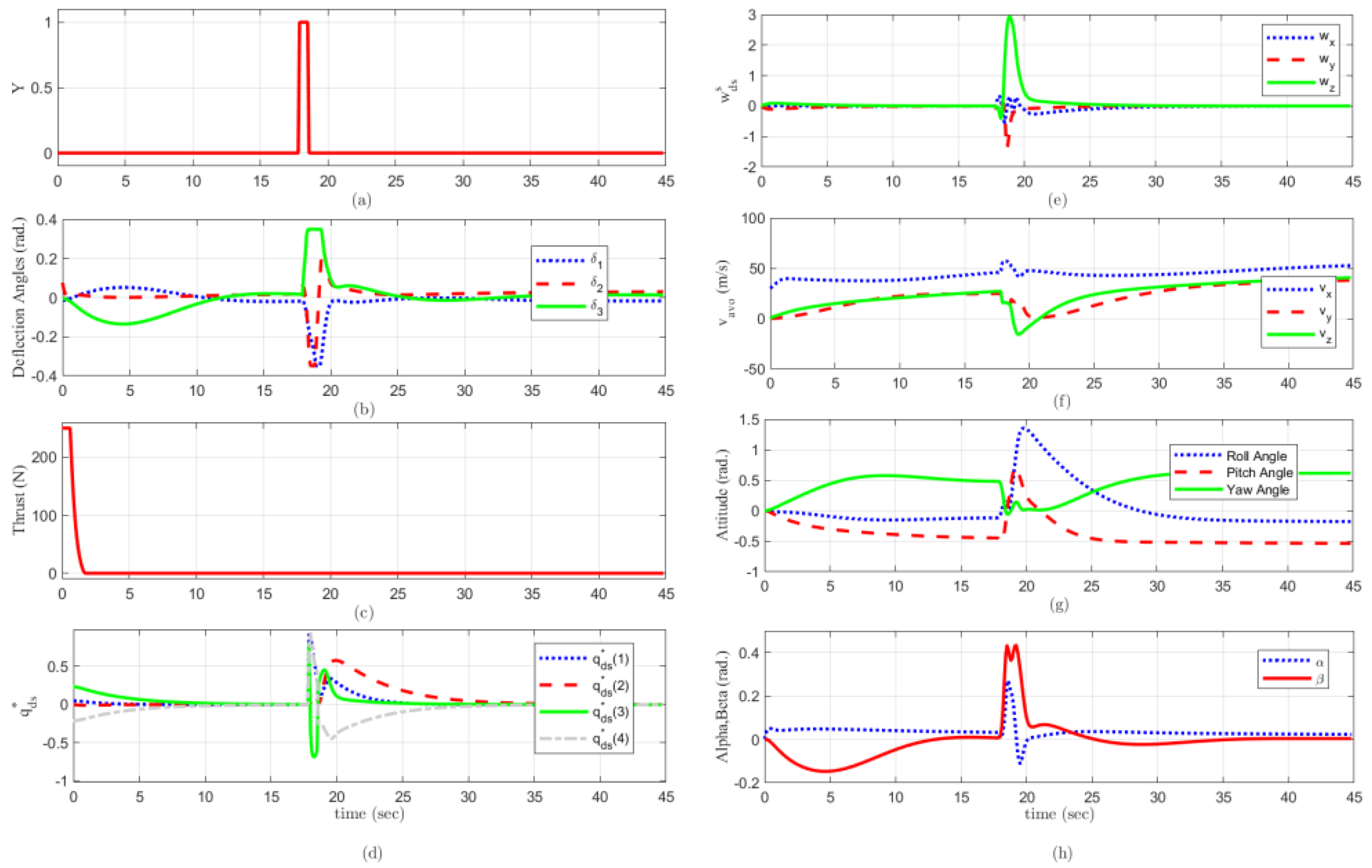
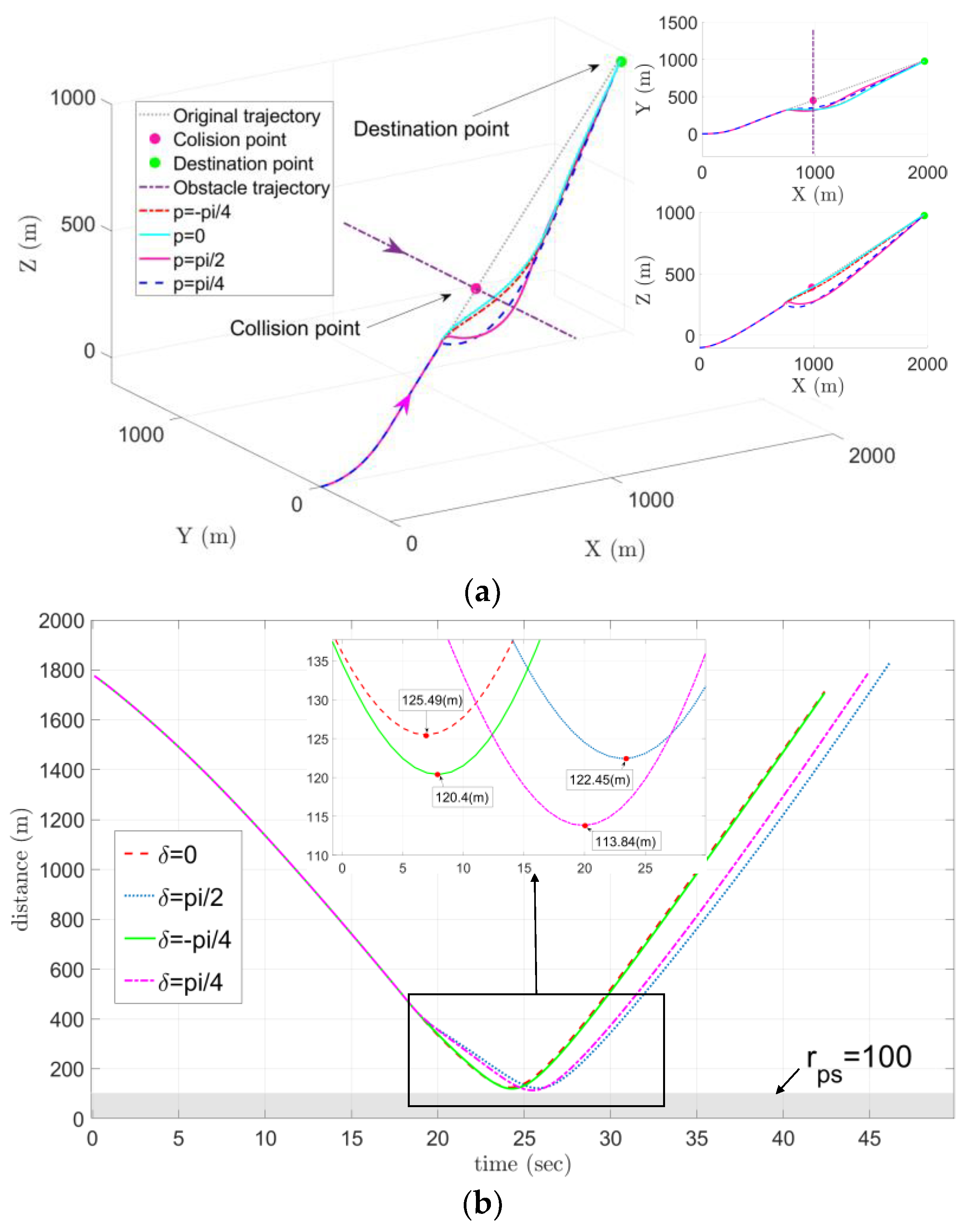
6. Simulation

We performed a numerical simulation on a laptop to verify the effectiveness of the three-dimensional obstacle avoidance guidance algorithm proposed above. The laptop ran Windows 10 Professional 64-bit with an AMD Ryzen 7 4800H with Radeon Graphics CPU (2.9 GHz) and 16 GB RAM. All simulations were developed in the MATLAB 2020b environment. The parameters of the UAV, collision avoidance algorithm, and control system are summarized in

Table 1. Parameters of the fixed-wing UAV, collision avoidance and control system.

Fixed-Wing UAV		3D-VO Collision Avoidance		Control System
$m=20.64\mathrm{kg}$	${\mathit{p}}_{UAV}^n\left(0\right)={[00-100]}^{\mathrm{{\rm T}}}$	$r_{ps}=100\mathrm{m}$	$d_{safe}=500\mathrm{m}$	$k_1=2$	$k_2=2$
$v_{UAV}^b\left(0\right){=\left[3000\right]}^{\mathrm{{\rm T}}}$	$q_{nb}\left(0\right)={[1000]}^{\mathrm{{\rm T}}}$	${\lambda }^{\ast }=90°$	$v_d=40\mathrm{m}/\mathrm{s}$	${\kappa }_1=2$	${\kappa }_2=2$
$w_{nb}^b\left(0\right)={[000]}^{\mathrm{{\rm T}}}$	${\mathit{p}}_d^n={[201010]}^{\mathrm{{\rm T}}}\ast {10}^3$	${\alpha }_{\max }=90°$	$\tau =0.5\mathrm{s}$	$K_s=2{\rm I}$	$\mathrm{\Lambda }=5\mathrm{m}$

Simulation 1: Use the algorithm that updates the avoidance plane in real time.

. The initial states of the obstacle are set as ${\mathit{p}}_{OBS}^n\left(0\right)={[\begin{array}{ccc}984.4& 1396.43& 390.1\end{array}]}^{\mathrm{{\rm T}}}$, and ${\mathsf{v}}_{OBS}={[\begin{array}{ccc}0& -40& 0\end{array}]}^{\mathrm{{\rm T}}}$. The deflection angle is constrained in the range of $\pm 15°$, and the maximum thrust of the engine is limited to 250 N.

Figure 9 a shows the trajectory of the UAV and the obstacle in the inertial coordinate system. The solid line represents the flight trajectory of the UAV. It can be seen from Figure 9a that the controller of the UAV leads to a smooth and continuous trajectory. Dashed and dotted lines respectively represent the moving target and the UAV in a non-avoidance mode. They intersect at a collision point (t = 23.8 s), indicating that if the avoidance maneuver is not performed, a collision will occur at that time. Figure 9b shows the change of the distance between the UAV and the moving obstacle over time, and the minimum distance between the UAV and the moving obstacle is greater than $r_{ps}$ as expected. It took 41.35 s to complete the task.

Figure 10 shows the control input of the rotation loop and the translation loop, the velocity, the angular velocity, and the attitude information of the UAV.

Figure 10c shows that the thrust engine is started in the initial stage (t = 0–2.1 s), pushing the UAV to a predetermined velocity. As shown in Figure 10d,e during the period (t = 0–17.2 s), the quaternion ${\mathit{q}}_{\mathrm{ds}}^{\ast }$ representing the error between the d-frame and the s-frame gradually converges to zero, indicating that the UAV can be directed toward the destination point. When an obstacle is detected and Equation (15) is satisfied, signal Y becomes 1 and the controller continuously controls the UAV keeps a certain safety distance with the obstacle, as in Figure 10a,b. In Figure 10f, the dotted, dashed, and solid lines represent ${\mathit{v}}_{av{o}_x},{\mathit{v}}_{av{o}_x}$ and ${\mathit{v}}_{av{o}_z}$, respectively. In the avoidance mode (t = 17.2–18.8 s), ${\mathit{v}}_{av{o}_x}$ increases, ${\mathit{v}}_{av{o}_x}$ as well as ${\mathit{v}}_{av{o}_z}$ decrease, and the thrust remains at 0, indicating that the UAV has only changed the direction of the velocity. Due to the avoidance maneuver, the attitude of the UAV changes drastically. Figure 10 g shows the attitude, including the roll, pitch and yaw angle. During the period (t = 17.2–18.8 s), the yaw angle continues to decrease, indicating that the UAV has adopted the strategy of avoiding obstacles on the right side. The sudden increase in the attack angle and the sideslip angle are shown in Figure 10h reflects the fact that the b-frame cannot be aligned with the s-frame immediately due to the existence of the UAV’s moment of inertia. As shown in Figure 10d, $q_{ds}^{\ast }$ has undergone two obvious divergence and reconvergence processes after experiencing the initial disturbance and then converging to 0. The first time is the process of converging to the obstacle avoidance point in the avoidance mode, and the latter is the process of re-converging to the destination point in the guidance mode.

Simulation 2: Fixed avoidance plane with different rotation angles: ${\delta }_1=0°,{\delta }_2=45°,{\delta }_3=-45°$ and ${\delta }_4=90°$.

We also performed a simulation where the UAV does not update the avoidance plane but chooses a fixed avoidance plane with a pre-set rotation angle, while the initial state and control parameters are the same as before. The simulation was implemented to quantify the impact of the rotation angle of the obstacle avoidance plane on the obstacle avoidance. Figure 11a shows four trajectories of the UAV with different avoidance planes. It can be seen from Figure 11b that different avoidance planes mainly affect the minimum distance and avoidance time in the macroscopic view.

When the obstacle avoidance plane rotation angle is $\delta =90°,45°$, the flight time is 46.2 s and 44.9 s, respectively. However, the flight time is 42.4 s when the obstacle avoidance plane rotation angle is $\delta =0°\mathrm{or}-45°$, and the trajectory is smoother. When we adopted the strategy of updating the rotation angle, under the same initial conditions, the flight time was 41.35 s, which is less than that in the fixed avoidance plane case. By analyzing the minimum distance between the UAV and the moving obstacle, we can observe that the algorithm adopting an updated avoidance plane can guarantee a less conservative avoidance trajectory. The reason for this difference is that in the fixed-angle avoidance plane, the choice of the avoidance velocity cannot always be guaranteed to be the smallest deviation from the original velocity; thus, the UAV flew over an unnecessarily long path. As shown in Figure 11b the minimum distance between the UAV and the obstacle was 113.84 m when the rotation angle of avoidance planes was defined as $\frac{\mathit{\pi }}{4}$. This is because the velocity of the UAV and the moving obstacle are almost simultaneously in the $S^{\delta }$ plane during the avoidance stage. Therefore, comparing the fixed avoidance plane and updated avoidance plane implementations of the method, we found that the latter guarantees the trajectory to be a less conservative and faster process.

7. Conclusions

In this work, we present a guidance framework that can enable the UAV to move along the collision-free smooth reference trajectory. In particular, we extend the traditional 3D-VO methods to kinodynamic constrained nonholonomic UAVs. The approach was to limit the set of feasible velocities to those that can be achieved with a position error below a predefined value. A reference collision-free trajectory resulting from the 3D-VO approach can be retained by integrating the updated avoidance velocity. The simulation results verified that the UAV can implement collision avoidance maneuvers under allowable trust and torque. We discussed fixed avoidance plane and updated avoidance plane implementations of the method and showed that the latter guarantees the trajectory to be more optimized but processed slower. Compared with other VO-based algorithms, the main innovation of this method is reflected in the extension of the 3D-VO to underactuated systems. The approach is to map underactuated variables to existing actuators. The method we proposed in this paper allows for fast online control and low computational cost, and flexible task assignment was presented in the detailed simulation experiments.

Although the guidance framework proposed in this paper is desirable, there is still large room for improvement. This algorithm was not tested in a multi-obstacle scenario. The extension to cooperative obstacle avoidance of UAV formation is yet to be considered, which will become our next research focus. The robustness against external disturbances, such as wind gusts, was not discussed.