Goal Programming and Mathematical Modelling for Developing a Capacity Planning Decision Support System-Based Framework in Higher Education Institutions

Abstract

Achieving the Saudi Kingdom’s vision 2030 in the higher education sector requires higher education institutions to make a significant simultaneous change in their current practices. This encompasses the transitioning of government-funded educational institutions to be financially independent. Therefore, a prompt, agile transition is required while maintaining a positive socioeconomic impact, entrepreneurship and innovation, and high-quality education. This necessitates the transition to lean processes and the review of current practices. One of the most vital processes in educational institutions is student admission/enrollment capacity planning. This study puts forward a capacity planning decision support system (DSS)-based framework for university student enrollment. The framework was applied to the case of KAU, where current practice and challenges are presented, and from which data were collected. A top-down/bottom-up approach was followed and applied using the goal programming technique and a developed mathematical model, respectively. Results show that the proposed framework effectively affects student admission/enrollment capacity planning on strategic and operational levels. Moreover, it can be used in other planning aspects of higher education in universities, such as human resources planning, teaching load planning, faculty-to-student ratios, accreditation, quality requirements, lab capacity planning, equipment/teaching aids procurement, and financial planning, to mention a few. The implications of this study include assisting decision-makers in higher education institutions in matching their admission/enrollment capacity of student numbers between the macro-strategic and the micro-operational level.

1. Introduction

Higher education, also known as post-secondary education or tertiary education, has seen enormous worldwide growth in the last decade, and it has become a global phenomenon. According to UNESCO data, the enrollment of 150 million students around the globe has been recorded in higher education institutions at the close of the last decade. This reflected a growth trend of around 50% from the previous decade. Another key indicator is the global enrollment ratio, defined as the percentage of total students enrolled in higher education within the total population of individuals eligible for school enrollment. This indicator has also seen growth from a total of 19% to approximately 26%. These growth results are unprecedented and may be due to several factors: more involvement of females and minority groups who are often socially under-represented, the growth of higher education in the private sector domain, diversity and variability in higher education systems, and the observed global deterioration of non-elite higher education institutions. Concurrently, higher education is considered a vital factor in driving a relatively new concept commonly known as the knowledge economy. Owing to these factors, higher education institutions—and research-rich higher education institutions in specific—have attained central roles in modern societies [1].

Higher education institutions have gradually transitioned to universal institutions and from elite institutions to mass institutions. Universal higher education systems—specifically those obligated to middle and upper classes and serving the entire population for technological and social transformation—are categorized by generally high enrollment rates of above 50%. Mass higher education institutions are categorized by enrollment rates between 16 and 50%. These institutions are accessed by a population with minimum qualifications and serve elite roles ranging from economic to technological. Elite higher education institutions are categorized by enrollment rates ranging from 0–15% and serve to address technological, economic, and governance needs in a country [2].

As mentioned earlier, higher education demand and growth necessitate higher education institutions to invest in planning and capacity enhancements. These enhancements can be found in academic and administrative aspects, infrastructure, and staff [3]. They keep in view the increase in enrollment demand. In a practical sense, however, job market competition in the government and private sectors obstructs higher education institutions from receiving qualified graduates [4]. The situation also deteriorates when higher education institution income does not match the increase in student enrollment numbers. This leads to inadequate investments in infrastructure and facilities, resulting in under-resourcing in the provision of equipment, books, and other necessary facilities [2]. Staff to student ratios also decrease, giving rise to situations where there is inadequate space for students in the classroom. Economic growth also demands that these higher education institutions perform better to produce more graduates for a growing job market with various disciplines. However, it has been indicated in various reports that a supply and demand gap exists for higher education graduates, leading to an ultimate slowing down—if not a choking—of economic growth [4].

Since the 1970s, admission officers have introduced enrollment management terminology intending to define a new discourse to maintain the number of newly admitted students. During that period, enrollment management consisted of analyzing population data, segregating the target population, and increasing marketing campaigns to attract more students. By the 1980s, this new management function was enhanced to incorporate other functionalities, such as student registration, records, fee payments and financial aid, graduation rates, retention mechanisms, etc., thus creating a direct relationship with academics. This garnered sophisticated financial modeling techniques that connected enrollment and retention rates with institutions’ revenues. In the late 1980s, its scope grew to include institutional operations, and the new term of strategic enrollment management was coined [2,3,4].

The authorities responsible for higher education in a country raise this very issue of higher education institutions’ admission capacity and prepare them to cope with the challenge. Traditionally, authorities have tackled the issue in their respective countries by designing separate plans for each higher education institution individually [2,3,4].

For the purpose of this research, the authors choose King Abdulaziz University (KAU) of Saudi Arabia as a case study as it is one of the leading and developing universities in the Middle East; it is the 1st in Times Higher Education Ranking [5]. According to a UNESCO report in 2019, there is an increasing rate of admission and enrollment each year in the Saudi education system [6]. The report showed the youth literacy rate for the population aged between 15 and 24 years old, both sexes, is 99%, which indicates a high demand for education. A total of 17% of students are enrolled in tertiary education. The Saudi government expenditure on education as a percentage of total government expenditure is almost 15.0%, which also indicates that high priority is given to the education system in the country.

Universities are not immune from such challenges. For instance, King Abdulaziz University (KAU) in Saudi Arabia is also undergoing a unique set of challenges; according to the QS Top Universities, KAU is a massive leading public university classified as a very high research output university that is ranked 109th worldwide and 1st in the Arab region [7]. Challenges, however, come as a result of the economic transition of the country to a non-oil-based economy.

In July 2020, the Saudi Minister of Education issued a decree selecting three universities that will be subject to the new system of universities for the gradual implementation and the follow-up of its regulations and provisions on a trial basis in those universities, including King Abdulaziz University [8]. The project of the new system has many goals that it was set to achieve. The chief aims of these goals are to improve the productivity of education in a distinct way, serve the community and be in line with the requirements of the labor market and the needs of the country. The system consists of 14 chapters and includes 58 articles to consolidate education based on technology and independence by providing financial support resources from within the university to spend on its projects and approving its internal regulations in a manner that does not conflict with the constants of higher education in the Kingdom and the values of Saudi society. These goals require a dynamic response through the KAU’s knowledge of its capability and capacity to respond to all new variables, and this is one of this study’s aims [9].

Thus, several newly imposed regulations and legislation have pushed such government-funded institutions to be financially independent and more agile, creating a positive socioeconomic impact, leading entrepreneurship and innovation, and maintaining a high-quality undergraduate and graduate education offering. In theory, the objective of this research study was to put forward a capacity planning admission/decision support system (DSS)-based framework for student enrollment and admission for universities. The case of KAU was presented in terms of its current practice and challenges. In order to achieve these objectives, this research went through several stages, as shown in Figure 1.

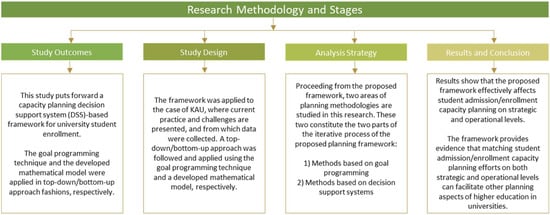
Figure 1. Research methodology and stages.

2. Motivations

The main motivations of this research study lie in achieving the Kingdom’s vision in the higher education sector. This constitutes the need for prompt and lean adaptation of the newly imposed regulations, as well as the need to transition from the current student admission practice to a more systematic and effective practice based on student enrollment capacity planning in KAU. One purpose of this study is to present the current student enrollment capacity planning practice in KAU and its associated challenges. Additionally, this study seeks to review the methods proposed in the literature to overcome such challenges in higher education institutions.

3. Objectives

Proceeding from the motivations of the dire need to change the business-as-usual (BAU) framework into one which is more agile and responsive to the changes imposed and required by the new universities’ regulations and mandates, the objectives of this article are devised. These objectives target King Abdulaziz University as a case study to identify the issues, propose solutions, and provide narrative, recommendations, and conclusions. They can be summarized as follows:

• Analyze the gap between the BAU framework and the new mandates of higher operational efficiencies and lowering costs;
• Assess the current infrastructure and what sources and resources are available or required;
• Explore the possible techniques to address the capacity planning problem in the King Abdulaziz University environment, as well as the future plans;
• Transition planning of a possible roadmap to a gradual change from the BAU framework into a new effective framework;
• Suggest and recommend the steps for implementing the framework in KAU and any similarly structured university locally, regionally, or even internationally.

4. Student Capacity Planning Problem Description in King Abdulaziz University

The following section introduces the problem of student capacity planning in KAU from different perspectives. First, it provides a preamble to the situation in the form of historical background on the origination of the issue and its contemporary relevance.

4.1. The Deanship of Admission and Registrations’ (DAR) Perspective on Capacity

4.1.1. Historical Introduction

The university began its first academic year in 1967 with the preparatory education program’s opening and a small number of students (68 males and 30 females). The first college in the university opened the following year (Faculty of Economics and Management), and a year after, the Faculty of Arts and Humanities was established [10].

The university transitioned from a private university to a state university after issuing the distinguished Council of Ministers resolution in 1974, incorporating it into the state. Another decision was issued to include the faculties of education, Shariaa, and graduate studies at King Abdulaziz University. These faculties were founded in 1949 in Mecca. They were subsequently separated and joined the University of Um al-Qura after its initiation.

The Kingdom’s adoption of this emerging university and its great support has impacted its transformation into a modern university with a current number of 140,000 students. Since then, it has retained a privileged position among higher education institutions in the Kingdom [10].

Following its establishment, King Abdulaziz University included branches of other universities. This included the University of Taiba in Medina, which eventually separated from it and later became independent. The branch of Tabuk University and the branch of Jazan University are of similar backgrounds and have now separated to become independent universities and the University of Northern Frontier branch. The university also includes two branches of the faculties of Araar and Rafha. The most recent of these is Jeddah University, a branch of the university which was later separated.

The university has established a curriculum for regular education and external education to facilitate studying for all citizens. In addition, the university has not been restricted to traditional teaching methods. Thus, it established the Deanship of Distance Education to keep pace with scientific, technical, and civilizational developments and enable the students who desire to continue their studies in university education to move forward towards a better future.

4.1.2. Students Admission

Currently, the university has around 141 scientific departments and 32 colleges in the main center and branches, serving approximately 140,000 students. The Deanship of Admission and Registration (DAR) performs its role in students’ admissions processes in each academic year. In all earlier historical stages, the university relied on simplified estimates of the capacity to admit bachelor’s and diploma students in university programs, thus accommodating them in the colleges and academic programs [11].

DAR annually reports the numbers of students admitted for the following year based on simplified statistics. The expected graduates are studied and replaced with the expected admitted number of students for the next year. However, this method inaccurately calculates the admission capacity and requires an advanced mechanism to support decision making. There are many significant challenges facing DAR and the university, as listed below.

4.1.3. Students’ College Enrollment Allocation (CEA)

After admission, students study the preparatory year programs, which usually accept between 12,000 and 18,000 students each year. After students complete the preparatory year, DAR discusses the numbers that each college can accommodate in a way that is not based on mathematical equations. This is carried out to determine the faculty’s ideal capacity and causes an accumulation of students in some colleges, while others have smaller numbers than they should; this is considered the first challenge [12].

After CEA, the second challenge is the confrontation between the students and DAR. The students approach DAR and apply thousands of requests to enroll in different colleges; most of these requests are rejected due to capacity issues. This is a distressing job for the deanship employees and leaders [13].

4.1.4. Students Transfer

The third challenge after admission and CEA is students’ requests to transfer from one college to another within the university. Through this, DAR provides an opportunity to students who did not have the chance to register after the preparatory year at their desired colleges. This transfer has several conditions. Some of these conditions are applied to all students as central conditions at the university level, such as [14]:

• The student must meet the transfer requirements and the college’s specified capacity;
• There should be no disciplinary sanctions in their academic record;
• The transfer should take place only once during the whole academic phase;
• In their current major, the student should not have studied more than half of the graduation requirements;
• All preparatory year courses should be completed;
• The student should have completed one or more semesters in their current faculty.

On the other hand, colleges have some precise requirements, such as accepting transfers from specific colleges and not from others or specifying standard courses that students must complete with specific grades to enter the differentiation system. Nevertheless, beyond all these conditions, the biggest challenge remains in the number of students that colleges can accept in the inter-college transfer phase.

Therefore, DAR’s vice dean in charge of the transfer conducts detailed negotiations with the colleges to accept as many students as possible and meet the students’ wishes in the best possible ways. This method’s flaw is the inability to accurately determine these colleges’ capacity.

4.1.5. The Major Rationale

The real suffering lies in the inability to identify the correct number of students that each college can accept, making it difficult for DAR leaders to agree with the colleges. DAR plays its part in raising the issues related to admission capacity and reviewing the transferring and registration criteria in the competent committees communal between the colleges and the deanship’s vice deans. Despite this fact, colleges impose more complex standards for students and accept smaller numbers than expected. The truth is that colleges cannot be blamed for their concern for educational and output quality; however, this requires the rationing of numbers.

To solve all of these challenges, equations should be in place (such as the models proposed in Section 6) to calculate all variables that help define the real numbers. However, collecting information on admission capacity requires obtaining data from various sources (as shown in Section 5) in the university, including the IT Deanship, the Curricula Centre, the Human Resources, and DAR, which requires considerable time and effort. Even if the information is available, there are difficulties in analyzing data and finding the right link between them. Therefore, a need arises to unite all relevant authorities in amalgamated teamwork with a group of experts and specialists.

4.1.6. KAU’s Attempt to Overcome the Challenges

In 2019, His Excellency, the President of the University, issued a decision to form a Standing Committee to study the colleges’ capacity and set transfer controls. This was carried out based on a DAR recommendation along with the Vice President for Academic Affairs. The Committee held several meetings and formed a sub-technical team to study the admission capacity. It also made several recommendations regarding the organization of transfers and admission capacity calculations [15].

4.2. First, Regarding Transferring

Before the establishment of the Technical Subcommittee to calculate the colleges’ absorptive capacity, the main Committee made some organizational amendments to the mechanisms of transferring students between colleges. These mechanisms arose to respond to some of the challenges that affect the colleges’ absorptive capacity. In general, some colleges have the desire and capacity to increase the number of students, but there were some conditions that limited the completion of transfers to them. Therefore, the Committee removed some obstacles and issued some amendments, including:

• When setting conditions such as obtaining specific grades in specific courses, such conditions should not be applied only to preparatory-year courses. They should also include higher-level courses;
• Transferring students and transfer seats should not be considered within the CEA numbers after the preparatory year, and specific seats should be allocated for transfer between colleges;
• When transferring, the student’s average is not required to be 3 of 5;
• If the college requests the criteria for transferring between colleges to be raised, the average should be elevated gradually and should not increase more than 0.25 from 5 for each academic year. These criteria should be applied to the next batch of students in the following year of adopting the recommendation after the faculty’s justifications are approved. However, this can be excluded if the college has justifications to be presented to the Committee;
• All colleges must provide transfer seats without exception, following the standards and regulations adopted by the Committee, and the college must establish the minimum standards it deems appropriate, of which the Committee should approve;
• Colleges should provide a transfer track for talented students in the college specialties so that the college provides a set of standard courses of no less than 6 and no more than 12 h of study and determines a degree of superiority as a transfer criterion without considering the average, termed the Transfer Path of Excellence;
• Subjects of the last semester for which no final score is recorded, such as IP, IC, and CN, are removed from the student’s grade sheet when transferring to another college;
• The transfer from external or distance learning to the regular program is not counted as a transfer opportunity, and the student can transfer from one college to another in the regular program.

On the contrary, there are some colleges that are in great demand by students wishing to transfer to them. There is also a branch in the city of Rabigh from which most students wish to transfer to the colleges of the main branch in the city of Jeddah. For this, the main Committee also developed some organizational solutions and added some requirements to put an end to the pressure for an absorptive capacity more than what is possible, including:

• The minimum average of a student transferred from the Rabigh branch to the main branch should be 4 of 5, plus a competition for seats to the transferred college;
• Transfer seats should suit the college’s size, the number of faculty members, and the rest of the faculty’s potential.;
• The admission capacity should be linked to the Committee’s findings, and the calculation capacity mechanism should be approved later;
• Requests to adopt the new conditions of the Committee are submitted in the minutes of the College Council before they are included and approved to ensure that the conditions are free from any violations of the education and exams regulation for the university stage and its executive rules.

4.3. Second, Regarding Capacity

Initially, the Committee formed a small commission to work on a form that includes almost all the relevant factors. They conducted a meeting with the colleges to adopt the form. They also conducted a survey and collected information from the colleges so that the relevant authorities and their scientific departments could be involved in achieving the best methods to calculate the capacity.

This is a summary of the small committee findings:

• A total of 18 colleges participated in the survey, with 37 scientific departments;
• This included 122 professors, 99 associate professors, 245 assistant professors, 170 lecturers, and teaching assistants;
• There were 7140 teaching hours in 4048 classroom seats, laboratories, studios, and clinics;
• Overall, there were 4800 teaching units in all programs for diplomas, bachelor, and postgraduate studies.

The Committee also accepted a study carried out by Said El-Quliti and others [16] to investigate the admission capacity at King Abdulaziz University, but the study posed many challenges:

• The urgent need to manage the academic load and distribute educational resources;
• The need to achieve acceptance policies proportionate to the academic workload;
• The need to assess educational capacities and plan for their distribution and use;
• The importance of a decision support system allowing the evaluation of various proposals and scenarios;
• Speed in planning procedures and thorough development of data and statistics to develop supportive academic management.

Hence, the Committee has confirmed the issues and the inputs that must be considered in the proper calculation of capacity, thus leading to high reliability at King Abdulaziz University regarding:

• The college’s infrastructure and spatial capabilities such as buildings, halls, laboratories, and training rooms;
• Supervision hours for graduate students;
• Assigning administrative work to faculty members;
• Attributing students to faculty members varying from one subject to another and from one college to another;
• The need for some colleges to teach courses to other colleges’ students in addition to teaching in the preparatory year;
• Not counting lab hours in some colleges;
• Increased capacity in some colleges or specialties that may affect the output quality, quality standards, and academic and institutional accreditation;
• The proposed admission numbers, which have been approved by the University Council, especially in health colleges that must be adhered to due to capacity limitations in laboratories and hospitals and for the sake of maintaining the quality of outputs;
• Considering the labor market needs as some specialties will witness future turnout, a fact that must be considered to keep up with future needs;
• Calculating non-traditional hours for faculty members such as health colleges requires working at the university hospital;
• A dynamic in recalculating the admission capacity based on variables each academic year, at least through electronic services and decision-making support systems;
• The admission capacity being counted at a lower level than the college level, as the department and specialization are more relevant due to some departments having more demand than others and also being subject to change;
• Using the available data from past years as a baseline for improving capacity calculations;
• Imposing a student ratio for a professor as recognized according to the college type (scientific—1:15, theoretical—1:30, health—1:5);
• Section characteristics in terms of section capacity based on academic accreditations and the nature of specialization;
• Data that should be read directly on electronic systems and not entered manually, as in the case of the current situation for the university education allowance;
• Instead of distributing the load on different terms, a load is assigned to the same professor for more than one semester, such as cooperative training and graduation projects;
• Calculating contact hours, not credit hours;
• Studying the possibility of removing under-performing students in colleges for more than the permissible period;
• Considering the training phase for health college students (internship year);
• Considering the time allowed to teach in the halls;
• Considering expansion plans and growth factors for colleges;
• The need to standardize and deal with data systems to overcome their duplication and inappropriateness;
• Starting from the fact that the university is classified as being for research and education and considering the support of faculty members who wish to reduce their load;
• Knowing the factors on which global standards are based and looking at past experiences;
• Reflecting on the relevance of the curriculum to the needs of the labor market.

4.4. The Departments’ Perspective on Capacity

Departments are the basic units forming the university organizational structure. However, they are the main and most salient operating units in the educational process and its outcomes. The total university capacity is highly dependent on the capacity of its departments and their available resources. The dynamic nature of demand in student numbers places departments under pressure to satisfy the job market and the community’s needs. Departments are constrained from accepting students beyond their capacities. This limitation is usually due to limited available educational resources (i.e., the number of instructors in each major domain in their programs and their teaching load capacity, classroom and seating capacity, lab capacity and available equipment, available daily time slots and schedule, etc.), the current number of students in their programs, quality of the education process, and accreditation requirements. Therefore, escalating student numbers, coupled with limited resources, necessitates effective capacity planning from a departmental perspective. Thus, from the departments’ perspective, for the university capacity planning to be accurate and effective, it should be conducted in a bottom-up fashion, which determines the maximum intake of students considering the constraints mentioned above to ensure a sustainable level of quality in the educational process. This framework requires capacity planning to start at the program level, which subsequently constitutes the departments, colleges, and ultimately the university’s total capacity, as shown in Figure 2. Bottom-up capacity planning imposed on the departments creates live data repositories to develop data-driven decision support systems, and this enables evidence-based planning. This data management requires the exchange of roles between the DAR and the departments. DAR needs to change from the planning and student’s assignment/allocation role to the strategic support/facilitator role of capacity planning from the top-down perspective, as seen in Figure 2.

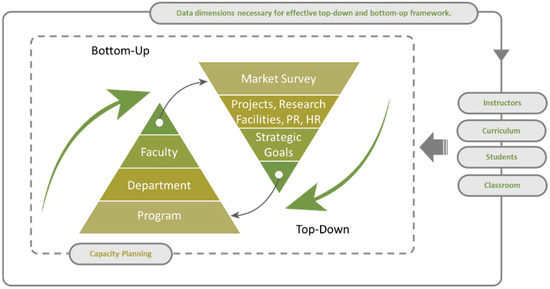
Figure 2. The proposed bottom-up and top-down framework of university student enrollment capacity planning.

5. Proposed Planning Framework for KAU Student Enrollment

The framework proposed for KAU student capacity planning is depicted in Figure 2. This procedure in an institution such as KAU must be iterative to account for the dynamic nature of the problem. The top-down part of the framework is surveyed, assessed, and studied in Section 6.1, where the bottom-up practice is in Section 6.2. The iterative process is repeated with adjustments with the goal of reaching a tolerance-based convergence between both parts of the framework.

The goal of the top-down process is to reflect external high-management expectations, strategies, and goals into the planned capacities. These expectations can be in the form of constraints, objectives, and/or input into the optimization problem. In contrast, departments need to effectively take the planning role of capacity considering all educational process aspects. In this manner, departments plan their capacity to support the deanship in high-level transparency, where the university capacity can be traced back to the program level. Despite the extensive data required and efforts that need to be exerted from the departments’ side, implications of the bottom-up approach exceed the accurate and effective capacity planning to enable evidence-based decisions, specifically those concerning human resources and recruitment, equipment procurement, classroom buildings, and extensions, scheduling, and other data dimensions, as can be seen in Figure 2.

To implement the proposed framework of this study, there is a need for data sources, which may include data of students currently in faculties, data of faculty members, number of classrooms, and training laboratories. There are additional details that must be obtained from the Human Resources Department, including the faculty members who have leadership positions, which affect the teaching load and thus affect the calculation of the absorptive capacity. Therefore, the authors prepared a table with data of the most important parties involved in capacity planning, including the name of the system or database at the university (Table 1). The required data were retrieved through the KAU’s Deanship of Information Technology.

Table 1. Data required for streamlining and automating the framework and their respective depository.

Classification	Data	Sector/Electronic Web-Based Systems
Faculty data	Job number	Human resources and Anjez system
	Faculty member’s name
	College
	Department
	Semester number
	Degree
	Weekly load according to degree	According to the organization’s list of faculty affairs (language instructor 18, teaching assistant and lecturer 16, assistant professor 14, associate professor 12, professor 10) and registered in the Anjez system according to the job title in human resources (employee information), human resources (salaries), and University Education Allowance System (Anjez).
	Number of leadership hours of administrative position assignment	Administrative decisions, human resources (salaries), University Education Allowance System (Anjez)
	Hours allocated for committees’ administrative work	University Education Allowance System (Anjez)
	Hours allocated for supervisory administrative assignment
	Hours allocated for the university teacher’s diploma
	Hours allocated for scientific theses supervision
	Hours allocated for joint supervision
	Actual teaching communication hours	University Education Allowance System (Anjez), ODUS-approved teaching load requests
Subject sections and students’ data	College	Admission, registration, ODUS system and educational affairs system
	Scientific department
	Subject code
	Subject number
	Semester number
	Section number
	Name of the subject teacher
	Number of students enrolled in the section
	Number of subject units approved in the student plan	Admission and registration, curricula center, and ODUS system using the students’ grade sheet
	Number of approved communication hours for the section	University Education Allowance System (Anjez), teaching load approval requests accredited by the ODUS Curricula Center
	The total number of students enrolled in subjects is calculated in the teaching load of faculty members	Admission, registration, ODUS, and educational affairs systems
	The total number of students enrolled in each program
	The total number of students enrolled in each department
	The total number of students enrolled in each college
Classroom and laboratory data	Number of classrooms allocated to each scientific department	University Vice-deanship for Projects, Deanship of Admission and Registration, and colleges’ Educational Affairs Vice-deanships
	Number of classrooms per college
	Number of laboratories per college
	Number of seats per semester
	Number of seats per lab
	Scheduling of classrooms and laboratories	Admission, registration, ODUS, and educational affairs systems
	Maximum capacity of students in one section according to the requirements of the program’s academic accreditation	Deanship of Quality and Academic Accreditation, Curricula Center, Colleges’ Development Vice-deanships

Central sectors related to providing services to all the above electronic sectors and systems: decision-making support center and IT Deanship. Anjez: web-based systems for human resources transactions. ODUS: On-Demand University Services, a web-based system for academic affairs.

6. Higher Education Student Enrollment Capacity Planning Methods & Techniques

Proceeding from the proposed framework in Section 5, two areas of planning methodologies are studied in the following sections. These two constitute the two parts of the iterative process of the proposed planning framework.

Many research studies exist in the literature, proposing methods and techniques to solve admission planning problems in higher education institutions. Since the 1960s, a diverse range of optimization techniques has been proposed to tackle higher education admissions planning problems. Some researchers have proposed solutions based solely on goal programming methods. Some have combined goal programming with other intelligent optimization techniques, such as classical mathematical modeling or decision support systems, whereas some have devised methods based on analytical approaches.

6.1. Methods Based on Goal Programming

6.1.1. Background and Literature

The goal programming method (GP) is one of the most powerful and result-oriented programming techniques within the last five decades. It is used to formulate and solve problems related to optimization mathematically. This method, either used alone or in conjunction with other classical optimization techniques, has been applied very successfully to solve higher education institutions’ admission planning problems. Numerous researchers and academicians have welcomed this method as the most suitable in problems related to optimization due to its capability to satisfy various end goals simultaneously. It also mediates the conflict of their priorities concerning the decision-making problem.

Lee and Clayton first devised the goal programming method in 1972 to allocate resources in higher education institutions. They studied a single college’s data in a single university in a single-year planning period. The model was developed for Virginia Polytechnic Institute and State University’s business college in the USA considering a single year’s data. It took into account variables and constraints related to the academic staff; for instance, it included their total number, distribution, and the number of graduate assistants for research. However, it did not take into account other factors related to educational processes [17].

In 1974, Schroeder devised a new method based on goal programming for academic recourse and budget planning in higher education institutions. The study was based on three years of data for three academic departments collected from the University of Minnesota, USA. The goal was to find the optimal faculty-to-staff ratio, faculty lecture load, faculty-to-teacher assistant ratio, and faculty ranking. The goals were subject to constraints related to the available planned budget in the three years and faculty availability. Decision variables included staff, faculty, and teacher assistant levels in various academic departments in the three years [18].

In 1974, Lee and Moore devised a new method based on goal programming to calculate students enrolled in various academic departments in higher education institutions. The study was based on data from a university in the USA. Decision variables included the number of admitted students in the in/out of state categories, new inductions, re-admissions, transfer cases, and all probable male/female combinations [19].

In 1981, Kendall and Luebbe devised a new method based on goal programming to manage student enrollment for a year in a college in Nebraska, USA. The study identified which activities were to be completed every three months in a year to achieve enrollment goals. The considered activities were human resources, time, budget, and marketing strategies. The study’s goal was to enable enrollment officers to enroll students within the planned budget [20].

In 1986, Soyibo and Lee devised a new method based on goal programming for optimal resource allocation over five years at the Ibadan University in Nigeria. The proposed model considered enrollment and faculty/staff goals for eight departments [21].

In 2009, Khan devised a new method based on goal programming for efficient enrollment management in higher education institutions. The study aimed to determine optimal faculty levels based on an optimal student mix [22].

In 2013, Kassa devised a new method based on goal programming to place enrolled students in departments for Bahir Dar University, Ethiopia, by streamlining the process and reducing the requisite staff hours [23].

In 2015, Qulity and Wagdy devised a new method based on non-linear integer goal programming to solve KSA’s student enrollment capacity planning problems. It used a modified differential evolution algorithm and utilized demographic data of KSA to present the experimental results [24].

In 2015, Quliti and Ragab et al. devised a new method based on a non-linear goal programming model (GPM) to solve the KSA student enrollment capacity planning problem. The proposed method was tested at King Abdulaziz University in the KSA to accomplish the crucial objectives of a 5-year plan in addition to a 25-year plan known as AAFAQ for higher education in the country [25].

In 2016, Quliti and Ragab et al. devised a new method based on large-scale non-linear integer goal programming to solve student enrollment capacity planning problems in the KSA. It used an improved differential evolution algorithm and utilized demographic data from the KSA to present the experimental results [26].

In 2016, Quliti and Ragab et al. devised a new method based on linearized integer goal programming to solve student enrollment capacity planning problems in the KSA. It used demographic data of KSA to present the experimental results [27].

In 2021, Ordu and Demir et al. applied a hybrid model that includes simulation, forecasting, and optimization. They created a linear optimization model to predict the needed bed capacity and staff demands of an England mid-size hospital. These findings were meant to provide important decision-makers with a new viewpoint by providing a decision support tool for short- and long-term strategic planning, allowing them to generate more reasonable and realistic plans, as well as highlighting the benefits of hybrid models [28].

Proceeding from the background introduced in this section, it is clear that goal programming-based techniques can be a valuable tool in developing a capacity planning framework. They can especially guide high-level strategic goals such as expansions and increasing the workforce.

6.1.2. Proposed Top-Down Process

In Equation (1), the general form of the objective function is introduced. This objective is subject to constraints acquired from the top-down process as well as the input. It is important to mention that Ω is the control variable; in this case, it is the allocated ‘planned’ students’ capacity.

$$f\left(\mathsf{\Omega }\right)=\underset{\mathsf{\Omega }}{\max }{\displaystyle \sum }_{h=1}^{H}SP{C}_h$$

(1)

This objective function is subject to several constraints; however, for the case of KAU as an illustration, the following constraints in Equations (2) and (3) are considered in the test case:

$$X={\displaystyle \sum }_{b=1}^B{\displaystyle \sum }_{c=1}^C{x}_c^b$$

(2)

$$CF={\displaystyle \sum }_{f=1}^F{P}_f$$

(3)

where $c$ is the classroom number in building number $b$, $C$ and $B$ are the total numbers of classrooms and buildings, respectively, $f$ is the faculty index, $F$ is the total number of faculties at the university, and $P_f$ represents the available hours for a faculty $f$.

In Figure 3, the general algebraic modeling system (GAMS) optimization platform has been used to test the validity of the proposed model. The optimization is interfaced with MATLAB using the GDX functionality to better incorporate data and access plotting functionality. The results in Table 2 show different strategic decisions; in this case, operational hours, the model provides the number of students planned.

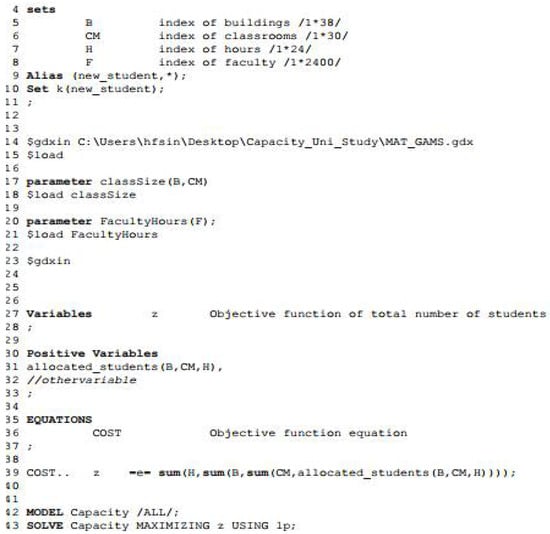
Figure 3. An excerpt of code used in GAMS to develop the top-down part of the planning framework.

Table 2. Results of the top-down method, showing different capacities based on the number of operational hours.

Operational Hours	Capacity
2	80,999
3	121,499
4	161,999
5	202,499
6	242,999
7	283,499
8	323,999
9	364,499
10	404,999

6.2. Methods Based on Decision Support Systems

6.2.1. Background and Literature

Decision support systems (DSS) have been devised as a relatively new and innovative approach to goal programming for higher education institutions to plan financials, allocate resources, devise admission policy, manage enrollment and funds, plan budgets, and schedule classrooms. DSS employs complex systems and gigantic databases to achieve the above-mentioned goals. Therefore, researchers have made several attempts to develop DSS to cope with one or more of these goals. One of the areas of DSS which has received special attention from researchers is related to resource allocation in higher education institutions.

In 1981, Franz and Lee et al. devised a DSS based on goal programming tested in a large higher education institution in the USA to support four decision-makers having varied problem-solving views to fulfill multiple conflicting objectives [29].

In 1991, Eliman devised a DSS to determine an optimal enrollment policy for a higher education institution in Kuwait. The proposed DSS consisted of an academic performance analysis module, demographic growth/regression analysis module, and student allocation module. This method had received positive feedback from the concerned decision-makers [30].

In 2005, Vinnik and Scholl devised a university capacity planning (UNICAP) DSS for a German university to optimize enrollment capacity planning and decision making employing the simulation/evaluation of strategic plans. The DSS integrated data from varied sources, applied online analytical processing (OLAP) techniques and allowed the interaction of decision-makers to test various strategies and their implications [31]. Additionally, in 2007, Mansmann and Scholl also presented an assessment methodology for educational capacity planning and resource utilization using a DSS with integrated input data sources and a graphical front-end for decision-makers for output presentation [32].

In 2010, Dahlan and Yahaya developed a decision support system to meet an academic program’s supply and demand needs contributing directly to optimal resource management. A system dynamics model was devised to achieve the goals [33].

In 2013, Alsharafat devised an intelligent DSS for enrollment management in higher education institutions employing multi aggregator models and evolutionary computing such as fuzzy logic, genetic algorithms, neuro-networks, and probabilistic reasoning [34].

In 2015, Kaur and Hasija presented a conceptual model of the admission system to assess university admission capacity with different factors affecting students’ performance [35].

Kaur and Hasija (2015), Trivedi (2013), and Baradwaj and Pal (2012) have all emphasized the importance of data mining and the potential advantages of using it in higher education, showing the need for more systematic decision-making support systems [35,36,37].

In 2017, Hallak and Ayoubi et al. devised a system dynamics approach to build simulation models that could be utilized to study the dynamic and dynamic interactions between student flows, infrastructure investments, and staff ratios in Syrian higher education institutions [38].

In 2018, Quliti and Ragab et al. devised a new method based on a hybrid strategic decision support system to solve the KSA student enrollment capacity planning problem. It used demographic data of KSA to present the experimental results [16].

In 2020, Win used statistical data analysis of a DSS on students’ intake for university admission using Dagon University students’ data for an effective decision-making process [39].

It could be observed from the previous literature that DSS is a strong approach advising the decision-making process, especially when making decisions in complex system situations with the existence of big databases. Student admission/enrollment capacity planning is regarded as a complex process in educational institutions. However, there is a perceived need for DSS frameworks that consider both the operational and the strategic sides of decision-making for the student capacity planning problem. Therefore, such a DSS-based framework will be the focus in this study to optimize and assist the student capacity planning decision-making process in universities based on the efficient utilization of their resources.

6.2.2. Proposed Bottom-Up Procedure

Following the proposed bottom-up framework demonstrated in Figure 2 and proceeding from the collected data in Table 1, the exercise to collect data for a sample faculty was conducted on the instructor, curriculum, and student data dimensions. Then, by fixing (maintaining) the student to faculty ratio, Equation (4) develops the model of the proposed formulation to plan the program-level capacity planning in a bottom-up approach. It converts the program input data acquired from the different data centers into one number, i.e., the student planned capacity for faculty ‘F’. This equation is then repeated for each faculty or program, all mounting up to a total student planned capacity for the university that is then compared to the top-down methodology for better tolerance management. The hierarchy of the cascading and summation of in each program ‘p’ for every department ‘d’ in college ‘c’ will provide the student planned capacity in the university for all colleges ‘C’ using all their departments ‘D’ for all their programs ‘P’. For better illustration, this hierarchical process is shown in Figure 4.

$$\mathrm{SPC}={\displaystyle \sum }_{c=1}^C{\displaystyle \sum }_{d=1}^D{\displaystyle \sum }_{p=1}^{\mathrm{P}}\frac{\left({\sum }_{\mathrm{f}=1}^{\mathrm{F}}{\mathsf{\Psi }}_{\mathrm{f}}\left(p\right) \right) * {\mathsf{\mu }}_{\mathrm{s}}^{\mathrm{c}}\left(p\right) }{{\overline{\mathrm{x}}}_{\mathrm{sc}}^{\mathrm{s}}\left(p\right){*\overline{\mathsf{\lambda }}}_{\mathrm{cn}}^{\mathrm{cr}}\left(p\right){*\overline{\mathrm{y}}}_{\mathrm{cr}}^{\mathrm{cs}}\left(p\right)}$$

(4)

where $\mathrm{SPC}$ is the student planned capacity for all programs in the university measured in students (st) for a pre-determined set of operational hours; ${\mathsf{\Psi }}_{\mathrm{f}}\left(p\right)$ represents the available contact hours for faculty ‘$\mathrm{f}$’ in program ‘$p$’ measured in hours per person (faculty), i.e., hr/f; ${\mathsf{{\rm M}}}_{\mathrm{s}}^{\mathrm{c}}\left(p\right)$ is the number of students registered in a course in program ‘$p$’; ${\overline{\mathrm{x}}}_{\mathrm{sc}}^{\mathrm{s}}\left(p\right)$ is the average number of sections, ‘courses’, each student is registered per semester in program ‘$p$’; ${\overline{\mathsf{\lambda }}}_{\mathrm{cn}}^{\mathrm{cr}}\left(p\right)$ represents the average rate to convert student credit hours to required faculty contact hours in program ‘$p$’; and ${\overline{\mathrm{y}}}_{\mathrm{cr}}^{\mathrm{cs}}\left(p\right)$ is the average credit hours for each section ‘course’ in program ‘$p$’.

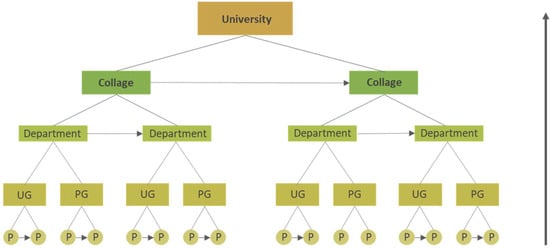
Figure 4. Bottom-up framework for KAU student capacity planning.

Given the extensive and expansive task of data acquisition required to perform the bottom-up procedure for KAU, a sample college has been chosen to provide conceptual validity and illustrate the significance of the proposed method. The college under study is the College of Engineering in KAU, which includes 8 different departments offering 14 undergraduate programs and 22 graduate programs.

Following the bottom-up model using Equation (4), the results are presented in Table 3. Figure 5 provides a visual summary of the results and demonstrates the optimal student capacity for the faculty of engineering. The horizontal axis represents the average number of students per section in the faculty charted versus the primary and secondary vertical axes representing the total number of students/faculty members and the consequential percentages of over/under capacity in contact hours on faculty members’ teaching load, respectively. Figure 5 shows that for the faculty of engineering to maintain a 1:10 faculty to student ratio and run on 100% teaching load capacity in terms of available contact hours (i.e., 0% over/underload in contact hours), the average number of students per section should be 17.1 students. This implies having a capacity of 3482 students and 353 faculty members with a teaching load of 3608 contact hours.

Table 3. Results of the bottom-up model, showing the different cases of utilization levels *.

The Average Number of Students per Section	Total Number of Students	Over/Under Capacity in Number of Students	Total Number of Faculty Members	Contact Hours	Over/Under Capacity in Number of Faculty Members	Over/Under Capacity in Total Contact Hours of Faculty Members’ Teaching Load	Percentages of Over-/Under Capacity in Total Contact Hours of Faculty Members’ Teaching Load	Percentage of Utilized Teaching Capacity Relative to Available Teaching Load Based on Number of Students
1	204	−3278	21	211	−333	−3397	−94%	6%
2	407	−3075	41	422	−312	−3186	−88%	12%
3	611	−2871	62	633	−291	−2975	−82%	18%
4	814	−2668	83	844	−271	−2764	−77%	23%
5	1018	−2464	103	1055	−250	−2553	−71%	29%
6	1221	−2261	124	1266	−229	−2342	−65%	35%
7	1425	−2057	145	1477	−209	−2131	−59%	41%
8	1629	−1853	165	1687	−188	−1920	−53%	47%
9	1832	−1650	186	1898	−167	−1709	−47%	53%
10	2036	−1446	207	2109	−147	−1499	−42%	58%
11	2239	−1243	227	2320	−126	−1288	−36%	64%
12	2443	−1039	248	2531	−105	−1077	−30%	70%
13	2647	−835	269	2742	−85	−866	−24%	76%
14	2850	−632	289	2953	−64	−655	−18%	82%
15	3054	−428	310	3164	−43	−444	−12%	88%
16	3257	−225	331	3375	−23	−233	−6%	94%
17	3461	−21	351	3586	−2	−22	−1%	99%
** 17.1041	3481.9985	0	353.3172	3607.8735	0	0	0%	100%
18	3664	182	372	3797	19	189	5%	105%
19	3868	386	392	4008	39	400	11%	111%
20	4072	590	413	4219	60	611	17%	117%
21	4275	793	434	4430	80	822	23%	123%
22	4479	997	454	4641	101	1033	29%	129%
23	4682	1200	475	4852	122	1244	34%	134%
24	4886	1404	496	5062	142	1455	40%	140%
25	5089	1607	516	5273	163	1666	46%	146%
26	5293	1811	537	5484	184	1876	52%	152%
27	5497	2015	558	5695	204	2087	58%	158%
28	5700	2218	578	5906	225	2298	64%	164%
29	5904	2422	599	6117	246	2509	70%	170%
30	6107	2625	620	6328	266	2720	75%	175%
31	6311	2829	640	6539	287	2931	81%	181%
32	6514	3032	661	6750	308	3142	87%	187%
33	6718	3236	682	6961	328	3353	93%	193%
34	6922	3440	702	7172	349	3564	99%	199%

* All scenarios are based on an approximately 1:10 faculty-to-student ratio. ** Shaded cells represent the optimal student capacity scenario (i.e., 100% utilization).

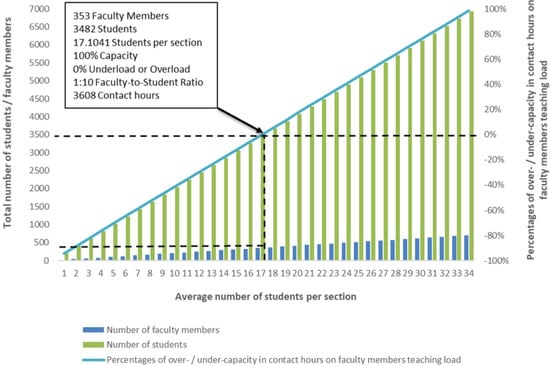
Figure 5. Utilization levels pertaining to the number of faculty members and the number of students and their relationship with the average number of students per section.

The Faculty of Engineering currently has 3515 students and 350 faculty members, with an available teaching load of 3574 contact hours. Therefore, it can be concluded that the faculty is over the student capacity by 33 students (i.e., 3515 − 3482 = 33), is short by three faculty members (i.e., 353 − 350 = 3), and is running over the available teaching load capacity by 34 contact hours (i.e., 3608 − 3574 = 34).

This approach is beneficial to calculating the student capacity and supporting admission/enrollment-related decisions. Furthermore, it can be used for human resources planning, teaching load planning, faculty-to-student ratio sensitivity analysis for programs accreditation and quality requirements, lab capacity planning, equipment/teaching aids procurement, and financial planning, only to mention a few, especially if used at the program level.

7. Roadmap

The following chart shown in Figure 6 represents the transitional roadmap for institutions undergoing similar mandates. It requires a deep understanding of the current situation (BAU) and modifying the policies via technical and non-technical means. This process is iterative, as it involves continuous improvement. The first three steps of the roadmap (input and policy adjustments, assessment, and committees) are established in Section 4 and Section 5. Moreover, data streamlining is summarized in Table 1. Additionally, the remaining parts of the roadmap are proposed in the framework.

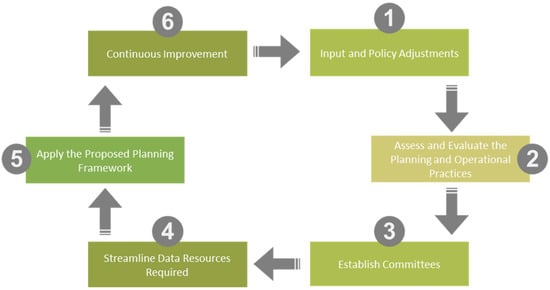
Figure 6. Transitional roadmap to an enhanced capacity planning practice.

8. Conclusions

The objective of this research study was to put forward a capacity planning admission/decision support system (DSS)-based framework for student enrollment and admission for universities. The case of KAU was presented in terms of current practice and challenges. Furthermore, the goal programming technique and the developed mathematical model were applied in top-down/bottom-up approach fashions, respectively. Results show that the proposed framework effectively affects student admission/enrollment capacity planning on both the strategic (top-down) and operational (bottom-up) levels. Moreover, the framework provides evidence that matching student admission/enrollment capacity planning efforts on both strategic and operational levels can facilitate other planning aspects of higher education in universities, including in human resources planning, teaching load planning, faculty-to-student ratios, accreditation, quality requirements, lab capacity planning, equipment/teaching aids procurement, and financial planning, to mention a few.

Resource planning in higher education institutions is currently an open research area. Further research is needed in various directions to devise effective, efficient, and integrated decision support systems over national levels for large planning periods. Applying the proposed framework to other programs, departments, faculties, and universities is a future research direction that ensures its validity and generalizability. Moreover, the development of capacity planning admission/decision support system (DSS)-based frameworks following other techniques and approaches involving simulation-based studies and artificial intelligence (AI)-enabled learning methods are other future research directions. Finally, the development of a user-friendly, web-based DSS for student admission/enrollment capacity planning is becoming a necessity.