1. Introduction
Search-based software engineering (SBSE) applies search-based techniques to software engineering tasks, of which an important one is the improvement and generation of software. This task is difficult to achieve due to several reasons, including the complexity of modern programming languages, the difficulty in evaluating the generated software, and the linearity of code—a small change might “break” the entire program’s behavior. To overcome these difficulties we propose the use of genetic programming (GP) to evolve behavioral programs.
Context-oriented behavioral programming (COBP) [
1] is a software development and modeling paradigm designed to allow users to program reactive systems in a natural and intuitive manner that is aligned with how humans perceive the system requirements. A behavioral program consists of a set of context-dependent scenarios (that state what to do) and anti-scenarios (that state what not to do), which are interwoven at run-time to generate a combined reactive system. Each scenario and anti-scenario is specified as a sequential thread of execution that isolates a specific aspect of the system behavior, preferably an individual requirement; it is referred to as a
b-thread. An application-agnostic execution mechanism repeatedly collects these scenarios, chooses actions that are consistent with all the scenarios, executes them, and continuously informs them of each selection. We elaborate on COBP in
Section 3.
A behavioral program has unique characteristics that makes it an excellent candidate for code evolution:
Repetitive structure, which allows for a simple representation of a program as an abstract syntax tree (AST).
Small independent components that are easier to change and adjust, since in many cases breaking one b-thread has little effect on the other b-threads.
Synthesis, formal reasoning, and verification algorithms can be used to evaluate a generated program’s performance.
In this paper we demonstrate how COBP programs can be evolved through GP, showcasing the benefits of COBP by focusing on the game of tic-tac-toe. Specifically, we evolve
from scratch a highly competent O player specified as a set of b-threads. Creating such a player requires the specification of different behaviors, such as place third “O” when possible, block “X” from winning, etc. We will show evolution created from scratch a complete program that consists of different modules that specify these behaviors. Most work on code evolution focuses on genetic improvements of existing code and code evolution of small modules, such as methods (elaborated in
Section 2). Thus, while tic-tac-toe may be seen as a toy problem, creating a complete program from scratch is complicated. We are aware of no attempt at generating from scratch a complete program for tic-tac-toe.
As we will show, our evolved individuals have the repetitive structure of behavioral programs. Most modules of our best individual are self-explanatory and adhere to a known strategy for the game.
For evolving COBP programs, we design the following: a domain-independent grammar for behavioral programs, augmented with terminals for tic-tac-toe; type-based, COBP-oriented genetic operators; and a fitness function that uses a behavioral program’s flow of events.
The contributions of our work are as follows:
- 1.
We provide a methodology and tools for evolving complete programs from scratch.
- 2.
We design a domain-independent grammar for behavioral programs.
- 3.
We design domain-independent, type-based, COBP-oriented genetic operators.
- 4.
We evolve a highly competent player for tic-tac-toe.
- 5.
Our evolved programs are well structured, consisting of multiple modules that are explainable and similar to our handcrafted program.
We first present a short survey on the field of SBSE and code-generation in
Section 2, followed by a short primer on behavioral programming in
Section 3. We then explain our method in
Section 4 in detail, and present our results in
Section 5. Finally, we present concluding remarks in
Section 6.
2. Previous Work
The earliest example of code generation is probably that of [
2], who evolved small multiplication functions using two specially designed languages. Koza notably took this idea several steps forward [
3]. A more recent example is that of Orlov and Sipper [
4,
5], who were able to generate Java functions by evolving Java bytecode directly. Despite these examples and others, automated programming has never managed to achieve a substantial breakthrough. In fact, Dijkstra stated that automated programming was a contradiction in terms [
6]:
…computing science is—and will always be—concerned with the interplay between mechanized and human symbol manipulation, usually referred to as “computing” and “programming”, respectively. An immediate benefit of this insight is that it reveals “automatic programming” as a contradiction in terms.
Petke et al. [
7] explains that many influential authors regard the challenge of automated programming to be simply unattainable, and thus more recent research focuses on automated testing and genetic improvements of software, rather than complete automated code generation.
Genetic improvement (GI) uses GP and other automated search methods to improve upon existing programs. The benefit of improving existing code instead of generating it from scratch is clear: GI starts with an existing base and as such involves a far more focused search space. GI touches on a number of different topics such as program transformation, program synthesis, GP, testing, and SBSE [
7].
GI uses the fact that naturally occurring code is very repetitive [
8,
9], and as such the practical space of naturally occurring code is much smaller than its theoretical space. We examined several core GI papers (defined as such by Petke et al. [
7]) to understand how these semi-generated programs can be represented, evaluated, and evolved.
2.1. Representation
There are number of ways to represent programs for GI, such as source code, bytecode, and the most common way—abstract syntax trees (ASTs). ASTs are a very natural approach to represent programs for use with GP techniques, since they are already in tree form. ASTs can also be applied to many different types of languages, including C [
10,
11], Java [
11], Python [
12], and b-programs. When introducing
GenProg, a tool for automatic bug repair, Le Goues et al. [
13] represented individuals as patches, a sequence of edit operations for an AST, a solution that drastically improves space complexity for large programs.
Another viable representation is binary or bytecode representation, examples of which include Schulte et al. [
14], who repaired defects in ARM, x86 assembly, and ELF binaries, and Orlov and Sipper [
4,
5], who evolved Java bytecode. This representation offers several benefits, stated by Schulte et al. [
15], including potentially being applicable to many programming languages, a small set of instructions, and simple syntax; these benefits also apply to b-programs.
Evolving b-programs combines the benefits of both approaches: We employ the natural and convenient representation of ASTs, while still maintaining benefits gained from a binary representation, since the paradigm has been implemented in many underlying languages, including Java [
16], JavaScript [
1], C [
17], LSC [
18], and more.
Petke et al. [
7] noted that a natural question in GI is concerned with translating code for parallel processing, and cited early work on
Paragen [
19,
20]. It is worth noting that COBP is inherently parallel—b-threads run internal logic in parallel [
16].
2.2. Evaluation
Most GI works use testing as the main fitness criterion, with the simplest way to calculate fitness based on the number of total tests passed [
21,
22], or using a weighting of tests [
23]. Arcuri and Yao [
24] evaluated fitness using a distance function based on a formal software specification. They also introduced the process of co-evolving test cases, and generating unit tests that pass on the original program but fail on the modified ones.
Overall, it is apparent that testing is the most dominant evaluation parameter for fitness calculation; however, with COBP, formal methods and verification techniques can also be used to evaluate the correctness of b-programs, due to the mathematical properties of COBP semantics.
3. A Short Primer on Context-Oriented Behavioral Programming
In context-oriented behavioral programming, requirements are implemented
independently from each other. Each requirement is encapsulated by a behavioral thread, or
b-thread. A collection of such b-threads forms a
b-program. The COBP paradigm has emerged from the behavioral programming paradigm [
16], extending it with context idioms that enable the definition of context-dependent requirements. In this paper we use a JavaScript implementation of COBP, called COBPjs (
https://github.com/bThink-BGU/BPjs-Context, accessed on 28 January 2022). The code in this paper can be found at
https://github.com/RoyPoli99/BPCodeGenerator, accessed on 28 January 2022.
To render these ideas more concrete we demonstrate the paradigm on the game of tic-tac-toe. There are several reasons for choosing this game:
While simple to play, a tic-tac-toe strategy is far from simple to evolve. The strategy for the game has eight different behavioral aspects (elaborated below) and learning all of them from scratch is a complex task.
The game rules include scenarios and anti-scenarios that demonstrate the power and simplicity of the paradigm in specifying reactive systems.
The number of possible game traces is relatively small, allowing us to formally prove the quality of our solution.
We begin with a behavioral program for the game that specifies only the requirements of the game’s rules. The requirements are as follows:
A cell can be marked only once.
X and O take alternate turns playing, with X starting.
The first player to obtain three marks in a line is the winner.
If no player wins and all nine squares are marked, a tie is declared.
The game ends upon a tie or a win.
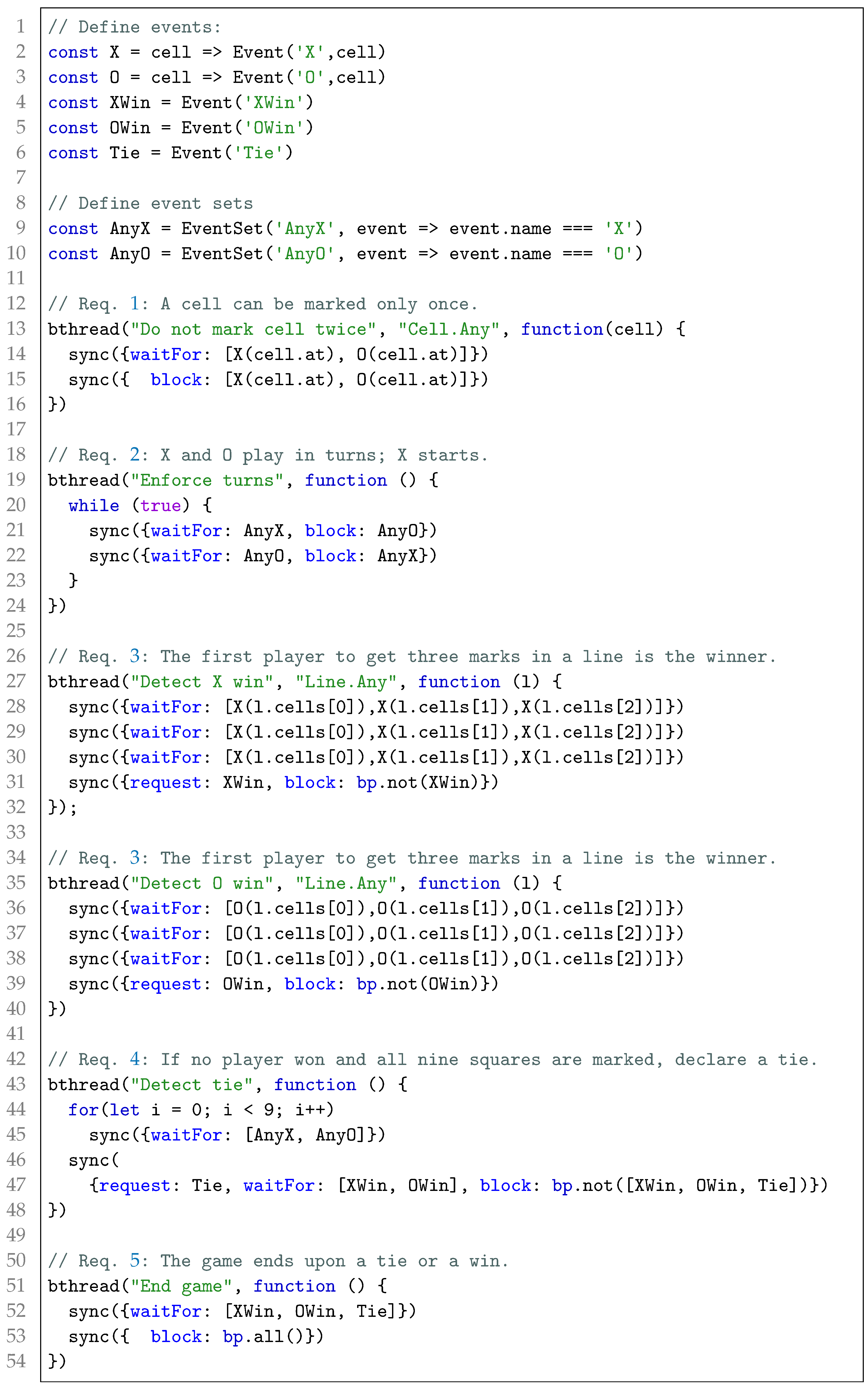
We note that the context of Requirement 1 is a cell and the context of Requirement 3 is a line. To define the behavior of these requirements, we first need to define the system context, as presented in Listing 1. The code begins (lines 1–16) with a definition of the contextual data as a set of entities, each having a unique identifier (the first parameter of the
ctx.Entity function), a type (second parameter), and data (third parameter). In addition, the context definition also includes two named functions—
Cell.Any and
Line.Any (lines 18–28). These functions are used to query the contextual data and return only the relevant entities. In this example, the queries always return the same answer since the context does not change throughout the lifetime of the game (e.g., cells and lines are not added/removed during the game). Nevertheless, COBP also supports dynamic changes to the context. To support such dynamics, the queries can be defined as functions rather than a predefined array of entities (see [
1] for further information).
Now that we have the context definition, we can define the rule requirements, including the context-dependent requirements, as presented in Listing 2. We begin with a syntax explanation, followed by an an outline of the execution semantics (the full semantics are defined in [
1]).
Listing 1. The context definition in COBPjs for the game of tic-tac-toe.
Listing 2. Tic-tac-toe rules, specified in COBPjs.
B-threads in COBP interact through events; thus, we begin with the definition of the possible events in the game (lines 1–6). X and O are functions that takes a cell entity and return an event with the name X or O, respectively, and the given cell as the event’s data. A set of events can be defined using an array of events (e.g., line 14), or using a function that takes an event and returns true if the event is in the set (i.e., AnyX and AnyO in lines 9–10). Another way to define event sets is using bp.not(e) and bp.all functions (i.e., lines 39 and 53). The first returns true for events that are not e, and the latter for all events.
The first b-thread (lines 1–5) specifies the first requirement: a cell can be marked only once. The context of the requirement is a cell, therefore the b-thread is bound to the Cell.Any query. As a result, for each answer to this query (i.e., for each cell entity), the execution mechanism of COBPjs will spawn and execute a live-copy of this behavior with the specific answer (i.e., cell) given as a parameter. The behavior itself (lines 3–4) waits for X or O events with this cell and then blocks any attempt to place another X or O there. The second b-thread (lines 7–13) defines the “turns” requirement, repeatedly blocking O while X is playing, and vice versa. This b-thread is not bound to any query since the requirement is not context-dependent. Similarly, the following b-threads handle winning and tie situations.
We note that the code in Listing 2 only imposes a correct behavior according to the game rules. When no one requests X or O events the game does not start. To start, we can create random X and O players by binding an additional b-thread to the Cell.Any query that has a single line: sync({request: [X(cell), O(cell)]}).
Although b-threads are independent from each other, they still need a way to synchronize with other b-threads. In COBP, whenever b-threads reach a sync statement, they submit their statement—what they request, waitFor, or block—to an application-agnostic central event arbiter, and halt. The arbiter selects an event that was requested but not blocked, and resumes all b-threads that are waiting for, or requested, the selected event, until the next synchronization statement. This simple protocol generates a cohesive behavior that is consistent with all b-threads. Notably, the protocol does not dictate the order in which actions are performed (e.g., given the random X and O player, the first X may be placed at any of the nine cells). To create a highly competent player for the game, which does not lose, and wins when possible, we need additional strategy b-threads that will prioritize the possible actions.
3.1. Hand-Crafted Strategy B-Threads for Tic-Tac-Toe
In the sections ahead we will use GP for evolving strategy b-threads for tic-tac-toe. Herein, we present a hand-crafted version for these b-threads, toward which end we begin with a description of Newell and Simon’s strategy [
25], consisting of eight rules with diminishing priorities, meaning that at each turn the players should play the first available rule:
- 1.
Win: If the player has two tokens in a line, then the player should place the last cell.
- 2.
Block: If the opponent has two tokens in a line, then the player should place the last cell.
- 3.
Fork: Cause a scenario where the player has two ways to win (two non-blocked lines with two tokens).
- 4.
Blocking an opponent’s fork: If there is only one possible fork for the opponent, the player should block it. Otherwise, the player should block all forks in any way that simultaneously allows them to make two-in-a-row. Otherwise, the player should make a two-in-a-row to force the opponent into defending, as long as it does not result in their producing a fork.
- 5.
Center: A player marks the center.
- 6.
Opposite corner: If the opponent is in the corner, the player plays the opposite corner.
- 7.
Empty corner: The player plays in a corner square.
- 8.
Empty side: The player plays in a middle square on any of the four sides.
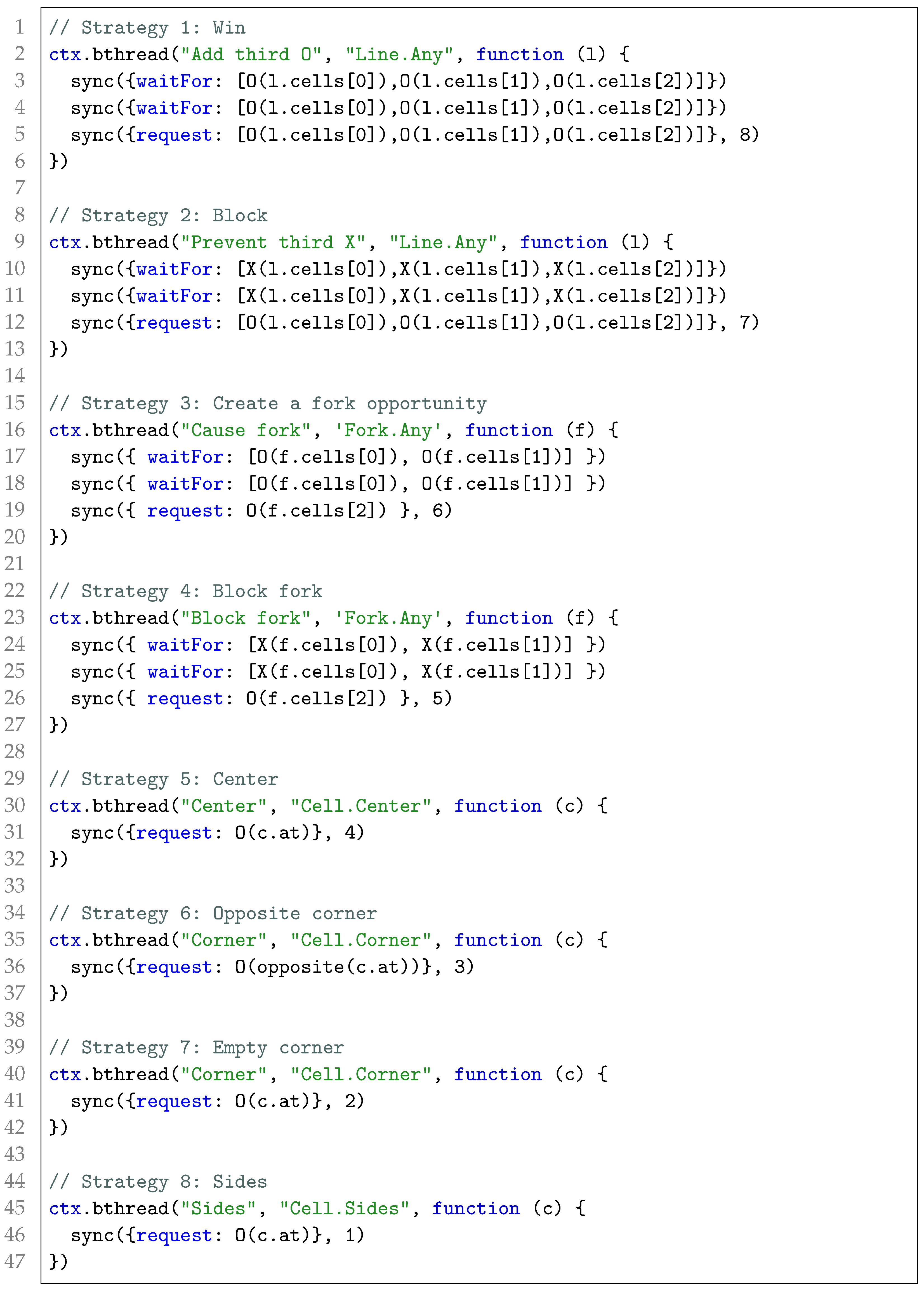
Listing 3. Strategy b-threads for an O player.
Listing 3 presents the code for a highly competent O player. The numbers at the end of the sync statements represent the priority of the events. The selected event will have the highest priority. Listing 3 also introduces new queries:
Fork.Any,
Cell.Center,
Cell.Sides, and
Cell.Corners. We do not elaborate the definition of these queries, though evolution will find them, as shown below. In
Section 5 we compare the evolved strategy b-threads to these hand-crafted ones.
We note that most rules are well defined and their implementation is thus straightforward. Nevertheless, the two fork rules (3 and 4) are unclear and the implementation is thus not aligned to them. While in the next section we will evolve the entire strategy b-threads, we note that in complex domains users may add hand-crafted strategy b-threads to the base individuals’ programs, and learn others.
3.2. COBP Characteristics
The code in the above listings reveals some of the unique characteristics of behavioral programs.
First, we observe the repetitive structure of many b-threads, with each having roughly the same body. This structure allows for a simple representation of a program as an abstract syntax tree (AST).
Second, because each b-thread defines a single aspect of the system’s behavior, the behavioral programs are self explanatory. As we will show in
Section 5, the evolved programs share this same characteristic, resulting in simple and explainable programs generated by evolution.
Third, COBP’s execution mechanism is based on the mathematically rigorous nature of the COBP semantics. These semantics afford the application of formal methods and verification algorithms to verify the correctness of a program, i.e., that it behaves correctly for any input. Here, we do not use this property for evaluating the individuals during evolution, though we will use it for validating the quality of the evolved individuals.
4. Method
In this section we describe our experimental setup for evolving behavioral programs. Aside from the fitness function and some parameters, the approach is domain-independent and may be applied to any behavioral program. The algorithm requires baseline b-threads (here, the entities and the rule b-threads from Listings 1 and 2), a fitness function, and terminals for the grammar (elaborated below). The algorithm outputs a set of b-threads that together with the baseline b-thread construct a complete, modular behavioral program. In our case, we want the algorithm to generate the strategy b-threads that constitute, along with the baseline b-threads, a program of a highly competent O player.
4.1. Grammar
We use grammar-based GP to evolve the program. The grammar is mostly domain-independent (except for the terminal set) and utilizes the repetitive nature of a behavioral program.
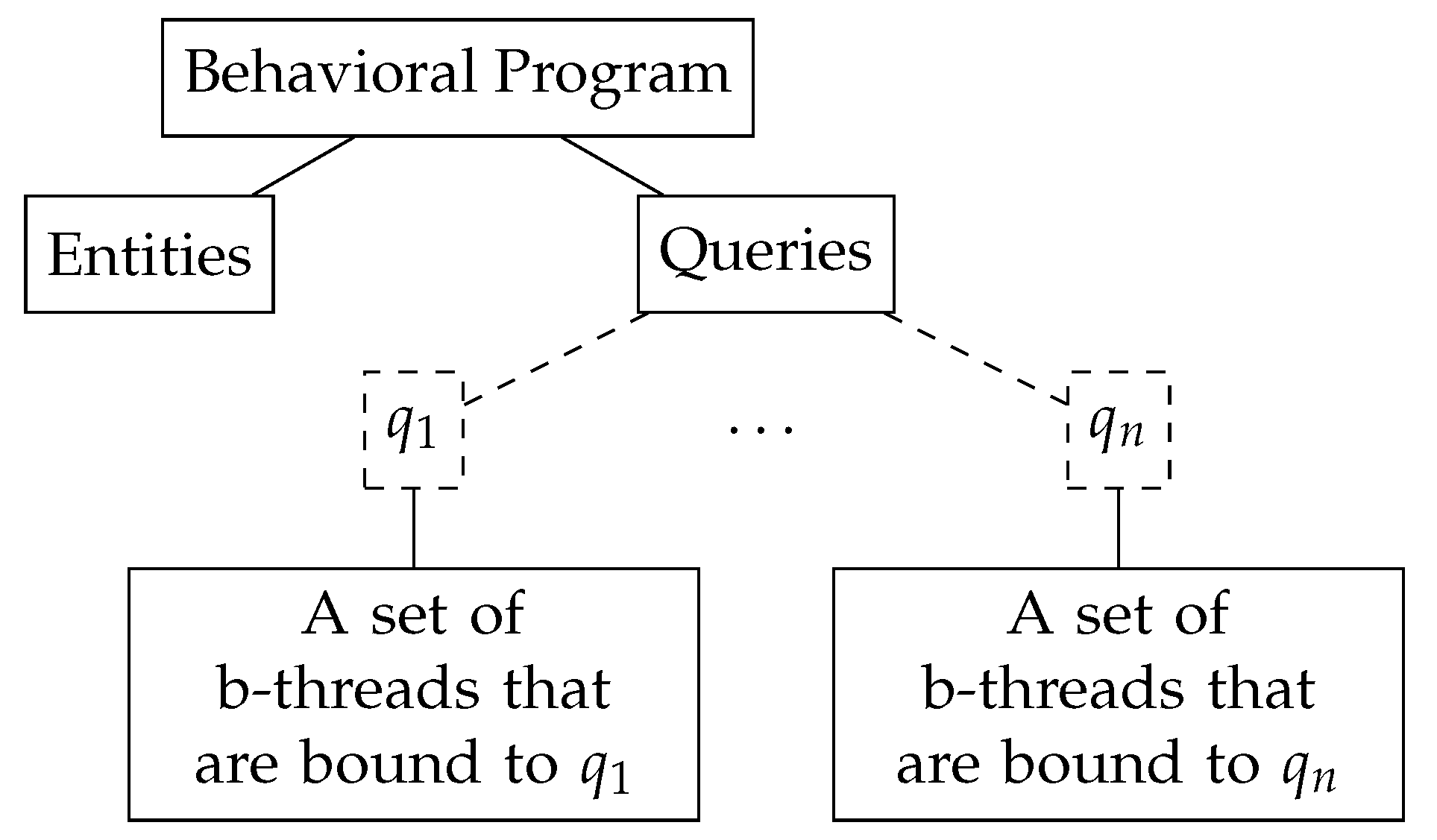
The structure of a general behavioral program is illustrated in
Figure 1. The program consists of contextual data, represented as a set of entities, queries on these entities, and context-dependent behaviors, each bound to a single query. For example, in Listing 2, there are two types of entities—
cell and
line. The queries are
Cell.Any and
Line.Any, and each of the context-dependent b-threads is bound to one of these queries. We recall that for generating strategy b-threads, additional queries and behaviors are required (
Cell.Sides,
Cell.Corners, etc.).
In the following experiments we want evolution to find both the b-threads and all context queries, including Cell.Any and Line.Any. We note that a context query is essentially defined as a set of entities. For example, Cell.Any is a set of nine sets, each containing a single cell entity. Similarly, Line.Any is a set of eight sets (three rows, three columns, and two diagonals), each containing three cell entities in a line. Thus, the queries in our grammar are parameterized by the size of the internal sets.
The grammar is presented in Listing 4; it is divided into two parts: a general grammar for any COBP programs, and specific terminals for tic-tac-toe. The general grammar can be generalized even more, e.g., by allowing multiple requests or by allowing waitFor and request in the same synchronization statement. Nevertheless, this grammar is general enough for our task and, from our experience with COBP, it is popular in programs as well. The specific grammar for tic-tac-toe is also general, in the sense that it only defines the entities and events that were defined by the rule b-threads. In addition, this part of the grammar configures the maximal possible priority and the maximal number of queries, behaviors per query, and entities. These values act as estimations that help evolution by placing boundaries on the size of the individuals.
Listing 4. Grammar for evolving strategy b-threads for tic-tac-toe.
4.2. Fitness Function
To evaluate an individual program we let it play 100 games as follows:
A total of 25 games vs. a player that does not lose, where the generated program plays first.
A total of 25 games vs. a player that does not lose, where the generated program plays second.
A total of 25 games vs. a random player, where the generated program plays first.
A total of 25 games vs. a random player, where the generated program plays second.
The player alternated between playing first and playing second in order to prevent evolution from succumbing to a bias, since the first player has an advantage because it has the opportunity to make more moves in a single game. Further, we alternated between players that do not lose and and random players because playing only against the first type of players did not allow the generated programs to learn how to win games. In addition, playing only against random players did not allow the generated programs to learn how to block the opponent from winning.
Given these 100 games, the fitness function was
Number of times that the individual missed an opportunity to win/block the opponent from winning.
The first two parts take into account how decisively the generated program won when given the opportunity, and how decisively it blocked the enemy from winning when possible. Additionally, to complete the game (i.e., reach a tie or a win), the individual must request for at least one event that is not blocked, whenever it is the turn of the O player. To address this, we added a penalty part to the fitness that reduces one point for each non-completed game. Finally, to push evolution further, we used fitness pressure (denoted by ) for each of the two parts. Thus, the fitness values were in the range of .
4.3. Genetic Operators
Our design of the genetic operators is based on two observations. First, generally speaking, b-threads may be correlated in several ways. For example, the strategy b-threads in Listing 3 have different priorities, thus defining an order for applying each strategy. As another example, consider the “turns” b-thread to be missing, in which case the program will not be able to generate correct game traces.
The second observation relates to the method for selecting the node for performing crossover or mutation. It makes no sense to perform crossover in the middle of a behavior, since it is a single logical unit with a high correlation between its different lines. Similarly, replacing an entire behavior will most likely result in a behavior that does not work well with the other behaviors. Therefore, uninformed, domain-independent genetic operators (e.g., single point crossover) yield poor results.
To keep the correlation between the different behaviors, we set the probabilities for applying mutation and crossover operators to be 70% and 5%, respectively. Thus, evolution was driven mostly by exploitation, rather then exploration.
For selecting the nodes for the operators, we grouped the nodes into four types, and defined a different probability for selecting each type, depending on the operator. The operators first selected a group type, and then uniformly selected a node in the group. The node types and the probabilities for selecting them are summarized in
Table 1. These probabilities were reached through empirical testing.
After selecting the node, the mutation operator replaces its sub-tree by growing another sub-tree instead, and the crossover operator replaces the sub-tree with a sub-tree from the second individual. Since the grammar is strongly typed, the crossover operator has additional constraints for selecting the node in the second individual.
4.4. “Smart” Test-Driven Genetic Operators
The first genetic operators served as a baseline for future enhancements and for presenting the capabilities of behavioral programming as a tool for evolving source code. In our second experiment, we proposed to evaluate tree nodes according to their contribution to the entire program—whether the contribution was “good” or “bad”. Then, we used these evaluations for developing smart genetic operators, by selecting the nodes according to their evaluation values.
Our smart, test-driven mutation and crossover operators are rooted in the field of
fault diagnosis [
26]. Fault diagnosis is the process of determining the type, size, location, and time of detection of a fault. We considered “bad moves” the generated program performed as faults in the code. We then applied diagnosis techniques to find “faulty” nodes in our program. Additionally, we used the same strategy to find “good” components in the code. For each win, win miss, block, and block miss, we noted the last node that was involved, and calculated each component’s score accordingly—wins and blocks increased the score, while win misses and block misses decreased the score. For example, if the last event was
OWin, then the win counter will be increased for the following nodes: the
node that represents the b-thread that requested the last O event, the
node of the behavior (i.e., the context of the b-thread), and the
node that contains the entity and the behavior. We also added a small bonus for every move the component was involved in, in order to discourage “timid” components, which did nothing. The smart operators still selected the node type using the same probabilities, but the node inside the group was selected according to the component score, rather than uniformly, with contrastive formulas for mutation and recombination:
The reason for this change is that in recombination we provide a higher chance for exchanging good nodes among individuals, and in mutation we provide a higher chance for replacing bad nodes. To select the actual node we used the same proportionate-selection mechanism of roulette wheel. Thus, the node score acts as an estimation for the node quality, but other nodes still stand a chance of being selected. For the same reason, a score of zero or less was reset to one.
5. Results
We tested our approach both with the basic operators and with the smart ones—and compared the results. Further, we also examined the playing capabilities of the evolved programs. The evolutionary hyperparameters are summarized in
Table 2. Notably, on a computer with an Intel i7 CPU, running 100 random games sequentially takes roughly three seconds and 500 MB. The memory footprint can be reduced to 4 MB at the expense of an additional second, by running the garbage collector after each run. Thus, while we executed 3 M random games at each generation, complete runs with no parallelization took less than four hours.
Over several experiments the basic operators managed to achieve an individual with maximum fitness score of 94 out of 100; the best individuals from these experiments consistently appeared as early as generation 250. The smart operators managed to generate a better best-performing individual, with a fitness value of 97.5. It is worth noting that this specific individual missed a block only seven times, throughout all 100 games, and it did not miss a single win opportunity. Individuals with fitness above 95 consistently appeared as early as generation 150, nearly 100 generations faster than the basic mutation operators.
To compare the performance of the operators, we selected the best two individuals at generations 50, 150, and 300. We then applied the operators 1000 times on these individuals, cloning the original individuals before applying the operators.
Table 3 shows the percentage each operator improved the fitness of the individual it was performed on, based on these 1000 runs. As results show, the smart operators were far more effective than the basic operators. The basic mutation performed worse almost always. The smart crossover outperformed the basic crossover in both parameters, except for generation 150, probably due to the fact that runs with the smart crossover had already reached a high fitness by this time.
5.1. Validation of the Evolved Players
To validate the correctness of our (O-playing) individuals, i.e., that they behave correctly for any opponent X player, we used the verification mechanism of COBPjs. Using this tool we mapped the state space of a game between two random players, thus generating all possible states of tic-tac-toe. Next, we traversed the graph and generated all possible 255,168 game traces (excluding symmetry). The first player wins 131,184 of these, the second player wins 77,904 traces, and the remaining 46,080 are a tie. To validate our individuals, we performed the same computation for our evolved players and compared the generated traces.
Table 4 presents the results for our best individual of all runs. This individual reduces the number of times X wins to less than 1% and the number of missed possible wins to less than 0.01%. The results were similar no matter who started.
5.2. Individual Representation
Listing 5 presents the context definition and the strategy b-threads of the best individual of all runs. The individual is different from the handcrafted strategy b-threads (Listing 3), both in context and in behaviors; nevertheless, it ultimately exhibits similar behavior. Upon inspection of the evolved solution we found that part of the code is straightforward to understand. For example, the second b-thread, bt_0_1, waits for one X and then places an O on the same line. The context of this b-thread, ctx1, defines a list of pairs of cells, each pair consisting of two cells on the same line. This behavior resembles the behavior of our handcrafted “Prevent third X" b-thread (second b-thread of Listing 3), which waits for two Xs in a line before placing an O in the third cell. Some behaviors are covered by more than one behavior. For example, part of the possible forks are covered by a combination of bt_0_1 and bt_0_0.
Listing 5. Best evolved individual.
6. Concluding Remarks
We presented the use of genetic programming to evolve behavioral programs from scratch, performing an in-depth analysis, using as a case study the game of tic-tac-toe. We demonstrated the advantages of context-oriented behavioral programming (COBP) in general, and in particular as they pertain to amenability to evolution. To this end, we presented novel, domain-independent, grammar and genetic operators for behavioral programs. Using these grammar and genetic operators, we evolved highly competent players for tic-tac-toe.
To validate our findings, we utilized the mathematical characteristics of COBP to verify the correctness of evolved programs. Compared to all possible ways that a player can lose or miss an opportunity to win, our best evolved player reduced these cases to less than one percent.
Another strength of our approach is the ability to understand the generated programs. Due to the simple and repetitive structure of behavioral programs, we were able to observe that evolved individuals ultimately exhibited similar behavior to the handcrafted program.
While tic-tac-toe may seem like a toy problem, evolution of this magnitude has not been performed before for this domain. Evolving a complete program from scratch is a complex task that was made possible by the unique characteristics of COBP.
Given our study we believe that using GP, and evolution in general, to evolve behavioral programs is a viable research pursuit, well worth undertaking.
During our work, we identified some possible shortfalls of our approach that we wish to examine in future research:
Restricted context grammar: The contexts (i.e., cell, line, fork) in tic-tac-toe are constant, in the sense that they do not change over time—cells are not dynamically added or removed. Dynamic contexts are important for many domains. In chess, for example, the “check” context needs to be activated whenever an opponent piece is threatening the king. While COBP supports dynamic context, the grammar defined here limits this ability. To support it, we will need to extend the grammar to allow more complex entities and queries. Relaxing the constraint of static context should be approached carefully, since it may dramatically increase the search space.
Evolving more-complex behavior: In terms of computing resources (CPU and RAM), our approach is very efficient and scalable. Nevertheless, it may be less successful on larger problems with more-complex behaviors, such as chess or connect-four. For such problems, we will likely employ a hybrid approach, wherein programmers provide some behaviors and evolution is set to find others; programmers then refine evolution’s solutions by adding handcrafted behaviors, after which evolution is launched—and so on. Such a methodology may constitute a natural relationship between programming and optimization.
Finally, in this research we used game simulations for evaluating our individuals. Another interesting direction is to use a data-driven approach for evaluating individuals, without actually running them. For example, we may learn the rule b-threads, given a similar grammar and a labeled set of both possible and impossible game traces. The evaluation can be carried out by checking, on a training set, if the evolved program does not generate impossible traces and that all possible traces are indeed possible. This approach presents a complication because the grammar must include the block idiom as well, which forbids events from happening and may lead most games to deadlocks.