In-Target Proton–Boron Nuclear Fusion Using a PW-Class Laser
Abstract
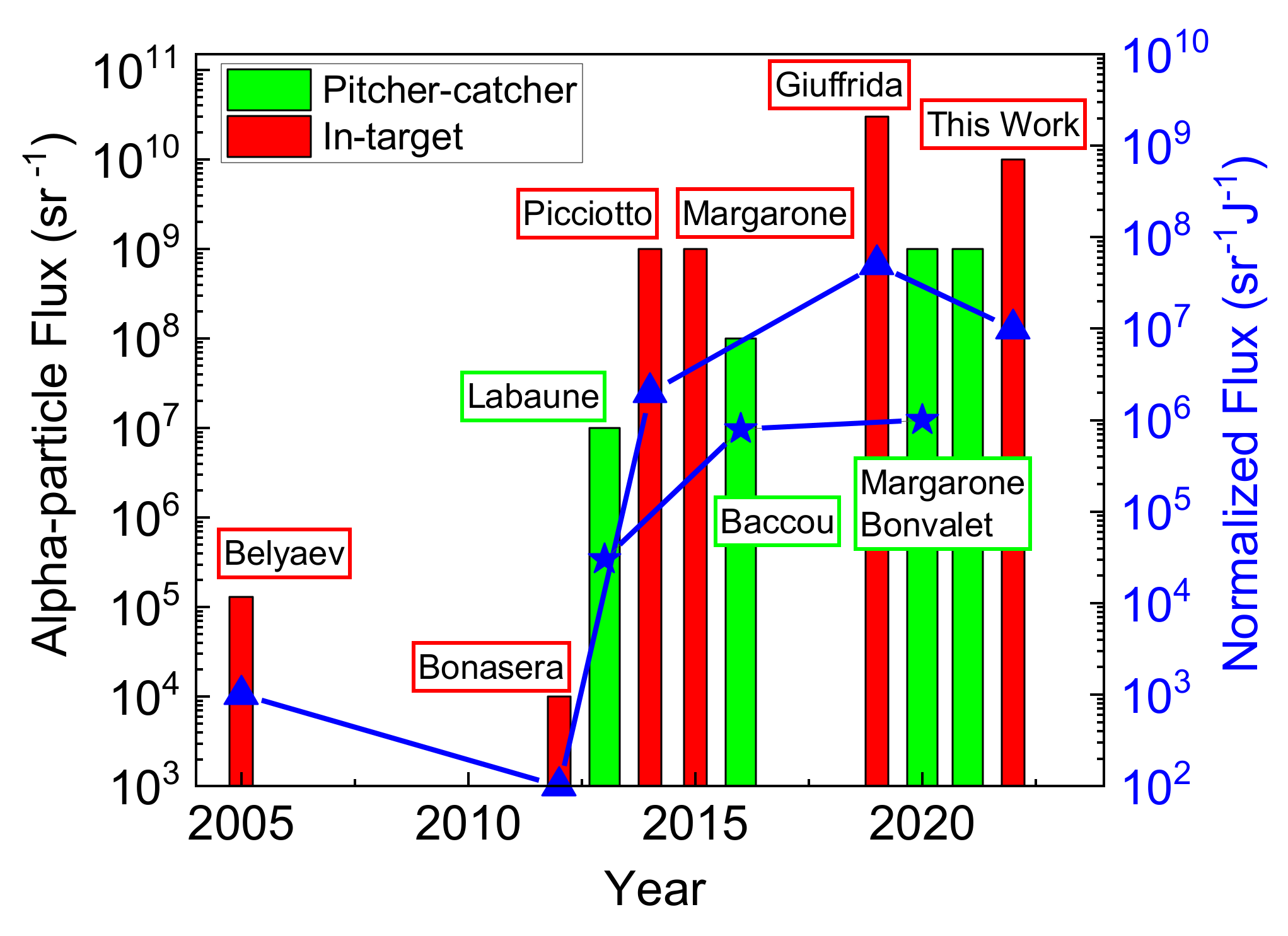
1. Introduction
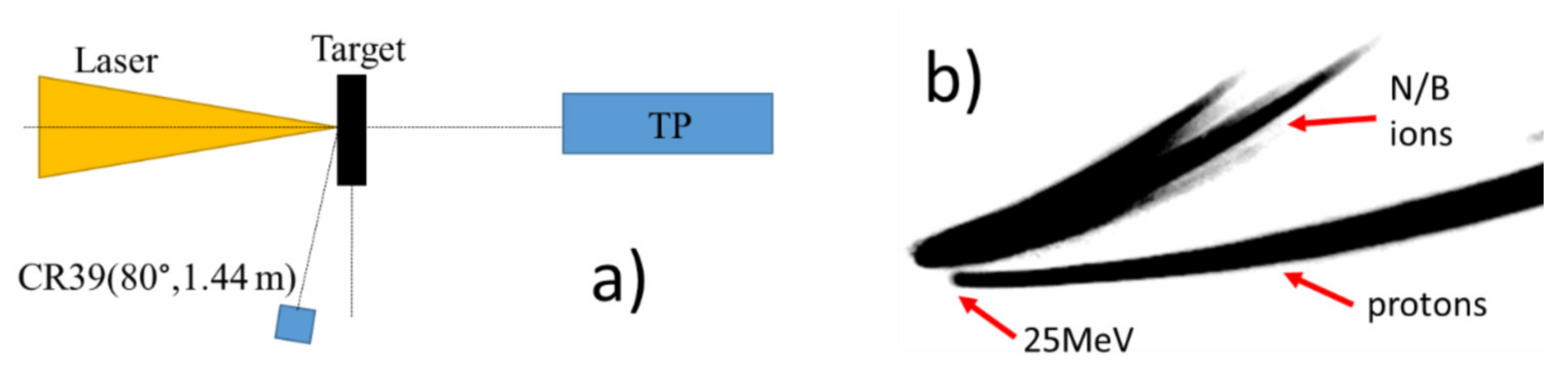
2. Materials and Methods
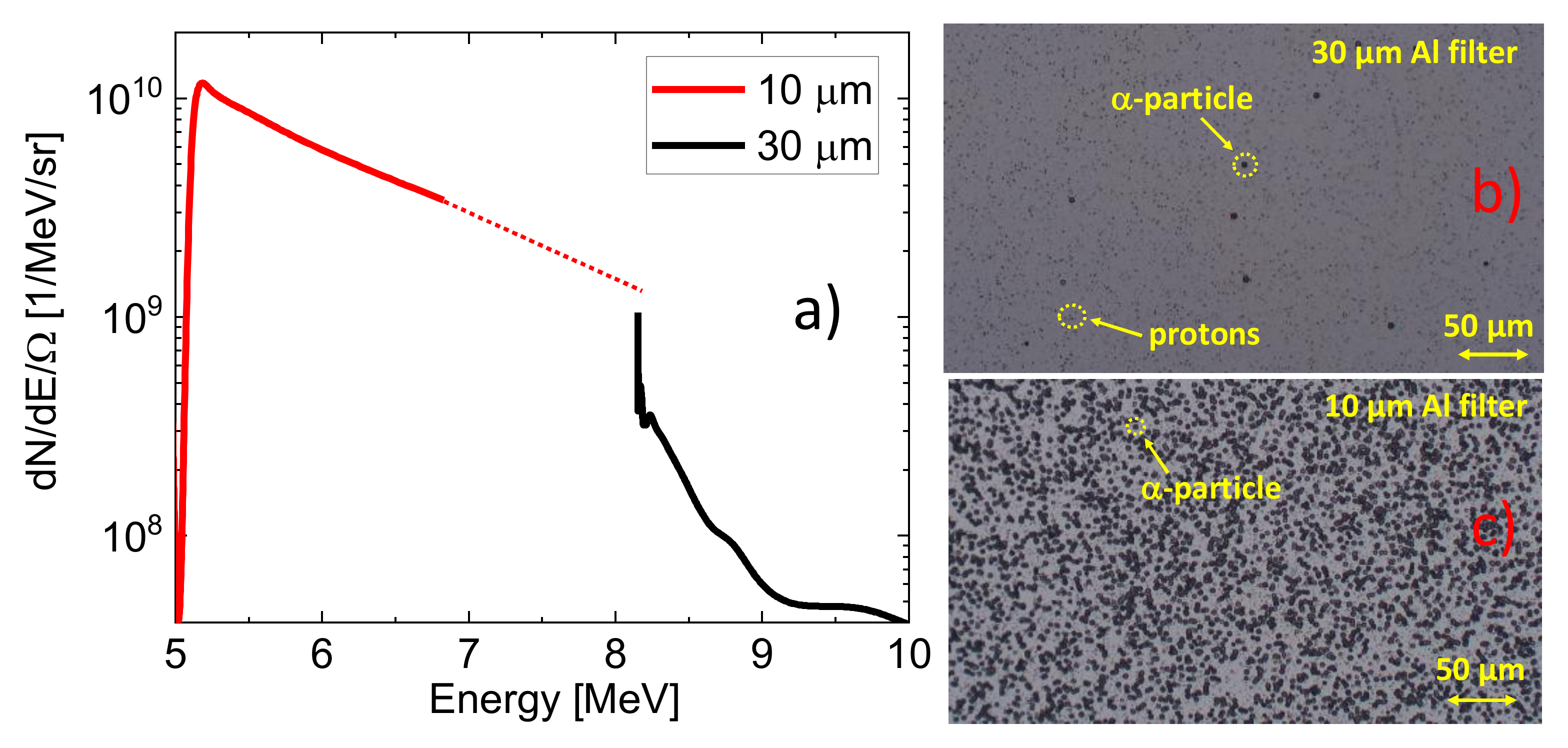
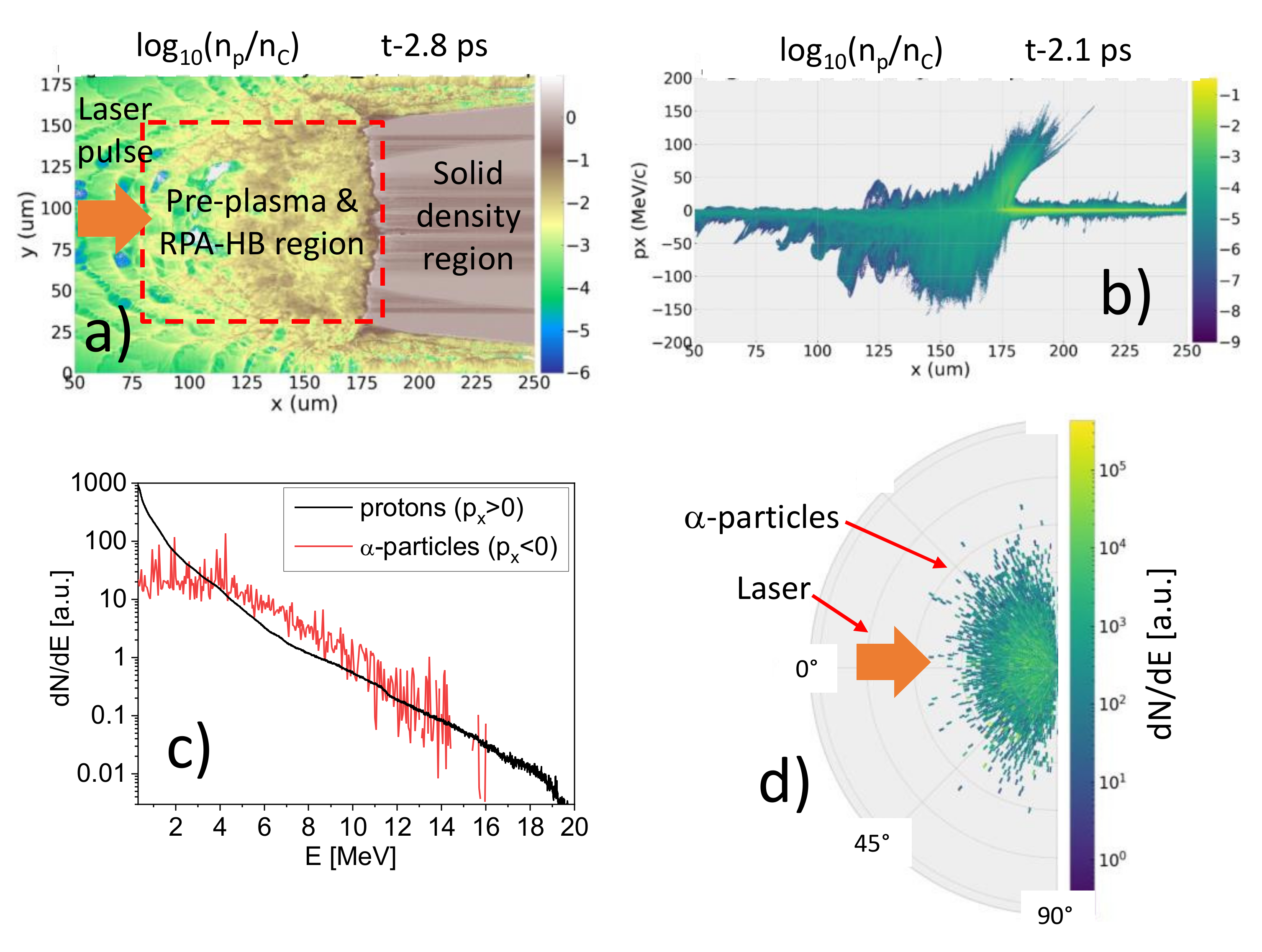
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stave, S.; Ahmed, M.W.; France, R.H.; Henshaw, S.S.; Müller, B.; Perdue, B.A.; Prior, R.M.; Spraker, M.C.; Weller, H.R. Understanding the B11(p,α)αα reaction at the 0.675 MeV resonance. Phys. Lett. B 2011, 696, 26. [Google Scholar] [CrossRef]
- Picciotto, A.; Margarone, D.; Velyhan, A.; Bellutti, P.; Krasa, J.; Szydlowsky, A.; Bertuccio, G.; Shi, Y.; Mangione, A.; Prokupek, J.; et al. Boron-Proton Nuclear-Fusion Enhancement Induced in Boron-Doped Silicon Targets by Low-Contrast Pulsed Laser. Phys. Rev. X 2014, 4, 031030. [Google Scholar] [CrossRef]
- Margarone, D.; Picciotto, A.; Velyhan, A.; Krasa, J.; Kucharik, M.; Mangione, A.; Szydlowsky, A.; Malinowska, A.; Bertuccio, G.; Shi, Y.; et al. Advanced scheme for high-yield laser driven nuclear reactions. Plasma Phys. Contr. Fusion 2015, 57, 014030. [Google Scholar] [CrossRef][Green Version]
- Giuffrida, L.; Belloni, F.; Margarone, D.; Petringa, G.; Milluzzo, G.; Scuderi, V.; Velyhan, A.; Rosinski, M.; Picciotto, A.; Kucharik, M.; et al. High-current stream of energetic α particles from laser-driven proton-boron fusion. Phys. Rev. E 2020, 101, 013204. [Google Scholar] [CrossRef] [PubMed]
- Margarone, D.; Morace, A.; Bonvalet, J.; Abe, Y.; Kantarelou, V.; Raffestin, D.; Giuffrida, L.; Nicolai, P.; Tosca, M.; Picciotto, A.; et al. Generation of α-Particle Beams with a Multi-kJ, Peta-Watt Class Laser System. Front. Phys. 2020, 8, 343. [Google Scholar] [CrossRef]
- Bonvalet, J.; Nicolai, P.; Raffestin, D.; D’humieres, E.; Batani, D.; Tikhonchuk, V.; Kantarelou, V.; Giuffrida, L.; Tosca, M.; Korn, G.; et al. Energetic α-particle sources produced through proton-boron reactions by high-energy high-intensity laser beams. Phys. Rev. E 2021, 103, 053202. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, V.S.; Matafonov, A.P.; Vinogradov, V.I.; Krainov, V.P.; Lisitsa, V.S.; Roussetski, A.S.; Ignatyev, G.N.; Andrianov, V.P. Observation of neutronless fusion reactions in picosecond laser plasmas. Phys. Rev. E 2015, 72, 026406. [Google Scholar] [CrossRef]
- Labaune, C.; Baccou, C.; Depierreux, S.; Goyon, C.; Loisel, G.; Yahia, V.; Rafelski, J. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat. Commun. 2013, 4, 2506. [Google Scholar] [CrossRef]
- Hora, H.; Korn, G.; Giuffrida, L.; Margarone, D.; Picciotto, A.; Krasa, J.; Jungwirth, K.; Ullschmied, J.; Lalousis, P.; Eliezer, S.; et al. Fusion energy using avalanche increased boron reactions for block-ignition by ultrahigh power picosecond laser pulses. Laser Part. Beams 2015, 33, 607–619. [Google Scholar] [CrossRef]
- ENERGY TOKEN. Available online: https://hb11.energy.com (accessed on 21 December 2021).
- MarvelFusion. Available online: https://marvelfusion.com (accessed on 21 December 2021).
- Qaim, S.M.; Spahn, I.; Scholten, B.; Neumaier, B. Uses of alpha particles, especially in nuclear reaction studies and medical radionuclide production. Radiochim. Acta 2016, 104, 601. [Google Scholar] [CrossRef]
- Belloni, F. On a fusion chain reaction via suprathermal ions in high-density H–11B plasma. Plasma Phys. Contr. Fusion 2021, 63, 055020. [Google Scholar] [CrossRef]
- Bonasera, A.; Caruso, A.; Strangio, C.; Aglione, M.; Anzalone, A.; Kimura, S.; Leanza, D.; Spitaleri, A.; Immè, S.; Morelli, D.; et al. Measuring the astrophysical S-factor in plasmas. In Proceedings of the 4th International Conference on Fission and Properties of Neutron Rich Nuclei, Sanibel Island, FL, USA, 11–17 November 2007; Hamilton, J.H., Ed.; World Scientific: Fort Lauderdale, FL, USA, 2013; pp. 503–507. [Google Scholar]
- Baccou, C.; Depierreux, S.; Yahia, V.; Neuville, C.; Goyon, C.; de Angelis, R.; Consoli, F.; Ducret, J.E.; Boutoux, G.; Rafelski, J.; et al. New scheme to produce aneutronic fusion reactions by laser-accelerated ions. Laser Part. Beams 2015, 33, 117. [Google Scholar] [CrossRef]
- Morace, A.; Iwata, N.; Sentoku, Y.; Mima, K.; Arikawa, Y.; Yogo, A.; Tosaki, S.; Vaisseau, X.; Abe, Y.; Kojima, S.; et al. Enhancing laser beam performance by interfering intense laser beamlets. Nat. Commun. 2019, 10, 2995. [Google Scholar] [CrossRef] [PubMed]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751. [Google Scholar] [CrossRef]
- Rabhi, N.; Batani, D.; Boutoux, G.; Ducret, J.-E.; Jakubowska, K.; Lantuejoul-Thfoin, I.; Nauraye, C.; Patriarca, A.; Sa’d, A.; Semsoum, A.; et al. Calibration of imaging plate detectors to mono-energetic protons in the range 1–200 MeV. Rev. Sci. Instrum. 2017, 88, 113301. [Google Scholar] [CrossRef] [PubMed]
- Breil, J.; Galera, S.; Maire, P.H. Multi-material ALE computation in inertial confinement fusion code CHIC. Comput. Fluids 2011, 46, 161. [Google Scholar] [CrossRef]
- Derouillat, J.; Beck, A.; Pérez, F.; Vinci, T.; Chiaramello, M.; Grassi, A.; Fle, M.; Bouchard, G.; Plotnikov, I.; Aunai, N.; et al. SMILEI: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 2018, 222, 351. [Google Scholar] [CrossRef]
- Robinson, A.P.L.; Gibbon, P.; Zepf, M.; Kar3, S.; Evans, R.G.; Bellei, C. Relativistically correct hole-boring and ion acceleration by circularly polarized laser pulses. Plasma Phys. Contr. Fusion 2009, 51, 024004. [Google Scholar] [CrossRef]
- Wilks, S.C.; Kruer, W.L.; Tabak, M.; Langdon, A.B. Absorption of ultra-intense laser pulses. PRL 1992, 69, 1383. [Google Scholar] [CrossRef]
- Bohlen, T.T.; Cerutti, F.; Chin, M.P.W.; Fasso, A.; Ferrari, A.; Ortega, P.G.; Mairani, A.; Sala, P.R.; Smirnov, G.; Vlachoudis, V. The FLUKA Code: Developments and Challenges for High Energy and Medical Applications. Nucl. Data Sheets 2014, 120, 211–214. [Google Scholar] [CrossRef]
- Ferrari, A.; Sala, P.R.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code; CERN-2005-10 (2005), INFN/TC_05/11, SLAC-R-773; CERN: Geneva, Switzerland, 2005. [Google Scholar]
- Tamburini, M.; Liseykina, T.V.; Pegoraro, F.; Macchi, A. Radiation-pressure-dominant acceleration: Polarization and radiation reaction effects and energy increase in three-dimensional simulations. Phys. Rev. E 2012, 85, 016407. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.N.; Atzeni, S.; Gangolf, T.; Gauthier, M.; Higginson, D.P.; Hua, R.; Kim, J.; Mangia, F.; McGuffey, C.; Marquès, J.-R.; et al. Experimental evidence for the enhanced and reduced stopping regimes for protons propagating through hot plasmas. Sci. Rep. 2018, 8, 14586. [Google Scholar] [CrossRef] [PubMed]
- Zylstra, A.B.; Frenje, J.A.; Grabowski, P.E.; Li, C.K.; Collins, G.W.; Fitzsimmons, P.; Glenzer, S.; Graziani, F.; Hansen, S.B.; Hu, S.X.; et al. Measurement of Charged-Particle Stopping in Warm Dense Plasma. Phys. Rev. Lett. 2015, 114, 215002. [Google Scholar] [CrossRef] [PubMed]
- Cayzac, W.; Frank, A.; Ortner, A.; Bagnoud, V.; Basko, M.M.; Bedacht, S.; Bläser, C.; Blaževic, A.; Busold, S.; Deppert, O.; et al. Experimental discrimination of ion stopping models near the Bragg peak in highly ionized matter. Nat. Comm. 2017, 8, 15693. [Google Scholar] [CrossRef]
- Temporal, M.; Canaud, B.; Cayzac, W.; Ramis, R.; Singleton, R.L. Effects of alpha stopping power modelling on the ignition threshold in a directly-driven inertial confinement fusion capsule. Eur. Phys. J. D 2017, 71, 132. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margarone, D.; Bonvalet, J.; Giuffrida, L.; Morace, A.; Kantarelou, V.; Tosca, M.; Raffestin, D.; Nicolai, P.; Picciotto, A.; Abe, Y.; et al. In-Target Proton–Boron Nuclear Fusion Using a PW-Class Laser. Appl. Sci. 2022, 12, 1444. https://doi.org/10.3390/app12031444
Margarone D, Bonvalet J, Giuffrida L, Morace A, Kantarelou V, Tosca M, Raffestin D, Nicolai P, Picciotto A, Abe Y, et al. In-Target Proton–Boron Nuclear Fusion Using a PW-Class Laser. Applied Sciences. 2022; 12(3):1444. https://doi.org/10.3390/app12031444
Chicago/Turabian StyleMargarone, Daniele, Julien Bonvalet, Lorenzo Giuffrida, Alessio Morace, Vasiliki Kantarelou, Marco Tosca, Didier Raffestin, Philippe Nicolai, Antonino Picciotto, Yuki Abe, and et al. 2022. "In-Target Proton–Boron Nuclear Fusion Using a PW-Class Laser" Applied Sciences 12, no. 3: 1444. https://doi.org/10.3390/app12031444
APA StyleMargarone, D., Bonvalet, J., Giuffrida, L., Morace, A., Kantarelou, V., Tosca, M., Raffestin, D., Nicolai, P., Picciotto, A., Abe, Y., Arikawa, Y., Fujioka, S., Fukuda, Y., Kuramitsu, Y., Habara, H., & Batani, D. (2022). In-Target Proton–Boron Nuclear Fusion Using a PW-Class Laser. Applied Sciences, 12(3), 1444. https://doi.org/10.3390/app12031444









