2.1. Alternative Definitions of the Informational Measure of Symmetry
Consider a 2D pattern built of 1D and/or 2D shapes or lines, demonstrating a number of symmetry elements (rotational symmetry, centers of symmetry, axes of symmetry, etc.), denoted as
,
, where
k is a number of non-identical symmetry operations. Pattern is understood as a 2D arrangement made from repeated lines or shapes on a surface. Element
forms the symmetry group of the shape
G (which should be clearly distinguished from the symmetry group of the entire pattern). Thus, the informational measure of symmetry of the pattern (abbreviated to IMS) is defined in a Shannon-like form as follows:
where
is the probability of appearance of the symmetry operation
within the shapes (lines) constituting the pattern, defined as follows:
where
=
is the total number of symmetry elements (operations) appearing in the 1D or 2D shapes, recognized in a given pattern, and
is the number of the same symmetry elements (operations)
, calculated for a given pattern. The normalization condition given by Equation (4) takes place:
Let us explain in detail the meaning of the introduced Shannon measure of symmetry
Suppose that we have a pattern demonstrating
k distinguishable elements of symmetry with probability distribution
. If, say,
we are certain that an element of symmetry
is recognized within the shapes constituting the pattern; in other words, element
necessarily appears within all of the shapes constituting the pattern, and we are certain that it is present in the shapes. For any other value of
, we are less certain about the occurrence of the symmetry element labeled
i. Less certainty can be translated into more uncertainty [
32]. Therefore, the larger the value of
, the larger the extent of uncertainty about the presence of element
within the pattern [
32]. Multiplying
by
, and summing over all
i, we obtain an average uncertainty about the presence of symmetry elements
within the given pattern. When
, we are certain that element
is not met within the pattern (numerous examples of calculation of
are supplied below).
Alternatively, the symmetry of the pattern may be quantified with the parameter
, defined according to Equation (5):
where
n denotes the
total number of elements of symmetry recognized in a shape;
n changes from unity to the maximal number of elements of symmetry inherent for the shapes appearing in the pattern and denoted “
l”.
is the probability of finding the shape possessing
n elements of symmetry in total belonging to group
G within the pattern, defined as follows:
where
is the number of shapes possessing
n elements of symmetry in total and
is the total number of shapes in the given pattern. The normalization condition given by Equation (7) takes place:
The Shannon-shaped measure
is interpreted, in turn, as an average across the pattern uncertainty of finding the shape possessing in total
n elements of symmetry within a given pattern [
27,
28]. The definition of the Shannon measure of symmetry
provided by Equations (5)–(7) resembles the definition of the Voronoi entropy, provided by Equation (1) with the following difference: instead of the number of polygon edges appearing in the definition of the Voronoi entropy, in our definition, we exploit the number of elements of symmetry
n in the shape; thus, we label this measure as the Voronoi–Shannon measure of symmetry (VSMS). The definition of VSMS provided by Equations (5)–(7) latently implies that a more symmetrical shape is characterized by the larger number of symmetry elements. We illustrate the difference between the information-theoretic measure of symmetry (IMS) and the Voronoi–Shannon measure of symmetry with several examples. The paper is organized as follows: the measures of symmetry introduced by Equations (2)–(7) are calculated for the patterns built of (i) 1D shapes (curves); (ii) 2D shapes, namely triangles and ellipses; and (iii) mixed patterns comprised of 1D and 2D shapes.
2.2. Information-Theoretic Measures of Symmetry of the Patterns Built of 1D Objects
First, consider the IMS and the VSMS of the patterns comprising only 1D objects (lines) lying on a plane. It should be noted that the symmetry group of an object depends not only on the object itself but also on the space in which we view it. For example, the symmetry group of a line segment in R1 is of order 2, the symmetry group of a line segment considered as a set of points in R2 is of order 4, and the symmetry group of a line segments viewed as a set of points in R3 is of infinite order. Hereinafter, we assume that the considered objects (lines) are treated as sets of points in R2 space. Let us start from the pattern built of
p irregular lines, such as depicted in
Figure 1. The analysis should necessarily start from the establishment of the symmetry group of the pattern. In this case, we recognize that the single element of symmetry for the shapes constituting the pattern is the onefold rotational symmetry, reduced to the rotation of the lines by the angle
, denoted
, which is an identity element of the symmetry group.
Let us first calculate
for the pattern, shown in
Figure 1a. In this case,
thus,
, and consequently, we calculate
. Now, we establish
It is easily seen that, for the irregular shapes possessing a single element of symmetry,
hence,
The same conclusion, i.e.,
, holds for the pattern built from non-identical, irregular, non-symmetrical lines. It should be emphasized that the same conclusion., i.e.,
, is true for the regular pattern, comprising irregular, non-symmetrical lines, such as the pattern shown in
Figure 1b, demonstrating a pattern characterized by the translational symmetry. Thus, we concluded that both of the introduced measures of symmetry are insensitive to the long-range order. How should the obtained result be interpreted?
means that an averaged uncertainty to reveal symmetry operation
within the pattern is zero; indeed, all of the 1D shapes depicted in
Figure 1 possess this element of symmetry; in turn,
means an average uncertainty for finding the shape demonstrating the single element of symmetry is zero within the pattern; indeed, every shape in the pattern has only one element of symmetry, namely
(see Ref. [
28]). It should be emphasized that neither Voronoi entropy nor continuous measure of symmetry could be defined and calculated for the patterns presented in
Figure 1a,b.
Now, consider the patterns composed of straight line segments, shown in
Figure 2a,b, and seen as sets of points in R2 space. The symmetry group of the straight line segments is built of four elements, namely the unity element, which is the onefold rotational symmetry, which is the rotation by the angle
(denoted
; the twofold rotational symmetry by the angle
, denoted
; and the mirror axes, denoted
. Let us calculate
For the pattern, built of the
p segments, we obtain
; thus,
.
Now, let us establish
In
Figure 2a,b, all of the shapes in the patterns have four aforementioned elements of symmetry. Thus,
and hence,
Again, all of the measures of symmetry introduced coincide for the patterns presented in
Figure 2a,b, and they are insensitive to the long-range order (translational symmetry) of segments, shown in
Figure 2b.
Consider the patterns built of the
p arcs of a circle (or, perhaps, the symmetric segments of the parabola
, shown in
Figure 2c,d. The symmetry group of the shapes depicted in
Figure 2c,d is built of two elements, namely the unity element, which is the onefold rotational symmetry (denoted
, and the mirror axis, denoted
. For this kind of pattern, we obtain
; thus,
. Consequently, in this case,
(due to
and
); the long-range order, shown in
Figure 2d plays no role in the calculation of both measures of symmetry. Now, consider the patterns built of the
p symmetric segments of a cubic parabola
) shown in
Figure 2e,f. The considerations akin to the aforementioned ones immediately yield
,
Thus, we come to the conclusion that the patterns depicted in
Figure 2c–f are
equivalent from the point of view of the Shannon measures of symmetry introduced, namely,
and
. Moreover, the VSMS of the patterns depicted in
Figure 1 and
Figure 2 is equal; however, the IMS of the patterns shown in
Figure 1 and
Figure 2 are different. It should be emphasized that both of the Shannon and the Voronoi–Shannon information-theoretic measures of symmetry of the discussed patterns are
the intensive properties of the patterns and that they are independent of the area of the pattern or the density and size of the shapes, and in this sense, they are different from the true thermodynamic entropy, which is an extensive parameter of the system. It should be emphasized that the long-range order does not influence either of the information-theoretic measures of symmetry.
Consider now the mixed patterns, comprising 1D objects (lines), depicted in
Figure 3.
Let us start from the pattern comprising segments of a cubic parabola and arcs of a circle, shown in
Figure 3a. Both shapes are characterized by the symmetry group containing two symmetry elements: the unity element, which is the onefold rotational symmetry and the twofold rotational symmetry in the case of segments of a cubic parabola, and the onefold rotational symmetry and the mirror axis in the case of arcs of a circle. Thus,
. Both shapes have two elements of symmetry; hence,
Now, consider the pattern built from
p irregular, non-symmetrical curves and
p arcs of a circle, presented in
Figure 3b. We recognize two elements of symmetry in this pattern, namely the onefold rotational symmetry inherent for all of the shapes and denoted
, and the mirror axis labeled
inherent for the arcs only. Thus, the entire number of the symmetry elements in the pattern is
(see Equation (3)); consequently, we easily calculate
; and finally, we obtain
. Let us now calculate
for the mixed pattern, shown in
Figure 3b. For this pattern, we calculate (
:
; thus,
Again, the Voronoi entropy could not be introduced for the patterns presented in
Figure 3a,b.
2.3. Information-Theoretic Measures of Symmetry of Patterns Built of 2D Shapes
Next, we address the patterns composed of 2D shapes. Let us start from the completely disordered pattern built of
p irregular shapes depicted in
Figure 4a. In this case, we recognize for all of the non-symmetrical shapes constituting the pattern the single element of symmetry, namely the rotation
; thus,
and consequently,
0. It is easily seen that
takes place for the same pattern. Let us analyze the 2D pattern comprising
p identical equilateral triangles depicted in
Figure 4b. The symmetry group of the equilateral triangle is the dihedral symmetry group, usually labeled
. In the case of the equilateral triangles shown in
Figure 4b, we have
elements of symmetry, which are 3
p symmetry axes and 3
p rotations. The IMS calculated with Equation (2) equals
1.792. On the other hand, all of the shapes constituting the pattern shown in
Figure 4b have the same number of symmetry elements; thus,
.
Consider the fractal Sierpinski gasket built of equilateral triangles, shown in
Figure 4c [
33,
34]. It is easily seen that
;
for any scaling level of its fractal structure. Thus, we conclude that informational measures of symmetry are invariant with respect to the scaling of the Sierpinski gasket. Obviously, the conclusion holds for the Sierpinski gasket built of squares. The general problem of the calculation of the informational measures of symmetry of fractal structures deserves additional research. The pattern characterized by the informational measures of symmetry should not be necessarily close-packed, as shown in
Figure 4d, representing a set of randomly dispersed equilateral triangles of various areas. In this case,
1.792,
takes place. Again, the introduced informational measures of symmetry are insensitive to the presence/absence of the long-range order in a given pattern.
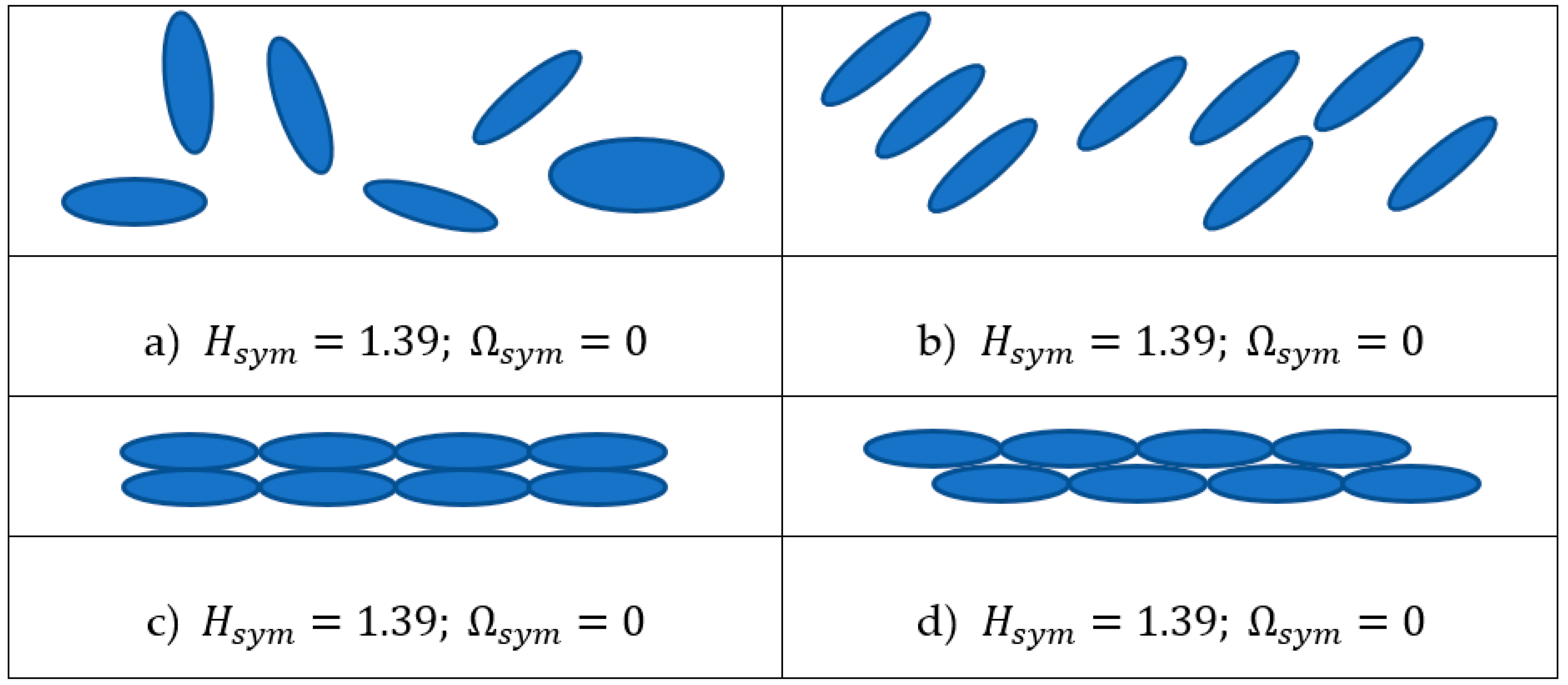
It is noteworthy that a pattern should not necessarily be built of polygons; it may comprise curvilinear shapes such as the ellipses, shown in
Figure 5.
Let us start from the pattern depicted in
Figure 5a comprising the dispersed random ellipses of various sizes. The group of symmetry of the ellipses includes four elements, namely the onefold rotational symmetry denoted
, the twofold rotational symmetry denoted
, and two distinguishable mirror axes denoted correspondingly as
and
; in this case,
. Thus, we calculate
All of the ellipses have in total four elements of symmetry; hence,
. The same is true for the dispersed identical long-range ordered ellipses, shown in
Figure 5b. The same conclusion holds for the close-packed ordered identical ellipses forming the patterns shown in
Figure 5c,d.
Figure 5c,d illustrate the idea that the set of the shapes should be clearly defined. Indeed,
holds for the patterns built of the ellipses
only. If we also consider the “interstitial” shapes emerging in the close-packed arranges (which are curvilinear quadrangles in
Figure 5c and curvilinear triangles in
Figure 5d), the informational measures of symmetry changes.
2.6. Information-Theoretic Measures of Information: How Do They Work? An Example from Chemistry
Let us exemplify the information-theoretic measure information introduced with an example taken from chemistry. Consider the benzene combustion reaction, represented by Equation (8):
Figure 9 depicts the reaction schematically and demonstrates the elements of symmetry for the molecules involved. All of these molecules possess planar molecular geometry, which allows us to consider a reaction that takes place in R2 space. The molecule of benzene in the R2 space is characterized by twelve elements of symmetry, namely:
and six mirror axes. The molecules of oxygen and
are linear ones and possess four elements of symmetry, namely
and
rotations, and two mirror axes. The molecule of water in R2 space possesses two elements of symmetry:
-rotation and the mirror axis, as shown in
Figure 9.
Let us calculate how the chemical reaction changes the symmetry of the system. Our calculation conducted according Equations (2) and (5) demonstrates that, before the reaction, we obtain . , which is due to the high symmetric benzene molecule, is as relatively high value. On the other hand, the value of is relatively low. This means that a certain group of symmetry (namely group with the symmetry involving a linear molecule of oxygen) dominates in the system addressed before the reaction. This is easily understood; indeed, 15 molecules of oxygen react with two molecules of benzene. After the reaction, the value of decreases (); this decrease is due to the diminished number of elements of symmetry inherent for the reaction products, namely water and molecules. The value of is contrastingly increased, namely we established , which points to the more homogeneous distribution of the symmetry elements among products of the reaction. Thus, we conclude that the suggested measures of symmetry may be applied for quantification of the symmetry change occurring under chemical reactions.