A Possible Information Entropic Law of Genetic Mutations

Featured Application

The results observed here have applications in all branches of medical sciences and genetics research, including evolutionary biology, pandemic monitoring, genetic therapies, pharmaceuticals, and bioinformatics.

Abstract

The current scientific consensus is that genetic mutations are random processes. According to the Darwinian theory of evolution, only natural selection determines which mutations are beneficial in the course of evolution, and there is no deterministic correlation between any parameter and the probability that these mutations will occur. Here, we investigate RNA genetic sequences of the SARS-CoV-2 virus using Shannon’s information theory, and we report a previously unobserved relationship between the information entropy of genomes and their mutation dynamics. Based on the analysis presented here, we are able to formulate a governing law of genetic mutations, stating that genomes undergo genetic mutations over time driven by a tendency to reduce their overall information entropy, challenging the existing Darwinian paradigm.

1. Introduction

The DNA or RNA genetic molecule is a highly complex information encoding system that displays incredible properties such as an extremely low error rate, high stability, and the ability to self-replicate, self-repair, and produce other molecules. The biological information is encoded in the sequence of nucleotides, and the time evolution of a genome is described by occasionally induced genetic mutations. Mutations are errors that appear during the process of self-replication when the genome is damaged and left unrepaired. These errors manifest in changes in the genetic sequence, ranging from simple substitutions that maintain the number of nucleotide constants to deletions and insertions that shift the sequence frame to a shorter or larger size, respectively. Genetic mutations can affect an organism’s phenotype and are essential for the diversity and evolution of living organisms. Due to the protective mechanisms such as DNA/RNA self-repair or proofreading during replication, mutation rates are very low, but avoiding mutations could become too energetically costly to living organisms, and they never reach zero. The scientific consensus on the dynamics of genetic mutations has accepted the Darwinian theory of evolution, in which genetic mutations are random processes [1]. This means that mutations occur randomly regardless of whether an organism will benefit from the DNA/RNA changes. Only natural selection determines which mutations are beneficial and preserved in the course of evolution [2], but there is no observed correlation between any parameter or variable and the probability that these mutations will occur.

A recent study reported that mutations in the plant Arabidopsis thaliana occur less often in functionally constrained regions of the genome, challenging the paradigm that a directionless force in evolution drives mutations and proposing that an adaptive mutation bias exists [3].

Nei also concluded that the driving force of phenotypic evolution is mutation, and natural selection is of secondary importance [4].

While the existence of an adaptive mutation force is indeed a strong counterargument to the evolutionary theory that mutations occur randomly with respect to their consequences, one has no means of predicting future genetic mutations without prior knowledge of the exact adaptive path that an organism would follow, which is still an unknown outcome.

Using a mathematical–physical approach, here, we report solid evidence of a truly predictive and quantifiable pattern of the dynamics of genetic mutations, and we formulate a possible governing law of genetic mutations.

2. Results

2.1. Information Theory Applied to Genomics

Our mathematical–physical analysis of genomic sequences is based on Shannon’s information theory [5] and the concept of information entropy (IE). For a given set of m independent and distinctive events, Y = {y₁, y₂,…, y_m}, which are described by a discrete probability distribution P = {p₁, p₂,…, p_m} on Y, the information content per event measured in bits, or the IE extracted when observing the set of events Y once is:

$$H(Y)={\displaystyle \sum _{i=1}^m{p}_i\cdot {\log }_2\frac{1}{p_i}}$$

(1)

where the function H(Y) is called the Shannon IE, and it is maximum when the events y_j have equal probabilities of occurring, $p_i=1/m$, so $H(Y)={\log }_{2}m$. Observing N sets of events Y, or N times the set of events Y, the information content is N·H(Y) bits. A DNA sequence can be represented as a long string of the letters A, C, G, and T. These represent the four nucleotides: adenine (A), cytosine (C), guanine (G), and thymine (T) (replaced with uracil (U) in RNA sequences). Hence, within Shannon’s information theory framework, a typical genome can be represented as a four-state probabilistic system, with m = 4 distinctive events, $Y=\left\{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\right\}$, and probabilities $p=\left\{p_{\mathrm{A}},p_{\mathrm{C}},p_{\mathrm{G}},p_{\mathrm{T}}\right\}$. Assuming the events have equal probabilities of occurring, using digital information units, i.e., the base of the logarithm is 2, and Equation (1) for m = 4, we determine that maximum Shannon IE is 2, indicating that the maximum information encodes per nucleotide is 2 bits, i.e., A = 00, C = 01, G = 10, T = 11. When the events occur with different probabilities, Relation (1) must be used to calculate the encoded information content. In order to clarify the procedure, let us consider an RNA subset consisting of N = 103 characters, which is exactly the window containing the first mutation (see LC542809 in Table 1 and window index 108 in Table 2):

CAATTTTGACTTCACTTTTAGTTTTAGTCCAGAGTACTCAATGGTCTTTGTTCTTTTTTTTGTATGAAAATGCCTTTTTACCTTTTGCTATGGGTATTATTGC

If the letters within this subset would occur with equal probabilities (1/4), then the subset would have H(Y) = 2, and a total entropy of N⋅H(Y) = 206 bits of information. However, counting the occurrences of each nucleotide, the above subset has the following probability distribution: $P=\left\{p_{\mathrm{A}}=\frac{20}{103},p_{\mathrm{C}}=\frac{16}{103},p_{\mathrm{G}}=\frac{16}{103},p_{\mathrm{T}}=\frac{51}{103}\right\}$. This results in the following:

$$H(X)=-\left(\frac{20}{103}{\log }_2\left(\frac{20}{103}\right)+\frac{16}{103}{\log }_2\left(\frac{16}{103}\right)+\frac{16}{103}{\log }_2\left(\frac{16}{103}\right)+\frac{51}{103}{\log }_2\left(\frac{51}{103}\right)\right)=1.7958$$

Therefore, the Shannon information entropy of this window is 1.7958 bits instead of 2 bits, and the total IE of the subset is 184.96 bits instead of 206 bits. After the mutation occurs (G → T), the new probability distribution is $P=\left\{p_{\mathrm{A}}=\frac{20}{103},p_{\mathrm{C}}=\frac{16}{103},p_{\mathrm{G}}=\frac{15}{103},p_{\mathrm{T}}=\frac{52}{103}\right\}$ and the IE of the mutated window is reduced to 1.779 bits.

Considering the genome as a non-equilibrium information coding system with a very long relaxation time, and given the highly complex nature of genome architecture, the main assumption here is that the IE profile of genetic sequences may represent a characteristic pattern able to highlight characteristic changes at sites where the nucleotide sequence is changed, such as single nucleotide polymorphisms (SNPs), deletions, and insertions, suggesting not only a role for IE in the determination of genomic variation as already proven [6] but also a role in developing a probabilistic quasi-deterministic approach to genetic mutations.

2.2. Information Entropy of SARS-CoV-2 Genomes

In order to test this assumption, we needed to examine the time evolution of the IE of a genome that undergoes frequent mutations in a short period of time. A system that perfectly fits this requirement is a virus genome, and we examined the RNA sequence of the novel SARS-CoV-2 virus, which emerged in December 2019, resulting in the current COVID-19 pandemic. The reference RNA sequence of SARS-CoV-2, representing a sample of the virus collected early in the pandemic in Wuhan, China, in December 2019 (MN908947) [7], has 29,903 nucleotides, so N = 29,903. For this reference sequence, we computed the Shannon IE using relation (1) and previously developed software, GENIES [8,9], designed to study the genetic mutations using Shannon’s IE [6]. The value obtained represents the reference Shannon IE at time zero before any mutation occurs. Using the NCBI virus database, we searched and extracted a number of SARS-CoV-2 variants sequenced at various locations around the globe at different times, starting from January 2020 to October 2021. Our search was centered on complete genome sequences containing the same number of nucleotides as the reference sequence. We also carefully selected variants that displayed an incremental number of SNP mutations, and we computed the Shannon IE corresponding to each variant. The full data set, including genome data references/links, collection times, number of SNP mutations, and the Shannon IE value of each genome are shown in Table 1.

Table 1. Tabulated results of the analysis performed on selected SARS-CoV-2 variants sequenced at various locations around the globe, over a period of 22 months.

Genome	Ref.	SNPs	Collection Time	Location	Shannon IE (Bits)
MN908947	[7]	0	December 2019	China	1.9570243
LC542809	[10]	4	March 2020	Japan	1.9569197
MT956916	[11]	6	May 2020	Spain	1.9569468
MT956915	[12]	7	May 2020	Spain	1.9569230
MW466798	[13]	9	July 2020	South Korea	1.9569327
OM098415	[14]	15	May 2021	China	1.9568149
OM098426	[15]	16	May 2021	China	1.9568117
MW679504	[16]	18	February 2021	USA	1.9568451
MW294011	[17]	19	October 2020	Ecuador	1.9567058
OK246811.1	[18]	21	March 2021	USA/PA	1.9568012
OK246805	[19]	22	March 2021	USA/PA	1.9567543
MW679505	[20]	25	February 2021	USA	1.9566630
MW735975	[21]	26	February 2021	USA/OH	1.9565714
MW695383	[22]	27	December 2020	USA/VA	1.9865744
OK546282.1	[23]	32	April 2021	USA/NE	1.9565675
OK104651.1	[24]	40	August 2021	Egypt	1.9564591
OL351371.1	[25]	49	October 2021	Egypt	1.9562614

Table 1. Tabulated results of the analysis performed on selected SARS-CoV-2 variants sequenced at various locations around the globe, over a period of 22 months.

Genome	Ref.	SNPs	Collection Time	Location	Shannon IE (Bits)
MN908947	[7]	0	December 2019	China	1.9570243
LC542809	[10]	4	March 2020	Japan	1.9569197
MT956916	[11]	6	May 2020	Spain	1.9569468
MT956915	[12]	7	May 2020	Spain	1.9569230
MW466798	[13]	9	July 2020	South Korea	1.9569327
OM098415	[14]	15	May 2021	China	1.9568149
OM098426	[15]	16	May 2021	China	1.9568117
MW679504	[16]	18	February 2021	USA	1.9568451
MW294011	[17]	19	October 2020	Ecuador	1.9567058
OK246811.1	[18]	21	March 2021	USA/PA	1.9568012
OK246805	[19]	22	March 2021	USA/PA	1.9567543
MW679505	[20]	25	February 2021	USA	1.9566630
MW735975	[21]	26	February 2021	USA/OH	1.9565714
MW695383	[22]	27	December 2020	USA/VA	1.9865744
OK546282.1	[23]	32	April 2021	USA/NE	1.9565675
OK104651.1	[24]	40	August 2021	Egypt	1.9564591
OL351371.1	[25]	49	October 2021	Egypt	1.9562614

Figure 1 shows the computed IE of each SARS-CoV-2 variant as a function of its number of SNP mutations. Remarkably, the data indicate that the Shannon IE of the RNA genomes decreases linearly with their corresponding number of mutations. The larger the number of mutations, the lower the corresponding Shannon IE value.

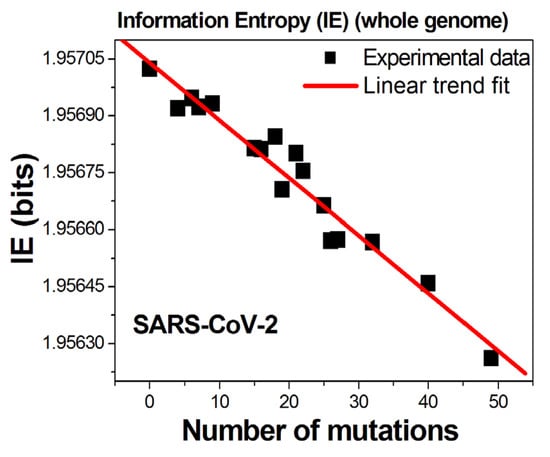
Figure 1. Information entropy values of variants of the SARS-CoV-2 virus as a function of the SNP mutations detected per variant.

All analyzed variants displayed the universal behavior of lowering the IE value relative to that of the original genome. The data in Figure 1 were selected to highlight this observation. Since the general consensus is that genetic mutations are random processes, one should not detect any correlation between the evolution of the genetic mutations and any other parameter.

2.3. The Governing Entropic Law of Genetic Mutations

Our novel data indicate that there is an intimate link between the dynamics of the genetic mutations and the mathematical value of their IE measured in bits. This interesting result naturally stimulates the thought that perhaps there is a hidden and undiscovered deterministic approach to genetic mutations. In fact, the observed trend has universal applicability to all information systems, beyond biological DNA/RNA information. It appears that all information systems are governed by an entropic law similar to the second law of thermodynamics, called the second law of infodynamics, which will be reported in a different article [26]. However, based on the data presented here, we are able to conclude this study by formulating a possible governing law of genetic mutations:

Biological RNA and DNA information systems tend to reduce their overall information entropy value by undergoing genetic mutations.

3. Predicting Mutations from Information Entropy Spectra

The careful application of this law facilitates a possible predictive approach to future genetic mutations before they take place. This is a matter for future studies and beyond the scope of this report, but a possible way of taking advantage of the observed law could be a methodology that involves splitting the entire genome into subsets, called “windows”. This is because our analysis was applied to the entire genetic sequences, each containing 29,903 characters, and the method revealed no relationship between the IE value and the location of the mutations within the genome sequence, making the possibility of finding a fully predictive algorithm for future genetic mutations not yet achievable. A “window” contains a given number of nucleotides (characters) called “window size” (WS). The window’s representation of the genome is obtained by sliding the window from left to right, across the whole genome [6]. Each new position of the window is obtained by sliding it for a fixed number of characters, called the “step size” (SS). In order to ensure that all sections of the genome are captured by this process, the SS must be at least 1 and maximum WS, so 1 < SS ≤ WS. By setting this rule, a given genome of N nucleotides will result in a total of N_w windows, given by the following formula:

$$N_w=\frac{N}{SS}-WS+SS$$

(2)

In order to produce an IE profile of the whole genome, one needs to compute the IE value of each window and plot the IE values obtained as a function of the window index location within the genome. The result is an IE spectrum, which is a numerical representation of the genome sequence containing all its biological information converted into a numerical spectrum. Using GENIES [8,9], we computed the IE spectra by counting and working out the probabilities of occurrence of single nucleotides for SS = WS = 103. Figure 2 shows the average IE per window of each SARS-CoV-2 spectrum for three different WS values as a function of the number of mutations. The data indicate again that the average IE per window within each genome decreases with an increase in the number of mutations. The larger the WS values, the better the correlation.

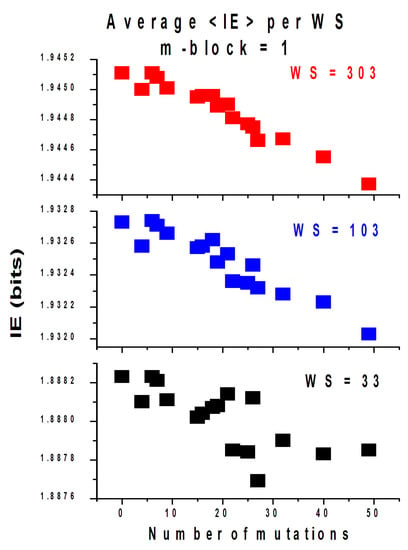
Figure 2. Average IE values per WS for each variant of SARS-CoV-2 studied, plotted as a function of the number of mutations.

This confirms that splitting the genome into windows retains the correlation to the IE observed in Figure 1, and the proposed governing law of genetic mutations is applicable not only to whole genomes but also to individual windows within the genomes.

In turn, this allows us to establish a link between the IE values and the index locations of the mutations, which could facilitate further studies to determine a fully predictive algorithm for genetic mutations, as diagrammatically shown in Figure 3.

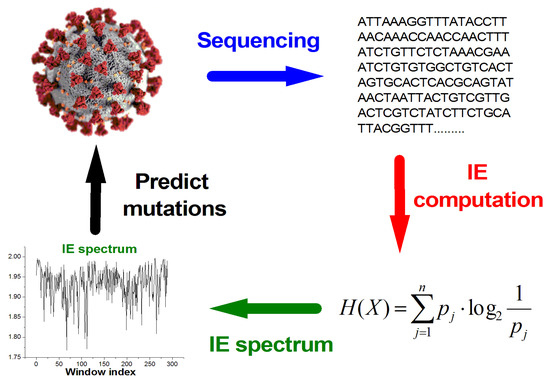
Figure 3. Diagrammatic representation of the methodology to produce the IE spectrum in order to facilitate studies of possible predictive algorithms of future genetic mutations.

To exemplify this technique, we computed the IE spectrum of the SARS-CoV-2 reference genome (MN908947) and the spectrum of the first mutated variant (LC542809) using WS = SS = 103. We performed a direct comparison of the two genomes, and four SNP mutations were identified in the LC542809 sequence (see Table 1), as follows: G11082T, C14407T, C26110T, and C29634T. The first character is the mutating nucleotide in the reference genome, the number is its location in the sequence, and the second character is what it mutated into in the new sequence.

Figure 4 shows the obtained IE spectra of the two sequences and their IE ratio (IER), i.e., IER = (IE mutated)/(IE reference). Although the two spectra appear identical, their ratio spectrum obtained by dividing the mutated spectrum to the reference spectrum can identify consistent changes between the two genomes.

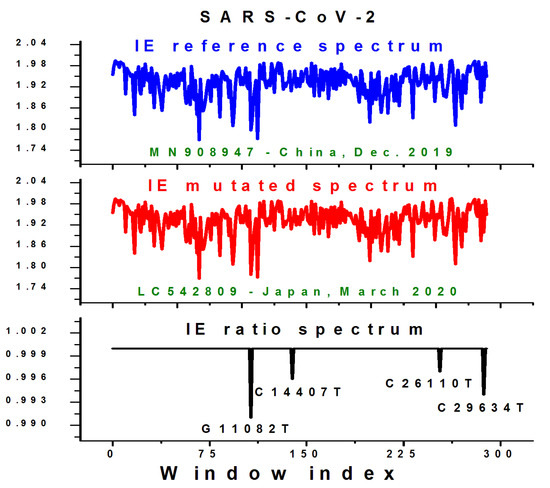
Figure 4. The IE spectra of the reference SARS-CoV-2 genome (top image), the mutated sequence (middle image), and their IE ratio (IER) spectrum (bottom image) obtained by dividing the two IE spectra. The four known mutations are captured in the IER spectrum and clearly marked. The IE of the corresponding window decreased in each case. Data obtained for WS = SS = 103.

Any value not equal to one in the IER spectrum indicates the presence of at least one mutation inside the corresponding window of the spectrum, resulting in a change in the information encoded at that position. The IE ratio spectrum (Figure 4, bottom image) successfully captured all four mutations and their corresponding locations within the genome’s IE spectrum, confirming the validity of this technique. Most importantly, the governing law of genetic mutations appears valid when applied to the individual windows where mutations were detected because each mutation resulted in a decrease in the IE value of the corresponding window, i.e., IER < 1 (Figure 4).

Table 2 shows the extracted string of nucleotides corresponding to each window that suffered a mutation in the reference spectrum. The nucleotide that mutated is highlighted in red. We also show the corresponding IE value of each window before and after the mutation occurs, indicating that mutations take place in a way that reduces the IE value within the selected window. Although in this example all four mutations resulted in a decrease in the IE values of their containing windows, it is important to mention that not all mutations display this behavior. Indeed, the majority of the mutations occur so that the IE value of their containing window decreases, but in some cases, only 70–80% of the mutations obey this information entropic rule, especially genomes that suffered a large number of mutations. When applied to entire genomes, the observed entropic law is always fully applicable.

Table 2. Details of the mutations that occurred in SARS-CoV-2 reference genome (MN908947) to result in the first mutated variant (LC542809), including the IE values of their corresponding windows where the mutations took place.

Window Index	SNP	Reference Window (WS = 103)	IE Reference (Bits)	IE Mutated (Bits)
108	G11082T	CAATTTTGACTTCACTTTTAGTTTTAGT CCAGAGTACTCAATGGTCTTTGTTCTT TTTTTTGTATGAAAATGCCTTTTTACCT TTTGCTATGGGTATTATTGC	1.796	1.779
140	C14407T	CATACCACCCAAATTGTGTTAACTGTT TGGATGACAGATGCATTCTGCATTGTG CAAACTTTAATGTTTTATTCTCTACAGT GTTCCCACCTACAAGTTTTGG	1.937	1.929
253	C26110T	CTGGTGTTGAACATGTTACCTTCTTCAT CTACAATAAAATTGTTGATGAGCCTGA AGAACATGTCCAAATTCACACAATCGA CGGTTCATCCGGAGTTGTTAA	1.963	1.956
287	C29634T	GCTATATAAACGTTTTCGCTTTTCCGTT TACGATATATAGTCTACTCTTGTGCAGA ATGAATTCTCGTAACTACATAGCACAAG TAGATGTAGTTAACTTTAA	1.909	1.898

Table 2. Details of the mutations that occurred in SARS-CoV-2 reference genome (MN908947) to result in the first mutated variant (LC542809), including the IE values of their corresponding windows where the mutations took place.

Window Index	SNP	Reference Window (WS = 103)	IE Reference (Bits)	IE Mutated (Bits)
108	G11082T	CAATTTTGACTTCACTTTTAGTTTTAGT CCAGAGTACTCAATGGTCTTTGTTCTT TTTTTTGTATGAAAATGCCTTTTTACCT TTTGCTATGGGTATTATTGC	1.796	1.779
140	C14407T	CATACCACCCAAATTGTGTTAACTGTT TGGATGACAGATGCATTCTGCATTGTG CAAACTTTAATGTTTTATTCTCTACAGT GTTCCCACCTACAAGTTTTGG	1.937	1.929
253	C26110T	CTGGTGTTGAACATGTTACCTTCTTCAT CTACAATAAAATTGTTGATGAGCCTGA AGAACATGTCCAAATTCACACAATCGA CGGTTCATCCGGAGTTGTTAA	1.963	1.956
287	C29634T	GCTATATAAACGTTTTCGCTTTTCCGTT TACGATATATAGTCTACTCTTGTGCAGA ATGAATTCTCGTAACTACATAGCACAAG TAGATGTAGTTAACTTTAA	1.909	1.898

4. Conclusions

In conclusion, we reported here the observation of an information entropic governing law of genetic mutations. The law states that genetic mutations are not merely random events, but they occur in a way that the information entropy (IE) of the whole genome reduces in value. In order to expand the applicability of this observation to the development of possible predictive algorithms of genetic mutations, we proposed a methodology that involves the conversion of the genetic sequences into IE numerical spectra by splitting them into segments of nucleotides called windows. The proposed entropic governing law of genetic mutations appears to be valid not only when applied to the full genome (Figure 1) but also when applied to the average IE per window (Figure 2), and most importantly when examining windows that contain specific mutations (Figure 4 and Table 2). This opens up the possibility of implementing this technique to obtain a fully deterministic approach to genetic mutations. By carefully studying the IE spectrum of a genome and its variants, combined with the observed law of genetic mutations and machine learning algorithms, one should be able to establish a deterministic algorithm for predicting future mutations before they occur. This article focused on mutations in the RNA of SARS-CoV-2 viruses, but we should keep in mind that DNA is subject to essentially the same entropic mutation forces, and we expect the observations reported here to be valid in all biological systems. It is also important to mention that this study was based on a single RNA virus family, and the proposed governing law of genetic mutations is a strong generalization. However, the governing law of genetic mutations is a particular case of a new physics law, called “the second law of infodynamics” [26], which states that the information entropy of all information systems decreases over time. While the second law of infodynamics underpins the generalization of these results to all biological systems, we acknowledge that further studies on other organisms are necessary to validate these results. We, therefore, hope that this work will stimulate future studies, leading to some form of a predictive algorithm for genetic mutations.