Numerical Simulation of Interaction between Plasma and Azithromycin Based on Molecular Dynamics

Abstract

Growing attention has been paid to nonthermal plasma treatment technology and its effects on the degradation of organic matter, especially for antibiotics. However, the majority of the conducted research has focused on the experimental results. Rare attempts were made to analyze the reaction mechanism at the microscopic level. In this paper, molecular dynamics simulation and reactive forcefields were used to investigate the reaction mechanism of different plasma particle interactions with azithromycin molecules. The simulation results indicated that the degradation of azithromycin was caused by the destruction of C-H and C-C bonds, followed by the formation of C=C and C=O bonds when reacted with the active particles. It was also found that the ability of degrading azithromycin varied among the different types of active particles. The oxygen atoms had the strongest ability to decompose the azithromycin molecule, with 38.61% of the C-H bonds broken as compared with other oxygenated species. The findings from this computational simulation could provide theoretical support and guidance for subsequent practical experiments.

1. Introduction

Nonthermal plasma treatment technology is an emerging technology with promising prospects in various applications. Intensive studies have been made in recent decades to develop this technology, especially in the field of biochemistry, such as [1] for pharmaceuticals [2,3], surface disinfection [4], tooth bleaching [5,6,7,8], the organic matter treatment of sewage, and [9] water purification.

Chemical degradation [10,11,12,13] and microbial degradation [14,15] are commonly used to treat the organic matter in sewage and waste liquids, but both approaches have limitations. The chemical degradation method mainly uses a combination of various chemical reagents to degrade substances, but it may cause secondary pollution due to excess chemical products. As for microbial degradation, microorganisms will develop resistance when degrading antibiotics, making the degradation effect worse. However, nonthermal plasma degradation technology will not have the above problems. The nonthermal plasma can continuously generate an appropriate amount of oxygen-containing active particles which can efficiently react with the pollutants to degrade them, producing eco-friendly products. In the literature [16,17,18,19], the plasma–active-oxygen group was used to improve the degradation rate of many antibiotics. The active-oxygen group and the catalyst could accelerate the degradation of antibiotics without producing pollutants. The literature [20,21,22] showed that oxygen-containing free radicals generated by plasma play a vital role in decomposing ofloxacin and other antibiotics, and that the degraded products are mainly carbon dioxide and water, which will not pollute the environment. In the above experiments, only the effectiveness of the oxygen-containing groups on degradation was studied, and the oxidation ability of each active species was not singly identified.

Despite the large numbers of practical experiments that have been conducted and reported, very few studies have focused on the fundamental mechanisms of plasma degradation of antibiotics, especially at the atomic level. Computer simulations are gradually recognized as a bridge connecting theory and experiment, and molecular dynamics simulations are one of them. Molecular dynamics [23] and reactive forcefields [24] can simulate the breaking and formation of chemical bonds so that the mechanism of interaction between substances can be explained. Zhang et al. [25,26,27] studied the interaction mechanism of plasma–active-oxygen groups with fatty acids, glucose, cell walls, and other organics through a molecular dynamics and reactive forcefield simulation, which provided strong support for the experimental research. Based on reactive forcefields, Zhao et al. [28,29] studied the mechanisms of surface modification of materials by plasma.

In this paper, a molecular dynamics and reactive forcefield simulations were used to study the mechanism of the nonthermal plasma degradation of azithromycin. The reactions between the azithromycin molecule with the plasma particles, including hydroxyl, ozone, and an oxygen atom, were also simulated. The specific modeling method will be elaborated in the second section; Section 3 describes the reaction products and pathways; the fourth section focuses on the analysis of the effect of different types and different amounts of active particles on azithromycin molecules; the conclusions and follow-up work will be elaborated in Section 5.

2. Modeling and Simulation

2.1. Reactive Forcefield Molecular Dynamics

Molecular dynamics [23] (MD) is a method that combines physics, mathematics, and other disciplines to simulate the motion of molecular systems by relying on Newtonian mechanics. Molecular dynamics can be roughly divided into two categories. The first category does not involve the breaking and forming of chemical bonds and can generally be used to study phenomena such as heating, compression, and stretching. The second category consists of the breaking and forming of chemical bonds, which requires using reaction potentials, namely reactive forcefield molecular dynamics (ReaxFF MD). This molecular simulation method combines the ReaxFF forcefield and molecular dynamics, which can be applied to simulate chemical reactions in complex systems. The ReaxFF forcefield is a bond-level-based reaction position proposed by van Duin [24] et al. in 2001. The bond level is determined according to the distance between atoms, thereby describing the interaction between substances in a bond-level-based chemical system. The reaction potential files used in this paper are built in the Materials studio software. In the ReaxFF forcefield [24], the total energy of the system can be expressed as the following formula:

$$E_{system}=E_{bond}+E_{over}+E_{unde}{}_r+E_{val}+E_{Coulomb}+E_{vdw}+E_{conj}+E_{tors}+E_{pen}$$

(1)

The first term on the right is the bond energy, and the other terms account for correction terms for over- and undercoordination, valence angles, Coulomb interactions, van der Waals interactions, conjugated systems, torsion terms, and the occurrence of unfavorable configurations, respectively.

2.2. Molecular Structure and Modeling of Azithromycin

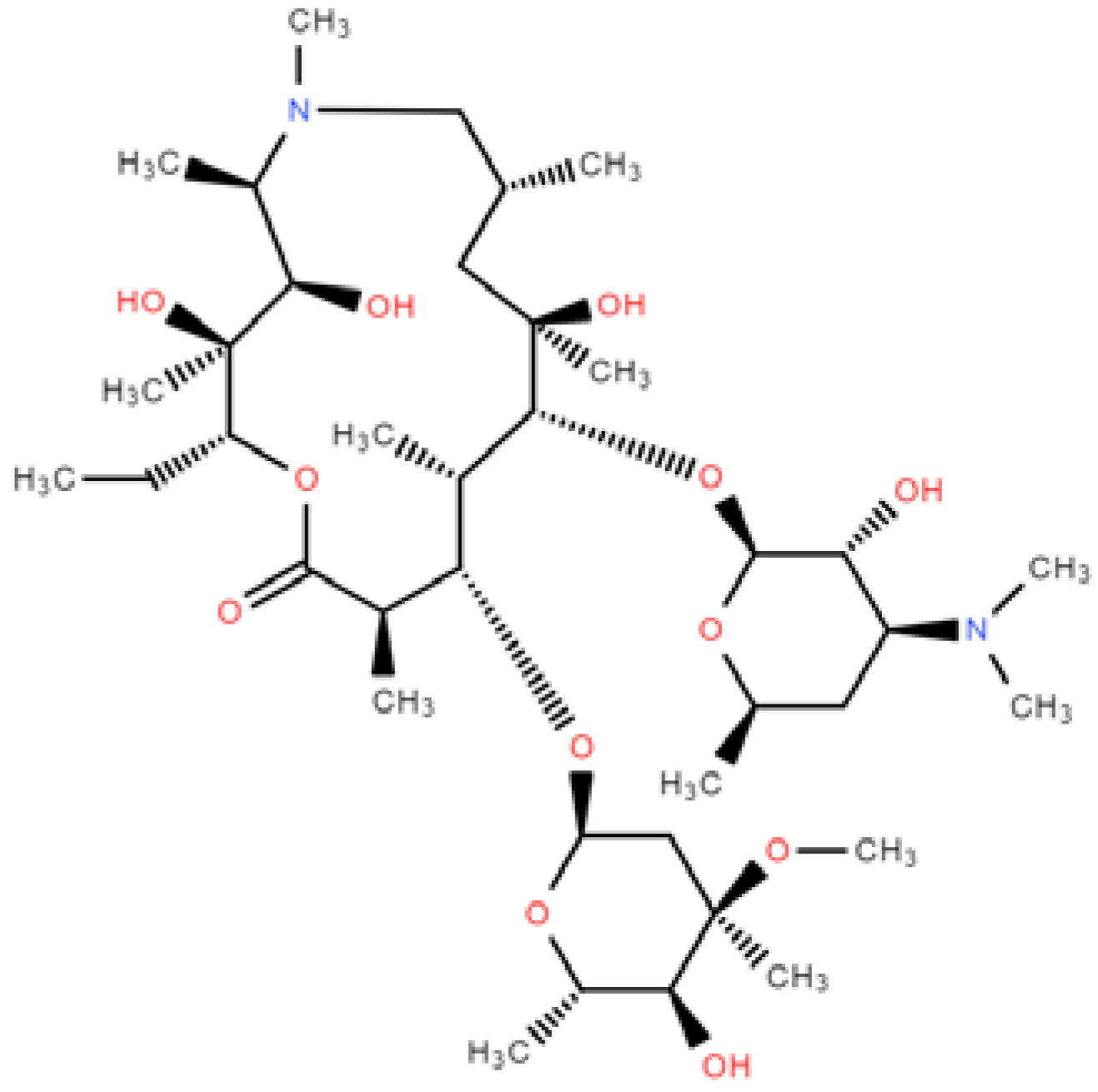
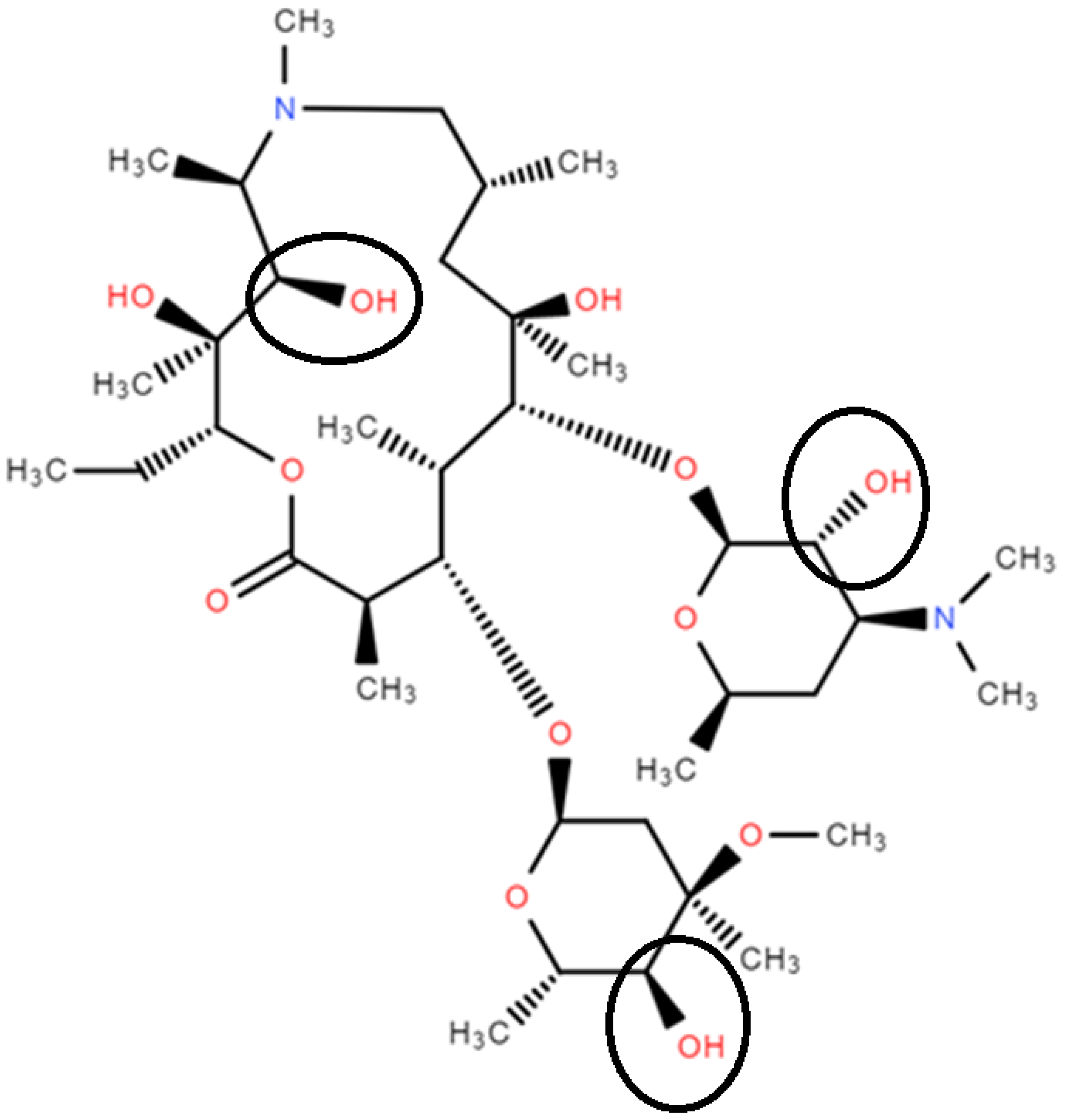
Azithromycin is a commonly used macrolide antibiotic which has a molecular formula of C₃₈H₇₂N₃. As a representative of ester antibiotics, azithromycin is commonly used in aquaculture and animal feeding. The molecular structure is shown in Figure 1. The structure comprises three-ring systems, and the rings are connected by carbon–oxygen bonds (ether bonds). Its molecule has five alcohol groups, three of which can be oxidized into ketones, one ester group, and five ether bonds.

The overall molecular dynamics simulation process is shown in Figure 2.

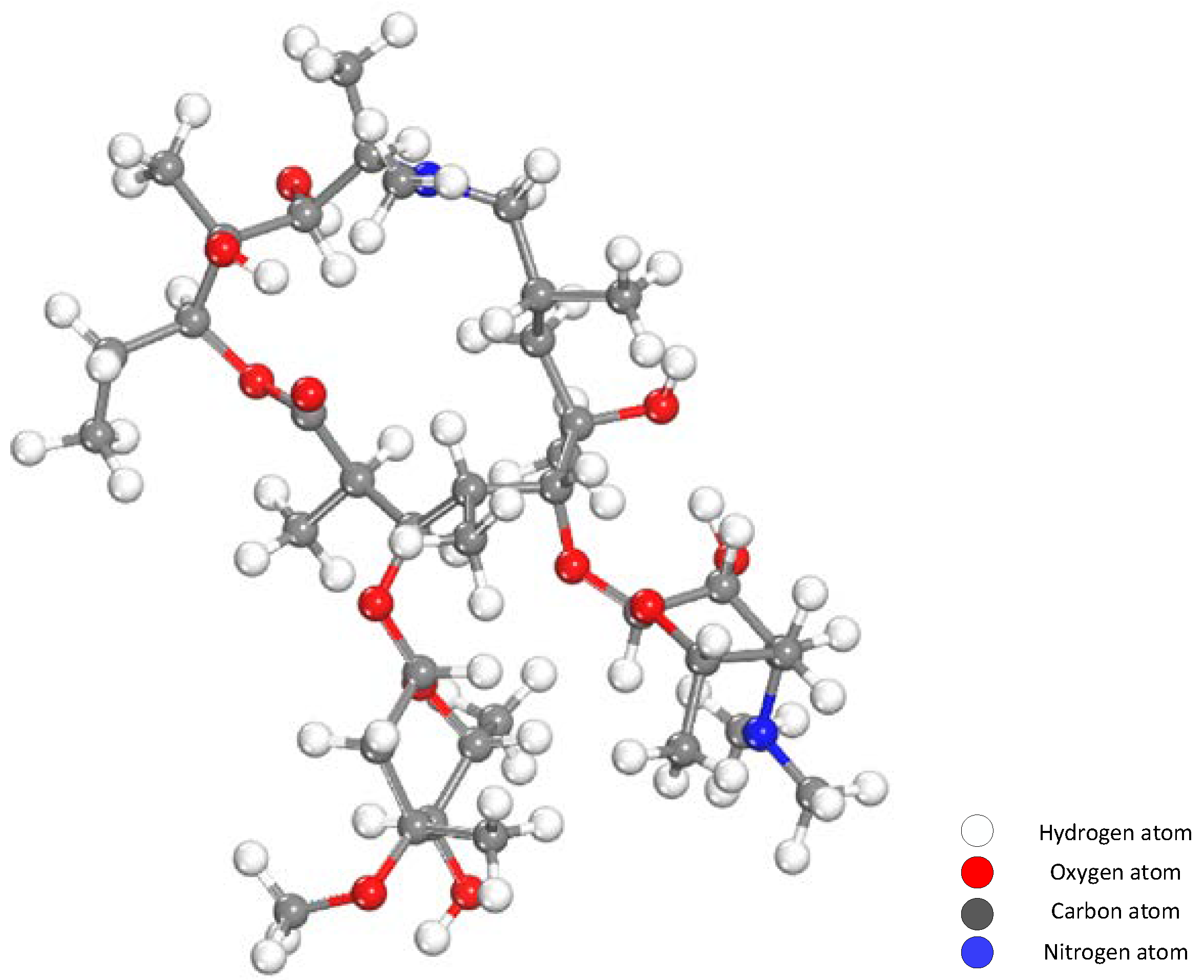
The modeling of the azithromycin molecule was achieved by using MaterialsStudio17.1. With the help of this software, the structure of the azithromycin molecule was drawn, and the correct chemical bonds and forcefields were set as well. The molecular structure was then geometrically optimized with the Forcite module to make it more stable with minimum energy. The specific steps of the simulation are as follows: using the geometry optimization task in the Forcite module, the selection of the NVT ensemble (N represents the number of determined particles, V represents the volume, and T represents the temperature) and the initial velocity of the particles is random. The temperature is set to 298 K, the time step is set to 0.1 fs, and the total simulation time is 100 ps. The processed molecules are shown in Figure 3. Next, using the amorphous cell module to encapsulate the azithromycin molecule with the active particle groups, the Compass forcefield is selected, and the size of the reaction box is about 15 Å × 15 Å × 15 Å. Then, the dynamics task in the Forcite module is used to balance the system energy, and the other settings are the same as above. The purpose is to compensate or remove part of the energy of the system to achieve a stable state with minimum energy.

Then, the ReaxFF reaction potential was used to simulate the reaction between the active-particle groups generated by the plasma and the azithromycin. According to the molecular dynamics principle, the molecular dynamics simulation’s step size should not be too large. Otherwise, the energy will change significantly during the reaction, and the system’s total energy will not be conserved. Moreover, if the simulation step is set for too long, the changes of the system cannot be reflected; if it is too short, the output results will be redundant. In this section, we used the dynamics task of the gulp module and selected the ReaxFF forcefield. Additionally, the charge of each atom was specified by the chosen electric forcefield. After several pre-simulations, it was found that the reaction was completed at about 80 ps, so the total reaction time was set to 100 ps to ensure the reaction was done. The temperature was set to 298 K, the system was set to the NVT ensemble, the simulation step time was set to 0.1 fs, the number of steps was 1,000,000 steps, and the results were output every 1000 steps. The size of the reaction box is about 15 Å × 15 Å × 15 Å. Every simulations was repeated 20 times independently. This paper focuses on the principle and decomposition path of azithromycin decomposition at the microscopic particle level, so to facilitate observation and analysis, only one azithromycin molecule was selected to react with different numbers of active-particle groups.

2.3. Active-Particle Modeling and Simulation

Ten, twenty, thirty, forty, and fifty reactive oxygen atoms (O), hydroxyl(·OH), and ozone (O3) were selected to react separately with an azithromycin molecule to observe its decomposition path and products. Each simulation was conducted 20 times independently. This ratio far exceeds the ratio of the active particle groups to the azithromycin in the actual reaction. Increasing the amount of the substance can speed up the response, get the results faster, and facilitate observation to study the reaction principle, which is reasonable for molecular dynamics. Due to the limitation of time, step size, and computation time, this simulation aims to explain the mechanism of the decomposition of antibiotics by plasma at the level of microscopic particles. Therefore, its simulation time cannot reach the actual.

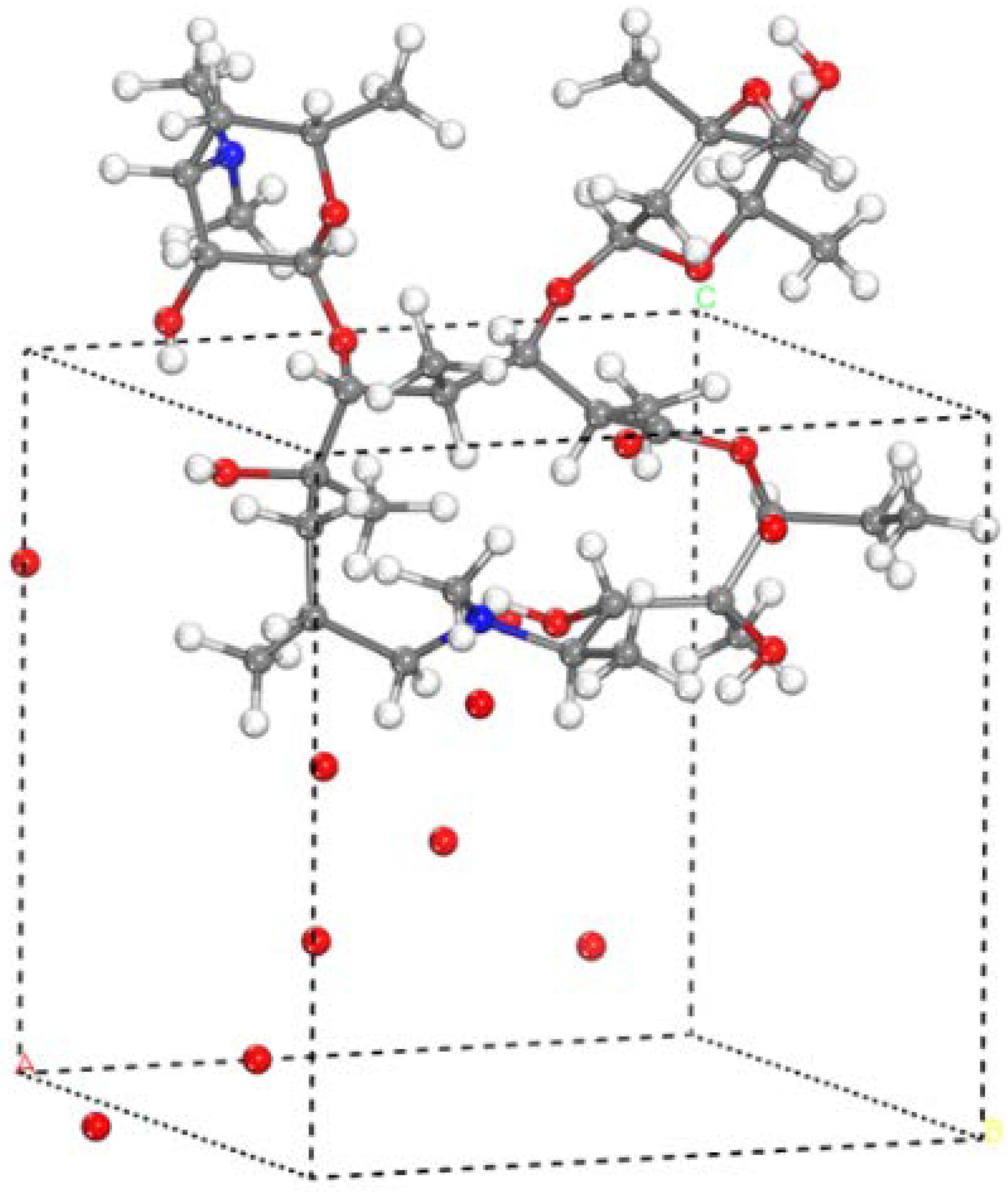
Figure 4 shows a periodic boundary reaction box containing ten oxygen atoms and one azithromycin molecule which can be infinitely extended in all three dimensions. The subsequent modeling of different numbers and types of ROS active particles is the same as above. By setting the periodic boundary, we can observe the changes in the whole system from a reaction box. During the reaction, some molecules run out of the reaction box from one side, but they will return to the reaction box from the other side, which will not affect the reaction result.

3. Results Analysis

3.1. Dehydrogenation Reaction

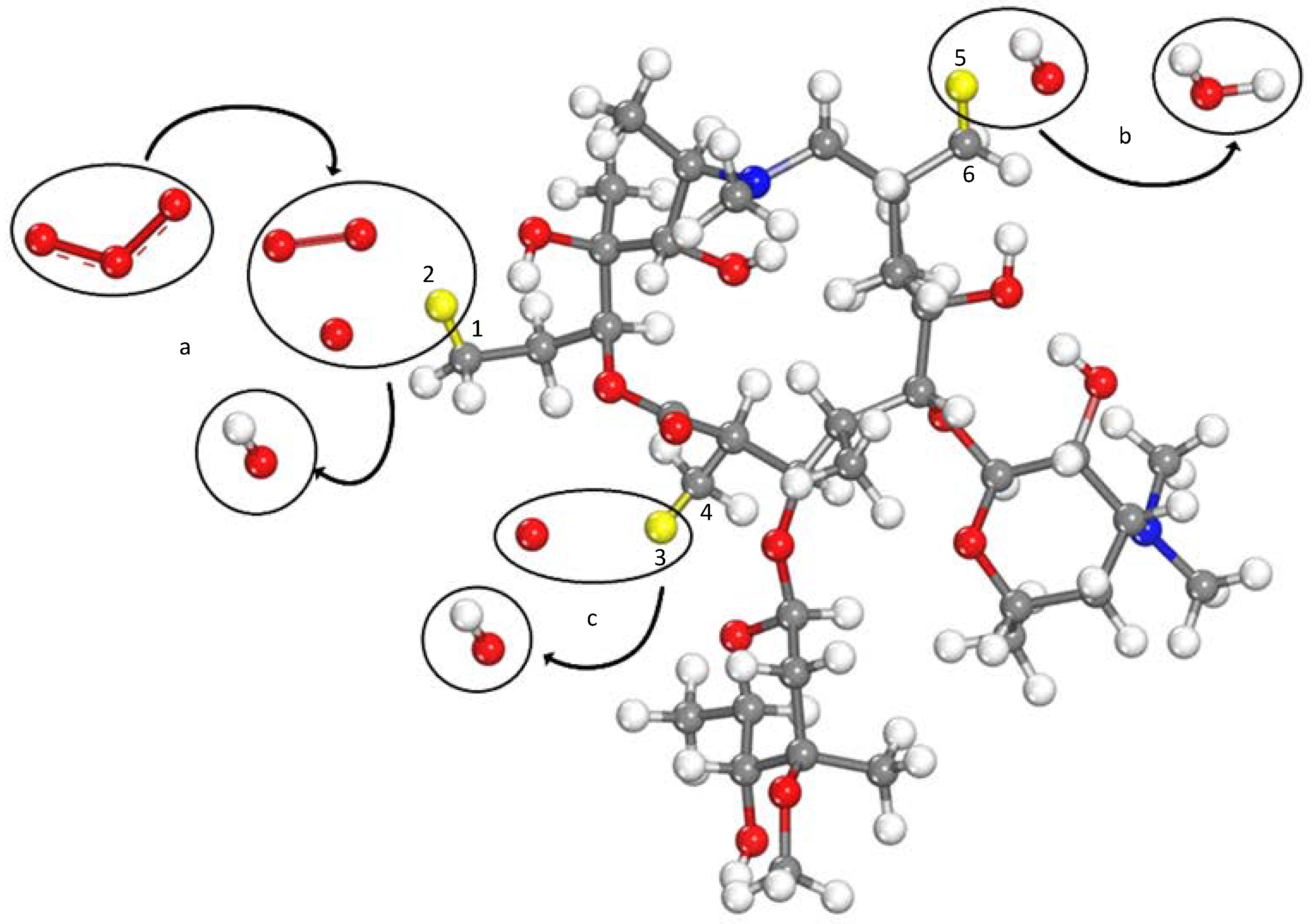
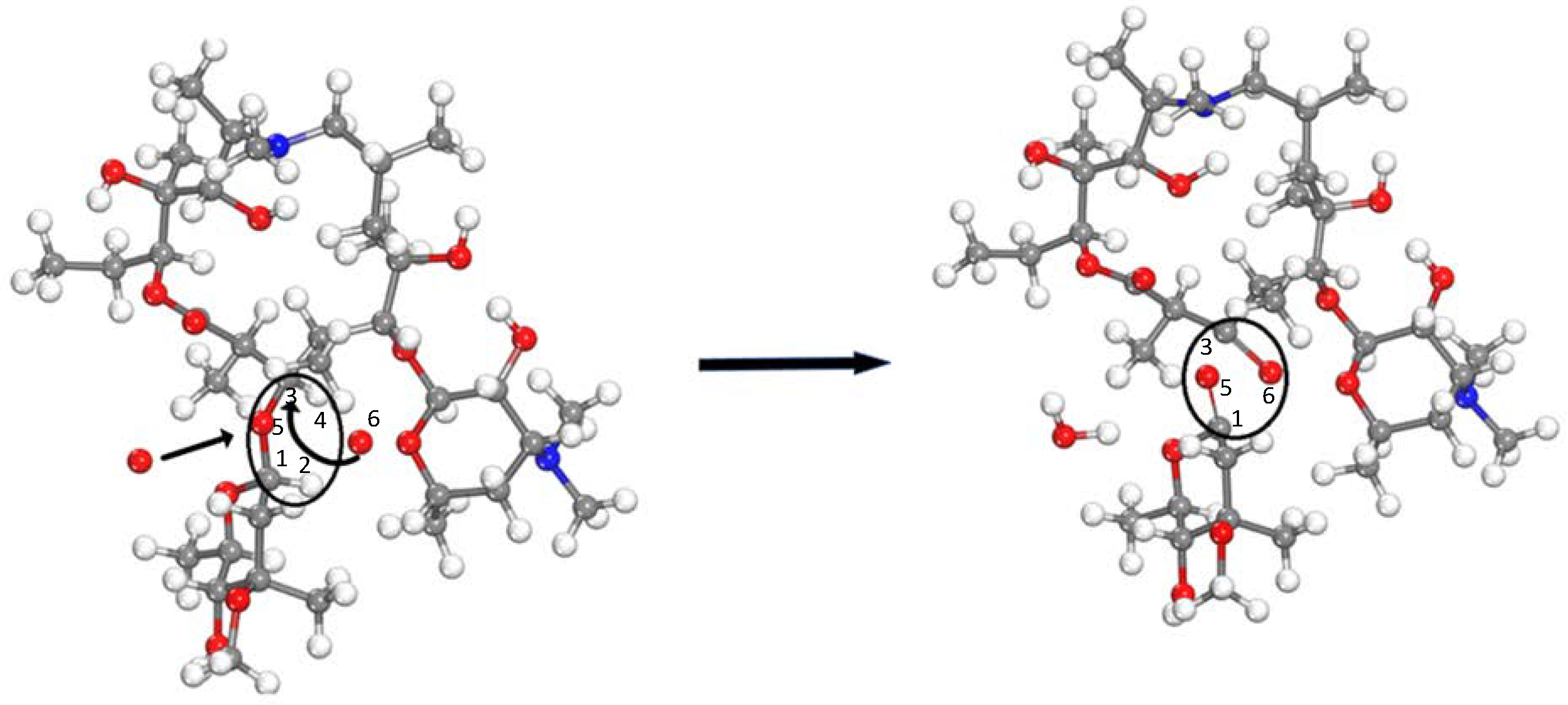
Through the reaction box, it can be observed that some of the C-H bonds are elongated, and the elongated chemical bonds are considered to have been broken when the reaction is complete. The most common response is that the active group abstracts hydrogen atoms from carbon atoms to form free hydroxyl groups, water, and other substances, as shown in Figure 5 (only some products are delivered). This reaction process generally occurs in the early stage of degradation. It acts as a starting reaction to trigger subsequent reactions, consistent with the results described in the literature [25,26]. At (a) in Figure 5, ozone decomposes into oxygen, acts on the C₁-H₂ chemical bond, and then breaks it. Subsequently, the hydrogen atom falls off and bonds with the oxygen atom to form a hydroxyl group; at (b), the hydroxyl group directly interacts with the C₆-H₅ chemical bond to abstract the hydrogen atom and create a water molecule. A single-oxygen atom at (c) interacts with C₄-H₃ to abstract a hydrogen atom to form a hydroxyl group. All three of the above behaviors leave carbon atoms with lone electrons, which make carbon atoms that can combine with other atoms or form C=C bonds with another of the same carbon atoms.

There are many sites where dehydrogenation can occur in practical reactions. If two oxygen atoms each take a hydrogen atom on the adjacent carbon atoms, a C=C double bond will be formed which increases the unsaturation of the reactant; if a carbon atom is taken from a hydrogen atom, and there is no surrounding carbon atom that can form a C=C bond, the carbon atom will have a bondable electron that can combine with the oxygen atom that then moves here to form a C-O bond or directly bond with a hydroxyl group, which is classified as an oxidation reaction, mentioned later. The dehydrogenation reaction accompanies the entire simulation, increasing azithromycin unsaturation over time. The more reactive particle groups there are, the more intense this process is.

After the dehydrogenation reaction, C=O and C=C bonds will be generated at various positions, and these phenomena have similar results [25].

3.2. Oxidation Reaction

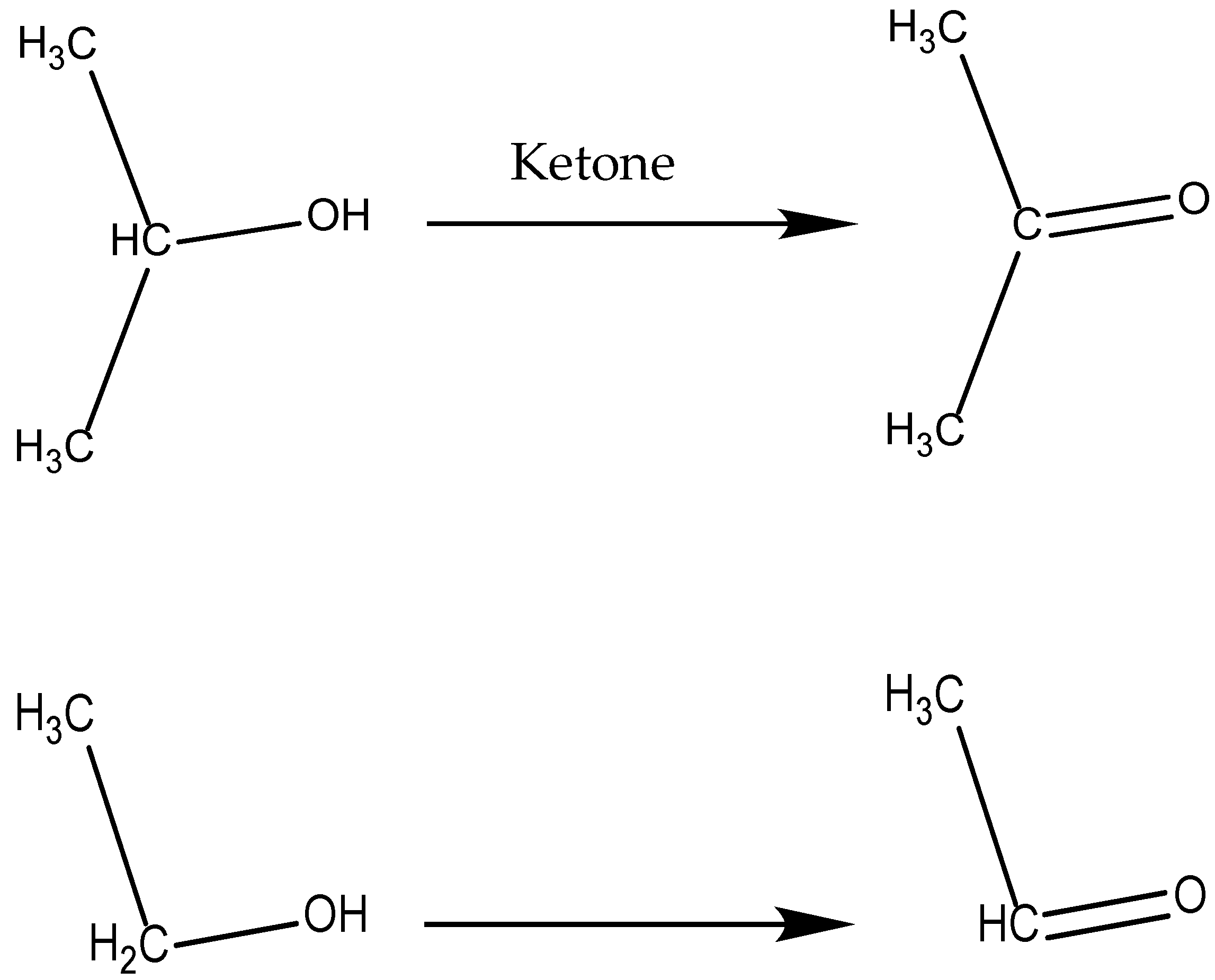
Due to the participation of active-oxygen groups, many oxidation reactions occurred, and now the common oxidation reactions in the simulation are listed. The functional group (-OH) shown in the molecular structure in Figure 6 is called the alcohol group. An oxidation reaction can make the alcohol group form a ketone or aldehyde group if a hydrogen atom is on the attached carbon.

As shown in the molecular structure of azithromycin in Figure 7, three alcohol groups can be oxidized. Figure 8 shows the process of the alcohol group being corrupted. Under the action of oxygen atoms, H₁-C₂ is broken, O₃-H₄ is broken, and the fractured hydrogen atoms and oxygen atom form a water molecule and simultaneously form a C₂=O₄ double bond.

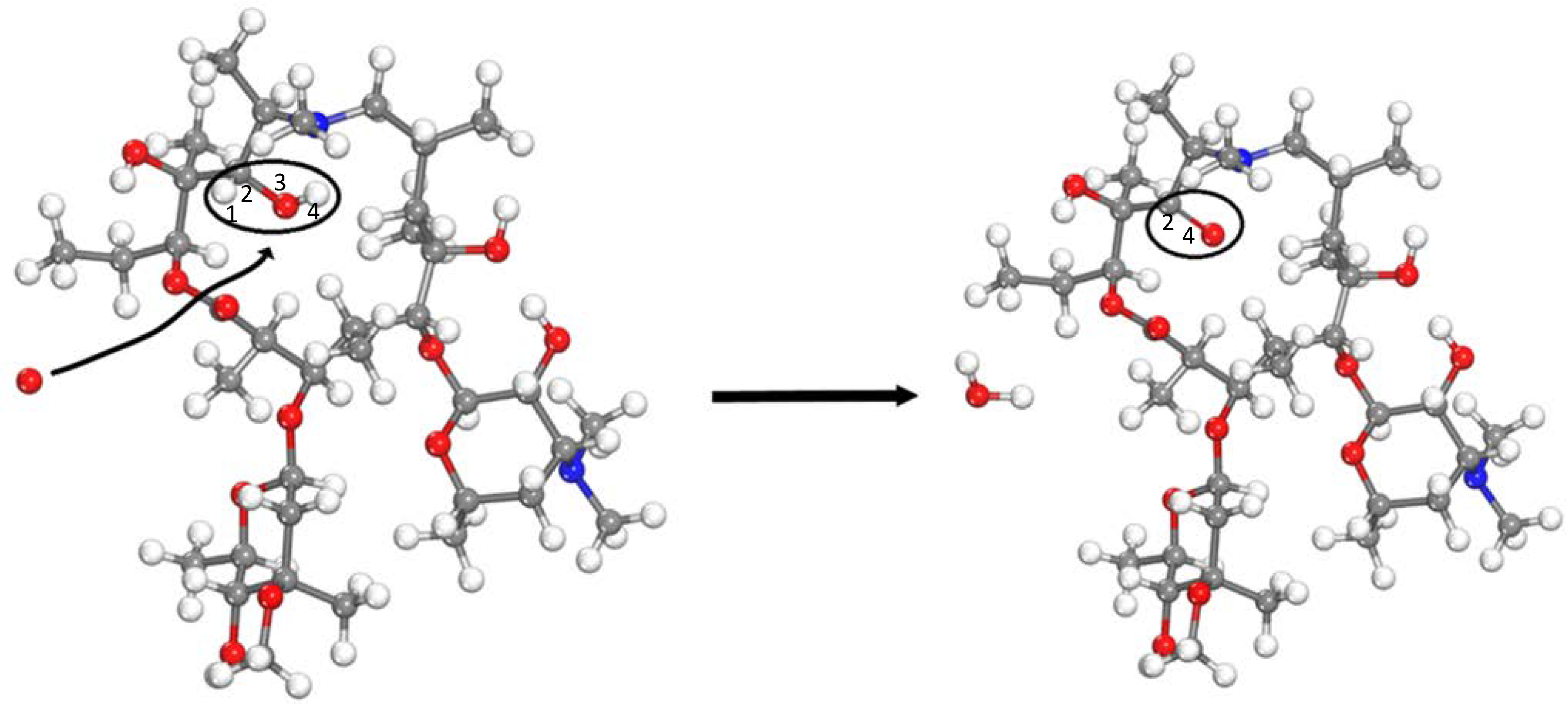
As mentioned in the dehydrogenation reaction above, a lone electron will be left after the carbon atom is dehydrogenated. In the simulation, it is found that this lone electron will combine with a nearby free hydroxyl group or with an oxygen atom to form a C-O bond, which can be further oxidized to form an aldehyde. As shown in Figure 9, the oxygen atom acts on the C₁-H₂ bond to break the bond and abstract the hydrogen atom to form the hydroxyl group 5. Then, the free hydroxyl group O₃-H₇ binds to C₁. The free oxygen atom continues to oxidize the hydroxyl group, the C₁-H₆ bond is broken, the O₃-H₇ bond is broken. Then, they shed hydrogen atoms and the oxygen atom forms a water molecule and simultaneously forms the C₁=O₃ double bond.

In the actual reaction, due to the large number of hydrogen atoms abstracted from carbon atoms, free hydroxyl groups will be combined with carbon atoms which are in diverse positions and maybe be oxidized. The above only shows one situation.

3.3. Inter-Ring and Intraring Fractures

As shown in Figure 10, azithromycin is composed of three-ring structures, ether bonds connect the rings, and the three rounds are not in the same plane. Figure 10 shows the bond length of each chemical bond of the azithromycin molecule. It can be seen from the chemical principle that the shorter the bond length of the covalent bond, the greater the bond energy and the more stable the bond structure. As shown in Figure 10, some C-C bonds and C-O bonds (ether bonds) have longer bond lengths and lower energy. Therefore, the ether bonds with lower bond energy are insufficient to support the ring structure in the interaction, being especially impacted by many active particles. The ether bond cleavage influenced by active-oxygen groups is also described in the literature [26]. As shown in Figure 11, influenced by the energetic particles, after breaking the C₃-O₅ bond, the C₃-H₄ and C₁-H₂ bonds are broken simultaneously, forming a C₁=O₅ double bond, and then the hydrogen atoms generated in this process and the free oxygen atoms form a water molecule. After C₃-O₅ is broken, carbon atoms containing lone electrons recombine with active particles to form C₃=O double bonds.

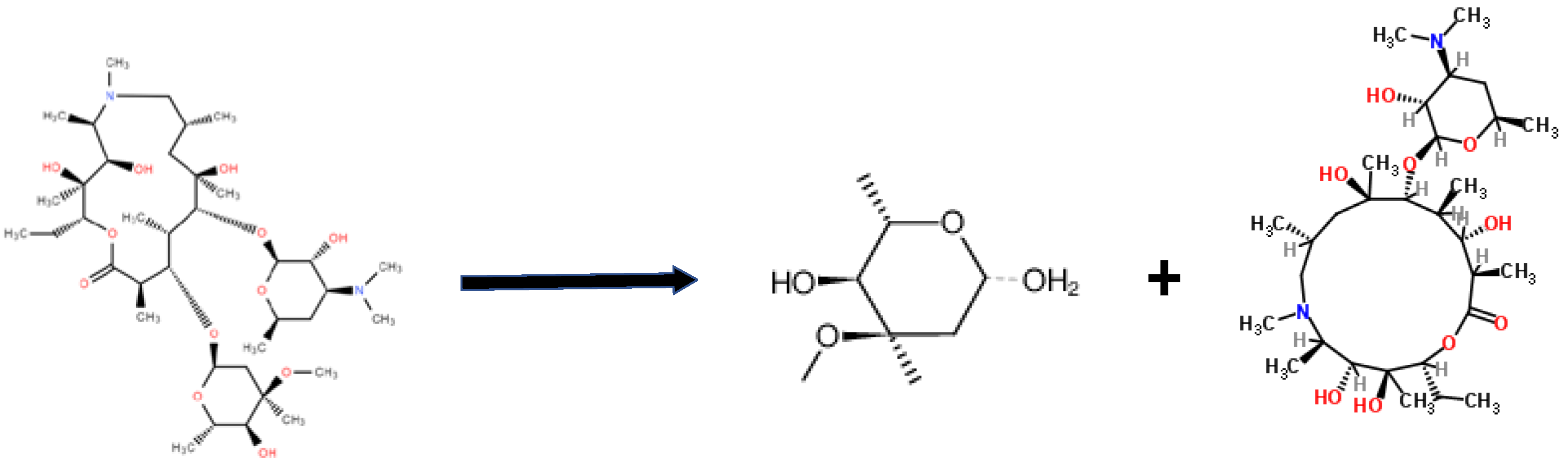
The product prototype formed after the detachment of the nitrogen-containing ring in the molecule is called Descladinose Azithromycin. The product prototype after the reaction of the nonnitrogen-containing ring is called L-cladinose, as shown in Figure 12. However, due to the dehydrogenation and oxidation reactions under the action of many active particles, the unsaturation and functional groups of the obtained product have undergone significant changes. However, from the skeleton’s perspective, it can still be seen that it is very similar to the prototype molecule.

After the ring is detached, the ether bond inside the ring may also be broken under the impact of active particles. Then, an alcohol group is generated, which can be further oxidized to an aldehyde group. The ether bond may be broken under the influence of acidity or alkalinity, so in the actual plasma degradation experiment of azithromycin, there will be more than one induction mechanism of this ring opening.

Under the action of a large number of active particles, azithromycin undergoes a hydrogen abstraction reaction. Then, the carbon–carbon bond is broken under the impact of the energetic particles, and the breaking positions depend on the length of the bond. The longer the bond length, the easier it is to break the chemical bond. The longer the treatment time and the more active atoms, the faster the fracture and the greater the number of fractures.

This section shows some essential plasma degradation products, critical chemical reactions, and the breaking and formation of crucial chemical bonds. After the reaction, there are many oxides, peroxides such as hydrogen superoxide, hydrogen peroxide, and carbon dioxide, as well as small molecules of carbon-containing organic compounds. This chapter aims to analyze its kinetic principle and the changes in vital chemical reactions to provide guidance and reasonable predictions for subsequent experiments.

4. Statistics and Analysis of Simulation Results

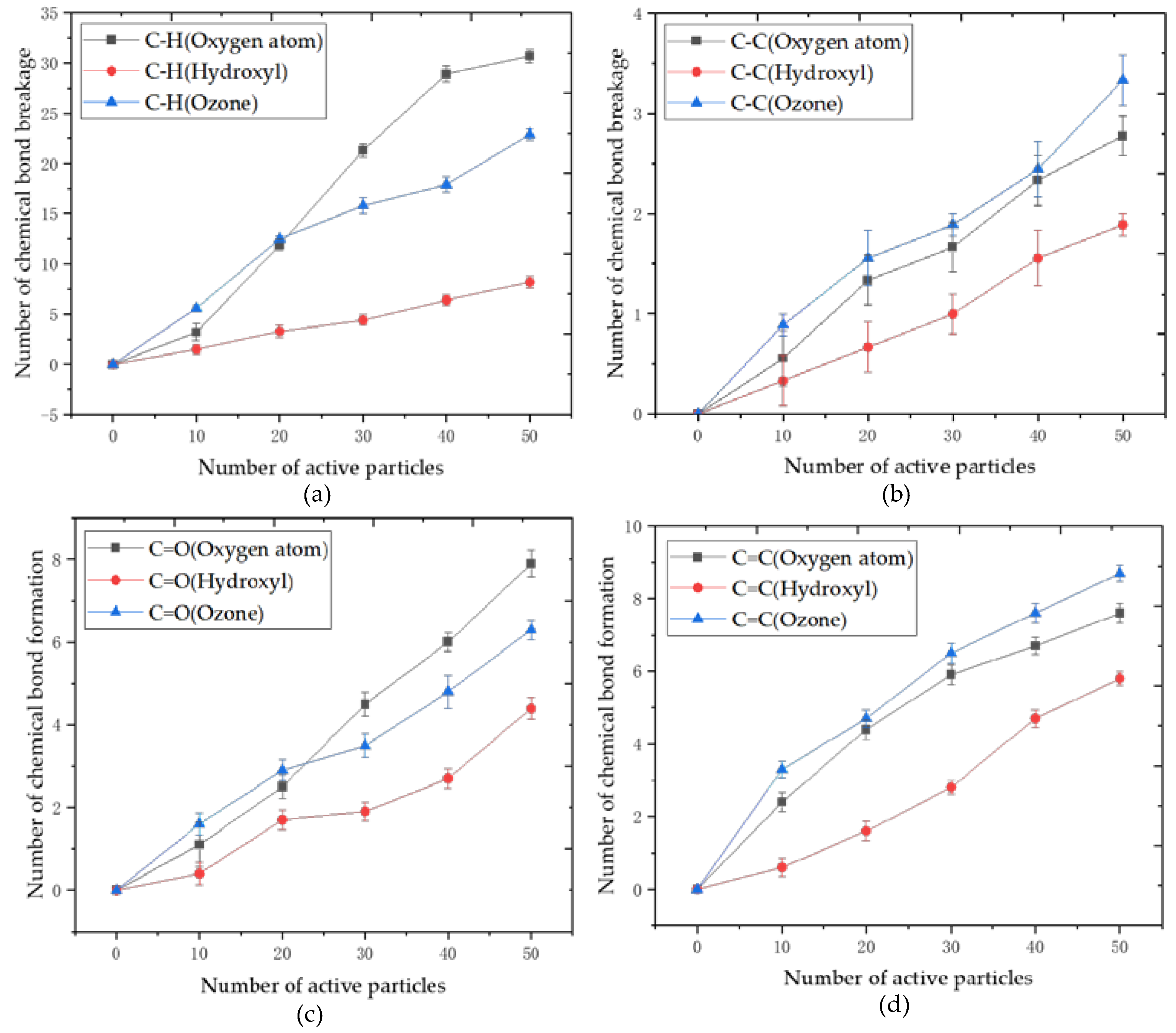
This part analyzes the azithromycin bond formation and bond-breaking with different active particles with the change of their number. According to the molecular structural formula of azithromycin, the number of C-H bonds that can be broken is 72, the number of C-C bonds is 29, and the percentage of C=C bonds is calculated as the percentage of double bonds formed in the original single bond. Moreover, the rate of C=O bonds is calculated as the percentage of double bonds in the original C-O bond. This calculation method is to more intuitively describe the degree of reaction to azithromycin molecules under the action of different active particles.

Figure 13 shows the specific number of broken or formed chemical bonds and the variance with multiple groups of samples. It can be seen that the variance of the C-H bond, C=O bond, and C=C bond are minor, while the variance of the C-C bond breakage is significant, as its breakage number is small. If the number of samples continues to increase, this error can be reduced.

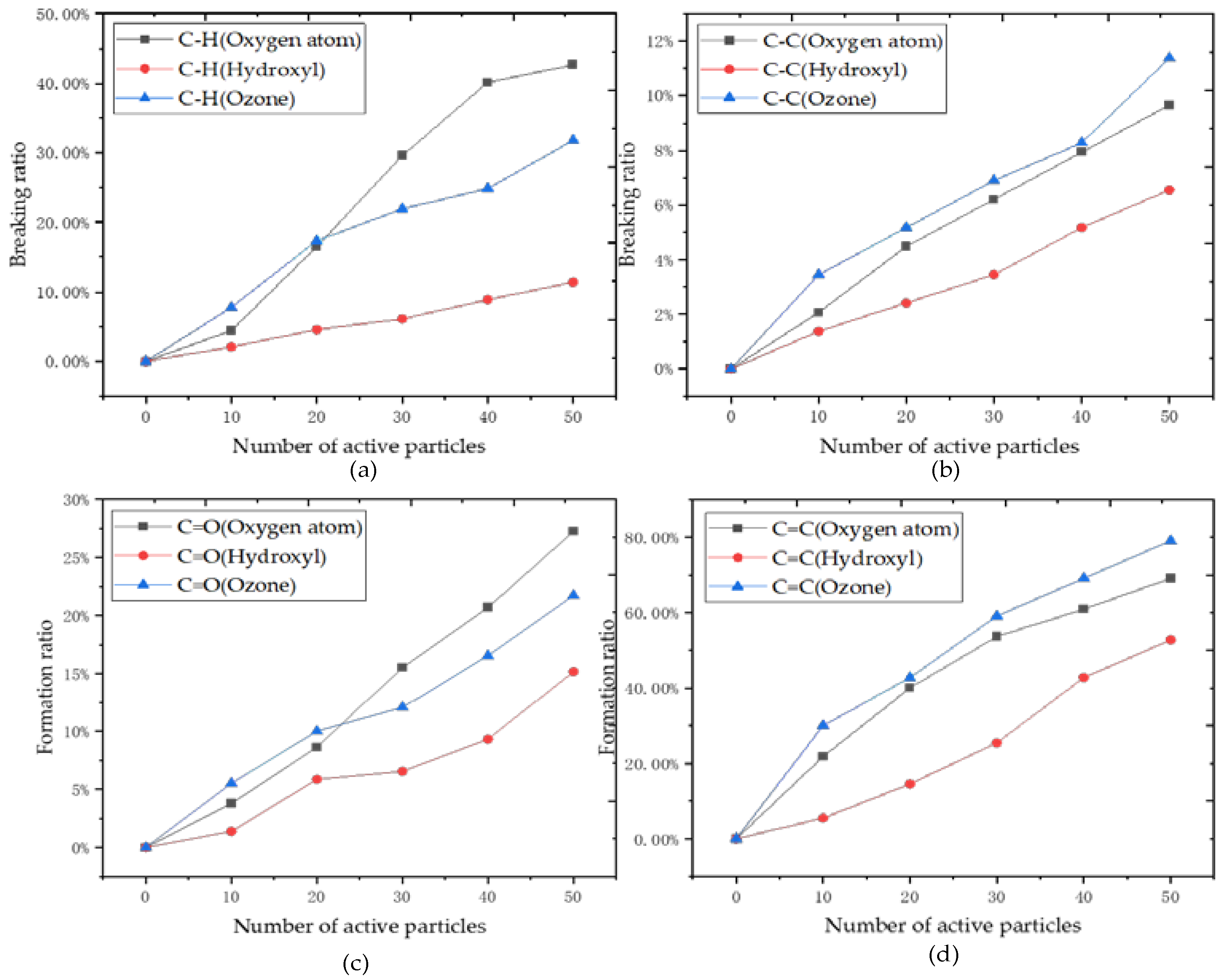
Figure 14 shows the percentage of each chemical bond change in the azithromycin molecule under the action of different active particles. It can be more intuitive to observe the degree of influence by active particles on the whole molecule.

The data of the breaking and formation of main chemical bonds is listed in

Table 1. The relationship between the changes of four key chemical bonds of azithromycin molecule and the number of active groups. The results in the table are the mean values from 20 independent simulations.

Incident Plasma Species	C-H Breaking Ratio (%)	C-C Breaking Ratio (%)	C=C Formation Ratio (%)	C=O Formation Ratio (%)
O (10)	3.89%	2.07%	3.79%	21.82%
O (20)	16.39%	4.48%	8.62%	40.00%
O (30)	29.72%	6.21%	15.52%	53.64%
O (40)	34.72%	7.93%	20.69%	60.91%
O (50)	38.61%	9.66%	27.24%	69.09%
OH (10)	1.81%	1.38%	1.38%	5.45%
OH (20)	4.17%	2.41%	5.86%	14.55%
OH (30)	5.56%	3.45%	6.55%	25.45%
OH (40)	8.06%	5.17%	9.31%	42.73%
OH (50)	10.69%	6.55%	15.17%	52.73%
O3 (10)	7.08%	3.45%	5.52%	30.00%
O3 (20)	15.69%	5.17%	10.00%	42.73%
O3 (30)	19.86%	6.90%	12.07%	59.09%
O3 (40)	22.36%	8.28%	16.55%	69.09%
O3 (50)	28.61%	11.38%	21.72%	79.09%

. The breakage of the C-H bond is almost throughout the entire reaction, and the oxidation reaction and the breaking of various chemical bonds firstly require a dehydrogenation reaction. It can be observed from Figure 14 that the dehydrogenation ability of ozone and reactive oxygen atoms is stronger, while the dehydrogenation ability of the hydroxyl group is weak. When ten active particles were added, the dehydrogenation capacity of ozone was the highest at about 7.08%. Ozone is unstable and can decompose more oxygen atoms to participate in the dehydrogenation reaction. Still, when 20 active particles or more are added, the dehydrogenation capacity of energetic oxygen atoms is the highest, reaching 38.61%. At the same time, the oxygen generated by the decomposition of ozone will react with hydroxyl groups to produce hydrogen peroxide or hydrogen superoxide instead of taking the hydrogen atoms on carbon atoms; that is to say, the products of ozone decomposition will react with the newly formed hydroxyl and other substances so that hydrogen atoms cannot be extracted from the carbon chain exclusively. Therefore, as the number increases, the hydrogen abstraction ability of oxygen atoms is stronger than that of ozone. Because the structure of the hydroxyl group is more stable than the oxygen atoms, its possibility of bonding with the hydrogen atom is not as urgent as oxygen atoms, and the C-H breaking rate is only 10.69%.

The breaking of the C-C bond is partly caused by the movement and impact of the active particles. The other reason is the formation of a large number of C=C bonds. In the C=C bond, it requires the bond and atoms to be in the same plane, so the breakage of the chemical bond occurs when the forces on the ends of the carbon atoms in the azithromycin molecule are not balanced. The C-C fragmentation ability of ozone is the strongest, reaching 11.38%, while the hydroxyl group is only 6.55%.

The reason for forming the C=C bond and C=O bond is that the active particle abstracts the hydrogen atoms, and the carbon atoms produce the lone electron. The above analysis shows that the oxygen atoms have a more robust and specific ability to abstract the hydrogen atoms. More C=C bonds are generated after interacting with active-oxygen atoms, and the bond-formation rate reaches 27.24% when the number of oxygen atoms is the largest. The ozone will be decomposed into oxygen and oxygen atoms, and oxygen will oxidize the hydroxyl groups to form C=O bonds, so the C=O double-bonds-bonding rate can reach 79.09%. The number of C=O and C=C bonds formed in the azithromycin molecule which has reacted with the hydroxyl group is the least, and the bonding rate is only 15.17% and 52.73% when the number of hydroxyl groups is the largest.

5. Conclusions

In the present study, a molecular dynamics simulation and reactive forcefields were used to investigate the mechanisms of nonthermal plasma particle degradation of azithromycin molecules. The simulation results indicated that the C-H and C-C bonds in the azithromycin molecules were firstly broken by the active groups in the nonthermal plasma, after which additional C=C and C=O bonds were formed. As a result, the azithromycin molecules were decomposed into mainly H₂O, CO₂, and other organic small molecules.

The ability of degrading azithromycin molecule for different types of active particles, namely, oxygen atom (O), ozone (O3), and hydroxyl radical (-OH), were also investigated in the present study. It was found that the oxygen atoms had the strongest ability to decompose the azithromycin molecule, with 38.61% of the C-H bonds broken, as compared with other oxygenated species. The findings from this computational simulation could provide theoretical support and guidance for subsequent practical experiments.

It was discovered during the study that the position where plasma particles interact with azithromycin could affect the chemical activities. Therefore, the effects of the reaction position of the azithromycin molecule should be investigated in further studies. In addition, the effects of other air–plasma species, such as active nitrogenous particles, on the degradation of antibiotics should also be studied.