Abstract
For both linear and nonlinear analysis, finite element method (FEM) software packages, whether commercial or in-house, have contributed significantly to ease the analysis of simple and complex structures with various working conditions. However, the literature offers other discretization techniques equally accurate, which show a higher meshing flexibility, such as meshless methods. Thus, in this work, the radial point interpolation meshless method (RPIM) is used to obtain the required variable fields for a nonlinear elastostatic analysis. This work focuses its attention on the nonlinear analysis of two benchmark plate-bending problems. The plate is analysed as a 3D solid and, in order to obtain the nonlinear solution, modified versions of the Newton–Raphson method are revisited and applied. The material elastoplastic behaviour is predicted assuming the von Mises yield surface and isotropic hardening. The nonlinear algorithm is discussed in detail. The analysis of the two benchmark plate examples allows us to understand that the RPIM version explored is accurate and allows to achieve smooth variable fields, being a solid alternative to FEM.
1. Introduction
Computational mechanics is the discipline concerned with the use of computational numerical methods to study phenomena governed by the principles of solid and fluid mechanics. It is used every day to help predict, develop, and improve not only structural and fluid applications in the industrial sense but also several other science areas, such as medicine, biology, chemistry, etc. [1]. With the constant evolution of engineering, the challenges for computational mechanics are numerous. For example, when analysing the simulation of manufacturing processes, such as extrusion or moulding, it is necessary to deal with large displacements of mesh, viscoplastic effects and contact conditions, whereas in simulations of failure processes, it is required to model the fracture initiation and its propagation path, leading to the development of demanding remeshing algorithms and fracture-damage criteria.
Problems dealing with large mesh distortions or localised remeshing requirements are not efficiently solved by mesh-dependent discretization techniques, such as the finite element method (FEM) [2]. Meshless methods are an alternative to classic mesh-dependent discretization methods. In meshless methods, the problem domain is discretized by a random set of nodes, without any preestablished connectivity, rather than a structured element mesh. To define the nodal connectivity, meshless methods use the influence-domain concept, allowing one to establish automatically the nodal connectivity in a later stage of the preprocessing phase [3,4].
Meshless methods and their origin can be traced to the smooth particle hydrodynamics method (SPH) [5]. It was applied to polytropic stellar models and used statistical techniques to recover analytical expressions for the physical variables from a known distribution of fluid elements, starting with a nonaxisymmetric distribution of approximately 80 particles in three dimensions. This method was applied to solid mechanics by Larry D. Libersky and A.G. Petschek [6] in 1991, in which an elastic-perfectly-plastic constitutive model was formulated. It was found that excellent features of the SPH, such as robustness, simplicity, and ease of adding new physics, could be transferred to the analysis of solid mechanics problems [7].
SPH is a particle method, in which the set of nodes (the particles) do not form a solid continuum in the same sense as in FEM, being more suited for free surface fluid analyses. Thus, other meshless technique started to be developed, such as the diffuse element method (DEM) [8], the first mature meshless method using a weak formulation and shape functions constructed by using the moving least-squares (MLS) approximants approach. Then, Belytschko and coworkers improved the DEM and proposed in 1994 the element free Galerkin method (EFGM) [9], one of the most popular meshless methods. At the same period, other approximation meshless techniques were developed, such as the reproducing kernel particle method (RKPM) [10] and the meshless local Petrov–Galerkin method (MLPG) [11], a truly meshless method (in the sense that it does not require a background nodal independent integration mesh) based on a local symmetric weak form (LSWF). MLPG does not need an element mesh for the interpolation of the solution variables. Integrals are solved over a regular-shaped domain and its boundaries. The generalized finite difference method (GFDM) is another popular approximation method [12,13]. Because it can be applied to solve problems discretized by using only an irregular nodal distribution, GFDM is also considered truly meshless. GFDM uses the Taylor series expansions and the MLS approximation to derive explicit expressions for the required partial derivatives of unknown variables. Collocation meshless methods are another class of meshless methods available in the literature, such as the local radial basis function collocation method (LRBFCM) [14,15], which uses the strong-form formulation to establish the system of equations and obtain the variable field. LRBFCM uses radial basis functions to construct trial functions, and it is highly dependent on the shape parameters of the corresponding radial basis function. The accuracy and efficiency of LRBFCM strongly depend on the values of such shape parameters, which must be analysed and optimised for distinct problems [14,15]. The literature offers several variants of collocation methods, such as the Trefftz collocation method [16,17].
Approximation methods, such as EFGM, RKPM, and MLPG, produce highly accurate solutions. However, their shape functions lack the Kronecker delta property, hindering the imposition of the essential and natural boundary conditions, which can only be enforced with exact technique, such Lagrange multipliers [1]. Therefore, efforts were made to develop interpolating meshless techniques. The natural element method (NEM), was one of the first to be developed [18]. Using the natural neighbour and Voronoï diagram concepts, the nodal connectivity, the background integration mesh and the shape functions (and corresponding spatial derivatives), are constructed automatically, producing a true meshless method approach with interpolating properties. In 2001, G.R. Liu and his research team developed the point interpolator method (PIM) [19], in which the shape functions are constructed by using a polynomial basis. Although simple and easy to apply, the process is not capable of producing shape functions when nodes are perfectly aligned (most common in regular nodal distributions). Therefore, a radial basis function was added to the formulation, allowing for the development of one of the most popular interpolating meshless methods: the radial point interpolation method (RPIM) [20]. The use of the radial-based functions eliminated the singularities occurring from the nodal alignment. Later, Belinha and coworkers included in the formulation the natural neighbour concept and developed the natural neighbour radial point interpolation method (NNRPIM) [1,21]. With the NNRPIM, both the nodal connectivity and the node-dependent integration background mesh are constructed resorting to the Voronoï tessellation and to the Delaunay triangulation. This procedure guarantees that the shape functions developed have the Kronecker delta property and a formulation that is truly meshless. The literature shows that both RPIM and NNRPIM are highly accurate and present high convergence rates [1], being solid alternatives for structural analysis.
It is possible to find in the literature several works successfully combining meshless methods with elastoplastic formulations. In 1999, Barry and Saigal [22] extended the EFGM to elastoplasticity considering a 3D formulation with small strains, analysing a thick-walled pressure vessel with internal pressure and an extension of a strip with a circular. Compared with reference solutions [23], the method was capable of producing results very close to the ones obtained in the FEM. In 2006, Belinha and Dinis [24,25,26] used the EFGM in the analysis of two-dimensional problems, plates, and laminates in the elastoplastic regime. Various modified Newton–Raphson algorithms were used to obtain the nonlinear solution. A Cook membrane and a sandwich material, under distributed load, were studied. The obtained results were in accordance with FEM solutions. Several modified Newton–Raphson algorithm versions were used to obtain the nonlinear solution and their performance and computational cost was also analysed. The results showed that the EFGM is a solid alternative to such nonlinear problems, being capable of obtaining similar results to the FEM analysis. More recently, in 2014, Cheng et al. [27], developed a novel interpolating EFGM (IEFGM) for two-dimensional elastoplasticity. By using the interpolating moving least-squares method (IMLS) to construct the shape functions, the Kronecker delta property is satisfied, and the essential boundary conditions can be applied directly. The method has some advantages, such as simpler formulae and the direct application of the boundary conditions. The results showed that the IEFGM is in good agreement with FEM, and it was also found that the IEFGM possesses a higher precision than the classic EFGM.
Regarding the RPIM, and its versios, in 2011, Dinis and coworkers [28] extended the NNRPIM to the large-deformation elastoplastic analysis, using the Newton–Rapson nonlinear solution algorithm and an efficient “forward-Euler” procedure to return the stress state to the yield surface. Then, in 2015, Zhang et al. [29] were capable of combining the node-based smoothed radial point interpolation method (NS-RPIM) with gradient-dependent plasticity to analyse the elastoplastic material behaviour of 2D solids. More recently, in 2019, Belinha and coworkers [30] extended both RPIM and NNRPIM to the elastoplastic analysis of aluminium alloys. In order to obtain comparable results, due to the lack of a suitable elastoplastic solution, an experimental test was performed in order to obtain the force/displacement curve and the corresponding mechanical properties. A dog-bone-shaped specimen was analysed with elastoplastic assumptions, under uniaxial tensile state conditions. Two different influence-cell degrees were considered—first degree and second degree—with the results showing that the second-degree influence cell returned a smooth result, whereas the first-degree cell had some discontinuities. Moreover, the results obtained with either the RPIM and NNRPIM showed a strong correlation with the experimental data. The main disadvantage of NNRPIM is clearly addressed: its higher computational cost when compared to the FEM and RPIM, which is due to the time spent establishing the natural neighbours and constructing the background integration points. Nevertheless, being a truly meshless method is also pointed out as its main advantage. Therefore, to fully discretize the problem domain, only a nodal discretization is required. The technique is then capable of automatically generating all the other required numerical structures (nodal connectivity, integration point, and shape functions).
In the present work, a radial point interpolation method version combined with a nonlinear solution algorithm was originally written and coded to study the elastoplastic bending behaviour of plates by using a classic 3D formulation. Thus, in the following sections, the RPI formulation and its extension to elastoplasticity are presented, and then 3D plate examples are solved by considering elastoplastic materials.
2. Meshless Methods
The majority of meshless methods follow a generic procedure, well discribed in the literature [1,2]. After the problem geometry and the natural and essential boundary conditions are described and established, the problem domain and the respective boundary are discretized by using a nodal set, which can follow a regular or irregular distribution. Similar to mesh-dependent methods combined with weak formulations and applied to elasticity problems, the accuracy of the solution provided by meshless methods depends on the nodal density of the discretization. Thus, a higher density of nodes generally returns more accurate results. Moreover, in specific problems wherein particular geometrical or loading details can have a considerable effect on the stress distribution (material discontinuities or concentrated loads), a higher nodal density in those locations is required to obtain better results. In meshless methods, the nodal distribution does not form a mesh because there is no preestablished connectivity between the nodes.
After the nodal discretization of the problem domain, the background integration points are defined. The complete set of integration points is known as integration mesh. Background integration meshes can be obtained by using background integration cells (fitted to the problem domain, as elements in the FEM) or by using nodal integration schemes (as the ones used in NEM or NNRPIM). This last procedure uses the mathematical concepts of natural neighbours, Voronoï diagrams and Delaunay tessellation to construct the integration points uniquely based on the nodal distribution, and thus producing truly meshless formulations.
After discretizing the problem domain with nodes and integration points, it is possible to establish the nodal connectivity. In FEM, as input, it is necessary to declare the nodes forming each element. Thus, integration points inside each element interact with the nodes forming that element, and elements interact with other elements possessing common nodes. In meshless methods, because there is no preestablished declared relation between the nodes, it is necessary to enforce such connectivity. Therefore, it is necessary to apply the concept of influence domain. Each integration point will search for nodes inside a certain radius. The nodes inside such radius will form the influence domain of . Due to its simplicity, several meshless formulations apply such concepts (RPIM, EFGM, MLPG, RKPM, etc.). There are several variants to this concept [1], some authors use fixed radial searches and other use variable radial searches. Fixing a radius will produce uneven influence domains. Integration points near a physical boundary will possess a lower number of nodes inside their influence domains when compared with the influence domains of the nodes inside the problem domain. Alternatively, fixing the number of nodes inside each influence domain (variable radius searches), will produce influence domains of the same size for all integration points. Alternatively, meshless formulations using the natural neighbour concept, such as NEM or NNRPIM, already possess the nodal connectivity established due to the Voronoï diagram [31] of the nodal discretization. Each integration point has an associated node , and each node possesses a set of natural neighbours: . Thus, the influence domain of is the set of natural neighbours of : , and itself.
Afterward, the shape functions are constructed by using approximation or interpolation functions according to the technique adopted. Regardless of the technique, the field variable can be approximated (or interpolated) at an integration point with
where n is the number of nodes inside the influence domain of the integration point , is a vector containing the field variable components of each node included in the influence domain of , and is the ith component of the shape function constructed for . Instead, the sum operation, the vectorized operation of Equation (1) can be used, in which and .
After constructing the shape function of each integration point, and its spatial partial derivatives, it is possible to apply then to a strong or weak form governing the problem domain and establish the system of equations, the resolution of which provides the problem’s solution variable fields (displacements, velocities, pressures, etc.)
2.1. The Radial Point Interpolation Method
In order to obtain the background integration points and to allow the numerical integration of the integro-differential equations governing the studied phenomenon, the RPIM classic formulation uses the Gauss–Legendre quadrature integration scheme. Therefore, the problem domain can be divided with regular integration cells, Figure 1, and then each integration cell is transformed into a isoparametric cube, in which the integration points are included following the Gauss–Legendre integration scheme (Figure 1). In the end, by using linear polynomial interpolating functions , whose generic equation is given by
considering
the isoparametric coordinates can be transformed back into Cartesian coordinates (Figure 1), with
For the RPIM formulation, inside each integration cell, it can be inserted in integration points, whose isoparametric coordinates and weights are, correspondingly,
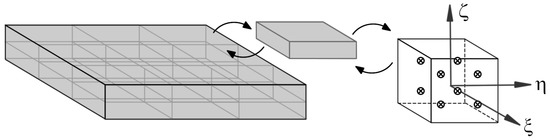
Figure 1.
Integration scheme for the RPIM, using rectangular parallelepiped integration cells.
The integration weight of each integration point can be calculated with
with being the total volume of the integration cell and the total volume of the isoparametric cell, which is .
Thus, following the Gauss–Legendre integration scheme, a given function defined inside a hexagonal domain discretized with integration points, can be integrated with
for which each is obtained with Equation (4) and the corresponding is indicated in Equation (5).
This procedure is repeated for each integration cell, allowing us to discretize the complete solid domain with a set of integration points (known as background integration mesh). Summing all integration points’ weight gives the solid domain total volume, :
As already mentioned, the RPIM enforces the nodal connectivity by establishing overlapped influence domains. In this work, a spherical influence domain will be used, imposing a fixed number of nodes inside each influence domain. Thus, each integration point will search for the n closest nodes and those nodes will set the influence domain of . According to Wang et al. [20], for a 2D problem, each influence domain should possess between and nodes. Thus, respectively, and in accordance with [32], for a 3D problem, each influence domain should possess between and nodes. Respecting the same number of nodes inside each influence domain allows the construction of shape functions with the same level of complexity for each integration point .
Regarding the construction of the shape functions, RPIM uses the radial point interpolating (RPI) technique. Thus, consider a function defined in the domain discretized by a set of N nodes: . Assuming an integration point, , possessing an influence domain with n nodes inside, it is possible to obtain the function’s interpolated value for by using the following construction:
where is a radial basis function, is a polynomial basis function, with m monomials, and and are nonconstant coefficients of and , respectively.
The vectors present in Equation (9) are defined by
Complete polynomial basis functions are added to the basis function to ensure the consistency of the RPI functions, e.g., adding to the RBF a linear polynomial ensures consistency and helps the RPI pass the standard patch test. Generally, low-order polynomial basis are considered, such as
As recommended in the literature [1], for efficiency purposes, in this work, a constant polynomial basis function is applied, .
Regarding the radial basis function, this work assumes the multiquadratic radial basis function (MQ-RBF), proposed initially by Hardy [33],
in which c and p are the MQ-RBF shape parameters. For 3D analyses, the literature [1] shows that c should be close to zero, but not be zero, and p should be close to one, but not be one. Therefore, following the literature recommendation, in this work the following MQ-RBF shape parameters are considered: and . The MQ-RBF shape parameters were obtained by optimizing the Kronecker delta function of the 3D RPI shape functions. The results shown in [1] proved to be accurate and stable, allowing us to reproduce highly complex variable fields.
The polynomial basis has to satisfy an extra requirement in order to obtain a unique solution,
with . Therefore, combining Equation (9) with Equation (13), a new equation matrix can be written as
where is given by
with the symmetric matrix obtained with
and matrix , of size , of the polynomial basis being given by
The moment matrix is symmetric because the distance is directionally independent. Solving Equation (14),
and substituting Equation (18) into Equation (9), the interpolation is obtained:
where is the interpolation of the integration point ,
In order to achieve a well-conditioned moment matrix, , the number of monomials, m, of the polynomial basis function should be much lower than the number of nodes, n, inside the influence domain of : . Such a relation is assured because in 3D analyses, the polynomials have , and for constant, linear, and quadratic polynomial basis functions, respectively, and the number of nodes inside the influence domain is typically .
The Galerkin weak form depends on the partial derivative of . Thus, in regard to a general direction , the partial derivatives can be written as
with the partial derivatives of the MQ-RBF in order to being defined as
As the literature shows, RPI functions possess several useful properties, such as the Kronecker delta property and satisfy the partition of unity. Being interpolating functions, they allow one to impose directly the essential and natural boundary conditions, reducing the overall computational cost of the analysis when compared with approximating meshless methods [1].
2.2. Discrete System of Equations
Being a discrete numerical technique, RPIM uses the Galerkin weak formulation to construct the global system of equations. Thus, considering the solid domain , with a body force , bounded by a surface boundary , submitted to external forces , on the natural boundary , and displacement constrains at the essential boundary , the Galerkin weak form can be expressed as
recalling that because , it is possible to interpolate all the components of the field variable with one operation:
and express the deformation vector as
being the deformation matrix of integration point , which can be defined as
where n is the number of nodes inside the influence domain of integration point .
Then, with the linear strain–stress relation , stress at an integration point can be defined by
where is the material constitutive matrix of integration point . Substituting the stress and the strain in Equation (23) allows us to obtain
because only the small strain will be considered, and , the expression can be presented as
leading to its final form, representing the system of equations
in which , , and are the global stiffness matrix, the global displacement field, and the global body and external force vectors, respectively. The discretization procedure allows us to obtain these entities by using a numerical integration:
Because the RPI function possesses the Kronecker delta property, the essential and natural boundary conditions can be directly imposed by using the direct imposition method or penalty methods, such as in other discrete numerical methods using interpolation functions.
3. Elastoplastic Analysis
The mathematical theory of plasticity provides a theoretical description for the relationship between stress and strain for a material exhibiting an elastoplastic behaviour [23]. Material plasticity is characterized by an irreversible deformation. Before occuring, plastic flow, the material shows a linear elastic behaviour, for which a linear relation following the generalized Hooke’s law is valid. After the yield stress is reached (established by the yield criterion), plastic behaviour occurs and the stress field starts following a flow rule. In order to implement material plasticity, it is necessary to establish three fundamental concepts:
- a yield criterion, indicating the stress level at which plastic flow initiates, and an initial yield surface, defining the elastic limit in a multiaxial stress state;
- a hardening law, describing the evolution of the subsequent yield surfaces; and
- a flow rule, relating the plastic deformation to the current stresses in the material and the stress increments outside the yield surface.
Concerning the yield criterion, in this work, the von Mises yield criterion is considered:
Assuming small strains, the total strain can be decomposed into two components [34,35],
where is the plastic component of the total strain and the elastic component. Concerning the hardening law, this work assumes that the yield surface grows linearly from the initial yield surface, only changing its size and expanding uniformly with the increase of the effective plastic strain, :
where is the plastic component of strain occurring during a strain increment.
The flow rule serves as a mathematical description of the evolution of the infinitesimal increments of the plastic strain in the course of the load history of the body [36]. As the incremental load increases, and the yield function f reaches a value equal to the yield stress of the material, , the frontier of elasticity starts to end and plasticity begins. The variation of the yield function can be written as a function of the variation of the stress field
where is the gradient of f, and therefore an orthogonal vector to the yield surface for a certain stress increment . Applying the Prandtl–Reuss flow rule, it is possible to write
where is the plastic multiplier (a scalar). The vector is a vector normal to the yield surface at the current stress state, as shown in Figure 2a [23,36], also known as a flow vector: .
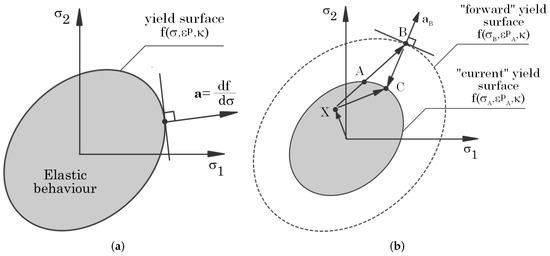
Figure 2.
(a) Flow vector representation. (b) Stress returning procedure.
3.1. Elastoplastic Constitutive Model
For its implementation in computational mechanics, it is convenient to present the previous elastoplastic theory in matrix formulation [23]. Thus, generically, the yield criterion of Equation (34) can be defined as
where is a generic hardening parameter (which in this work will be assumed as the effective plastic deformation, Equation (36)). By differentiating Equation (39), it is possible to write
which is equivalent to Equation (37) but for a material with hardening. Thus, Equation (40) can be written as function of the plastic multiplier ,
where the vector is termed the flow vector, . The hardening parameter A depends on the hardening rule [23], and it can be written as
From decomposition equation, Equation (35), it possible to write . Thus, with Equation (38), , and using the Hooke law,
it is possible to develop Equation (41) as
Substituting Equation (44) in Equation (43) permits us to obtain
with being the elastoplastic tangential constitutive matrix. The elastic constitutive matrix can be defined as
where E is the elastic modulus of the material (observed in the linear elastic phase) and the Poisson’s coefficient.
The hardening parameter A can be obtained by means of the hardening hypothesis [23] considering the associated flow rule. In this work, the analysed nonlinear materials exhibit a “linear-elastic/linear plastic” hardening behaviour. Thus, as shown in the literature [23], the hardening parameter A can be written as
where is the tangent modulus (tangent to the stress–strain curve in the plastic regime).
3.2. Stress-Returning Algorithm
In this work, an incremental procedure is adopted, in which an incremental stress leads to an incremental strain. Thus, trial stresses are a sum of a previous stress state with an incremental stress state. Consequently, it is possible to obtain trial stress states beyond the yield surface. For such case, the trial stress state must be forced to return to the yield surface. In this work, a “backward-Euler” procedure is adopted [23], Figure 2b.
Considering a trial stress state at a given integration point , the trial stress state is constituted by the previous stress state on the integration point, , and the incremental stress state of the present load increment (or iteration), ,
if the trial stress state does not respect the yield criterion, Equation (39), being observed:
then, it is necessary to return the stress state to the yield surface. As Figure 2b shows, consider a two-dimensional Westgaard stress space in which a stress state represented by point B has passed beyond the yield surface. In order to avoid extra, unnecessary computations, instead calculating the intersection stress state represented with point A, it is assumed a “forward” yield function , containing the stress state B,
in which is the updated yield stress, accounting for the hardening parameter
where is the accumulated effective plastic strain from the previous increment, .
Thus, the flow vector is calculated from stress state B, , and the plastic multiplier is given by
Now it is possible to estimate the stress in point C:
As can be observed, stress state is an estimated stress state. In order to achieve accurately stress state , it would be required to use the flow vector calculated directly in point C,
However, stress state is unknown, naturally hindering the calculation of . Therefore, an iterative procedure must be implemented to reach point C from point B. For each “stress return iteration”, the effective plastic strain is updated in order to apply Equation (51) and pass to the next “stress return iteration”, until point C is satisfactorily approximated, concluding the iterative process.
3.3. Nonlinear Solution Algorithm
The elastoplastic analysis of structures involves a set of nonlinear equations that need to be solved in order to obtain the problem’s corresponding solution. Generally, such nonlinear equations are solved by using iterative-incremental methods. In this work, the Newton–Raphson method is used as a nonlinear solution technique. Therefore, for a given increment i and iteration j, the the displacement, for each load increment is given by
and the total displacements are given by
During the incremental-iterative process, the increment of load acts as a predictor. It provides a starting solution, , in order for the iterative process to have a starting point to begin the convergence process. In addition, the complete version of the Newton–Raphson method, in which the stiffness matrix is calculated in each iteration (of each increment), there are several other versions documented in the literature [23]. For instance, the KT0 approach, in which only the initial stiffness matrix, calculated in the first iteration of the first increment (the elastic stiffness matrix), is considered for the complete analysis. Another version is the KT1, in which the stiffness matrix is calculated only at the first iteration of each increment, being then used in all the iterations of such increments. Both KT0 and KT1 versions allow us to reduce the number of computations in slightly nonlinear problems; however, for highly nonlinear problems the best approach is to use the complete version of the Newton–Raphson method, which allows us to significantly reduce the number of iterations in each increment.
The complete version of the Newton–Raphson used in this work can be summarised as follows. First, the problem domain is discretized with a nodal mesh, the background integration mesh is constructed and the nodal connectivity is imposed. Then, the RPI shape functions are constructed for each integration point. In this work, an incremental-iterative procedure was implemented for the elastoplastic deformation problem. Thus, the discretized system of equation represented in Equation (30) can be written as
where is the tangent stiffness matrix, the incremental displacement field, is the incremental load vector, and is the residual force vector. Thus, the process can start for the first increment ().
- 1.
- Set the incremental load, .
- 2.
- Loop over all integration points, .
- 3.
- Assemble the global tangent stiffness matrix: .
- 4.
- Solve .
- 5.
- Update the displacement field: .
- 6.
- Loop over all integration points, .
- (a)
- Evaluate the strain increment: .
- (b)
- Considering the elastic constitutive matrix, Equation (46), obtain the incremental stress state: .
- (c)
- Calculate the trial stress state: .
- (d)
- Verify if: . If so, . Otherwise, the algorithm presented in Section 3.2 is applied, which will lead to .
- (e)
- Update the stress field: .
- 7.
- Calculate the residual force vector: .
- 8.
- Apply a residual force convergence criteria: .
- (a)
- if , being a small threshold value (such as ), then, the process moves to point 2, initialising a new increment: , and assuming a new force increment: .
- (b)
- If , then the iterative process begins, attempting to achieve . Thus, the process moves to point 2, initialising iteration j, assuming a new force increment: .
4. Numerical Results
In this section, simply supported and clamped 3D square plates are analysed. The three nonlinear solution algorithms (KT-0, KT-1, and KT-ALL) are used and compared by using the RPIM and the FEM for both plate configurations. The results obtained are compared with solutions documented in the literature [26], which were obtained by using the element free Galerkin method (EFGM) and an equivalent single-layer deformation theory, the first order shear deformation theory, and matched/validated with advanced FEM formulations, equally assuming an equivalent single layered deformation theory.
Regarding the geometric properties of the plates, following Figure 3 representation, the length L and thickness h of all analysed cases are: m and m. Concerning the plate’s material, the following mechanical properties were considered: elasticity (Young’s) modulus: GPa, Poisson’s coefficient: , tangent elasticity modulus: GPa, and yield stress: MPa.
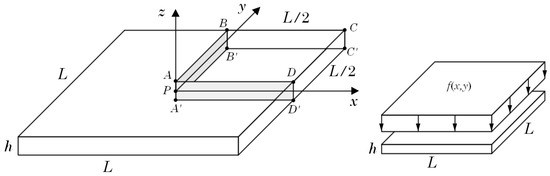
Figure 3.
Square plate representation showing the geometric properties, the symmetry assumption and the uniform distributed load considered in all analyses.
Regarding the loading conditions, all plates are submitted to a uniform distributed load covering the complete surface of the plate, as shown in Figure 3. In order to reduce the computational cost of the nonlinear analyses, instead computing the complete plate, only one quarter of the plate is analysed, assuming the corresponding boundary conditions. Thus, in surface the displacement on direction is assumed constrained: , in surface the displacement on direction is assumed constrained: , and in line both and directions are constrained: . These symmetry boundary conditions are common to both simply supported and clamped plate examples. In addition, for the simply supported plate, the line of nodes on the middle layer of the plate (with ) have all degrees of freedom constrained: . For the clamped plate, in addition to the symmetry boundary conditions, all the points belonging to surfaces and have all degrees of freedom constrained: .
All examples are analysed by using the FEM and the RPIM. Concerning FEM, eight-node hexagonal elements are considered, assuming full integration: integration points following the Gauss–Legendre quadrature scheme. Regarding the RPIM, the background integration mesh coincides with the FEM element mesh, being formed by hexagonal integration cells filled with integration points respecting the Gauss–Legendre quadrature scheme, and each influence domain is composed of 27 nodes. The RPI shape functions are constructed with a constant polynomial basis, , and the MQ-RPI shape parameters: and .
The problem domain is dicretized with a 3D regular nodal of nodes, which corresponds to hexagonal elements in FEM, or hexagonal integration cells in RPIM.
4.1. Normalized Central Displacement
In this section, the w displacements of point P (obtained along ) as a function of the applied load will be presented. Thus, in order to represent normalized load-displacement curves, the obtained w displacement are normalized with
and the force is normalized with
being,
and
where is the obtained transversal displacement (along ) on point P, h is the thickness of the plate, E the elasticity (Young’s) Modulus, the Poisson’s coefficient, the plastic moment, and the yield stress of the material being used.
The normalized load-transversal displacement curves are presented in Figure 4 for both simply supported and clamped plates, and for both numerical methods (FEM and RPIM).
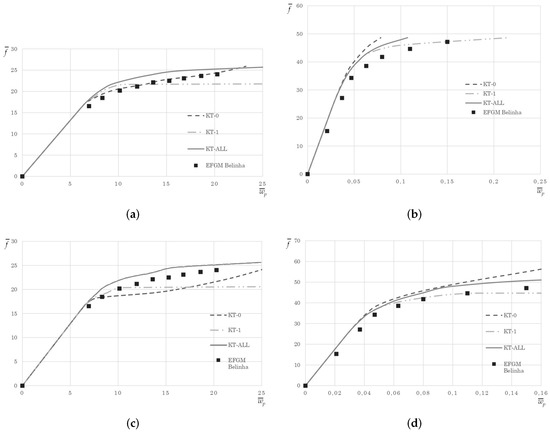
Figure 4.
Normalized load-transversal displacement curves obtained with three nonlinear solution algorithms (KT0, KT1, and full Newton–Raphson method—KT-ALL). FEM analysis for the (a) simply supported plate and (b) the clamped plate. RPIM analysis for the (c) simply supported plate and (d) the clamped plate.
Regarding the simply supported plate, it can be observed that by using the KT1 and KT-All nonlinear solution algorithms allows similar solutions for FEM and RPIM. Comparing the results with the literature, it is perceptible that both FEM and RPIM (using the KT-All nonlinear solution algorithm) are capable of achieving close results with the EFGM formulation by using an equivalent single layer theory [26].
For the clamped plate, Figure 4b shows that the FEM with KT1 and KT-All is capable of delivering a solution close to the reference solution. However, because the clamped plate is a more demanding benchmark, the solution is not as close as for the simply supported plate. FEM requires more nodes along the thickness to achieve a closer solution. For the RPIM (Figure 4d), both KT1 and KT-All algorithms produce solutions very close with the literature.
Notice that in the present work, a full 3D-deformation theory is considered, which is fundamentally different from the first-order shear deformation theory used by the reference solution. The full 3D-deformation theory strongly depends on the number of nodes along the thickness. Thus, the similarity between the obtained results and the solution documented in the literature indicates that both FEM and RPIM nonlinear solution algorithms were successfully implemented.
It would be expected that we would obtain similar results regardless of the nonlinear solution algorithm used (KT0, KT1 or KT-All). However, due to the total computational time of the analysis, per increment only a maximum of 100 iterations is allowed. The KT-All never requires more than roughly 10 iterations; however, when a large portion of integration point yield, KT1 starts to require more than 100 iterations per increment, and from third increment (very early), KT0 already requires more than 100 iterations per increment. This is because in each increment the solution is not fully corrected (the number of iterations is insufficient), the solutions start to accumulate convergence errors and, consequently, to diverge. This, observation highlights the advantage of using the full Newton–Raphson method (KT-ALL).
4.2. Stress Diagrams through the Plate’s Thickness
In this section, the stress distributions along with the plates’ thickness for distinct increment levels, and for the three numerical methods, will be presented. These results were obtained only with the KT-All nonsolution algorithm. As for units, the load increments are in [kN/m2], the stress value (horizontal axis) in MPa, and the thickness coordinate (vertical axis) is in meters.
First, the stress distribution along line A- is shown for the simply supported plate. Thus, in Figure 5, the FEM and RPIM results are shown side by side.

Figure 5.
Stress distribution along the thickness in line A-A′ for the simply supported plate. FEM analysis (a) , (c) , (e) and (g) . RPIM analysis (b) , (d) , (f) and (h) . Load increments in [kN/m2].
As a first observation, it is possible to visualise that the stress distribution along the thickness for the normal stresses and are virtually identical. Such an observation indicates that the symmetry was properly implemented. Additionally, the normal stresses obtained with RPIM are very similar to the ones obtained with the FEM. It is possible to visualise that, as the material starts to yield, the stress distribution along the thickness leaves the linear behaviour and starts showing a pronounced curve at the top and bottom layers, consistent with the maximum (yield) stress allowed.
The most significant differences can be found in the shear components of the stress tensor: and . However, the differences become smaller as the load increment grows. At the centre of the plate, along the thickness, the distribution of shear stresses and should be zero. This is true for the first increment (around 807–815 kN/m2). Figure 5e–h does not show such a null line for the first increment because the stress on the nodes is extrapolated from the integration points in its vicinity (which do not belong exactly to the centre of the plate, and therefore possess non-null shear stresses). Afterward, yielding starts to occur at the centre of the plate and the stress field of the integration points along the thickness starts to increase due to the reconfiguration of the stress, a consequence of the stress-returning algorithm.
For the clamped plate, four interest lines along the plate thickness are analysed. Thus, Figure 6, Figure 7, Figure 8 and Figure 9 represent the stress distributions obtained along lines A-, B-, C- and D-, as indicated in Figure 3, respectively.
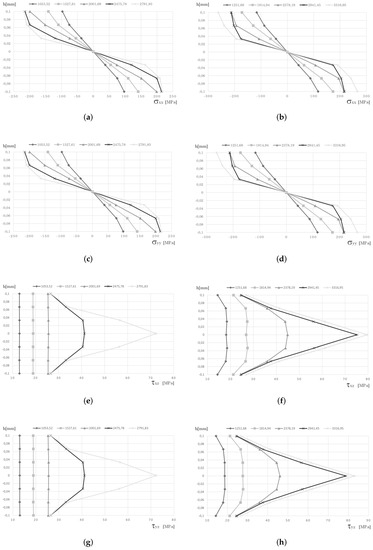
Figure 6.
Stress distribution along the thickness in line A-A′ for the clamped. FEM analysis (a) , (c) , (e) and (g) . RPIM analysis (b) , (d) , (f) and (h) . Load increments in [kN/m2].
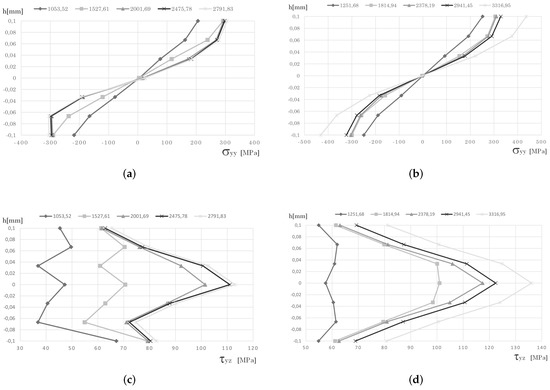
Figure 7.
Stress distribution along the thickness in line B-B′ for the clamped. FEM analysis (a) and (c) . RPIM analysis (b) and (d) . Load increments in [kN/m2].
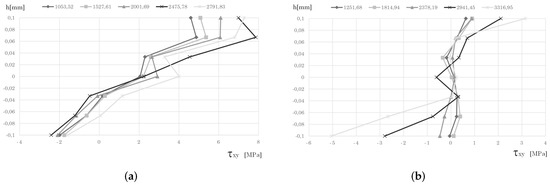
Figure 8.
Stress distribution along the thickness in line C-C′ for the clamped. FEM analysis (a) . RPIM analysis (b) . Load increments in [kN/m2].
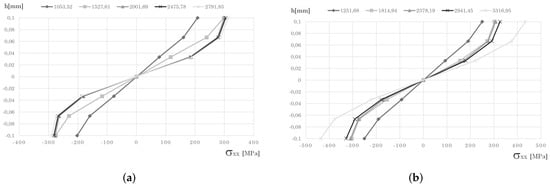
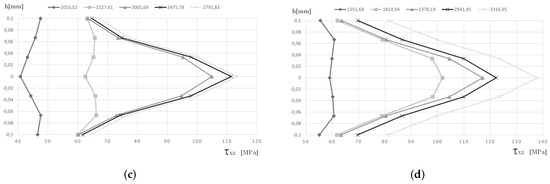
Figure 9.
Stress distribution along the thickness in line D-D′ for the clamped. FEM analysis (a) and (c) . RPIM analysis (b) and (d) . Load increments in [kN/m2].
Observing Figure 6, Figure 7, Figure 8 and Figure 9 it is noticeable that the load increments of FEM and RPIM are different. Such differences come from the elastoplastic algorithm implemented by the authors. The algorithm first identifies the load increment corresponding to the problem’s elastic limit, ; then such a load increment is multiplied by a factor, which in this work was 2.5, and an ultimate load is achieved: . Then, the number of increments is decided. In this work, 10 increments were used for each elastoplastic analysis. Thus, after the elastic limit, each incremental load will have the following magnitude: . Hence, if two distinct numerical methods predict two distinct elastic limits (because distinct numerical methods produce distinct numerical results), the ultimate load, and consequently the incremental load magnitude, of each numerical method will also be different.
Regarding line A-, Figure 6, it is possible to visualise that FEM and RPIM produce similar results for similar load increment levels. Additionally, as already observed in the simply supported plate, the normal stresses and evolve from a linear elastic distribution along the thickness to a curved yield configuration at the top and bottom layers of the plate. The shear stresses and start with a value very close to zero (it is not zero due to the same reason already discussed for the simply supported plate) and both evolve to a bilinear configuration, with lower shear stress values in the top and bottom layers of the plate and maximum stress in the plate’s middle layer. Such stress evolution is due to the material yielding and the consequent required stress returning procedure.
Along line B-, Figure 7 shows that the normal stresses obtained with FEM and RPIM are close for similar incremental load levels. However, the shear stress results are very different. The FEM obtains an expected shear stress distribution, showing an unsymmetrical irregular path. In opposition, the RPIM produces the expected result, a parabolic distribution, symmetric with respect to the plate’s middle layer, that becomes gradually shaped (with a central peak at the plate’s middle layer) as the material yielding evolves.
Line C- was selected to study the variation of the shear stress . Being the plate’s corner, shear stresses are at maximum at this location. Hence, Figure 8 presents, along the plate’s thickness, the evolution of shear stress with the plate’s yielding. At first sight, the most evident observation is the difference between FEM and RPIM results. The shear stress produced with FEM maintains its almost linear distribution along the thickness as the plate yields. On the other hand, with RPIM for the first load increments, maintains a relatively low magnitude; however, as the material starts to yield at this location, the stress level rises rapidly.
Concerning the stress distribution along the line D-, Figure 9, the FEM and RPIM results are consensual. The normal stress and the shear stress , obtain with FEM and RPIM, are very close. Furthermore, along this line D-, the shear stress obtained with FEM follows the same evolution as the one observed with RPIM as the plate yields.
4.3. Effective Stress Maps
In this section, the effective stress distribution maps for both plate configurations, simply supported and clamped plate, and both numerical method, FEM and RPIM, will be presented. The FEM and RPIM results were once again obtained assuming the full Newton–Raphson nonlinear solution algorithm (KT-All). After extrapolating the stress state from the integration points near the plate’s top layer to its closest nodes (belonging to the plate’s top surface), the (extrapolated) von Mises equivalent stress on each of those nodes was calculated:
The obtained FEM von Mises equivalent stress maps for the simply supported plate are presented in Figure 10, and the RPIM results are shown in Figure 11. The load increment is in [kN/m2], and the maximum and minimum stress values of each incremental load (subfigure) are the ones indicated in the caption of the corresponding subfigure. It is possible to observe that both FEM and RPIM produce very similar results. As expected, the simply supported plate forms a rupture line along the plate diagonal, connecting the plate’s centre and the plate’s corner. Notice that the material enters the plastic regime along that diagonal line first, and then expands from that line to the remaining area as the load increment increases.
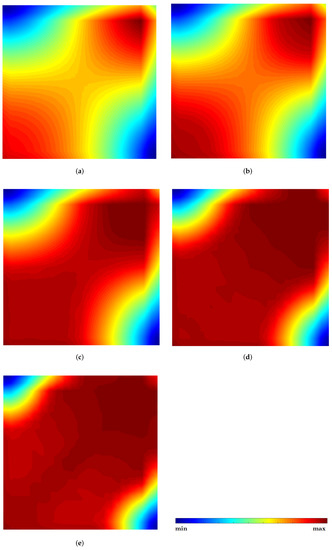
Figure 10.
Effective von Mises stress distribution maps obtained with FEM for five load increments considering the simply supported plate. For each load increment, the minimum and maximum effective stresses are: (a) KN/m2: = 0 MPa; = 170 MPa. (b) KN/m2: = 0 MPa; = 205 MPa. (c) KN/m2: = 0 MPa; = 210 MPa. (d) KN/m2: = 0 MPa; = 215 MPa. (e) KN/m2: = 0 MPa; = 220 MPa.
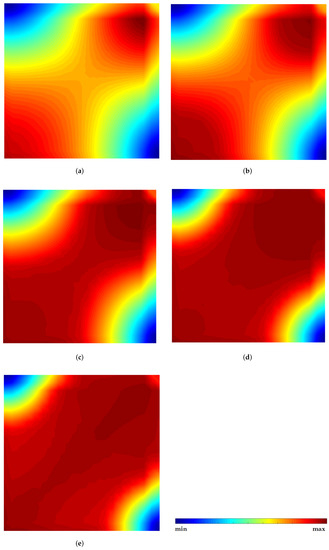
Figure 11.
Effective von Mises stress distribution maps obtained with RPIM for five load increments considering the simply supported plate. For each load increment, the minimum and maximum effective stresses are: (a) KN/m2: = 0 MPa; = 170 MPa. (b) KN/m2: = 0 MPa; = 205 MPa. (c) KN/m2: = 0 MPa; = 210 MPa. (d) KN/m2: = 0 MPa; = 215 MPa. (e) KN/m2: = 0 MPa; = 220 MPa.
Regarding the clamped plate results, the corresponding von Mises equivalent stress maps are presented in Figure 12 and Figure 13 for FEM and RPIM, respectively.
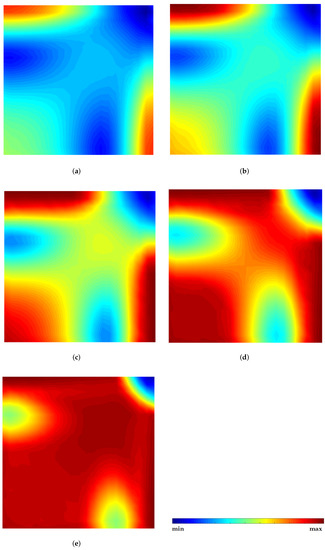
Figure 12.
Effective von Mises stress distribution maps obtained with FEM for five load increments considering the clamped plate. For each load increment, the minimum and maximum effective stresses are: (a) KN/m2: = 0 MPa; = 170 MPa. (b) KN/m2: = 0 MPa; = 205 MPa. (c) KN/m2: = 0 MPa; = 210 MPa. (d) KN/m2: = 0 MPa; = 215 MPa. (e) KN/m2: = 0 MPa; = 220 MPa.
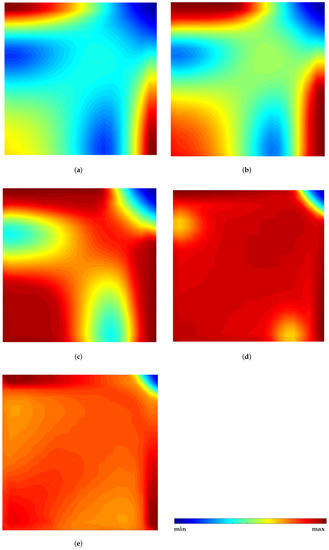
Figure 13.
Effective von Mises stress distribution maps obtained with RPIM for five load increments considering the clamped plate. For each load increment, the minimum and maximum effective stresses are: (a) KN/m2: = 0 MPa; = 170 MPa. (b) KN/m2: = 0 MPa; = 205 MPa. (c) KN/m2: = 0 MPa; = 210 MPa. (d) KN/m2: = 0 MPa; = 215 MPa. (e) KN/m2: = 0 MPa; = 220 MPa.
Both FEM and RPIM solutions are again very similar. It is clear that the initiation of material yields at the boundaries of the plate, and then it starts to yield at the centre of the plate. Afterward, the yielding advances to a diagonal line merging the boundary yield material to the yield material of the plate’s centre.
Both the rupture paths observed in the simply supported and clamped plates are the ones described in the literature for these two benchmarks [26].
5. Conclusions
In this work, the radial point interpolation method (RPIM) was combined with an elastoplastic formulation to analyse 3D plates. Original nonlinear RPIM and FEM codes were written in order to have a more detailed comprehension of the differences and similarities between both numerical methods (at the formulation and results levels). This process allowed us to directly compare performances (global computational times and efficiency) and the results accuracy.
Concerning the nonlinear solutions algorithms tested, it was found that using the KT-All algorithm is more efficient. Although it recalculates the stiffness matrix in every iteration, it required many fewer iterations than KT0 or KT1 when a large part of the material starts to yield. Thus, the overall computation time is less than the one required by KT0 or KT1 algorithms to achieve the same solution.
Regarding the stress distribution along the thickness of the plate, the results show that generally FEM and RPIM produce similar normal stresses distributions. However, concerning shear stresses, the results are not as close. In opposition to FEM, RPIM is capable of producing the expected parabolic shear stress distribution along the thickness, demonstrating an higher accuracy. The stress distributions shown were acquired at the nodes. Therefore, such results are an extrapolation of the stress values on the integration points. This explains why shear stress obtained with FEM and RPIM is not null at the top and bottom layers of the plate (as it should be).
The presented stress distribution maps allowed us to visualise the expected rupture lines of both benchmarks. In the simply supported plate, the diagonal rupture line can identified, as well as in the clamped plate the boundary rupture lines at first, and then the central rupture and, in the end, the diagonal lines. Such results indicate that the nonlinear solution algorithm was successfully combined with the linear RPIM formulation.
The main advantage of RPIM is its potential to be directly integrated in existing FEM software. For instance, the RPIM can assume the finite elements as integration cells, distributing inside them the required integration points (following the most appropriated scheme). Moreover, the element nodes can be utilised to form the global nodal discretization. Then, by using the influence-domain concept, the nodal connectivity can be established. Afterward, the process moves on, constructing the RPI functions, establishing the system of equations, obtaining the displacement, strain and stress fields and following the elastoplastic analysis. The final results can then be depicted in existent FEM software. Moreover, because RPIM is an interpolating numerical method, it can be combined with FEM. Allowing to use meshless methods in parts of the domain in which higher accuracy is required (for instance, the vicinity of cracks or other locations in which stress concentration is expected) and the FEM can be applied in the remaining part of the solid (to speed-up the analysis).
Author Contributions
Conceptualisation, J.B., methodology; J.B., software; J.B., validation; M.A. and J.B., formal analysis; J.B., investigation, J.B., resources; J.B., data curation; M.A. and J.B., writing—original draft preparation; J.B. and M.A., writing—review and editing; J.B., visualization; J.B., supervision; J.B., project administration; J.B., funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the funding provided by Ministério da Ciência, Tecnologia e Ensino Superior—Fundação para a Ciência e a Tecnologia (Portugal) and LAETA, under internal project UIDB/50022/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Belinha, J. Meshless Methods in Biomechanics; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Gu, Y. Meshfree methods and their comparisons. Int. J. Comput. Methods 2005, 2, 477–515. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Rabczuk, T.; Bordas, S.; Duflot, M. Meshless methods: A review and computer implementation aspects. Math. Comput. Simul. 2008, 79, 763–813. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G. Smooth particle hydrodynamics with strength of materials. In Advances in the Free-Lagrange Method Including Contributions on Adaptive Gridding and the Smooth Particle Hydrodynamics Method; Springer: Berlin/Heidelberg, Germany, 1991; pp. 248–257. [Google Scholar]
- Gharehdash, S.; Barzegar, M.; Palymskiy, I.B.; Fomin, P.A. Blast induced fracture modelling using smoothed particle hydrodynamics. Int. J. Impact Eng. 2020, 135, 103235. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Computat. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Hu, W.; Gu, Y.; Zhang, C.; He, X. The generalized finite difference method for an inverse boundary value problem in three-dimensional thermo-elasticity. Adv. Eng. Softw. 2019, 131, 1–11. [Google Scholar] [CrossRef]
- Xing, Y.; Song, L.; Fan, C.M. A generalized finite difference method for solving elasticity interface problems. Eng. Anal. Bound. Elem. 2021, 128, 105–117. [Google Scholar] [CrossRef]
- Noorizadegan, A.; Young, D.L.; Chen, C.S. A novel local radial basis function collocation method for multi-dimensional piezoelectric problems. J. Intell. Mater. Syst. Struct. 2022, 33, 1574–1587. [Google Scholar] [CrossRef]
- Chiang, Y.; Young, D.; Sladek, J.; Sladek, V. Local radial basis function collocation method for bending analyses of quasicrystal plates. Appl. Math. Model. 2017, 50, 463–483. [Google Scholar] [CrossRef]
- Solyaev, Y.O.; Lurie, S.A. Trefftz collocation method for two-dimensional strain gradient elasticity. Int. J. Numer. Methods Eng. 2021, 122, 823–839. [Google Scholar] [CrossRef]
- Wang, G.; Dong, L.; Atluri, S.N. A Trefftz collocation method (TCM) for three-dimensional linear elasticity by using the Papkovich-Neuber solutions with cylindrical harmonics. Eng. Anal. Bound. Elem. 2018, 88, 93–103. [Google Scholar] [CrossRef]
- Sukumar, N.; Moran, B.; Belytschko, T. The natural element method in solid mechanics. Int. J. Numer. Methods Eng. 1998, 43, 839–887. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y. A point interpolation method for two-dimensional solids. Int. J. Numer. Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G. A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Dinis, L.; Jorge, R.N.; Belinha, J. Analysis of 3D solids using the natural neighbour radial point interpolation method. Comput. Methods Appl. Mech. Eng. 2007, 196, 2009–2028. [Google Scholar] [CrossRef]
- Barry, W.; Saigal, S. A three-dimensional element-free Galerkin elastic and elastoplastic formulation. Int. J. Numer. Methods Eng. 1999, 46, 671–693. [Google Scholar] [CrossRef]
- Hinton, E.; Owen, D.R.J. Finite Elements in Plasticity: Theory and Practice; Pineridge Press: Swansea, Wales, 2017. [Google Scholar]
- Belinha, J.; Dinis, L. Análise elasto-plástica de problemas anisotrópicos considerando o método livre de elementos de Galerkin. Rev. Int. Métodos Numéricos Cálculo Diseño Ing. 2006, 22, 87–117. [Google Scholar]
- Belinha, J.; Dinis, L. Analysis of Plates and Laminates using the Element Free Galerkin Method. Comput. Struct. 2006, 84, 1547–1559. [Google Scholar] [CrossRef]
- Belinha, J.; Dinis, L. Elasto-plastic analysis of plates by the element free Galerkin method. Eng. Comput. 2006, 23, 525–551. [Google Scholar] [CrossRef]
- Cheng, Y.; Bai, F.; Peng, M. A novel interpolating element-free Galerkin (IEFG) method for two-dimensional elastoplasticity. Appl. Math. Model. 2014, 38, 5187–5197. [Google Scholar] [CrossRef]
- Dinis, L.; Jorge, R.N.; Belinha, J. The Natural Neighbour Radial Point Interpolation Meshless Method Applied to the Non-Linear Analysis. AIP Conf. Proc. 2011, 1353, 1175–1178. [Google Scholar]
- Zhang, G.; Li, Y.; Gao, X.; Hui, D.; Wang, S.; Zong, Z. Smoothed Point Interpolation Method for Elastoplastic Analysis. Int. J. Computat. Methods 2015, 12, 1540013. [Google Scholar] [CrossRef]
- Farahani, B.V.; Belinha, J.; Amaral, R.; Tavares, P.J.; Moreira, P.M. Extending radial point interpolating meshless methods to the elastoplastic analysis of aluminium alloys. Eng. Anal. Bound. Elem. 2019, 100, 101–117. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles Applications des Paramètres Continus à la Théorie des Formes Quadratiques. Deuxième Mémoire. Recherches sur les Parallélloèdres Primitifs. J. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G.; Gu, Y.; Wang, Y. A meshfree radial point interpolation method (RPIM) for three-dimensional solids. Comput. Mech. 2005, 36, 421–430. [Google Scholar] [CrossRef]
- Hardy, R.L. Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Rodrigues, D.; Belinha, J.; Jorge, R. The elastoplastic analysis of 3D-printed thermoplastics using the NNRPIM and a modified hill yield criterion. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1368–1381. [Google Scholar] [CrossRef]
- Rodrigues, D.; Belinha, J.; Jorge, R.N.; Dinis, L. Numerical simulation of compression and tensile tests on thermoplastics: A meshless approach. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 286–306. [Google Scholar] [CrossRef]
- Ochsner, A. Elastoplasticity of Frame Structure Elements; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).