Thermomechanical Analysis of Steel-to-Timber Connections under Fire and the Material Density Effect

Abstract

This work presents a thermomechanical numerical analysis of a steel-to-timber connection with dowels in tension when exposed to fire using ANSYS ^® software. Three different wood density materials were considered. The connection is built by a three-dimensional model with a thermomechanical boundary condition. A nominal temperature–time curve, ISO 834, was used to simulate the fire effect. Numerical simulation to determine the field of thermal and mechanical stresses was performed using a combined problem. A temperature field was imposed for a given time instant of fire exposure, calculated through a thermal analysis in a transient regime. This temperature profile was coupled to an incremental tensile load, allowing the determination of the maximum mechanical resistance of the connection. According to this methodology, the load-bearing capacity of the connections in each fire rating will be determined. In addition, the numerical results allow verification of the wood density influence on the mechanical resistance of the connection exposed to fire. In conclusion, the load-bearing capacity decreases with fire exposure and with lower material density. With the proposed methodology, the effect of the wood density on the heat transferred through the connection under fire can be verified, and a thermomechanical complex model is proposed to solve and analyze this type of problem, which is the great motivation in this work. The numerical methodology represents well the thermomechanical behavior of the connection under fire. This procedure can be used, considering other different parameters, to improve the design and allow the study of the connection behavior as an alternative to the experimental tests.

1. Introduction

The study of the thermomechanical behavior of a wood structural connection when exposed to fire is very important [1]. In a fire situation, temperatures and thermal gradients are very high. Wood loses mechanical resistance and steel is a good conductor of temperature, which generates thermal stresses and strains because of the overall strength of the connection. The use of wood material has increased in construction and engineering activities. This growth requires a high level of knowledge regarding the behavior of such structures in fire situations. Predicting the thermomechanical response in the steel-to-timber connection with dowels subjected to fire is a highly nonlinear problem, due to the thermal and mechanical properties dependent on the temperature of the materials involved. The thermomechanical analysis of connections has been recently studied [2]. Szász [2] studied a double shear steel-to-timber connection under fire using two different fire loads: a natural fire curve was created with OZone software, and a nominal temperature–time curve, ISO 834. The model was built using the ANSYS software. The authors verified the influence of the timber width cross-section and the diameter of the fastener with the same materials [2].

Initially, many studies were developed involving analytical models to predict temperature results on the behavior of structures exposed to the fire scenario [3,4]. Meanwhile, some research involving numerical and computational models was developed to study structures exposed to fire, for example, using the ANSYS software [5,6,7]. More recently, some of these studies included thermomechanical analyses in steel structures, concrete-filled steel columns, composite steel and concrete beams, composite concrete, and timber beams, among others [2,8,9]. The thermomechanical behavior of timber connections under fire is complicated because of the complexity of analyzing the wood’s thermal and mechanical properties and its degradation in fire [10].

This paper aims to present a consistent approach to accurately estimate the thermomechanical behavior of steel-to-timber connections. While some studies present structural finite element methods for predicting mechanical stresses, other work only emphasizes thermal analysis. The present methodology considers both thermal and mechanical structural analysis. The ability to obtain thermomechanical results makes these methodologies useful in comparison to other previous methods. The current study intends to evaluate, through an advanced calculation model using the finite element method, the behavior of steel-to-timber connections in fire situations, considering the nonlinearity and the elastoplastic regime of the materials. This work was developed with the ANSYS^® software [11], where the connection model was exposed to a nominal temperature–time curve recommended by the standard ISO 834 [12,13]. The mechanical and thermal properties were imposed on the numerical model according to the Eurocodes for each material [14,15].

The main objective of this manuscript is to study timber connections in tension and exposed to fire, identifying the load-bearing capacity that allows the dimensioning of safety in the connection. Simultaneously, it is intended to verify the effect of wood density on the heat transferred through the connection. To accomplish this, a three-dimensional numerical model was created to carry out a transient and thermomechanical analysis. Thus, the thermal and mechanical analysis is based on a two-step simulation process, submitting the connection to fire, and then, for each fire rated time, the load-bearing capacity is determined. Load-bearing capacity is the ability of the connection to withstand the imposed load (thermal and mechanical) without exceeding the material’s yield conditions.

2. Materials and Methods

The geometric model of the steel-to-timber connection under study was calculated according to Eurocode 5, part 1-1 [16,17], represented in Figure 1.

The main dimensions of the connection under study are symmetrical according to a vertical plane and consists of two external steel plates, an inner wooden member, and 18 steel dowels that work as connectors.

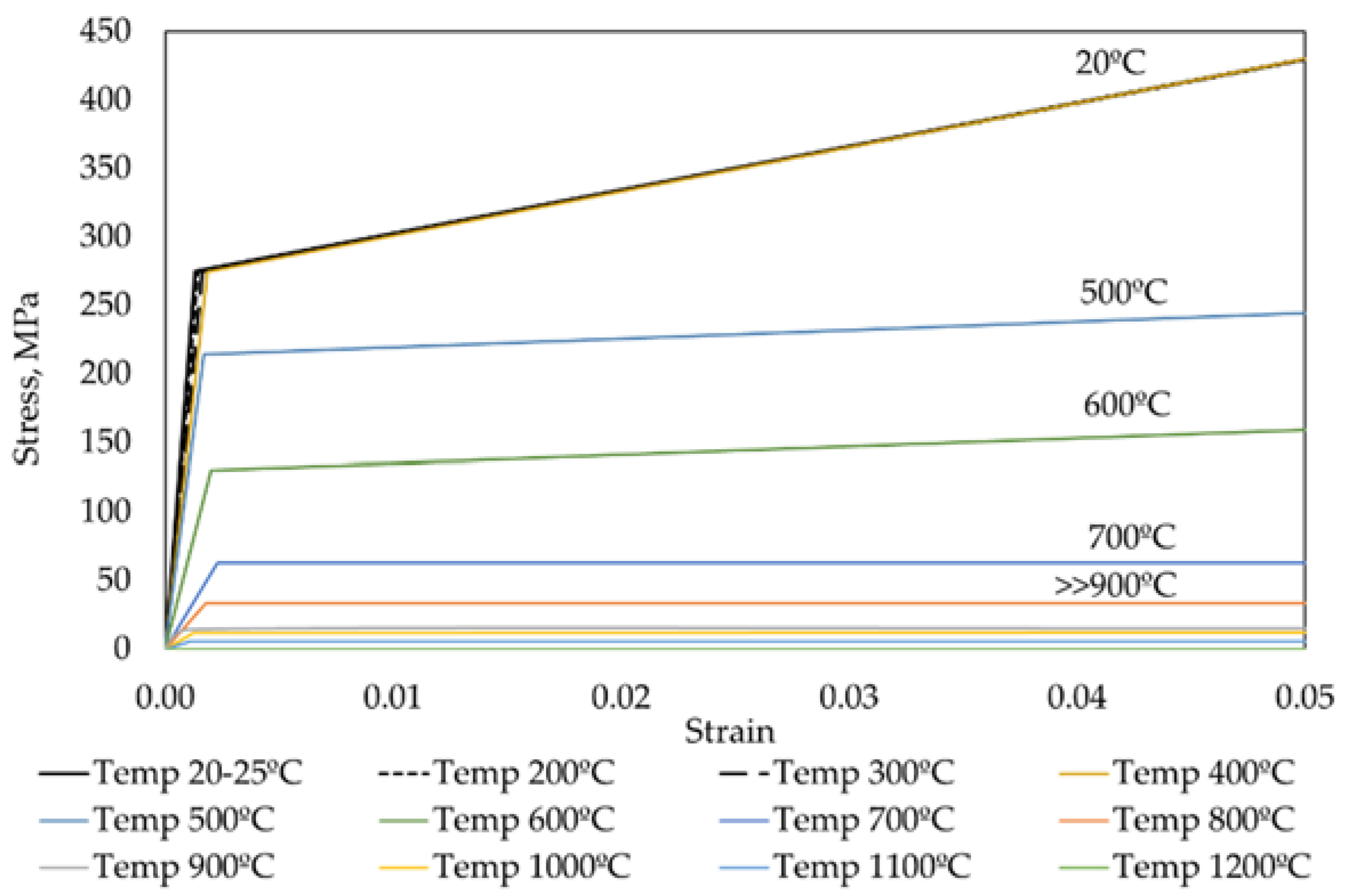
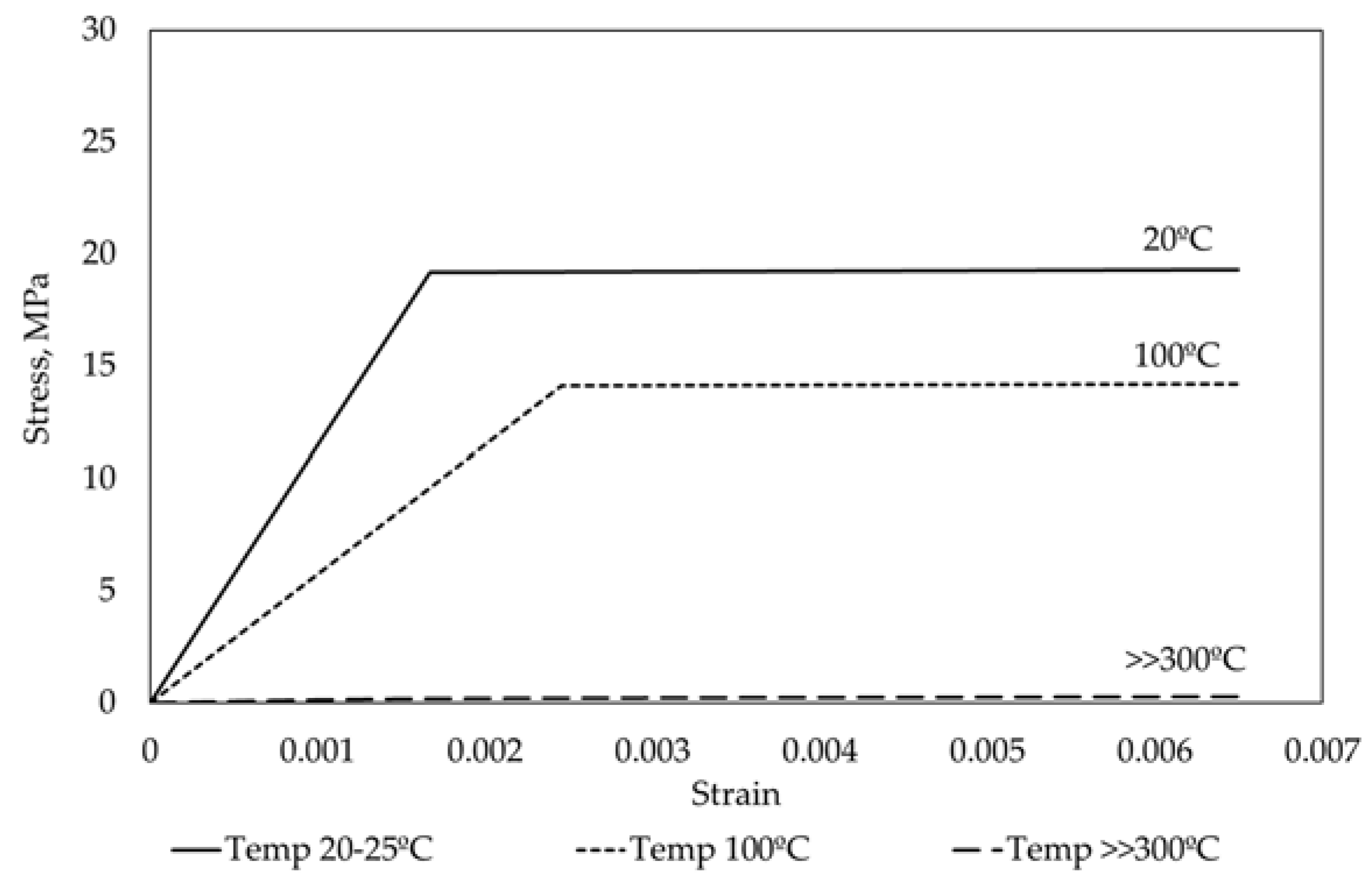
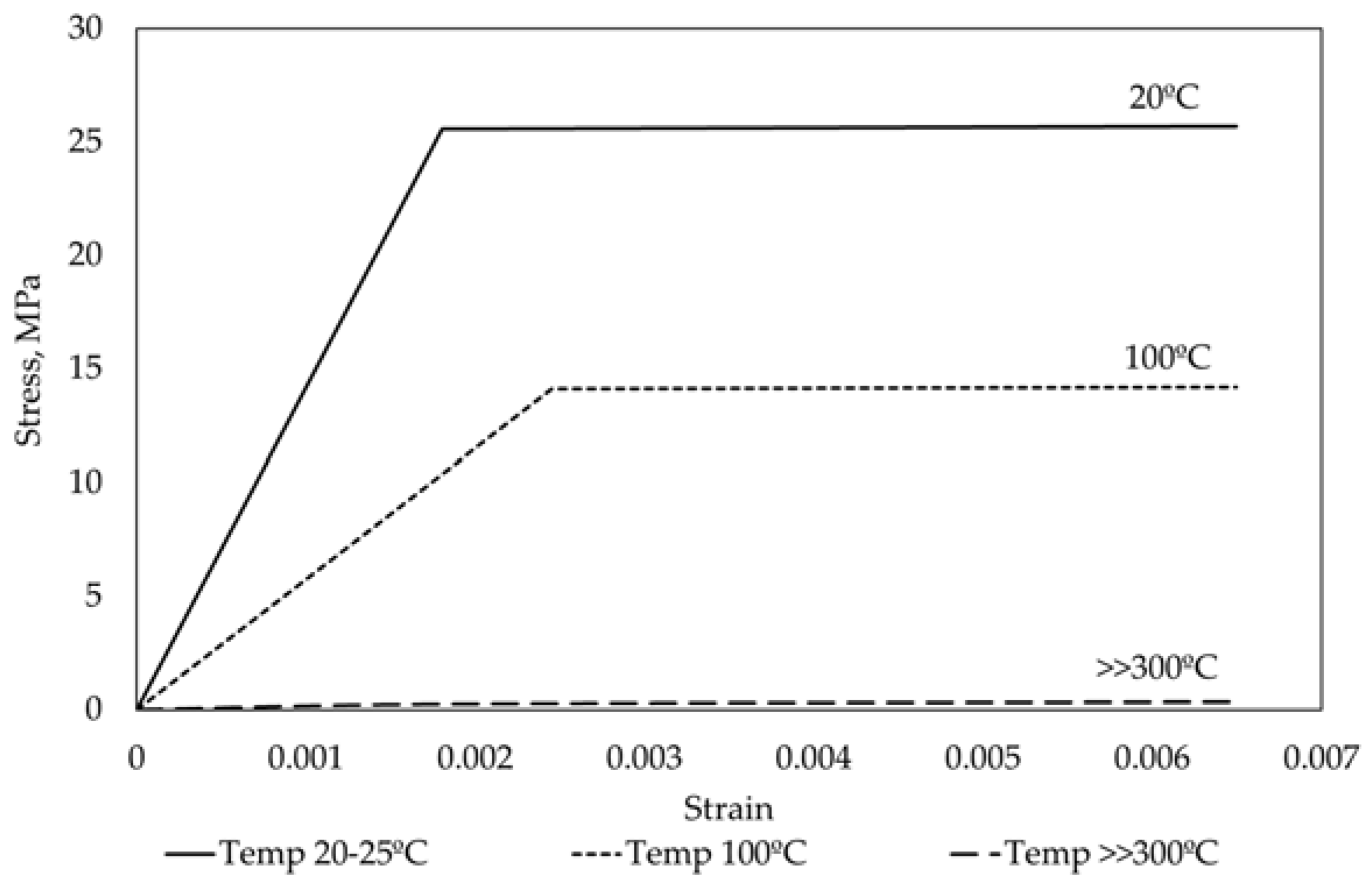
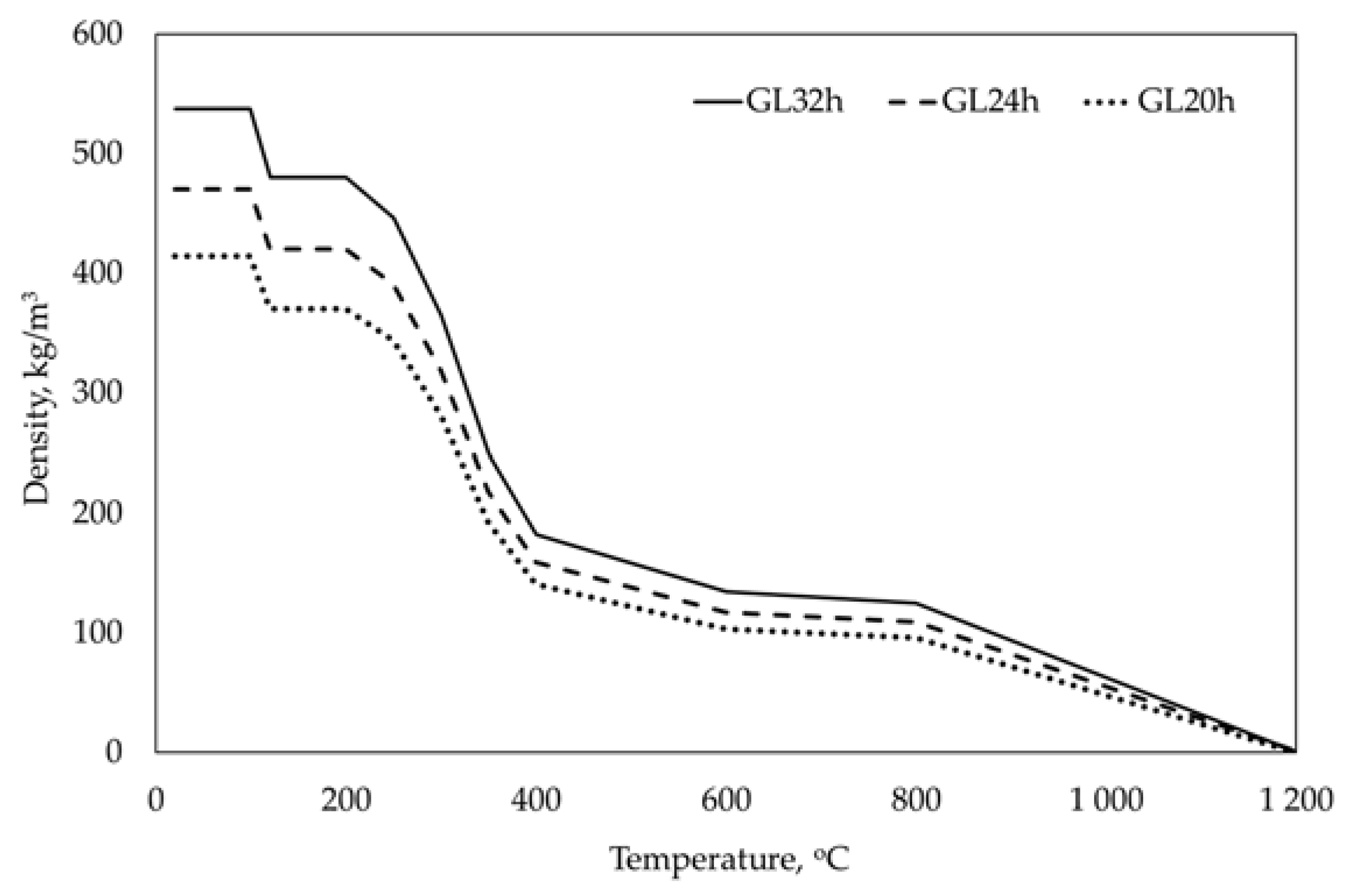
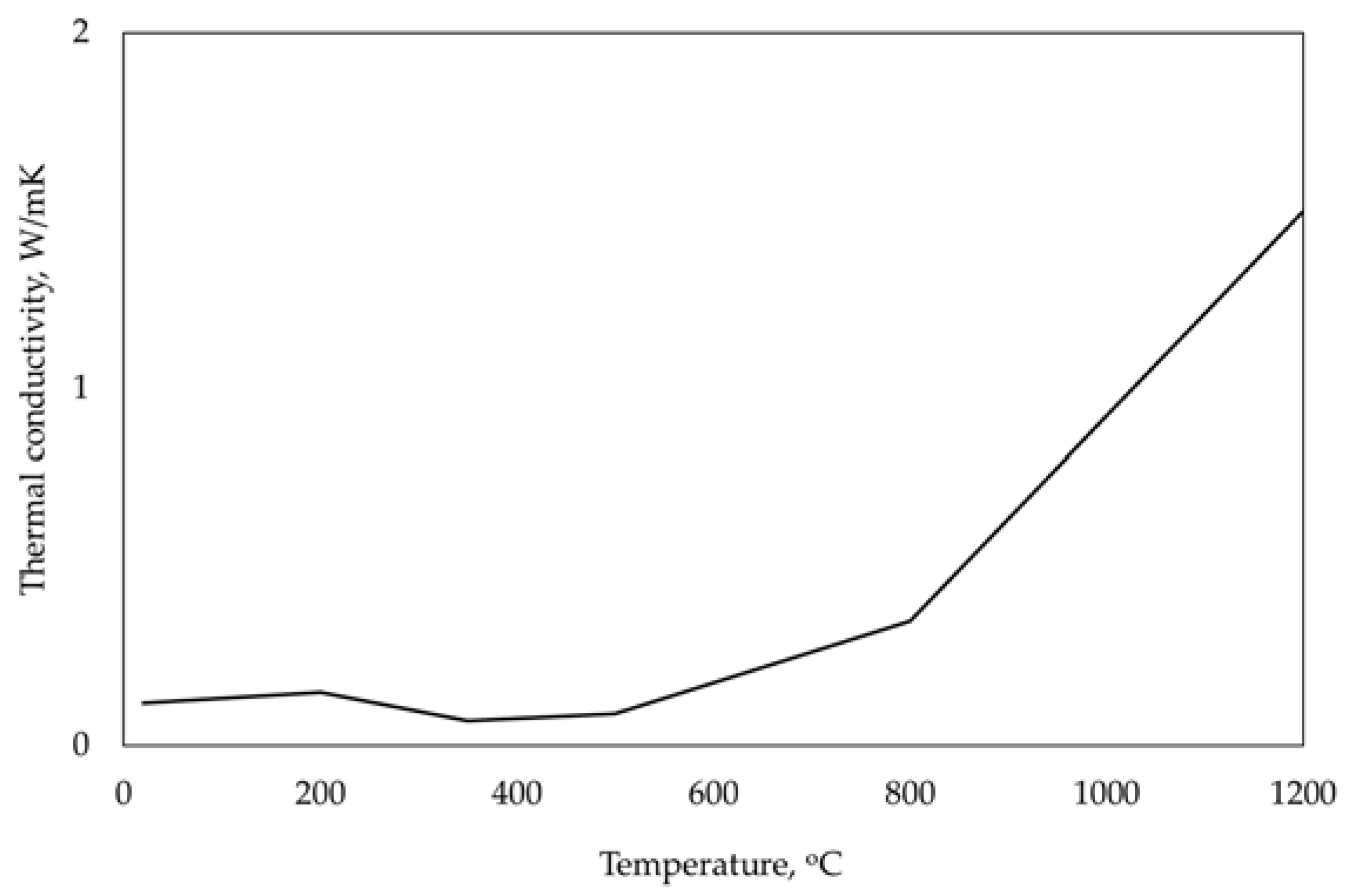
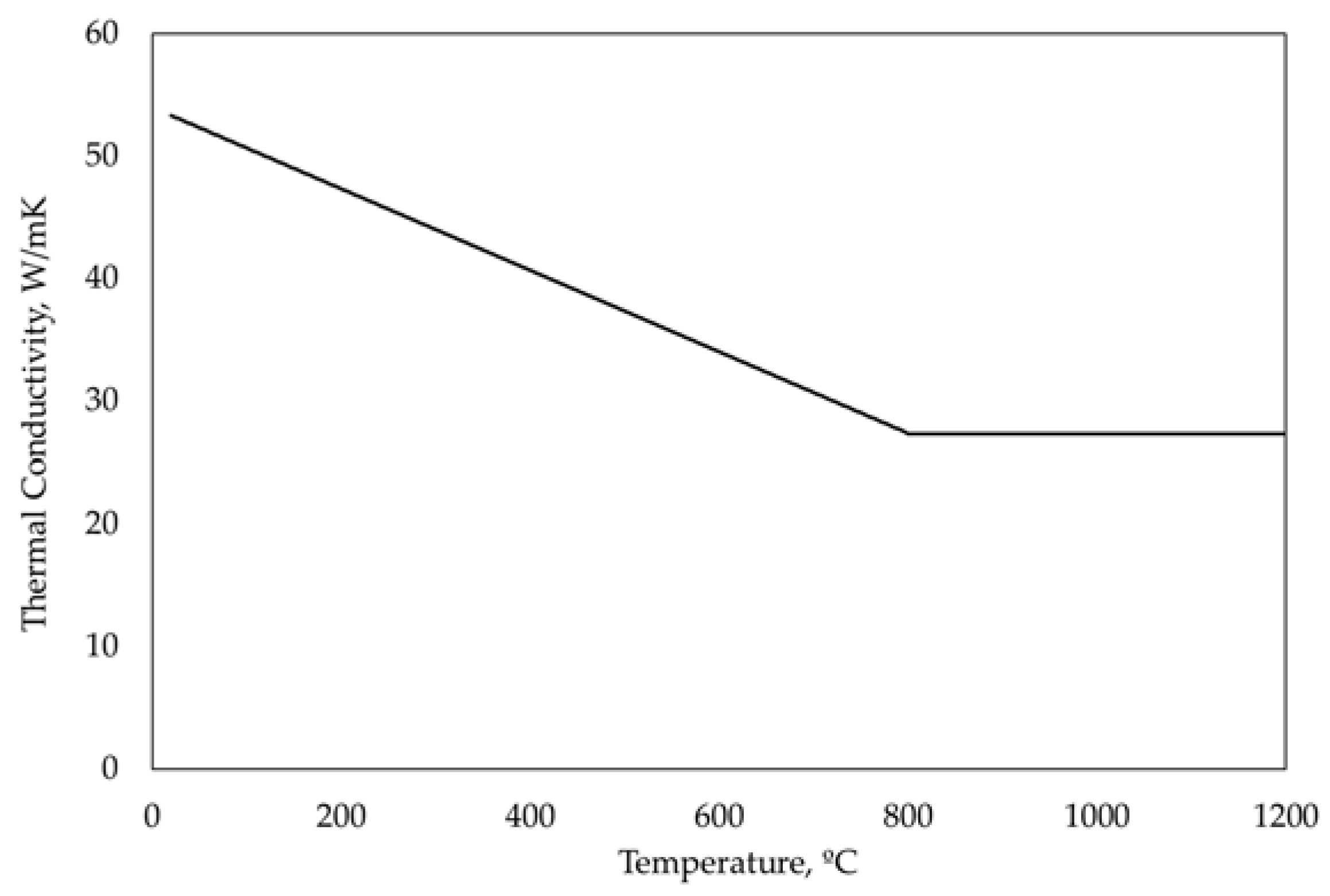
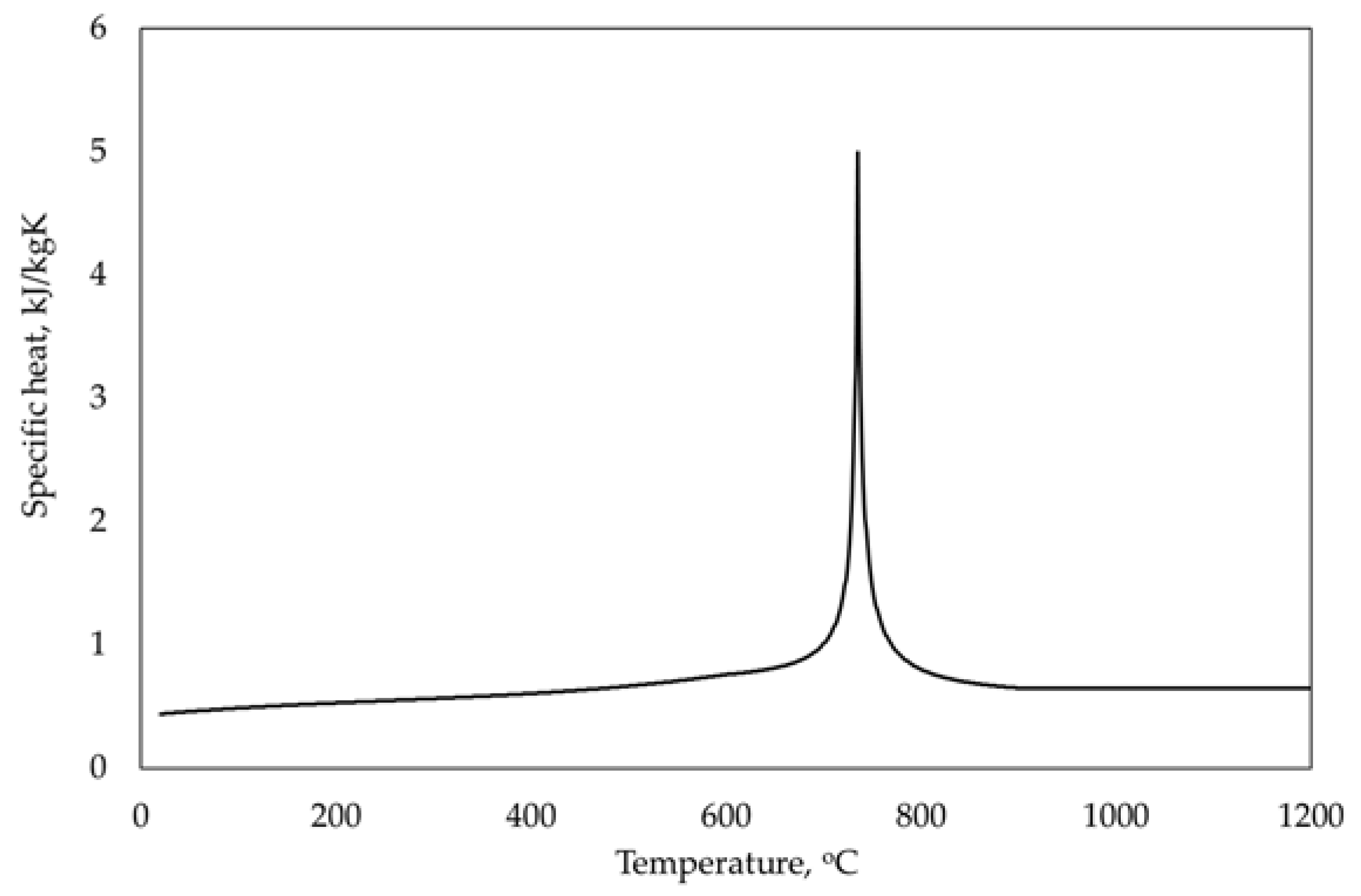
2.1. Material Properties and Fire Curve

As described in our previous work [17], the material properties are defined according to the standards. For mechanical and structural analysis, the material properties involved in the study are the mechanical properties of wood and steel material (with elastic and plastic behavior) and the thermal properties of both materials (conductivity, specific heat density, and emissivity). For the wooden members, three different species of glued laminate were considered: GL20H, GL24H, and GL32H [5,6,7,18].

The wood stiffness and strength properties vary as a function of the orientation between longitudinal, tangential, and radial directions. Stiffness and strength are greatest in the longitudinal direction. For this reason, only the properties parallel-to-grain were considered according to the direction the applied tensile load.

The mechanical properties of the glued laminated wood chosen for use in this study, at approximately 12% moisture content, have a Poisson ratio value equal to 0.4 and a coefficient of thermal expansion equal to 4 × 10⁻⁶/K in all species considered. In tests of both hardwoods and softwoods, the parallel-to-grain values ranging from 0.000031 to 0.0000045 per °K were considered [18,19,20]. The other mechanical properties can vary significantly among the glued laminated species. For GL20H, the yield strength parallel-to-grain is equal to 16 MPa, the Young’s modulus is equal to 8.4 GPa, and the density is equal to 370 kg/m³. For GL24H, the yield strength parallel-to-grain is equal to 19.2 MPa, the Young’s modulus is equal to 11.5 GPa, and the density is equal to 420 kg/m³. For GL32H, the yield strength parallel-to-grain is equal to 25.6 MPa, the Young’s modulus is equal to 14.2 GPa, and the density is equal to 480 kg/m³.

For the connectors and plate elements, steel material S275 was considered, according to the Eurocode 3 part 1-1 [21], where the yield strength is equal to 275 MPa, the ultimate tensile strength is equal 430 MPa, the Young’s modulus is 210 GPa, the Poisson’s ratio is 0.3, the density is equal to 7850 kg/m³, and the coefficient of thermal expansion was considered constant equal to 12 × 10⁻⁶/K.

The stress–strain curves for the steel and wood material at elevated temperatures are defined as multilinear with isotropic hardening plasticity (see Figure 2, Figure 3, Figure 4 and Figure 5).

The fire starts with a transient thermal analysis, resulting in the thermal response of the connection during the fire exposure. The nominal temperature–time standard curve ISO 834 is the one that has been used in fire tests to rate structural and separating elements [12], which is described by Equation (1) and shown in Figure 6.

$${\theta }_{\infty }=20+345{\log }_{10}\left(8t+1\right)$$

(1)

where $t$ is the time in min and ${\theta }_{\infty }$ is the gas temperature in the fire compartment expressed in °C.

The initial temperature in the steel-to-timber connection was considered equal to 20 °C. The external surface of the connection is exposed to the standard fire curve ISO 834 and the convection coefficient is 25 W/m²K [13]. The emissivity of the flames is considered constant and equal to 1 [13].

For thermal analysis, heat transfer is governed by material density, thermal conductivity, and specific heat. The wood properties are temperature dependent, being defined by Eurocode 5, part 1-2 [14] and presented in Figure 7, Figure 8 and Figure 9. The emissivity is also defined as equal to 0.8, Eurocode 5, part 1-2 [14].

For steel, density is assumed to be constant, as previously mentioned, for the entire range of temperatures produced during a fire, while thermal conductivity and specific heat are temperature dependent, being the respective variation with temperature represented in Figure 10 and Figure 11, Eurocode 3, part 1-2 [15]. The emissivity of the material is defined as equal to 0.7, Eurocode 3, part 1-2 [15].

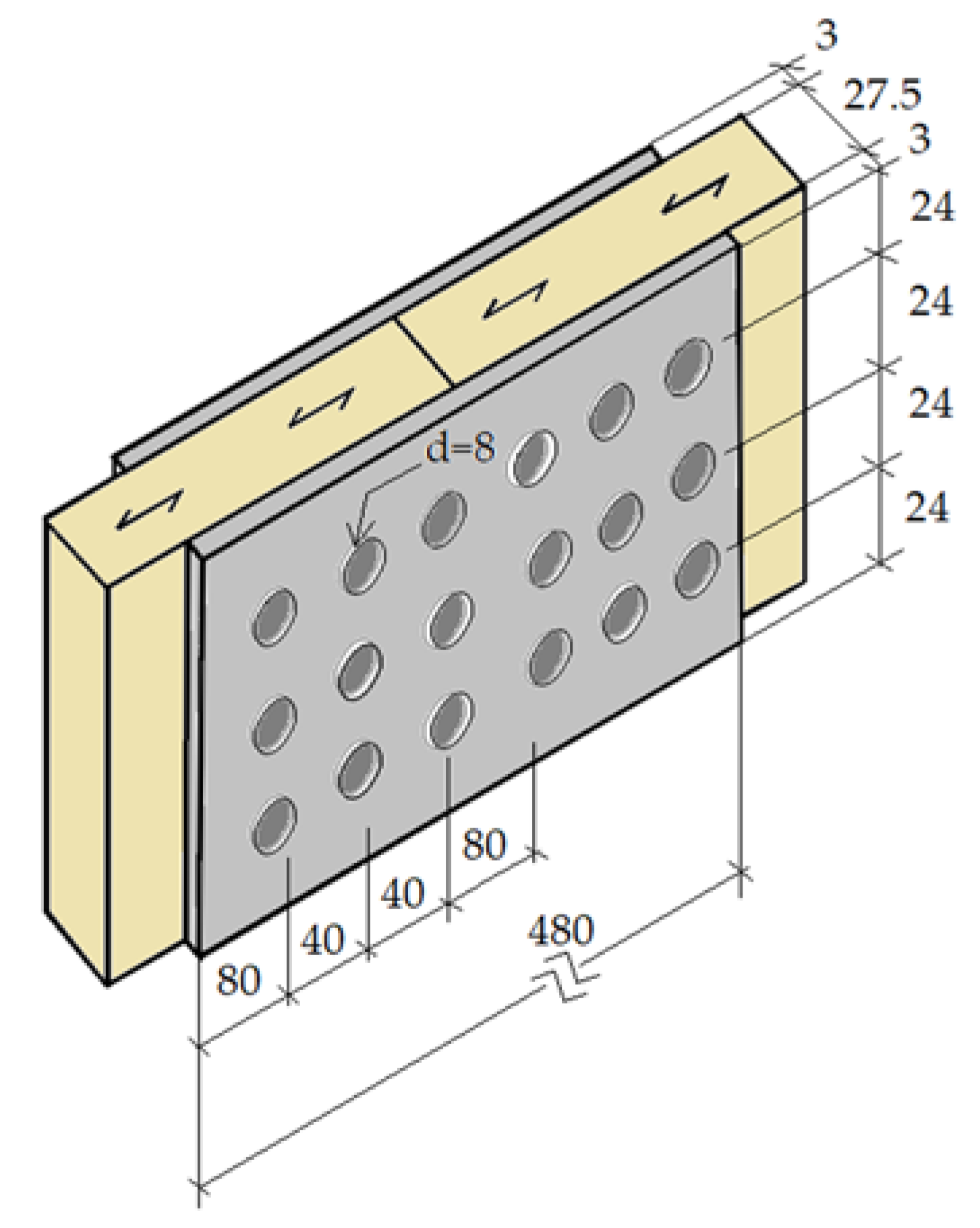
2.2. Geometric Model in the Study

For the steel-to-timber connection with external steel plates with 3 mm of thickness, the simplified equation from Eurocode 5, part 1-1 [16] helps to determine the characteristic load-carrying capacity per shear plane and fastener $F_{v,Rk}$ at ambient temperature and is given by Equation (2).

$$F_{v,Rk}=min\{\begin{array}{c}0.5f_{h,2,k}{t}_{2}d\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}a)\\ 1.15\sqrt{2M_{y,Rk}{f}_{h,2,k}d}+\frac{F_{ax,Rk}}{4}\hspace{1em}\hspace{1em}\hspace{1em}b)\end{array}$$

(2)

where $d$ is the dowel diameter equal to 8 mm, $t_2$ is the wooden board thickness member equal to 27.5 mm, $f_{h,2,k}$ is the characteristic embedment strength in timber member calculated with Equation (3), $M_{y,Rk}$ is the value of the characteristic yield moment of the fastener using Equation (4), and $F_{ax,Rk}$ represents the characteristic axial withdrawal capacity of the fastener equal to 0 in the studied connection [16].

The value of the characteristic embedment strength in the timber member parallel to the grain is obtained according to the value of the dowel diameter $d$ and the characteristic wood density ${\rho }_k$, given by:

$$f_{h,2,k}=0.082\left(1-0.01d\right){\rho }_k$$

(3)

The value of $M_{y,Rk}$ is calculated according to the dowel diameter d, and its material characteristic tensile strength $f_{u,k}$, [16], by following Equation (4).

$$M_{y,Rk}=0.3f_{u,k}{d}^{2.6}$$

(4)

After the calculated value of $F_{v,Rk}$, equal to 2821.456 N, it is required to determine the design value of the characteristic load-carrying capacity, which is obtained from Equation (5). In this equation, two safety factors are introduced, defined according to Eurocode 5 part 1-1 [16]. The partial factor for the material property ${\gamma }_M$ is equal to 1.25 for the glued laminated timber. The modification factor, considering the load duration and moisture content effect $k_{mod}$, was considered equal to 0.6 for the glued laminated timber.

$$F_{v,Rd}=\frac{F_{v,Rk}{k}_{mod}}{{\gamma }_M}$$

(5)

The calculated value is 1354.3 N, which enables the calculation of the number of dowels, an important parameter in the connection design with the arrangement of rows and columns [5,6,7]. The number of dowels is determined by Equation (6), after calculating $F_{v,Rd}$ [17], considering the applied tensile load $F_d$ as a resultant value equal to 10 kN.

$$N\ge \frac{F_d}{F_{v,Rd}}$$

(6)

The connection under study is symmetrical along a vertical plane and consists of two external steel plates and an internal wooden member with 18 steel dowels. Three rows and three lines of dowels were chosen for each symmetrical plane, and the spacing between the dowels is given by the equations of Eurocode 5 part 1-1 [16]. The dowels’ layout and their spacing are presented in Figure 1.

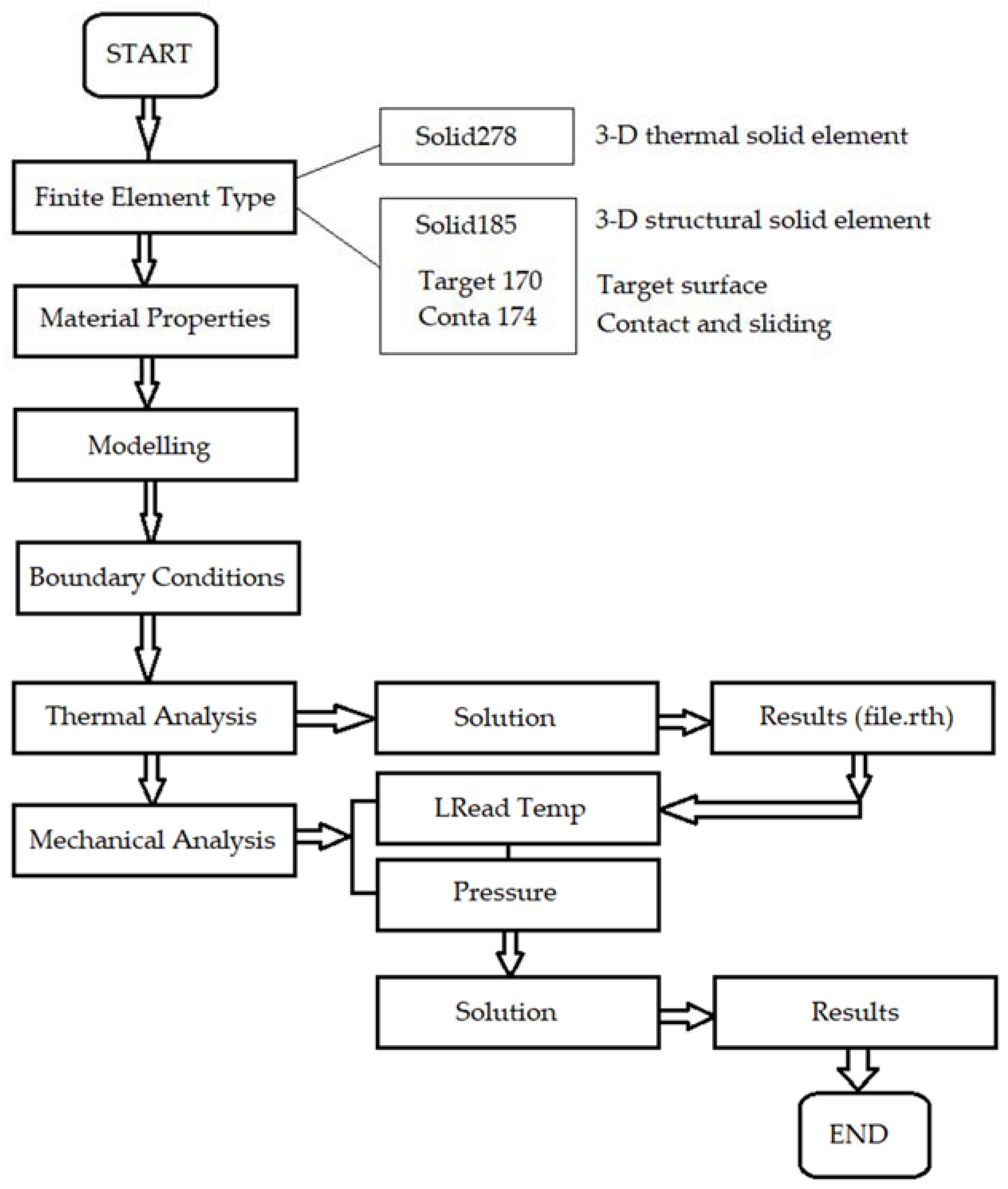
2.3. Thermomechanical Analysis

To create the thermomechanical model, at first, a thermal and transient analysis with nonlinear materials was performed.

The simulation was performed with ANSYS 2020.R2 [11], using combined analysis between the thermal process to read the temperature and running into a structural mechanical process, as shown in the flowchart presented in Figure 12.

ANSYS^® [11] is a commercial software program capable of performing several Multiphysics analyses, based on the numerical finite element method. ANSYS^® [11] was selected due to its thermal and structural numerical algorithms and its ability to model contact between components.

The analysis is usually performed by first conducting the thermal analysis and then the structural analysis. That is, the calculated temperature affects the structural and mechanical analysis, but the mechanical analysis does not affect the temperature field variation.

To satisfy the thermal or structural conditions of the problem, it is necessary to employ an iterative procedure in each time step. The modified Newton–Raphson method was adopted to solve the problem with an imposed time step and minimum time increment. The convergence criterion is based on the heat flow calculation for thermal analysis and displacement calculations for structural analysis, using an absolute tolerance of 0.1 with a maximum number of iterations equal to 15.

2.3.1. Thermal Analysis

The calculated temperature fields are then imported into the connection model as the thermal load at the specified time. The thermal analysis consists of determining the temperatures at each mesh node, used in the structural analysis defined in the next subitem.

The steel-to-timber connection is subjected to the nominal temperature–time curve ISO 834 applied on the front and the back surface of the model. The thermal response is calculated during 3600 s of fire exposure. The boundary conditions applied to the connection in this situation are the convection, with a coefficient equal to 25 W/m²K, on the sides exposed to fire and the radiation with the emissivity considered equal to 1, according to the according to Eurocode 1 part 1-2 [13]. The initial temperature applied on all model surfaces is constant and equal to 20 °C.

Firstly, through purely thermal analysis, the evolution of the thermal gradient in the connection is obtained. Then, the thermal outputs (nodal temperatures) are used as inputs in the structural analysis, through the LREAD command. Nodal temperatures act as body forces on the respective nodes. This approach requires that the mesh be the same for the thermal and mechanical analysis.

2.3.2. Structural Analysis

After the previous step, it is possible to proceed with the structural analysis, where the material’s mechanical properties must be properly attributed. The nodal temperatures are imposed for each time instant, reading the file.rth. The thermal load influences the mechanical behavior of the connection, through generated thermal strains and the degradation of the mechanical properties of the materials. Simultaneously, an incremental and linear tensile load is imposed on the timber element, whose main objective is to verify the maximum value that satisfies the safety of the project and the good working of the model. The structural analysis was carried out by considering wood material properties to GL20H, GL24H, and GL32H, and for the time instants of 0, 60, 120, 240, and 300 s.

2.4. Finite Elements

A three-dimensional (3D) numerical model was created using ANSYS^® [11] to carry out the thermomechanical analysis and consider the nonlinear properties of wood and steel materials. For the numerical model, the principle of symmetry is used, reducing the computational costs and analysis time. Due to the study of half of the connection, symmetrical boundary conditions (S) were applied on the left side of the connection on the steel elements’ sides, as shown in Figure 13. The solution method is incremental and iterative, based on displacement. The software uses the Newton–Raphson method to determine the new equilibrium position. Furthermore, the numerical model simulates the contact between all wood and steel components.

Figure 13 presents the mesh used for one half of the numerical model and a representative plane under study, where different points (K1, K2, and K3) and the length of the dowel are considered for further analysis.

To simulate the thermomechanical response, the connection is discretized using different types of elements available in the ANSYS^® [11] internal library, as described in the flowchart of Figure 12.

To represent the connection mesh for thermal analysis, the finite element SOLID 278 with a 3-D thermal conduction capability was chosen. This element has eight nodes with one degree of freedom, temperature, for each node. The element is applicable to a 3-D thermal analysis, in steady state or transient.

To represent the connection mesh for structural analysis, the SOLID 185 finite element was used for the 3-D modeling of solid structures. It is defined by eight nodes with three degrees of freedom at each node: translations in the x, y, and z nodal directions.

All contact interactions between different components were simulated using standard ANSYS^® Contact174 and Target170 finite elements. These elements were only used to attach the connection between the contacting surfaces and between the dowels to transfer mechanical forces.

CONTA174 is used to represent contact and sliding between 3-D target surfaces and a deformable surface defined by this element. The element is applicable to 3-D structural and coupled-field contact analyses. It can be used for both pair-based contact and general contact. TARGE170 is used to represent various 3-D “target” surfaces for the associated contact elements. The contact modeling requires the specification of the static friction coefficient for sliding surfaces, here considered a value of 0.3 [22]. In the study by Dorn [22], the static coefficients of friction for laminated veneer lumber on steel surfaces were experimentally determined. The authors concluded that the values were obtained between 0.1 and 0.3 for a smooth steel surface.

3. Results and Discussion

Figure 14 and Figure 15 show the three connections under study, with all the parameters involved in the project. For the study, dowel diameters equal to 8 mm and three wood materials (GL20H, GL24H, and GL32H) [17] were considered.

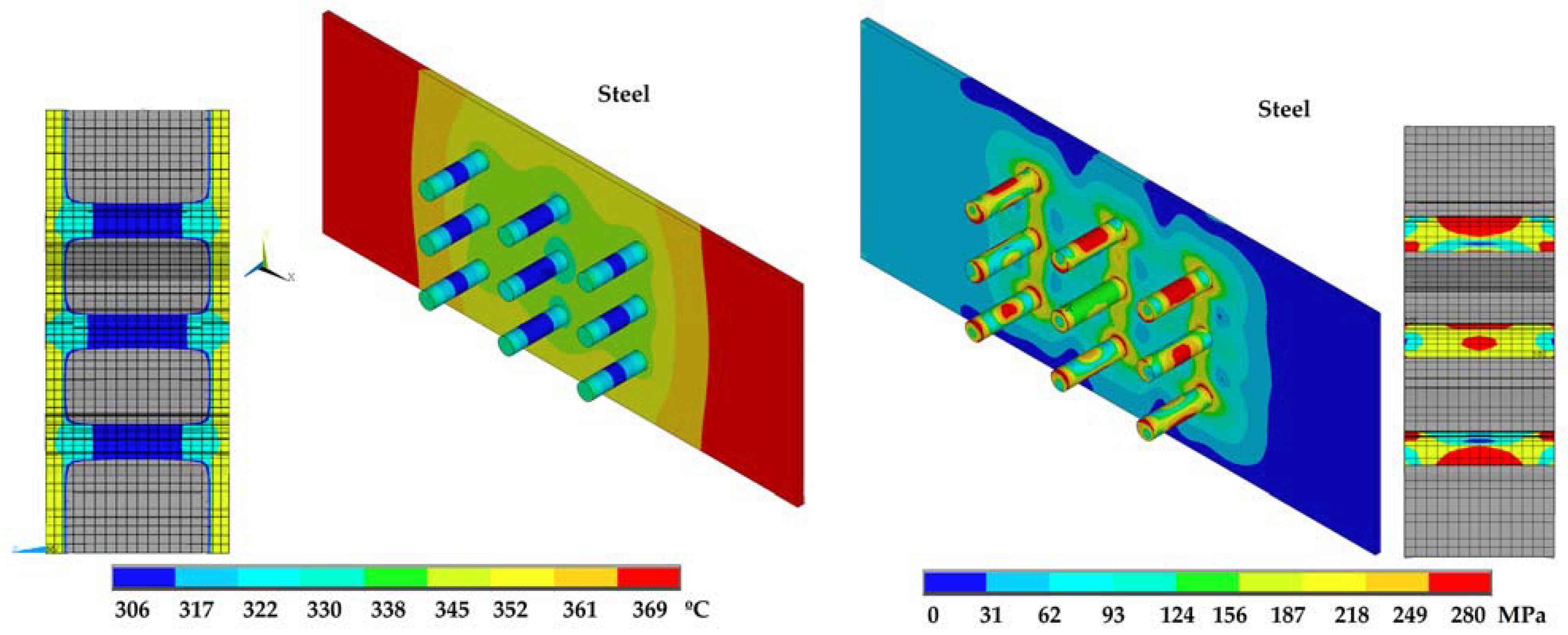
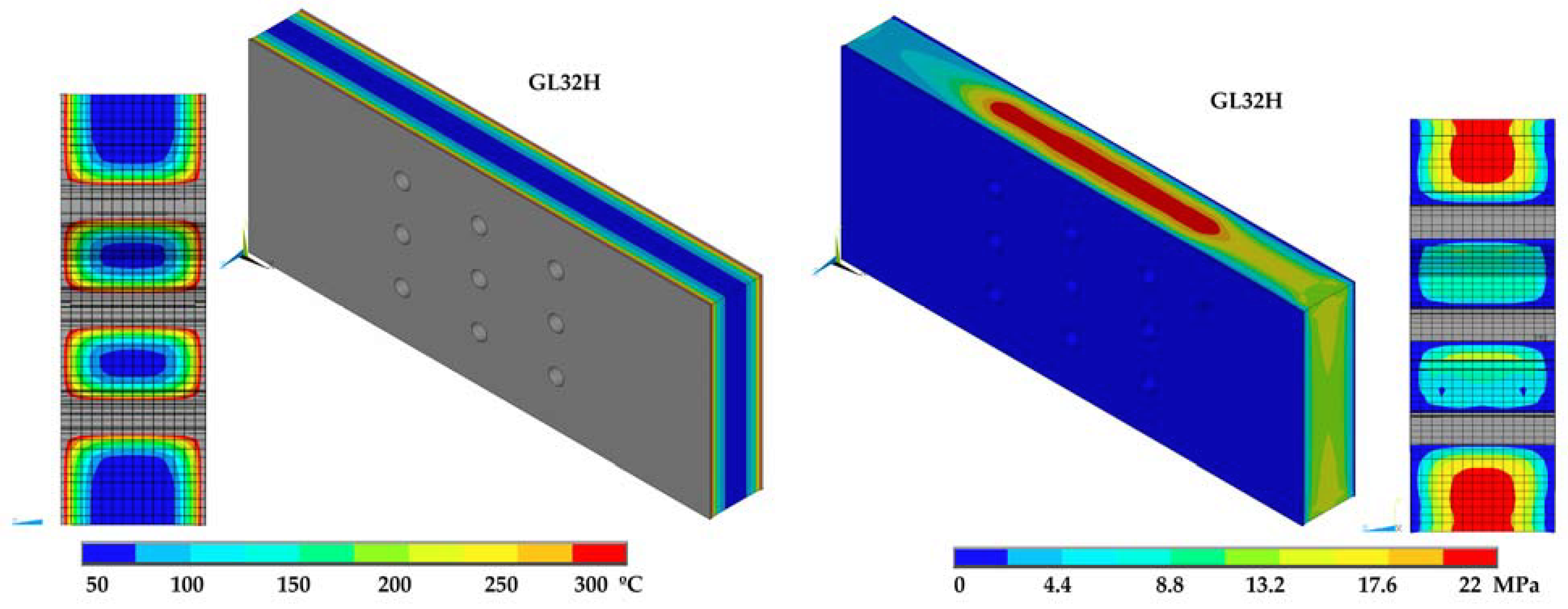
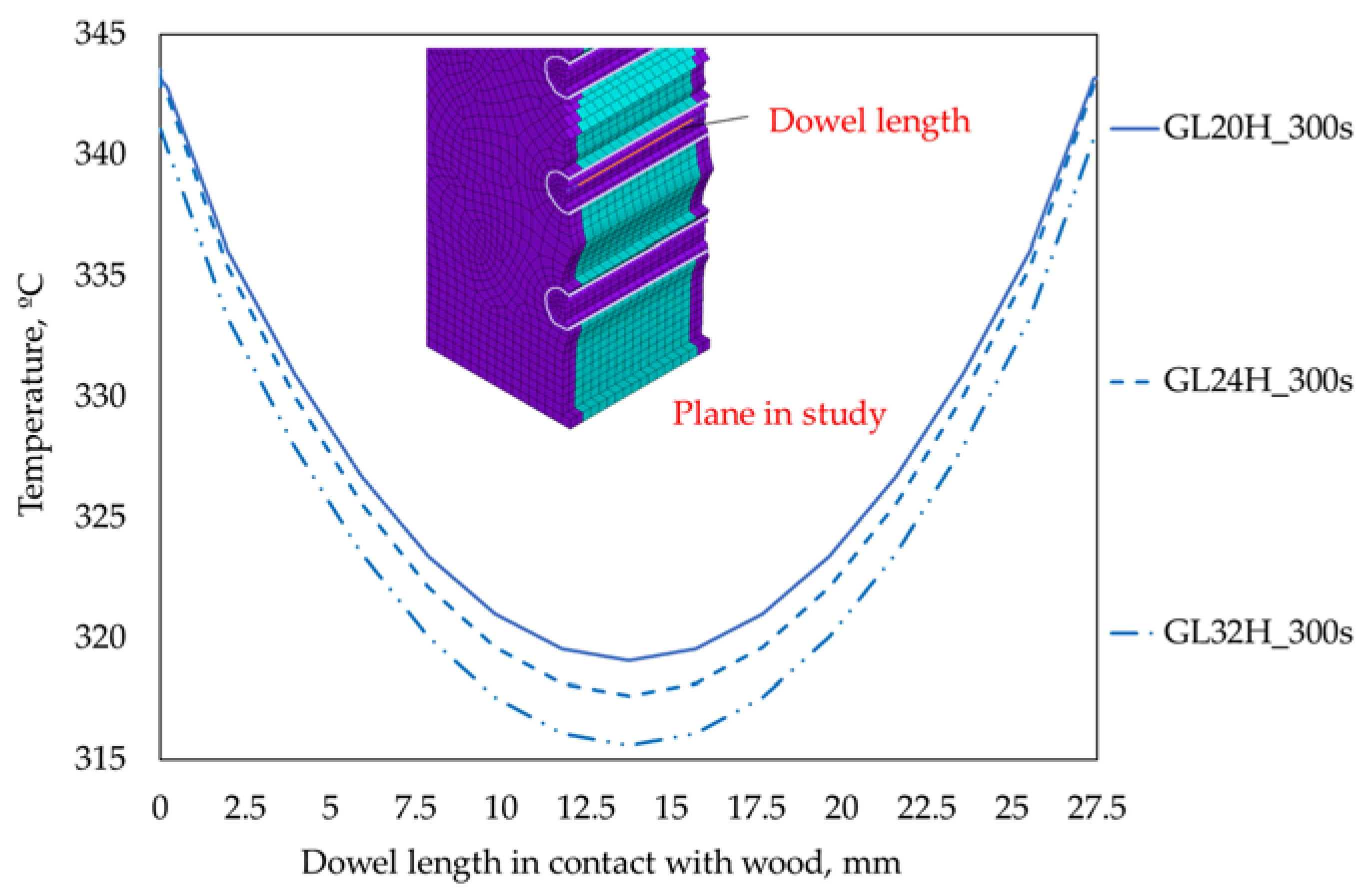
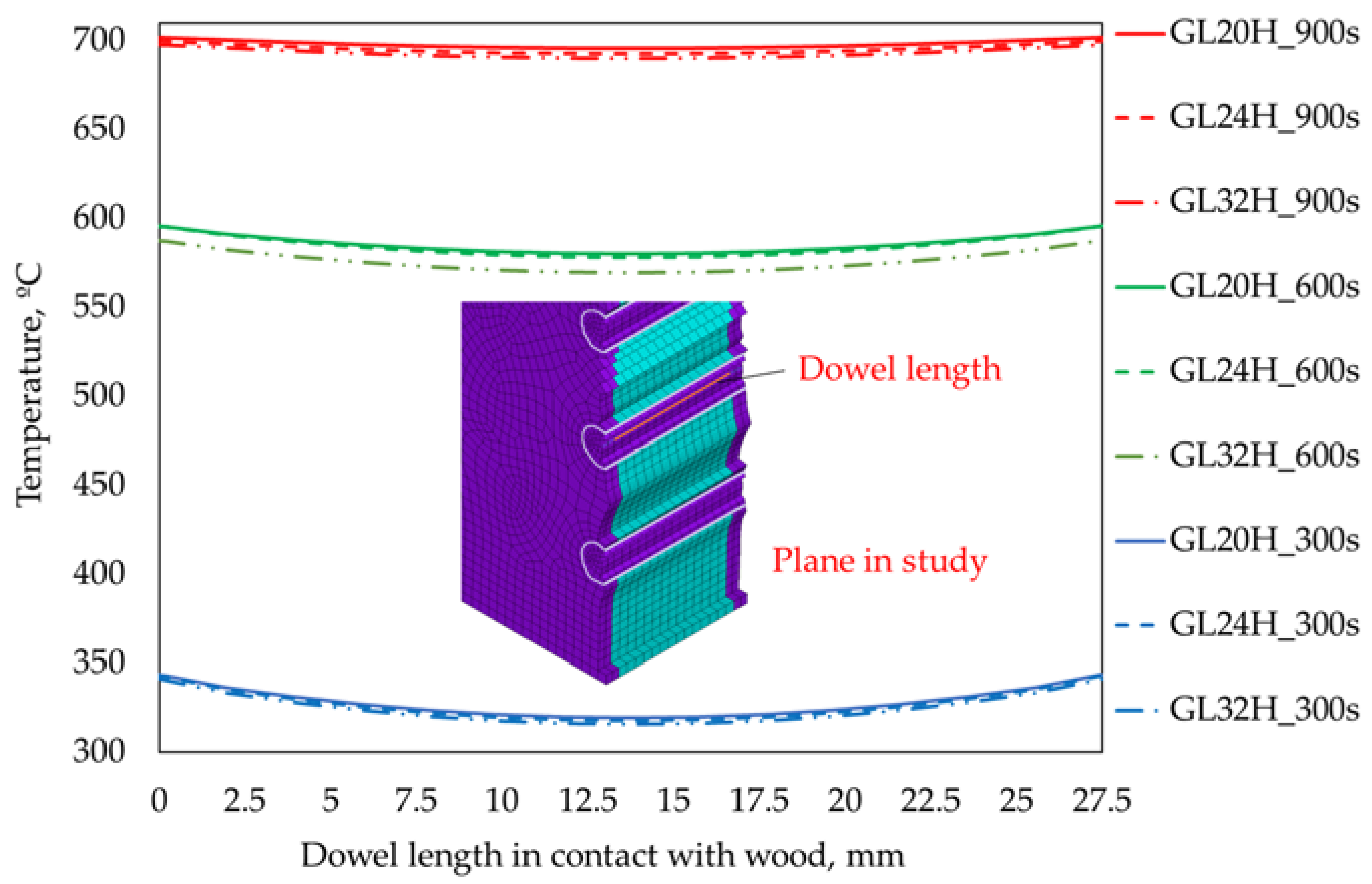
3.1. Temperature Evolution through Dowel Length in Contact with Different Wood Densities

The temperature evolution through the dowel length in the middle of the studied cross-section was obtained at different time instants of fire exposure to identify the variation between the external side exposed to fire and the internal side in contact with the wood element, as represented in Figure 14 and Figure 15.

The numerical results show that there is a small temperature variation between 25 and 30 °C throughout the dowel for time instant 300 s, being smaller for GL32H wood, and higher for GL20H wood. As expected, the temperature at the dowel edges in contact with the fire is higher than in the middle, which is the result of the neighboring wood material with lower conductivity.

The steel-to-timber connection in GL32H presents a lower temperature distribution due to its superior density in relation to the other species. The temperature inside the dowel increases by around 250 °C when the time goes from 300 s to 600 s, and increases by another 100 °C when the exposure to fire is 900 s. The temperature in the material depends on the boundary conditions, namely, exposure to fire and its logarithm curve effect. There is a great effect at the beginning of the fire, and then the heat effect increases more slowly.

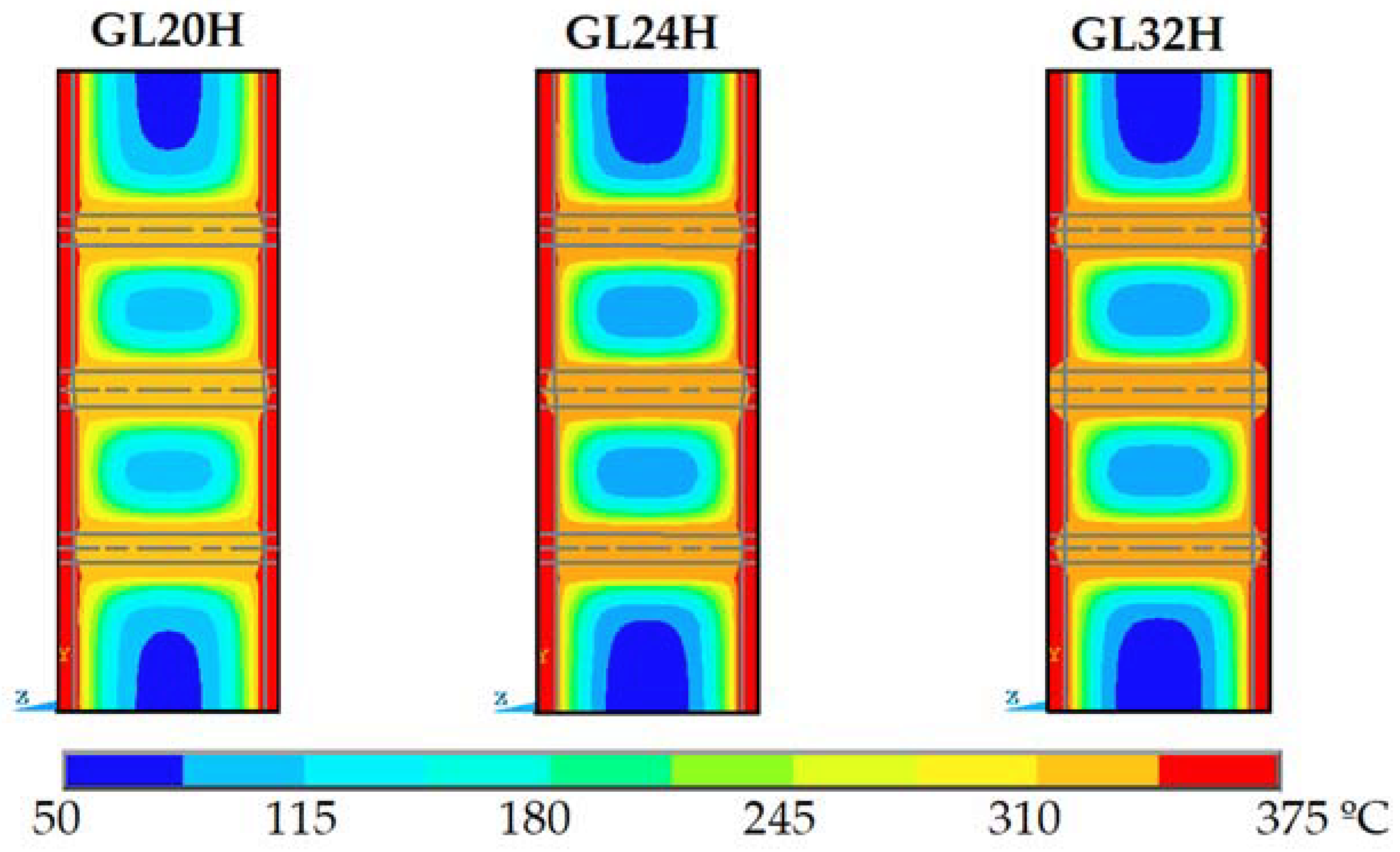
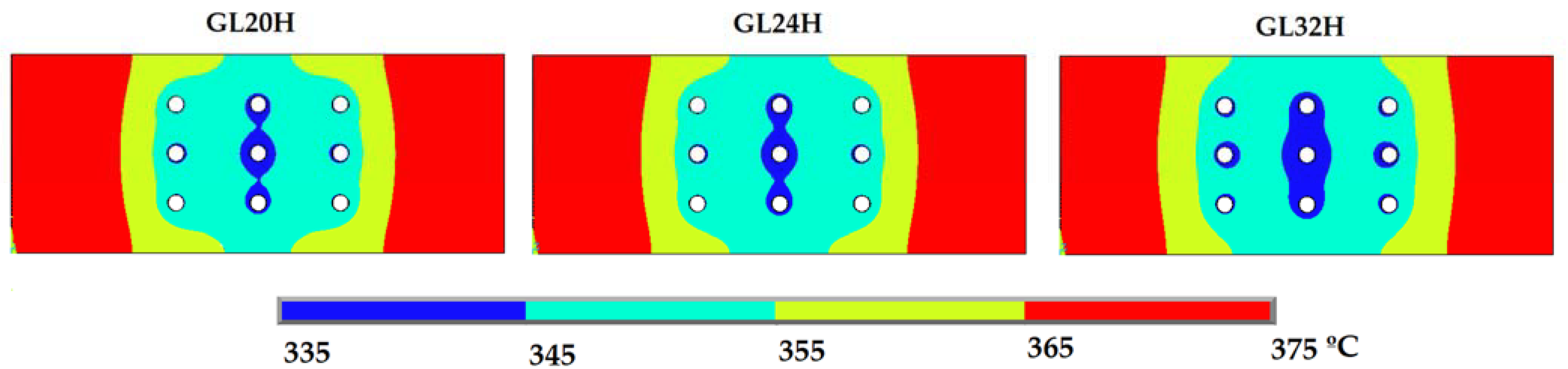
3.2. Temperature Evolution in the Connection with Different Wood Densities

Figure 16 shows the results of the temperature inside the middle cross-section of the connection. These were obtained for the three wood species under study and for a time exposure of 300 s.

The results show that the temperature can vary between 50 and 375 °C. On the surface of the steel plate exposed to the fire, the temperatures can reach 375 °C and on the dowels, a temperature of 310 °C is observed.

More regions with lower temperatures are observed for GL32H wood compared to the other wood species. Moreover, the region surrounding the dowels and near the steel plates presents higher temperatures. In all models, inside of the cross-section, the temperatures adjacent to the dowels are more pronounced than in the other internal regions, due to the steel’s heat-spreading effect in the dowels, as identified in [6].

Figure 17 shows the results of the temperatures in the front plane of the wood immediately in contact with the steel plate, for the three wood species under study and for the time of exposure to fire of 300 s.

The effect of heat transfer from the steel plate and the dowels to the wood element is noticeable. In the connection with GL20H wood, the temperature field reaches increased values even in the vicinity of the connectors compared to other types of wood connections. Indeed, the dowels in the middle show larger regions with lower temperatures, but this effect decreases with the distance to the middle. On the connection edges, the variation is not relevant. These observations complement the previous ones associated with Figure 16.

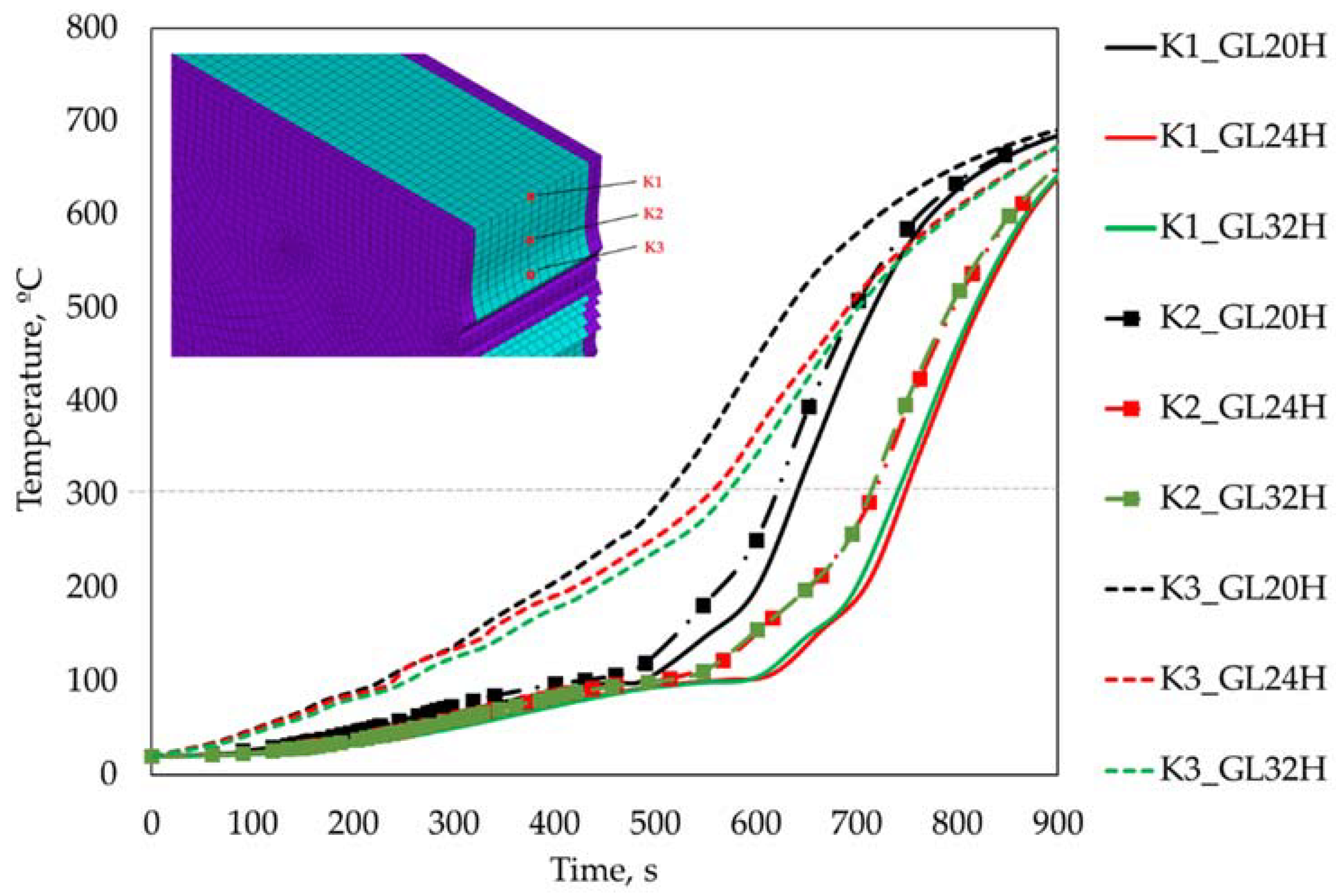
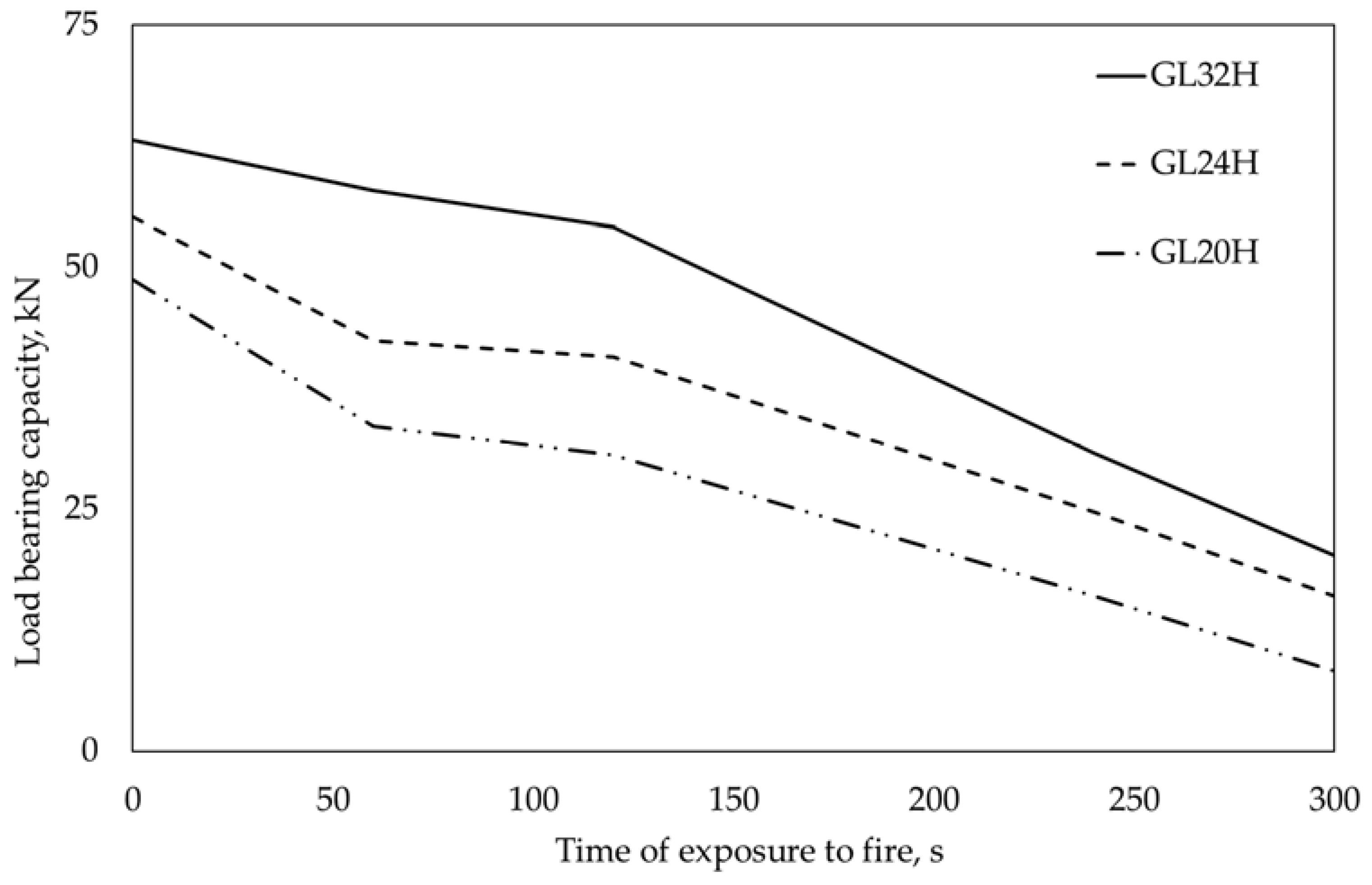
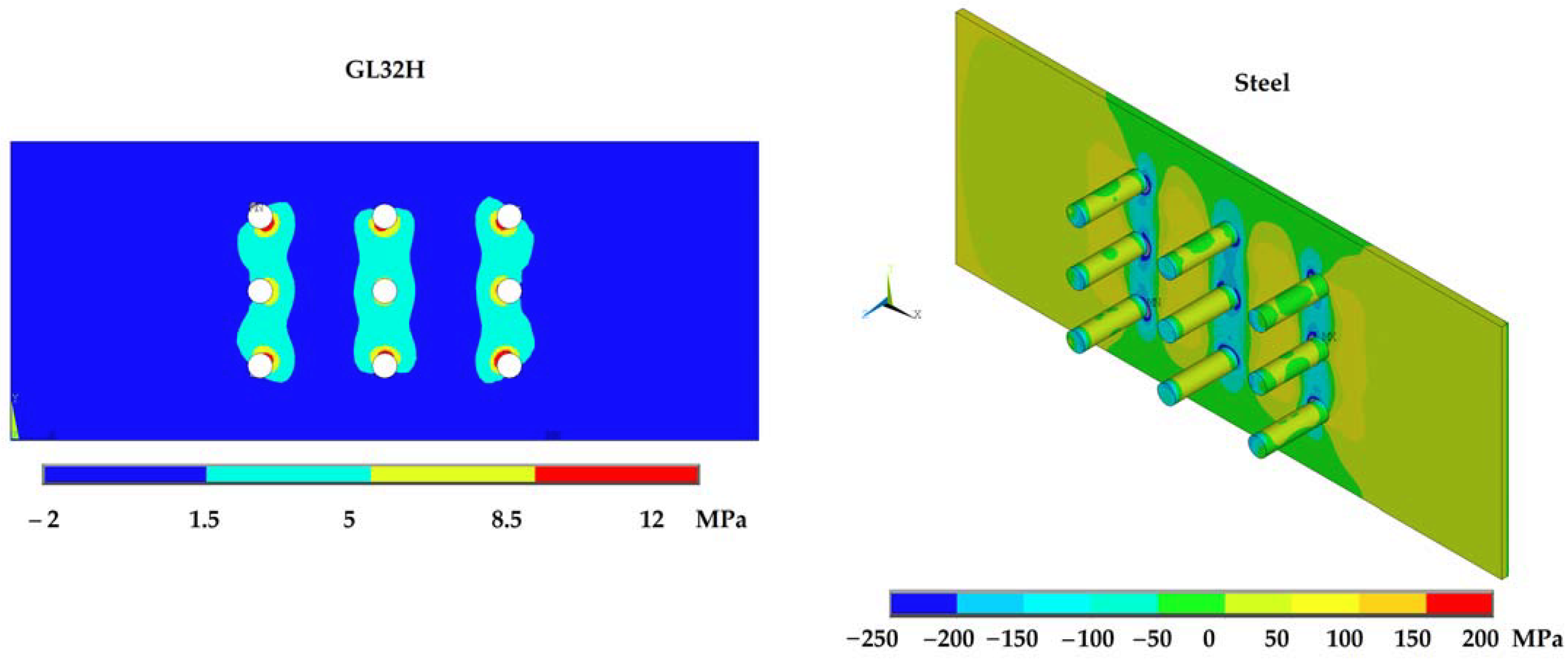
3.3. Temperature, Load-Bearing Capacity, and Stress Level in Connections with Different Wood Densities

The load-bearing capacity of the connection when submitted to tensile load and exposed to fire requires verification of the stress level and the temperature reached at the beginning of the wood char layer formation. According to Eurocode 5 part 1-2 [14], the point that the char layer appears in the wooden material corresponds to the temperature of 300 °C.

The temperature–time curves for points K1, K2, and K3 and the three wood species are represented in Figure 18.

The curves show a similar tendency for the same point of analysis, with an early rise in temperature being consistently observed for the GL20H wood. The connection made with GL20H wood presents the highest temperatures over time, being this followed by the connection with GL24H wood and the connection with GL32H wood. After 500 s, the temperature reaches 300 °C at the external point K3 for connection with GL20H wood, with a delay of 90 s to the connection with GL32H wood and 60 s to the connection with GL24H wood.

The temperature difference is evident due to the wood density effect, with a delay between the connection in GL20H and the other wood species being observed. The connection in GL32H has lower temperatures until the exposure to fire in the connection reaches 900 s, where all connections start to have the same behavior. The average temperature at 900 s is 688 °C for the connection with GL20H wood, 664 °C for the connection with GL24H wood, and 656 °C for the connection with GL32H wood.

In the work presented by Szász [2], the results of the temperature obtained on the timber element submitted to the fire curve has a similar tendency compared with the results in our study. The use of the ISO834 fire curve resulted in higher temperatures in the outer regions and in the steel elements.

In Figure 19, it is possible to analyze the load-bearing capacity of the studied connection for different times of exposure to fire and for the three wood species under study. These results are based on the material’s failure strength according to the material behavior at different temperature levels.

The results presented in Figure 19, at room temperature, correspond to the initial instance. The results only show the effect due to the applied mechanical load in the connection. These values are in accordance with the calculated load-bearing capacity given by Equation (2), Eurocode 5, part 1-1 [16].

The numerical value is 48.76 kN for connection with GL20H wood, 55.19 kN for connection with GL24H wood, and 63.09 kN for connection with GL32H wood. In this graphic, the results also show a decreasing load-bearing capacity with the exposure time to the fire. The GL32H connection has more resistance than other connections with lower wood density. On average, the connection with GL32H wood presents a superior load-bearing capacity of 16 kN compared to the connection with GL20H wood, and more than 6 kN more than the connection with GL24H wood. The decrease in load-bearing capacity in all connections is slightly linear with the increasing fire exposure time. These connections do not withstand more than 300 s at high temperatures. At the end of the fire exposure, and in relation to the applied load at ambient temperature, it was possible to observe that the GL20H connection has an 83% decrease in the load-bearing capacity, the GL24H connection has a reduction of 71%, and the GL32H connection decreases by 68%. The duration of fire exposure changes the load-bearing capacity in the connection because both materials (steel and wood) are also changing, a conclusion also reported by [2].

According to the work presented by Szász [2], the size of the fasteners considerably affected the fire performance of the connection. At ambient temperature, the big fastener diameter is favorable, but in a fire, it transfers more heat into the inner timber elements, thus charring the timber faster. This result is significant in the case of smaller timber cross-sections. The load-bearing capacity based on the tests had a reduction equal to 57% and 81% at different fire exposure times, with a similar tendency to the observed results in the present work.

Figure 20 presents the normal stress for GL30H wood, steel plates, and dowels for the time instant of 300 s. This confirms that the wood around the holes is in tensile when the contacting dowels are in compression. Once the mechanical load is applied to the wood component, with the contact effect of the steel elements, they receive the opposite load behavior.

The combination of tensile and thermal load leads to stress concentration in the holes of the GL32H wood. The normal stress presents a tensile value of 12 MPa in the upper and lower dowels. At the same time, the steel elements have a compressive value of 250 MPa for the same positions. The wood plate is in tensile and the steel elements in compression.

The following Figure 21 and Figure 22 represent the values of the stresses observed in the connection with the best performance: the connection with GL32H wood.

Figure 21 shows the corresponding temperature and the equivalent von Mises stresses on the steel plates, dowels, and the middle cross-section of the connection for the time 300 s.

Figure 21. Temperature (left) and equivalent stress (von Mises) (right) in the steel elements, both with the middle cross-section, at 300 s.

Figure 21. Temperature (left) and equivalent stress (von Mises) (right) in the steel elements, both with the middle cross-section, at 300 s.

The higher values are observed on the upper and lower dowels with the value of 200 MPa, which corresponds to the value of 22 MPa in the respective holes of the GL32H wood component. As expected, the cross-section exhibits a stress concentration near the dowels. In the middle of the connection, the values of stress are more relieved for both components. The steel plate presents superior to 306 °C, with the lower temperatures exhibited in the middle section of the dowels. The corresponding equivalent von Mises stress reveals that the maximum value of 280 MPa is also obtained in the middle section of the dowels.

Figure 22 represents the temperature and the von Mises stress for the wood element and the middle cross-section of the connection for the time of 300 s.

Figure 22. Temperature (left) and equivalent stress (von Mises) (right) in the wood element, both with the middle cross-section, at 300 s.

Figure 22. Temperature (left) and equivalent stress (von Mises) (right) in the wood element, both with the middle cross-section, at 300 s.

In the wood component, the indirect char layer depth is formed in contact with the steel elements, resulting in the loss of strength in this region. In the middle cross-section of the connection, it is observed that the von Mises stresses can reach 22 MPa for the intact regions of the wood component.

4. Conclusions

In this work, a numerical methodology was developed to evaluate the safe design of a typical steel-to-timber connection under exposure to fire and under a tensile load, by considering the wood properties of GL20H, GL24H, and GL32H. The numerical methodology presented makes it possible to predict the structural behavior of the steel-to-timber connection during the time of exposure to fire, considering the reduction of properties with the temperature of the steel and wood components. The load-bearing capacity for different times was evaluated by analyzing the stress level and the wood char layer formation. When exposed to fire, wooden materials exhibit thermal physical degradation. In steel-to-timber connections, the type of wooden material can limit the use of these constructive elements in terms of fire resistance. It was concluded that the wood density influenced the resistance of the connection under ambient and fire conditions.

This study concludes that the proposed thermomechanical model can offer good responses and enables several applications and analyses for future research involving this thematic. These constructive elements must be chosen in advance to prevent and delay the fire damage effect, allowing the connection to remain in service with more safety and durability. Future work will also consider different insulation materials, ensuring greater durability in these types of components. The main purpose of this study was to analyze a steel-to-timber connection in double shear with dowels under fire with the finite element method considering the material density effect, choosing three different wood species. The proposed methodology allowed the verification of the wood density effect on the heat transferred through the connection under fire, and a thermomechanical complex model was developed to analyze this type of problem, which was a great novelty in this work. The analysis in this study allows for the improvement of structural and safety designs, maximizing the load-bearing capacity of connections when exposed to fire.