Abstract
Construction projects are often delayed. Their budgets are being exceeded. This is partly because construction project models rarely take human factors into account. The article focuses on the repetitive multi-unit projects that are often found in construction practices. They are an excellent example of construction works for which the optimization of certain processes can bring measurable financial benefits. In particular, the focus was on improving the key investment success indicator, the total cost of a project. This article presents the use of learning and forgetting phenomenon to improve construction schedules. The authors proposed an innovative model of the construction phase and optimized the schedule using a proprietary calculation algorithm using the simulated annealing phenomenon. The method was verified by a series of experiments and showcased by a case study. The results show that the presented methods can improve the construction planning process and better reflect the current construction conditions. The findings may impact residential, infrastructure, industrial, and commercial construction branches.
1. Introduction
Solving the problems of scheduling construction projects is currently of interest to many researchers around the world. Repetitive multi-unit projects, which are often found in construction practice, deserve particular attention. Due to their nature, they are an excellent example of construction works for which the optimization of certain processes can bring measurable financial benefits.
They consist of the implementation of many different buildings with similar technology. Cases of such undertakings may occur in residential, infrastructure, industrial or commercial construction branches. The optimization model of a multi-object project presented in the article is intended to be used for projects consisting in the implementation of many different construction objects with a similar implementation technology, but significantly differing in the size of the works to be performed. For this reason, this model can be treated as a generalization of the approach to scheduling repetitive objects presented, for example, in the LOB method [1] and derivative methods [2]. As a result, the potential application of new implementations can be widely used in industry. As numerous reports show [3,4,5], a significant proportion of construction projects are overestimated or underestimated. This may result, inter alia, from incorrect construction of project models. This case hinders proper analysis and preparation of the implementation.
One of the factors causing large deviations of models from reality may be an insufficient consideration of the human factor. The learning and forgetting effect (LAF) is a phenomenon that allows to describe the increase in the efficiency of construction work groups and, thus, the decrease in the duration of construction works of one type in many different locations. This has been proven in the works of many researchers [6,7,8,9].
The article presents the application of this phenomenon in a multi-unit construction project. Considering the effect of learning and forgetting is a very important element of the actual work schedule. The article presents an optimization model of such a construction project. The search for the optimal schedule, taking into account the assumed constraints and the objective of the project implementation cost, is an NP-hard optimization task. The model of scheduling a multi-unit project presented in the article can be successfully used during the planning process of such projects by practitioners and decision makers of the construction sector.
2. Materials and Methods
2.1. Project Scheduling Problems—The Overview
Current research on project scheduling problems is focused on searching for optimal schedules considering existing constraints [10,11]. Construction cases of such problems are usually considered to be NP-hard optimization problems, as explained in [12,13]. Numerous categories—models of project scheduling problems (PSP) are being studied depending on various constraints and schedules’ objective functions. The most common approach for solving PSP optimization is a deterministic approach (due to its complexity and practical aspect). There are many well-known reviews of PSP deterministic models, e.g., [14,15,16,17]. One of the most frequently described and researched models is the Resource-Constrained Project Scheduling Problem (RCPSP) [18]. This is due to the wide applicability of this problem in the worldwide industrial production and the construction sector [10].
Classic RCPSP focuses on the makespan minimization. However, different objective functions, constraints, conditions (and the whole model) can be used in order to best meet the needs of the decision maker. The most frequently described objective functions in construction include optimization of total cost [19], quality [20], NPV [21], total project delay [22], monthly cash demand [23], cost minimization in regard to the base-plan [24], deviations from average employment level [25], schedule robustness [26], etc.
The procedures used to solve PSPs can be classified as: exact, heuristic, and metaheuristic [10,13]. Practical scheduling problems in construction are often classified as NP-hard (non-deterministic, polynomial-time hard) problems. Computing time needed for solving such problems grows exponentially with the increase of the problem’s size [12,13,27]. Therefore, according to many researchers, metaheuristic algorithms seem to be the most appropriate measures for task sequencing and scheduling (despite the fact that they do not guarantee finding the optimal solution) [19,21,27,28,29,30]. Different metaheuristic algorithms are being used for solving PSPs, e.g., Simulated Annealing (SA) [21], Genetic Algorithms (GA) [19,29], Tabu Search (TS) [21,31], Ant Colony Optimization (ACO) [32], Particle Swarm Optimization (PSO) [33], or hybrid algorithms [23,34,35].
2.1.1. Multi-Mode Problems
Currently, in the construction industry, there is a continuous increase in a number of contracts focusing on delivering non-standard products individually agreed with the client. Therefore, the scheduling of production processes is often in line with the principles of project management. The same principle is also characteristic of the construction industry [10]. This phenomenon can be modeled by a generalization version of a RCPSP—the Multi-Mode RCPSP (MRCPSP or sometimes MMRCPSP). In MRCPSP, each activity can be executed in one of the defined modes. Each mode has a specific duration and specific resource requirements [29]. Thanks to the introduction of modes, the decision makers are able to study different projects’ variants (e.g., in terms of different materials or technology used). Unfortunately, as the additional decision variables (activities’ modes) are being introduced, the possible solutions’ space (and, at the same time, the amount of computational time required to solve the problem) is growing [10]. Therefore, the computational time required for solving a MRCPSP is longer than that of a similar RCPSP without multiple modes [27].
MRCPS problems can be further complicated, for example by adding the dependencies between time and cost of a project—Multi-Mode Resource Constrained, Discrete Time-Cost Trade-Off problems MRC-DTCTP [25], which, in construction, are also often called Time-Cost Trade-Off (TCT) problems. The elaborated problems can also include discounted cash flows (MRCPSPDCF) [10,21,36].
2.1.2. Schedule Optimization for Multi-Unit Construction Projects
The problems of planning the execution of construction works are analyzed using various theoretical models. These models are usually of a deterministic or random approach. The most common methods of planning construction work (scheduling projects) are, e.g., CPM/PERT network planning (Critical Path Method/Program Evaluation and Review Technique) [37], Line of Balance (LOB) [1], methods based on LOB, such as the LSM (Linear Scheduling Model) or RSM (Repetitive Scheduling Method) [2], and Time Couplings Methods TCM [38].
Network planning is usually used to schedule construction projects that are unique, for example large-scale buildings (residential, service, or industrial). The second group of methods based on LOB is intended for scheduling repetitive projects.
Repetitive projects are characterized by the possibility of their clear division into parts (units), which may be individual working plots of the building (work zones), individual floors, entire building structures or sections of buildings with specific lengths, e.g., linear construction projects. Examples of such projects are multi-story buildings, estates consisting of single or multi-family houses, pipelines, and roads. In each part of a given repetitive project, specialized work crews carry out dedicated activities as they move from one part of the previous venture to the next [39].
Among the repetitive projects, a special group can be distinguished, which consists in the implementation of many similar buildings. Such projects are referred to in the literature as multi-unit projects. The flow shop theory of scheduling is used in order to describe and solve such problems [40]. Flow shop scheduling is a special case of job–shop scheduling in theory of scheduling where there is strict order of all operations to be performed on all jobs. Flow shop scheduling may apply as well to production facilities as to computing designs. The current research on multi-unit projects focuses on the continuous improvement of the theoretical models.
In article [41], a model of scheduling a multi-unit undertaking consisting in the implementation of many production halls was presented. The costs of works and directive deadlines for completion of works have been established for each unit. Penalties were charged for exceeding these deadlines. The task was to find the optimal order of execution of the halls, which would minimize the total cost of the project, including penalties for exceeding the directive deadlines. This task was solved using the metaheuristic scatter search algorithm. In [42], the NP-difficult problem of scheduling a construction project was considered with the criterion of the sum of penalties for exceeding the deadline for building construction. The parameters of this project were represented by fuzzy numbers or random variables with a normal distribution or the Erlang distribution. In [43], a scheduling model was presented with the possibility of performing one type of work by more than one working group and with sequence relationships given by any graph. The optimization task in this model was solved using the tabu search algorithm. In [44], the scheduling model for a multi-unit project assumes a linear relationship between the time and the cost of carrying out the activity. The criterion of minimizing the total value of the project cost determined on the basis of the mathematical programming model, taking into account direct and indirect costs, costs of missing deadlines and costs of workgroup discontinuities. The optimization task in this model was solved using the modified simulated annealing algorithm. In the paper [45] the author presents a model of a multi-site enterprise, in which he minimizes downtime during work to maintain the continuity of work of working groups. Additionally, he minimizes both the time and penalties for exceeding the deadlines for completion of works in the facilities. The problem was modeled and solved as a problem of multi-criteria optimization using the mixed-integer linear programming approach. In [10], the authors presented the model of a multi-unit project aimed at maximizing the investor’s total profit. Profit is calculated as the result of total accumulated cash flows from the entire project. The optimization task in the project model was solved using proprietary forms of simulated annealing and genetic search algorithms.
2.2. Learning and Forgetting Phenomena
The concepts of learning and forgetting (LAF) and learning curves have been discussed and written about for many years. This approach assumes that this phenomenon can have a strong impact on the effectiveness of our work. Regardless of whether we perform simple household tasks, complex office work, or construction works. Repeatability and regularity of performed tasks affect the quality of results and the duration of the work.
2.2.1. LAF Models
It is believed that the first application of learning curves in production and operations management was published by Wright in 1936 [46]. The learning-curve representation suggested by Wright is a geometric progression which expresses the decreasing cost required to accomplish a repetitive operation. According to his theory: as the total quantity of units produced doubles, the cost per unit declines by some constant percentage [47]. Wright’s learning curve (WLC) can be classified as a log-linear model and can be represented as:
- -
- —the time to produce the xth unit,
- -
- —the time to produce the first unit,
- -
- —the production count,
- -
- —the learning curve exponent.
Usually, the parameter value is equal to , where is a learning rate.
Over the years Wright’s learning curve model was modified in numerous ways—for example, by including prior experience level [48], by mixing manual and automated operations [49], by introducing a mixed model assembly (with two or more items being repetitively assembled) [50], or by introducing restoring interruptions [51].
Various studies tackled advantages and disadvantages of WLCs, and its modifications. This led numerous researchers (including Carlson, Kvålseth, Pegels, Mazur, and Hastie) to study and develop exponential and hyperbolic models for learning curves [46].
The models can be further divided into categories according to their characteristics, for example, by task duration (continuous or interrupted tasks); learning individuals (single workers, groups, or organizations); type of learning (motor or cognitive); and learning drivers (e.g., working time, cumulative number of produced units, number of setups, number of detected problems, completed projects, etc.) [52].
Many models of forgetting have also been developed. Although the phenomenon is the opposite of learning, it is usually not modelled as simply the mirror image of learning (Figure 1). Some of the most renown forgetting models include: the variable regression variable forgetting model (VRVF) [53], the variable regression invariant forgetting model (VRIF) [54], the learn–forget curve model (LFCM) [55], the power integration diffusion model (PID) [56], and the depletion power integration latency model (DPIL) [57].
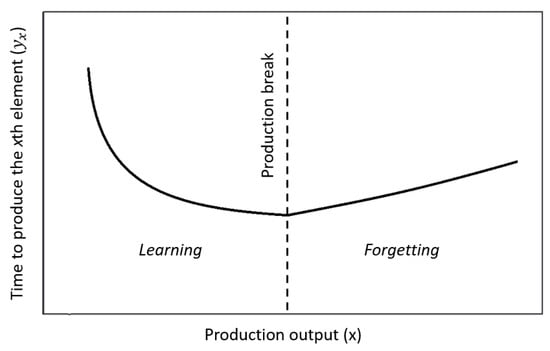
Figure 1.
Sample learning and forgetting process.
Both phenomena (learning and forgetting) are being studied both mathematically and empirically.
2.2.2. LAF in Construction Industry
The influence of the learning effect on the performance of groups of employees when performing repetitive activities has been studied in many articles. The article [58] presents the problem of the increase in efficiency observed during the research on efficiency in the construction of 15 multi-story reinforced concrete buildings located in Italy. The obtained research results allowed for the assessment of the learning rate at the level of 85% to 95%, which makes it possible to determine the costs and times of carrying more accurately out similar works in this country.
The publication [59] investigated the impact of the learning effect on the efficiency of installing slab formworks for building construction. The observed learning rates ranged from 95% to over 99%. Such high learning rates, according to the authors, could have been caused by the volatility of the conditions of the works: a change in the number of working groups, a change in the duration of working shifts or a change in the remuneration incentive system. The problem of establishing a learning curve model for the efficiency of works in the implementation of prefabricates in construction was presented in the article [60]. The authors, based on data from the period of 5 years, for 90% of works related to the production of prefabricated elements, determined a learning curve model based on exponential functions. According to the authors’ research, the obtained model has a satisfactory degree of fit and allows for a very accurate ability to predict future performance. The issue of determining the learning curve was also tackled in the paper [61]. This time, the authors dealt with repetitive and complex activities that occur when making prefabricated floating caissons. They used a simulation method to predict future performance outcomes generated by the generated learning curve. Another type of repetitive works in which the influence of the learning effect can be noticed are insulation renovation works during the construction of roofs of buildings [62]. Based on the questionnaire survey, the authors checked which of the known mathematical models better reflects the learning phenomenon for this type of works.
The presented literature review on taking into account the learning phenomenon for repetitive activities in construction shows a very wide range of types of construction works in which this phenomenon occurs. The research is currently being continued in order to find the best possible understanding of this phenomenon in construction.
The second problem faced by researchers is the inclusion of the phenomenon of learning, as well as learning and forgetting, in scheduling projects with repetitive activities. The best-known methods of scheduling such projects in construction are the LOB method and many other techniques based on it [1]. An article [6] presented research on including the learning effect during the calculation of parameters calculated for schedules created with the use of the LOB method. The following factors are taken into account: the number of activities in one facility/unit, the complexity of activities, and working and management conditions. When considering the learning process, there may be certain and uncertain information, which is why the fuzzy sets theory was used for this purpose.
The problem of taking into account learning and forgetting curves when setting the dates of commencement and completion of construction activities planned with the LOB method was presented in the article [7]. The authors stated that the use of such curves for the LOB method allows for more realistic schedules of repetitive undertakings. The article [8] presents an original learning curve developed by the authors for monitoring the improvement of employee performance as a result of learning. Additionally, the authors present an improved LOB method that takes into account the new learning curve and is based on the mechanism of optimal allocation of resources. The proposed improved LOB method takes into account the possibility of minimizing the use of resources while meeting the requirements for business continuity and the target date of completion of each activity. In turn, in [9] the authors present the application of the learning and forgetting effect for a repeatable project. The endeavor consists of the performance of five finishing works activities on each of the floors of a ten-story residential building (50 activities in total). The result of taking LAF into account is the reduction of the duration of the project by 24 days, i.e., by 18.8% in relation to the duration of the project, without taking these phenomena into account.
2.3. The Construction Project Model
The construction project presented in this article can be described as follows. The contractor’s task in the project is to construct n independent construction units (e.g., residential buildings, or any other suitable construction objects). In each unit, m different works/activities are being performed (e.g., earthworks, foundations, etc.), the size of which can be any size for each of the n units. These works will be performed by specialized working groups, each of which may perform only one type of job. After the completion of activities of a given type of work on the previous unit, specialized groups proceed without undue delay to the next unit, again performing the same type of work (the next step). Only one activity can be performed on a given unit at a time. A given workgroup can only perform an activity on one unit at a time. It is assumed that the order in which workgroups move between units (objects) for each workgroup is the same and is expressed by one order (permutation) of objects’ execution.
Each of the m works in n units performed by a given working group can be executed in several ways (the fact results from the possibility of adopting various technologies for carrying out the works). It is assumed that the more expensive method (mode) enables faster performance of a given activity, and the cheaper method allows only a slower performance of a given activity (the same assumption was made by [63]). For example, the use of more efficient, but more expensive resources (e.g., machines) allows for speeding up the performance of works. By using cheaper but less efficient resources, the duration is extended. The relationship between the cost of performing an activity and its duration for various modes of a single activity is presented in Figure 2. In the model of the project under consideration, the mode is selected for each activity. Each mode is characterized by a specific the duration of the activity and its cost. The selected modes for the whole project are presented in the form of a vector–array (with each element representing mode selected for a given activity).
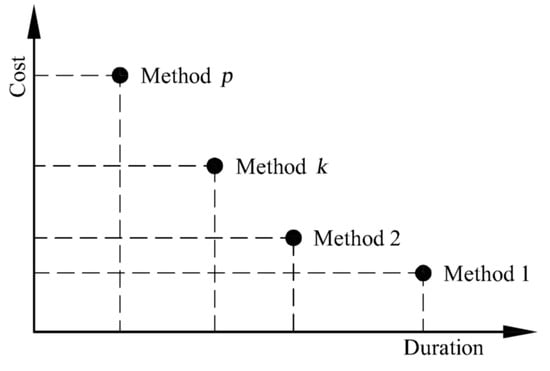
Figure 2.
A typical relationship between time and cost of an activity [63].
Another factor that is taken into account when creating a construction schedule is the effect of learning and forgetting. It concerns working groups performing repetitive activities on site. The learning effect makes it possible to take into account the possible shortening of the duration of subsequent activities of the same type when repeating them in the following construction units. The forgetting effect, in turn, allows taking into account the possible extension of the duration of subsequent activities of the same type when repeating them in the following construction units. The effects depend on the size of the time gap between activities of the same type. The impact of these effects (adopted according to the study [64]) on the duration of activities in the considered project is described in Section 2.3.1.
The creation of the construction schedule for the project depends on the two presented decision variables: the order (permutations) of the objects’ (units) execution and the vector of selected methods (modes) of performing the activities. The choice of the optimal schedule will depend on the assumed objective function. In this case, minimization of the total cost.
2.3.1. The Model of the Learning and Forgetting Effect Used in the Research
The proposed approach uses a modified hyperbolic model of learning and forgetting introduced by Nembhard & Uzumeri [64], which allows to determine the performance of working groups. For this purpose, the following formulas should be considered:
- -
- —current performance,
- -
- —asymptotic limit of y value,
- -
- —amount of accumulated work performed,
- -
- —previous experience in the same unit as ,
- -
- —amount of work to be performed to achieve efficiency of ,
- -
- —forgetting factor,
- -
- —the ratio of the time elapsed from the first timestamp to the time that has elapsed since the last unit x was produced.
The parameters were set so that the efficiency of the working groups varied from 0.7 to 1.3: , . The value of the r parameter is selected based on the complexity of the works. The more complex the work, the more experience it requires to achieve performance. The initial value of the parameter p depends on the experience of working groups. In this research the following assumptions were adopted: low-skilled working groups p = r (efficiency approx. 0.7), medium-skilled working groups p = 2 r (efficiency approx. 1.0), and highly qualified working groups p = 4 r (efficiency approx. 1.3).
The productivity of 1.3 means that during one working day a working group performs work equal to 1.3 working days of a working group with the capacity of 1.0. Productivity at the level of 0.7 means that a given working group performs work equal to 0.7 days of work of a working group with a capacity of 1.0. If the work under normal conditions (1.0 performance) and without taking into account the learning curve required 10 days of work, the qualified team (1.3 performance) will perform the work in approx. 7.7 days, and the unskilled working group (0.7 capacity) in approx. 14.3 days. Of course, taking into account the learning curve means that the unqualified working group gains experience, which increases their efficiency and reduces the time of task completion. Workgroups learn and forget any work carried out with a given technology independently.
2.3.2. The Optimization Model
The construction project presented above has the following optimization model:
Parameters:
- The task of the contractor in the project is to construct a set of construction units:
Z = {Z1, Z2, Z3, ..., Zi, ..., Zn}.
- The set of working groups performing one type of work is as follows:
B = {B1, B2, B3, ..., Bj, ..., Bm}.
- Each unit Zi ∈ Z requires implementation of m activities which form the set:
Oi = {Oi1, Oi2, Oi3, ..., Oij, ..., Oim}.
- Each working group Bj can perform activity Oij ∈ Oi using a maximum of p different methods (technologies) of execution:Dj = {Dj1, …, Djk, …, Djp},
- -
- Dj—set of possible execution modes (methods) for performing activity j by a working group Bj,
- -
- Djk—k method of performing activity j by a working group Bj, a k = 1 ... p.
- It is assumed that the activity Oij ∈ Oi can be done by the working group Bj. The durations of activities from the set Oi are defined by a vector:
ti = [ti1, ti2, ti3, ..., tij, ..., tim], tij = [tij1, …, tijk, …, tijp].
The duration tijk is subject to the method selection from the set of Dj modes of activity Oij.
- Similarly, as the above, it is assumed that the activity Oij ∈ Oi can be implemented by the working group Bj. The cost of realization of the activity Oij by the working group Bj defines a variable cijk ≥ 0. The set of possible costs of activities ci from the set Oi is defined by the vector:
ci = [ci1, ci2, ci3, ..., cij, ..., cim],
The cost of the work cijk is subject to the method selection from the set of Dj modes of activity Oij.
- The LAF effect is considered for the whole duration of activities from the set Oi within vector tu_i = [tu_i1, tu_i2, tu_i3, ..., tu_ik, ..., tu_im], where tu_ik is a real duration of activity Oij taking into account the LAF effect calculated in accordance with the formula:
- -
- —the efficiency (performance) of the jth working group in carrying out the ith job on the zth day in turn.
Constraints:
- The order of execution of the activities resulting from work technology is assumed such that:
- It is assumed that only one job can be performed at a time.
- It is assumed that the activity cannot be stopped during its performance (preemption is not allowed).
Decision variables:
- the order π of execution of units (permutation):
π = (π(1), π(2), π(3), ..., π(j), ..., π(n)),
- set of numbers of methods of activity execution (from k = 1 to k = p):
R = (R1, R2, R3, ..., Ri, ..., Rn),
tu_i = {tu_i1, tu_i2, tu_i3, ..., tu_ij, ..., tu_im},
ci = {ci1, ci2, ci3, ..., cij, ..., cim}.
The deadlines for the activities can be determined from the formula:
Fπ(i), j = max{Fπ(i−1),j, Fπ(i), j−1} + t u_π(i),j,
- -
- π(0) = 0,
- -
- F0,j = 0,
- -
- Fi,0 = 0.
The duration of the entire project Fn,m (duration of all works performed in the units) for π* and for the decision variable R* is
Fn,m(π*, R*) = Fπ*(n),m.
The deadlines for the performance of individual works and their cost can be found in time O(nm). The number of possible solutions to the presented model is n!∙pmn.
The objective function assumes minimization of the total cost of the construction project. It consists of:
- -
- direct costs , which are the sum of the costs of all activities in the project,
- -
- indirect costs (all costs that do not become a final part of the installation but are crucial for the operation of the contractor) depending on the duration of the project,
- -
- penalty costs (optional) charged in case of delays (failure to meet the directive deadlines for the completion of construction works),
- -
- cost bonuses (optional) awarded in case of finishing the works early (earlier than directive deadlines). Such bonuses reduce the overall cost of the project.
More precisely, the optimization task focuses on finding the minimum total cost of the project for the permutation π* and for the decision variable R*, for which:
where
- -
- —daily indirect construction costs,
- -
- —deadline for completion of works in the project,
- -
- —deadline for completion of works on i unit,
- -
- —the finish time for construction works on i unit,
- -
- —daily cost of the penalty for exceeding the directive deadlines for finishing works on units,
- -
- —the contractor’s daily bonus for not exceeding the directive deadlines for completion of works in the units,
- -
- —a set of all possible permutations in a given project,
- -
- n—number of all units (objects),
- -
- m—number of works (activities) to be completed on each of the units.
The presented problem of discrete optimization is a variant of the flow shop permutation problem. This problem is often considered in the theory of job scheduling. Due to the NP-difficulty of the presented problem and the existence of two different decision variables, it was solved using a dedicated algorithm using the metaheuristic simulated annealing algorithm.
2.4. The Optimization Method of the Multi-Unit Project Discussed in the Article
The optimization problem presented above is the NP-hard discrete optimization problem. A significant difficulty in solving it is introduced by the fact that there are two different decision variables influencing the value of the objective function, which is the cost of the project implementation: the order (permutation) of unit execution and a set of methods (technologies) for carrying out activities. To solve this problem, it is proposed to use the approximate simulated annealing algorithm (SA) belonging to the group of metaheuristics. This algorithm was used in a proprietary, dedicated algorithm enabling the solution of the presented problem of discrete optimization with two different decision variables.
2.4.1. Simulated Annealing Algorithm
Simulated annealing (SA) algorithm has been proposed in the work of Kirkpatrick [65]. This algorithm uses analogous to the thermodynamic process of cooling the solid in order to introduce the trajectory of the search of the local extremum. States of solid matter are seen analogously as individual solutions to the problem, whereas the energy of the body as the value of the objective function. During the physical process of cooling the temperature is reduced slowly in order to maintain energy balance. The SA algorithm starts with the initial solution (usually chosen at random). Then, in each iteration, according to established rules or randomly, there is solution π’ selected from the base neighborhood π. It becomes the base solution in the next iteration, if the value of the objective function is better than the current base solution or if it otherwise may become the base solution with the probability of (Boltzmann function):
where ∆ = c(π) − c(π’), Ti—the temperature of the current iteration i, and c—the objective function. In each iteration there are m draws from the neighborhood of the current basic solution performed. The parameter called the temperature decreases in the same way as in the natural process of annealing. The most frequently adopted patterns of cooling are geometrical or logarithmic ones. Below is the general algorithm of the SA method (Algorithm 1) used to solve flow problems, which will be used to solve the problem under consideration.
p = exp(−∆/Ti),
| Algorithm 1: SA |
| Step 0. Determine the initial solution π ∈ Π. Substitute πSA = π0, k = 0, T = T0.
Step 1. Perform steps 1.1–1.3 x times. Step 1.1. Substitute k: = k + 1. Choose at random π ∈ N(V, πk−1). Step 1.2. If c(π) > c(πSA) then substitute πSA = π. Step 1.3. If c(π) > c(πk-1) then substitute πk = π. Otherwise, accept solution π with a probability of p = exp((c(π) − c(πk-1))/T, where πk = π’. If solution π was accepted, and πk = πk-1 if solution π was not accepted. Step 2. Change the temperature T according to the defined pattern of cooling. Step 3. If T > TN return to the step 1; otherwise, STOP. |
SA algorithms are used to solve many optimization problems, including flow shop problems which are considered in the context of discrete optimization problems.
2.4.2. The Algorithm for Solving the Optimization Problem in the Presented Model of a Multi-Unit Project
Due to the existence of two different decision variables for the solution of the optimization task in the presented model of a multi-unit project, it is proposed to solve the optimization problem with the help of the following algorithm created by the authors, using the SA metaheuristic:
- Let π ∈ Π be any random permutation (π* the best solution found so far, π* = π to start with), let R be a randomly determined set of methods for performing activities (R* the best solution found so far, R* = R to start with), and let MaxIter be the accepted maximum number of iterations of the algorithm.
- Step 1. Find the solution of the optimization problem using the SA metaheuristic (permutation δ) minimizing the cost of the project with the assumption of R as a set of methods for the implementation of activities.
- Step 2. Find the solution of the optimization problem using the SA metaheuristic (set of ρ methods of carrying out activities) minimizing the cost of the project with the assumption of the order of implementation of the units expressed by the permutation ρ.
- Step 3. If U(δ, ρ) ≤ U(π*, R*), to π* = δ, R* = ρ. Assume that R = ρ.
- Step 4. If Termination_Condition, then STOP;otherwise, go to Step 1.
The above algorithm is designed to search the entire space of possible solutions, solving the problem of minimizing the cost of the entire project for the permutation found. As a result, it provides the minimum value of the project cost from the entire search trajectory. The algorithm ends with the termination condition, which is the execution of its iteration MaxIter.
In step 1, the task of minimizing the cost of the project is solved, assuming a given set of methods for the implementation of activities. The following assumptions were made regarding the form and parameters of the SA algorithm described in step 1:
- the Nπ neighborhood contains permutations generated from π by the “insert” movement,
- the Boltzmann acceptance function was used,
- a geometric cooling scheme was adopted, i.e., Ti+1 = λTi and T0 = 60, λ = 0.99, and the number of considered solutions at a fixed temperature—7,
- the maximum number of iterations of the SA algorithm in step 2—500.
In step 2, the task of minimizing the cost of the project is solved with the assumption of the found order of execution of the units (permutation). The assumptions regarding the form and parameters of the SA algorithm described in step 2 are described below:
- sets of numbers of the methods of carrying out works generated from R by means of a movement consisting in changing a randomly selected method of carrying out activities by a value selected at random +1 or −1 are contained in the neighboring set NR,
- the Boltzmann acceptance function was used,
- a geometric cooling scheme was adopted, i.e., Ti+1 = λTi and T0 = 60, λ = 0.99, and the number of considered solutions at a fixed temperature—35,
- the maximum number of iterations of the SA algorithm in step 3—20,000.
The software implementation of the presented algorithm for the model under consideration was made in the Python programming language.
3. Results
3.1. Testing the Accuracy of the Results Obtained Using the SA Algorithm
The verification of the results obtained with the use of the simulated annealing algorithm is presented in this chapter. The results were compared with the results obtained with the use of other algorithms. Due to its popularity and ease of use, the [66] method of experimental analysis was adopted to verify the algorithm’s effectiveness.
The method of experimental analysis is based on a posteriori evaluation of the behavior of the studied algorithm (in this case the approximation error). The evaluation is based on the results of calculations on a limited but representative sample of specific examples. Such a sample is most often created by randomly generating subsets of examples of a given problem or using previously created “difficult” test examples used by other researchers.
The quality of the obtained results is compared with one of the values: the optimal value, the lower limit, the suboptimal value obtained with another approximate algorithm, or the value obtained randomly. The method of experimental analysis used in the article has the following form. In the beginning, four groups of examples of construction projects were randomly generated with the following sizes: n = 6 units, n = 10 units, n = 15 units, and n = 20 units. In each group, five examples were randomly generated with sizes: m = 3 works (activities), m = 5 works, and m = 7 works. Hence the number of all examples was 60.
For each example, the schedule with the lowest cost to complete the project was searched for. Each example was solved five times with a dedicated simulated annealing algorithm and comparison algorithms: random search (RS) [67] and climbing search (CR) [68]. For each comparative algorithm, the percentage relative difference (PRD) was calculated according to the following relationships:
where:
- —the value of the adopted objective function obtained by means of the SA + SA algorithm,
- —the value of the adopted objective function obtained by means of the RS algorithm,
- —the value of the adopted objective function obtained by means of the CR algorithm.
The average PRD of the applied algorithms are presented in Table 1.

Table 1.
The verification results for examples n = 6, 10, 15, and 20 units obtained with the use of the SA + SA algorithm.
The mean values of PRD for the tested simulated annealing algorithm show that this algorithm always obtains better results than those obtained with the RS and CR comparative algorithms. The average PRD error of the tested simulated annealing algorithm in relation to the RS algorithm for all sizes of optimization tasks is −12.90% and usually increased with the increase in the size of the task (even up to approx. −20%). The average PRD error of the tested simulated annealing algorithm in relation to the CR algorithm for all sizes of optimization tasks is −7.16% and usually showed a decrease in its values for sizes n = 15 and n = 20 units and sizes m = 5 and m = 7 works.
3.2. Case Study
The analyzed construction project involves the construction of n = 7 units—residential buildings (building shells in a raw state). Each of the buildings requires m = 5 works. The order of the works is fixed. One construction company, which has m = 5 different working groups specialized in ordered works, is commissioned by the client. For each activity in the units under construction, there are three modes (methods) of implementation, which are characterized by a specific cost of execution (expressed in EUR) and duration (expressed in working days). Data on the modes of performing activities in a construction project are included in Table 2.

Table 2.
The duration of the activities and their cost according to the mode for n = 7 units of a construction project.
In order to prepare a case study, data for a single residential building were used. Authors determined the duration of activities and their cost on the basis of labor intensity catalogs for construction and unit prices of works. Data for the remaining buildings were randomly generated using a uniform distribution ranging from −30% to +30%. The principle was applied that each reduction in the duration of activity increases its cost, which is related to the use of more expensive technology.
During the performance of works by working groups, the impact of gaining experience (learning) by employees is taken into account. This results in a significant reduction in the duration of works of one type during the course of the project. In addition, the impact of forgetting how to perform a given work is taken into account depending on the size of the break between activities of one type. This results in a corresponding extension of the time needed to perform the next steps. It is assumed that these influences are determined by the modified hyperbolic learning model developed by [64]. It was assumed that the maximum efficiency is k = 1.3. The forgetting coefficient is α = 0.3. The value of the r coefficient was assumed depending on the type of works at the level of 30, 90, 210, 45, and 30 for individual works, depending on the complexity of their execution. The value of the p coefficient was assumed at the level of r, 2 r, or 4 r, depending on the experience of the working group.
A construction company carrying out a given project has to respect the deadlines for the completion of individual units, which are imposed by the client. For subsequent units, these deadlines are as follows: 30, 50, 90, 130, 170, 200, and 240. The penalty for exceeding the imposed deadline for building completion is 1/100 of the average cost of the unit, i.e., 1.72, 1.24, 1.93, 2.08, 1.99, 1.84, or 2.32 thousand EUR for one day of delay for corresponding units. The reward (bonus) for the earlier performance of all activities in a building is 1/300 of the average cost of the facility, i.e., 0.57, 0.41, 0.64, 0.69, 0.66, 0.61, or 0.77 thousand EUR per day for corresponding units. The enterprise incurs indirect costs amounting to EUR 10,000 for each day of the project. The manager’s task is to find a project implementation schedule that will minimize the adopted objective function, i.e., the total cost, assumed in accordance with the relationship (20).
The number of possible schedules in a given project is equal to 7!∙35∙7 ≈ 2.5∙1020. An initial schedule is adopted for the project, assuming the order of units according to their numbering (permutation of units π0 = (1,2,3,4,5,6,7)) and the choice of mode no. 2 for carrying out all activities. According to the initial schedule, the cost of the project is EUR 4,970.66 thousand, and its duration is 306.2 working days. The schedule is presented in Figure 3.
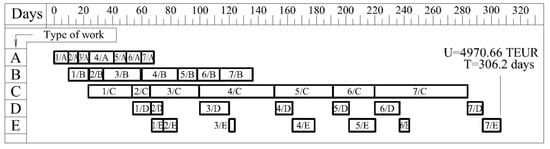
Figure 3.
Permutation π0—construction project schedule considering LAF.
LAF has a clear effect on the duration of the schedule. It affects not only the duration but also the cost of the project. A schedule for the baseline solution without LAF was presented in Figure 4. The cost of the project is EUR 5196.30 thousand, and its duration is 320.0 working days (both values are higher than the ones presented in Figure 3).
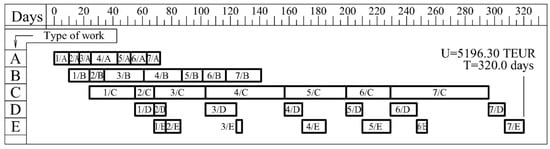
Figure 4.
Permutation π0—construction project schedule not considering LAF.
Then, the two-stage algorithm was used in order to find the optimal solution. The algorithm was using the simulated annealing algorithm, as presented in Section 2.3. The resulting schedule (with specific decision variables) is presented below: πSA = (2,1,6,3,5,4,7) and R = (R1, R2, R3, R4, R5, R6, R7) where:
- R1 = (2,2,2,2,1),
- R2 = (2,2,2,3,2),
- R3 = (2,1,2,2,2),
- R4 = (2,2,2,1,1),
- R5 = (3,3,2,2,2),
- R6 = (1,1,2,2,1),
- R7 = (1,1,3,2,1).
The calculated total cost for this project is EUR 4622.84 thousand, and the duration is 295 working days. The cost of the project implementation is lower by 7.0% compared to the cost of the project implementation according to the initial schedule. The duration of the suboptimal schedule is 3.7% shorter than that of the baseline schedule. The obtained suboptimal schedule is presented in Figure 5.
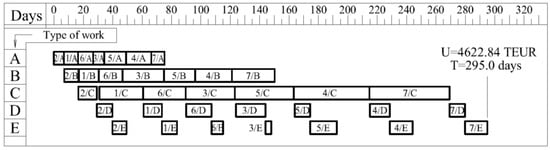
Figure 5.
Permutation πSA—optimized construction project schedule.
4. Conclusions
The article presents an optimization model of a multi-unit construction project. The described scheduling problem was solved by two proprietary, dedicated algorithms using a metaheuristic simulated annealing algorithm. In addition, the authors conducted a comparative experimental analysis of the proposed method for solving the optimization problem. The approach was highly effective, and a satisfactory suboptimal solution was obtained. Additionally, the operation of the proposed model was presented on the computational example of a multi-unit undertaking taking into account the effect of learning and forgetting. The results obtained in the case study confirmed the effectiveness of the applied method of solving optimization tasks.
As shown by the results obtained by the authors, the effect of learning and forgetting can have a significant impact on the financial results of construction projects. This phenomenon may allow for better modeling of construction processes and, thus, the better preparation of projects. Practical problems in modern construction show that many schedules and budgets are underestimated or overestimated. This may be due to the omission of aspects related to the so-called human factors (such as the process of learning and forgetting). It is only logical that the LAF phenomenon has a particularly strong impact on repetitive projects, such as the multi-unit projects presented in the article.
In the future, the authors plan to compare the classic schedule and schedule taking into account the LAF with the implementation of the multi-unit facility actually being constructed. Such studies could even more clearly confirm the dependencies discovered during the research, as well as the possibilities of a new way of modeling such a problem.
Moreover, due to the computational successes, the authors plan to find additional applications for the algorithm developed in the research.
Author Contributions
Conceptualization, B.S., J.R. and M.P.; methodology, B.S., J.R. and M.P.; software, B.S.; validation, J.R. and M.P.; formal analysis, M.P.; investigation, B.S., J.R. and M.P.; resources, B.S., J.R. and M.P.; data curation, M.P.; writing—original draft preparation, B.S., J.R. and M.P.; writing—review and editing, J.R. and M.P.; visualization, M.P.; supervision, B.S., J.R. and M.P.; and project administration, B.S., J.R. and M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arditi, D.; Tokdemir, O.B.; Suh, K. Challenges in Line-of-Balance Scheduling. J. Constr. Eng. Manag. 2002, 128, 545–556. [Google Scholar] [CrossRef]
- Mattila, K.G.; Park, A. Comparison of Linear Scheduling Model and Repetitive Scheduling Method. J. Constr. Eng. Manag. 2003, 129, 56–64. [Google Scholar] [CrossRef]
- Sobieraj, J.; Metelski, D. Project Risk in the Context of Construction Schedules—Combined Monte Carlo Simulation and Time at Risk (TaR) Approach: Insights from the Fort Bema Housing Estate Complex. Appl. Sci. 2022, 12, 1044. [Google Scholar] [CrossRef]
- Krzemiński, M. Conctruction scheduling and stability of the resulting schedules. Arch. Civ. Eng. 2016, 62, 89–100. [Google Scholar] [CrossRef][Green Version]
- Nicał, A.; Anysz, H. The quality management in precast concrete production and delivery processes supported by association analysis. Int. J. Environ. Sci. Technol. 2020, 17, 577–590. [Google Scholar] [CrossRef]
- Arditi, D.; Tokdemir, O.B.; Suh, K. Effect of learning on line-of-balance scheduling. Int. J. Proj. Manag. 2001, 19, 265–277. [Google Scholar] [CrossRef]
- Lam, K.C.; Lee, D.; Hu, T. Understanding the effect of the learning-forgetting phenomenon to duration of projects construction. Int. J. Proj. Manag. 2001, 19, 411–420. [Google Scholar] [CrossRef]
- Zhang, L.; Zou, X.; Kan, Z. Improved Strategy for Resource Allocation in Repetitive Projects Considering the Learning Effect. J. Constr. Eng. Manag. 2014, 140, 04014053. [Google Scholar] [CrossRef]
- Biruk, S.; Rzepecki, L. Scheduling Repetitive Construction Processes Using the Learning-Forgetting Theory. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 112039. [Google Scholar] [CrossRef]
- Sroka, B.; Rosłon, J.; Podolski, M.; Bożejko, W.; Burduk, A.; Wodecki, M. Profit optimization for multi-mode repetitive construction project with cash flows using metaheuristics. Arch. Civ. Mech. Eng. 2021, 21, 1–17. [Google Scholar] [CrossRef]
- Rosłon, J.; Książek-Nowak, M.; Nowak, P. Schedules Optimization with the Use of Value Engineering and NPV Maximization. Sustainability 2020, 12, 7454. [Google Scholar] [CrossRef]
- Herroelen, W. Project Scheduling-Theory and Practice. Prod. Oper. Manag. 2009, 14, 413–432. [Google Scholar] [CrossRef]
- Węglarz, J. Project Scheduling—Recent Models, Algorithms and Applications; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Kolisch, R.; Padman, R. An integrated survey of deterministic project scheduling. Omega 2001, 29, 249–272. [Google Scholar] [CrossRef]
- Herroelen, W.; De Reyck, B.; Demeulemeester, E. Resource-constrained project scheduling: A survey of recent developments. Comput. Oper. Res. 1998, 25, 279–302. [Google Scholar] [CrossRef]
- Brucker, P.; Drexl, A.; Möhring, R.; Neumann, K.; Pesch, E. Resource-constrained project scheduling: Notation, classification, models, and methods. Eur. J. Oper. Res. 1999, 112, 3–41. [Google Scholar] [CrossRef]
- Kulejewski, J.; Ibadov, N.; Krzemiński, M. Scheduling Construction Projects Under Fuzzy Modelling of Resource Constraints. MATEC Web Conf. 2018, 196, 04045. [Google Scholar] [CrossRef][Green Version]
- Habibi, F.; Barzinpour, F.; Sadjadi, S.J. Resource-constrained project scheduling problem: Review of past and recent developments. J. Proj. Manag. 2018, 55–88. [Google Scholar] [CrossRef]
- Senouci, A.B.; Eldin, N.N. Use of Genetic Algorithms in Resource Scheduling of Construction Projects. J. Constr. Eng. Manag. 2004, 130, 869–877. [Google Scholar] [CrossRef]
- Tiwari, V.; Patterson, J.H.; Mabert, V.A. Scheduling projects with heterogeneous resources to meet time and quality objectives. Eur. J. Oper. Res. 2009, 193, 780–790. [Google Scholar] [CrossRef]
- Mika, M.; Waligóra, G.; Węglarz, J. Simulated annealing and tabu search for multi-mode resource-constrained project scheduling with positive discounted cash flows and different payment models. Eur. J. Oper. Res. 2005, 164, 639–668. [Google Scholar] [CrossRef]
- Geiger, M.J. A multi-threaded local search algorithm and computer implementation for the multi-mode, resource-constrained multi-project scheduling problem. Eur. J. Oper. Res. 2017, 256, 729–741. [Google Scholar] [CrossRef]
- Rosłon, J.H.; Kulejewski, J.E. A hybrid approach for solving multi-mode resource-constrained project scheduling problem in construction. Open Eng. 2019, 9, 7–13. [Google Scholar] [CrossRef]
- Deblaere, F.; Demeulemeester, E.; Herroelen, W. Reactive scheduling in the multi-mode RCPSP. Comput. Oper. Res. 2011, 38, 63–74. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Eshtehardian, E.; Jooybanpour, S.; Javanmardi, A. Multi-mode resource-constrained discrete time-cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Autom. Constr. 2012, 30, 216–227. [Google Scholar] [CrossRef]
- Chen, A.H.-L.; Liang, Y.-C.; Padilla, J.D. An Entropy-Based Upper Bound Methodology for Robust Predictive Multi-Mode RCPSP Schedules. Entropy 2014, 16, 5032–5067. [Google Scholar] [CrossRef]
- Rosłon, J. The multi-mode, resource-constrained project scheduling problem in construction: State of art review and research challenges. Tech. Trans. 2017, 5, 67–74. [Google Scholar] [CrossRef]
- Zhou, J.; Love, P.; Wang, X.; Teo, K.L.; Irani, Z. A review of methods and algorithms for optimizing construction scheduling. J. Oper. Res. Soc. 2013, 64, 1091–1105. [Google Scholar] [CrossRef]
- Van Peteghem, V.; Vanhoucke, M. A genetic algorithm for the preemptive and non-preemptive multi-mode resource-constrained project scheduling problem. Eur. J. Oper. Res. 2010, 201, 409–418. [Google Scholar] [CrossRef]
- Liao, T.W.; Egbelu, P.; Sarker, B.; Leu, S. Metaheuristics for project and construction management—A state-of-the-art review. Autom. Constr. 2011, 20, 491–505. [Google Scholar] [CrossRef]
- Mika, M.; Waligóra, G.; Węglarz, J. Tabu search for multi-mode resource-constrained project scheduling with schedule-dependent setup times. Eur. J. Oper. Res. 2008, 187, 1238–1250. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H. Ant colony optimization-based multi-mode scheduling under renewable and nonrenewable resource constraints. Autom. Constr. 2013, 35, 431–438. [Google Scholar] [CrossRef]
- Jarboui, B.; Damak, N.; Siarry, P.; Rebai, A. A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems. Appl. Math. Comput. 2008, 195, 299–308. [Google Scholar] [CrossRef]
- Sebt, M.H.; Afshar, M.R.; Alipouri, Y. Hybridization of genetic algorithm and fully informed particle swarm for solving the multi-mode resource-constrained project scheduling problem. Eng. Optim. 2016, 49, 513–530. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Zhang, Y. Hybrid Particle Swarm and Differential Evolution Algorithm for Solving Multimode Resource-Constrained Project Scheduling Problem. J. Control Sci. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Rosłon, J.; Książek-Nowak, M.; Nowak, P.; Zawistowski, J. Cash-Flow Schedules Optimization within Life Cycle Costing (LCC). Sustainability 2020, 12, 8201. [Google Scholar] [CrossRef]
- Galloway, P.D. Survey of the Construction Industry Relative to the Use of CPM Scheduling for Construction Projects. J. Constr. Eng. Manag. 2006, 132, 697–711. [Google Scholar] [CrossRef]
- Rogalska, M.; Hejducki, Z. The application of time coupling methods in the engineering. Tech. Trans. 2017, 9, 67–74. [Google Scholar] [CrossRef]
- Li-hui, Z.; Xi, Z. Repetitive Project Scheduling Theory and Methods, 1st ed.; Elsevier: New York, NY, USA, 2015. [Google Scholar]
- Gupta, J.N.; Stafford, E.F. Flowshop scheduling research after five decades. Eur. J. Oper. Res. 2006, 169, 699–711. [Google Scholar] [CrossRef]
- Bożejko, W.; Hejducki, Z.; Wodecki, M. Applying metaheuristic strategies in construction projects management. J. Civ. Eng. Manag. 2012, 18, 621–630. [Google Scholar] [CrossRef]
- Bozejko, W.; Hejducki, Z.; Wodecki, M. Flowshop scheduling of construction processes with uncertain parameters. Arch. Civ. Mech. Eng. 2019, 19, 194–204. [Google Scholar] [CrossRef]
- Podolski, M. Management of resources in multiunit construction projects with the use of a tabu search algorithm. J. Civ. Eng. Manag. 2016, 23, 263–272. [Google Scholar] [CrossRef]
- Podolski, M.; Sroka, B. Cost Optimization of Multiunit Construction Projects Using Linear Programming and Metaheuristic-Based Simulated Annealing Algorithm. J. Civ. Eng. Manag. 2019, 25, 848–857. [Google Scholar] [CrossRef]
- Tomczak, M. Modeling of the harmonization method for executing a multi-unit construction project. Open Eng. 2019, 9, 282–291. [Google Scholar] [CrossRef]
- Glock, C.H.; Grosse, E.H.; Jaber, M.Y.; Smunt, T.L. Applications of learning curves in production and operations management: A systematic literature review. Comput. Ind. Eng. 2018, 131, 422–441. [Google Scholar] [CrossRef]
- Wright, T.P. Factors affecting the cost of airplanes. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Badiru, A.B. Multivariate analysis of the effect of learning and forgetting on product quality. Int. J. Prod. Res. 1995, 33, 777–794. [Google Scholar] [CrossRef]
- De Jong, J.R. The effects of increasing skill on cycle time and its consequences for time standards. Ergonomics 1957, 1, 51–60. [Google Scholar] [CrossRef]
- Thomopoulos, N.T.; Lehman, M. The Mixed Model Learning Curve. AIIE Trans. 1969, 1, 127–132. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Guiffrida, A.L. Learning curves for imperfect production processes with reworks and process restoration interruptions. Eur. J. Oper. Res. 2008, 189, 93–104. [Google Scholar] [CrossRef]
- Grosse, E.H.; Glock, C.; Müller, S. Production economics and the learning curve: A meta-analysis. Int. J. Prod. Econ. 2015, 170, 401–412. [Google Scholar] [CrossRef]
- Carlson, J.G.; Rowe, A.J. How much does forgetting cost. Ind. Eng. 1976, 8, 40–47. [Google Scholar]
- Elmaghraby, S.E. Economic manufacturing quantities under conditions of learning and forgetting (EMQ/LaF). Prod. Plan. Control 1990, 1, 196–208. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. Production breaks and the learning curve: The forgetting phenomenon. Appl. Math. Model. 1996, 20, 162–169. [Google Scholar] [CrossRef]
- Sikström, S.; Jaber, M.Y. The power integration diffusion model for production breaks. J. Exp. Psychol. Appl. 2002, 8, 118–126. [Google Scholar] [CrossRef]
- Sikström, S.; Jaber, M.Y. The Depletion-Power-Integration-Latency (DPIL) model of spaced and massed repetition. Comput. Ind. Eng. 2012, 63, 323–337. [Google Scholar] [CrossRef]
- Pellegrino, R.; Costantino, N.; Pietroforte, R.; Sancilio, S. Construction of multi-storey concrete structures in Italy: Patterns of productivity and learning curves. Constr. Manag. Econ. 2012, 30, 103–115. [Google Scholar] [CrossRef]
- Jarkas, A.; Horner, M. Revisiting the applicability of learning curve theory to formwork labour productivity. Constr. Manag. Econ. 2011, 29, 483–493. [Google Scholar] [CrossRef]
- Tai, H.-W.; Chen, J.-H.; Cheng, J.-Y.; Hsu, S.-C.; Wei, H.-H. Learn Curve for Precast Component Productivity in Construction. Int. J. Civ. Eng. 2021, 19, 1179–1194. [Google Scholar] [CrossRef]
- Panas, A.; Pantouvakis, J.P. Simulation-Based and Statistical Analysis of the Learning Effect in Floating Caisson Construction Operations. J. Constr. Eng. Manag. 2014, 140, 04013033. [Google Scholar] [CrossRef]
- Mályusz, L.; Pém, A. Prediction of the learning curve in roof insulation. Autom. Constr. 2013, 36, 191–195. [Google Scholar] [CrossRef]
- Hegazy, T. Optimization of construction time-cost trade-off analysis using genetic algorithms. Can. J. Civ. Eng. 1999, 26, 685–697. [Google Scholar] [CrossRef]
- Nembhard, D.A.; Uzumeri, M.V. Experiential learning and forgetting for manual and cognitive tasks. Int. J. Ind. Ergon. 2000, 25, 315–326. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Błażewicz, J. Złożoność Obliczeniowa Problemów Kombinatorycznych; Wydawnictwa Naukowo-Techniczne: Kraków, Poland, 1988. [Google Scholar]
- Karnopp, D.C. Random search techniques for optimization problems. Automatica 1963, 1, 111–121. [Google Scholar] [CrossRef]
- Taillard, E. Some efficient heuristic methods for the flow shop sequencing problem. Eur. J. Oper. Res. 1990, 47, 65–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).