Abstract
Smoothness is a commonly used measure of motion control. Physiological motion is characterized by high smoothness in the upper limb workspace. Moreover, there is evidence that smoothness-based models describe effectively skilled motion planning. Typical smoothness measures are based on wrist kinematics. Despite smoothness being often used as a measure of motor control and to evaluate clinical pathologies, so far, a smoothness map is not available for the whole workspace of the upper limb. In this work, we provide a map of the upper limb workspace comparing four smoothness metrics: the normalized jerk, the speed metric, the spectral arc length, and the number of speed peaks. Fifteen subjects were enrolled, performing several reaching movements in the upper limb workspace in multiple directions in five planes (frontal, left, right, horizontal and up). Smoothness of the wrist of each movement was computed and a 3D workspace map was reconstructed. The four smoothness metrics were in general accordance. Lower smoothness was found in the less dexterous sectors (up and left sectors), with respect to the frontal, horizontal, and right sectors. The number of speed peaks, frequently used for evaluating motion in neurological diseases, was instead not suitable for assessing movements of healthy subjects. Lastly, strong correlation was found especially between the normalized jerk and speed metric. These results can be used as a benchmark for motor control studies in various fields as well as clinical studies.
1. Introduction
Smoothness usually describes the quality of a movement and is recognized as a feature of coordinated and skilled motor behavior [1], characterizing goal-directed movements [2]. Movement smoothness is commonly used as a measure of motor performance and motion control with wide application in healthy subjects [3] and neurological patients [4,5]. Physiological motion is characterized by high smoothness in the upper limb workspace. It was proposed that smoothness is a motion planning criterium for determining limb trajectories [6,7]. A reduced movement smoothness reflects deficits in movement planning and execution. Therefore, smoothness has become an important metric for the evaluation of patients with deficits in motor control and for the assessment of their recovery [8], such as patients suffering from stroke [9], cerebral palsy [10], Parkinson’s disease [11], or multiple sclerosis [12].
The most frequently used methods for evaluating movement performance in clinical scenarios are clinical scales and functional tests, e.g., Jebsen-Taylor Hand Function (JTHF) [13], Arm Research Assessment Test (ARAT) [14], and Nine-Hole Peg test (NHPT) [15]. Although these measures are easy to administer, they are partially dependent on the observers that score the tests [16]. Therefore, objective smoothness metrics based on kinematics have been developed. Smoothness can be measured with indexes referred to wrist motion. These indexes are based on the velocity profile of the wrist and its derivatives and include: the number of velocity peaks [17,18], the speed metric [19,20], defined as the ratio between the mean and the maximum velocity; the jerk, which is the third order derivative of the position profile, and related indexes such as the normalized jerk [11], the log dimensionless jerk [21], or the normalized squared jerk [22]; the arc length of the velocity or of the power spectrum [21,23].
Jerk is also frequently used as a measure for motion dexterity [24]. Kinematic assessment can detect changes in movement performance that cannot be captured by clinical scales and tests and provides a more objective measure [25]. Kinematics measures have been compared to clinical scales usually adopted for the evaluation of patient performance, proving their validity as indicators of smoothness and motion dexterity [25,26]. Therefore, smoothness analyses may help clinicians in the evaluation of dexterity and motor control.
However, so far, smoothness has not been investigated in a comprehensive set of directions in the workspace of the upper limb, and comparative maps of smoothness based on multiple indexes have not been created before. In this paper, we aim at (i) reconstructing a map of smoothness in the upper limb workspace of healthy subjects that can be used as reference data in clinical applications and (ii) comparing several metrics based on wrist motion. First, fifteen subjects performed a variety of point-to-point reaching movements in multiple directions in five planes of motion. Then, the normalized jerk (NJ), the speed metric (SM), the spectral arc length (SAL), and the number of speed peaks (NP) were computed in order to evaluate the smoothness in each movement direction. A smoothness map was reconstructed in both the 3D space and with respect to shoulder articular angles and the difference between sectors were evaluated. Finally, the correlations between pairs of metrics were computed.
2. Materials and Methods
A scheme of the work is portrayed in Figure 1.
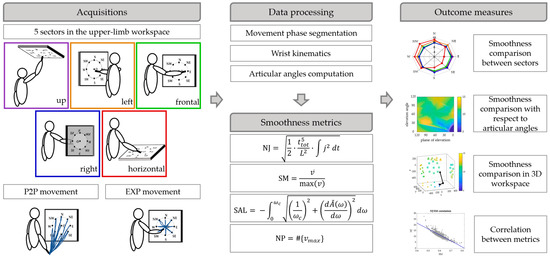
Figure 1.
Scheme of the work. Upper limb movements (P2P and EXP) were performed in 5 sectors of the workspace by 15 subjects. The data were segmented in phases and the wrist kinematics and the articular angels were computed. Then, four smoothness metrics based on wrist motion were computed and smoothness was compared between sectors, mapped with respect to articular angles and in the 3D workspace for each of the smoothness metric. Finally, the correlations between pairs of metrics were computed.
2.1. Participants
Fifteen healthy subjects were recruited to participate in this study (68 ± 11 kg; 1.73 ± 0.08 m; 9 males and 6 females). Exclusion criteria were the presence of pain, and neurological or musculoskeletal disorders affecting motion capabilities. All the recruited subjects were right-handed. Ethical approval was granted by the CNR Ethical Committee (Rome, Italy) and the experimental trial was conducted in compliance with the Declaration of Helsinki [27]. The participants provided written informed consent to participate in this study and for the publication of any data included in this article.
2.2. Laboratory Acquisition Set Up
Kinematic data recordings were made with the Vero Vicon system, consisting of 10 infrared cameras. During the acquisitions, 5 retroreflective markers were placed on specific anatomical landmarks of each subject in order to reconstruct the right upper limb. Markers were placed on D5 and C7 vertebras, acromion (shoulder; S), right elbow epicondyle (elbow; E), and on the styloid process of the ulna (wrist; W). Subjects held a 20-cm-long pointer, which was identified with two markers. Marker positioning is shown in Figure 2.

Figure 2.
Marker positioning and articular angles. Markers were placed on D5 and C7 vertebras, acromion (shoulder—S), right elbow epicondyle (elbow—E), and on the styloid process of the ulna (wrist—W). Shoulder elevation angle is shown in the first panel, shoulder plane of elevation in the second one and the elbow flexion angle in the last panel.
The subject stood in the middle of the area tracked with the motion capture system and executed a set of point-to-point movements (P2P) and multi-directional exploration tasks (EXP). The P2P movement consisted of reaching 9 targets (markers) placed on a target board at 8 cardinal points (NE, E, SE, S, SW, W, NW, N) and in the center of a circle (labelled as O), starting from a reference position R; the EXP task consisted of moving the pointer from the central point O to the cardinal directions, as in previous similar protocols [28,29]. The subject was asked to perform natural movements at a relatively fast speed [29] and to wait in isometric configuration for one second after reaching each target before moving to the following one. The target board was positioned with 5 orientations, in order to cover a comprehensive volume of the workspace of the upper limb. The board was positioned frontally, with vertical orientation (Frontal), laterally on the left (Left) and on the right (Right), upwards (Up) and frontally in horizontal position (Horizontal). The movements were performed only with the right upper limb. Movements were repeated ten times for every direction.
2.3. Data Analysis
2.3.1. Movement Segmentation
Markers were labelled in the Vicon Nexus software and their 3D position in time was imported into Matlab 2021b (Natick, MA, USA) tables. Marker trajectories were sampled at 100 Hz and were filtered with a 3rd order Butterworth low pass filter, cut-off frequency = 5 Hz. The time series of the velocity of the wrist marker was used to identify movement phases: the onset and the offset of the movements were computed when a predefined threshold was exceeded (5% of the maximum absolute velocity of the wrist). Only the forward phases, identified as the movements from the initial position to each target in the P2P movements and from the center to the cardinal points for the EXP tasks, were considered for the analysis.
2.3.2. Articular Kinematics
The kinematics of the upper limb was computed in intrinsic articular coordinates. Three articular angles were computed as the arccosine of the scalar product between two vectors, defined as in Scano et al. [30]. The arm vector is defined as the vector having module equal to the length of the arm, direction connecting the shoulder marker to the elbow marker, and orientation from the shoulder to the elbow, while the forearm vector is defined as the vector having a module equal to the length of the forearm, direction connecting the elbow marker to the wrist marker, and orientation from the elbow to the wrist. The arm unit vector is the arm vector divided by its norm; the forearm unit vector is the forearm vector divided by its norm. The shoulder elevation is the angle between the arm unit vector (projected in the sagittal plane for frontal, up and horizontal sectors and in the coronal plane for left and right sectors) and the vertical axis pointing downwards. The shoulder plane of elevation is the angle between the arm unit vector (projected in the horizontal plane) and the x-axis pointing towards the right of the subject. The elbow flexion is the angle between the arm unit vector and the forearm unit vector. Articular angles are shown in Figure 2.
2.3.3. Smoothness Metrics
Four smoothness metrics based on wrist kinematics were computed. The normalized jerk (NJ) [11] was computed as follows:
where is the task execution time, is the third derivative of the wrist 3D trajectory, and is the length of the wrist trajectory during the execution of the task. Low NJ indicates high smoothness.
The speed metric (SM) [20] is defined as the average velocity divided by the maximum velocity:
where is the velocity profile of the wrist and is the average velocity. SM increases with the smoothness of the movement.
The spectral arc length (SAL) is computed from the arc length of the power spectrum of the Fourier transform of the velocity [21] or of the acceleration [23] profile, as follows:
where is the frequency band, the Fourier magnitude spectrum of the acceleration signal , and is the normalized magnitude spectrum. High SAL corresponds to high smoothness.
Last, the number of speed peaks (NP) [18] metric is defined as the number of local maxima of the speed profile :
NP increases with the smoothness decrease and is near 1 in smooth reaching movements.
The smoothness metrics were computed for each repetition in each movement phase.
2.4. Outcome Measures and Statistical Analysis
First, the smoothness metrics were compared between directions in the same sector and between sectors, in order to evaluate movement in the entire workspace and the average values across subjects were reported in spider plots.
Then, the smoothness metrics were analyzed with respect to the shoulder plane of elevation and elevation angle (that define most of the limb orientation) in a compact colormap representation so that the smoothness of the movement was reported also in function of the intrinsic articular angles. Furthermore, a smoothness 3D map was reconstructed in which the smoothness metric was reported in the position of the wrist at the end of the movement with respect to the initial shoulder position in order to represent smoothness in the 3D workspace with respect to the subject.
Statistical analyses were performed between sectors for each smoothness metric to discriminate smoothness differences in the workspace. The distributions were tested for normality through the Kolmogorov–Smirnov test and the ANOVA test was performed, setting the alpha level of significance to 0.05. Then, the Tukey–Kramer post-hoc test was used to identify the significant differences between sectors.
Finally, the correlations between all the smoothness metric pairs were performed and the regression line was reported in scatter plots. All the analyses were performed for P2P and EXP movement separately.
3. Results
Smoothness Maps
The radar plot showing the smoothness metrics (NJ, SM, SAL, and NP) averaged across repetitions and subjects in each direction for all the sectors is reported in Figure 3 for P2P movements.
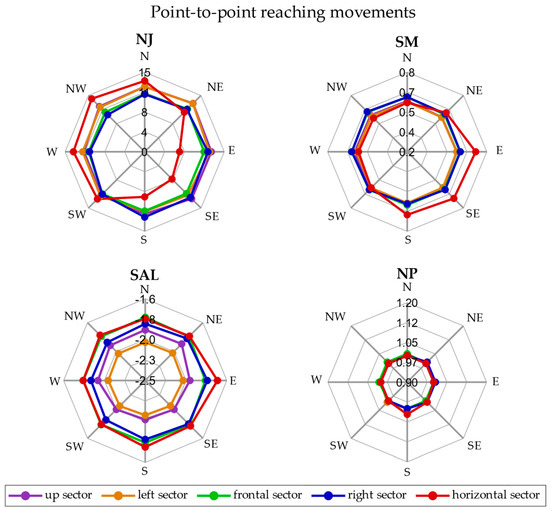
Figure 3.
Radar plot for P2P movements. The smoothness metrics are represented in separate plots. In each radar plot, the five sectors—up (purple), left (orange), frontal (green), right (blue) and horizontal (in red)—are reported and each point is the average of the metric across repetitions and subjects.
In the P2P movement, the NJ was between 10 and 12.5 in all the directions and sectors, except in the horizontal sector, in which the SW, W, NW, and N directions presented the highest values (12.6, 13.4, 14.1 and 13.6), while the S, SE, and E directions showed the lowest values (6.6, 7.3, and 8.5). The SM ranged between 0.55 and 0.63 in all the directions and sectors, except in the horizontal sector in which the SM was 0.72 in the E direction. The SAL, instead, varied between sectors and the highest value was −1.70 in the E direction of the horizontal sector and the lowest one was −2.12 in the SE and S directions of the left sector. Finally, the NP was on average about 1 for all the directions and sectors.
The radar plot representing the smoothness metrics (NJ, SM, SAL, and NP) averaged across repetitions and subjects in each direction for all the sectors is reported in Figure 4 for the EXP movement.
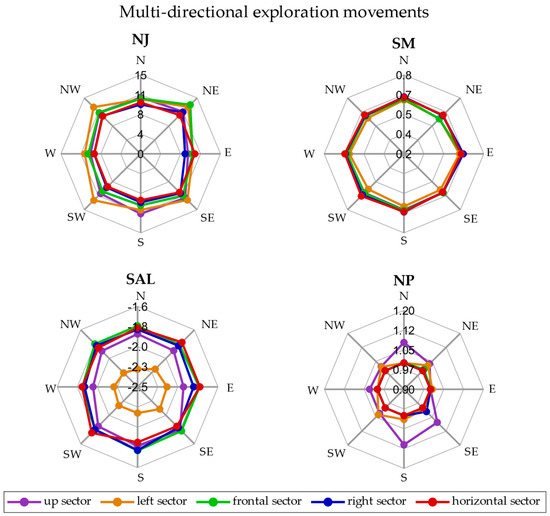
Figure 4.
Radar plot for EXP movements. The smoothness metrics are represented in separate plots. In each radar plot, the five sectors—up (purple), left (orange), frontal (green), right (blue) and horizontal (in red)—are reported and each point is the average of the metric across repetitions and subjects.
In the EXP movements, the NJ was between 8 and 13, while the SM ranged between 0.57 and 0.65 in all the directions and sectors. The SAL was between −1.20 and −1.77, except for the left sector in which the SAL was between −2.30 and −2.15. Finally, the NP was on average about 1 in all the sectors and directions, except for the up sector in which the NP was higher than 1 in some directions.
The color maps in Figure 5 represent the metrics with respect to the articular angles of the shoulder, plane of elevation, and elevation angle.
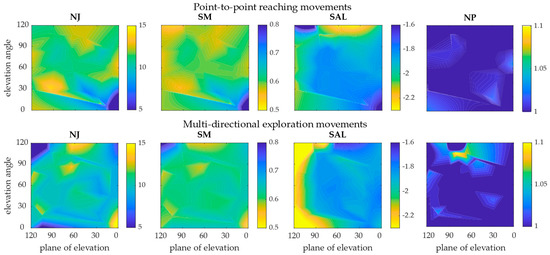
Figure 5.
Color maps representing the level of smoothness with respect to articular angles. Results of the P2P movements (first row) and of the EXP movements (second row) are reported with respect to shoulder plane of elevation and shoulder elevation angle. The four metrics are represented in the columns. The blue areas represent the regions of the workspace in which the performed movement was smoother (lower NJ and NP, and higher SM and SAL); the yellow areas are the regions in which the movements were less smooth.
In P2P movements, the color maps of NJ, SM, and SAL indicated that smoother movements were performed where both the plane of elevation and the elevation angle were low. If the angles were above 90°, the smoothness decreased. The NP indicated almost the same smoothness for all the angles. In EXP movements, the NJ and the SM found high smoothness when both angles were high and low smoothness when angles were very small. The SAL, instead, showed that the whole region in which the plane of elevation angle was high was a low smoothness area. The NP indicated almost the same smoothness for all the angles, except with plane of elevation between 60° and 90° and elevation angle between 90° and 120°.
The representation of the smoothness metrics in the 3D workspace of the upper limb is reported in P2P movements in Figure 6 and in EXP movements in Figure 7.
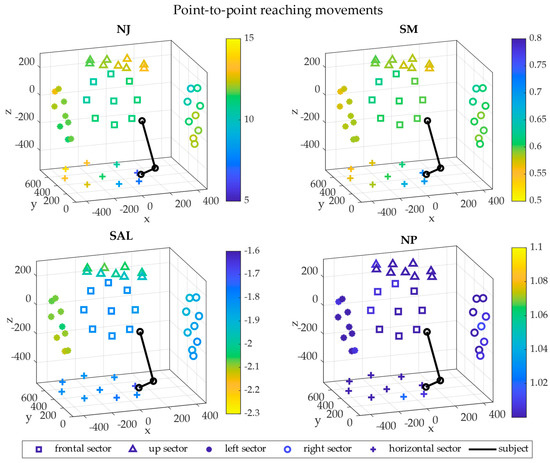
Figure 6.
3D maps in cartesian coordinates—P2P movements. The 3D maps representing the level of smoothness are reported in cartesian coordinates referred to the shoulder. The five sectors are visualized in the 3D space with different shapes: frontal (square), up (triangle), left (bullet), right (circle) and horizontal (cross). The upper limb starting position is represented in black for a typical subject for visual reference. Each point is the average across repetitions and subjects and their colors indicate the magnitude of the metrics. The x axis points to the right of the subject, the y axis points frontally and the z axis is vertical.
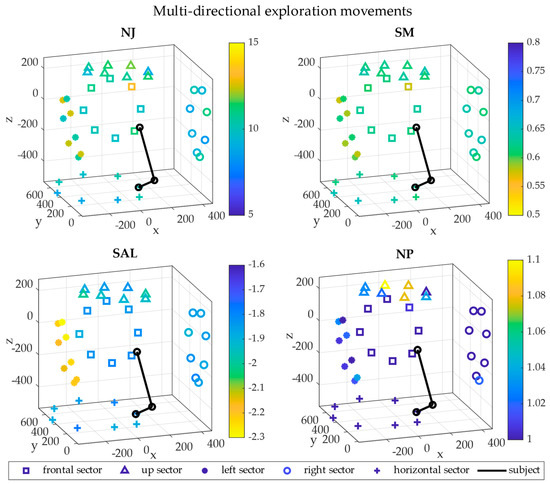
Figure 7.
3D maps in cartesian coordinates—EXP movements. The 3D maps representing the level of smoothness are reported in cartesian coordinates referred to the shoulder. The five sectors are visualized in 3D space with different shapes: frontal (square), up (triangle), left (bullet), right (circle) and horizontal (cross). The upper limb starting position is represented in black for a typical subject for visual reference. Each point is the average across repetitions and subjects and their colors indicate the magnitude of the metrics. The x axis points to the right of the subject, the y axis points frontally and the z axis is vertical.
In P2P movements, the lowest NJ in the horizontal sector was found in the directions close to the subjects, while the highest values were in the left and up sectors and in the north-west side of the horizontal sectors. The right and the frontal sectors presented similar values of NJ. The same smoothness distribution was found with the SM. The SAL was higher in the horizontal, the right and the frontal sectors, while it was lower in the left and up sectors. Finally, the NP was almost the same in all the sectors, with higher values in the horizontal one.
In EXP movements, the NJ was higher in the left sectors with respect to the others and the highest NJ was in the NE direction of the frontal sector. The same smoothness distribution was found with the SM. The SAL was higher in the left sector; the other sectors presented similar values. Finally, the NP was almost the same in all the sectors, with higher values in the up one.
Smoothness differences between sectors were investigated with statistical tests for each metric and the results are reported in Figure 8.
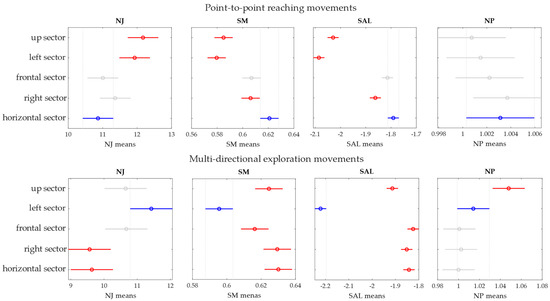
Figure 8.
The statistical tests between sectors are reported for each metric (in the column). Both P2P (first row) and EXP (second row) are reported.
In P2P movements, the NJ in the frontal and the horizontal sectors was significantly lower than the NJ in the up (p = 0.003, p = 10−4) and left sectors (p = 0.04, p = 0.01). The SM was significantly higher in the frontal, right and horizontal sectors with respect to the up (p = 10−4, p = 10−4, p = 10−11) and left (p = 10−6, p = 10−6, p = 10−14) sectors. Moreover, the SM in the right sector was lower than in the horizontal sector (p = 0.04). The SAL was significantly lower in the left (p = 10−14) and in the up (p = 10−14) sectors. Moreover, the SAL in the right sector was higher than in the right sector (p = 0.02) and in the horizontal sector (p = 10−4). The NP, instead, was not significantly different between sectors.
In EXP movements, the NJ in the left sector was significantly higher than for the right (p = 10−4) and horizontal (p = 0.001) sectors, while the SM was lower in the left sector (p < 10−3) with respect to the other sectors. The SAL in the left sector was significantly lower than the other sectors (p < 10−3) and was lower in the up sector (p < 10−3) with respect to the frontal, right and horizontal sectors. Finally, the NP was higher in the up sector (p < 0.02).
Correlation plots between each possible pairs of metrics are shown for each repetition and subject in Figure 9 for the P2P movements and in Figure 10 for the EXP movements.
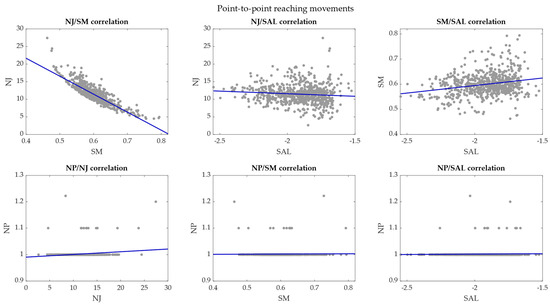
Figure 9.
Correlation plots between each possible pair of smoothness metrics—P2P movements. The correlations between pairs of smoothness metrics are reported in each plot and the regression lines are marked in blue.
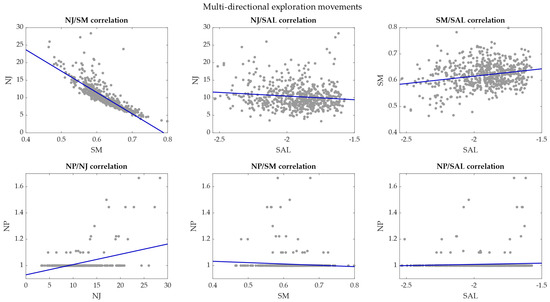
Figure 10.
Correlation plot between smoothness metrics—EXP movements. The correlations between pairs of smoothness metrics are reported in each plot and the regression lines are marked in blue.
In P2P movements, the NJ had a very high negative correlation with the SM with r coefficient = −0.86 (p < 0.001). The NJ had r correlation coefficient = −0.10 (p = 0.01) with the SAL and r = 0.16 (p = 10−5) with the NP. The correlation coefficient was 0.23 (p = 10−10) between SM and SAL, 0.01 (p = 0.71) between SM and NP, and 0.03 (p = 0.44) between SAL and NP.
In EXP movements, the NJ had a very high negative correlation with the SM with r coefficient = −0.83 (p < 0.001). The NJ showed r coefficient = −0.12 (p = 0.003) with SAL and r = 0.43 (p < 0.001) with NP. The SM had a low correlation coefficient with SAL (0.24, p = 10−9) and no correlation with NP (−0.08, p = 0.06). The correlation coefficient between SAL and NP was 0.06 (p = 0.14).
4. Discussion
Smoothness metrics represent the basis of many motor control tests performed in clinical environments to assess the patients’ motor performance [4,9,23]. Upper limb gestures are typically evaluated with jerk-based indexes and associated to pathologies that involve motor impairment. It was found that smoothness is correlated with motor impairment [31] and with standard clinical measures [32,33,34]. Smoothness is used as a parameter for motor performance evaluation during rehabilitation in post-stroke patients [20], parkinsonian patients [35] and spinal cord injury [36]. In the previous studies, motor recovery was associated with increased smoothness. Moreover, smoothness measures can be also used for detailed evaluation of motor performance that cannot easily be assessed with clinical scales. For example, the normalized jerk was sensible enough to identify a limited motor performance of the ipsilesional limb in post-stroke patients [37]. Smith et al. [38], instead, found that smoothness metrics could detect motor dysfunctions related to Huntington’s disease before clinical tests.
However, no studies so far have investigated the sensibility of these measurements in a wide mapping of the upper limb in healthy subjects as benchmark values for clinical applications.
In this paper, four smoothness metrics based on wrist motion were used to reconstruct a map of movement smoothness in the upper limb workspace in a cohort of fifteen healthy subjects. First, two upper limb movements, namely point-to-point reaching movements and multi-directional exploration tasks, were acquired from fifteen subjects in five sectors of the workspace: frontal, up, left, right and horizontal. Then, the smoothness was computed with the NJ, the SM, the SAL, and the NP. A smoothness map of each metric was reported for all the sectors, in the 3D space and with respect to the shoulder articular angles, that describe the direction of movements. Statistical tests were performed between sectors in order to investigate which sectors could be discriminated with the smoothness metrics. Finally, correlation coefficients between pairs of metrics were computed. Thus, the outcomes of this work include comprehensive smoothness maps, established in a wide variety of directions in the upper limb workspace, and a comparison between four commonly adopted metrics for movement smoothness.
Smoother movements correspond to lower NJ and NP and higher SM and SAL. The NJ presented similar results between directions in each sector, except for P2P movements in the horizontal sector. In general, the left and the up sectors showed higher NJ in P2P movements and these sectors also correspond to the regions in which the plane of elevation and/or the elevation angle were higher. In EXP movements, the NJ was lower in the horizontal and frontal plane, while it was high in the left sector. The SM was always in accordance with the results of the NJ, and it shows strong discriminative sensibility between sectors. The NJ and the SM showed a very high negative correlation. The SAL presented results similar to NJ and SM, interestingly detecting lower smoothness in the up and the left sectors, probably due to the fact that the limb has less dexterous control in such sectors, that are “at the borders” of the upper limb workspace. The SAL could discriminate smoothness differences between the sectors in a similar way with respect to the SM, presenting a positive correlation with SM. The NP, instead, was for almost all the conditions = 1 and could discriminate only some of the directions of the up sector in EXP movements as less smooth. The NP showed no correlation with the other metrics, and it had low positive correlation with NJ in EXP movements. This index was not suitable for analyzing the smoothness of reaching movements performed by healthy subjects, since in reaching movements the number of velocity peaks is usually one. In fact, healthy persons’ movements are mainly characterized by bell-shaped velocity profiles with only one velocity peak [6,39]. The NP could be more suitable for more complex movements and especially for evaluating patients’ performances [30,40]. It was shown that in post-stroke patients, the number of velocity peaks may increase despite the reduced articular range of motion (due to neurological diseases) with respect to healthy people motion [30]. In a previous study [21], the NP showed to have high variability and failed to capture the trend of the performance of healthy subjects. This effect is also related to the choice of the filtering parameters; the lower the cutoff frequency of the low pass-filter, the less is the capability of NP of discriminating different levels of smoothness. While this is true for all the smoothness metrics, this is particularly crucial for NP.
The areas of the workspace that presented the lowest smoothness were the up and left sectors, in which the movement execution was less comfortable and dexterous due to the high shoulder flexion angles, that require effort and coordinated control in poorly used areas of the upper limb workspace [41]. Furthermore, in P2P movements, the length of the trajectory and the execution time were higher, leading to generally less smooth movements, as already demonstrated in other studies [42,43].
The application of different smoothness metrics on healthy subjects in a large set of upper limb movements covering the workspace provided reference values for four commonly used metrics that may be useful for the understanding of the physiological mechanisms related to smoothness and may find use when assessing motor performance of impaired patients. Since smoothness is considered as the result of a cognitive process and the improvement of motor control in patients, the use of smoothness metrics can be important for the appropriate evaluation of the motor recovery in impaired subjects [8,20]. This work provides reference values that may be used as benchmark for the evaluation of smoothness related measurement in a clinical context, as well as deepens the relationships found between such movements.
This work has some limitations. First, only movements of healthy people were considered, reducing the range of application for some of the indexes, such as the NP. However, this study is the first step towards the application of these metrics in clinical assessments and its aim is to provide reference values for future studies on specific diseases. Moreover, the use of only healthy subjects allowed us to have coherence between the smoothness metrics and to interpret the results in consistent experimental conditions. Future work may involve patients suffering from neurological and neuromuscular diseases. Second, gender differences in smoothness metrics were not investigated since the sample size of this study was limited and we could not provide statistical evidence of gender differences. Future work could include a larger cohort of subjects, with a balanced number of males and females in order to assess the smoothness differences between genders. Finally, despite us providing a quantification of smoothness computed with several metrics, covering a comprehensive set of 3D directions in the upper limb workspace, the movements we considered were all approximately rectilinear or with little curvature. Developments of this concept may include more complex movements of the activity of daily living that require more complex coordination.
5. Conclusions
In this study, a smoothness map on the 3D workspace of the upper limb was computed, comparing four smoothness metrics based on wrist motion, namely the normalized jerk, the speed metric, the spectral arc length, and the number of speed peaks. Fifteen healthy subjects performed reaching movements and exploration tasks in multiple directions in five sectors of the workspace. The smoothness metrics were in accordance, discriminating well the sectors, identifying low smoothness in the up and left sectors, while the number of peaks was a metric not suitable for assessing movements of healthy subjects. However, strong correlation was found only between normalized jerk and speed metrics. These results can be used as a benchmark for clinical studies.
Author Contributions
Conceptualization, A.S.; methodology, A.S. and C.B.; software, A.S. and C.B.; validation, A.S. and C.B.; formal analysis, A.S. and C.B.; investigation, A.S. and C.B.; resources, A.S. and M.A.; data curation, A.S. and C.B.; writing—original draft preparation, A.S., C.B., H.M. and M.A.; writing—review and editing, A.S., C.B., H.M. and M.A.; visualization, A.S. and C.B.; supervision, A.S., M.A. and H.M.; project administration, A.S. and M.A.; funding acquisition, A.S. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the CNR Ethical Committee (CNR Ethics, Rome, Italy).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kiely, J.; Pickering, C.; Collins, D.J. Smoothness: An Unexplored Window into Coordinated Running Proficiency. Sport. Med.-Open 2019, 5, 43. [Google Scholar] [CrossRef]
- Gulde, P.; Hermsdörfer, J. Smoothness metrics in complex movement tasks. Front. Neurol. 2018, 9, 615. [Google Scholar] [CrossRef] [PubMed]
- Scano, A.; Chiavenna, A.; Malosio, M.; Tosatti, L.M. Kinect V2 Performance Assessment in Daily-Life Gestures: Cohort Study on Healthy Subjects for a Reference Database for Automated Instrumental Evaluations on Neurological Patients. Appl. Bionics Biomech. 2017, 2017, 8567084. [Google Scholar] [CrossRef]
- Caimmi, M.; Carda, S.; Giovanzana, C.; Maini, E.S.; Sabatini, A.M.; Smania, N.; Molteni, F. Using kinematic analysis to evaluate constraint-induced movement therapy in chronic stroke patients. Neurorehabil. Neural Repair 2008, 22, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.A.; Willén, C.; Sunnerhagen, K.S. Kinematic variables quantifying upper-extremity performance after stroke during reaching and drinking from a glass. Neurorehabil. Neural Repair 2011, 25, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Flash, T.; Hogan, N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef]
- Cruse, H.; Wischmeyer, E.; Brüwer, M.; Brockfeld, P.; Dress, A. On the cost functions for the control of the human arm movement. Biol. Cybern. 1990, 62, 519–528. [Google Scholar] [CrossRef]
- Van Kordelaar, J.; Van Wegen, E.; Kwakkel, G. Impact of time on quality of motor control of the paretic upper limb after stroke. Arch. Phys. Med. Rehabil. 2014, 95, 338–344. [Google Scholar] [CrossRef]
- Mohamed Refai, M.I.; Saes, M.; Scheltinga, B.L.; van Kordelaar, J.; Bussmann, J.B.J.; Veltink, P.H.; Buurke, J.H.; Meskers, C.G.M.; van Wegen, E.E.H.; Kwakkel, G.; et al. Smoothness metrics for reaching performance after stroke. Part 1: Which one to choose? J. Neuroeng. Rehabil. 2021, 18, 154. [Google Scholar] [CrossRef]
- Montes, V.R.; Quijano, Y.; Chong Quero, J.E.; Ayala, D.V.; Perez Moreno, J.C. Comparison of 4 different smoothness metrics for the quantitative assessment of movement’s quality in the upper limb of subjects with cerebral palsy. In Proceedings of the Pan American Health Care Exchanges, PAHCE, Brasilia, Brazil, 7–12 April 2014. [Google Scholar]
- Teulings, H.L.; Contreras-Vidal, J.L.; Stelmach, G.E.; Adler, C.H. Parkinsonism reduces coordination of fingers, wrist, and arm in fine motor control. Exp. Neurol. 1997, 146, 159–170. [Google Scholar] [CrossRef]
- De Sire, A.; Bigoni, M.; Priano, L.; Baudo, S.; Solaro, C.; Mauro, A. Constraint-Induced Movement Therapy in multiple sclerosis: Safety and three-dimensional kinematic analysis of upper limb activity. A randomized single-blind pilot study. NeuroRehabilitation 2019, 45, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Jebsen, R.H.; Taylor, N.; Trieschmann, R.B.; Trotter, M.J.; Howard, L.A. An objective and standardized test of hand function. Arch. Phys. Med. Rehabil. 1969, 50, 311–319. [Google Scholar] [PubMed]
- Lyle, R.C. A performance test for assessment of upper limb function in physical rehabilitation treatment and research. Int. J. Rehabil. Res. 1981, 4, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Mathiowetz, V.; Weber, K.; Kashman, N.; Volland, G. Adult norms for the nine hole peg test of finger dexterity. Occup. Ther. J. Res. 1985, 5, 24–38. [Google Scholar] [CrossRef]
- De Los Reyes-Guzmán, A.; Dimbwadyo-Terrer, I.; Trincado-Alonso, F.; Monasterio-Huelin, F.; Torricelli, D.; Gil-Agudo, A. Quantitative assessment based on kinematic measures of functional impairments during upper extremity movements: A review. Clin. Biomech. 2014, 29, 719–727. [Google Scholar] [CrossRef]
- Merlo, A.; Longhi, M.; Giannotti, E.; Prati, P.; Giacobbi, M.; Ruscelli, E.; Mancini, A.; Ottaviani, M.; Montanari, L.; Mazzoli, D. Upper limb evaluation with robotic exoskeleton. Normative values for indices of accuracy, speed and smoothness. NeuroRehabilitation 2013, 33, 523–530. [Google Scholar] [CrossRef]
- Brooks, V.B.; Cooke, J.D.; Thomas, J.S. The Continuity of Movements; Springer: Boston, MA, USA, 1973; pp. 257–272. [Google Scholar]
- Adams, R.J.; Lichter, M.D.; Krepkovich, E.T.; Ellington, A.; White, M.; Diamond, P.T. Assessing Upper Extremity Motor Function in Practice of Virtual Activities of Daily Living. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 287–296. [Google Scholar] [CrossRef]
- Rohrer, B.; Fasoli, S.; Krebs, H.I.; Hughes, R.; Volpe, B.; Frontera, W.R.; Stein, J.; Hogan, N. Movement smoothness changes during stroke recovery. J. Neurosci. 2002, 22, 8297–8304. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Melendez-Calderon, A.; Burdet, E. A robust and sensitive metric for quantifying movement smoothness. IEEE Trans. Biomed. Eng. 2012, 59, 2126–2136. [Google Scholar] [CrossRef]
- Hogan, N.; Sternad, D. Sensitivity of smoothness measures to movement duration, amplitude, and arrests. J. Mot. Behav. 2009, 41, 529–534. [Google Scholar] [CrossRef]
- Beck, Y.; Herman, T.; Brozgol, M.; Giladi, N.; Mirelman, A.; Hausdorff, J.M. SPARC: A new approach to quantifying gait smoothness in patients with Parkinson’s disease. J. Neuroeng. Rehabil. 2018, 15, 49. [Google Scholar] [CrossRef] [PubMed]
- Temporiti, F.; Mandaresu, S.; Calcagno, A.; Coelli, S.; Bianchi, A.M.; Gatti, R.; Galli, M. Kinematic evaluation and reliability assessment of the Nine Hole Peg Test for manual dexterity. J. Hand Ther. 2022. [Google Scholar] [CrossRef] [PubMed]
- Johansson, G.M.; Häger, C.K. A modified standardized nine hole peg test for valid and reliable kinematic assessment of dexterity post-stroke. J. Neuroeng. Rehabil. 2019, 16, 8. [Google Scholar] [CrossRef] [PubMed]
- Van Dokkum, L.; Hauret, I.; Mottet, D.; Froger, J.; Métrot, J.; Laffont, I. The contribution of kinematics in the assessment of upper limb motor recovery early after stroke. Neurorehabil. Neural Repair 2014, 28, 4–12. [Google Scholar] [CrossRef] [PubMed]
- Rickham, P.P. Human Experimentation Code of Ethics of the World Medical Association. Br. Med. J. 1964, 2, 177. [Google Scholar] [CrossRef]
- D’Avella, A.; Portone, A.; Fernandez, L.; Lacquaniti, F. Control of fast-reaching movements by muscle synergy combinations. J. Neurosci. 2006, 26, 7791–7810. [Google Scholar] [CrossRef]
- Scano, A.; Dardari, L.; Molteni, F.; Giberti, H.; Tosatti, L.M.; D’Avella, A. A comprehensive spatial mapping of muscle synergies in highly variable upper-limb movements of healthy subjects. Front. Physiol. 2019, 10, 1231. [Google Scholar] [CrossRef]
- Scano, A.; Molteni, F.; Tosatti, L.M. Low-Cost Tracking Systems Allow Fine Biomechanical Evaluation of Upper-Limb Daily-Life Gestures in Healthy People and Post-Stroke Patients. Sensors 2019, 19, 1224. [Google Scholar] [CrossRef]
- Schiefelbein, M.L.; Salazar, A.P.; Marchese, R.R.; Rech, K.D.; Schifino, G.P.; Figueiredo, C.S.; Cimolin, V.; Pagnussat, A.S. Upper-limb movement smoothness after stroke and its relationship with measures of body function/structure and activity–A cross-sectional study. J. Neurol. Sci. 2019, 401, 75–78. [Google Scholar] [CrossRef]
- Rech, K.D.; Salazar, A.P.; Marchese, R.R.; Schifino, G.; Cimolin, V.; Pagnussat, A.S. Fugl-Meyer Assessment Scores Are Related With Kinematic Measures in People with Chronic Hemiparesis after Stroke. J. Stroke Cerebrovasc. Dis. 2020, 29, 104463. [Google Scholar] [CrossRef]
- Celik, O.; O’Malley, M.K.; Boake, C.; Levin, H.S.; Yozbatiran, N.; Reistetter, T.A. Normalized movement quality measures for therapeutic robots strongly correlate with clinical motor impairment measures. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 433–444. [Google Scholar] [CrossRef] [PubMed]
- Scano, A.; Caimmi, M.; Chiavenna, A.; Malosio, M.; Tosatti, L.M. Kinect One-based biomechanical assessment of upper-limb performance compared to clinical scales in post-stroke patients. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015; Volume 2015, pp. 5720–5723. [Google Scholar]
- Schuch, C.P.; Balbinot, G.; Bonilla, M.N.; Guedes Machado, A.; Oliveira, A.A. de Feasibility of a Short-Term Virtual Reality Balance Intervention to Improve Mobility Smoothness in Parkinson’s Disease. Front. Virtual Real. 2020, 1, 7. [Google Scholar] [CrossRef]
- Gutiérrez, Á.; Sepúlveda-Muñoz, D.; Gil-Agudo, Á.; de los Reyes Guzmán, A. Serious game platform with haptic feedback and EMG monitoring for upper limb rehabilitation and smoothness quantification on spinal cord injury patients. Appl. Sci. 2020, 10, 963. [Google Scholar] [CrossRef]
- Scano, A.; Guanziroli, E.; Mira, R.M.; Brambilla, C.; Molinari Tosatti, L.; Molteni, F. Biomechanical assessment of the ipsilesional upper limb in post-stroke patients during multi-joint reaching tasks: A quantitative study. Front. Rehabil. Sci. 2022, 3, 943397. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.A.; Brandt, J.; Shadmehr, R. Motor disorder in Huntington’s disease begins as a dysfunction in error feedback control. Nature 2000, 403, 544–549. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, R.; Alimi, A.M.; Yergeau, P.; Leclerc, F. Modelling velocity profiles of rapid movements: A comparative study. Biol. Cybern. 1993, 69, 119–128. [Google Scholar] [CrossRef]
- Kahn, L.E.; Zygman, M.L.; Rymer, W.Z.; Reinkensmeyer, D.J. Effect of robot-assisted and unassisted exercise on functional reaching in chronic hemiparesis. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology-Proceedings, Istanbul, Turkey, 25–28 October 2001; Volume 2, pp. 1344–1347. [Google Scholar]
- Yang, N.; Zhang, M.; Huang, C.; Jin, D. Motion quality evaluation of upper limb target-reaching movements. Med. Eng. Phys. 2002, 24, 115–120. [Google Scholar] [CrossRef]
- Ao, D.; Song, R.; Tong, K.Y. Sensorimotor control of tracking movements at various speeds for stroke patients as well as age-matched and young healthy subjects. PLoS ONE 2015, 10, e0128328. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Melendez-Calderon, A.; Roby-Brami, A.; Burdet, E. On the analysis of movement smoothness. J. Neuroeng. Rehabil. 2015, 12, 112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).