Featured Application
The proposed enhanced single-probe method can be used to measure the impedance of energized devices or systems, which is usually not possible with traditional direct measurement methods. The online impedance measure is helpful in filter design/selection, system monitoring, and fault diagnosis. In addition, the obtained online impedances allow the prediction of converter-generated electromagnetic interference in both DC, AC single-phase, and AC three-phase systems, as well as estimation of the insertion loss of EMI filters, which is beneficial to filter assessment and design.
Abstract
Due to the widespread integration of renewable energy sources connected to AC and DC power systems by means of power electronics converters, electromagnetic noise propagates along lines, and metallic earth-return structures. EMI filters are commonly used to mitigate the common mode and differential mode noise at the interface of distribution lines, and their suppression characteristics are usually assessed in standard test setups, the impedances of which are, however, scarcely representative of real-world applications. In this paper, an online, inductively coupled impedance measurement method is proposed. A sensitivity analysis to highlight the benefits of the proposed setup and experimental verification is performed. The proposed method enables non-intrusive impedance measurement in energized systems, including power converters. These measures, in turn, allow the evaluation of modal insertion losses of EMI filters in real-world operating conditions. The three-phase example considered in this study shows significant deviations from manufacturer specifications, thus justifying the need for more advanced estimation techniques.
1. Introduction
Due to the widespread integration of renewable energy facilities, electromagnetic interference (EMI) issues are significantly growing in both AC and DC power systems [,]. Specifically, electromagnetic disturbances from power electronics converters that interface renewable energy sources to the power grid propagate along lines and metallic earth-return structures [,]. Passive EMI filters are commonly used to suppress common mode (CM) and differential mode (DM) emissions exiting power converters to mitigate the noise propagating along distribution lines []. Filter performance is usually assessed in terms of insertion loss (IL), defined in CISPR 17 as the ratio of the voltages across a specific reference load in the absence and presence of the filter []. For IL measurement, a reference test setup is used, which is characterized by source and load impedances defined by the standard (50 Ω/50 Ω, 100 Ω/0.1 Ω, and 0.1 Ω/100 Ω) []. However, in real-world applications, the actual IL of the filter (hereinafter called “in-circuit IL”) depends on the actual frequency-depending impedances of the devices connected with the filter, which scarcely replicate the reference impedances in the CISPR 17 test setup.
Therefore, assessing the in-circuit IL based on the actual load/source impedance is of great importance to selecting or designing proper filters for a specific system. Several contributions to the assessment of IL focused on the worst-case scenario (minimum IL). For instance, the theoretical minimum IL of the filter derived from its network parameters under extreme reference impedances revealed a substantially lower level than the so-called ‘approximate worst case’ in the CISPR 17 setup, which considers only two scenarios of mismatched load/source impedances (100 Ω/0.1 Ω and 0.1 Ω/100 Ω) []. Taking into account the impedance of the EMI source, a more realistic IL was predicted, which, at some frequencies, was smaller than the approximate worst-case estimated by CISPR 17 [].
Some works are devoted to thorough characterization of filters intended for IL prediction. For instance, in [,], the standard or in-circuit IL was predicted using the EMI filter scattering parameters (S-parameter) obtained by modeling or experiments. In [], a black-box model of EMI filters compatible with circuit solvers was proposed using the vector fitting technique, which can predict the IL in both time and frequency-domain simulation [,]. In [], a single setup was presented to evaluate all modes of insertion loss and extended to an approximate worst-case measurement.
Besides predicting the IL, some contributions have focused on designing EMI filters based on the actual source/load impedances in the targeted applications []. For instance, in [], the EMI filter design took into account the terminal impedances of an inverter-driven motor system that were measured offline by an LCR meter. However, recent research has shown that the impedance of power electronics converters measured offline may not coincide with the actual impedance when the system is powered on [,]. Hence, the online impedance measurement is more appropriate for optimal filter design. Note that, in this context, the online measurement is to be intended: a) a measure performed without physical modification of the circuit under test, just clamping a suitable probe on one or more cables, and b) a measure that can be performed while the circuit under test is working. Examples of filter design exploiting online impedance measurement were presented in [] and [] for inverter-driven motor systems and switched-mode power supplies, respectively.
The available methods for online impedance measurement can be classified into voltage-current strategy and capacitive/inductive coupling approaches []. Among them, inductive coupling methods allow for non-intrusive (intended as not requiring direct connection to live parts or physical modification to the system) measurements as well as less complex setups since they do not require direct electrical contact with the energized system. The first implementation made use of two probes and was proposed for measuring power line in-circuit impedances []. Further applications of such a method were presented in [,]. A more recent implementation [] foresees the use of one instead of two probes, with the advantage of, besides requiring less instrumentation, eliminating possible issues due to mutual coupling between the two probes. This method was applied to measure the in-circuit DM and CM impedances at the AC input of a motor-drive system [,].
This paper fits into this line of research with a twofold objective. The first objective is to enhance the single-probe method by simplifying the test setup and the calibration procedure. To this end, a sensitivity analysis is carried out to optimize the characteristics and assess the effectiveness of the measurement and calibration setup. The second objective is to exploit the obtained in-circuit measurements of modal impedances to investigate the effectiveness of the measurement setup foreseen by the standard in providing realistic information on the actual suppression performance (filter IL) of EMI filters when installed in a real system. The proposed methodology is applied to measure the modal impedances of a motor drive system and to assess the effectiveness of two three-phase EMI filters installed in such a motor drive system for different operating conditions.
The manuscript is organized as follows. Section 2 presents the enhanced single-probe method and its verification by measuring discrete RLC components. Besides, a sensitivity analysis is carried out to assess the effectiveness of the proposed setup. In Section 3, the procedure to measure the modal impedances of a motor drive system is introduced. In Section 4, the theoretical derivation of CM/DM ILs of three-phase EMI filters is proposed. Additionally, the measured in-circuit modal impedances of a motor drive system and the predicted IL of two three-phase filters are presented and discussed. Finally, Section 5 summarizes the obtained results and draws some conclusions.
2. Enhanced Single-Probe Method and Verification
2.1. Enhanced Single-Probe Method
In this section, an enhanced single-probe setup to measure the unknown impedance (Zx), as shown in Figure 1a, is presented. In the proposed setup, the bulk current injection (BCI) probe is connected to one port of the vector network analyzer (VNA) through a coaxial cable. A short wire connecting the unknown impedance is wound on the core of the BCI probe forming multiple turns. In each of these turns, the wire enters the probe inner window from a side, crosses the probe leaving the opposite side, and runs back to the entering side. The turn number of this looped wire is called Nturns. Inside the BCI probe, there is a feeding winding whose number of turns is Nprobe (this number is out of the operator’s control since it is related to the probe manufacturer and model). It is worth noting that it is possible to use not only BCI probes but also current monitor probes, as they are basically the same instrument, and many models are declared for both purposes by manufacturers. However, their design is usually optimized for one of the two scopes. Monitor probes have a high number of turns Nprobe in order to reduce the loading impedance ( Ω) on the clamped cable, which would perturb the circuit under test. Conversely, BCI probes usually have a very low Nprobe to be effective in inducing a longitudinal voltage source onto the clamped cable.
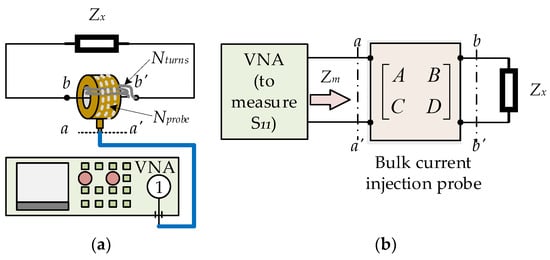
Figure 1.
(a) Enhanced single-probe setup and (b) its corresponding equivalent circuit.
The main improvements of this setup over previous solutions come in two folds. First, the signal amplification and protection module in [], which comprises extra radio-frequency components (including a directional coupler, a signal amplifier, and surge protectors) to allow a gain/phase meter to operate as VNA, is eliminated, and substituted by a real VNA with low-frequency extension capabilities (Keysight, E5061B, 5 Hz—1.5 GHz). As a result, the lowest frequency can be extended to 10 kHz instead of 150 kHz (directional couplers and other radio-frequency devices for use below hundreds of kHz are often commercially unavailable or exhibit limited performance parameters). Second, in order to improve the sensitivity of this setup in a simplified approach, i.e., to enhance coupling effects and signal-to-noise ratio (SNR), we propose the use of multiple turns Nturns instead of only one turn [], and to specifically make the number of wire turns Nturns exactly equal to the turns Nprobe of the feeding winding inside the BCI probe. The sensitivity analysis in Section 2.2 will support this choice.
The instrument calibration is carried out at the probe port (a-a’). Thus, the input impedance (Zm) seen at a-a’ can be extracted from the measured scattering parameter (S11) by []:
where Z0 is the internal reference impedance of the VNA.
The equivalent circuit of the setup is shown in Figure 1b, where the transmission (ABCD) matrix T of the two-port network (port a-a’ and b-b’) accounts for the BCI probe and the two-turn loop wire and its parasitic components:
Thus, the unknown impedance Zx can be computed from []:
Substituting (1) into (3) and further simplifying, Zx can be expressed in terms of S11 and three coefficients (k1, k2, and k3) []:
where
The three coefficients depend on the internal impedance of the VNA (Z0) and the ABCD parameters of the two-port network, which is determined by the calibration setup (the BCI probe, the multiple-turn wire, and the parasitic components). The calibration procedure presented in Section 2.3 allows skipping the determination of the ABCD parameters (e.g., by probe modeling and accounting for all parasitic effects).
2.2. Sensitivity Analysis for Justification of the Two-Turn Loop Setup
The derivative-based local sensitivity analysis is proposed to study how sensitive the obtained impedance Zx is to the measured S11, keeping other parameters (k1, k2, and k3) fixed. Under the assumption that S11 is a real number (i.e., resistive load), the sensitivity coefficient is obtained by differentiating (4):
This sensitivity coefficient should be high to obtain a good accuracy of the derived impedance. To further investigate how to make this coefficient as high as possible in principle, we consider the circuit representation in Figure 2, where the probe is modeled as an ideal transformer.
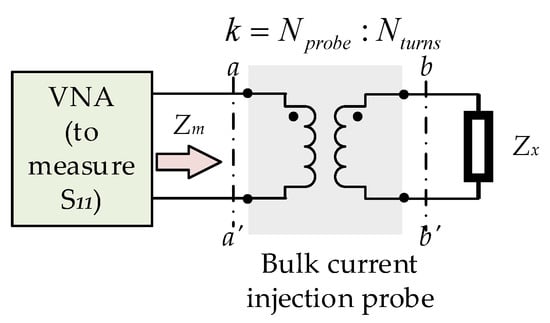
Figure 2.
Equivalent circuit involving an ideal transformer to model the BCI probe.
Such a probe model represents a large approximation, valid only in an intermediate frequency range (in-band region) of the whole working band declared by probe manufacturers, after the inductive behavior of the low-frequency region and before the very high-frequency region where magnetic-flux leakage and parasitic effects (e.g., stray capacitances) play a fundamental role. Anyway, this basic model is sufficient to investigate and justify the choice of Nturns.
The ABCD parameters between ports a-a’ and b-b’ can be obtained according to the characteristics of the ideal transformer:
where the is the turn ratio.
Substituting the ABCD parameters into (5)–(7), the three coefficients can be computed as:
In this general scenario, the sensitivity coefficient is associated with the turn ratio of the ideal transformer (k), the measured scattering parameters (S11), and the reference impedance of the VNA (Z0):
The sensitivity of the setup needs to be increased for high accuracy. To this end, we investigate two extreme cases when the port b-b’ is an open or short circuit. For the open circuit condition (S11 = 1), the sensitivity coefficient is singular and reaches infinity, indicating that the single-probe setup can provide high accuracy in measuring high impedances. On the contrary, the short circuit condition (S11 = −1) is the worst case, exhibiting the minimum sensitivity as:
Thus, the accuracy of the single-probe setup degrades when measuring low impedances. The minimum sensitivity coefficient in (12) should be kept as high as possible to improve the measurement accuracy for low impedances, i.e., the ideal transformer ratio k should stay small. This can be achieved in two ways, increasing the turn number Nturns of the loop wire or choosing probes with a small Nprobe. For the latter, commercial BCI probes are already designed with a small number Nprobe (usually one to three) to maximize coupling efficiency in BCI testing. In this respect, the category of BCI probes is best suited for the proposed impedance-measured method compared to other inductive probes, like current-monitor probes, which usually involve many primary turns. Anyway, after a specific BCI probe is selected (this choice is based on the working band), this number Nprobe is fixed and out of the control of the test operator.
In terms of selecting the turn number Nturns of the loop wire, there is a trade-off between many factors. On the one hand, increasing this number is helpful in improving the worst-case sensitivity (12). On the other hand, this choice can introduce two critical issues. First, when this setup is employed to measure the impedance of an active device like an operating power converter (this application will be presented in the next section), if , then an interference-noise current In generated by such a converter and flowing in the secondary would result in an increased noise current In/k injected in the VNA port connected to the primary, which could cause measurement errors and even possible instrument damage. Second, the use of too many hand-made wire turns would increase the uncertainty of the geometrical arrangement, which reduces the repeatability of the test setup.
Therefore, considering the trade-off between sensitivity and other aspects, the optimal solution appears to be a number of wire turns equal to the number of turns of the probe inner winding, i.e., . For the available BCI probe, the optimal choice results to be 2.
2.3. Calibration Procedure and Validation of the Proposed Method
Purpose of the calibration procedure is to directly measure the three coefficients (k1, k2, and k3) needed in (4), in order to be able to correctly measure the impedance of the circuit under test with no need for an explicit probe model []. This allows users to avoid the determination of an accurate model of the BCI probe as a two-port network to be used for computing A, B, C, and D. Additionally, the calibration procedure can be repeated with any BCI probe with no need for a specific setup.
Calibration is performed from 10 kHz to 30 MHz. The calibration setup shown in Figure 3a consists of a short loop wire with two turns. The calibration procedure requires measuring the S11 parameters of three known resistors (nominal values 1.1 Ω, 50 Ω and 1 kΩ), whose actual impedances (see Figure 3b) are determined with an impedance analyzer by reflectometric measure. The VNA is configured to measure 1601 points from 10 kHz up to 30 MHz, with 100 Hz resolution bandwidth and 8 dBm transmitted power. The same configurations have been used both for the calibration discussed in this section and for the tests reported in the following sections.
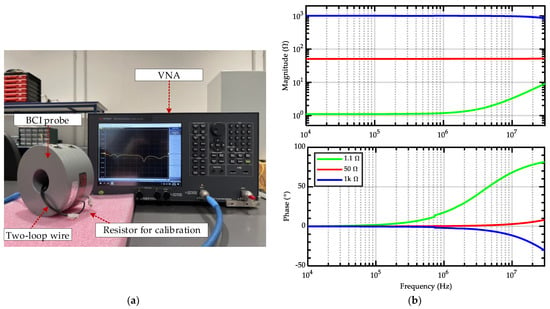
Figure 3.
(a) Calibration setup and (b) measurements of the magnitude and phase of the three resistors used for calibration (obtained by reflectometric measure with impedance analyzer).
The three coefficients can be calculated by this equation system derived from (4):
where Z1.1Ω, Z50Ω, and Z1kΩ are actual impedances of three resistors measured by an impedance analyzer, and S1.1Ω, S50Ω, and S1kΩ are the measured S11 parameters in the calibration setup (see Figure 3a).
The amplitude and phase of k1, k2, and k3 obtained from the calibration procedure are plotted in Figure 4a, and are consistent with the ideal theoretical expectations (10) in the in-band region (1–5 MHz). Specifically, since the turn ratio k is equal to 1 in our setup, the coefficients become k1 = k2 = −Z0 = −50 Ω and k3 = −1. Outside that narrow in-band region, the coefficients exhibit a non-trivial frequency response, which is determined by all the possible complex phenomena (e.g., lossy and dispersive ferrite core, inductive and capacitive parasitic effects) associated with the specific BCI probe model.
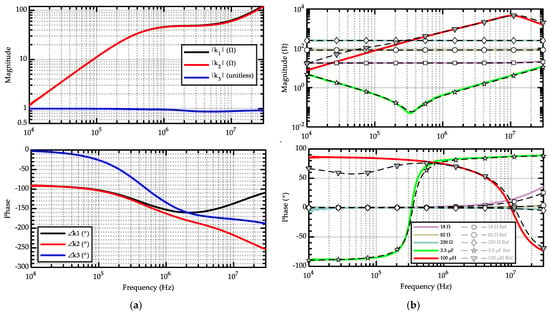
Figure 4.
(a) Calibrated three coefficients and (b) verification with discrete RLC components.
Several discrete components have been used in the calibrated setup, not only by resistors (like the three calibration loads) but also by capacitors and inductors. For instance, some discrete RLC components are reported in Figure 4b. Their impedances have been measured both through the proposed methodology using the calibrated coefficients k1, k2, and k3, and by an impedance analyzer. The minor discrepancies of the 3.3 µF capacitor around its self-resonance frequency are expected due to the low sensitivity at low impedance, confirming the conclusions of sensitivity analysis. The deviations of the 100 µH inductor are likely due to the different shape of the impedance analyzer fixture (involving a small ground plane below the component under test) and the proposed method (without ground plane), which has an impact on capacitive parasitic effects.
The magnitude relative error calculated from the data in Figure 4b is reported in Figure 5a, while the phase error calculated from the data in Figure 4b is reported in Figure 5b. The maximum values of magnitude error [Ω], magnitude relative error, and phase error [°] are reported in Table 1, while average error and standard deviation are reported in Table 2 both for magnitude and phase. It is possible to appreciate that resistor measures are very accurate, with small errors at low frequency, where the probe coupling is weaker, and moderate errors in the tens of MHz range where inductively coupled methods are known to suffer from undesired parasitic effects.
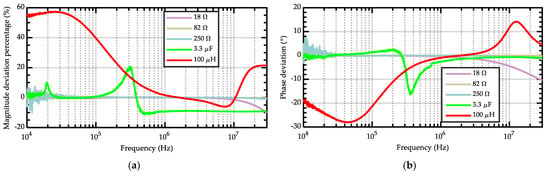
Figure 5.
(a) Magnitude error (percentage) and (b) phase error from the measure of discrete RLC components.

Table 1.
Maximum magnitude and phase errors from the measure of discrete RLC components.

Table 2.
Average magnitude and phase errors from the measure of discrete RLC components.
The capacitor measure shows moderate error around its self-resonance, where the impedance is minimum: this is not unexpected, since the sensitivity analysis presented in Section 2.2 showed that the accuracy of the method is reduced when measuring small impedances, even in ideal conditions. An almost constant error is present at frequencies higher than the capacitor self-resonance frequency, which can be ascribed to the parasitic capacitance between the component under test and the impedance analyzer fixture ground. In fact, this additional capacitance is negligible at low frequency, where the capacitance of the capacitor under test is dominant, but its effect is evident at frequencies higher than the capacitor self-resonance frequency, where the capacitor under test behaves as a small inductor.
Lastly, as far as the inductor measure is concerned, the same considerations drawn for resistors measures apply both in the tens of kHz and MHz ranges. Additionally, as mentioned, in the 10–100 kHz range a significant error due to capacitive effects is present. However, considering the percentage errors reported in Figure 5a, in the frequency range from 110 kHz up to 30 MHz, the inductor impedance measure is not less accurate than the other component ones.
3. Setups to Extract Equivalent Modal Circuits
This section introduces the application of the proposed single-probe method for extracting the equivalent DM/CM circuits of a motor drive system, which are further elaborated in setups to predict in-circuit ILs of EMI filters. Figure 6a shows the diagram of a typical setup of a motor drive system, which includes a variable-frequency drive, a three-phase induction motor, and cables. The AC power from the grid is transferred to the motor drive system through a line impedance stabilization network (LISN), which provides a stable impedance regardless of possible variations of the power grid impedance in the specified frequency range []. Figure 6b shows a picture of the motor drive system along with the proposed single-probe setup. The details of the motor drive system and instruments used in this setup are collected in Table 3.
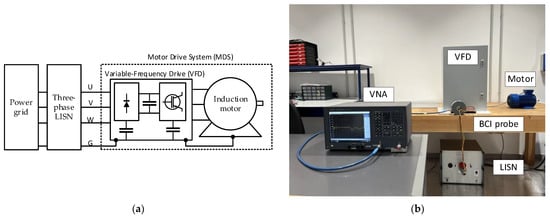
Figure 6.
(a) Diagram of the motor drive system, and (b) a picture of the single-probe setup used to measure the motor drive system impedances.

Table 3.
Specifications of motor drive system and instruments.
3.1. Measurement Setups to Extract the Equivalent Modal Circuits
The equivalent DM and CM circuits need to be extracted separately. For each mode, the measurements should be carried out twice to determine the equivalent modal circuits of both the motor drive system and external circuits (i.e., LISN with cables).
It is worth mentioning that the noise generated by the motor drive system is assumed to be negligible with respect to the signal injected by the VNA. Thus, the accuracy of the measured impedance is supposed not significantly degraded when the motor drive system is turned on. It is also assumed that the system is symmetric. Therefore, the corresponding DM circuit can be represented by two impedances only (see Figure 7b), where ZMDS_DM and ZLISN_Cable_DM stand for the DM impedances of the motor drive system and external circuit, respectively.
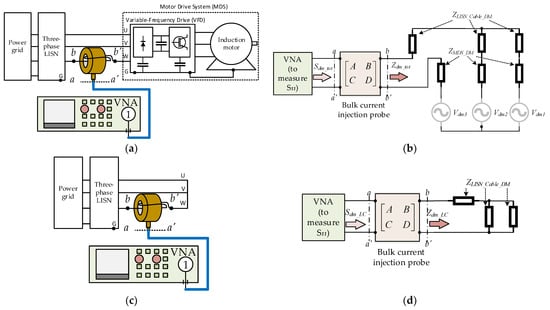
Figure 7.
Setups to determine the DM equivalent circuit: (a,b) in the presence and (c,d) in the absence of the motor drive system.
Two setup configurations are employed to determine these two impedances. In the first configuration, the probe is clamped on any phase of the motor drive system with (see the example for phase W in Figure 7a). Meanwhile, the ground cable between the motor drive system and the LISN is disconnected. No matter which phase is measured, the equivalent circuit of this setup can be represented as in Figure 7b. The measured reflection coefficient (Sdm_tot) can be used to calculate the impedance (Zdm_tot) seen at b-b’ by (14). In the second configuration in Figure 7c,d, the motor drive system is taken out, and the cable terminals of phases U, V, and W on the motor drive system side are connected to assess the external circuit (Zdm_LC), which is derived from the measured Sdm_LC by (15). Eventually, the two impedances of the DM equivalent circuit (ZLISN_Cable_DM and ZMDS_DM) can be computed from (16) and (17) by circuit theory. Due to the symmetry assumption, the minor differences between measurements on each phase are assumed to be non-intentional deviations. Consequently, the results in the next section are based on the average values calculated from three measurements on each phase.
The extraction technique of the CM equivalent circuit is similar to the DM procedure (see Figure 8). Additionally, also in this case, the method requires two setups: one in the presence and one in the absence of the motor drive system. Unlike for DM, here the ground cable between the motor drive system and LISN, where the probe is clamped, is part of the CM configuration. Moreover, instead of three measurements on each phase, in the CM setups a single measurement on the ground wire is performed. Indeed, clamping the three-phase wires would produce, in principle, the same results as clamping the ground wire. However, the need to wind the three-phase wires in the probe two times produces non-negligible difficulties in setup repeatability. The measured impedances (Zcm_tot and Zcm_LC), and the equivalent impedances (ZLISN_Cable_CM and ZMDS_CM) are derived according to (18)–(21).
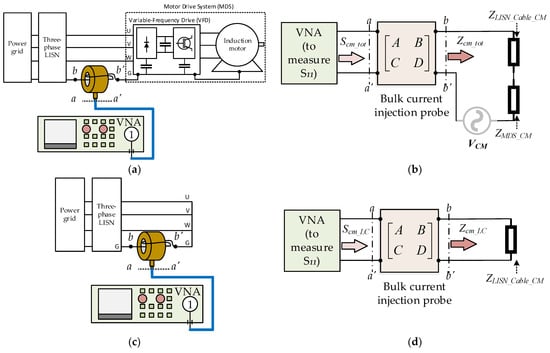
Figure 8.
Setups to determine CM equivalent circuit: (a,b) in the presence and (c,d) in the absence of the motor drive system.
In order to investigate the motor drive system modal impedances under different operating conditions, several scenarios will be implemented, including (1) power OFF, (2) power ON and motor drive system OFF, and (3) power ON and motor drive system ON with different switching frequencies (5 kHz, 10 kHz, and 15 kHz).
3.2. Measurement Setup for Three-Phase EMI Filters
To estimate the in-circuit IL, it is necessary to characterize the filter in addition to the equivalent modal circuit of a particular configuration. To accomplish this, the S-parameters of the three-phase EMI filter are measured by a four-port VNA (see the setup in Figure 9). Three sets of measurements are performed at different combinations of the filter ports with the other ports terminated in 50 Ω loads to get the complete 6×6 S-parameter matrix. In order to determine the in-circuit IL, the ABCD parameters of the filter are then deduced from the S-parameters using the analytical expressions in []. To compare the IL of different filters, we characterize two different topologies: one-stage and two-stage (manufacturer and model are undisclosed since they are not relevant).

Figure 9.
(a) Setup for S-parameter measurement of a three-phase filter and (b) filter arrangement inside a metallic enclosure equipped with SMA connectors.
4. Measurement Results and IL Prediction
4.1. Impedances of the Equivalent Modal Circuits of the Motor Drive System Setup
Based on the enhanced single-probe setup in Section 2 and the measurement procedure in Section 3.2, the modal impedances of the motor drive system equivalent modal circuits are determined (see Figure 10).
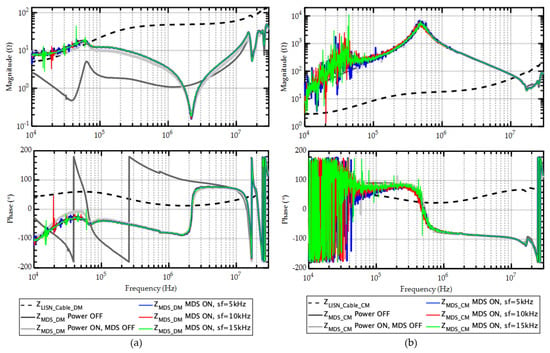
Figure 10.
Impedances in the motor drive system equivalent modal circuits: (a) DM and (b) CM.
The impedances of the LISN and cable in the equivalent modal circuits (see black dash line in Figure 10: ZLISN_Cable_DM and ZLISN_Cable_CM) are almost equal to 50 Ω and 50/3 Ω in the intermediate frequency range as expected. However, at higher frequencies, these impedances increase owning to cable effects, thus confirming the necessity to evaluate not only the source but also the load CM and DM actual impedance.
The impedance ZMDS_DM of the motor drive system shows a significantly different behavior depending on the power being turned OFF and ON (see the black curve and other curves in Figure 10a). Thus, the online DM impedance cannot be represented by the one measured offline in this motor drive system setup. This conclusion is in line with other research works []. Except for a small portion below 70 kHz, where the switching frequency and its harmonics affect measurement accuracy, the impedance ZMDS_DM does not exhibit significant variations if the switching frequency is changed (sf = 5 kHz, 10 kHz, and 15 kHz). When power is ON, and the motor drive system is OFF (grey curve), it displays almost the same impedance as the other three operating conditions but with less noise at low frequency. This result suggests measuring the online DM impedance by simply turning ON the power while leaving the motor drive system OFF.
None of the cases exhibit significant variations of the CM equivalent impedance ZMDS_CM, except for frequencies below 100 kHz, where the measured impedance is more affected by the switching frequency and its harmonics than in the DM case. However, no significant variations are observed if the CM impedance is measured online or offline. As a consequence, offline impedance measurement can be effectively used for the CM. These conclusions are consistent with those in [,].
4.2. Definition of CM/DM IL of Three-Phase Filters
According to CISPR 17, the filter IL is defined as the ratio of the voltages measured across a reference load in the presence and in the absence of the filter when a source with a specific reference impedance is fed to the system. In the symmetrical scenario, both the load and source impedances take the value of 50 Ω. In a three-phase system, this choice leads to equivalent load and source impedances equal to ) Ω for the DM, and to 50/3 Ω for the CM equivalent circuit of the measurement setup.
To estimate the in-circuit IL of a three-phase filter installed in the motor drive system under analysis, the actual modal impedances obtained by the one-probe method are used instead of the canonical impedances foreseen by the standard. Specifically, the actual load impedance is defined as the impedance of the cable and LISN, while the EMI source impedance is defined as the impedance of the motor drive system in a specific operating condition.
DM and CM in-circuit ILs of the filter can be evaluated by solution of the modal circuits shown in Figure 11. Panels on the left represent the modal setups in the absence of the filter, and can be readily solved to evaluate the modal voltages Vwo_DM, Vwo_CM across the load in the absence of the filter.
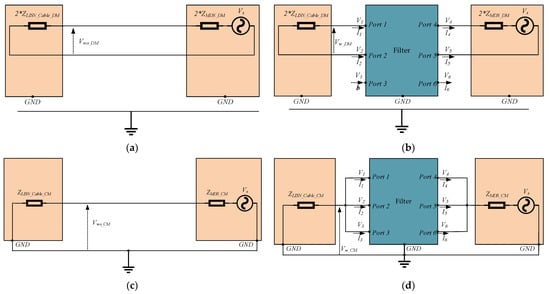
Figure 11.
Setups for computing the in-circuit IL. Left and right panels show the (a,b) DM and (c,d) CM setups without and with the filter, respectively.
Modal ILs can be therefore cast as follows:
where ZLISN_Cable_DM and ZMDS_DM are the load and source impedances, respectively, in the DM test setup, and ZLISN_Cable_CM and ZMDS_CM are the same impedances in the CM setup.
The voltages V1 and V2 in (22), and V1 in (23) involved in these expressions can be evaluated by combining the filter ABCD-parameter representation, relating voltages and currents at the filter ports, i.e.,
with the terminal constraints imposed by the DM and CM tests setups, respectively:
It should be noted that for simplicity of notation in (22)–(23), the same symbol was used to denote the voltage V1 measured in the DM setup [(22), (25) set of equations on the left], and in the CM setup [(23), (25) set of equations on the right].
4.3. Predictions of the DM and CM IL
Based on the IL expressions derived in Section 4.2, the DM and CM IL of two three-phase EMI filters under various operating conditions of the motor drive system are predicted.
The first filter considered for the analysis is a single-stage filter sample. Figure 12 shows the frequency behavior of the DM ILs obtained by connecting three different pairs of ports of the filter and the CM IL. The standard modal IL evaluated with symmetrical 50 Ω load/source impedances is also plotted for comparison (black dash curves).
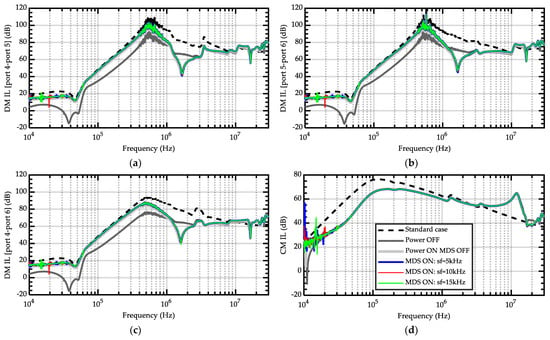
Figure 12.
One-stage filter: DM ILs between (a) port 4–5, (b) port 5–6 and (c) port 4–6, and (d) CM IL.
For the DM, it can be observed that the offline DM IL (black curve) significantly underestimates the actual (i.e., when the motor drive system is working) effectiveness of the filter in the frequency band below 10 MHz. Hence, the online DM impedance shall be used in order to achieve reliable estimates of the in-circuit DM IL. Conversely, the specific operation condition (power ON, motor drive system OFF, and different switching frequencies) does not significantly affect the DM IL. The IL measured according to the standards significantly overestimates the actual DM IL from 500 kHz to 10 MHz.
On the other hand, the CM IL is not influenced by the operating conditions, confirming the possibility of using the offline CM impedance to estimate the CM IL. Likewise for DM, the CM IL measurement obtained in the test setup foreseen by the standard does not provide reliable information on the actual filter performance, since this setup can overestimate (below 3 MHz) or underestimate (above 3 MHz) the actual CM IL.
For comparison, Figure 13 shows the results obtained for a two-stage filter. Again, for DM IL, the estimated value based on the DM impedance measured offline does not correspond to the actual DM IL. The setup foreseen by the standard leads to overestimates of the actual DM IL from 200 kHz to around 10 MHz. For the CM IL, the insensitivity to the working conditions is confirmed. Additionally, the CM IL measured according to the standard underestimates the actual CM IL of the filter from 10 kHz to around 15 MHz.
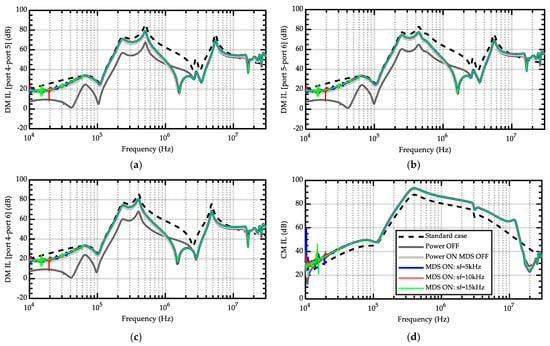
Figure 13.
Two-stage filter: DM IL between (a) port 4–5, (b) port 5–6 and (c) port 4–6, and (d) CM IL.
5. Conclusions
This work proposes an improved single-probe method for online, in-circuit impedance measurement with an extended frequency range down to 10 kHz. With respect to the approaches available in the literature, the proposed method eliminates the complex composition of the signal amplification and makes use of a simpler test setup. This is achieved by performing a sensitivity analysis, which indicates that the number of turns of the wire (twisted around the BCI probe) should match the same number of windings inside the BCI probe. The proposed setup is verified by discrete RLC components. The analysis shows that the general single-probe setup has a high sensitivity for measuring high impedances. In contrast, low impedance measurement accuracy suffers from low sensitivity, which can be improved by selecting a bulk current injection probe with only one-turn winding or increasing the turn numbers of the wire twisted on the probe.
The enhanced single-probe technique is then utilized to extract the equivalent CM/DM circuits for a motor drive system by measuring its online impedances. Finally, using the network theory and the knowledge of equivalent modal circuits, in-circuit modal ILs are predicted under different operating conditions of the motor drive system.
From the analysis, two main conclusions can be drawn. The DM impedance is significantly different if the system is powered ON and OFF. Once the system is powered ON, even if the variable-frequency device is not turned ON, the measured DM impedance can be used for in-circuit DM IL prediction because no significant differences can be observed for different operating conditions. Conversely, it has been proven that the CM impedance does not depend on the ON and OFF status of the system, conclusion that is in line and confirmed by other works in the literature.
Consequently, the predicted DM IL based on the DM impedance measured offline cannot reflect the actual DM IL of the filter, even if the in-circuit DM IL does not depend on the switching frequency of the system. Conversely, the CM impedance measured offline can be used to predict the in-circuit CM IL. However, in both CM and DM cases, the modal IL evaluated in the test setup foreseen by the standard cannot provide a reliable estimate of the actual IL of the filter installed in the motor drive system under analysis.
Author Contributions
Conceptualization, L.W., S.N., G.S., F.G. and S.A.P.; methodology, S.N. and G.S.; software, L.W.; validation, S.N., L.W. and G.S.; formal analysis, S.N. and G.S.; investigation, L.W., S.N. and G.S.; resources, F.G.; data curation, L.W.; writing—original draft preparation, L.W.; writing—review and editing, S.N., G.S., F.G. and S.A.P.; visualization, L.W.; supervision, S.A.P. and F.G.; project administration, S.A.P. and F.G.; funding acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 812753.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smolenski, R. Conducted Electromagnetic Interference (EMI) in Smart Grids; Power systems; Springer: London, UK, 2012; ISBN 978-1-4471-2959-2. [Google Scholar]
- Jettanasen, C.; Ngaopitakkul, A. The Conducted Emission Attenuation of Micro-Inverters for Nanogrid Systems. Sustainability 2019, 12, 151. [Google Scholar] [CrossRef]
- Wan, L.; Beshir, A.H.; Wu, X.; Liu, X.; Grassi, F.; Spadacini, G.; Pignari, S.A.; Zanoni, M.; Tenti, L.; Chiumeo, R. Black-Box Modelling of Low-Switching-Frequency Power Inverters for EMC Analyses in Renewable Power Systems. Energies 2021, 14, 3413. [Google Scholar] [CrossRef]
- Baranowski, J.; Drabek, T.; Piątek, P.; Tutaj, A. Diagnosis and Mitigation of Electromagnetic Interference Generated by a Brushless DC Motor Drive of an Electric Torque Tool. Energies 2021, 14, 2149. [Google Scholar] [CrossRef]
- Wunsch, B.; Skibin, S.; Forsström, V.; Stevanovic, I. EMC Component Modeling and System-Level Simulations of Power Converters: AC Motor Drives. Energies 2021, 14, 1568. [Google Scholar] [CrossRef]
- CISPR 17:2011; Methods of Measurement of the Suppression Characteristics of Passive EMC Filtering Devices. 2nd ed. International Special Committee on Radio Interference: Geneva, Switzerland, 2011.
- Mardiguian, M.; Raimbourg, J. An Alternate, Complementary Method for Characterizing EMI Filters. In Proceedings of the 1999 IEEE International Symposium on Electromagnetic Compatability. Symposium Record (Cat. No.99CH36261); IEEE: Seattle, WA, USA, 1999; Volume 2, pp. 882–886. [Google Scholar]
- Kostov, K.S.; Kyyrä, J.J. Insertion Loss and Network Parameters in the Analysis of Power Filters. In Proceedings of the Nordic Workshop on Power and Industrial Electronics (NORPIE/2008), Espoo, Finland, 9–11 June 2008; Helsinki University of Technology: Helsinki, Finland, 2008. [Google Scholar]
- Kovacevic, I.; Krismer, F.; Schroth, S.; Kolar, J.W. Practical Characterization of EMI Filters Replacing CISPR 17 Approximate Worst Case Measurements. In Proceedings of the 2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 23–26 June 2013; pp. 1–10. [Google Scholar]
- Kim, K.; Hwang, H.; Nah, W. An EM-Circuit Co-Simulation Model to Predict Insertion Loss in a Busbar-PCB Type EMI Filter. In Proceedings of the 2021 IEEE International Joint EMC/SI/PI and EMC Europe Symposium, Raleigh, NC, USA, 26 July–13 August 2021; pp. 313–317. [Google Scholar]
- Cuellar, C.; Idir, N. Determination of the Insertion Loss of EMI Filters Using a Black-Box Model. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2644–2649. [Google Scholar]
- Negri, S.; Spadacini, G.; Grassi, F.; Pignari, S. Black-Box Modeling of EMI Filters for Frequency and Time-Domain Simulations. IEEE Trans. Electromagn. Compat. 2022, 64, 119–128. [Google Scholar] [CrossRef]
- Negri, S.; Spadacini, G.; Grassi, F.; Pignari, S.A. Prediction of EMI Filter Attenuation in Power-Electronic Converters via Circuit Simulation. IEEE Trans. Electromagn. Compat. 2022, 64, 1086–1096. [Google Scholar] [CrossRef]
- Nemashkalo, D.; Koch, P.; Moonen, N.; Leferink, F. Multichannel EMI Filter Performance Assessment. In Proceedings of the 2022 International Symposium on Electromagnetic Compatibility—EMC Europe, Gothenburg, Sweden, 5–8 September 2022; pp. 69–73. [Google Scholar]
- Dey, S.; Mallik, A. A Comprehensive Review of EMI Filter Network Architectures: Synthesis, Optimization and Comparison. Electronics 2021, 10, 1919. [Google Scholar] [CrossRef]
- Luna, M.; La Tona, G.; Accetta, A.; Pucci, M.; Di Piazza, M.C. An Evolutionary EMI Filter Design Approach Based on In-Circuit Insertion Loss and Optimization of Power Density. Energies 2020, 13, 1957. [Google Scholar] [CrossRef]
- Mazzola, E.; Grassi, F.; Amaducci, A. Novel Measurement Procedure for Switched-Mode Power Supply Modal Impedances. IEEE Trans. Electromagn. Compat. 2020, 62, 1349–1357. [Google Scholar] [CrossRef]
- Wan, L.; Hamid, A.; Grassi, F.; Spadacini, G.; Pignari, S.A. SPICE Simulation of Modal Impedances in Automotive Powertrains under Different Operating Conditions. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–5. [Google Scholar]
- Fan, F.; See, K.Y.; Liu, X.; Li, K.; Gupta, A.K. Systematic Common-Mode Filter Design for Inverter-Driven Motor System Based on In-Circuit Impedance Extraction. IEEE Trans. Electromagn. Compat. 2020, 62, 1711–1722. [Google Scholar] [CrossRef]
- Tarateeraseth, V.; See, K.Y.; Canavero, F.G.; Chang, R.W.-Y. Systematic Electromagnetic Interference Filter Design Based on Information from In-Circuit Impedance Measurements. IEEE Trans. Electromagn. Compat. 2010, 52, 588–598. [Google Scholar] [CrossRef]
- Jie, H.; Zhao, Z.; Fei, F.; See, K.Y.; Simanjorang, R.; Sasongko, F. A Survey of Impedance Measurement Methods in Power Electronics. In Proceedings of the 2022 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar]
- Southwick, R.; Dolle, W. Line Impedance Measuring Instrumentation Utilizing Current Probe Coupling. IEEE Trans. Electromagn. Compat. 1971, EMC-13, 31–36. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, F.; Jie, H.; Sun, Q.; Tu, P.; Wang, W.; See, K.Y. Inductively Coupled In-Circuit Impedance Measurement and Its EMC Applications. arXiv 2022, arXiv:2204.01546. [Google Scholar]
- Zhao, Z.; Fan, F.; Jie, H.; Yang, Z.; Dong, M.; Chua, E.K.; Yak See, K. In-Circuit Impedance Measurement Setups of Inductive Coupling Approach: A Review. In Proceedings of the 2022 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Beijing, China, 1–4 September 2022; pp. 228–230. [Google Scholar]
- Weerasinghe, A.; Zhao, Z.; Narampanawe, N.; Yang, Z.; Svimonishvili, T.; See, K.Y. Single-Probe Inductively Coupled In-Circuit Impedance Measurement. IEEE Trans. Electromagn. Compat. 2022, 64, 2–10. [Google Scholar] [CrossRef]
- Weerasinghe, A.; Zhao, Z.; Fan, F.; Tu, P.; See, K.Y. In-Circuit Differential-Mode Impedance Extraction at the AC Input of a Motor Drive System. In Proceedings of the 2021 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Bali, Indonesia, 27–30 September 2021; pp. 1–4. [Google Scholar]
- Zhao, Z.; Fan, F.; Weerasinghe, A.; Tu, P.; See, K.Y. Measurement of In-Circuit Common-Mode Impedance at the AC Input of a Motor Drive System. In Proceedings of the 2021 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Bali, Indonesia, 27–30 September 2021; pp. 1–4. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-63155-3. [Google Scholar]
- Wan, L.; Khilnani, A.; Hamid, A.; Grassi, F.; Spadacini, G.; Pignari, S.; Sumner, M.; Thomas, D. Limitations in Applying the Existing LISN Topologies for Low Frequency Conducted Emission Measurements and Possible Solution. In Proceedings of the 2021 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Bali, Indonesia, 27–30 September 2021; pp. 1–4. [Google Scholar]
- Frickey, D.A. Conversions between S, Z, Y, H, ABCD, and T Parameters Which Are Valid for Complex Source and Load Impedances. IEEE Trans. Microw. Theory Tech. 1994, 42, 205–211. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).