Analysis of All-Optical Generation of Graphene Surface Plasmons by a Frequency-Difference Process
Abstract
:1. Introduction
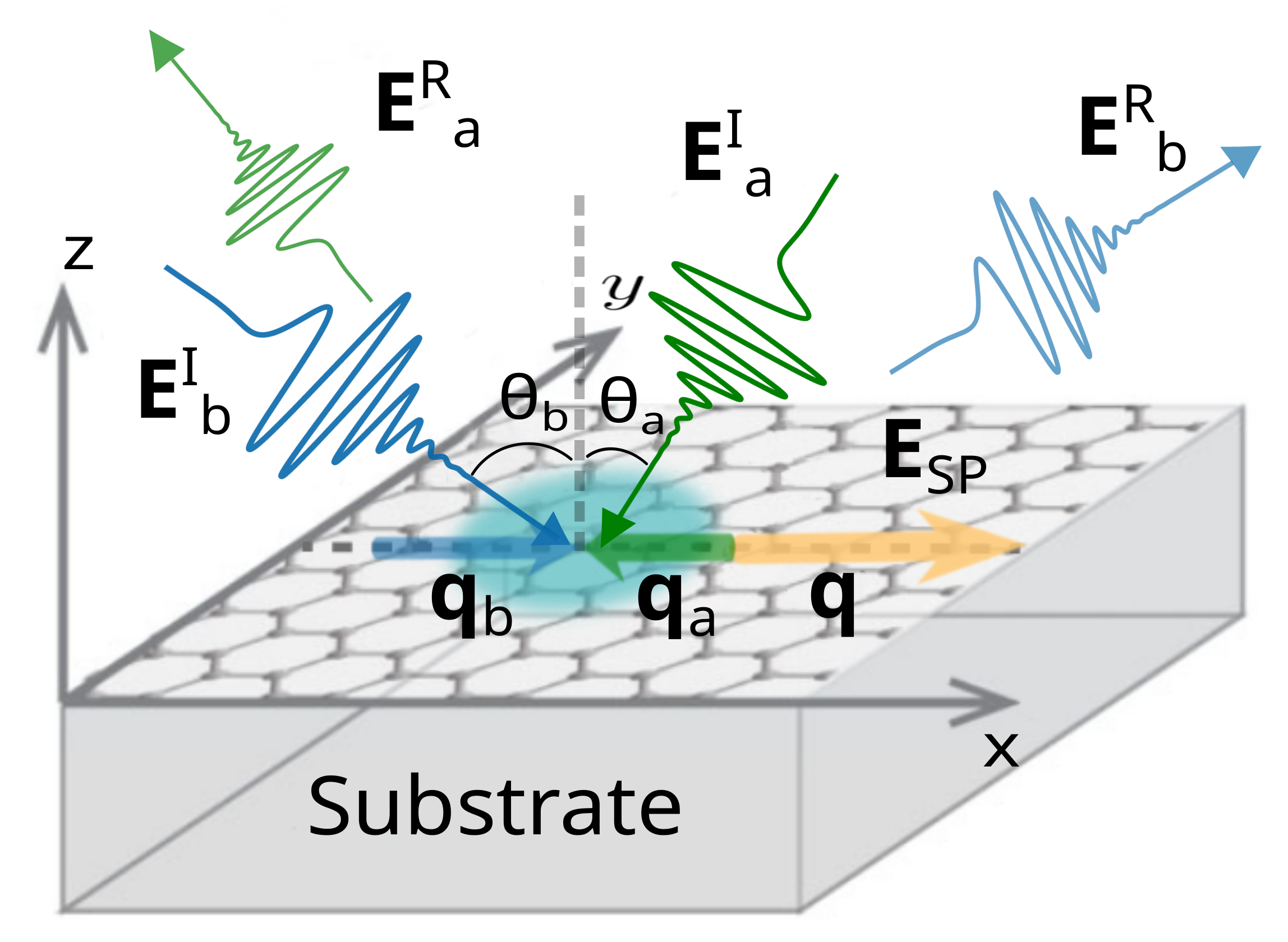
2. Materials and Methods
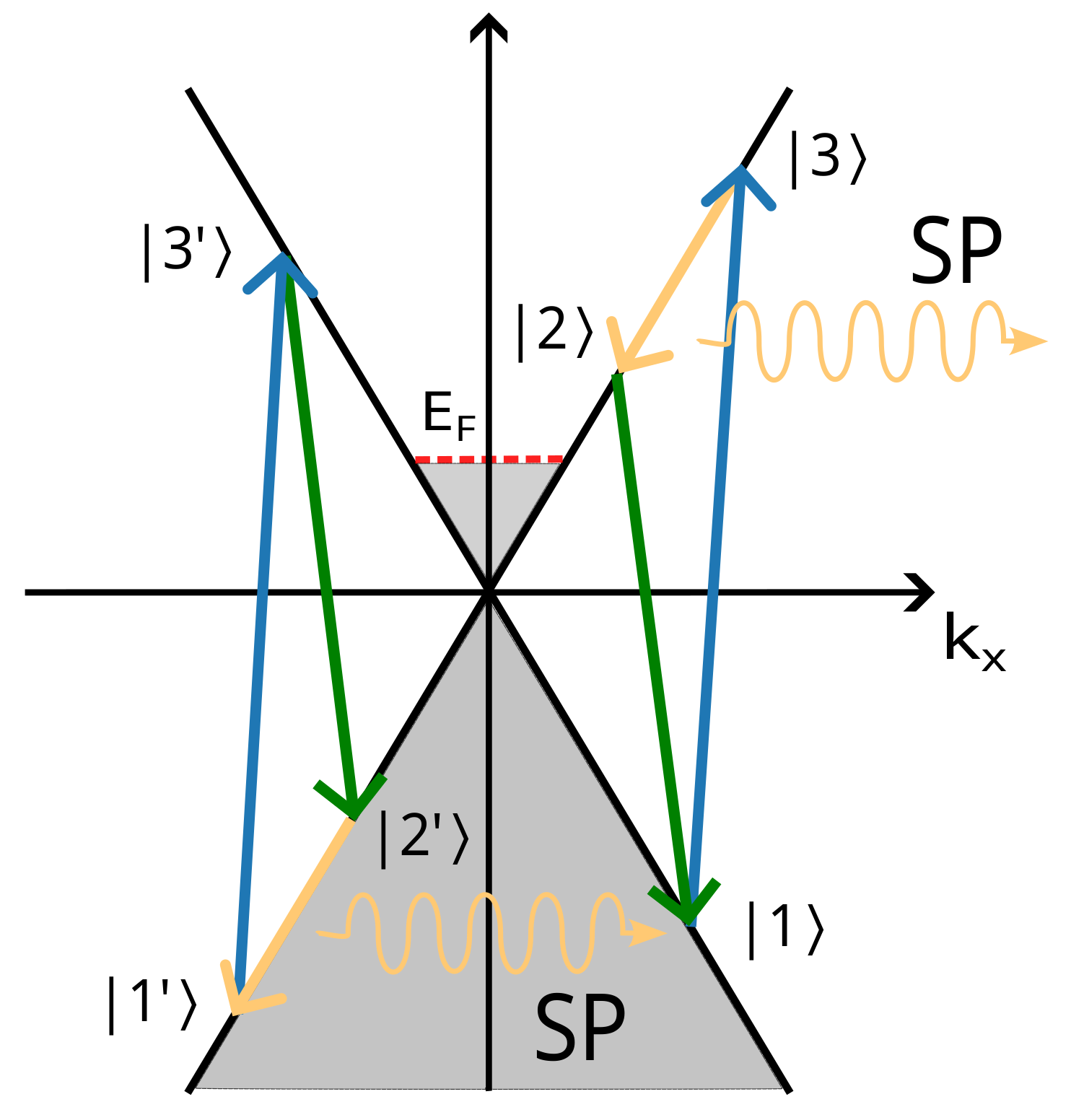
2.1. Second-Order Conductivities
2.2. Reflection Coefficients of the Optical Beams
3. Results and Discussion
3.1. Calculated Optical Spectra
3.2. How to Detect the Optically Generated SPs?
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gonçalves, P.A.D.; Peres, N.M.R. An Introduction to Graphene Plasmonics; World Scientific: Singapore, 2016. [Google Scholar]
- Fei, Z.; Rodin, A.S.; Andreev, G.O.; Bao, W.; McLeod, A.S.; Wagner, M.; Zhang, L.M.; Zhao, Z.; Dominguez, G.; Thiemens, M.; et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 2012, 487, 82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Badioli, M.; Alonso-González, P.; Thongrattanasiri, S.; Huth, F.; Osmond, J.; Spasenovic, M.; Centeno, A.; Pesquera, A.; Godignon, P.; et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 2012, 487, 77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photon. 2012, 6, 749. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.R.; Vasilevskiy, M. A Primer on Surface Plasmon-Polaritons in Graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef] [Green Version]
- Constant, T.J.; Hornett, S.M.; Chang, D.E.; Hendry, E. All-optical generation of surface plasmons in graphene. Nat. Photon. 2016, 12, 124. [Google Scholar] [CrossRef] [Green Version]
- Tao, J.; Dong, Z.; Yang, J.K.W.; Wang, Q.J. Plasmon excitation on flat graphene by spolarized beams using four-wave mixing. Opt. Express 2015, 23, 7809. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Tokman, M.; Belyanin, A. Efficient Nonlinear Generation of THz Plasmons in Graphene and Topological Insulators. Phys. Rev. Lett. 2014, 112, 055501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikhailov, S.A. Non-linear electromagnetic response of graphene. EPL 2007, 79, 27002. [Google Scholar] [CrossRef] [Green Version]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent Nonlinear Optical Response of Graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Dadap, J.I.; Petrone, N.; Yeh, P.C.; Hone, J.; Osgood, R.M., Jr. Optical third-harmonic generation in graphene. Phys. Rev. X. 2013, 3, 021014. [Google Scholar] [CrossRef]
- Cheng, J.L.; Vermeulen, N.; Sipe, J.E. Third order optical nonlinearity of graphene. New J. Phys. 2014, 16, 053014. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Quantum theory of the third-order nonlinear electrodynamic effects of graphene. Phys. Rev. B 2016, 93, 085403. [Google Scholar] [CrossRef] [Green Version]
- Ooi, K.J.A.; Tan, D.T.H. Nonlinear graphene plasmonics. Proc. Math. Phys. Eng 2017, 473, 20170433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hafez, H.A.; Kovalev, S.; Deinert, J.C.; Mics, Z.; Green, B.; Awari, N.; Chen, M.; Germanskiy, S.; Lehnert, U.; Teichert, J.; et al. Extremely efficient terahertz high-harmonic generation in graphene by hot Dirac fermions. Nature 2018, 561, 507. [Google Scholar] [CrossRef] [PubMed]
- Peres, N.M.R.; Bludov, Y.V.; Santos, J.E.; Jauho, A.P.; Vasilevskiy, M.I. Optical bistability of graphene in the terahertz range. Phys. Rev. B 2014, 90, 125425. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, V.; Carey, T.; Viti, L.; Li, L.; Linfield, E.H.; Davies, A.G.; Tredicucci, A.; Yoon, D.; Karagiannidis, P.G.; Lombardi, L.; et al. Terahertz saturable absorbers from liquid phase exfoliation of graphite. Nat. Commun. 2017, 8, 15763. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: Boston, MA, USA, 2008. [Google Scholar]
- Lin, K.H.; Weng, S.W.; Lyu, P.W.; Tsai, T.R.; Su, W.B. Observation of optical second harmonic generation from suspended single-layer and bi-layer graphene. APL 2014, 105, 151605. [Google Scholar] [CrossRef]
- Yao, B.; Liu, Y.; Huang, S.W.; Choi, C.; Xie, Z.; Flor Flores, J.; Wu, Y.; Yu, M.; Kwong, D.L.; Huang, Y.; et al. Broadband gate-tunable terahertz plasmons in graphene heterostructures. Nat. Photon. 2018, 12, 1749. [Google Scholar] [CrossRef] [Green Version]
- Constant, T.J.; Hornett, S.M.; Chang, D.E.; Hendry, E. Intensity dependences of the nonlinear optical excitation of plasmons in graphene. Phil. Trans. R. Soc. A 2017, 375, 20160066. [Google Scholar] [CrossRef] [Green Version]
- Tollerton, C.J.; Bohn, J.; Constant, T.J.; Horsley, S.A.R.; Chang, D.E.; Hendry, E.; Li, D.Z. Origins of All-Optical Generation of Plasmons in Graphene. Sci. Rep. 2019, 9, 3267. [Google Scholar] [CrossRef]
- Wang, Y.; Tokman, M.; Belyanin, A. Second-order nonlinear optical response of graphene. Phys. Rev. B 2016, 94, 195442. [Google Scholar] [CrossRef] [Green Version]
- Ventura, G.B.; Passos, D.J.; Lopes dos Santos, J.M.B.; Viana Parente Lopes, J.M.; Peres, N.M.R. Gauge covariances and nonlinear optical responses. Phys. Rev. B 2017, 96, 035431. [Google Scholar] [CrossRef] [Green Version]
- Passos, D.J.; Ventura, G.B.; Lopes, J.M.V.P.; Santos, J.M.B.L.d.; Peres, N.M.R. Nonlinear optical responses of crystalline systems: Results from a velocity gauge analysis. Phys. Rev. B 2018, 97, 235446. [Google Scholar] [CrossRef] [Green Version]
- Blount, E. Formalisms of Band Theory. Solid State Phys. 1962, 13, 305. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Vasilevskiy, M.I.; Peres, N.M.R. Mechanism for graphene-based optoelectronic switches by tuning surface plasmon-polaritons in monolayer graphene. EPL 2010, 92, 68001. [Google Scholar] [CrossRef] [Green Version]
- Ulbricht, R.; Hendry, E.; Shan, J.; Heinz, T.F.; Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 2011, 83, 543. [Google Scholar] [CrossRef] [Green Version]
- Doukas, S.; Sharma, P.; Goykhman, I.; Lidorikis, E. Electrical detection of graphene plasmons for mid-infrared photodetection and chemical sensing: A computational study. APL 2022, 121, 051103. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Theory of the strongly nonlinear electrodynamic response of graphene: A hot electron model. Phys. Rev. B 2019, 100, 115416. [Google Scholar] [CrossRef] [Green Version]
- Pogna, E.A.A.; Tomadin, A.; Balci, O.; Soavi, G.; Paradisanos, I.; Guizzardi, M.; Pedrinazzi, P.; Mignuzzi, S.; Tielrooij, K.J.; Polini, M.; et al. Electrically Tunable Nonequilibrium Optical Response of Graphene. ACS Nano 2022, 16, 3613. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias, R.; Viana Gomes, J.C.; Vasilevskiy, M.I. Analysis of All-Optical Generation of Graphene Surface Plasmons by a Frequency-Difference Process. Appl. Sci. 2022, 12, 12376. https://doi.org/10.3390/app122312376
Dias R, Viana Gomes JC, Vasilevskiy MI. Analysis of All-Optical Generation of Graphene Surface Plasmons by a Frequency-Difference Process. Applied Sciences. 2022; 12(23):12376. https://doi.org/10.3390/app122312376
Chicago/Turabian StyleDias, Rui, José C. Viana Gomes, and Mikhail I. Vasilevskiy. 2022. "Analysis of All-Optical Generation of Graphene Surface Plasmons by a Frequency-Difference Process" Applied Sciences 12, no. 23: 12376. https://doi.org/10.3390/app122312376
APA StyleDias, R., Viana Gomes, J. C., & Vasilevskiy, M. I. (2022). Analysis of All-Optical Generation of Graphene Surface Plasmons by a Frequency-Difference Process. Applied Sciences, 12(23), 12376. https://doi.org/10.3390/app122312376






