Suitability of an Artificial Viscosity Model for Compressible Under-Resolved Turbulence Using a Flux Reconstruction Method
Abstract
1. Introduction
2. Numerical Methods
2.1. Governing Equations
2.2. Flux Reconstruction Method
2.3. Subgrid Scale Models
2.3.1. Functional Models
2.3.2. Structural Models
2.4. Artificial Viscosity
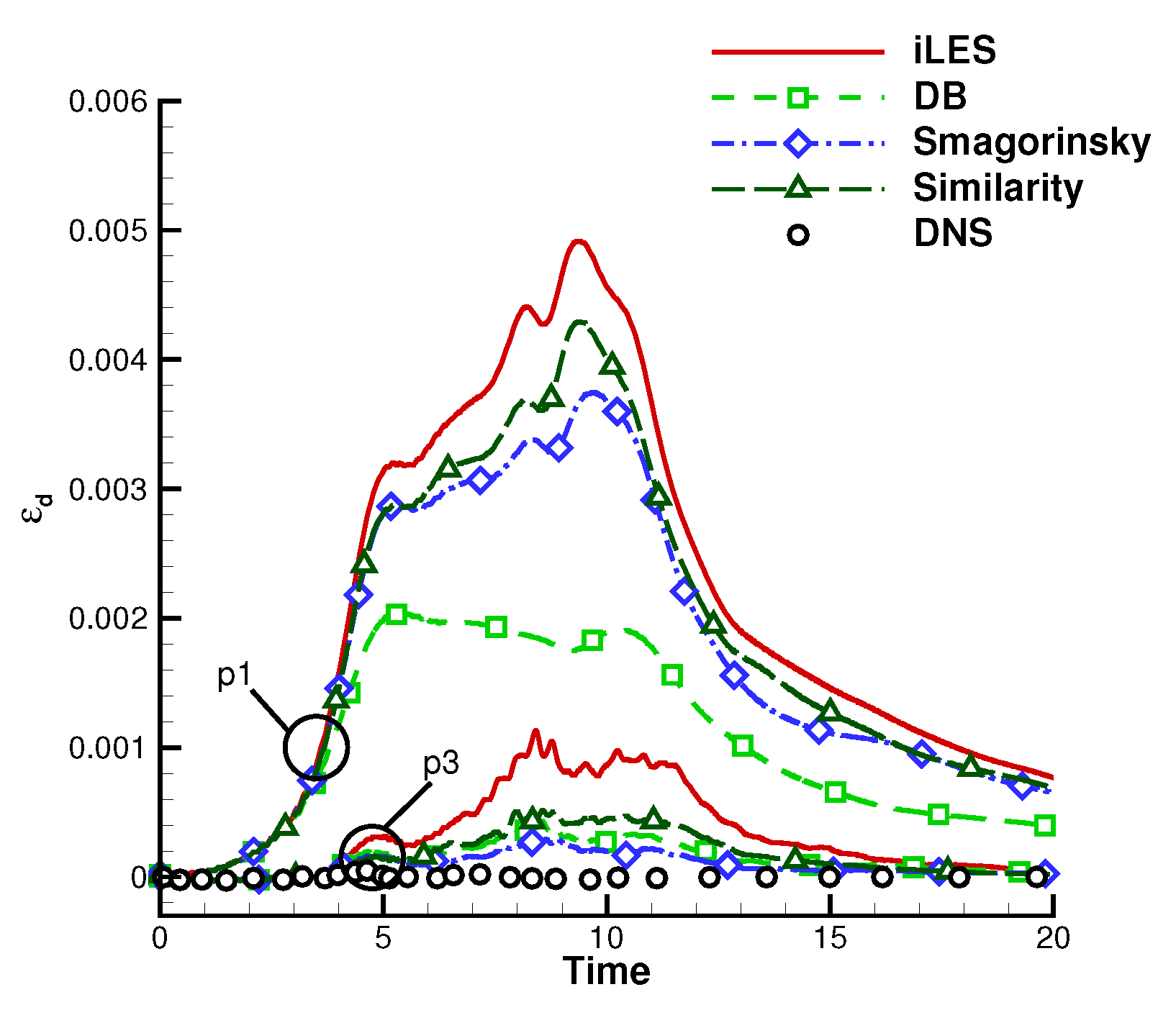
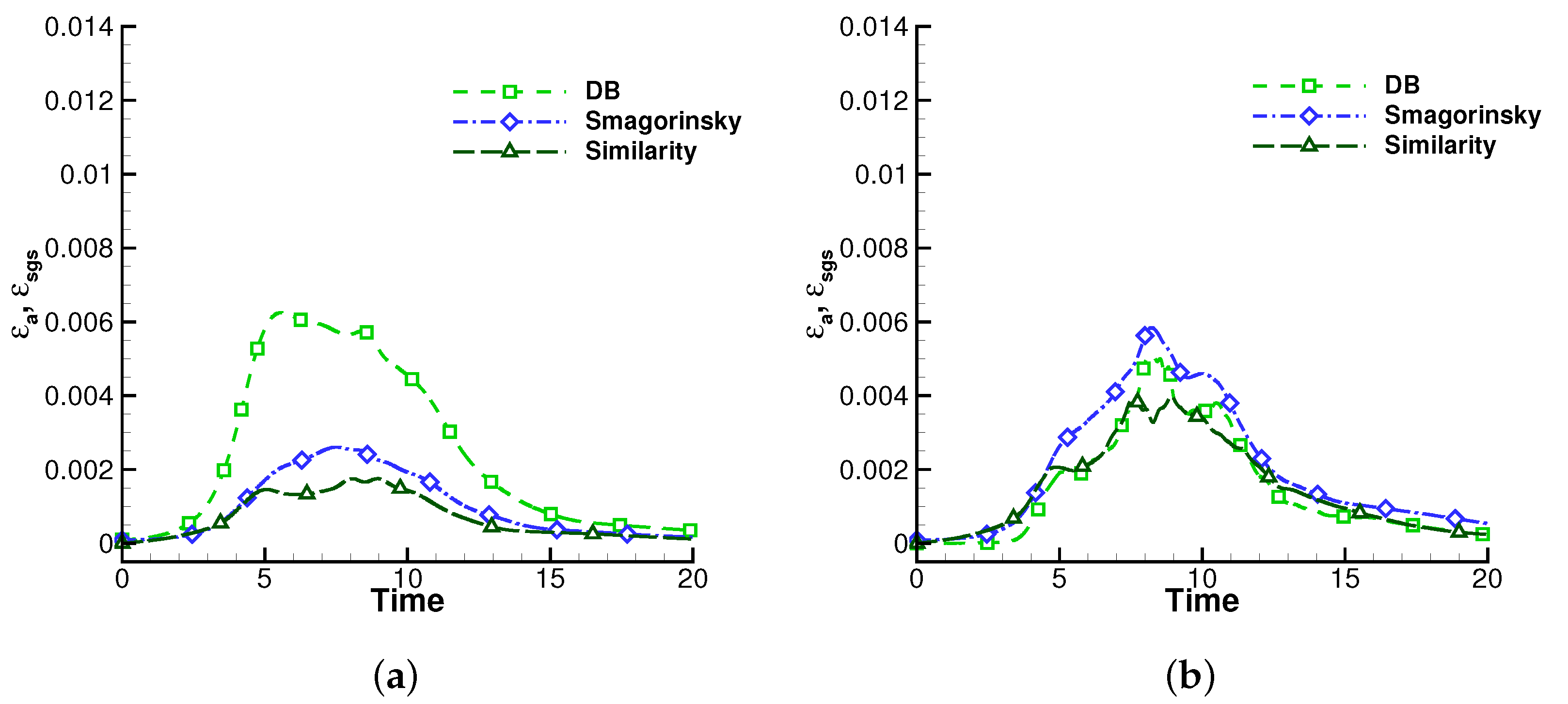
3. Decomposition of Total Turbulent Energy Dissipation Rate
4. Results and Discussion
4.1. Incompressible Taylor-Green Vortex
4.1.1. Effects of Polynomial Orders
4.1.2. Effects of the Explicit SGS Models and the DB Model
4.1.3. Discussion on Computational Cost
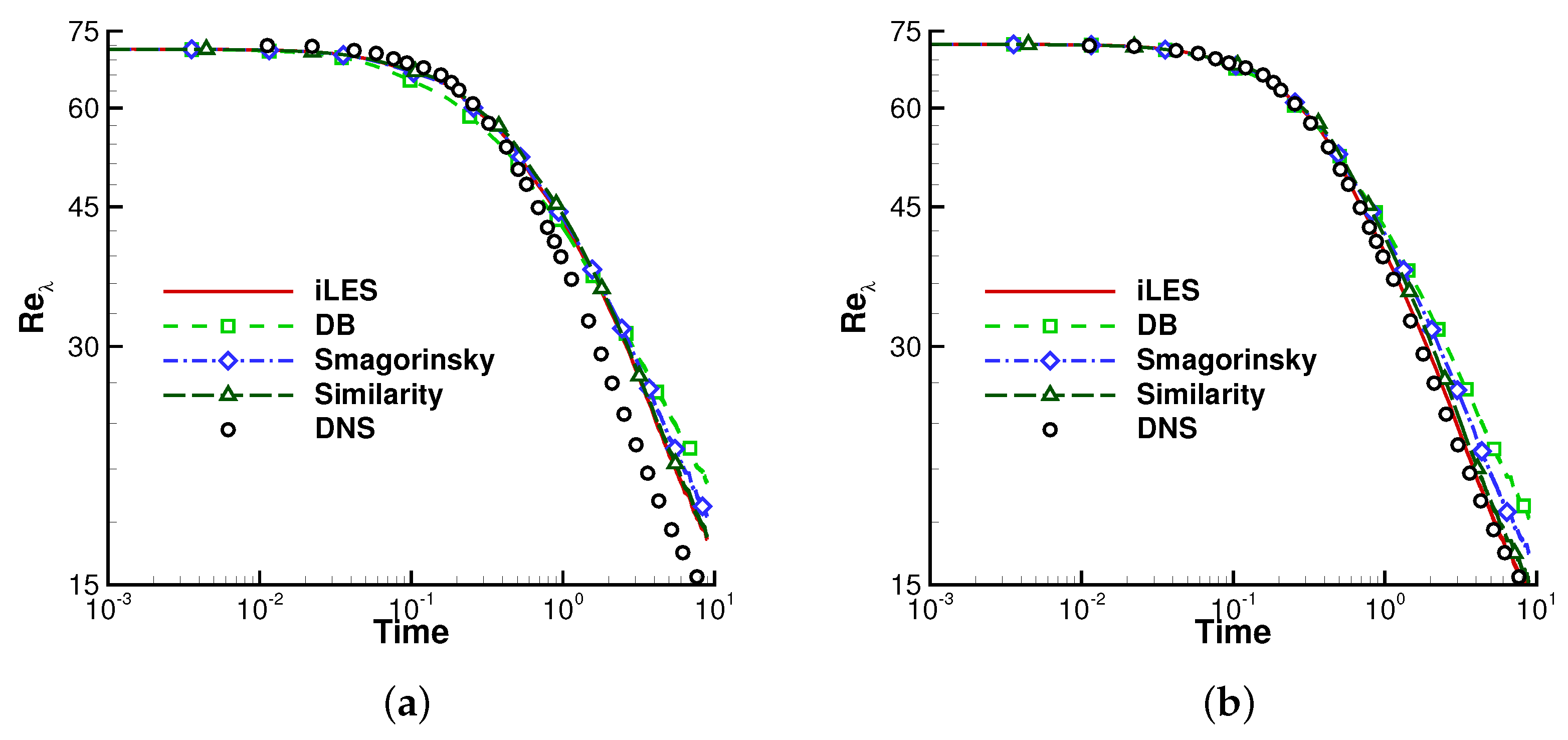
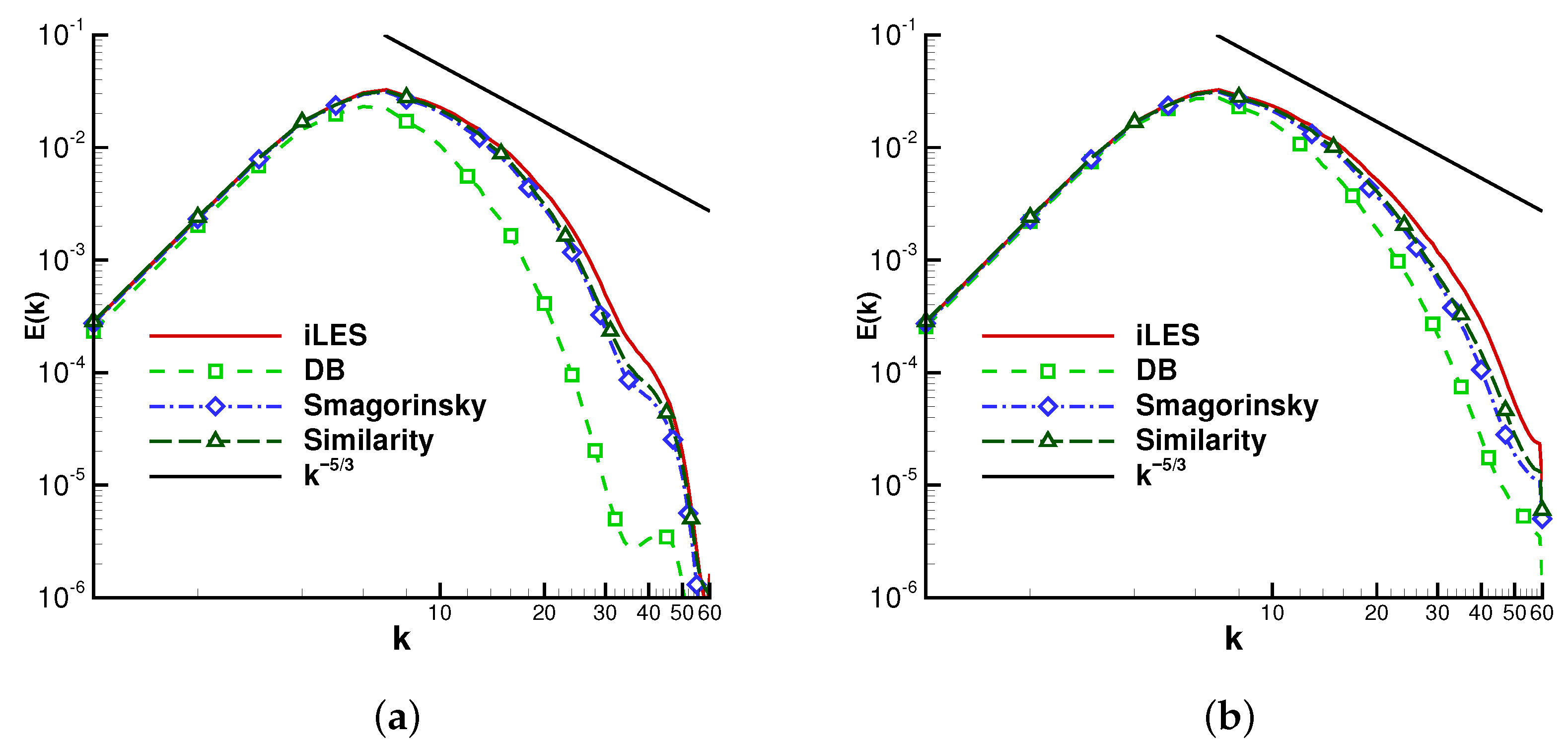
4.2. Homogeneous Isotropic Turbulence
4.2.1. Effects of Polynomial Orders
4.2.2. Effects of the Explicit SGS Models and the DB Model
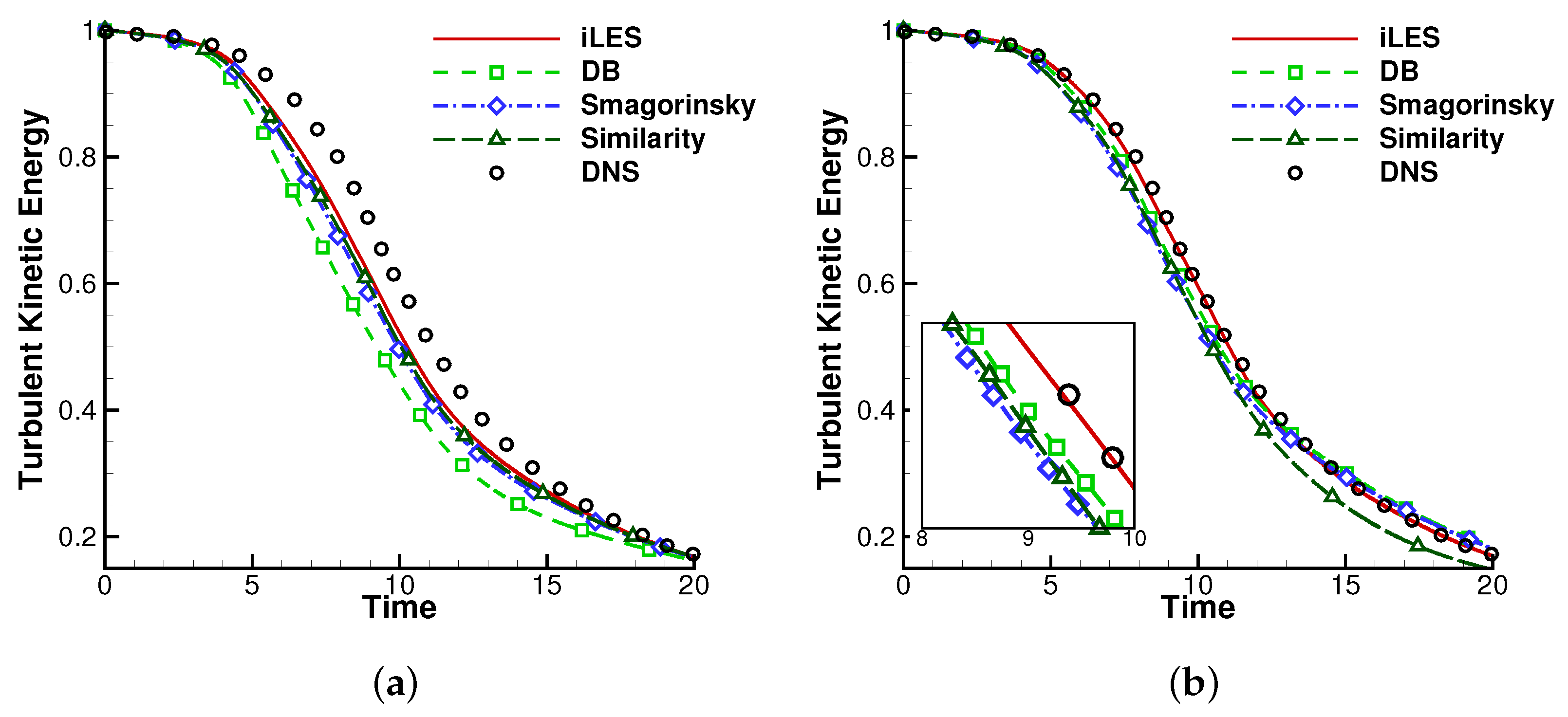
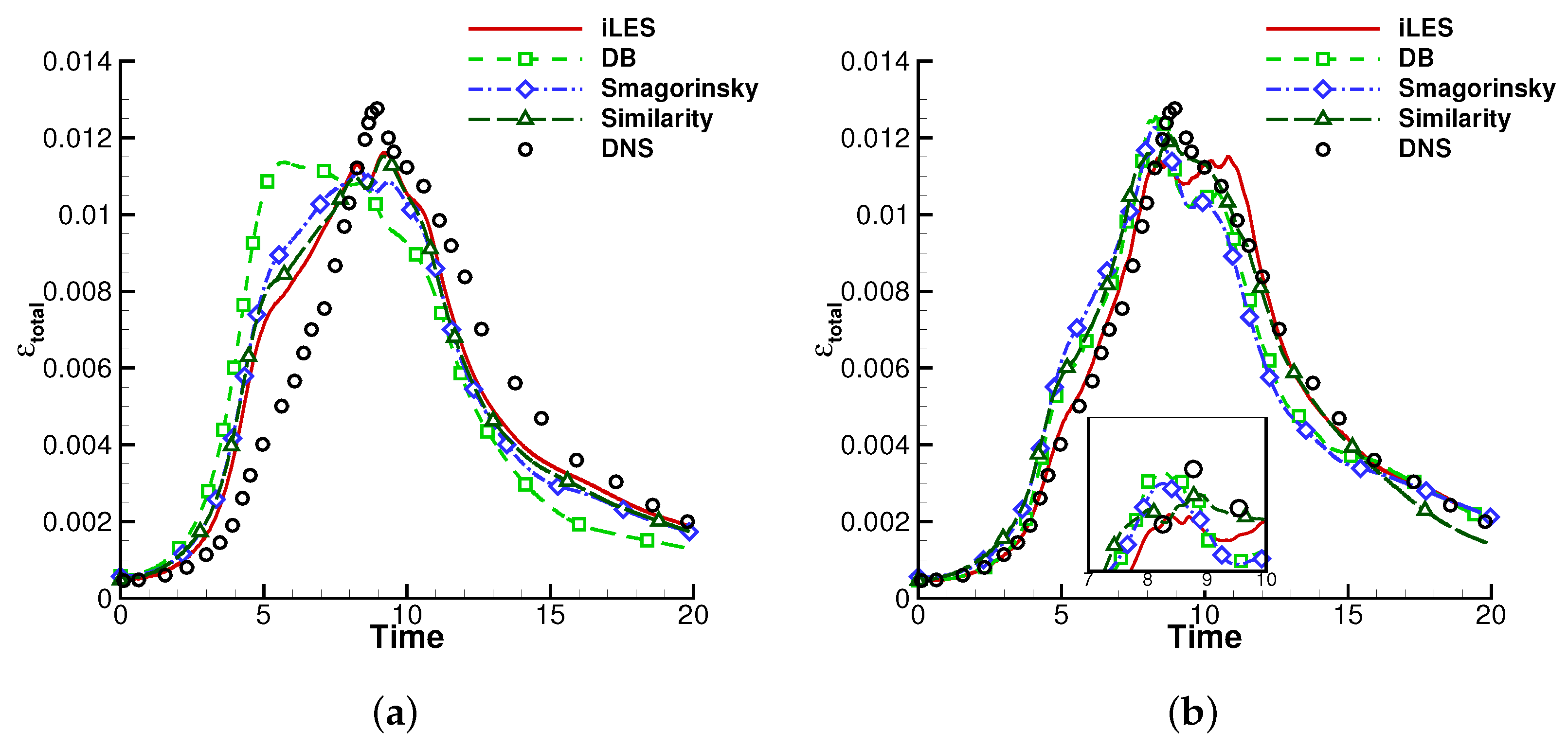
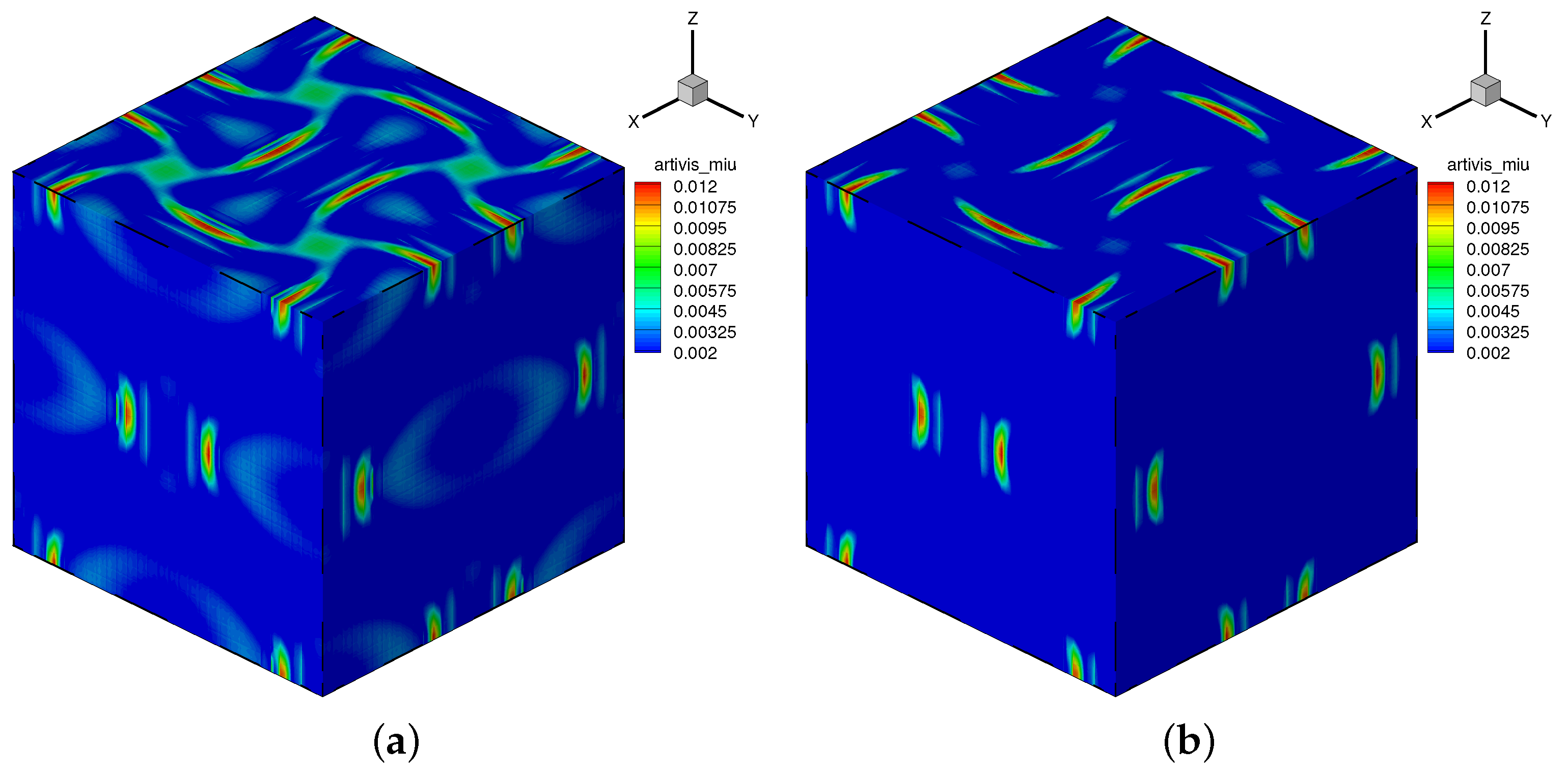
4.3. Compressible Taylor-Green Vortex
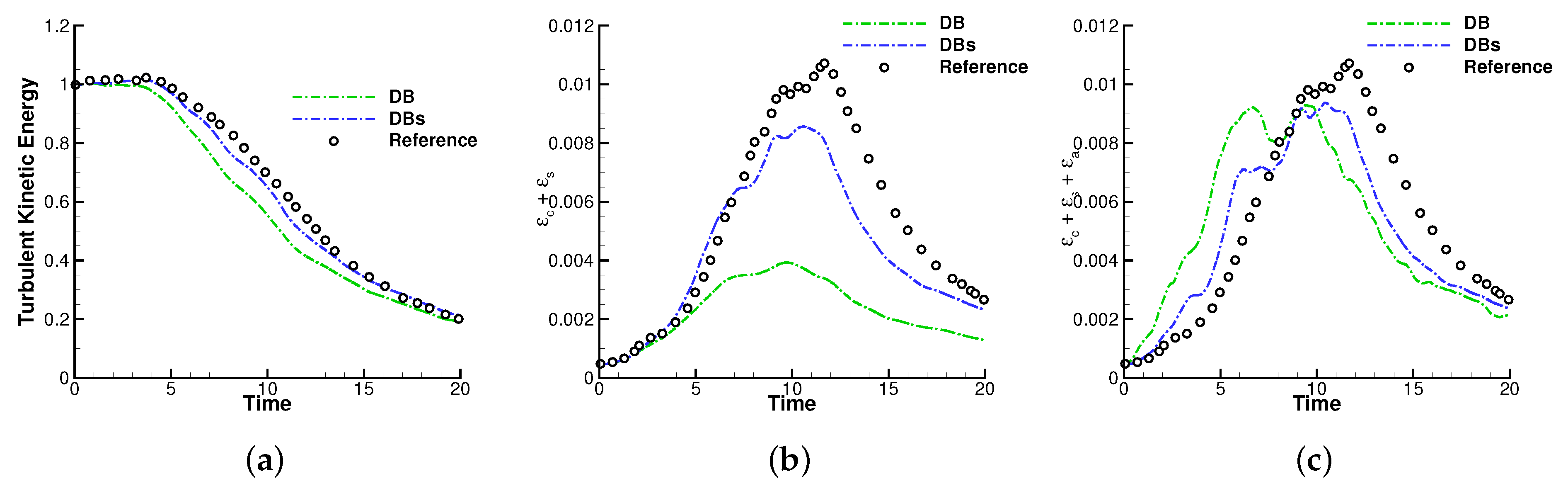
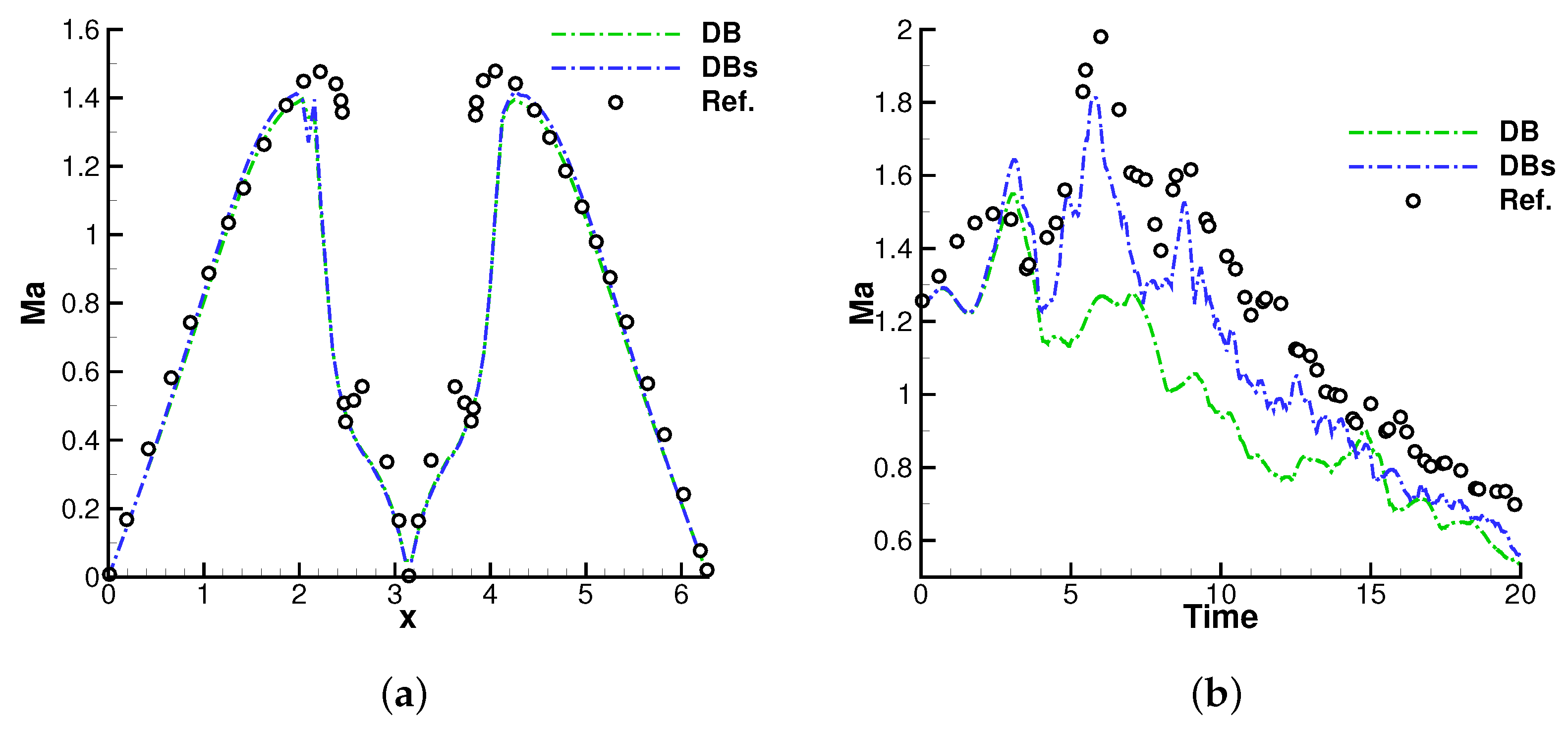
4.4. Compressible Channel Flow
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| LES | large eddy simulation |
| RANS | Reynolds Averaged Navier-Stokes |
| DNS | Direct Numerical Simulation |
| FVM | finite volume method |
| DG | discontinuous Galerkin |
| SD | spectral difference |
| FR | flux reconstruction |
| CPR | correction procedure via reconstruction |
| DOFs | degrees of freedom |
| DPW | DOFs per wave |
| ESFR | energy-stable flux reconstruction |
| TVB | total variation bounded |
| WENO | weighted essentially non-oscillatory |
| DB | dilation-based |
| SGS | subgrid scale |
| TGV | Taylor-Green vortex |
| HIT | homogeneous isotropic turbulence |
| iLES | implicit large eddy simulation |
| SPs | solution points |
| SSPRK54 | strong stability preserving five-stage fourth-order Runge-Kutta |
References
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Technical Report; NASA: Washington, DC, USA, 2013. [Google Scholar]
- Paliath, U.; Premasuthan, S. Large eddy simulation for jet installation effects. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2137. [Google Scholar]
- Wei, X.; Zhang, M.; An, Z.; Wang, J.; Huang, Z.; Tan, H. Large eddy simulation on flame topologies and the blow-off characteristics of ammonia/air flame in a model gas turbine combustor. Fuel 2021, 298, 120846. [Google Scholar] [CrossRef]
- Asada, K.; Kawai, S. Large-eddy simulation of airfoil flow near stall condition at Reynolds number 2.1 ×106. Phys. Fluids 2018, 30, 085103. [Google Scholar] [CrossRef]
- Garnier, E.; Adams, N.; Sagaut, P. Large Eddy Simulation for Compressible Flows; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Vermeire, B.C.; Nadarajah, S.; Tucker, P.G. Implicit large eddy simulation using the high-order correction procedure via reconstruction scheme. Int. J. Numer. Methods Fluids 2016, 82, 231–260. [Google Scholar] [CrossRef]
- Garnier, E.; Mossi, M.; Sagaut, P.; Comte, P.; Deville, M.O. On the Use of Shock-Capturing Schemes for Large-Eddy Simulation. J. Comput. Phys. 1999, 153, 273–311. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Jia, F.; Laskowski, G.; Kopriva, J.; Paliath, U.; Bhaskaran, R. Towards industrial large eddy simulation using the FR/CPR method. Comput. Fluids 2017, 156, 579–589. [Google Scholar] [CrossRef]
- Cockburn, B.; Karniadakis, G.E.; Shu, C.W. Discontinuous Galerkin Methods: Theory, Computation and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 11. [Google Scholar]
- Liu, Y.; Vinokur, M.; Wang, Z. Spectral difference method for unstructured grids I: Basic formulation. J. Comput. Phys. 2006, 216, 780–801. [Google Scholar] [CrossRef]
- Huynh, H.T. A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods. In Proceedings of the Collection of Technical Papers—18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; Volume 1, pp. 698–739. [Google Scholar] [CrossRef]
- Haga, T.; Gao, H.; Wang, Z.J. A High-Order Unifying Discontinuous Formulation for the Navier-Stokes Equations on 3D Mixed Grids. Math. Model. Nat. Phenom. 2011, 6, 28–56. [Google Scholar] [CrossRef]
- Lodato, G.; Castonguay, P.; Jameson, A. Structural Wall-modeled LES Using a High-order Spectral Difference Scheme for Unstructured Meshes. Flow Turbul. Combust. 2014, 92, 579–606. [Google Scholar] [CrossRef]
- Yi, L.U.; Kai, L.; Dawes, W.N. Flow simulation system based on high order space-time extension of flux reconstruction method. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Uranga, A.; Persson, P.O.; Drela, M.; Peraire, J. Implicit Large Eddy Simulation of transition to turbulence at low Reynolds numbers using a Discontinuous Galerkin method. Int. J. Numer. Methods Eng. 2011, 87, 232–261. [Google Scholar] [CrossRef]
- Vermeire, B.; Witherden, F.; Vincent, P. On the utility of GPU accelerated high-order methods for unsteady flow simulations: A comparison with industry-standard tools. J. Comput. Phys. 2017, 334, 497–521. [Google Scholar] [CrossRef]
- Fernandez, P.; Nguyen, N.C.; Peraire, J. On the ability of discontinuous Galerkin methods to simulate under-resolved turbulent flows. arXiv 2018, arXiv:1810.09435. [Google Scholar]
- Witherden, F.D.; Vermeire, B.C.; Vincent, P.E. Heterogeneous Computing on Mixed Unstructured Grids with PyFR. Comput. Fluids 2014, 120, 173–186. [Google Scholar] [CrossRef]
- Lodato, G.; Castonguay, P.; Jameson, A. Discrete filter operators for large-eddy simulation using high-order spectral difference methods. Int. J. Numer. Methods Fluids 2013, 72, 231–258. [Google Scholar] [CrossRef]
- Blackburn, H.M.; Schmidt, S. Spectral element filtering techniques for large eddy simulation with dynamic estimation. J. Comput. Phys. 2003, 186, 610–629. [Google Scholar] [CrossRef]
- Vincent, P.E.; Castonguay, P.; Jameson, A. A new class of high-order energy stable flux reconstruction schemes. J. Sci. Comput. 2011, 47, 50–72. [Google Scholar] [CrossRef]
- Castonguay, P.; Williams, D.M.; Vincent, P.E.; Jameson, A. Energy stable flux reconstruction schemes for advection–diffusion problems. Comput. Methods Appl. Mech. Eng. 2013, 267, 400–417. [Google Scholar] [CrossRef]
- Williams, D.M.; Castonguay, P.; Vincent, P.E.; Jameson, A. Energy stable flux reconstruction schemes for advection–diffusion problems on triangles. J. Comput. Phys. 2013, 250, 53–76. [Google Scholar] [CrossRef]
- Williams, D.; Jameson, A. Energy stable flux reconstruction schemes for advection–diffusion problems on tetrahedra. J. Sci. Comput. 2014, 59, 721–759. [Google Scholar] [CrossRef]
- Wang, Z.J.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck, H.; Hartmann, R.; Hillewaert, K.; Huynh, H.T.; et al. High-order CFD methods: Current status and perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar] [CrossRef]
- Vermeire, B.; Cagnone, J.S.; Nadarajah, S. ILES using the correction procedure via reconstruction scheme. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 1001. [Google Scholar]
- Lodato, G.; Chapelier, J.B. Evaluation of the spectral element dynamic model for large-eddy simulation on unstructured, deformed meshes. Flow Turbul. Combust. 2018, 101, 271–294. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Liu, Y. Spectral (finite) volume method for conservation laws on unstructured grids IV: Extension to two-dimensional systems. J. Comput. Phys. 2004, 194, 716–741. [Google Scholar] [CrossRef]
- Shu, C.W. TVB uniformly high-order schemes for conservation laws. Math. Comput. 1987, 49, 105–121. [Google Scholar] [CrossRef]
- Biswas, R.; Devine, K.D.; Flaherty, J.E. Parallel, adaptive finite element methods for conservation laws. Appl. Numer. Math. 1994, 14, 255–283. [Google Scholar] [CrossRef]
- Burbeau, A.; Sagaut, P.; Bruneau, C.H. A problem-independent limiter for high-order RungeKutta discontinuous Galerkin methods. J. Comput. Phys. 2001, 169, 111–150. [Google Scholar] [CrossRef]
- Krivodonova, L. Limiters for high-order discontinuous Galerkin methods. J. Comput. Phys. 2007, 226, 879–896. [Google Scholar] [CrossRef]
- Qiu, J.; Shu, C.W. Runge–Kutta Discontinuous Galerkin Method Using WENO Limiters. SIAM J. Sci. Comput. 2005, 26, 907–929. [Google Scholar] [CrossRef]
- Luo, H.; Baum, J.D.; Lohner, R. A Hermite WENO-based limiter for discontinuous galerkin method on unstructured grids. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Cook, A.W.; Cabot, W.H. Hyperviscosity for shock-turbulence interactions. J. Comput. Phys. 2005, 203, 379–385. [Google Scholar] [CrossRef]
- Mani, A.; Larsson, J.; Moin, P. Suitability of artificial bulk viscosity for large-eddy simulation of turbulent flows with shocks. J. Comput. Phys. 2009, 228, 7368–7374. [Google Scholar] [CrossRef]
- Yu, J.; Hesthaven, J.S. A study of several artificial viscosity models within the discontinuous galerkin framework. Commun. Comput. Phys. 2020, 27, 1309–1343. [Google Scholar]
- Blaisdell, G.A. Review of “Implicit Large Eddy Simulation: Computing Turbulent Fluid Dynamics”. AIAA J. 2008, 46, 3168–3170. [Google Scholar] [CrossRef]
- Fernandez, P.; Nguyen, N.C.; Peraire, J. A physics-based shock capturing method for large-eddy simulation. arXiv 2018, arXiv:1806.06449. [Google Scholar]
- Kawai, S.; Shankar, S.K.; Lele, S.K. Assessment of localized artificial diffusivity scheme for large-eddy simulation of compressible turbulent flows. J. Comput. Phys. 2010, 229, 1739–1762. [Google Scholar] [CrossRef]
- Ansorge, R.; Bijl, H.; Meister, A.; Sonar, T. Recent Developments in the Numerics of Nonlinear Hyperbolic Conservation Laws: Lectures Presented at a Workshop at the Mathematical Research Institute, Oberwolfach, Germany, 15–21 January 2012; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 120. [Google Scholar]
- Lusher, D.J.; Sandham, N.D. Assessment of low-dissipative shock-capturing schemes for the compressible Taylor–Green vortex. AIAA J. 2021, 59, 533–545. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Lodato, G.; Vervisch, L.; Domingo, P. A compressible wall-adapting similarity mixed model for large-eddy simulation of the impinging round jet. Phys. Fluids 2009, 21, 35102. [Google Scholar] [CrossRef]
- Roe, P. Efficient construction and utilization of approximate Riemann solutions. Comput. Methods Appl. Sci. Eng. 1984, 6, 499–518. [Google Scholar]
- Peraire, J.; Persson, P.O. The compact discontinuous galerkin (CDG) method for elliptic problems. SIAM J. Sci. Comput. 2007, 30, 1806–1824. [Google Scholar] [CrossRef]
- Gottlieb, S. On high order strong stability preserving Runge-Kutta and multi step time discretizations. J. Sci. Comput. 2005, 25, 105–128. [Google Scholar] [CrossRef]
- Smagorinsky, J.S. General Circulation Experiments with the Primitive Equations. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Bardina, J.; Ferziger, J.; Reynolds, W. Improved subgrid-scale models for large-eddy simulation. In Proceedings of the 13th Fluid and Plasmadynamics Conference, Snowmass, CO, USA, 14–16 July 1980; p. 1357. [Google Scholar]
- Carton de Wiart, C.; Hillewaert, K.; Duponcheel, M.; Winckelmans, G. Assessment of a discontinuous Galerkin method for the simulation of vortical flows at high Reynolds number. Int. J. Numer. Methods Fluids 2014, 74, 469–493. [Google Scholar] [CrossRef]
- Samtaney, R.; Pullin, D.I.; Kosović, B. Direct numerical simulation of decaying compressible turbulence and shocklet statistics. Phys. Fluids 2001, 13, 1415–1430. [Google Scholar] [CrossRef]
- Taylor, G.I.; Green, A.E. Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 158, 499–521. [Google Scholar] [CrossRef]
- Debonis, J.R. Solutions of the Taylor-Green vortex problem using high-resolution explicit finite difference methods. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Bogey, C.; Bailly, C. A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 2004, 194, 194–214. [Google Scholar] [CrossRef]
- Shu, C.W.; Don, W.S.; Gottlieb, D.; Schilling, O.; Jameson, L. Numerical convergence study of nearly incompressible, inviscid Taylor–Green vortex flow. J. Sci. Comput. 2005, 24, 1–27. [Google Scholar] [CrossRef]
- Bull, J.R.; Jameson, A. Simulation of the Taylor–Green vortex using high-order flux reconstruction schemes. AIAA J. 2015, 53, 2750–2761. [Google Scholar] [CrossRef]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; National Aeronautics and Space Administration: Washington, DA, USA, 1981; Volume 81315. [Google Scholar]
- Ristorcelli, J.R.; Blaisdell, G.A. Consistent initial conditions for the DNS of compressible turbulence. Phys. Fluids 1997, 9, 4–6. [Google Scholar] [CrossRef][Green Version]
- Movahed, P.; Johnsen, E. The mixing region in freely decaying variable-density turbulence. J. Fluid Mech. 2015, 772, 386–426. [Google Scholar] [CrossRef]
- Ducros, F.; Ferrand, V.; Nicoud, F.; Weber, C.; Darracq, D.; Gacherieu, C.; Poinsot, T. Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 1999, 152, 517–549. [Google Scholar] [CrossRef]
- Modesti, D.; Pirozzoli, S. Reynolds and Mach number effects in compressible turbulent channel flow. Int. J. Heat Fluid Flow 2016, 59, 33–49. [Google Scholar] [CrossRef]
- Le Bras, S.; Deniau, H.; Bogey, C.; Daviller, G. Development of compressible large-eddy simulations combining high-order schemes and wall modeling. AIAA J. 2017, 55, 1152–1163. [Google Scholar] [CrossRef]
- Huang, P.; Coleman, G.; Bradshaw, P. Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 1995, 305, 185–218. [Google Scholar] [CrossRef]


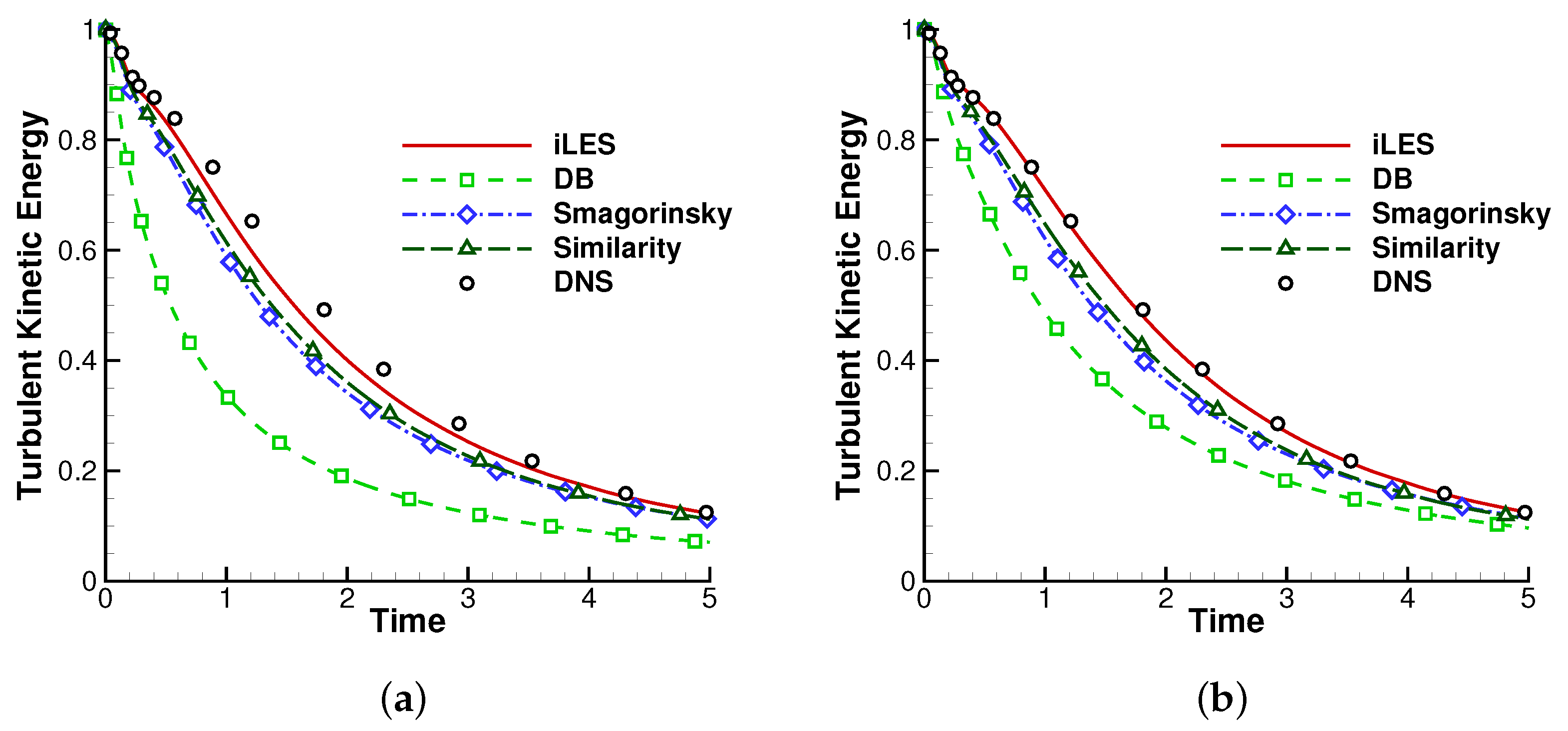
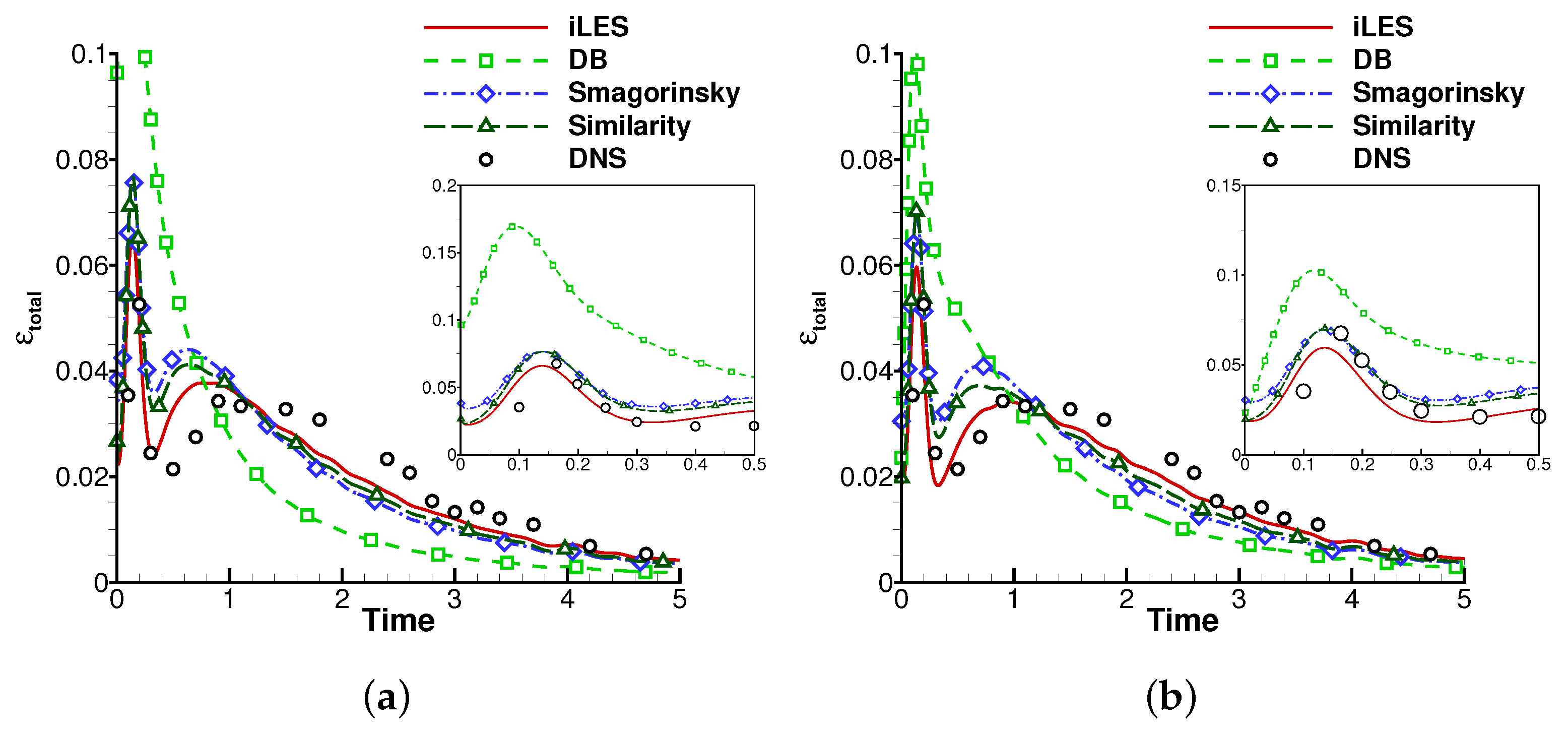
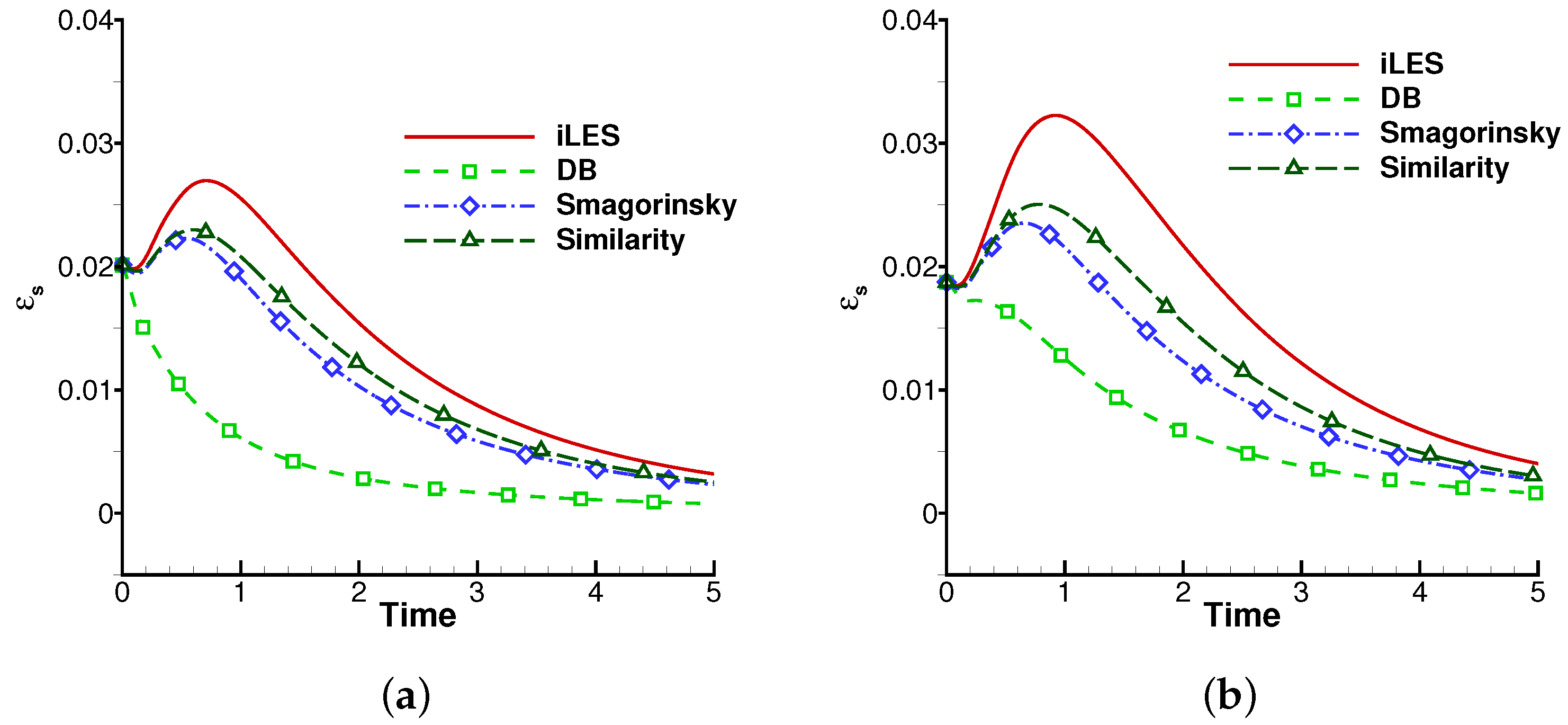
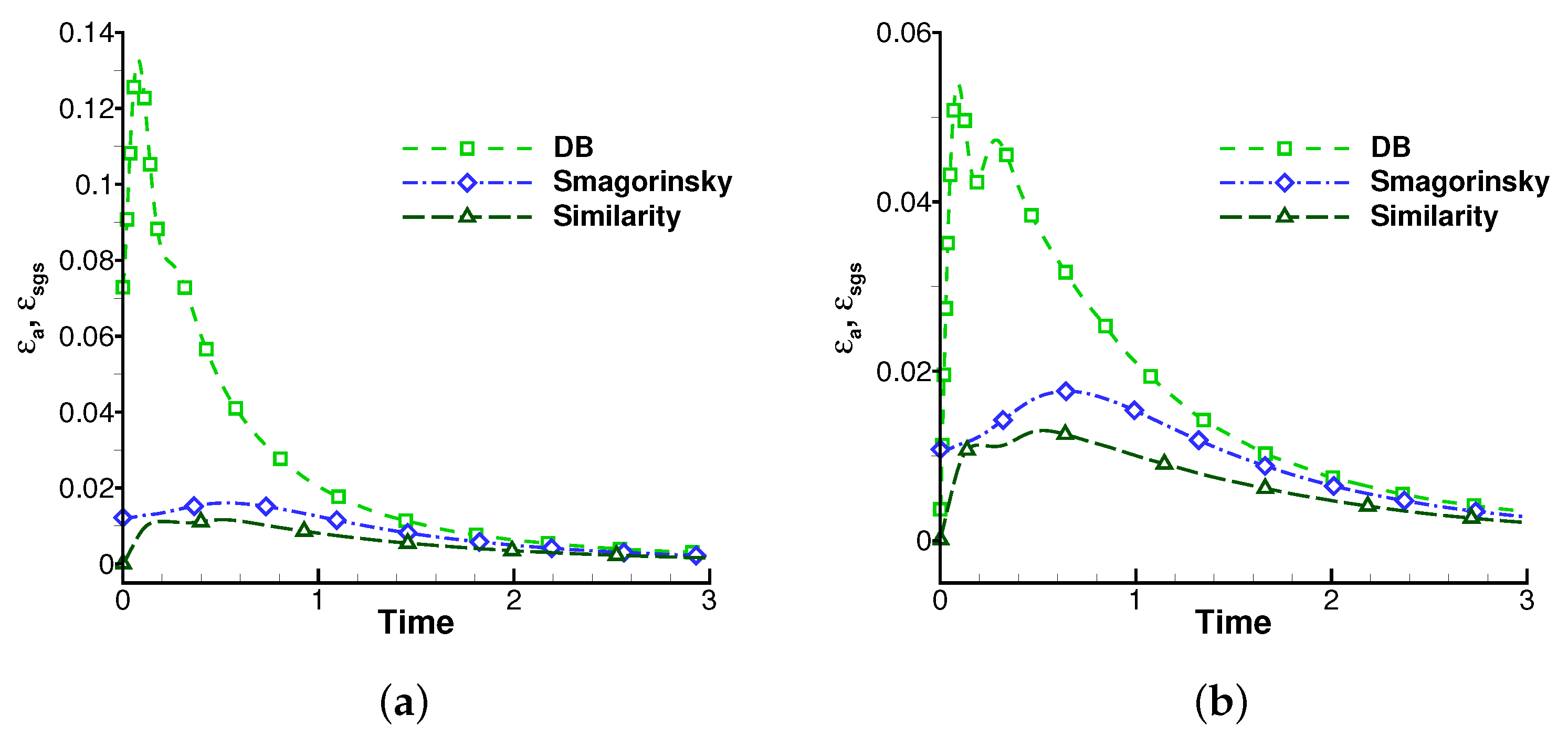

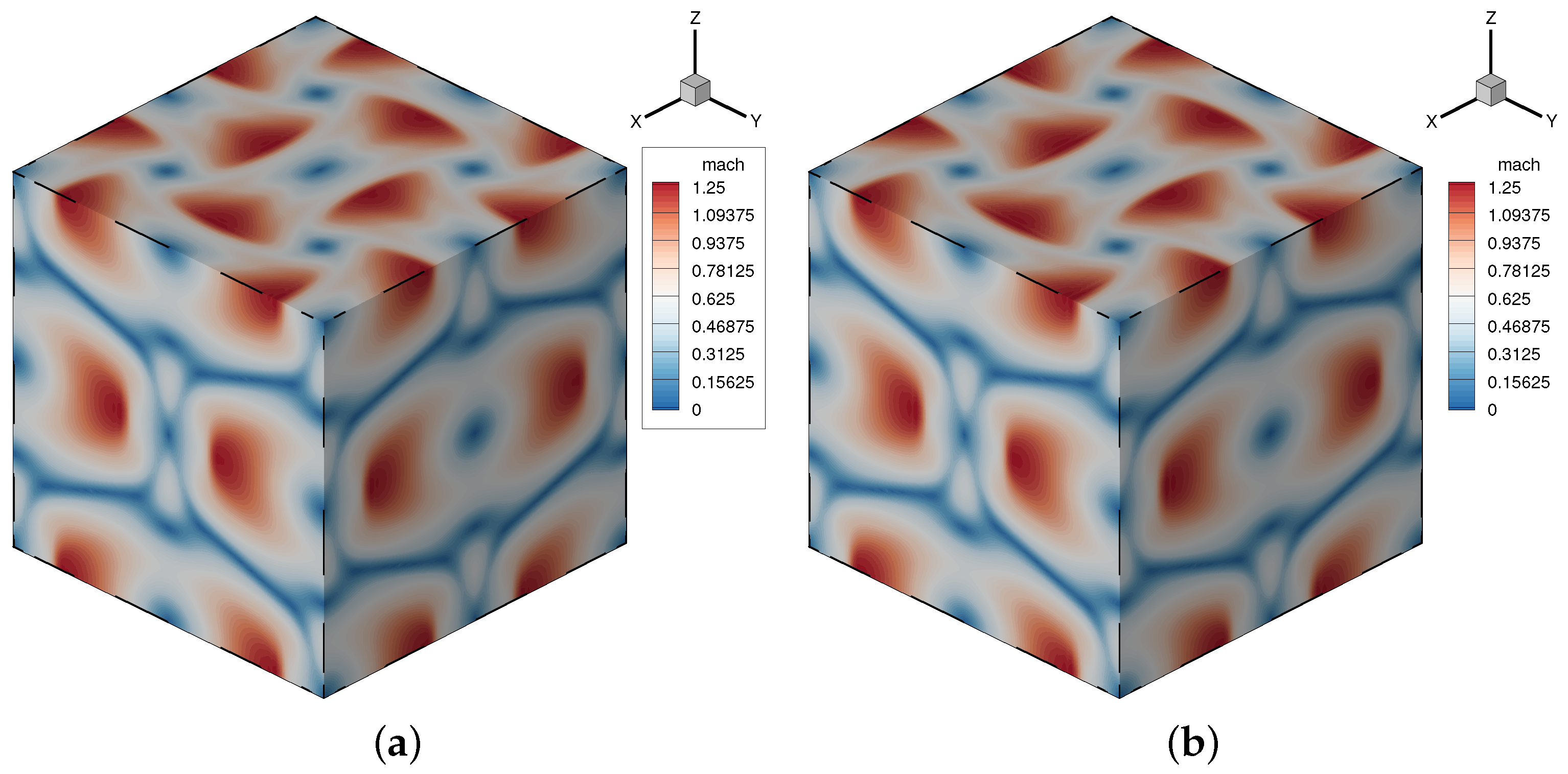


| Discretization | DOFs | Model | Runtime(s) | Ratio |
|---|---|---|---|---|
| elements, | 120 | iLES | 3443 | 1.0 |
| DB | 3935 | 1.14 | ||
| Smagorinsky | 4631 | 1.35 | ||
| similarity | 4823 | 1.40 | ||
| elements, | 120 | iLES | 3686 | 1.07 |
| DB | 4246 | 1.23 | ||
| Smagorinsky | 5197 | 1.51 | ||
| similarity | 5200 | 1.51 |
| Computation | DOF | ||||
|---|---|---|---|---|---|
| LES with DB method | 26 | 26 | 10 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Yan, C.; Yu, J. Suitability of an Artificial Viscosity Model for Compressible Under-Resolved Turbulence Using a Flux Reconstruction Method. Appl. Sci. 2022, 12, 12272. https://doi.org/10.3390/app122312272
Ma L, Yan C, Yu J. Suitability of an Artificial Viscosity Model for Compressible Under-Resolved Turbulence Using a Flux Reconstruction Method. Applied Sciences. 2022; 12(23):12272. https://doi.org/10.3390/app122312272
Chicago/Turabian StyleMa, Libin, Chao Yan, and Jian Yu. 2022. "Suitability of an Artificial Viscosity Model for Compressible Under-Resolved Turbulence Using a Flux Reconstruction Method" Applied Sciences 12, no. 23: 12272. https://doi.org/10.3390/app122312272
APA StyleMa, L., Yan, C., & Yu, J. (2022). Suitability of an Artificial Viscosity Model for Compressible Under-Resolved Turbulence Using a Flux Reconstruction Method. Applied Sciences, 12(23), 12272. https://doi.org/10.3390/app122312272





