Human Randomness in the Rock-Paper-Scissors Game
Abstract
1. Introduction
2. Evaluation of RPS Time Series
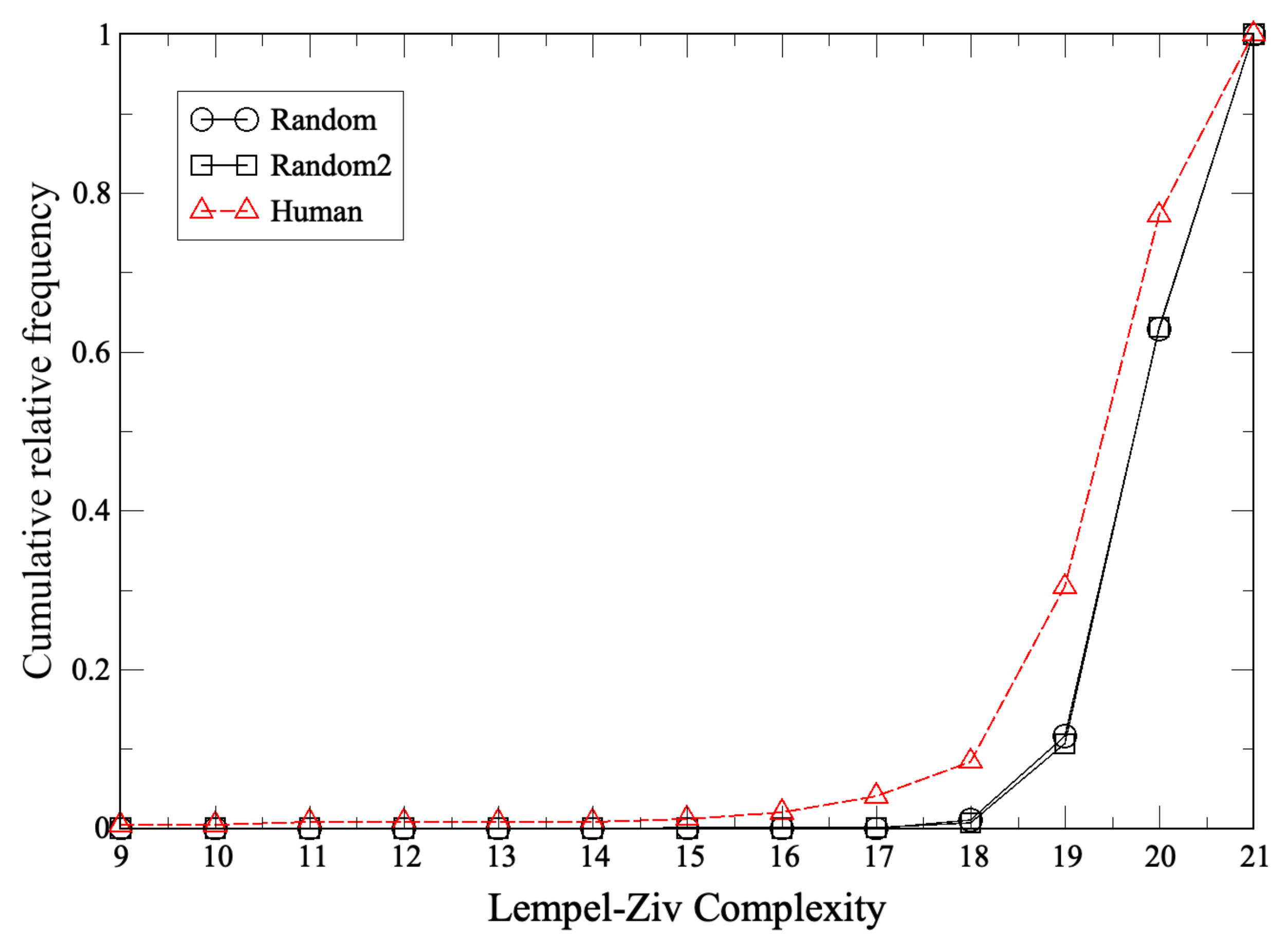
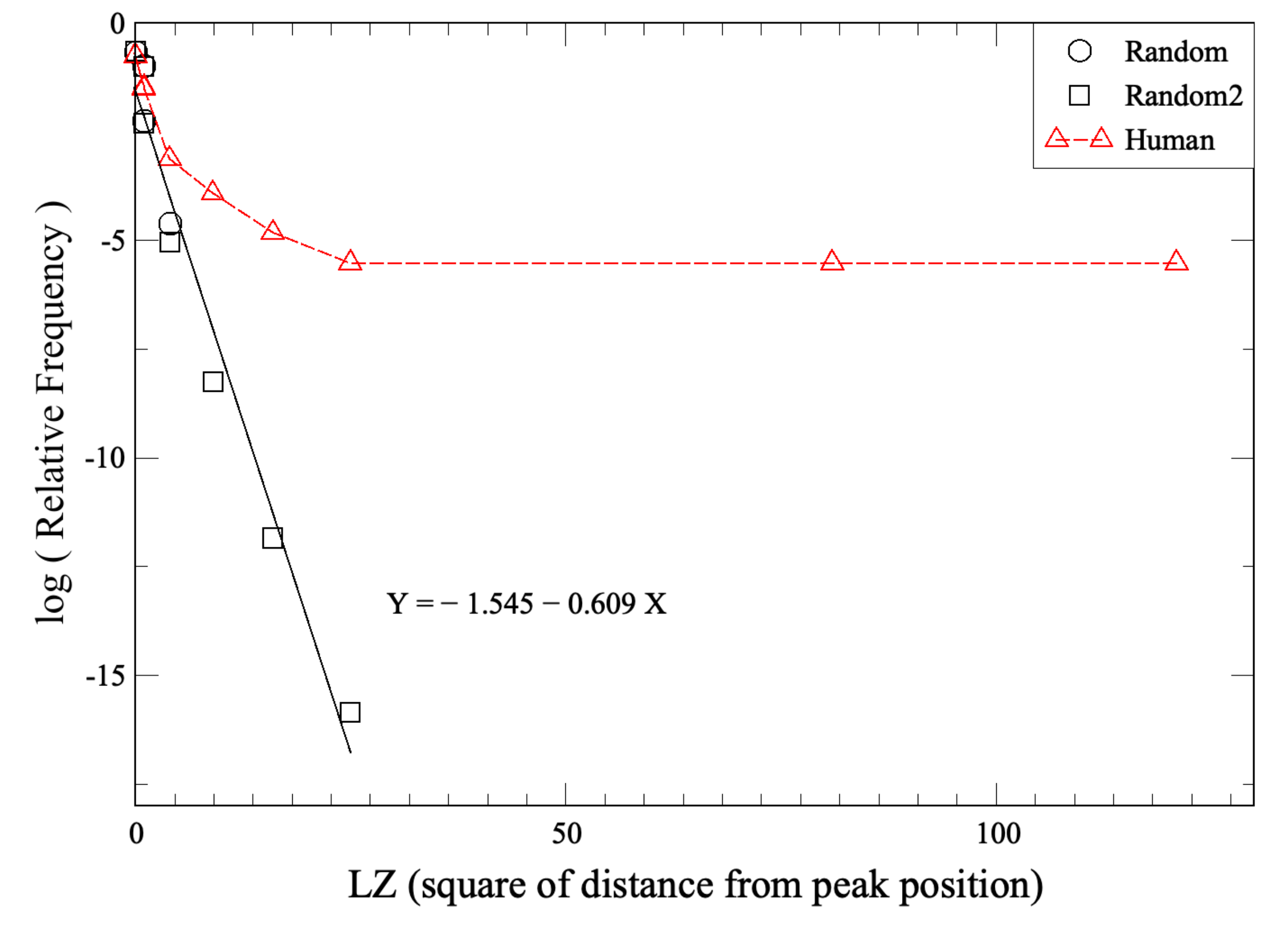
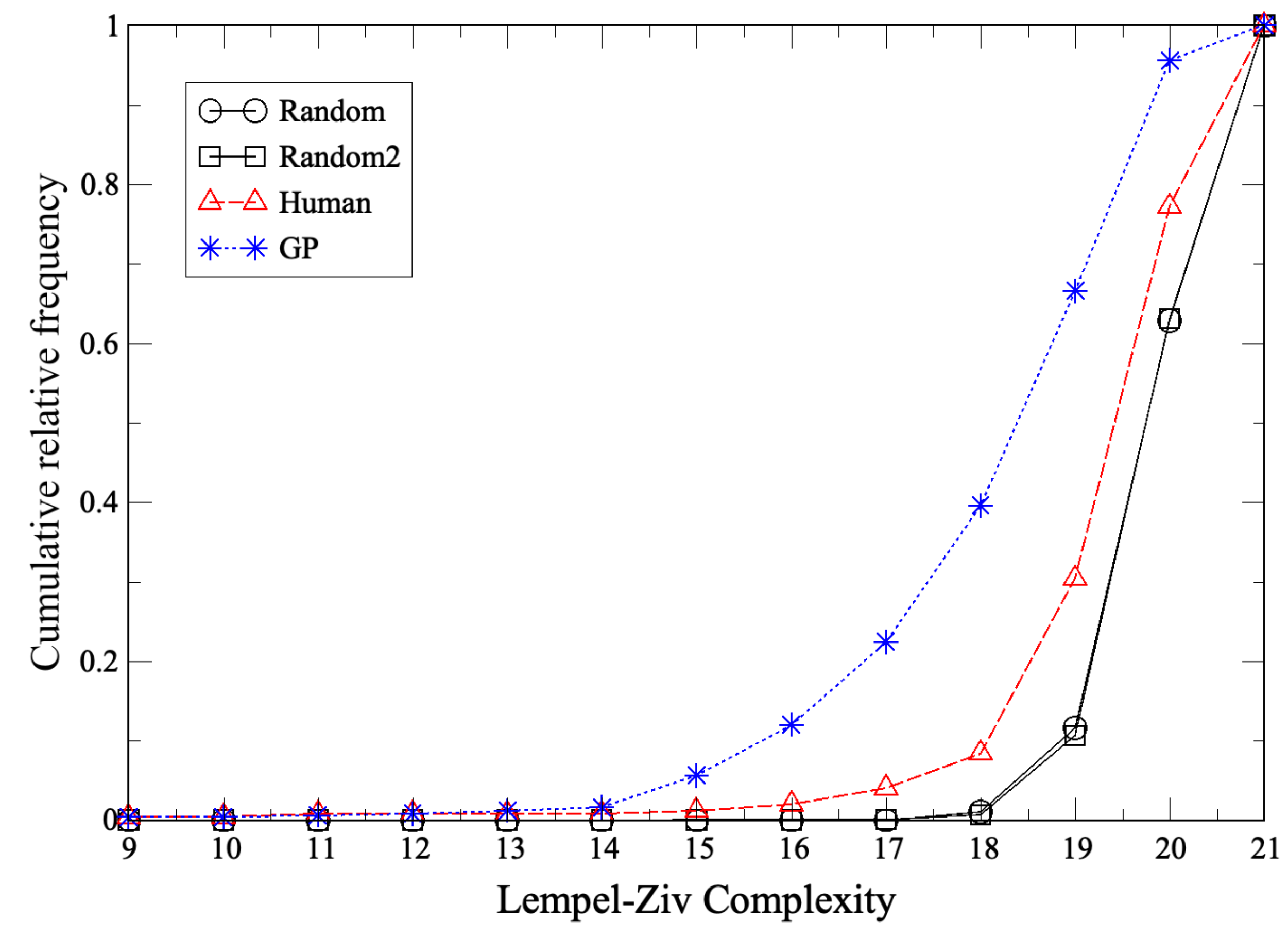
2.1. Lempel–Ziv Complexity
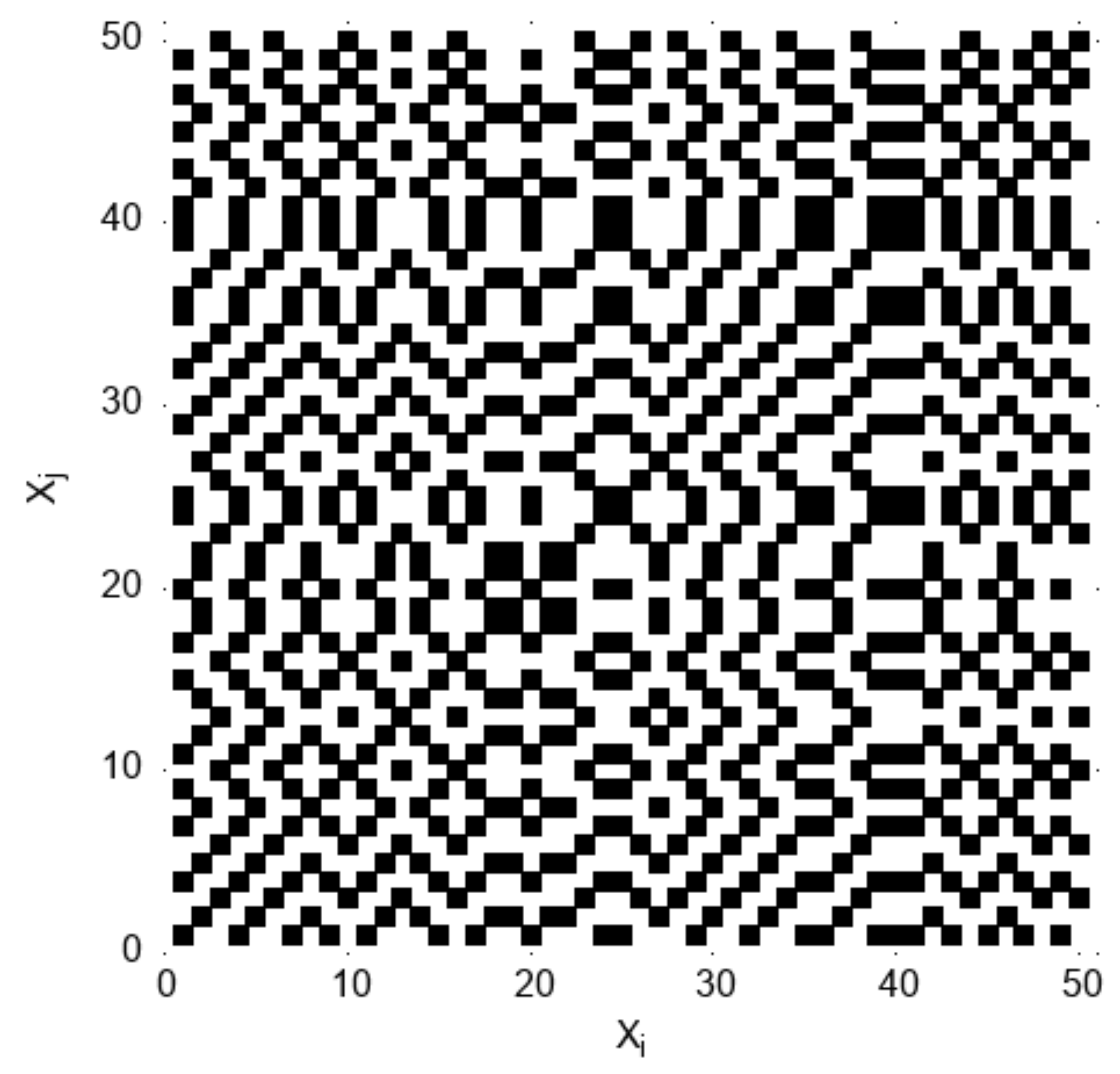
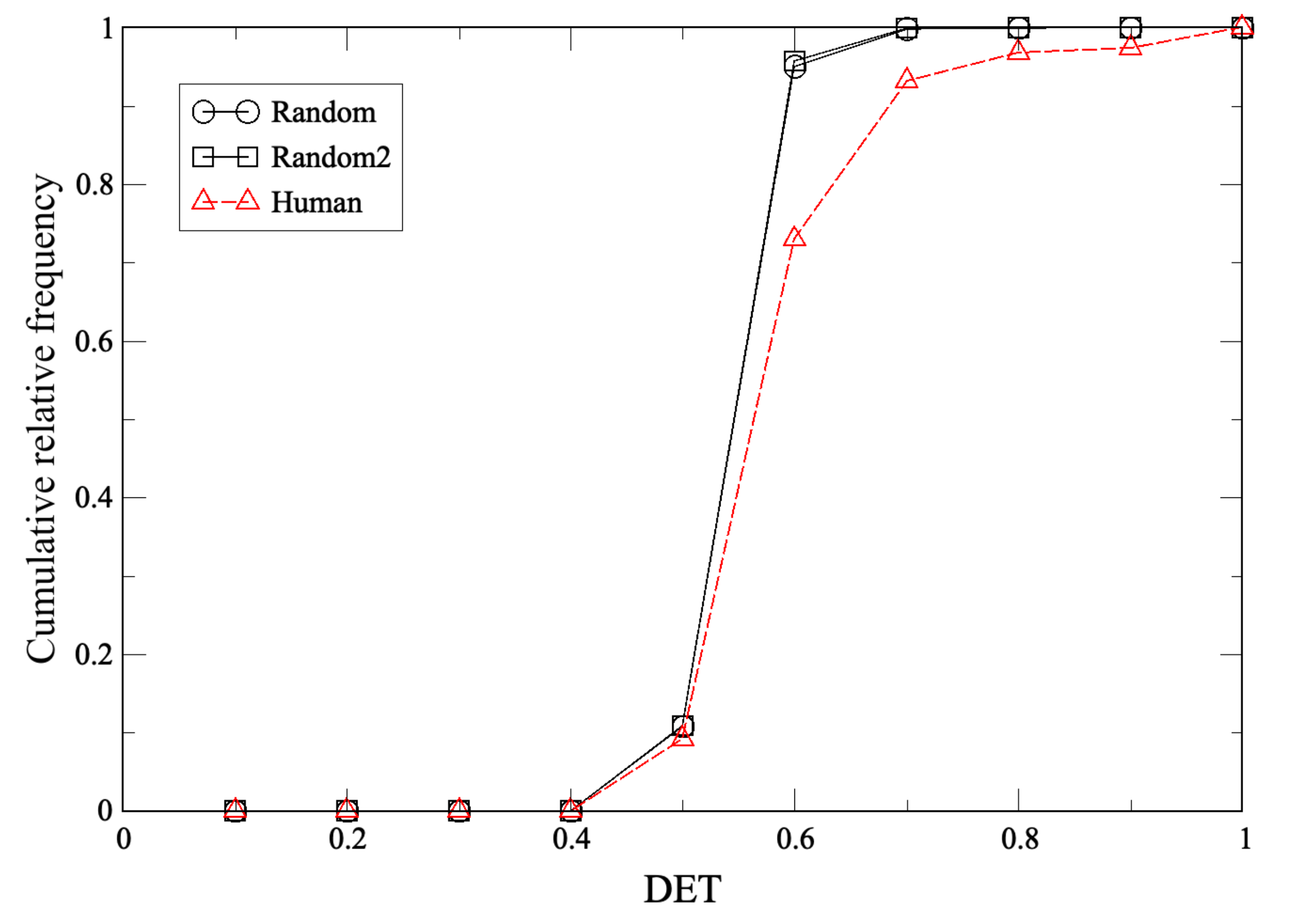
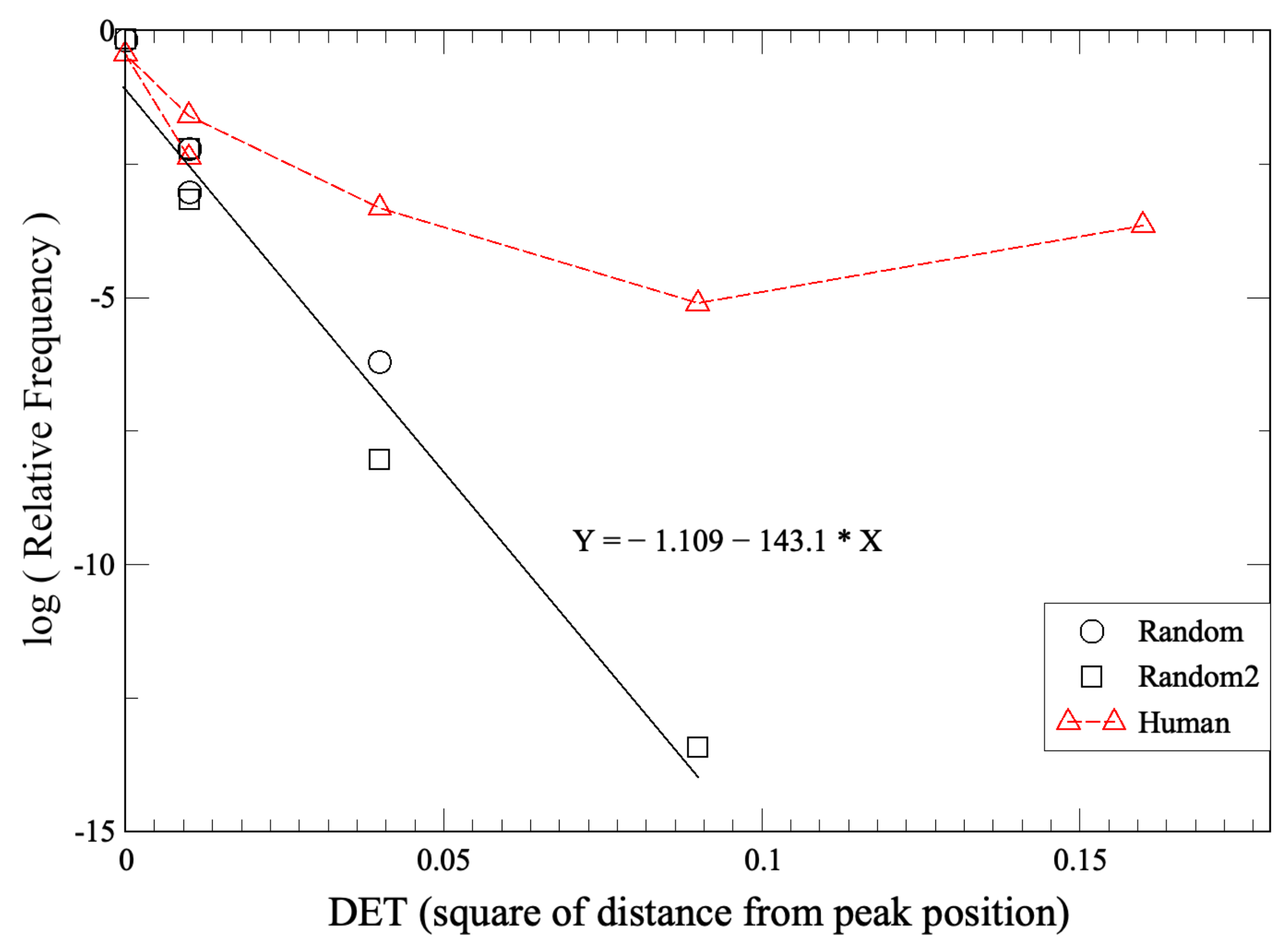
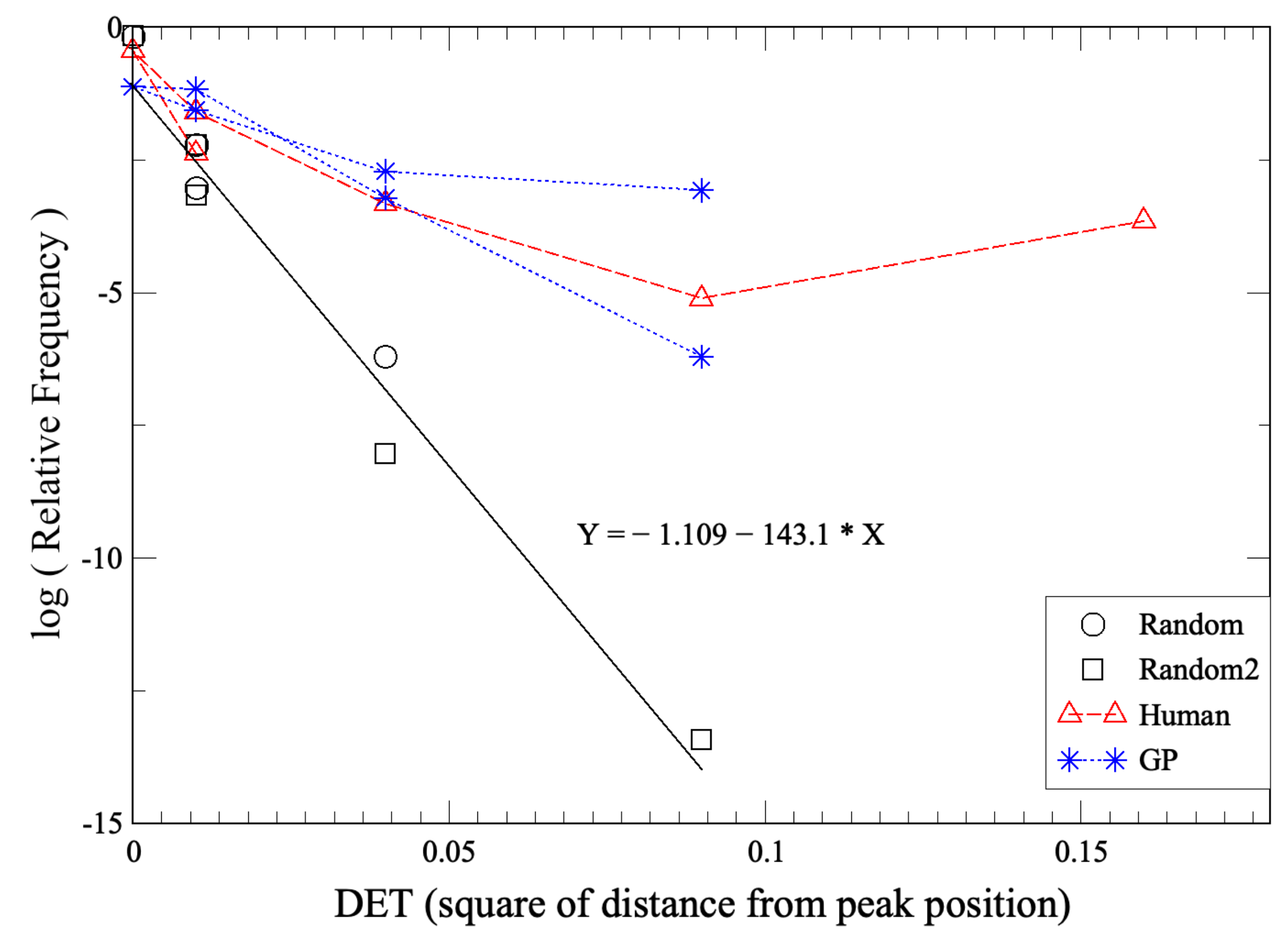
2.2. Recurrence Plot
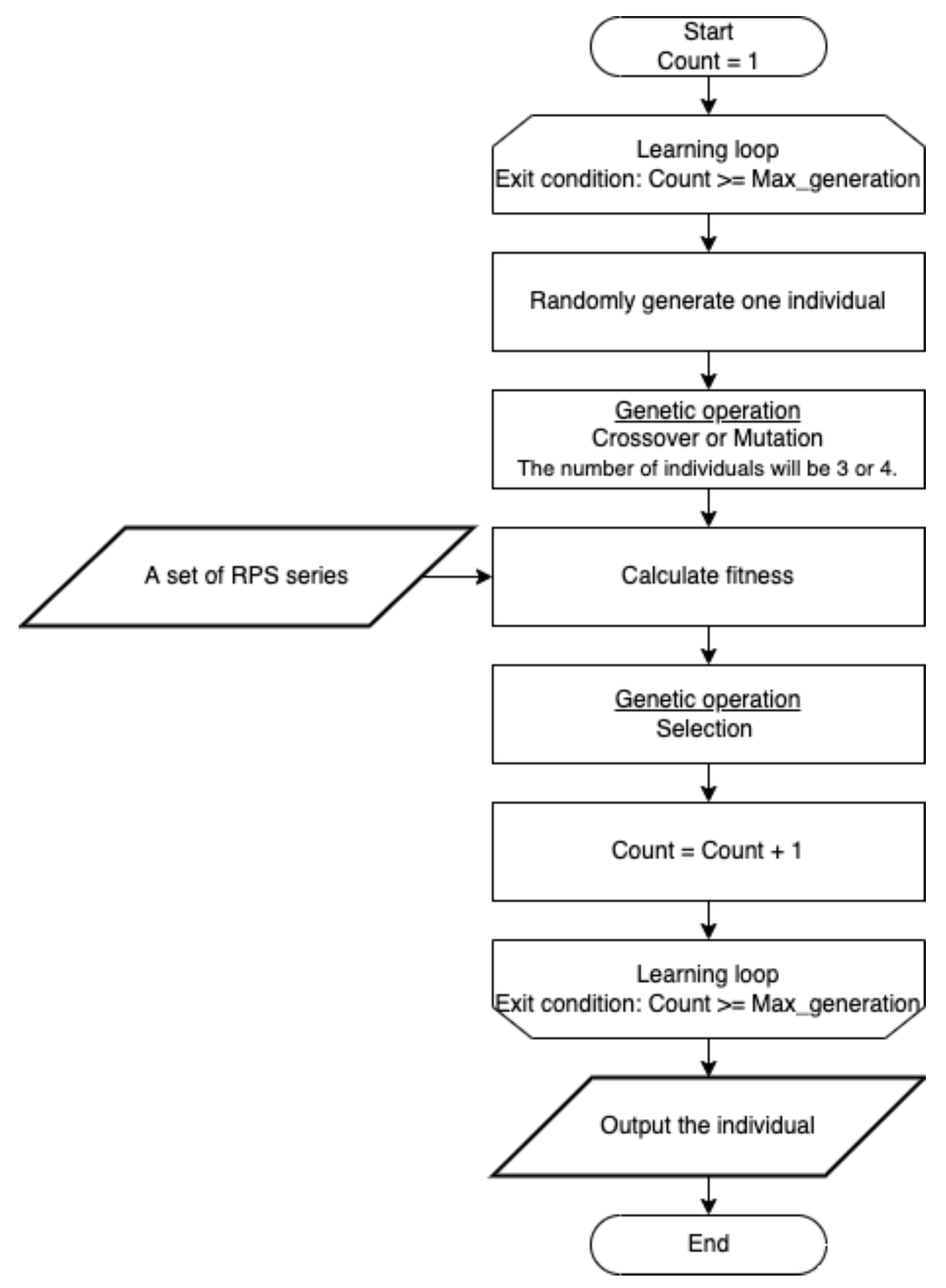
3. Strategy Inference from RPS Time Series Using Genetic Programming
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RPS | Rock-Paper-Scissors |
| DET | DETerminism |
| GA | Genetic Algorithm |
| GP | Genetic Programming |
Appendix A. Lempel–Ziv Complexity
| Algorithm A1 pseudocode to calculate Lempel–Ziv complexity |
|
Appendix B. DET from Recurrence Plot and Application to RPS Time Series
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the NeurIPS 2012, Lake Tahoe, NV, USA, 3 December 2012. [Google Scholar]
- Schulz, H.; Behnke, S. Deep Learning. Künstl. Intell. 2012, 26, 357–363. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the NeurIPS 2014, Montreal, QC, Canada, 9 December 2014. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Is Artificial Intelligence Set to Become art’s Next Medium? Available online: https://www.christies.com/features/a-collaboration-between-two-artists-one-human-one-a-machine-9332-1.aspx (accessed on 5 May 2022).
- Here’s DALL-E: An Algorithm Learned to Draw Anything You Tell It. Available online: https://www.nbcnews.com/tech/innovation/here-s-dall-e-algorithm-learned-draw-anything-you-tell-n1255834 (accessed on 5 May 2022).
- Hodassman, S.; Vardi, R.; Tugendhaft, Y.; Goldental, A.; Kanter, I. Efficient dendritic learning as an alternative to synaptic plasticity hypothesis. Sci. Rep. 2022, 12, 6571. [Google Scholar] [CrossRef]
- Shen, G.; Zhao, D.; Zeng, Y. Backpropagation with biologically plausible spatiotemporal adjustment for training deep spiking neural networks. Patterns 2022, 3, 100522. [Google Scholar] [CrossRef] [PubMed]
- Colbrooka, M.J.; Antunb, V.; Hansena, A.C. The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale’s 18th problem. Proc. Natl. Acad. Sci. USA 2022, 119, e2107151119. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- AlphaGo, The Challenge Match. Available online: https://www.deepmind.com/research/highlighted-research/alphago/the-challenge-match (accessed on 5 May 2022).
- Kim, S.-J.; Takahashi, T.; Sano, K. A balance for fairness: Fair distribution utilising physics. Humanit. Soc. Sci. Commun. 2021, 8, 131. [Google Scholar] [CrossRef]
- Kim, S.-J.; Takahashi, T. Performance for Multi-armed Bandit Tasks Depending on Ambiguity-Preference of Learning Algorithm. Front. Appl. Math. Stat. 2018, 4, 27. [Google Scholar] [CrossRef]
- Taleb, N.N. Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets; Penguin Books: London, UK, 2007. [Google Scholar]
- The Official History of Rock Paper Scissors. Available online: https://wrpsa.com/the-official-history-of-rock-paper-scissors (accessed on 5 May 2022).
- Kako, S. Densho Asobi Kou 4 Janken Asobi Kou; Komine Shoten: Tokyo, Japan, 2008. (In Japanese) [Google Scholar]
- van den Nouweland, A. Rock-paper-scissors; a new and elegant proof. Econ. Bull. 2007, 3, 1–6. [Google Scholar]
- Batzilis, D.; Jaffe, S.; Levitt, S.; List, J.A.; Picel, J. Behavior in Strategic Settings: Evidence from a Million Rock-Paper-Scissors Games. Games 2019, 10, 18. [Google Scholar] [CrossRef]
- Brockbank, E.; Vul, E. Humans fail to outwit adaptive rock, paper, scissors opponents. Proc. Annu. Meet. Cogn. Sci. Soc. 2021, 43, 1740–1746. [Google Scholar]
- Wang, Z.; Xu, B.; Zhou, H.J. Social cycling and conditional responses in the Rock-Paper-Scissors game. Sci. Rep. 2014, 4, 5830. [Google Scholar] [CrossRef] [PubMed]
- Rock, Paper, Scissors| Kaggle. Available online: https://www.kaggle.com/competitions/rock-paper-scissors (accessed on 5 May 2022).
- Rock Paper Scissors Programming Competition. Available online: http://www.rpscontest.com (accessed on 5 May 2022).
- Nippon Janken Kyoukai (Japan Jan-ken Association). Available online: https://japan-rps.jimdofree.com (accessed on 5 May 2022). (In Japanese).
- World Rock Paper Scissors Association. Available online: https://wrpsa.com (accessed on 5 May 2022).
- Yu, Q.; Fang, D.; Zhang, X.; Jin, C.; Ren, Q. Stochastic Evolution Dynamic of the Rock-Scissors-Paper Game Based on a Quasi Birth and Death Process. Sci. Rep. 2016, 6, 28585. [Google Scholar] [CrossRef]
- Wang, L.; Huang, W.; Li, Y.; Evans, J.; He, S. Multi-AI competing and winning against humans in iterated Rock-Paper-Scissors game. Sci. Rep. 2020, 10, 13873. [Google Scholar] [CrossRef] [PubMed]
- Hajihashemi, M.; Aghababaei, S.K. Multi-strategy evolutionary games: A Markov chain approach. PLoS ONE 2022, 17, e0263979. [Google Scholar] [CrossRef]
- Aphiratsakun, N.; Blake, X.J.; Tin, K.K.; Ngwe, T. AI-based Rock-Paper-Scissors plug and play system. In Proceedings of the 2020 5th International STEM Education Conference, Hua Hin, Thailand, 4–6 November 2020; pp. 30–33. [Google Scholar]
- Yuge, T.; Shirai, H.; Nishino, J.; Odaka, T.; Ogura, H. Evolutional Acquisition of a Strategy Using Genetic Programming. Mem. Fac. Eng. Univ. 2001, 49, 129–139. (In Japanese) [Google Scholar]
- Komai, T.; Kim, S.-J.; Kurokawa, H. Characteristic extraction method of human’s strategy in the Rock-Paper-Scissors game. In Proceedings of the 2018 RISP International Workshop on Nonlinear Circuits, Communications and Signal Processing, Honolulu, HI, USA, 4–7 March 2018; pp. 592–595. [Google Scholar]
- Komai, T.; Kim, S.-J.; Kousaka, T.; Kurokawa, H. A Human Behavior Strategy Estimation Method Using Homology Search for Rock-Scissors-Paper Game. J. Signal Process. 2019, 23, 177–180. [Google Scholar] [CrossRef]
- Bédard-Couture, R.; Kharma, N.N. Playing Iterated Rock-Paper-Scissors with an Evolutionary Algorithm. In Proceedings of the 11th International Joint Conference on Computational Intelligence, Vienna, Austria, 17–19 September 2019; pp. 205–212. [Google Scholar]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Kim, S.-J.; Umeno, K.; Hasegawa, A. On the NIST Statistical Test Suite for Randomness. Tech. Rep. IEICE 2003, ISEC2003-87, 21–27. [Google Scholar]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D. Recurrence plots of dynamical systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Webber, C.L., Jr.; Zbilut, J.P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Hirata, Y. Recurrence plots for characterizing random dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 94, 105552. [Google Scholar] [CrossRef]
- Hacking, I. The Emergence of Probability; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Kim, S.-J.; Naruse, M.; Aono, M.; Hori, H.; Akimoto, T. Random Walk with Chaotically Driven Bias. Sci. Rep. 2016, 6, 38634. [Google Scholar] [CrossRef]
- Pedro Castro-Rodrigues, P.; Akam, T.; Snorasson, I.; Camacho, M.; Paixão, V.; Maia, A.; Barahona-Corrêa, J.B.; Dayan, P.; Simpson, H.B.; Costa, R.M.; et al. Explicit knowledge of task structure is a primary determinant of human model-based action. Nat. Hum. Behav. 2022, 6, 1126–1141. [Google Scholar] [CrossRef]


| No. | Function | Note |
|---|---|---|
| 1 | add() | |
| 2 | sub() | |
| 3 | multiple() | |
| 4 | divide() | |
| 5 | mod() | |
| 6 | plus1(x) | |
| 7 | plus2(x) | |
| 8 | gp-hand(x) | |
| 9 | opp-hand(x) | |
| 10 | If-r() | |
| 11 | If-s() | |
| 12 | If-p() |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komai, T.; Kurokawa, H.; Kim, S.-J. Human Randomness in the Rock-Paper-Scissors Game. Appl. Sci. 2022, 12, 12192. https://doi.org/10.3390/app122312192
Komai T, Kurokawa H, Kim S-J. Human Randomness in the Rock-Paper-Scissors Game. Applied Sciences. 2022; 12(23):12192. https://doi.org/10.3390/app122312192
Chicago/Turabian StyleKomai, Takahiro, Hiroaki Kurokawa, and Song-Ju Kim. 2022. "Human Randomness in the Rock-Paper-Scissors Game" Applied Sciences 12, no. 23: 12192. https://doi.org/10.3390/app122312192
APA StyleKomai, T., Kurokawa, H., & Kim, S.-J. (2022). Human Randomness in the Rock-Paper-Scissors Game. Applied Sciences, 12(23), 12192. https://doi.org/10.3390/app122312192







