Performance Analysis of Magnetorheological Porous Fabric Composite
Abstract
1. Introduction
2. Preparation and Experiments
2.1. Material Preparation
2.2. Experiments
3. Discussion
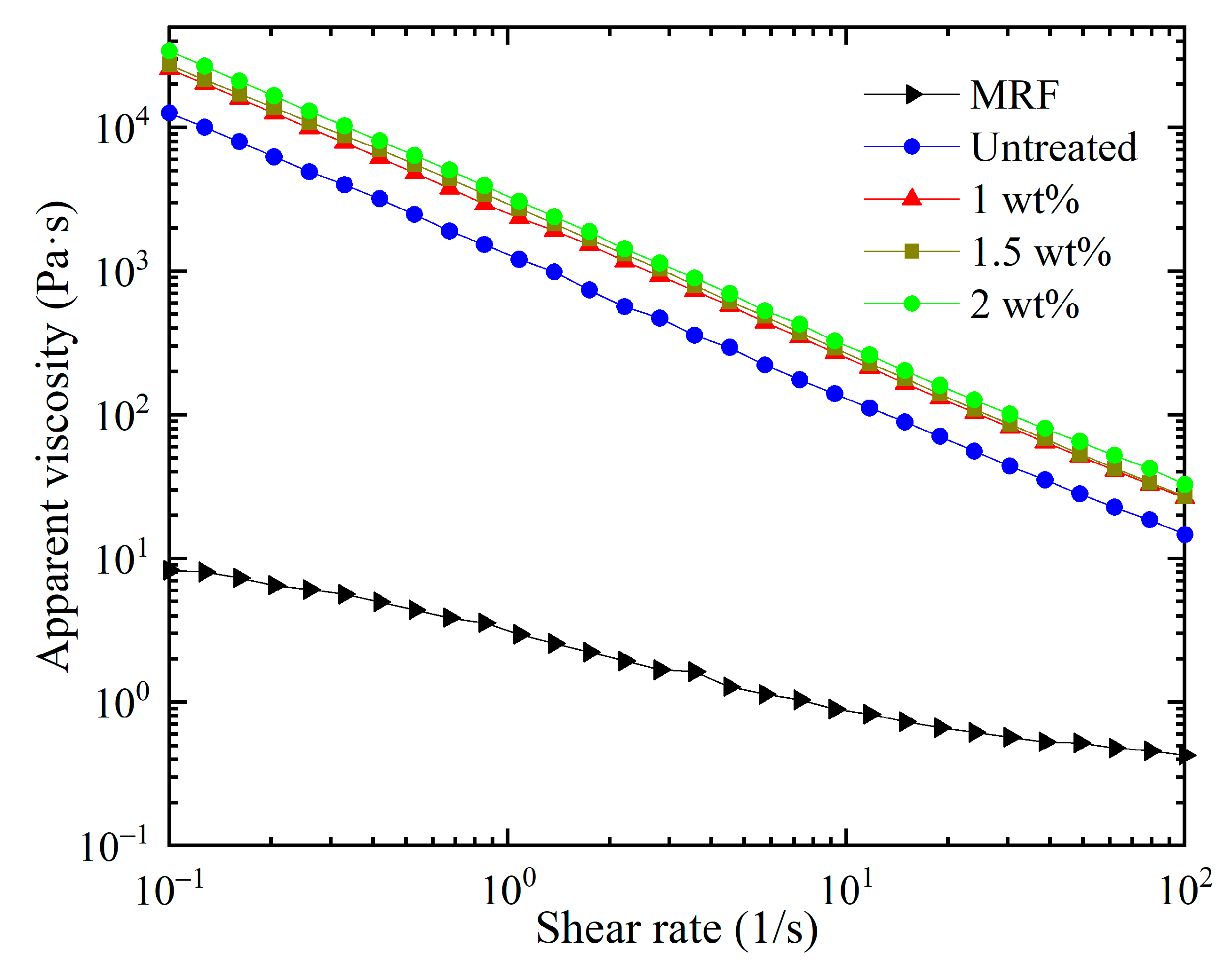
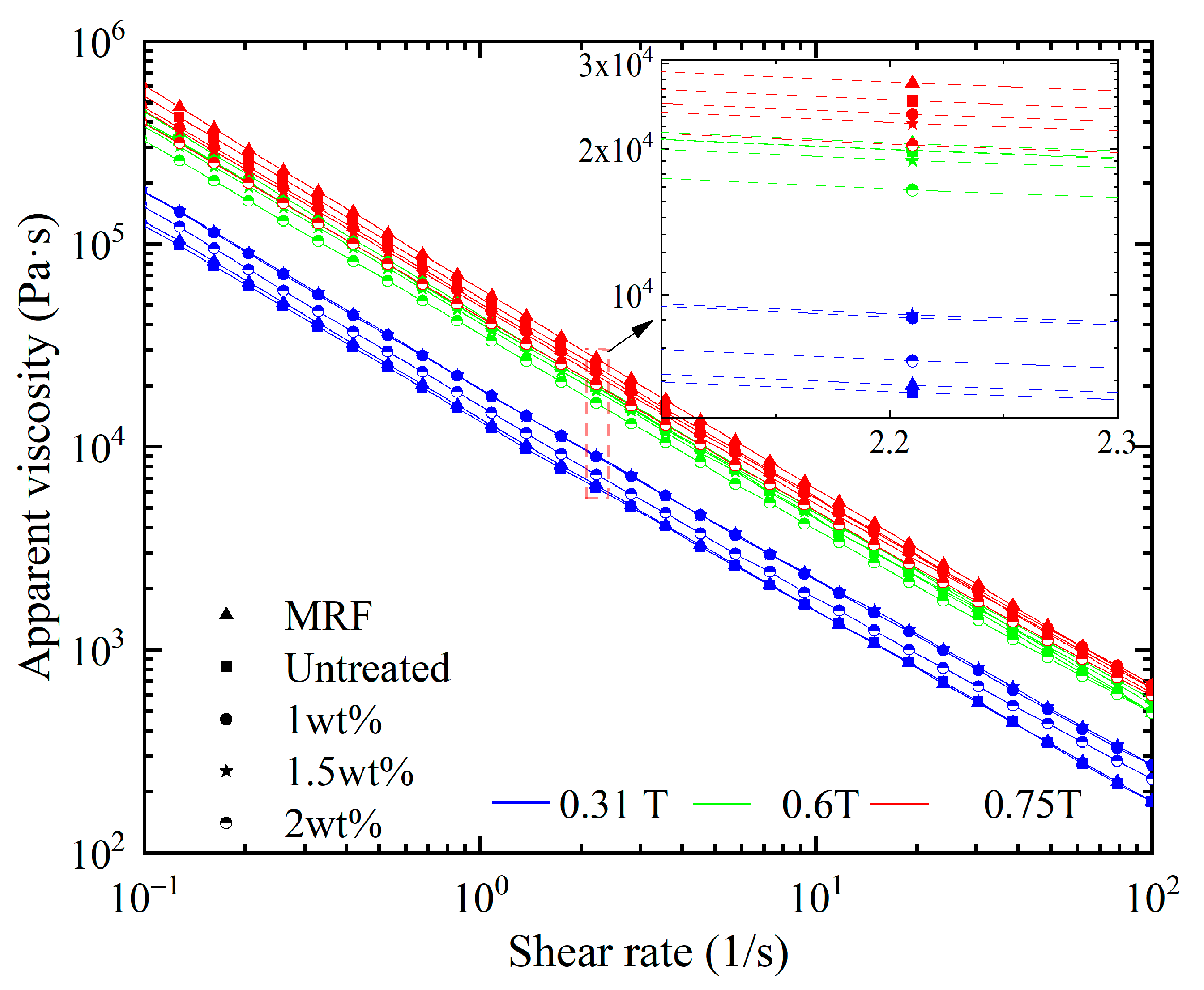
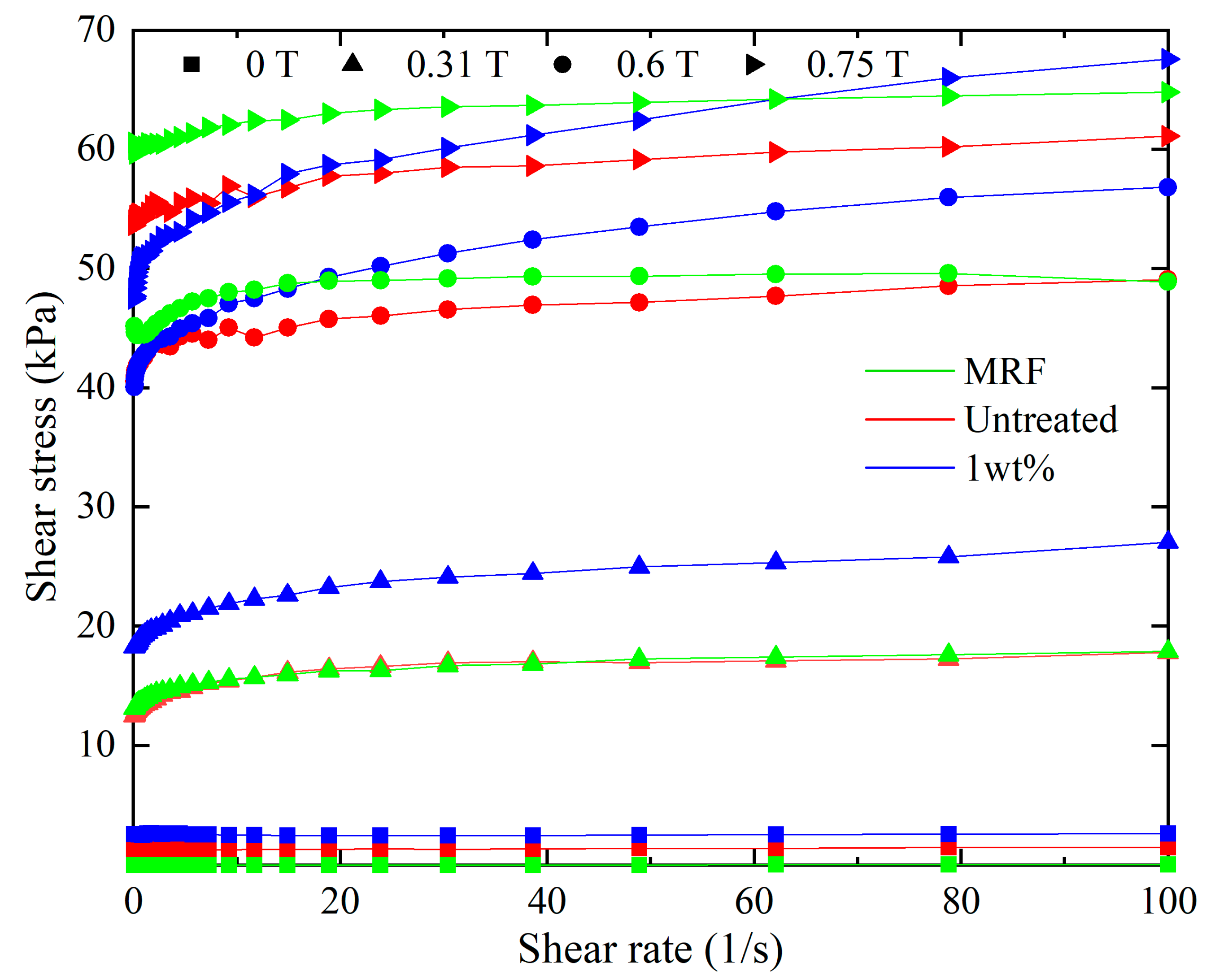
3.1. Viscosity Changeability
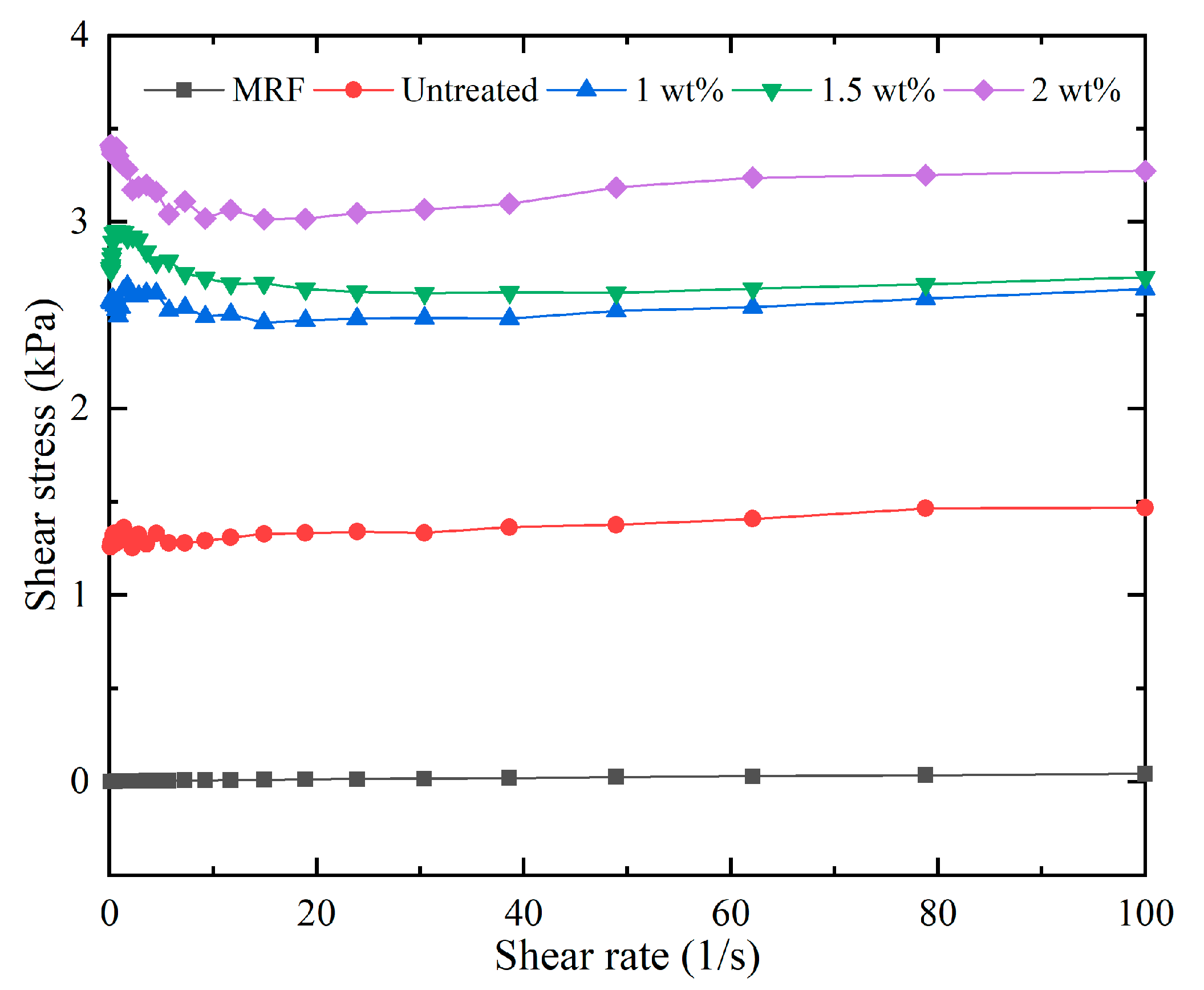
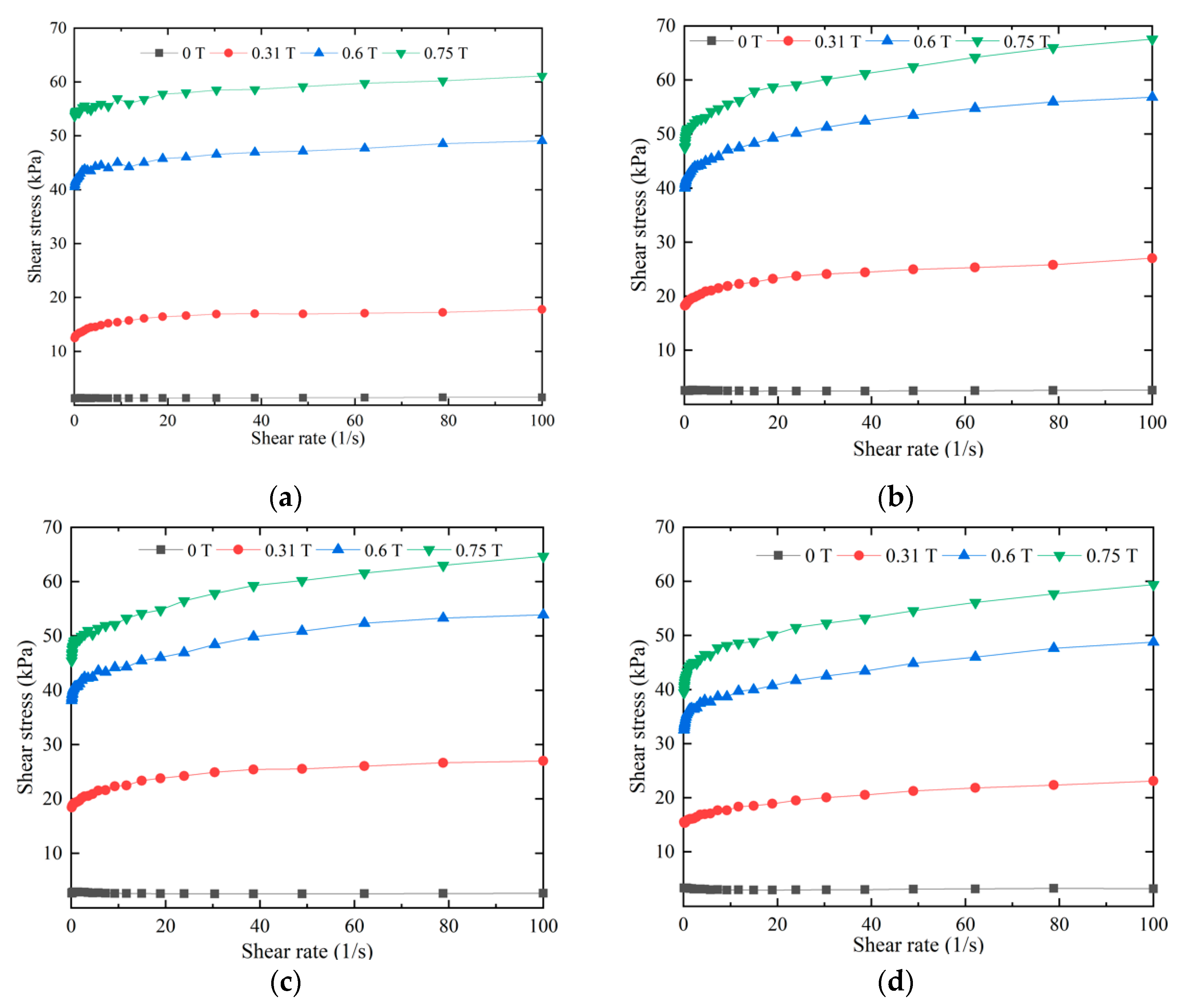
3.2. Shear Stress
3.3. Dynamic Viscoelasticity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yarali, E.; Farajzadeh, M.A.; Noroozi, R.; Dabbagh, A.; Khoshgoftar, M.J.; Mirzaali, M.J. Magnetorheological elastomer composites: Modeling and dynamic finite element analysis. Compos. Struct. 2020, 254, 112881. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, W.; Jiang, W.; Ye, F.; Mao, Y.; Xuan, S.; Gong, X. Multifunctional polymer composite with excellent shear stiffening performance and magnetorheological effect. J. Mater. Chem. C 2014, 2, 7133–7140. [Google Scholar] [CrossRef]
- Manoharan, R.; Vasudevan, R.; Jeevanantham, A.K. Dynamic characterization of a laminated composite magnetorheological fluid sandwich plate. Smart Mater. Struct. 2014, 23, 25022. [Google Scholar] [CrossRef]
- de Souza Eloy, F.; Gomes, G.F.; Ancelotti, A.C.; da Cunha, S.S.; Bombard, A.J.F.; Junqueira, D.M. Experimental dynamic analysis of composite sandwich beams with magnetorheological honeycomb core. Eng. Struct. 2018, 176, 231–242. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Q.; Zhu, K.; Jiang, S.; Wu, H.; Yi, L. Preparation and characterization of magnetorheological elastic polishing composites. J. Intel. Mat. Syst. Str. 2019, 30, 1481–1492. [Google Scholar] [CrossRef]
- Powell, L.A.; Hu, W.; Wereley, N.M. Magnetorheological fluid composites synthesized for helicopter landing gear applications. J. Intel. Mat. Syst. Str. 2013, 24, 1043–1048. [Google Scholar] [CrossRef]
- Chen, W.; Huang, J.; Yang, Y. Research on the transmission performance of a high-temperature magnetorheological fluid and shape memory alloy composite. Appl. Sci. 2022, 12, 3228–3243. [Google Scholar] [CrossRef]
- Chibulu, C.; Yardimci, M.Y.; De Schutter, G. Effect of volume fraction of fine sand on magnetorheological response and blocking mechanisms of cementitious mixtures containing Fe3O4 nanoparticles. Appl. Sci. 2022, 12, 10104–10117. [Google Scholar] [CrossRef]
- Ramamoorthy, M.; Rajamohan, V.; AK, J. Vibration analysis of a partially treated laminated composite magnetorheological fluid sandwich plate. J. Vib. Control 2016, 22, 869–895. [Google Scholar] [CrossRef]
- Dai, S.; Du, C.; Yu, G. Design, testing and analysis of a novel composite magnetorheological fluid clutch. J. Intel. Mat. Syst. Str. 2013, 24, 1675–1682. [Google Scholar] [CrossRef]
- Arumugam, A.B.; Ramamoorthy, M.; Rajamohan, V. Dynamic characterization and parametric instability analysis of rotating magnetorheological fluid composite sandwich plate subjected to periodic in-plane loading. J. Sandw. Struct. Mater. 2019, 21, 2099–2126. [Google Scholar] [CrossRef]
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A review of challenges and solutions in the preparation and use of magnetorheological fluids. Int. J. Mech. Mater. Eng. 2019, 14, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Li, W.; Du, H. A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Lee, C.J.; Kwon, S.H.; Choi, H.J.; Chung, K.H.; Jung, J.H. Enhanced magnetorheological performance of carbonyl iron/natural rubber composite elastomer with gamma-ferrite additive. Colloid Polym. Sci. 2018, 296, 1609–1613. [Google Scholar] [CrossRef]
- Zając, P.; Kaleta, J.; Lewandowski, D.; Gasperowicz, A. Isotropic magnetorheological elastomers with thermoplastic matrices: Structure, damping properties and testing. Smart Mater. Struct. 2010, 19, 45014. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the particle size on the magnetorheological effect of magnetorheological elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Carlson, J.D.; Jolly, M.R. MR fluid, foam and elastomer devices. Mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Kang, T.J.; Hong, K.H.; Jeong, H. Preparation and properties of ap-aramid fabric composite impregnated with a magnetorheological fluid for body armor applications. Polym. Eng. Sci. 2015, 55, 729–734. [Google Scholar] [CrossRef]
- Gürgen, S.; Yıldız, T. Stab resistance of smart polymer coated textiles reinforced with particle additives. Compos. Struct. 2020, 235, 111812. [Google Scholar] [CrossRef]
- Gavrilovici, A.M.; Anitas, E.M.; Chirigiu, L.; Bica, I.; Negrutiu, M.L. Magnetodielectric effects in magnetorheological elastomers based on polymer fabric, silicone rubber, and magnetorheological suspension. Adv. Polym. Tech. 2019, 2019, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Li, T.T.; Wang, Y.; Shiu, B.C.; Peng, H.K.; Lou, C.W.; Lin, J.H. Hydrogel with high toughness and strength for fabricating high performance stab-resistant aramid composite fabric. J. Mater. Res. Technol. 2021, 15, 1630–1641. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Hong, S.W.; Park, Y.J.; Kim, S.H.; Kim, G.W.; Choi, S.B. Tunable Young’s moduli of soft composites fabricated from magnetorheological materials containing microsized iron particles. Materials 2020, 13, 3378–3393. [Google Scholar] [CrossRef] [PubMed]
- Ivaneyko, D.; Toshchevikov, V.P.; Saphiannikova, M.; Heinrich, G. Magneto-sensitive elastomers in a homogeneous magnetic field: A rectangular lattice model. Macromol. Theor. Simul. 2011, 20, 411–424. [Google Scholar] [CrossRef]
- Karl, C.W.; McIntyre, J.; Alshuth, T.; Klüppel, M. Magneto-rheological elastomers with switchable mechanical properties. KGK-Kaut. Gummi Kunst. 2013, 66, 46–53. [Google Scholar]
- Kaleta, J.; Królewicz, M.; Lewandowski, D. Magnetomechanical properties of anisotropic and isotropic magnetorheological composites with thermoplastic elastomer matrices. Smart Mater. Struct. 2011, 20, 85006. [Google Scholar] [CrossRef]
- Małecki, P.; Królewicz, M.; Krzak, J.; Kaleta, J.; Pigłowski, J. Dynamic mechanical analysis of magnetorheological composites containing silica-coated carbonyl iron powder. J. Intel. Mat. Syst. Str. 2015, 26, 1899–1905. [Google Scholar] [CrossRef]
- Son, K.J.; Fahrenthold, E.P. Evaluation of magnetorheological fluid augmented fabric as a fragment barrier material. Smart Mater. Struct. 2012, 21, 75012. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A. Flexural analysis of laminated composite porous plate. Asian J. Civ. Eng. 2022. [Google Scholar] [CrossRef]
- Mistik, S.I.; Shah, T.; Hadimani, R.L.; Siores, E. Compression and thermal conductivity characteristics of magnetorheological fluid–spacer fabric smart structures. J. Intel. Mat. Syst. Str. 2012, 23, 1277–1283. [Google Scholar] [CrossRef]
- Glaser, R.; Caccese, V.; Shahinpoor, M. Development of magneto-rheological fluid composites with rigidification characteristics. Smart Mater. Struct. 2011, 20, 45018. [Google Scholar] [CrossRef]
- Kaleta, J.; Lewandowski, D. Inelastic properties of magnetorheological composites: I. Fabrication, experimental tests, cyclic shear properties. Smart Mater. Struct. 2007, 16, 1948–1953. [Google Scholar] [CrossRef]
- Nakano, M.; Yang, J.; Sun, S.; Totsuka, A.; Fukukita, A. Development and damping properties of a seismic linear motion damper with MR fluid porous composite rotary brake. Smart Mater. Struct. 2020, 29, 115043. [Google Scholar] [CrossRef]
- Dong, X.; Xi, J.; Chen, P.; Li, W. Magneto-rheological variable inertia flywheel. Smart Mater. Struct. 2018, 27, 115015. [Google Scholar] [CrossRef]
- Tong, Y.; Dong, X.; Qi, M. High performance magnetorheological fluids with flower-like cobalt particles. Smart Mater. Struct. 2017, 26, 25023. [Google Scholar] [CrossRef]




| Property | Values | Property | Values |
|---|---|---|---|
| Density/kg·m−3 | 2960 | Shear stress at 0.5 T/kPa | ≥50 |
| Viscosity of zero-field ( = 51/s, 20 °C)/Pa·s | ≤1.5 | Operating temperature/°C | −40~150 |
| Bulk modulus/MPa | 200 | Magnetic properties/kA·m−1 | 379.64 |
| Ingredient | Density/kg·m−3 | Average Thickness/mm |
|---|---|---|
| Polypropylene | 200 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Wu, L.; Li, P.; Li, X.; Zhao, J.; Dong, X. Performance Analysis of Magnetorheological Porous Fabric Composite. Appl. Sci. 2022, 12, 12062. https://doi.org/10.3390/app122312062
Yan H, Wu L, Li P, Li X, Zhao J, Dong X. Performance Analysis of Magnetorheological Porous Fabric Composite. Applied Sciences. 2022; 12(23):12062. https://doi.org/10.3390/app122312062
Chicago/Turabian StyleYan, Hua, Lifan Wu, Pingyang Li, Xuan Li, Junxin Zhao, and Xiaomin Dong. 2022. "Performance Analysis of Magnetorheological Porous Fabric Composite" Applied Sciences 12, no. 23: 12062. https://doi.org/10.3390/app122312062
APA StyleYan, H., Wu, L., Li, P., Li, X., Zhao, J., & Dong, X. (2022). Performance Analysis of Magnetorheological Porous Fabric Composite. Applied Sciences, 12(23), 12062. https://doi.org/10.3390/app122312062







