Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review
Abstract
1. Introduction
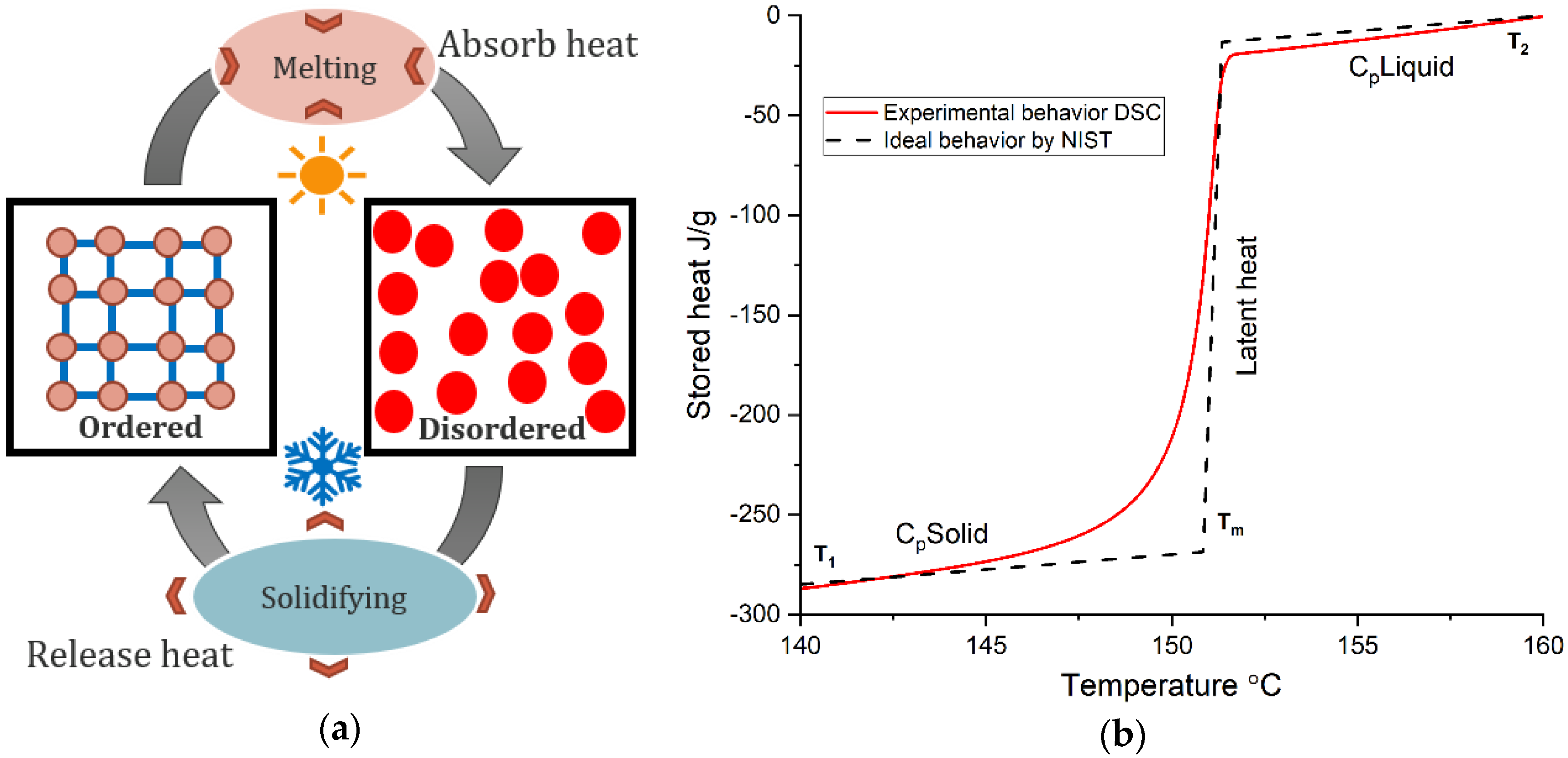
2. Phase Change Materials and Base Concepts
3. Calorimetric Characterization
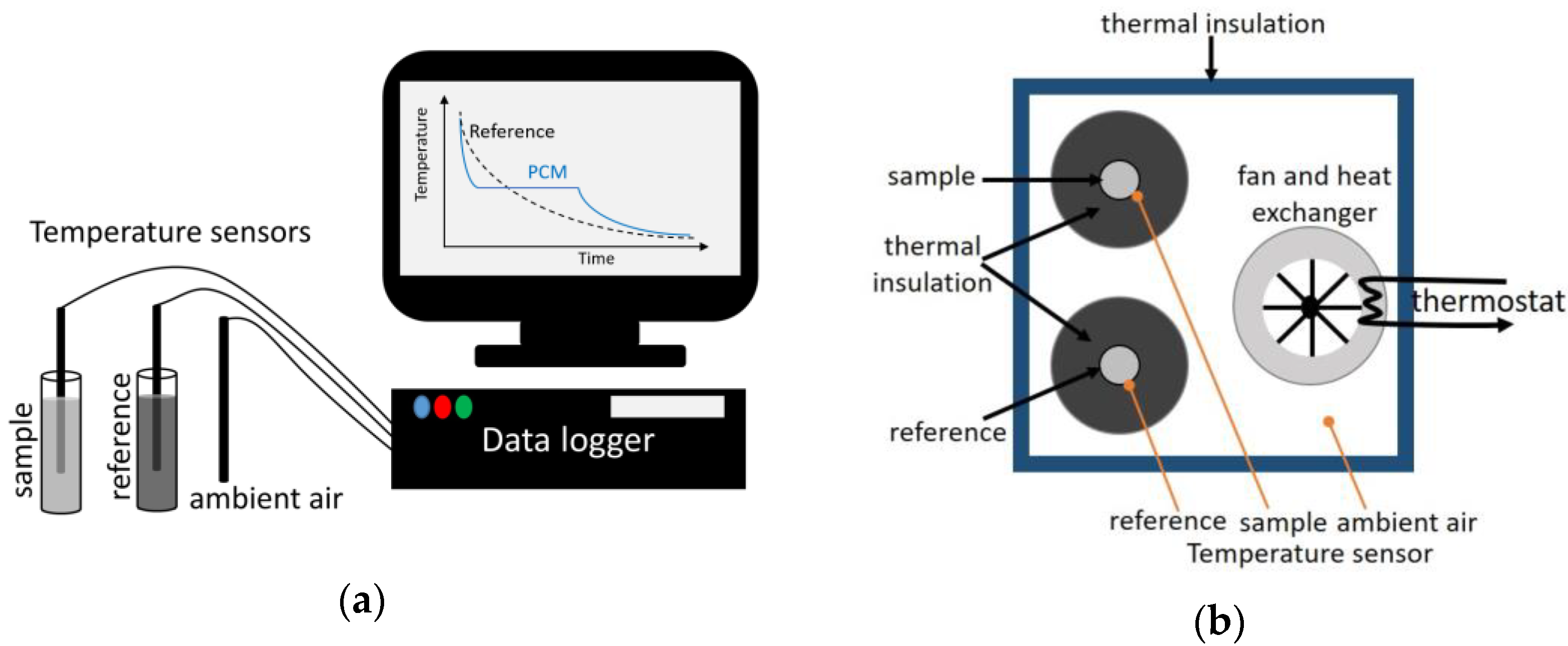
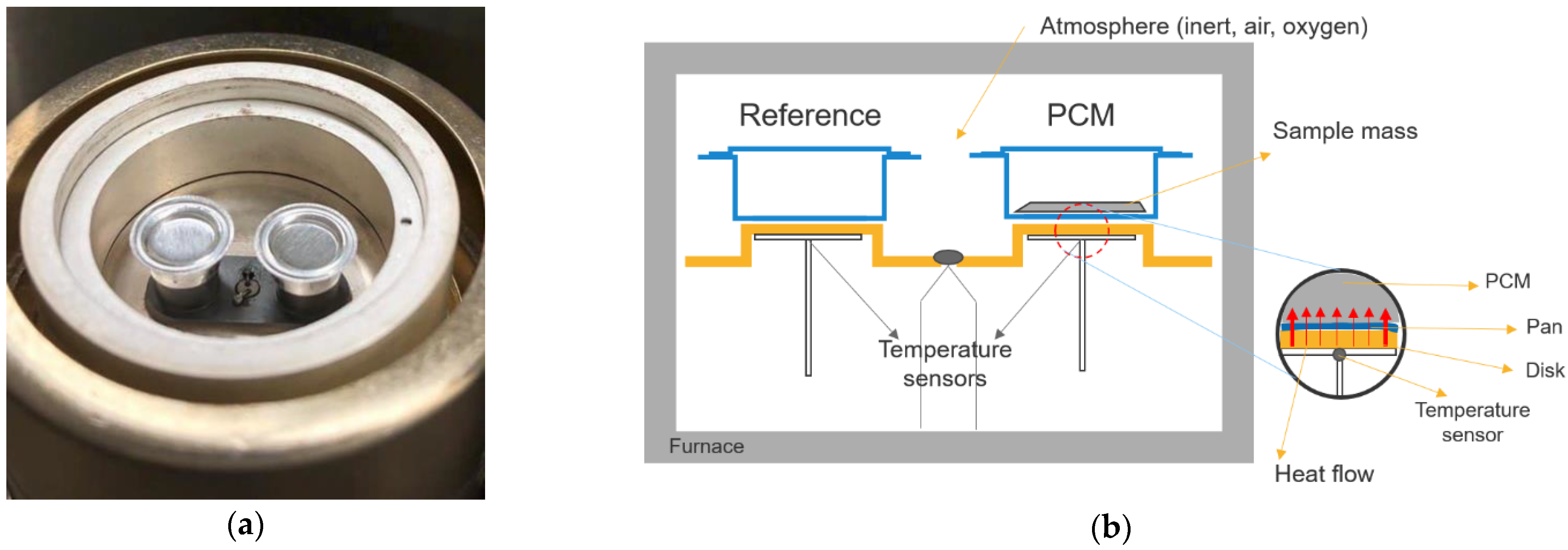
3.1. Calorimetric Methods
- ✓
- The most important one is the ability to measure large samples.Note that in the following, small samples contain typically tens of milligrams while large samples are of the order of tens of grams;
- ✓
- Due to the fast heating up/cooling down process, less time is consumed in the range where little heat is stored;
- ✓
- The obtained signal is not dependent on the heating rate, so the signal/noise ratio is always high.
| Test Type | Sample Size | Calibration | Advantages | Disadvantages | References |
|---|---|---|---|---|---|
| Heat-flux DSC | (10–100 µL) | All reference materials for melting point and enthalpy, and sapphire for heat capacity | Widely available, wide temperature range from sub-ambient to hundreds of degrees | Small sample size Unsuitable for PCM composite and PCM with subcooling | [6] |
| T-history | (10–20 mL) | Water (Cp), Copper (Cp), Indium (T, Δh) [28] | Self-built, can cover large samples Suitable for heterogenous material, volume dependent behavior Fast heating up/cooling down High signal to noise ratio | Time-consuming (one heating/cooling cycle can be done within a day) Narrow temperature range compared to DSC | [6,10,22,28,29] |
| 3-layer calorimeter (3LC) | (100 mL) | Only by the manufacturer with (water and hexadecane) | Uniquely built for large samples of PCM | Only available from a single company Temperature range (-20 to 100 °C) Time-consuming | [6,26] |
| Adiabatic calorimetry Adiabatic scanning calorimetry (1970) Peltier-element-based ASC (pASC) | Tens of mg in pASC | Do not need calibration | Heat flow calibration is not needed | Can only measure during heating cycle, not during cooling | [30,31,32,33,34] |
| Heat flow meter (HFM), guarded hot plate (GHP), and longitudinal guarded comparative calorimeter | Large samples | ASTM C1784-14 [35] was developed for HFM method Stainless steel [36] | Large samples, PCM composite or encapsulated PCM | Non-conventional method | [36] |
3.2. Calibration Step and Measurement Accuracy
| Material | Melting Point (°C) | Enthalpy | Remarks | References |
|---|---|---|---|---|
| Mercury | −38.8344 °C | 11.443 ± 0.004 J/g | Short shelf-life Unsafe | [41] |
| Water | 0.01 °C | 335 ± 0.6 J/g | Liquid water is suitable for Cp measurement, especially for large-scale measurement | [6,41] |
| Gallium | 29.8 °C | 80.097 ± 0.032 J/g [34] | Incompatible with Al crucibles | [34,39] |
| Biphenyl | 68.97 ± 0.01 °C | 122.5 ± 0.4 J/g | Suitable for large sample calibration | [33] |
| Benzoic acid | 122.37 °C | 147.4 ± 0.1 J/g | [19,41,42] | |
| Diphenylacetic acid | 147.19 ± 0.03 °C | 146.8 ± 0.6 J/g | Should be used in hermetic crucibles due to mass losses | [27] |
| Indium | 156.61 ± 0.02 °C | 28.71 ± 0.08 J/g | Promising reference to calibrate temperature and heat of fusion Can be re-melted up to ten times | [27] |
| Tin | 231.928 °C | 60.6 ± 0.2 J/g | [41] | |
| Bismuth | 271.442 | 53.07 ± 0.58 J/g | [38,41] | |
| Zinc | 419.527 °C | 108 ± 0.6 J/g | Amalgam with aluminum at 450 °C | [41] |
| Solid copper | 1084.62 °C | 205.4 ± 6.6 J/g | Oxidizes easily and reacts with alumina | [6] |
| Solid alumina (Sapphire) | Not precise | Not precise | Suitable for heat flow calibration in Cp measurement | [19,43,44] |
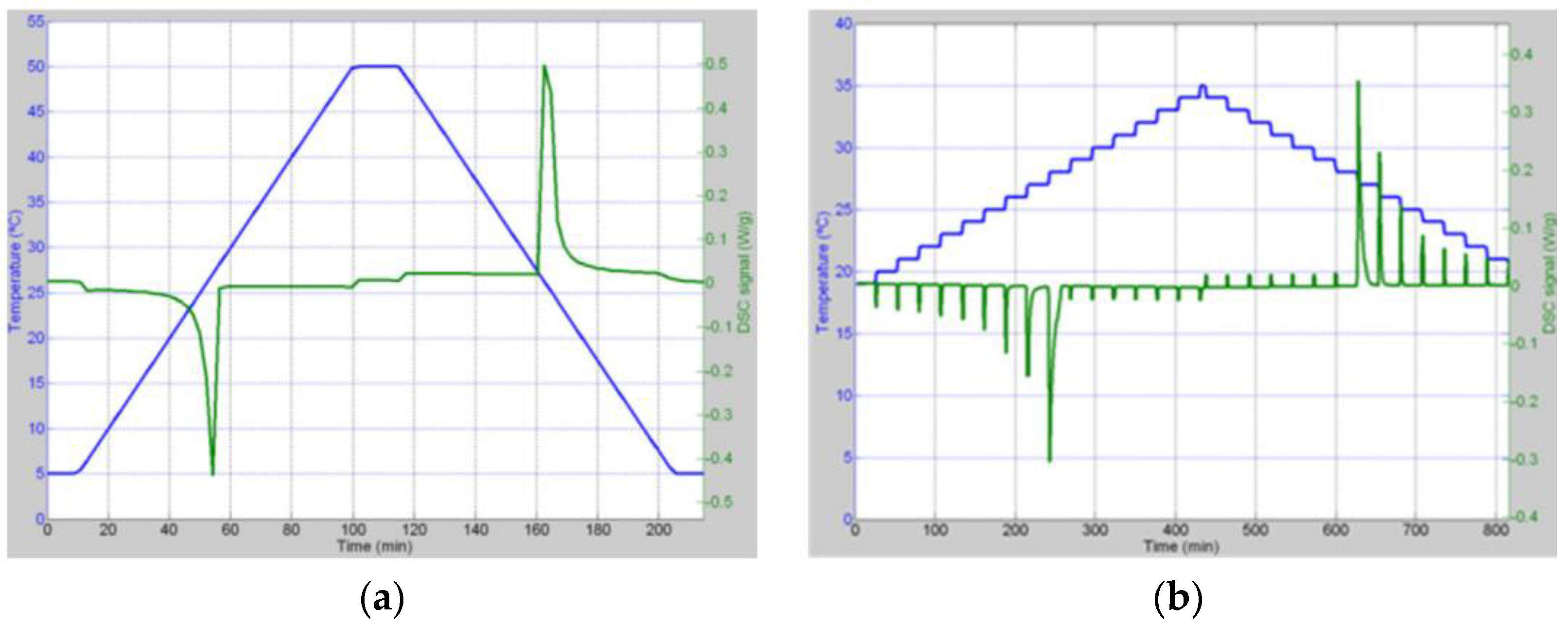
3.3. Temperature Program (Heating Mode)
3.4. DSC Tests for PCMs
3.5. Data Communication
4. PCM Properties Achieved by DSC
4.1. Transition Temperatures
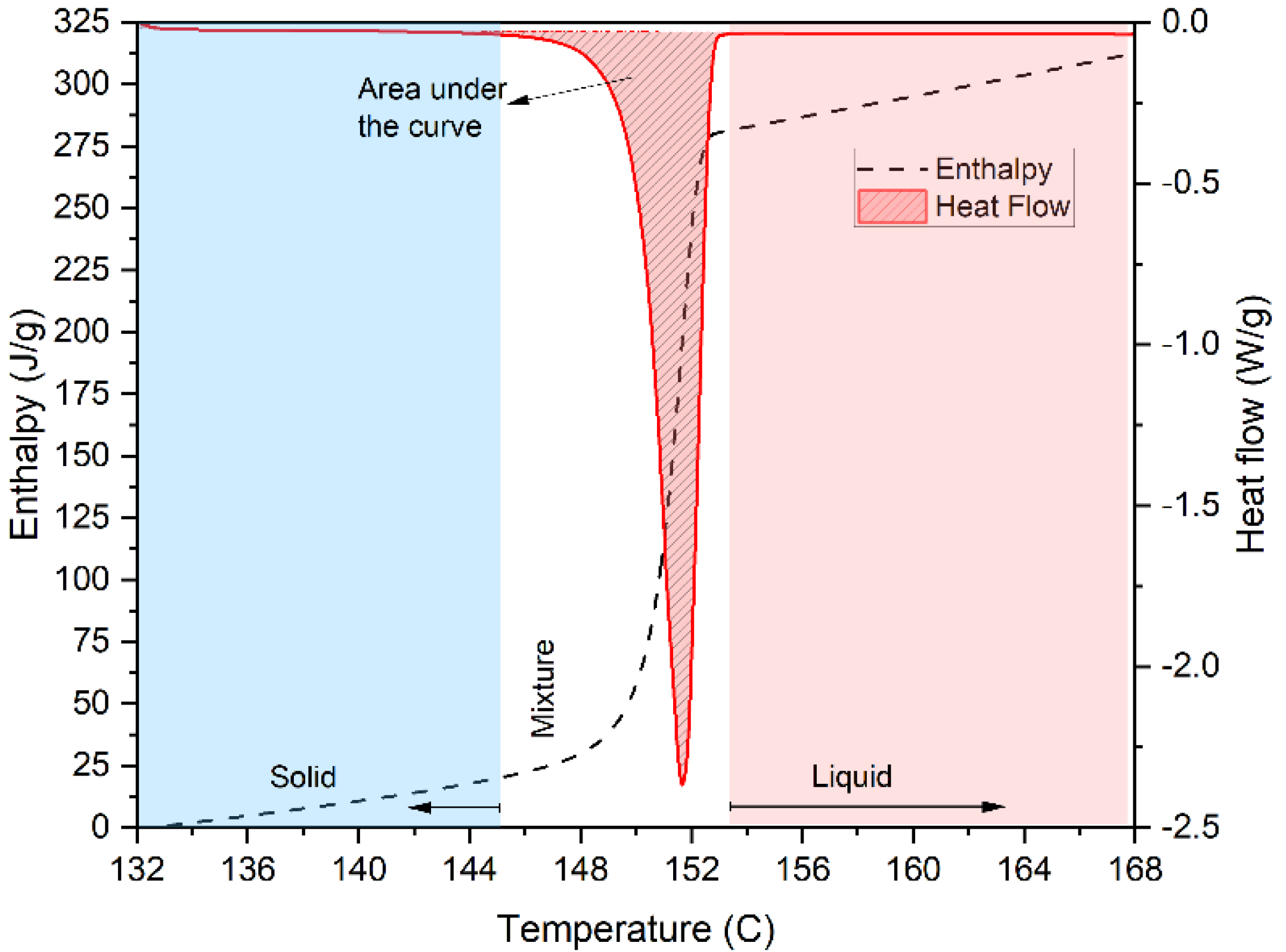
4.2. Enthalpy
4.3. Specific Heat Capacity
4.4. Thermal Stability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Abbreviations |
| Cp: specific heat capacity (J·g−1·°C−1) D: distance between empty crucible and sample signal (m) h: enthalpy (J) I: electrical current (A) Kσ: stress constant P: power (W) Q: thermal energy (J) : heat flow difference (J·s−1) R: thermal resistance (K·W−1) m: mass (kg) t: time (s) T: temperature (K) U: voltage difference (V) | AC: adiabatic calorimetry ASC: adiabatic scanning calorimetry ASTM: American society for testing and materials CAES: compressed air energy storage DSC: differential scanning calorimetry HDR: hear rate determination Hf-DSC: heat-flux DSC IEA: international energy agency IWH: industrial waste heat LHTES: latent heat thermal energy storage NIST: National Institute of Standard and Technology pASC: Peltier based adiabatic scanning calorimetry PCM: phase change material RRT: round robin tests SEM: scanning electron microscopy TES: thermal energy storage TGA: thermogravimetric analysis 3LC: three layers calorimeter |
| Greek Symbols | Subscript |
| β: heating/cooling rate (°C·min−1) ϕ: heat flow (mW) Δ: difference δ: uncertainty | a: ambient a–s: between ambient and sample a–r: between ambient and reference el: electric s: sample r: reference st: sapphire 1: temperature in point 1 2: temperature in point 2 |
References
- Barreneche, C.; Solé, A.; Miró, L.; Martorell, I.; Fernández, A.I.; Cabeza, L.F. Study on differential scanning calorimetry analysis with two operation modes and organic and inorganic phase change material (PCM). Thermochim. Acta 2013, 553, 23–26. [Google Scholar] [CrossRef]
- Feng, P.H.; Zhao, B.C.; Wang, R.Z. Thermophysical heat storage for cooling, heating, and power generation: A review. Appl. Therm. Eng. 2020, 166, 114728. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Huang, R.; Chang, J.; Yu, X.; Jiang, R.; Yu, X.; Roskilly, A.P. Applications and technological challenges for heat recovery, storage and utilisation with latent thermal energy storage. Appl. Energy 2021, 283, 116277. [Google Scholar] [CrossRef]
- Miró, L.; Brückner, S.; Cabeza, L.F. Mapping and discussing Industrial Waste Heat (IWH) potentials for different countries. Renew. Sustain. Energy Rev. 2015, 51, 847–855. [Google Scholar] [CrossRef]
- Franquet, E.; Gibout, S.; Bédécarrats, J.P.; Haillot, S.; Dumas, J.P. Inverse method for the identification of the enthalpy of phase change materials from calorimetry experiments. Thermochim. Acta 2012, 546, 61–80. [Google Scholar] [CrossRef]
- Mehling, H.; Leys, J.; Glorieux, C.; Thoen, J. Potential new reference materials for caloric measurements on PCM. SN Appl. Sci. 2021, 3, 202. [Google Scholar] [CrossRef]
- Gschwander, S.; Haussmann, T.; Hagelstein, G.; Sole, A.; Cabeza, L.F.; Diarce, G.; Hohenauer, W.; Lager, D.; Ristic, A.; Rathgeber, C.; et al. Standardization of PCM Characterization Via DSC; Greenstock: Beijing, China, 2015. [Google Scholar]
- He, B.; Martin, V.; Setterwall, F. Phase transition temperature ranges and storage density of paraffin wax phase change materials. Energy 2004, 29, 1785–1804. [Google Scholar] [CrossRef]
- Schmit, H.; Rathgeber, C.; Hoock, P.; Hiebler, S. Critical review on measured phase transition enthalpies of salt hydrates in the context of solid-liquid phase change materials. Thermochim. Acta 2020, 683, 178477. [Google Scholar] [CrossRef]
- Solé, A.; Miró, L.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Review of the T-history method to determine thermophysical properties of phase change materials (PCM). Renew. Sustain. Energy Rev. 2013, 26, 425–436. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.; Zhang, X.; Ma, J.; Shen, T.; Li, S.; Dong, B. A review on synthesis, characterization and application of nanoencapsulated phase change materials for thermal energy storage systems. Appl. Therm. Eng. 2021, 185, 116326. [Google Scholar] [CrossRef]
- Min, K.E.; Jang, J.W.; Kim, J.K.; Wern, C.; Yi, S. Thermophysical Properties of Inorganic Phase-Change Materials Based on MnCl2·4H2O. Appl. Sci. 2022, 12, 6338. [Google Scholar] [CrossRef]
- Fleischer, A.S. Thermal Energy Storage Using Phase Change Materials: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Rathgeber, C.; Miró, L.; Cabeza, L.F.; Hiebler, S. Measurement of enthalpy curves of phase change materials via DSC and T-History: When are both methods needed to estimate the behaviour of the bulk material in applications? Thermochim. Acta 2014, 596, 79–88. [Google Scholar] [CrossRef]
- Fatahi, H.; Claverie, J.; Poncet, S. Experimental investigation of the rheological and phase change behavior of adipic acid as a phase change material (PCM) for thermal energy storage at 150 °C. Thermochim. Acta 2022, 711, 179206. [Google Scholar] [CrossRef]
- Irfan Lone, M.; Jilte, R. A review on phase change materials for different applications. Mater. Today Proc. 2021, 46, 10980–10986. [Google Scholar] [CrossRef]
- Rolka, P.; Przybylinski, T.; Kwidzinski, R.; Lackowski, M. The heat capacity of low-temperature phase change materials (PCM) applied in thermal energy storage systems. Renew. Energy 2021, 172, 541–550. [Google Scholar] [CrossRef]
- Mehling, H.; Cabeza, L.F. Heat and Cold Storage with PCM An up to Date Introduction into Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Höhne, G.W.H.; Hemminger, W.F.; Flammersheim, H.-J. Differential Scanning Calorimetry, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Arkar, C.; Medved, S. Influence of accuracy of thermal property data of a phase change material on the result of a numerical model of a packed bed latent heat storage with spheres. Thermochim. Acta 2005, 438, 192–201. [Google Scholar] [CrossRef]
- Gabbott, P. Principles and Applications of Thermal Analysis; Blackwell Publishing Ltd.: Oxford, UK, 2008. [Google Scholar]
- Günther, E.; Hiebler, S.; Mehling, H.; Redlich, R. Enthalpy of phase change materials as a function of temperature: Required accuracy and suitable measurement methods. Int. J. Thermophys. 2009, 30, 1257–1269. [Google Scholar] [CrossRef]
- Yinping, Z.; Yi, J. A simple method, the -history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials. Meas. Sci. Technol. 1999, 10, 201–205. [Google Scholar] [CrossRef]
- Marín, J.M.; Zalba, B.; Cabeza, L.F.; Mehling, H. Determination of enthalpy–temperature curves of phase change materials with thetemperature-history method: Improvement to temperature dependentproperties. Meas. Sci. Technol. 2003, 14, 184. [Google Scholar] [CrossRef]
- Lázaro, A.; Günther, E.; Mehling, H.; Hiebler, S.; Marín, J.M.; Zalba, B. Verification of a T-history installation to measure enthalpy versus temperature curves of phase change materials. Meas. Sci. Technol. 2006, 17, 2168. [Google Scholar] [CrossRef]
- Höhlein, S.; König-Haagen, A.; Brüggemann, D. Thermophysical characterization of MgCl2·6H2O, xylitol and erythritol as phase change materials (PCM) for latent heat thermal energy storage (LHTES). Materials 2017, 10, 444. [Google Scholar] [CrossRef]
- Charsley, E.L.; Laye, P.G.; Markham, H.M.; Le Goff, T. Calibration of differential scanning calorimeters: A comparison between indium and diphenylacetic acid. Thermochim. Acta 2010, 497, 72–76. [Google Scholar] [CrossRef]
- Rathgeber, C.; Schmit, H.; Hennemann, P.; Hiebler, S. Calibration of a T-History calorimeter to measure enthalpy curves of phase change materials in the temperature range from 40 to 200 °C. Meas. Sci. Technol. 2014, 25, 035011. [Google Scholar] [CrossRef]
- Rathgeber, C.; Schmit, H.; Miró, L.; Cabeza, L.F.; Gutierrez, A.; Ushak, S.N.; Hiebler, S. Enthalpy-temperature plots to compare calorimetric measurements of phase change materials at different sample scales. J. Energy Storage 2018, 15, 32–38. [Google Scholar] [CrossRef]
- Archer, D.G.; Kirklin, D.R. NIST and standards for calorimetry. Thermochim. Acta 2000, 347, 21–30. [Google Scholar] [CrossRef]
- Archer, D.G. New NIST-traceable standards for calibration and validation of DSC. J. Therm. Anal. Calorim. 2006, 85, 131–134. [Google Scholar] [CrossRef]
- Leys, J.; Duponchel, B.; Longuemart, S.; Glorieux, C.; Thoen, J. A new calorimetric technique for phase change materials and its application to alkane-based PCMs. Mater. Renew. Sustain. Energy 2016, 5, 4. [Google Scholar] [CrossRef]
- Leys, J.; Losada-Pérez, P.; Slenders, E.; Glorieux, C.; Thoen, J. Investigation of the melting behavior of the reference materials biphenyl and phenyl salicylate by a new type adiabatic scanning calorimeter. Thermochim. Acta 2014, 582, 68–76. [Google Scholar] [CrossRef]
- Archer, D.G. The Enthalpy of Fusion of Gallium. J. Chem. Eng. Data 2002, 47, 304–309. [Google Scholar] [CrossRef]
- Standard Test Method for Using a Heat Flow Meter Apparatus for Measuring Thermal Storage Properties of Phase Change Materials and Products. Available online: https://www.astm.org/c1784-20.html (accessed on 21 March 2022).
- Göbel, A.; Vidi, S.; Klinker, F.; Hemberger, F.; Brütting, M.; Ebert, H.P.; Mehling, H. Method for the Thermal Characterization of PCM Systems in the Volume Range from 100 ml to 1000 ml. Int. J. Thermophys. 2017, 38, 67. [Google Scholar] [CrossRef]
- Moukhina, E. Enthalpy calibration for wide DSC peaks. Thermochim. Acta 2011, 522, 96–99. [Google Scholar] [CrossRef]
- Price, D.M. Temprature calibration of differential scanning calorimeters. J. Therm. Anal. 1995, 45, 1285–1296. [Google Scholar] [CrossRef]
- Su, W.; Gao, L.; Wang, L.; Zhi, H. Calibration of differential scanning calorimeter (DSC) for thermal properties analysis of phase change material. J. Therm. Anal. Calorim. 2021, 143, 2995–3002. [Google Scholar] [CrossRef]
- Pishchur, D.P.; Drebushchak, V.A. Recommendations on DSC calibration: How to escape the transformation of a random error into the systematic error. J. Therm. Anal. Calorim. 2016, 124, 951–958. [Google Scholar] [CrossRef]
- Thermal Analysis & Rheology. Available online: https://www.tainst.com (accessed on 15 March 2022).
- Fatahi, H.; Poncet, S.; Claverie, J. Thermal storage properties of organic PCMs with operating temperature of 150 °C by DSC. In Proceedings of the 13th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, Vicenza, Italy, 1–3 September 2021; pp. 1–8. [Google Scholar]
- Ferrer, G.; Barreneche, C.; Solé, A.; Martorell, I.; Cabeza, L.F. New proposed methodology for specific heat capacity determination of materials for thermal energy storage (TES) by DSC. J. Energy Storage 2017, 11, 1–6. [Google Scholar] [CrossRef]
- ASTM E1269-11; Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2018. [CrossRef]
- Castellón, C.; Günther, E.; Mehling, H.; Hiebler, S.; Cabeza, L.F. Determination of the enthalpy of PCM as a function of temperature using a heat-flux DSC—A study of different measurement procedures and their accuracy. Int. J. Energy Res. 2008, 32, 1258–1265. [Google Scholar] [CrossRef]
- Li, L.; Yu, H.; Wang, X.; Zheng, S. Thermal analysis of melting and freezing processes of phase change materials (PCMs) based on dynamic DSC test. Energy Build. 2016, 130, 388–396. [Google Scholar] [CrossRef]
- Del Barrio, E.P.; Dauvergne, J.L. A non-parametric method for estimating enthalpy-temperature functions of shape-stabilized phase change materials. Int. J. Heat Mass Transf. 2011, 54, 1268–1277. [Google Scholar] [CrossRef]
- Haillot, D.; Bauer, T.; Kröner, U.; Tamme, R. Thermal analysis of phase change materials in the temperature range 120–150 °C. Thermochim. Acta 2011, 513, 49–59. [Google Scholar] [CrossRef]
- Rathgeber, C.; Gutierrez, A. Analysis of supercooling of phase change materials with increased sample size-Comparison of measurements via DSC, T-History and at pilot plant scale Caloric measurements on PCM-collection of key publications and discussion View project MERITS View project. In Proceedings of the 13th International Conference on Energy Storage Greenstock, Beijing, China, 19–21 May 2015. [Google Scholar]
- Zhao, Y.; Zhang, X.; Xu, X.; Zhang, S. Research progress in nucleation and supercooling induced by phase change materials. J. Energy Storage 2020, 27, 101156. [Google Scholar] [CrossRef]
- Zeng, J.L.; Chen, Y.H.; Shu, L.; Yu, L.P.; Zhu, L.; Bin Song, L.; Cao, Z.; Sun, L.X. Preparation and thermal properties of exfoliated graphite/erythritol/mannitol eutectic composite as form-stable phase change material for thermal energy storage. Sol. Energy Mater. Sol. Cells 2018, 178, 84–90. [Google Scholar] [CrossRef]
- Zeng, J.-L.; Zhou, L.; Zhang, Y.-F.; Sun, S.-L.; Chen, Y.-H.; Shu, L.; Yu, L.-P.; Zhu, L.; Song, L.-B.; Cao, Z. Effects of some nucleating agents on the supercooling of erythritol to be applied as phase change material. J. Therm. Anal. Calorim. 2017, 129, 1291–1299. [Google Scholar] [CrossRef]
- Jin, X.; Hu, H.; Shi, X.; Zhang, X. Energy asymmetry in melting and solidifying processes of PCM. Energy Convers. Manag. 2015, 106, 608–614. [Google Scholar] [CrossRef]
- Kahwaji, S.; Johnson, M.B.; White, M.A. Thermal property determination for phase change materials. J. Chem. Thermodyn. 2021, 160, 106439. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Tao, W.; Cao, X.; He, Y. Fatty acids as phase change materials: A review. Renew. Sustain. Energy Rev. 2014, 29, 482–498. [Google Scholar] [CrossRef]
- Venkata Krishnan, R.; Nagarajan, K. Evaluation of heat capacity measurements by temperature-modulated differential scanning calorimetry. J. Therm. Anal. Calorim. 2010, 102, 1135–1140. [Google Scholar] [CrossRef]
- Sun, X.; Lee, K.O.; Medina, M.A.; Chu, Y.; Li, C. Melting temperature and enthalpy variations of phase change materials (PCMs): A differential scanning calorimetry (DSC) analysis. Phase Transitions 2018, 91, 667–680. [Google Scholar] [CrossRef]
- ASTM E967-08; American Society for Testing and Materials (ASTM®), Standard Test Method for Temperature Calibration of Differential Scanning Calorimeters and Differential Thermal Analyzers. ASTM International: West Conshohocken, PA, USA, 2014.
- Lazaro, A.; Peñalosa, C.; Solé, A.; Diarce, G.; Haussmann, T.; Fois, M.; Zalba, B.; Gshwander, S.; Cabeza, L.F. Intercomparative tests on phase change materials characterisation with differential scanning calorimeter. Appl. Energy 2013, 109, 415–420. [Google Scholar] [CrossRef]
- Dolado, P.; Mazo, J.; Lázaro, A.; Marín, J.M.; Zalba, B. Experimental validation of a theoretical model: Uncertainty propagation analysis to a PCM-air thermal energy storage unit. Energy Build. 2012, 45, 124–131. [Google Scholar] [CrossRef]
- Wang, G.; Harrison, I.R. Polymer melting: Heating rate effects on DSC melting peaks. Thermochim. Acta. 1994, 231, 203–213. [Google Scholar] [CrossRef]
- Sam, M.N.; Caggiano, A.; Mankel, C.; Koenders, E. A Comparative Study on the Thermal Energy Storage Performance of Bio-Based and Paraffin-Based PCMs Using DSC Procedures. Materials 2020, 13, 1705. [Google Scholar]
- Kousksou, T.; El Rhafiki, T.; Jamil, A.; Bruel, P.; Zeraouli, Y. PCMs inside emulsions: Some specific aspects related to DSC (differential scanning calorimeter)-like configurations. Energy 2013, 56, 175–183. [Google Scholar] [CrossRef]
- Jin, X.; Xu, X.; Zhang, X.; Yin, Y. Determination of the PCM melting temperature range using DSC. Thermochim. Acta 2014, 595, 17–21. [Google Scholar] [CrossRef]
- Müller, L.; Rubio-Pérez, G.; Bach, A.; Muñoz-Rujas, N.; Aguilar, F.; Worlitschek, J. Consistent DSC and TGA Methodology as Basis for the Measurement and Comparison of Thermo-Physical Properties of Phase Change Materials. Materials 2020, 13, 4486. [Google Scholar] [CrossRef] [PubMed]
- Phase Change Materials (Phasenwechselmaterial) Gütesicherung Quality Assurance RAL-GZ 896. 2018. Available online: www.mybeuth.de (accessed on 9 March 2022).
- Vélez, C.; Ortiz De Zárate, J.M.; Khayet, M. Thermal properties of n-pentadecane, n-heptadecane and n-nonadecane in the solid/liquid phase change region. Int. J. Therm. Sci. 2015, 94, 139–146. [Google Scholar] [CrossRef]
- Saeed, R.M.; Schlegel, J.P.; Sawafta, R. Characterization of high-temperature PCMs for enhancing passive safety and heat removal capabilities in nuclear reactor systems. Energy 2019, 189, 116137. [Google Scholar] [CrossRef]
- Zeng, J.-L.; Shu, L.; Jiang, L.-M.; Chen, Y.-H.; Zhang, Y.-X.; Xie, T.; Sun, L.-X.; Cao, Z. Thermodynamic and thermal energy storage properties of a new medium-temperature phase change material. J. Therm. Anal. Calorim. 2018, 135, 3171–3179. [Google Scholar] [CrossRef]
- Han, L.; Xie, S.; Ma, G.; Sun, J.; Jia, Y.; Jing, Y. Test and improvement of the cyclic stability of oxalic acid dihydrate for thermal energy storage. Thermochim. Acta 2016, 645, 24–30. [Google Scholar] [CrossRef]
- Salyan, S.; Suresh, S. Liquid metal gallium laden organic phase change material for energy storage: An experimental study. Int. J. Hydrogen Energy 2018, 43, 2469–2483. [Google Scholar] [CrossRef]
- Gasia, J.; Martin, M.; Solé, A.; Barreneche, C.; Cabeza, L.F. Phase change material selection for thermal processes working under partial load operating conditions in the temperature range between 120 and 200 °C. Appl. Sci. 2017, 7, 722. [Google Scholar] [CrossRef]


| Application | Classification | Ideal Properties |
|---|---|---|
Thermal storage:
| Organic (Paraffin and non-Paraffin)
| Technical properties
|
Physical properties
| ||
Kinetic properties
| ||
Chemical properties
| ||
Environmental properties
| ||
Economic
|
| Ref. | References | Test Conditions | Objectives | Remarks |
|---|---|---|---|---|
| [27] | Diphenylacetic acid Indium | Dynamic mode Stepwise 1, 2.5, 5, 7.5 and 10 °C/min 2.5 and 10 | Comparison between organic and metallic Solid or powder Pre-melting or not | Pre-melting the reference will improve the reliability of measurement; Solid shape reference would be preferred compared to powder or granular |
| [40] | Indium | 3, 9 and 15 °C/min | Melting enthalpy of indium was measured | Placing the sample crucible leads to 0.5 error in enthalpy |
| [39] | Gallium Indium Tin | 1, 2, 5 and 10 °C/min | Influence of various calibration method on the accuracy of temperature and enthalpy of n-eicosane | The accuracy of calibration could be improved by multipoint calibration |
| [6] | Not precise | Not precise | Introducing new reference material for DSC calibration | n-alkanes (C12, C14, C16 and C18) for temperature and enthalpy (-10 °C–30 °C); there is demand for sub-ambient references |
| Challenges | Explanations | Suggestions | References |
|---|---|---|---|
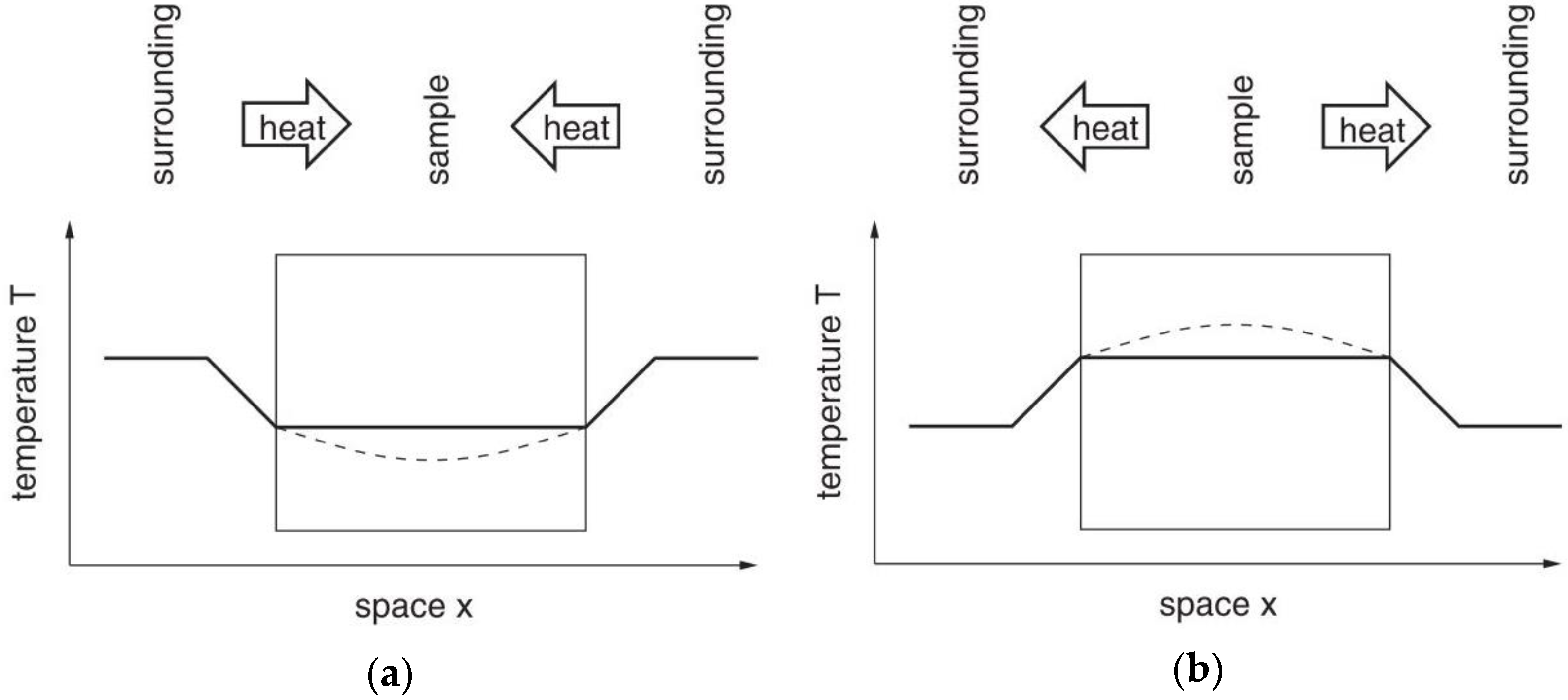
| High heat capacity Low thermal conductivity Phase change over a narrow temperature range | Thermal gradient inside a PCM sample is larger compared to other materials. Difference between apparent and real temperatures of the sample. | Smaller sample sizes, and lower heating and cooling rates, reduce the temperature shift. However, both of them lead to a weaker signal and a decreased accuracy in enthalpy. Using a method like IEA can help us to determine the suitable heating rate. | [45] |
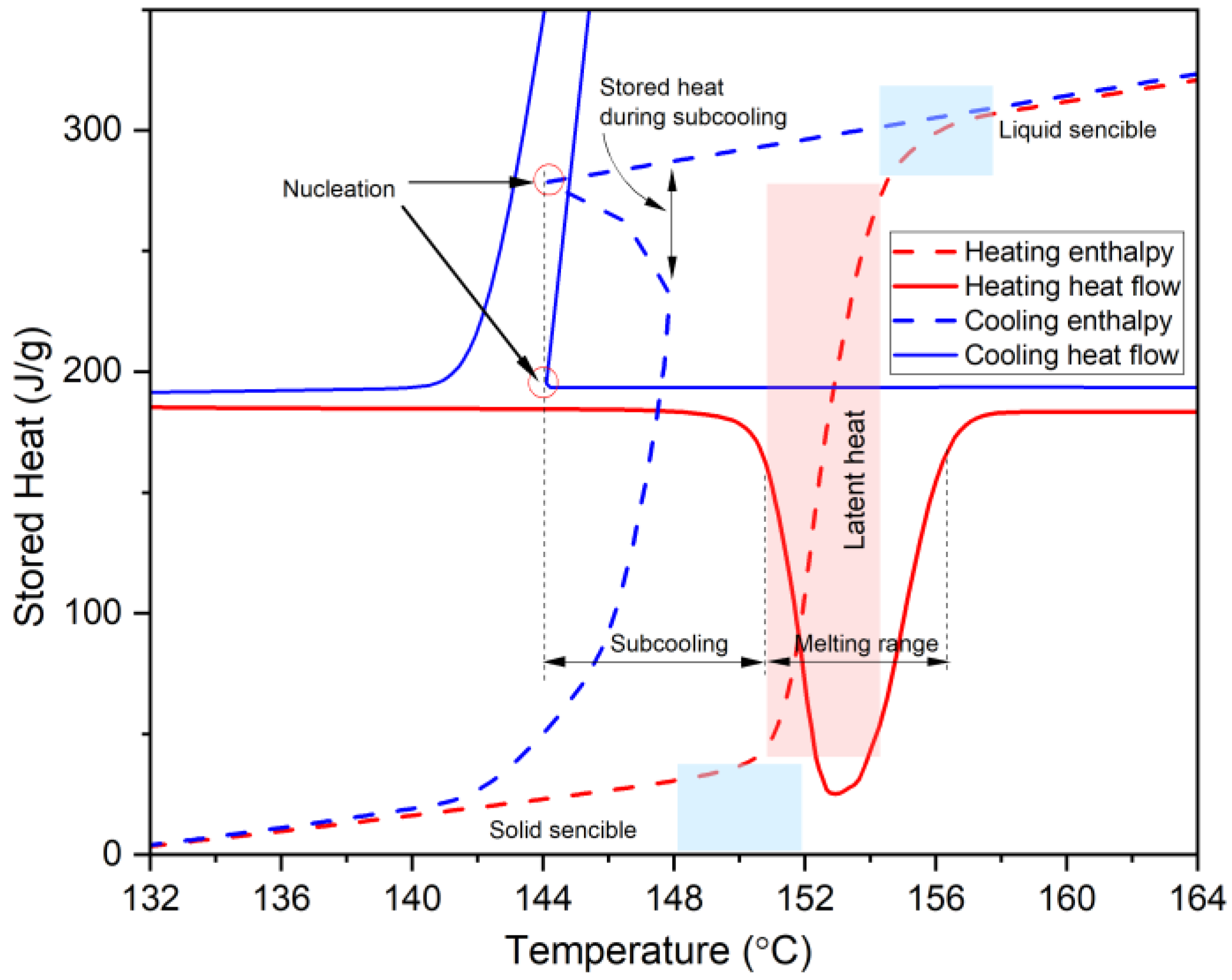
| Subcooling | Subcooling deforms the cooling curve and gets stronger for smaller samples. External effects such as container or crucible wall. Small and moderate subcooling can be up to 5 and 10 °C, respectively. | Subcooling is a highly volume dependent phenomenon. So, at the DSC scale, PCMs show larger subcooling. Adding nucleating agents is a useful method to reduce subcooling. Using a DSC equipped with a cooling system provides one with better temperature control over the solidification cycle. For samples showing subcooling, DSC in medium to slow dynamic mode (under 2 °C/min) is recommended. Combining DSC and T-history helps distinguish between real properties of a PCM and effects from test conditions. Adding nucleating agents is a useful method to reduce subcooling. | [14,26,48,52] |
| Impure PCMs (enhancers, nucleating agents) | Sampling | Small sample might not be representative of bulk material. Repeating DSC tests by taking different samples. Using methods such as T-history allows testing of a larger sample size. | [22] |
| Impure PCMs (mixture of several constituents) | Peak separation and incongruent phase change process | Large heating rates result in disappearing or merging small peaks into a larger one. Slow dynamic mode is recommended. | [46] |
| Incomplete phase change process | Partly melting/freezing due to the non-continuous load of energy | Large heating/cooling rate would not simulate correctly the real heat transfer into/out of PCM in the application. Slow dynamic mode is recommended. | [46] |
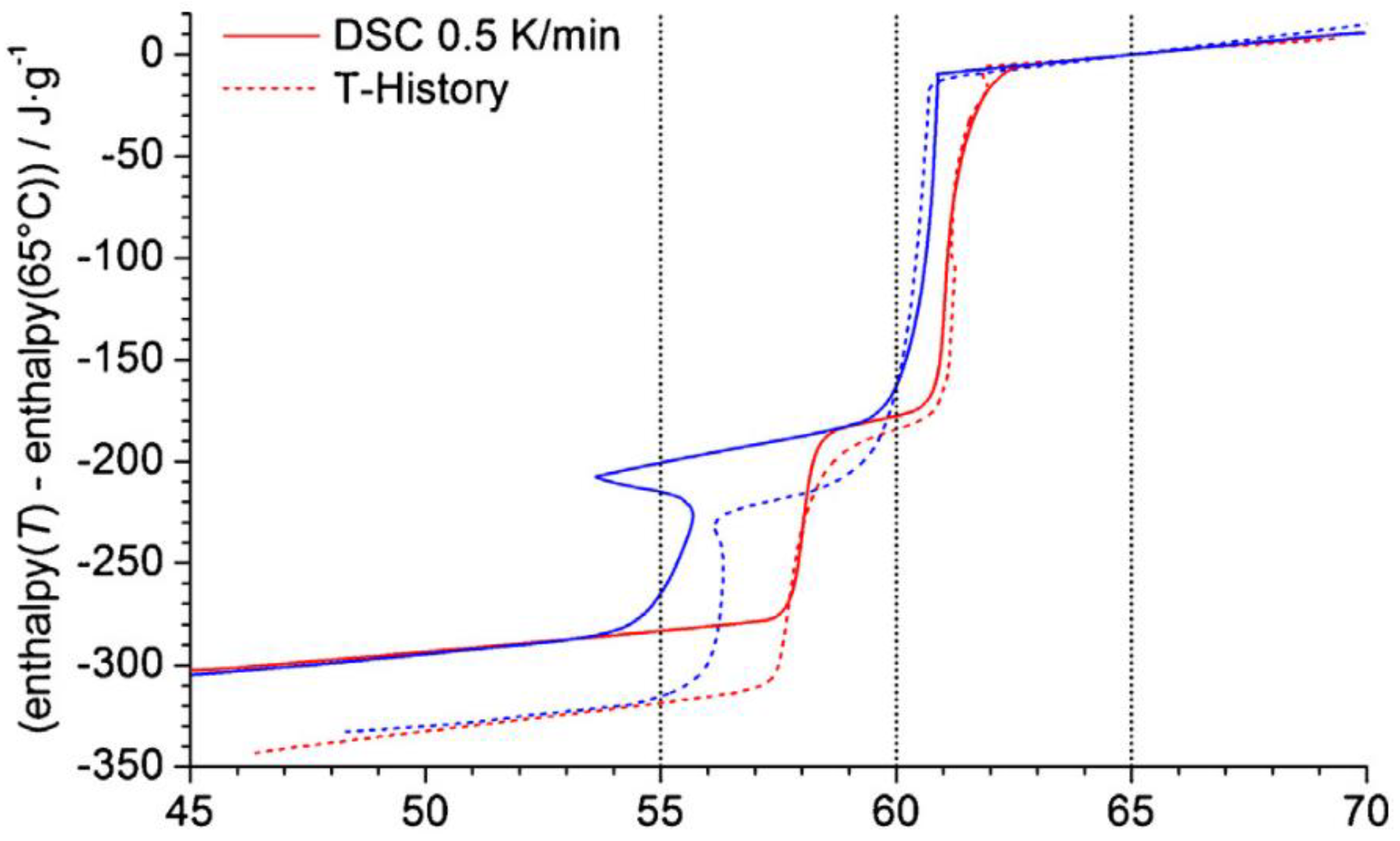
| Asymmetrical process of melting and solidification | In heat transfer modeling of PCMs, melting and solidification are assumed symmetrical | It is found out that melting and solidification are not symmetrical. Therefore, the enthalpy of a PCM is not only dependent on temperature, but also on the previous state of the PCM. | [53] |
| Ref. | PCM | Objective | Recommendations to Determine the Transition Temperature |
|---|---|---|---|
| [54] | Not precise | Recommendations concerning accurate property measurements | Low heating rate (~2 °C/min) Sample in good thermal contact with DSC pan Multi point calibration or use of a calibrant with a close melting point to the sample Reporting the test conditions |
| [64] | RT27 26.8 °C | Accurate determination of PCM melting range | Proposed a new method to determine actual endset of melting that is not dependent on the heating rate |
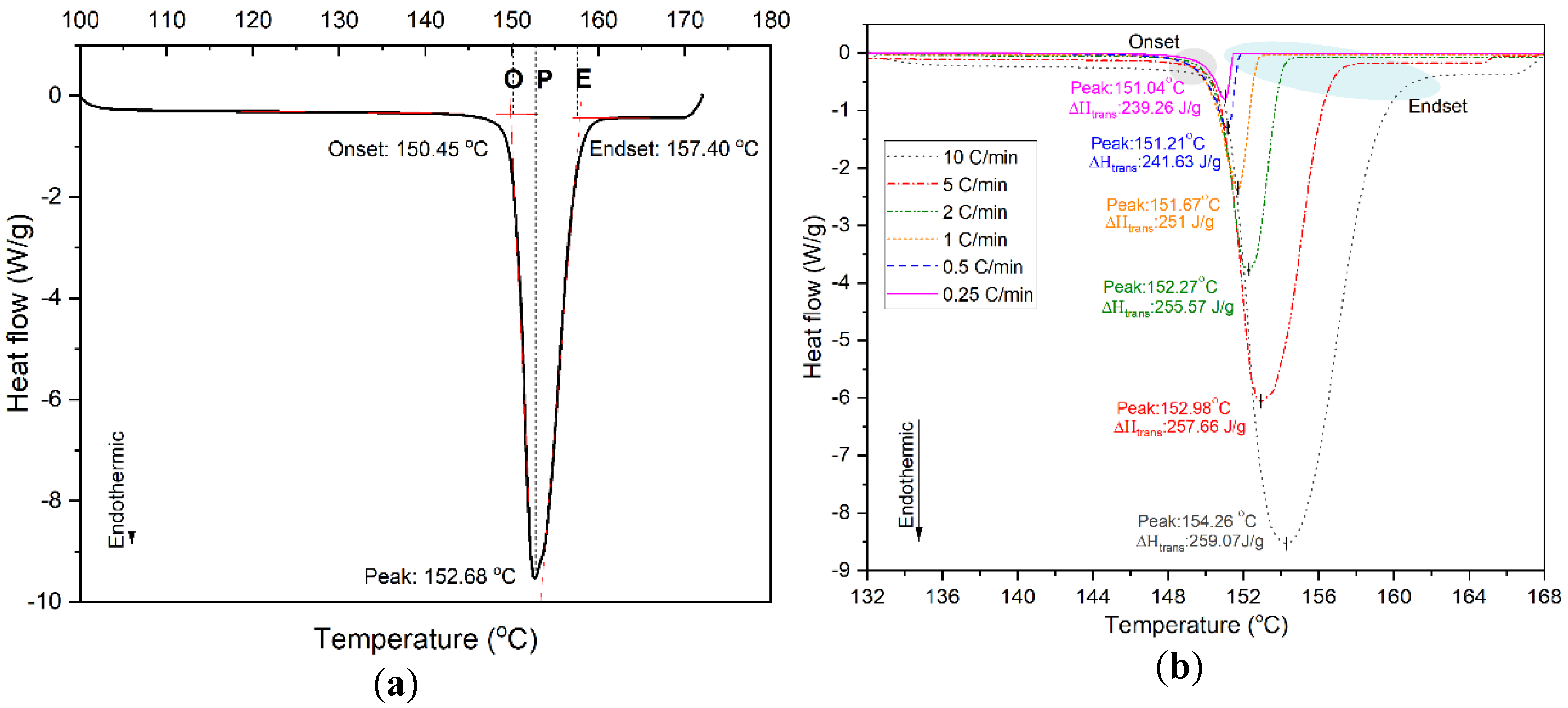
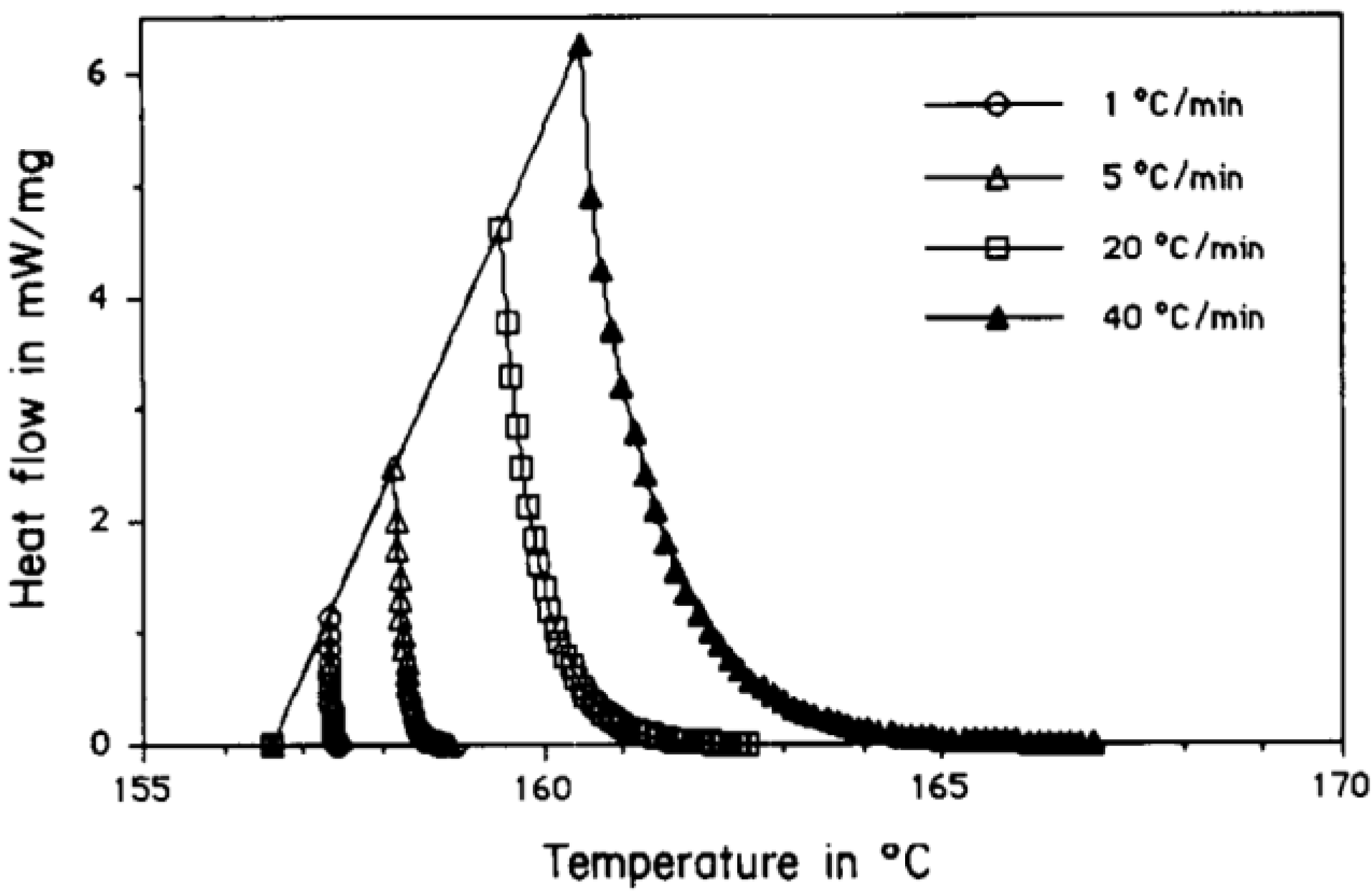
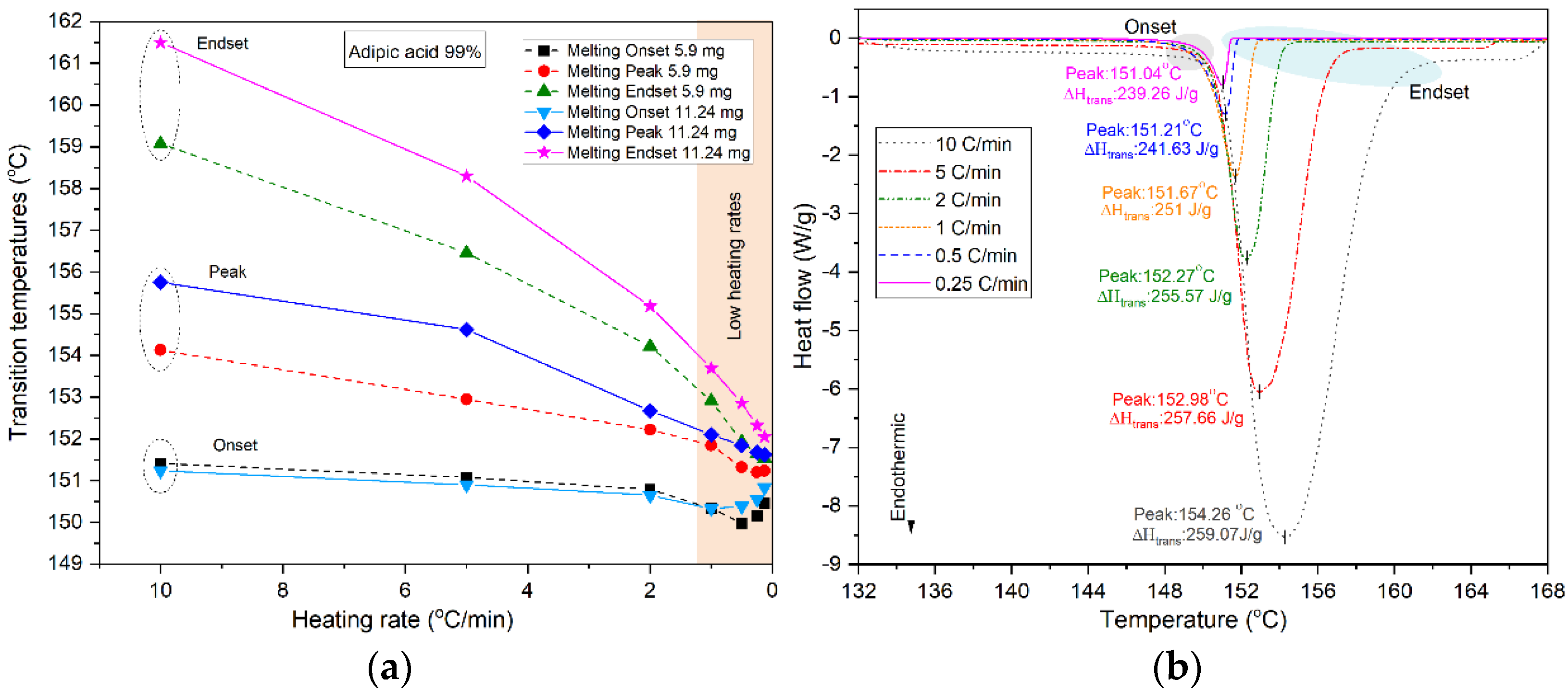
| [57] | Paraffin-based 15 °C Hydrated salt 25 °C | Investigating the influence of heating rate and sample mass on transition properties of organic and inorganic PCMs | By increasing mass and heating rate, peak and endset temperatures shift to higher values. In case of hydrated salts, high heating rates hide more information about the kinetics. To achieve smaller deviation with larger sample, lower heating rate should be preferred. |
| [63] | Hexadecane 18 °C Heptadecane 21.8 °C Octadecane 28 °C | Physical modelling of a heat transfer inside a DSC sample | In order to describe accurately the melting process inside a DSC cell, use lower heating rate. In case of mixture of PCMs, high heating rates hide more information about the kinetics of melting. |
| [65] | 23 organic and inorganic PCMs in the range of (−50 to 190 °C) | Establishing a consistent method to determine the phase transition temperatures and enthalpy | A combination of low heating rate (2 °C/min) for temperature measurement and high heating rate (10 °C/min) for enthalpy were used in a single temperature program. |
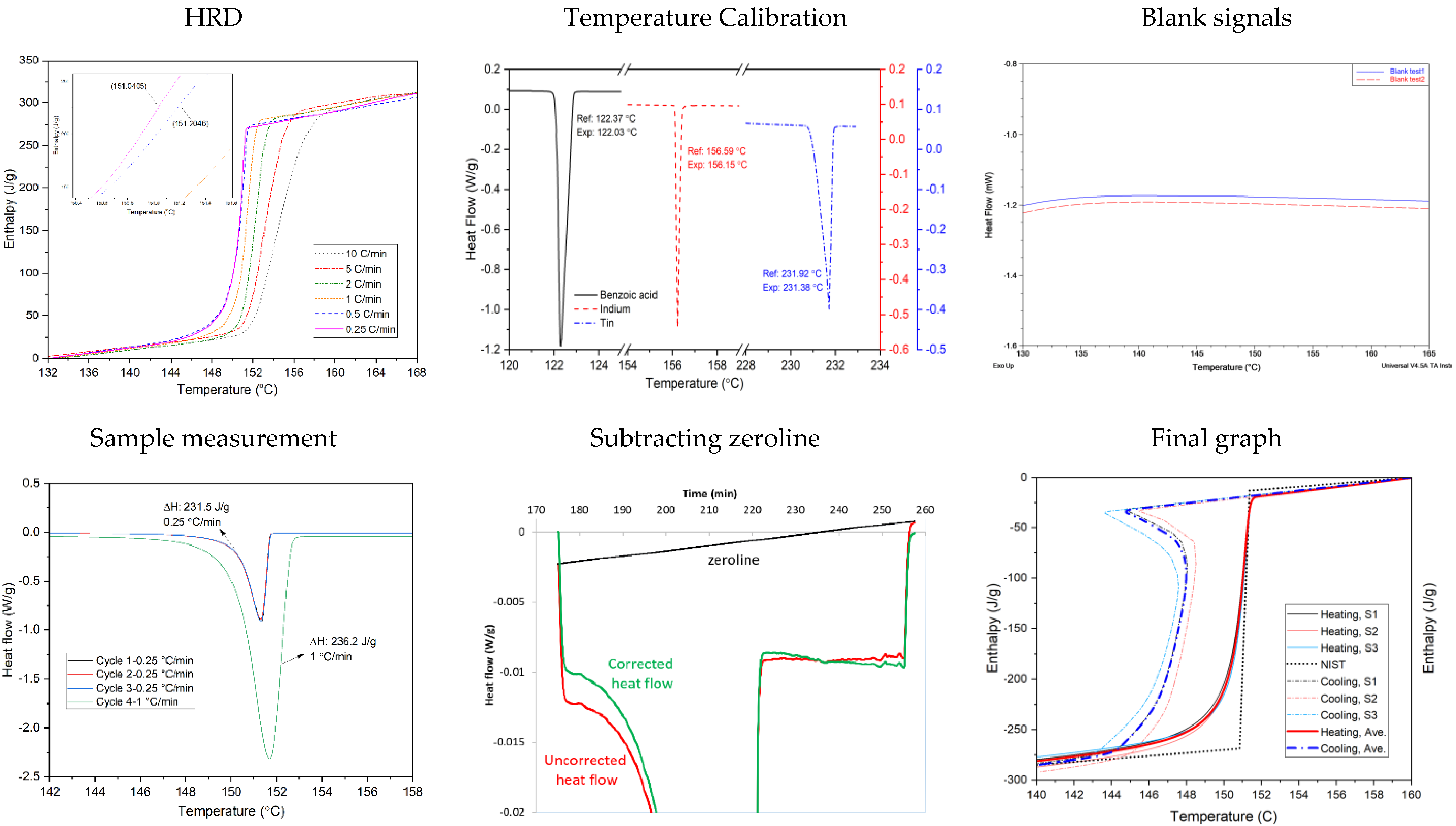
| Steps | Explanation | |
|---|---|---|
| 1 | Determination of the heating rate | Apply several heating rates from fast rate and slow down by half in the subsequent runs. When the temperature difference is less than 0.2 K between inflection points of two different heating rates, or less than 0.5 K between heating and cooling curves, criteria is met. |
| 2 | Calibration with determined heating rate | Temperature calibration using three different references by determined heating rate. |
| 3 | Measurement with empty crucible | Measurement of empty crucible as a baseline |
| 4 | Sample measurement | Measure three samples per PCM, each for four cycles, using the determined heating rate and a similar mass |
| 5 | Data Analysis | Subtract the baseline signal from sample signal Subtract the zeroline Representing the enthalpy graph |
| Ref. | PCM | Objective | Recommendations to Determine Transition Temperatures |
|---|---|---|---|
| [54] | PT-37 Paraffin (eicosane) | Indistinctive effect of heating rates on the value of transition enthalpy | 10 K/min heating rate or above 1 K/min Sample in a good thermal contact with DSC pan (pre-melt the sample) Calibration with indium just prior to the experiment Reporting the test conditions |
| [64] | Commercial RT27 | Finding the phase transition range by determining the endset of transition | Proposed a new method to determine actual endset of melting peak that is independent of heating rate. |
| [57] | n-octadecane 15 °C calcium chloride hexahydrate 25 °C | Determining suitable heating rate and sample mass using DSC | In case of hydrated salts, high heating rates hide more information about the kinetics. To achieve smaller deviation with larger sample, lower heating rate should be chosen. PCMs with higher thermal conductivity are more sensitive to heating rate rather than sample mass. |
| [59] | Octadecane (98.11%), | Study dynamic and step method and test their accuracy on the h(T) relationship | Run a baseline test Use low heat rate Applying same method leads to repeatable results in different labs with different machines |
| [45] | Commercial RT27 | Influence of two different modes of heating (dynamic and step modes) on the accuracy of enthalpy–temperature relationship. | The step method is less sensitive to the measurement parameters. In dynamic mode, by decreasing heating rate the uncertainty is decreased, but at the cost of increasing uncertainty. |
| [22] | Salt hydrate | Investigating the enthalpy change of a PCM as a function of temperature | Calorimetric measurements were carried out by three different methods (DSC, T-history and large-scale set-up). T-history method allows one to test a larger amount of sample. This is suitable in case of heterogenous PCMs. |
| [9] | Salt hydrate | Review of the studies concerning the phase transition enthalpy of salt hydrates | In case of salt hydrates, it is important to indicate the preparation, verification of sample composition and water content of the sample. This review paper includes the experimental results regarding the calorimetry of salt hydrates. |
| [66] | Not precised | Preparing quality and testing specifications for PCMs | Determining heating rates for each test condition in order to measure enthalpy |
| Ref. | PCMs | Instrument/Method | Test Conditions | Calibration | Highlights | Recommendations |
|---|---|---|---|---|---|---|
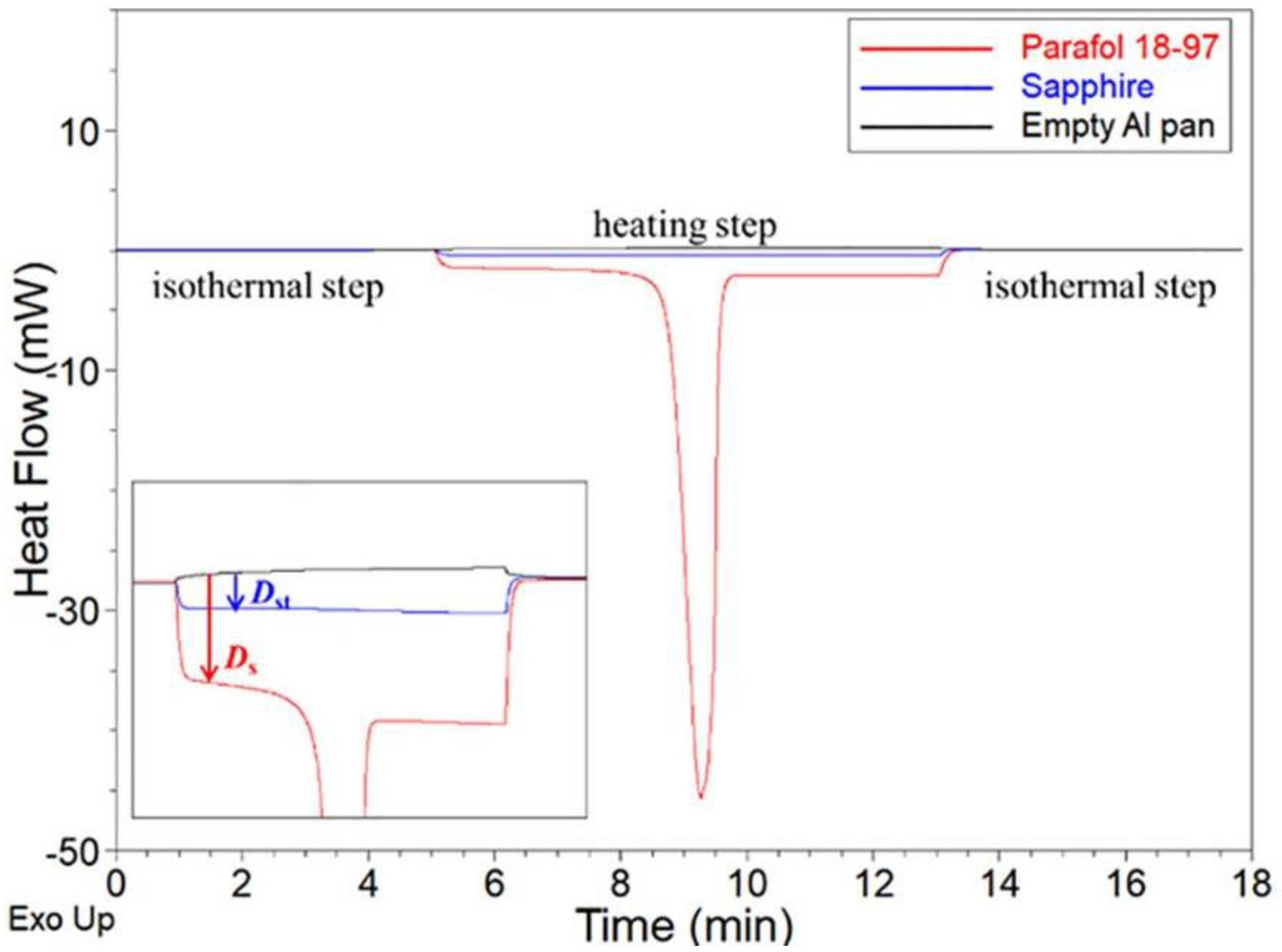
| [54] | Parafol 18–97 | TA-Q200 Three steps ASTM-E1269-11 | Isotherm-5 min Ramp 10 °C/min Isotherm-5 min | Baseline Indium (cell constant check) | Following the ASTM-E1269-11, DSC can determine the Cp within 10% error | Reproducible baseline Good contact between the sample and the pan and between the pan and the DSC Same condition and same pan for the three steps |
| [17] | RT15 RT22 HC | TA-Q2000 | Isotherm-3 min Ramp 10 °C/min Isotherm-3 min | Indium | The effects of heating rate and sample mass on Cp have been studied | Studying the effect of heating rate on heat capacity can provide the designer with a simulation of heat transfer conditions |
| [68] | Octadecanoic acid Tm: 70 °C | TA-modulated DSC (Discovery DSC) | Equilibrium step for 10 min Heating rate 3 °C/min PCM was melted prior to starting measurements | Sapphire | Heat capacity measurements during the phase transition (less than 5% error) | Use modulated DSC for heat capacity measurement during the thermal events |
| [62] | RT24 RT25 RT26 PT25 | Netzsch 214 Polyma heat-flux DSC | Before and after the phase transition by 10 °C/min according to DIN 51007 During the transition by 0.25 or 0.125 °C/min, according to IEA | Three steps based on DIN 51007 | Their Cp results showed negligible deviation | Using two different heating rates to measure heat capacity of PCM High rates for sensible regions Low rates for transition |
| [57] | Paraffin based (n-octadecane) Hydrated salt (calcium chloride hexahydrate) | TA-DSC 2920 | Measurement in the range of (0–50 °C) | Baseline (empty pan) | By increasing heating rate and sample mass, the peak height decreases | |
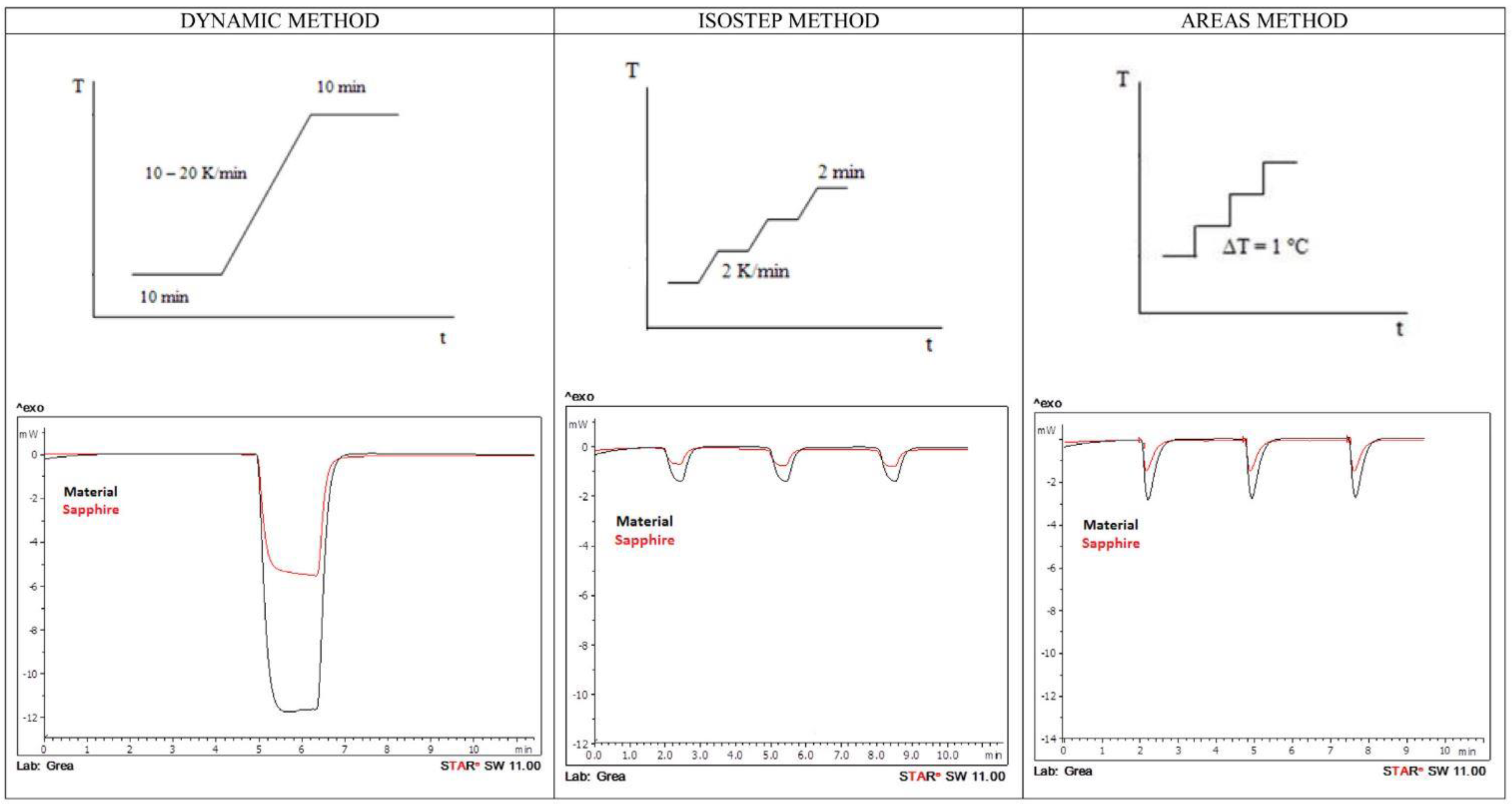
| [43] | Sensible storage materials (water, slate and potassium nitrate (KNO3) | Mettler Toledo 822e DSC | Three steps method Three modes of heating: dynamic, isostep and areas | Zinc Indium | 3% error in areas method 6% error in dynamic method 16% error in Isostep method | The wider temperature range of interest should be considered in dynamic method |
| [69] | (E)-3-phenylbut-2-enoic acid Tm: 95 °C | TA-Q1000 | Isothermal period -5 min Ramp 5 °C/min Zero the heat flow in the middle of temperature range | Indium Sapphire Benzoic acid | The overall uncertainty was less than 5% for benzoic acid Cp was measured to calculate thermodynamic properties such as enthalpy and entropy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatahi, H.; Claverie, J.; Poncet, S. Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review. Appl. Sci. 2022, 12, 12019. https://doi.org/10.3390/app122312019
Fatahi H, Claverie J, Poncet S. Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review. Applied Sciences. 2022; 12(23):12019. https://doi.org/10.3390/app122312019
Chicago/Turabian StyleFatahi, Hazhir, Jérôme Claverie, and Sébastien Poncet. 2022. "Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review" Applied Sciences 12, no. 23: 12019. https://doi.org/10.3390/app122312019
APA StyleFatahi, H., Claverie, J., & Poncet, S. (2022). Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review. Applied Sciences, 12(23), 12019. https://doi.org/10.3390/app122312019







