Evaluation of Different Control Algorithms for Carbon Dioxide Removal with Membrane Oxygenators
Abstract
1. Introduction
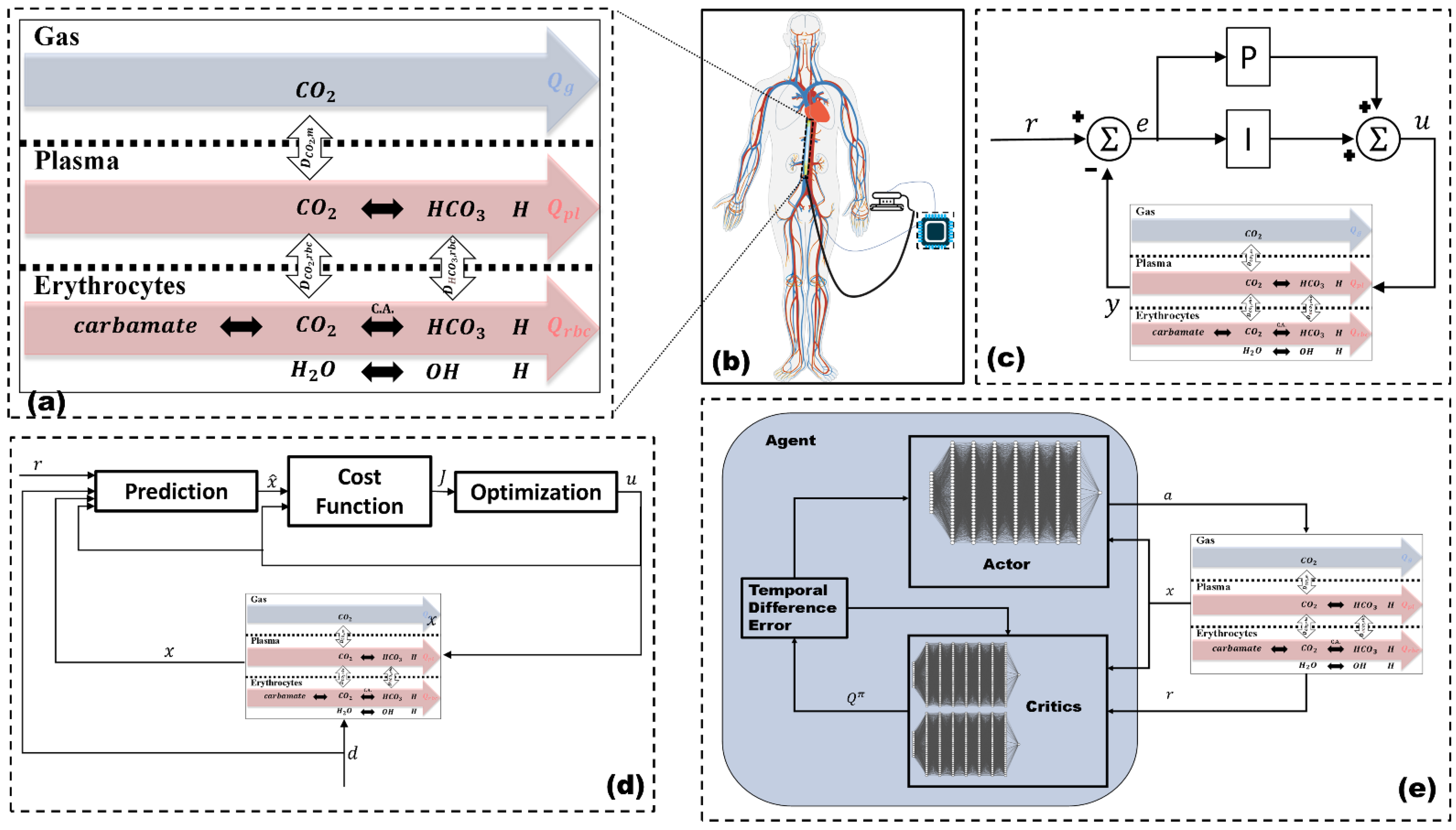
2. Modeling and Control
2.1. Mathematical Model
2.1.1. Gas Compartment
2.1.2. Plasma Compartment
2.1.3. Erythrocytes Compartment
2.1.4. Model Adjustment
2.1.5. Model Implementation
2.2. Control
2.2.1. PI Controller
2.2.2. Non-Linear Model Predictive Controller
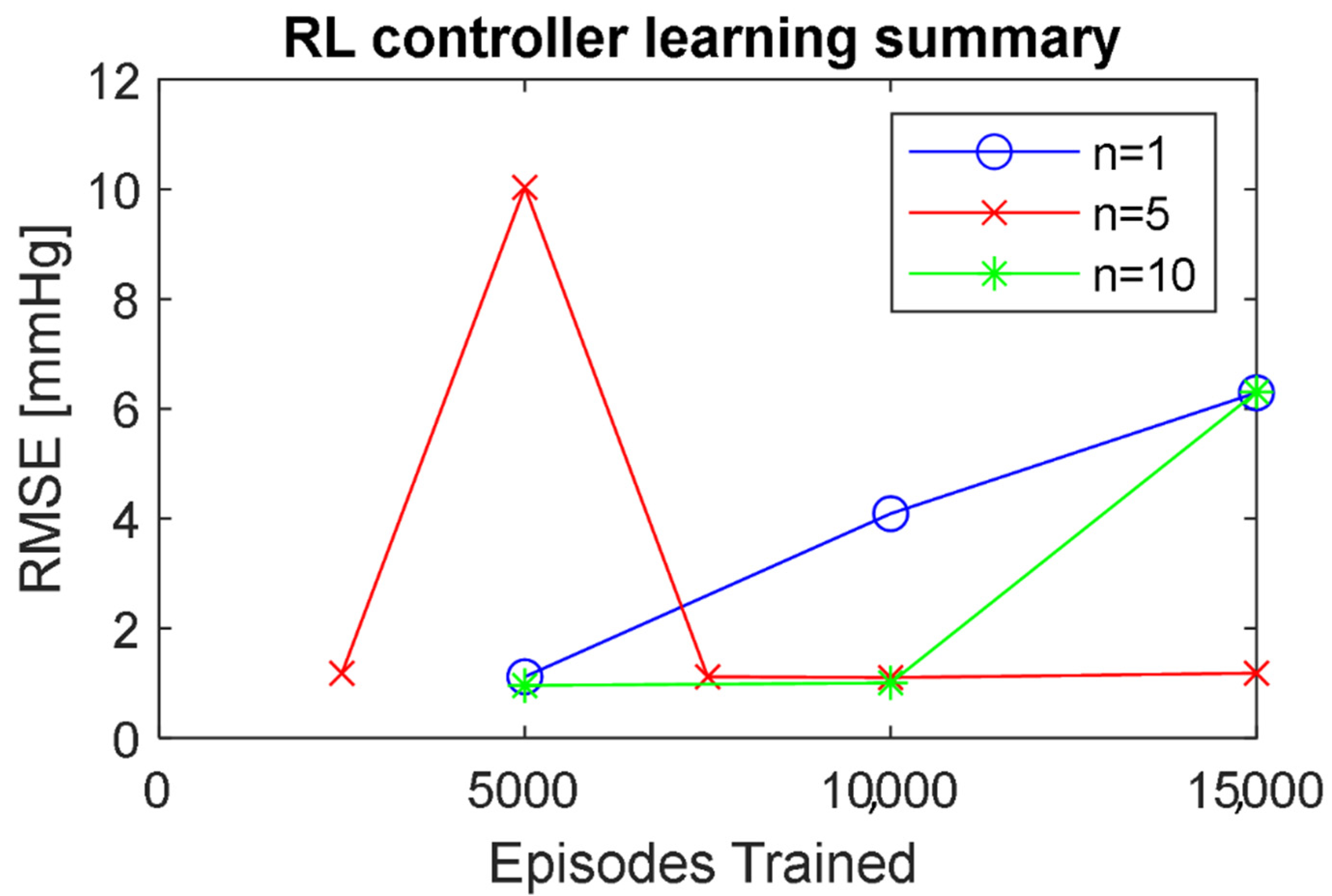
2.2.3. Reinforcement Learning Controller
2.2.4. Imitation Learning
2.2.5. Controller Implementation
2.3. Control Experiments
2.3.1. Rise Time
2.3.2. Settling Time
2.3.3. Root-Mean-Squared Error
2.3.4. Action Power
2.3.5. Action Standard Deviation
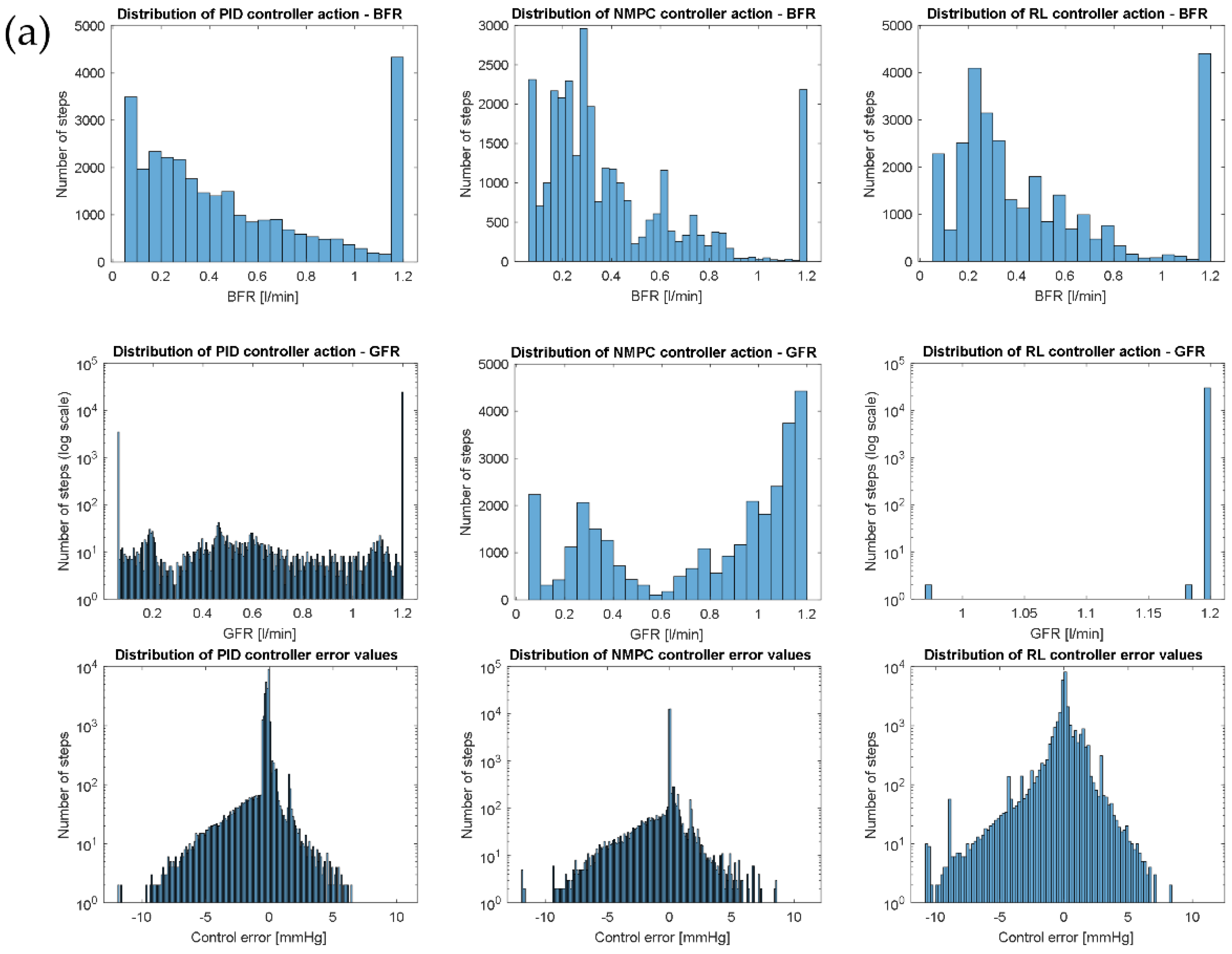
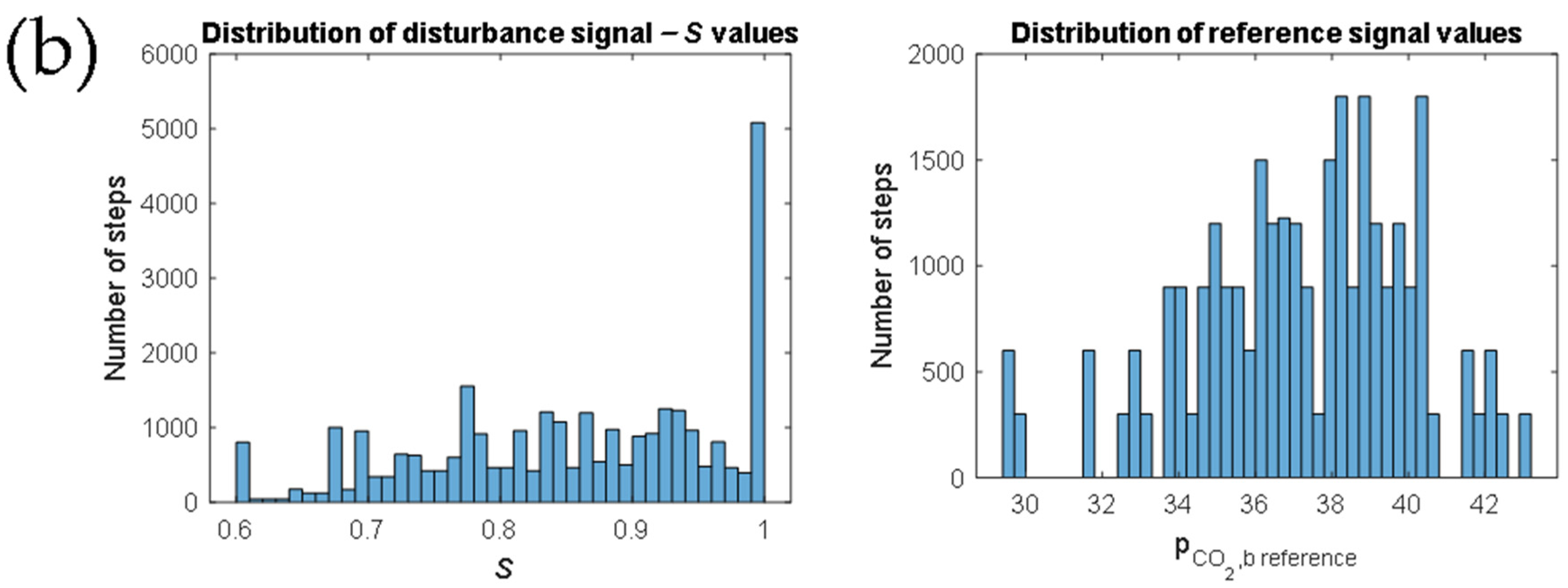
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| Gas compartment | |
| (A1) | |
| Plasma compartment | |
| (A2) | |
| (A3) | |
| (A4) | |
| (A5) | |
| Erythrocytes compartment | |
| (A6) | |
| (A7) | |
| (A8) | |
| (A9) | |
| (A10) | |
| (A11) | |
| (A12) | |
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Gas volume | 0.0055 | L | |
| Blood volume | 0.0121 | L | |
| Plasma volume | L | ||
| Erythrocyte volume | L | ||
| Membrane diffusion capacity | 5.4 × 10−6 | L (mmHg s)−1 | |
| Gas pressure | 760 | mmHg | |
| CO2 solubility coefficient | 3.5 × 10−5 | M mmHg−1 | |
| CO2 molar volume | 25.64 | M−1 | |
| Erythrocyte diffusion capacity for CO2 | M L (mmHg s)−1 | ||
| Erythrocyte diffusion capacity for HCO3 | M L (mmHg s)−1 | ||
| CO2 half-time erythrocyte membrane diffusion | 0.001 | s | |
| HCO3 half-time erythrocyte membrane diffusion | 0.2 | s | |
| Buffer capacity plasma | 6 × 10−3 | M pH−1 | |
| Buffer capacity erythrocytes | 57.7 × 10−3 | M pH−1 | |
| CO2 hydration reaction forward constant | 0.12 | s−1 | |
| CO2 hydration reaction reverse constant | 89 | s−1 | |
| Carbonic acid dissociation equilibrium constant | 5.5 × 10−4 | M | |
| Carbamate generation forward constant | 5 × 103 | (M s)−1 | |
| Oxygenated hemoglobin ionization constant | 8.4 × 10−9 | M | |
| De-oxygenated hemoglobin ionization constant | 7.2 × 10−8 | M | |
| Carbamate ionization constant | 2.4 × 10−5 | - | |
| Carbonic anhydrase catalytic factor | 13,000 | - | |
| Hemoglobin concentration | 20.7 × 10−3 | M |
| Symbol | Variable | Description | Unit | Value |
|---|---|---|---|---|
| Partial pressure CO2 gas oxygenator | state | mmHg | 0.695 | |
| Partial pressure CO2 gas venous | disturbance | mmHg | 0 | |
| Partial pressure CO2 plasma oxygenator | state, output | mmHg | 43 | |
| Partial pressure CO2 plasma venous | disturbance | mmHg | 46 | |
| Partial pressure CO2 erythrocyte oxygenator | state | mmHg | 43.1 | |
| Partial pressure CO2 erythrocyte venous | disturbance | mmHg | 46 | |
| Bicarbonate concentration plasma oxygenator | state | M | 263 × 10−4 | |
| Bicarbonate concentration plasma venous | disturbance | M | 263 × 10−4 | |
| Bicarbonate concentration erythrocyte oxygenator | state | M | 183 × 10−4 | |
| Bicarbonate concentration erythrocyte venous | disturbance | M | 182 × 10−4 | |
| Hydrogen concentration plasma oxygenator | state | M | 42.3 × 10−9 | |
| Hydrogen concentration plasma venous | disturbance | M | 42.3 × 10−9 | |
| Hydrogen concentration erythrocyte oxygenator | state | M | 61 × 10−9 | |
| Hydrogen concentration erythrocyte venous | disturbance | M | 61 × 10−9 | |
| Virtual pH | state | - | 7.37 | |
| Carbamate concentration | state | M | 184 × 10−5 | |
| Carbamate concentration venous | disturbance | M | 235 × 10−5 | |
| Blood oxygen saturation | measured disturbance | - | - | |
| Hematocrit | disturbance | - | 0.45 | |
| Sweep gas flow rate | manipulated variable | L/s | - | |
| Blood flow rate | manipulated variable | L/s | - |
| Symbol | Meaning |
|---|---|
| CO2 | Carbon dioxide |
| O2 | Dioxygen |
| N2 | Dinitrogen |
| HCO3 | Bicarbonate Ion |
| H | Hydrogen |
| pH | Potential of hydrogen |
| Oxygen molar concentration | |
| Oxygen partial pressure | |
| Blood oxygen capacity | |
| Virtual partial pressure of oxygen | |
| Temperature | |
| Oxygen solubility in blood | |
| Venous oxygen molar concentration | |
| Membrane diffusion capacity for oxygen | |
| Oxygen molar volume | |
| Oxygen partial pressure in sweep gas | |
| Future state vector | |
| Function of x and u | |
| State vector | |
| Input vector | |
| Minimizing function | |
| Control horizon number of samples, number of transitions | |
| Cost | |
| Sample index | |
| Cost function | |
| Regularization parameter | |
| Policy | |
| Q-value function | |
| Time | |
| Agent action at time t | |
| Environment state at time t | |
| Reward | |
| Future reward discount factor | |
| Policy function | |
| Function parameters (weights of the neural net) | |
| Target Q-value function | |
| Target function update rate |
References
- Makdisi, G.; Wang, I.W. Extra Corporeal Membrane Oxygenation (ECMO) review of a lifesaving technology. J. Thorac. Dis. 2015, 7, E166–E176. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, R.G.; Lund, L.; Frankowski, B.; Federspiel, W.J. An extracorporeal carbon dioxide removal (ECCO 2 R) device operating at hemodialysis blood flow rates. Intensive Care Med. Exp. 2017, 5, 41. [Google Scholar] [CrossRef]
- Kneyber, M.C. Mechanical ventilation during extra-corporeal membrane oxygenation: More questions than answers. Minerva Anestesiol. 2019, 85, 91–92. [Google Scholar] [CrossRef] [PubMed]
- Ficial, B.; Vasques, F.; Zhang, J.; Whebell, S.; Slattery, M.; Lamas, T.; Daly, K.; Camporota, N.A. Physiological basis of extracorporeal membrane oxygenation and extracorporeal carbon dioxide removal in respiratory failure. Membranes 2021, 11, 225. [Google Scholar] [CrossRef]
- Teber, O.O.; Altinay, A.D.; Mehrabani, S.A.N.; Tasdemir, R.S.; Zeytuncu, B.; Genceli, E.A.; Dulekgurgen, E.; Pekkan, K.; Koyuncu, İ. Polymeric hollow fiber membrane oxygenators as artificial lungs: A review. Biochem. Eng. J. 2022, 180, 108340. [Google Scholar] [CrossRef]
- Bouchez, S.; de Somer, F. The evolving role of the modern perfusionist: Insights from transesophageal echocardiography. Perfusion 2021, 36, 222–232. [Google Scholar] [CrossRef] [PubMed]
- Boeken, U.; Ensminger, S.; Assmann, A.; Schmid, C.; Werdan, G.; Michels, O.; Miera, F.; Schmidt, S.; Klotz, C.; Starck, K. Einsatz der extrakorporalen Zirkulation (ECLS/ECMO) bei Herz- und Kreislaufversagen. Kardiologe 2021, 15, 526–535. [Google Scholar] [CrossRef]
- Utley, J.R. Techniques for avoiding neurologic injury during adult cardiac surgery. J. Cardiothorac. Vasc. Anesth. 1996, 10, 38–44. [Google Scholar] [CrossRef]
- Misgeld, B.J.E.; Werner, J.; Hexamer, M. Simultaneous automatic control of oxygen and carbon dioxide blood gases during cardiopulmonary bypass. Artif. Organs 2010, 34, 503–512. [Google Scholar] [CrossRef]
- Manap, H.H.; Wahab, A.K.A.; Zuki, F.M. Control for Carbon Dioxide Exchange Process in a Membrane Oxygenator Using Online Self-Tuning Fuzzy-PID Controller. Biomed. Signal Process. Control. 2021, 64, 102300. [Google Scholar] [CrossRef]
- Sadati, S.J.; Noei, A.R.; Ghaderi, R. Fractional-order control of a nonlinear time-delay system: Case study in oxygen regulation in the heart-lung machine. J. Control Sci. Eng. 2012, 2012, 478346. [Google Scholar] [CrossRef]
- Allen, J.; Fisher, A.C.; Gaylor, J.D.S.; Razieh, A.R. Development of a digital adaptive control system for PO2 regulation in a membrane oxygenator. J. Biomed. Eng. 1992, 14, 404–411. [Google Scholar] [CrossRef]
- Hill, E.P.; Power, G.G.; Longo, L.D. A mathematical model of carbon dioxide transfer in the placenta and its interaction with oxygen. Am. J. Physiol. 1973, 224, 283–299. [Google Scholar] [CrossRef]
- Lukitsch, B.; Ecker, P.; Elenkov, M.; Janeczek, C.; Haddadi, B.; Jordan, C.; Krenn, C.; Ulrich, R.; Gfoehler, M.; Harasek, M. Computation of global and local mass transfer in hollow fiber membrane modules. Sustainability 2020, 12, 2207. [Google Scholar] [CrossRef]
- Klocke, R.A. Velocity of CO2 exchange in blood. Annu. Rev. Physiol. 1988, 50, 625–637. [Google Scholar] [CrossRef]
- Hexamer, M.; Werner, J. A mathematical model for the gas transfer in an oxygenator. IFAC Proc. Vol. 2003, 36, 409–414. [Google Scholar] [CrossRef]
- Misgeld, B.J.E. Automatic Control of the Heart-Lung Machine. Ph.D. Thesis, Ruhr-Universität Bochum, Universitätsbibliothek, Bochum, Germany, 2007. [Google Scholar]
- Manap, H.H.; Wahab, A.K.A.; Zuki, F.M. Mathematical Modelling of Carbon Dioxide Exchange in Hollow Fiber Membrane Oxygenator. IOP Conf. Ser. Mater. Sci. Eng. 2017, 210, 012003. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Lukitsch, B.; Ecker, P.; Elenkov, M.; Janeczek, C.; Jordan, C.; Krenn, C.G.; Ulrich, R.; Gfoehler, M.; Harasek, M. Suitable CO2 solubility models for determination of the CO2 removal performance of oxygenators. Bioengineering 2021, 8, 1–25. [Google Scholar] [CrossRef]
- Harasek, M.; Elenkov, M.; Lukitsch, B.; Ecker, P.; Janeczek, C.; Gfoehler, M. Design of Control Strategies for the CO2 Removal from Blood with an Intracorporeal Membrane Device. In Proceedings of the 11th Biomedical Engineering International Conference (BMEiCON), Chiang Mai, Thailand, 21–24 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. J. Dyn. Syst. Meas. Control. Trans. ASME 1993, 115, 220–222. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control Theory and Algorithms; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2015; Volume 4, pp. 2587–2601. [Google Scholar]
- François-lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. In Foundations and Trends® in Machine Learning; Mike Casey: University of California, Berkeley, CA, USA, 2018; Volume II, pp. 1–140. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Dulac-Arnold, G.; Mankowitz, D.; Hester, T. Challenges of Real-World Reinforcement Learning. arXiv 2019, arXiv:1904.12901. [Google Scholar]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. Ser. B 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Waltz, R.A.; Morales, J.L.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Program. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Rizvi, A.S.A.; Pertzborn, A.J.; Lin, Z. Reinforcement Learning Based Optimal Tracking Control Under Unmeasurable Disturbances with Application to HVAC Systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Amodei, D.; Olah, C.; Steinhardt, J.; Christiano, P.; Schulman, J.; Mané, D. Concrete Problems in AI Safety. arXiv 2016, arXiv:1606.06565. [Google Scholar]
- Potra, F.A.; Wright, S.J. Interior-point methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
- Mills, N.L.; Ochsner, J.L. Massive air embolism during cardiopulmonary bypass. Causes, prevention, and management. J. Thorac. Cardiovasc. Surg. 1980, 80, 708–717. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Doron, Y.; Strub, F.; Hessel, M.; Sonnerat, N.; Modayil, J. Deep Reinforcement Learning and the Deadly Triad. arXiv 2018, arXiv:1812.02648. [Google Scholar]
- Elenkov, M.; Lukitsch, B.; Ecker, P.; Janeczek, C.; Harasek, M.; Gföhler, M. Non-parametric dynamical estimation of blood flow rate, pressure difference and viscosity for a miniaturized blood pump. Int. J. Artif. Organs 2022, 45, 207–215. [Google Scholar] [CrossRef] [PubMed]

| PI | NMPC | RL | |
|---|---|---|---|
| RT [s] | 1.18 | 1.33 | 4.9 |
| ST [s] | 2.24 | 3.57 | 7.6 |
| RMSE [mmHg] | 1.06 | 1.09 | 1.37 |
| [L2s−2] | 6.7 × 10−3 | 4.1 × 10−3 | 8 × 10−3 |
| [L2s−2] | 2.2 × 10−3 | 1.4 ×10−3 | 2 × 10−3 |
| [mLs−1] | 6.53 | 6.53 | 0.03 |
| [mLs−1] | 6.3 | 5.05 | 5.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elenkov, M.; Lukitsch, B.; Ecker, P.; Janeczek, C.; Harasek, M.; Gföhler, M. Evaluation of Different Control Algorithms for Carbon Dioxide Removal with Membrane Oxygenators. Appl. Sci. 2022, 12, 11890. https://doi.org/10.3390/app122311890
Elenkov M, Lukitsch B, Ecker P, Janeczek C, Harasek M, Gföhler M. Evaluation of Different Control Algorithms for Carbon Dioxide Removal with Membrane Oxygenators. Applied Sciences. 2022; 12(23):11890. https://doi.org/10.3390/app122311890
Chicago/Turabian StyleElenkov, Martin, Benjamin Lukitsch, Paul Ecker, Christoph Janeczek, Michael Harasek, and Margit Gföhler. 2022. "Evaluation of Different Control Algorithms for Carbon Dioxide Removal with Membrane Oxygenators" Applied Sciences 12, no. 23: 11890. https://doi.org/10.3390/app122311890
APA StyleElenkov, M., Lukitsch, B., Ecker, P., Janeczek, C., Harasek, M., & Gföhler, M. (2022). Evaluation of Different Control Algorithms for Carbon Dioxide Removal with Membrane Oxygenators. Applied Sciences, 12(23), 11890. https://doi.org/10.3390/app122311890






