1. Introduction
Complex decision-making and optimization problems occupy a very important position in smart cities. Swarm intelligence methods have become one of the important means to solve complex optimization problems in smart cities by simulating the emergence mechanism of intelligent behavior of social animals in nature [
1]. The ant colony algorithm in swarm intelligence has a wide range of application scenarios in the field of smart cities, and is widely used in smart transportation, path planning, and smart cities.
An important problem facing simulations relying on neuromorphic computing architecture is how to map complex neural networks to node networks; that is, how to achieve the mapping between logical and physical networks. A logic network, namely problem network and task network, when simulating a biological neural network, has a huge scale which is reflected in two aspects: one is the huge number of neurons, and the other is the complex connection between neurons. In addition, the logical network targets different application scenarios, and it is impossible to design the topology of the physical network structure for a specific logical network. At the same time, the nodes of physical networks have a limited capacity, a limited number of neurons capable of support, and a limited ability to route cells. Thus, mapping a logical network with a physical network has become a key challenge in system design.
In this context, many scholars have proposed a variety of algorithms; for example, an innovative ant colony optimization based on parameter tuning to solve the matching problem [
2]. To sum up, it can be roughly divided into four categories [
3].
- (1)
The greedy algorithm and its variants.
The greedy algorithm is the simplest mapping algorithm; it is divided into local greedy and global greedy [
4]. In local greedy, a starting node is first selected in each of the two graphs, and then one of the adjacent nodes is selected and added to the map. Global greedy will be based on a specific global strategy, such as the weights of the edges in the connection matrix. There are also algorithms that combine local and global, taking advantage of their respective characteristics.
- (2)
Graphical division.
The second common mapping algorithm is a graph division-based algorithm, such as a k-way graph division that divides the problem graph and the node topological graph recursion into smaller partitions, and then maps while expanding the recursion.
- (3)
Algorithm based on graph similarity.
Another mapping algorithm is a graph similarity-based algorithm, where the adjacency matrix of the problem graph and the node topological graph are arranged into a corresponding canonical form by some strategy, and are then mapped based on this rearranged adjacency matrix.
- (4)
The heuristic algorithm.
Heuristic algorithms summarize the past experience, and include genetic algorithms (GA), ant colony algorithms (ACA), particle swarm optimization (PSO) algorithms, etc. In general, such algorithms will have an objective function and will iterate based on this goal to gradually find the optimal strategy. The ant colony algorithm is fast in computation and has received attention from researchers due to its unique advantages [
5,
6,
7]. He et al. [
8] proposed an adaptive variable neighborhood search ant colony algorithm (AVNSACA) to make up for the lack of pheromones in the algorithm’s early stage, which avoid the algorithm falling into local optimum. Reed et al. [
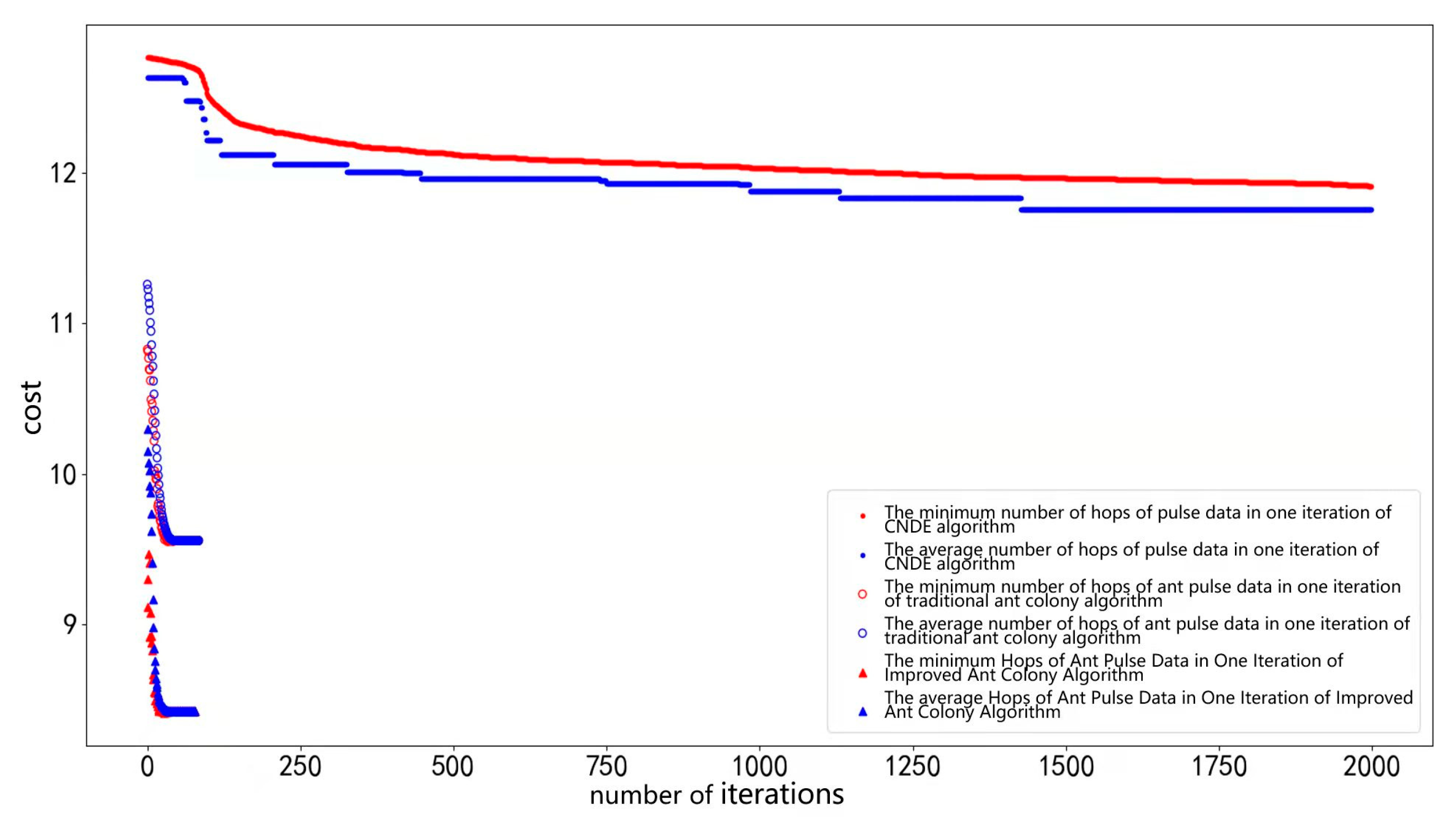
9] proposed an ant colony algorithm for the multi-compartment vehicle routing problem. Besides the differential evolution algorithm based on the complex networks algorithm (CNDE) are proposed for the topology mapping problem [
10,
11].
Because neural networks have a 3-dimensional (3D) structure, each neuron has multiple inputs and provides outputs to multiple neurons, making the application of the greedy algorithm difficult. The algorithms based on graph division and graph similarity are essentially greedy. As they lack global information and have no backtracking mechanism, they cannot provide a good mapping scheme [
12,
13]. Heuristic algorithms are widely studied in the global optimization literature and have become an effective method for solving complex optimization problems. When applied for many-to-one topological mapping, the traditional methods are limited by the node capacity, and it is difficult to carry out the corresponding combinatorial selection step. Therefore, to overcome these issues, a mapping method based on the ant colony algorithm is proposed here and is verified through simulation analysis and alignment.
The design purpose of the mapping algorithm is to study the optimal mapping scheme, which can effectively reduce the cost of solving problems. The core of the mapping algorithm is to design the objective function of the algorithm optimization. At present, the common optimization objective functions and evaluation indicators are summarized as follows [
14].
- (1)
Average hop count.
In the logical network, the communication between the connected neurons is realized by pulses. Due to the capacity limitation of the physical network nodes, the connected neurons often cannot be deployed on the same physical node. Therefore, the pulse generated by the source neuron needs to be transmitted to the destination neuron through the routing algorithm and forwarded by the communication unit. When the source neuron and the destination neuron are on the same node, the number of forwarding times required for the impulse data, that is, the number of hops, is 0. When the source neuron and the destination neuron are on adjacent nodes, the impulse data needs to be transmitted. The number of times is 1 [
14]. When the source neuron is farther from the physical node where the destination neuron is located, the number of hops required for the impulse data to reach the destination neuron will naturally increase.
The increase in the average hop count of pulse data means that the power consumption of the system increases, and the congestion problem that the system is faced with may be aggravated. Therefore, it is one of the optimization goals to choose an appropriate mapping method to reduce the average hop count of the pulse.
More specifically, the average hop count of the system is expressed as:
is the average hop count,
is the number of hops between the i-th neuron and the j-th neuron, as well as the number
of pulse data packets sent by the i-th neuron to the j-th neuron per unit time. There is no connection from the i-th neuron to the j-th neuron [
15]; then
.
In the case of multicast, this expression is different because when the forwarding direction required by the destination neuron is the same, only one forwarding is required. Therefore, the expression becomes:
Here, is the number of times the pulse sent for the i-th neuron needs to be retransmitted.
- (2)
Link load balancing.
Balancing the link load can effectively alleviate congestion, thereby reducing the waiting time of pulse packets on each node. The evaluation index of link load balancing is the link load variance:
is the link load variance, is the load on the i-th link, is the average link load, and is the total number of links.
- (3)
Node load balancing.
Node load balancing refers to the number of neurons deployed on each physical node. Balancing the node load can avoid a large number of neurons on the same physical node, resulting in excessive computing pressure and communication pressure on this node. This may lead to problems such as excessive delay and loss of pulse data packets. The evaluation index of node load balancing is the node load variance:
In the formula, is the node load variance, is the load on the i-th node, that is, the number of neurons, is the average node load, and is the total number of links.
- (4)
Energy consumption.
In a neuromorphic computing architecture computer, the energy consumption of the system can come from a variety of sources, including:
Computational energy consumption: neuron processing impulse data inevitably brings energy consumption.
Suspended state node energy consumption: In a scenario where a neuromorphic computer simulates a large-scale biological nervous system, many nodes will wait for the arrival of pulse data due to relatively sparse connections and other reasons. Therefore, in order to save energy, such nodes should be suspended state; the end of the suspended state is triggered by the arrival of the node.
Communication energy consumption: The energy consumption caused by the propagation of pulse data between nodes, including routing units, links, etc.; this part of the energy consumption is determined by factors such as the generation frequency and hop count of the system’s pulse data packets.
- (5)
Forwarding delay.
A pulse data from generation to response corresponds to its delay. In the biological nervous system, this delay also exists, whether it is the response time of biological neurons to electrical signals or the transmission time of electrical signals in axons and other parts, all of which cause delays in biological nervous systems. In neuromorphic computing, this time delay can be simulated by code inside the node. However, the delay caused by the forwarding of pulse data is difficult to predict, and this part of the delay may include the waiting time of the pulse data caused by the congestion problem, the delay caused by the communication link, and so on. Therefore, the forwarding delay is also one of the indicators to measure the system performance.
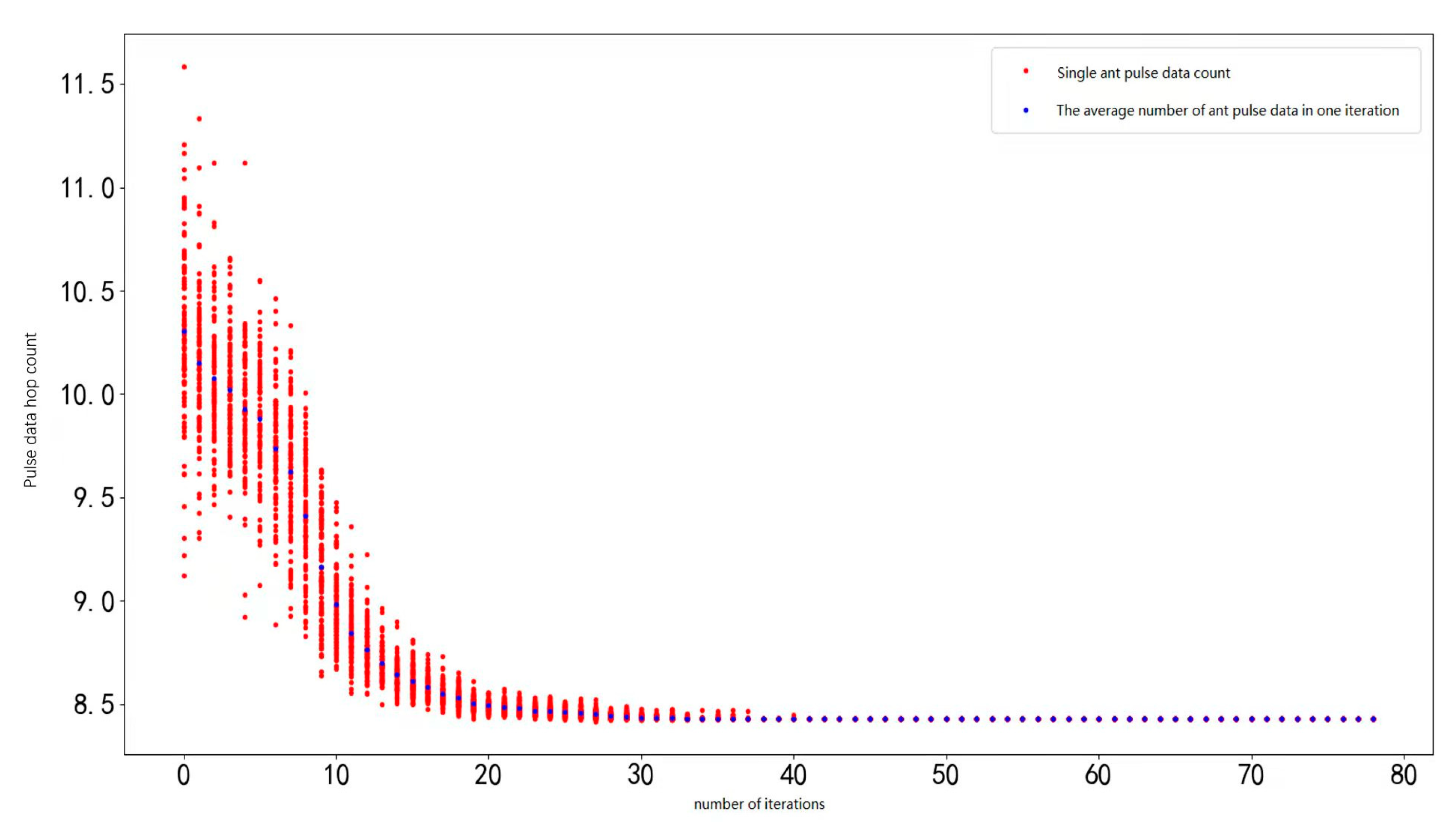
Considering the above factors, the average hop count is the most important indicator to measure the entire system. The smaller the average hop count, the less the pulse data needs to be forwarded, which can reduce the communication pressure of the system, reduce congestion, reduce the energy consumption caused by communication, and reduce the delay from the generation of pulse data to the response, etc. Therefore, this paper chooses the average hop count as the optimization objective, and reduces the average hop count by designing a mapping algorithm.
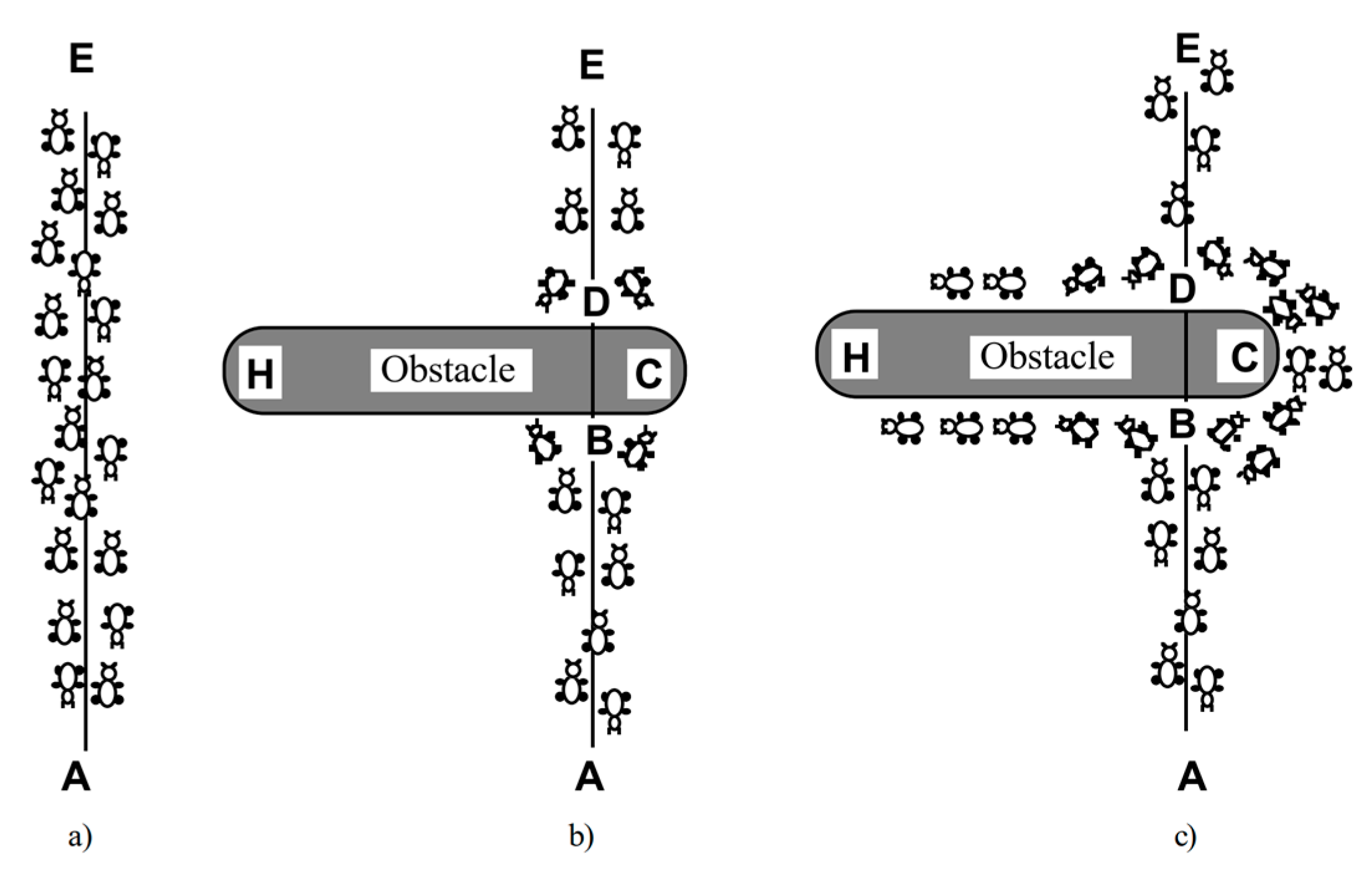
In 1991, Marco Dorigo proposed a simulated evolutionary algorithm, Ant Colony Optimization (ACO), inspired by the behavior of ant groups in finding the optimal path in their search for food [
16,
17]. As shown in
Figure 1, the colonies travel to and from points A and E (e.g., nest and food), following the shortest route. When an obstacle between A and E emerges, ants need to choose a side to pass around the obstacle. As ants leave pheromones on their path initially, without any pheromones on either side, the colony will make a random decision. However, as time passes, after more and more ants pass around the shorter edge of the obstacle, the pheromone concentration on that side becomes higher, resulting in more ants following this path. Eventually, the entire colony will adopt this new path from point A to point E.
The ant colony algorithm can be roughly divided into three stages:
The initialization includes two parts. One refers to the related hyperparameters, including the number of ants in the ant colony and the pheromone updates, among others. The other pertains to heuristic information: the decision basis of the ants, without any historical information.
- (2)
Solution construction.
The most critical point in the algorithm is how each ant chooses a path based on the available information.
- (3)
Pheromone update.
Pheromones affect ants’ decision making, and pheromone update strategies mimic pheromone updates in actual ant colonies, including volatilization and release. Therefore, pheromones automatically evaporate over time and colonies release pheromones on the selected path.
2. Improved Ant Colony Mapping Algorithm
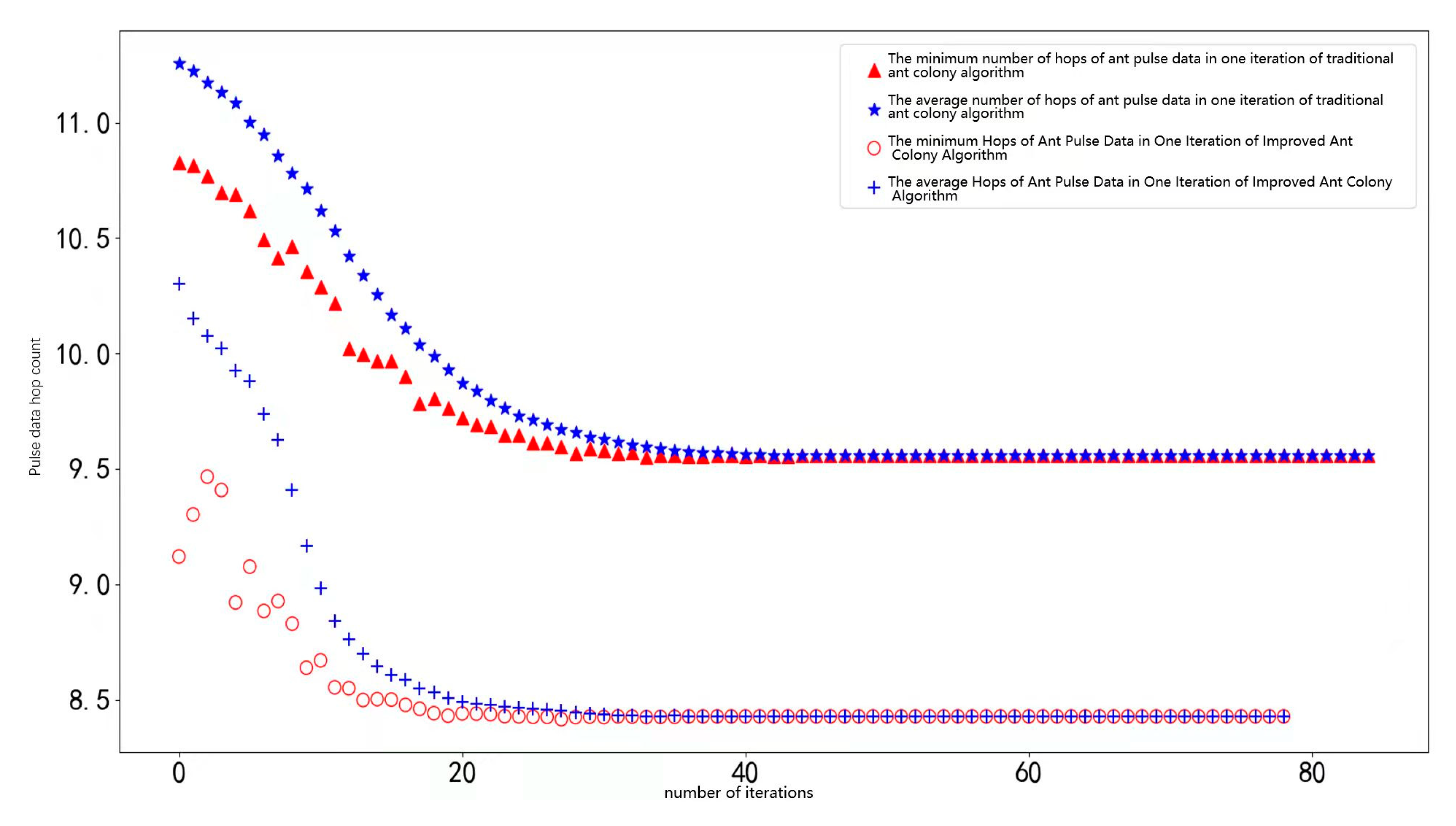
The ant colony algorithm has been widely used in various fields and topological mapping is one of its application scenarios, but current research focuses primarily on one-to-one scenarios leaving many-to-one scenarios inadequately explored. Therefore, an improved ant colony algorithm for a many-to-one topological mapping scenario is developed here, and is defined as:
That is, a given index of neurons through the mapping algorithm obtains the deployed node index. The goal of optimization is to average jumps and the objective function as follows:
C(v) is the forwarding number required for the pulse emitted by the neuron v. The p(v) refers to the proportion of neuron v generating pulses to all neuronal pulses; in random cases, all neurons in the same proportion.
2.1. Initialization
Heuristic information is defined as follows:
The heuristic information of neuron
mapping to node
is determined by the importance of neurons and the centers of the nodes. The number of neuron connections represents its importance,
.
The degree of the center of the node is determined by its Manhattan distance from the remaining nodes.
The center degree of the node is the sum of its Manhattan distance from other nodes. This value reflects the communication ability of the node; the smaller the Manhattan distance, the higher the center degree of the node. The more neurons the output of the neuron is connected to, the greater the communication pressure of the neuron, so it should be placed on a node with a high degree of centrality. Therefore, the heuristic information should be proportional to the importance of neurons and inversely proportional to their centrality, so that neurons with high communication pressure are more likely to be deployed on nodes with strong communication capabilities.
2.2. Solution Construction
In the traditional ant colony algorithm, the probability of t (that the ant
k maps the neuron
to the node
in the first iteration) is:
In the above formula,
is the
t cycle,
is the occupancy of node
in the
t cycle, and
is the normalized pheromone concentration of the node.
In this paper, some improvements have been made to the above decision probability. Compared to the traditional ant colony algorithm, is added to the probability, representing the occupancy rate of node in the t-th cycle. That is, it is more inclined to deploy neurons on nodes with high occupancy, and deploying different neurons on the same node directly avoids the traffic between them. When the occupancy is 0, is placed as the same as deploying a neuron.
and mean the weight. The larger the value of , the more likely the ants choose to take the path with high pheromone concentration; that is, the greater the possibility of choosing the path that has been tried before, thus reducing the randomness of the search. With larger values, it is easier for colonies to choose locally shorter paths, which can accelerate convergence, but are easier to fall into local optima.
is the set of nodes that can still deploy neurons at present. Because the capacity of nodes is limited, some nodes will be filled with the deployment process of neurons, so only nodes that are not full can be selected.
2.3. Pheromone Update
The update rules for pheromones are as follows:
Among them, p is the decay factor. In the natural state, the pheromone left by the ants will decay over time, and q is the magnification. If the neuron is mapped to the node in the minimum cost mapping mode of all the ants in this iteration, the corresponding pheromone is amplified by q times.
Based on the above formula, the mapping algorithm based on the ant colony algorithm (Algorithm 1) is obtained as follows:
First, the neuron importance and node center degree are calculated based on the connections among the neurons and the number of nodes to further obtain the map-inspired information.
Second, the pheromone information is initialized.
Third, in each iteration, all ants generate a mapping method based on the probability jointly determined by the current pheromones and inspired confidence, and then calculate the cost of these mapping methods, selecting the least costly mapping method for this iteration.
Then, the pheromones are updated according to the minimum cost mapping mode of this iteration and the intrinsic decay.
If the maximum number of iterations is reached or the cost meets the requirements, the process terminates; otherwise the iteration is repeated.
| Algorithm 1: Given the neuron connection matrix and the number of nodes, iteratively optimise 2D Mesh mapping functions |
Input: Neuronal connection matrix CM,
Number of ants ant _num, the maximum number of iterations max _iter_num,
Decay factor p, magnification q,
pheromone index, enlightening information index
Output: Mapping function
1: Calculational neuronal importance: importance (i)
2: Degree of calculation of node centre: centre (i)
3: Calculate the mapping heuristic information: i,j
4: The initialised pheromone matrix is the full 1: pheromone_matrix
5: for iter = 1:max _iter_num:
6: for ant_group in group_num:
7: for ant =1:ant_num:
8: Generate the mapping matrix map _matrix by strategy
9: The mapping matrix, m in_map_matrix _one_iter that calculates the minimum cost
10: Update the pheromone matrix
11: Updates the global minimum cost mapping matrix, m in_map_matrix
12: end for
13: return m in_map_matrix |