Abstract
The effects of advanced nonlinear varied shear coefficient and third-order shear deformation theory (TSDT) on the dynamic responses of thick functionally graded material (FGM) plates under thermal vibration are investigated. The nonlinear coefficient of the displacement field of TSDT is used to obtain the expression of advanced varied shear coefficient for the thick FGM plates. The dynamic displacements, shear rotations and stresses in numerical results under sinusoidal applied heat loads are obtained and investigated. Two parametric effects of environment temperature and FGM power law index on the dynamic responses of thermal stress and center deflection of thick FGM plates are also investigated. The transient responses of center deflection are found for the cases of simply homogeneous equation and fully homogeneous equation. Also, the transient responses of center deflection are found for cases of nonlinear and linear varied-modified coefficient of shear correction.
1. Introduction
There are some investigations of shear deformation effects in composited plates. In 2020, Zenkour and El-Shahrany [1] used various displacement theories, e.g., third-order shear deformation theory (TSDT), first-order shear deformation theory (FSDT), etc., to study laminated magnetostrictive plates; in their research, the numerical dynamic results of vibration suppression are presented. There are some dynamical investigations of thermal vibrations in the temperature environment. In 2020, Wu et al. [2] used an experimental test for hypersonic vehicles to investigate the vibration of lightweight ceramic insulating material in extremely thermal conditions. In 2020, Shariyat and Mohammadjani [3] applied a three-dimensional (3D) nonlinear variable thermos-viscoelastic numerical theory to investigate the dynamic stress and time response of vibration in thick functionally graded material (FGM) rotating annular plates undergoing temperature rises. In 2020, Fan et al. [4] presented the numerical analysis of a 3D integrated package to investigate the fatigue of through-silicon-via copper (TSV-Cu) structures under thermal and vibration coupled loads. In 2019, Su et al. [5] used FSDT in a numerical approach to investigate the flutter and vibration of stiffened FGM plates under different temperature conditions. In 2019, Fang et al. [6] used two versions of Euler–Bernoulli beam theory (EBT) and Timoshenko beam theory (TBT) in a numerical approach to study the thermal vibration behaviors of rotating FGM micro-beams. In 2016, Duc et al. [7] used FSDT in a numerical approach to calculate the dynamic and vibration for piezoelectric FGM plates under different temperature conditions. In 2006, Huang and Shen [8] used higher-order shear deformation theory (HSDT) in a numerical approach to investigate the time response of piezoelectric FGM plates under different temperature conditions. In 2004, Huang and Shen [9] used HSDT in a numerical approach to investigate the time response of FGM plates under different temperature conditions.
The generalized differential quadrature (GDQ) method has been applied for FGM plates. In 2019, Hong [10] studied the dynamic responses of thick FGM plates by using the TSDT effect and fully homogeneous equation under different temperature conditions. The simply modified factor of shear correction was used without considering the nonlinear terms of TSDT. In 2014, Hong [11] studied the dynamic responses of Terfenol-D FGM plates by considering the FSDT effect and the simply modified factor of shear correction under different temperature conditions. In 2012, Hong [12] presented the dynamic responses for Terfenol-D FGM plates by using the FSDT effect and constant value of shear correction equal to 5/6 under rapid heating. It is interesting to further study the dynamic responses of stresses and deflection in the TSDT approach of GDQ computations, and the advanced nonlinear varied-modified coefficient of shear correction for thick FGM plates under different temperature condition. The parametric effects of temperature and power law index of FGM on the dynamic responses of stress and deflection are investigated for thick FGM plates.
This paper will proceed as follows. Firstly, the advanced nonlinear varied-modified coefficient of shear correction including the coefficient term z3 of TSDT is presented. Secondly, the dynamic responses of stresses and deflection in GDQ computation are presented. Finally, the parametric effects of temperature and power law index of FGM on the dynamic responses of stress and deflection are presented.
2. Formulation Procedures
The two constituent materials of the FGM plate (e.g., FGM material 1 and FGM material 2) are shown in Figure 1. Along the axes of and , the lengths are and , respectively. The thickness of FGM material 1 is , the thickness of FGM material 2 is and the total thickness of the FGM plates is in the direction of in the Cartesian system. Young’s modulus of thick FGM plates in power law function are used in the standard form of index under environment temperature . The other properties are assumed in the average values of forms. The individual properties of the constituent material of the FGMs are functions of which can be obtained. The time dependent of displacements and of the thick FGM plates can be assumed in the nonlinear forms with respect to direction by using the coefficient term of TSDT equations [13] as follows,
in which is time. Coefficient for is given in the TSDT approach, and , and are the displacements in the , and axes of the middle-plane of the thick FGM plates, respectively. and are the shear rotations in the and directions.
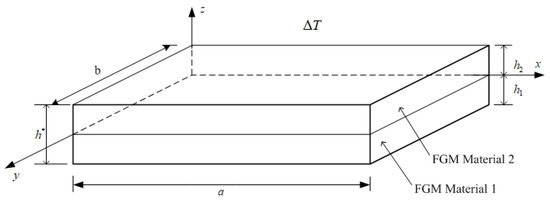
Figure 1.
Thick FGM plate under sinusoidal applied heat loads.
The stresses in normal direction ( and ) and in the shear direction (, and ) for the thick FGM plate under temperature difference can be obtained and expressed in terms of the products of stiffness and strains with thermal coefficients , and . The parameter between the thick FGM plate and the curing environment area can be obtained in linear form with z, also in sinusoidal form with x, y and t that can be expressed by Hong as follows [10],
in which is the frequency of applied heat flux, is the temperature amplitude of applied heat loads.
The dynamic equations of motion with nonlinear TSDT for a thick FGM plate can be obtained by assuming that the first partial differentation in displacements and shear rotations with respect to z are going to zero in the strain-displacement relations [14]. The dynamic equilibrium differential equations with nonlinear TSDT of thick FGM plates could be obtained by Hong [10] with the following integrals for the stiffness and in the direction, respectively,
where is the advanced nonlinear varied-modified coefficient of shear correction.
In the advanced nonlinear varied expression including the terms for the thick FGM plates in terms of Young’s modulus and in constituent material 1 and 2, respectively, can be obtained as follows,
where
- ,
- ,
The values of advanced nonlinear are usually functions of , and , but is independent to the value of . The GDQ numerical method is used in the computation for the derivative of a smooth function at a coordinate of an arbitrary grid point , in which subscripts and in a domain [11,15,16,17]. The clarification of expression in Equation (4) can be presented in more detail and is referred to in 2022 by Hong [18]. The non-dimensional parameters (X, Y, U, V and W) are used in the GDQ approaches under no in-plane distributed forces and no external pressure load () as follows,
The displacement and shear rotations are assumed in time sinusoidal form of vibrations and expressed in the following,
in which is the natural frequency of the thick FGM plate with subscript mode shape numbers and . Boundary equations of displacements and shear rotations with amplitudes: , , , , and for four-sided simply supported plates are given explicitly in Appendix A.
3. Some Numerical Results and Discussions
The coordinates and in the computational domain for the grid points and of the thick FGM plates are implemented to calculate the displacements and shear rotations of GDQ results under applied heat loads and listed as follows.
Also, the dynamic inter-laminar stresses in the constituent layer could be calculated when the displacements and shear rotations are obtained for the given and time. The simply homogeneous equation can be obtained by assuming that matrix elements in (row, column) with (1,3)–(1,5); (2,3)–(2,5); (3,1)–(3,2); (4,1)–(4,2) and (5,1)–(5,2) are neglected in the coefficient matrix of fully homogeneous equation in 2019 by Hong [10]. The determinant of the coefficient matrix in a simply homogeneous equation going to zero could be obtained in the simply five degree polynomial equation, thus the values could be calculate.
3.1. Dynamic Convergence Study
The FGM constituent material 1 located at lower position is stainless steel (SUS304); the FGM constituent material 2 located at upper position is silicon nitride () used with h1 = h2 under applied heat temperature and . The convergence of center displacement amplitude (unit mm) are studied for the thick FGM plates at t = 6 s with , = 0.925925/mm2, h1 = h2 = 0.6 mm, T = 100 K and = 100 K. The calculated values of for = 10 with applied heat flux = 0.2618004/s and = 5 with = 0.2618019/s, respectively, are obtained and listed in Table 1 by using the advanced nonlinear varied and under three values of . For = 10, the values are calculated and used in case 1: = 0.059249/s and = 0.5; in case 2: = 0.061595/s and = 1; in case 3: = 0.064255/s and = 2. For = 5, the values are calculated and used in case 1: = 0.018034/s and = 0.5; in case 2: = 0.032166/s and = 1; in case 3: = 0.032121/s and = 2. The error accuracy of the amplitude is 2.702918E-05 for = 0.5 and = 10. The grid point 13 × 13 could be considered in enough grid numbers to provide the acceptable convergence for the amplitude and used continuously in the next time response of calculations. The advanced nonlinear values for under T = 100 K are shown in Table 2, they are typically varied with the three parameters: , and . The typical (unit 1/s) vs. mode shapes and (from 1 to 9) of the vibrating plate are reported in Table A1 and listed in Appendix A.

Table 1.
Dynamic convergence of considering advanced nonlinear .

Table 2.
Nonlinear varied vs. c1 and under T = 100 K.
3.2. Time Responses of Deflection and Stress
In Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, the horizontal and vertical axes have units, e.g., in Figure 2, the unit for in the vertical axis is “mm”, and the unit for t in the horizontal axis is “sec”. In Figure 3, the unit for in the vertical axis is “GPa”, the unit for t in the horizontal axis is “sec”. In Figure 4, the unit for in the vertical axis is “mm”, the unit for in the horizontal axis is “K”. In Figure 5, the unit for in the vertical axis is “GPa”, the unit for in the horizontal axis is “K”. The time responses of deflection and stress are computed with the value decreasing from = 15.707964/s at t = 0.1 s to = 0.523601/s at t = 3.0 s. Figure 2 shows the time response of (unit mm) for = 5 and 10, respectively, with = 0.925925/mm2, , T = 600 K and = 100 K. The maximum absolute value of is 0.006138 mm at = 0.1 s found for = 5 with advanced = −3.535402 and = 15.707964/s. The time responses of are converging at around 0.0 for = 5 and 10.
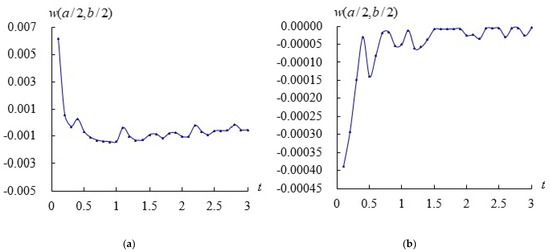
Figure 2.
(unit mm) vs. t (unit s): (a) for ; (b) for .
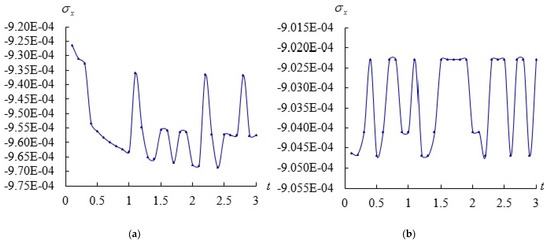
Figure 3.
Stress (unit GPa) vs. t (unit s): (a) ; (b) for .
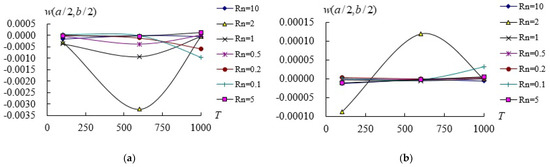
Figure 4.
(unit mm) vs. T (unit K): (a) for ; (b) for .
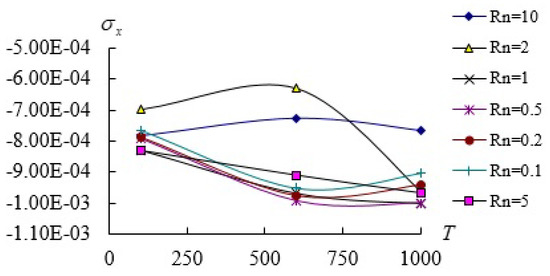
Figure 5.
(unit GPa) vs. T (unit K) for .
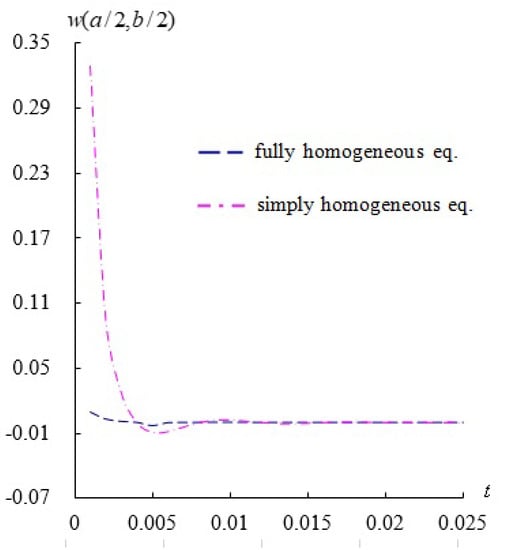
Figure 6.
Transient response of (unit mm) vs. t (unit s) compared with simply and fully homogeneous eq.
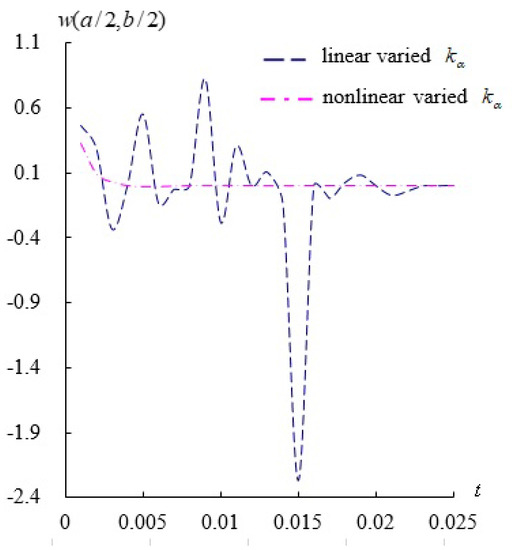
Figure 7.
Transient response of (unit mm) vs. t (unit s) compared with nonlinear and linear varied .
Typically the stress values vary through the plate thickness by considering the effect of advanced nonlinear varied values. Figure 3a,b show the time responses of the dominated stresses (unit GPa) at the center position of lower surface z = −0.5 as the analyses of deflection case in Figure 2 for = 1, = 5 and 10, respectively. The absolute value of maximum stresses is −9.685218 × 10−4 GPa found at t = 2.4 s for thick = 5. The time responses of stresses are oscillating around − 9.50 × 10−4 GPa for = 5 and around −9.035 × 10−4 GPa for = 10.
3.3. Deflection and Stress vs. T and Rn
Figure 4 shows (unit mm) vs. (unit K) for (from 0.1 to 10) at = 2.4 s with = 0.654498/s, advanced nonlinear , = 0.925925/mm2, = 100 K, = 5 and 10, respectively. Figure 4a shows the curves in = 5; the absolute value of maximum is −0.003227 mm found at T = 600 K for = 2. The absolute values of for = 0.5, 1 and 2 can proceed in higher T = 1000 K of temperature condition. The center deflection amplitude values are almost keep constant versus T for = 10. Figure 4b shows the curves in = 10; the value of maximum is 0.000119 mm found at T = 1000 K for = 2. The absolute values of for = 2 can proceed in higher T = 1000 K of temperature condition.
Figure 5 shows the dominated stresses (unit GPa) vs. T (unit K) and at center position of z = −0.5 for = 5. The values of for = 0.1 and 0.2 can proceed in higher T = 1000 K of temperature condition. The absolute value of maximum is −1.001130 × 10−3 GPa found at T = 1000 K for = 0.5 and 1.
3.4. Transient Responses of Deflection and Stress
The transient responses of (unit mm) are computed for = 10 with fixed = 0.065469/s under = 0.925925/mm2, , advanced nonlinear = −3.535402, T = 600 K and = 100 K. Figure 6 shows the transient compared by using simply homogeneous equation and fully homogeneous equation with = 785.3982/s, respectively, for t = 0.001 s–0.025 s. The amplitudes in the simply homogeneous equation are found in greater values and overestimated in the approach. The explanation provided more clearly for Figure 6. There are two equation types (simply homogeneous equation and fully homogeneous equation) used to calculate the values of for Equation (6). The simply homogeneous equation and fully homogeneous equation are listed in the Appendix A. Figure 7 also shows the transient compared with values of nonlinear varied (expression with containing the factor) and linear varied (expression without containing the factor) for the = 10 case of = 785.3982/s. The transient values in linear varied case are overestimated with respect to the nonlinear varied case.
3.5. Future Works
There is some recent research in the field of FGMs, e.g., in 2023, Sirimontree et al. [19] presented a vibroacoustic study for the sandwich magneto-electro-elastic cylindrical FGM nanoshell in the external flow and under thermal environment. Based on the fundamental study for thermal vibration of thick FGM plates in 2019 by Hong [10], it would be interesting to further study the advanced dynamic vibration of FGM plates/cylindrical shells in supersonic flow.
4. Conclusions
The dynamic responses of deflection and stress computed by the GDQ method in TSDT thick FGM plates under sinusoidal applied heat loads by considering the parameter effects of advanced , and . By using the simply homogeneous equation to calculate the natural frequency. The advanced nonlinear are usually in functions of , and . The maximum absolute value of is 0.006138 mm at t = 0.1 s found for = 5 with advanced = −3.535402 and = 15.707964/s. The amplitudes in simply homogeneous equation are found in greater values and overestimated in the approach. The transient responses of are compared with the cases of simply homogeneous equation and fully homogeneous equation. Also, the transient responses of are compared with the cases of nonlinear and linear varied .
Funding
The funding of this paper is by a grant MOST 111-2221-E-164-001 from National Science and Technology Council (NSTC), Taiwan, ROC.
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Informed Consent Statement
Not applicable for studies not involving humans.
Data Availability Statement
The manuscript completely presented the data used to generate the figures and tables. Data are all available on request. All the data are generated by the author; data are openly available.
Conflicts of Interest
The author has declared no conflict of interest. There is no funder for this study. There is only the author stated in the manuscripts.
Appendix A
The boundary equations of displacements and shear rotations with amplitudes: , , , , and for 4-sided simply supported plates are given explicitly as follows,
The fully homogeneous equation is expressed as follows,
where , (i = 0, 1, 2, …, 6), is the density of k th constituent ply, , etc. all of the parameters and coefficients can be referred [10].
The simply homogeneous equation is expressed as follows,
The typical (unit 1/s) vs. mode shapes and (from 1 to 9) of the vibrating plate are reported in the Table A1 under nonlinear varied , , and T = 300 K.

Table A1.
vs. and under nonlinear varied , , and T = 300 K.
Table A1.
vs. and under nonlinear varied , , and T = 300 K.
| (unit 1/s) | |||||||||
| 5 | 0.030248 | 0.012079 | 0.010355 | 0.005455 | 0.003399 | 0.007451 | 0.006401 | 0.005629 | 0.005048 |
| 10 | 0.060513 | 0.042673 | 0.035361 | 0.020371 | 0.015934 | 0.031821 | 0.014847 | 0.011815 | 0.006108 |
| (unit 1/s) | |||||||||
| 5 | 0.019082 | 0.009523 | 0.010442 | 0.004176 | 0.007139 | 0.007156 | 0.006237 | 0.005555 | 0.005061 |
| 10 | 0.023112 | 0.030248 | 0.014602 | 0.012079 | 0.015355 | 0.010355 | 0.015735 | 0.005455 | 0.006460 |
| (unit 1/s) | |||||||||
| 5 | 0.008481 | 0.007713 | 0.010970 | 0.009022 | 0.007734 | 0.006781 | 0.006089 | 0.006744 | 0.001734 |
| 10 | 0.027054 | 0.023712 | 0.012403 | 0.016924 | 0.009628 | 0.011476 | 0.015462 | 0.004309 | 0.006783 |
| (unit 1/s) | |||||||||
| 5 | 0.010463 | 0.009661 | 0.008689 | 0.007765 | 0.007011 | 0.006711 | 0.002147 | 0.001856 | 0.001620 |
| 10 | 0.012677 | 0.019082 | 0.010558 | 0.009523 | 0.012944 | 0.010442 | 0.013141 | 0.004176 | 0.007080 |
| (unit 1/s) | |||||||||
| 5 | 0.005210 | 0.007929 | 0.007340 | 0.006738 | 0.006999 | 0.002301 | 0.001972 | 0.001712 | 0.001502 |
| 10 | 0.010366 | 0.015779 | 0.014532 | 0.008480 | 0.008050 | 0.017151 | 0.011124 | 0.004087 | 0.008826 |
| (unit 1/s) | |||||||||
| 5 | 0.006944 | 0.006693 | 0.006307 | 0.005852 | 0.005405 | 0.004941 | 0.004526 | 0.004152 | 0.003821 |
| 10 | 0.008856 | 0.008481 | 0.008063 | 0.007713 | 0.008185 | 0.010970 | 0.009856 | 0.009022 | 0.003542 |
| (unit 1/s) | |||||||||
| 5 | 0.005915 | 0.005753 | 0.005469 | 0.005921 | 0.005027 | 0.004625 | 0.004279 | 0.003964 | 0.003679 |
| 10 | 0.012552 | 0.008211 | 0.011614 | 0.010954 | 0.010263 | 0.009585 | 0.006448 | 0.008361 | 0.007834 |
| (unit 1/s) | |||||||||
| 5 | 0.005130 | 0.005009 | 0.006575 | 0.005036 | 0.004590 | 0.004284 | 0.004006 | 0.003746 | 0.003506 |
| 10 | 0.010707 | 0.010463 | 0.010102 | 0.009661 | 0.009180 | 0.008689 | 0.004282 | 0.007765 | 0.007361 |
| (unit 1/s) | |||||||||
| 5 | 0.004509 | 0.007183 | 0.005173 | 0.004502 | 0.004205 | 0.003967 | 0.003743 | 0.003530 | 0.003328 |
| 10 | 0.005754 | 0.005626 | 0.005439 | 0.005199 | 0.004907 | 0.007963 | 0.007584 | 0.007228 | 0.006915 |
References
- Zenkour, A.M.; El-Shahrany, H.D. Vibration suppression of advanced plates embedded magnetostrictive layers via various theories. J. Mater. Res. Technol. 2020, 9, 4727–4748. [Google Scholar] [CrossRef]
- Wu, D.; Lin, L.; Ren, H. Thermal/vibration joint experimental investigation on lightweight ceramic insulating material for hypersonic vehicles in extremely high-temperature environment up to 1500 °C. Ceram. Int. 2020, 46, 14439–14447. [Google Scholar] [CrossRef]
- Shariyat, M.; Mohammadjani, R. 3D nonlinear variable strain-rate-dependent-order fractional thermoviscoelastic dynamic stress investigation and vibration of thick transversely graded rotating annular plates/discs. Appl. Math. Model. 2020, 84, 287–323. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Y.; Chen, X.; Jiang, Y.; Zhang, S.; Wang, Y. Research on fatigue of TSV-Cu under thermal and vibration coupled bade on numerical analysis. Microelectron. Reliab. 2020, 106, 113590. [Google Scholar] [CrossRef]
- Su, Z.; Wang, L.; Sun, K.; Wang, D. Vibration characteristic and flutter analysis of electrically restrained stiffened functionally graded plates in thermal environment. Int. J. Mech. Sci. 2019, 157–158, 872–884. [Google Scholar] [CrossRef]
- Fang, J.; Gu, J.; Wang, H.; Zhang, X. Thermal effect on vibrational behaviors of rotating functionally graded microbeams. Eur. J. Mech. A/Solids 2019, 75, 497–515. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H.; Quang, V.D. Nonlinear dynamic and vibration analysis of piezoelectric eccentrically stiffened FGM plates in thermal environment. Int. J. Mech. Sci. 2016, 115–116, 711–722. [Google Scholar] [CrossRef]
- Huang, X.L.; Shen, H.S. Vibration and dynamic response of functionally graded plates with piezoelectric actuators in thermal environments. J. Sound Vib. 2006, 289, 25–53. [Google Scholar] [CrossRef]
- Huang, X.L.; Shen, H.S. Nonlinear vibration and dynamic response of functionally graded plates in thermal environments. Int. J. Solids Struct. 2004, 41, 2403–2427. [Google Scholar] [CrossRef]
- Hong, C.C. GDQ computation for thermal vibration of thick FGM plates by using fully homogeneous equation and TSDT. Thin-Walled Struct. 2019, 135, 78–88. [Google Scholar] [CrossRef]
- Hong, C.C. Thermal vibration and transient response of magnetostrictive functionally graded material plates. Eur. J. Mech. A/Solids 2014, 43, 78–88. [Google Scholar] [CrossRef]
- Hong, C.C. Rapid heating induced vibration of magnetostrictive functionally graded material plates. Trans. ASME J. Vib. Acoust. 2012, 134, 021019. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N.; Rostam-Abadi, F. Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem. Anal. Des. 2004, 40, 463–483. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Hong, C.C. Thermal vibration of magnetostrictive material in laminated plates by the GDQ method. Open Mech. J. 2007, 1, 29–37. [Google Scholar] [CrossRef][Green Version]
- Bert, C.W.; Jang, S.K.; Striz, A.G. Nonlinear bending analysis of orthotropic rectangular plates by the method of differential quadrature. Comput. Mech. 1989, 5, 217–226. [Google Scholar] [CrossRef]
- Shu, C.; Du, H. Implementation of clamped and simply supported boundary conditions in the GDQ free vibration analyses of beams and plates. Int. J. Solids Struct. 1997, 34, 819–835. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced frequency analysis of thick FGM plates using third-order shear deformation theory with a nonlinear shear correction coefficient. J. Struct. Eng. Appl. Mech. 2022, 5, 143–160. [Google Scholar] [CrossRef]
- Sirimontree, S.; Thongchom, C.; Saffari, P.R.; Refahati, N.; Saffari, P.R.; Jearsiripongkul, T.; Keawsawasvong, S. Effects of thermal environment and external mean flow on sound transmission loss of sandwich functionally graded magneto-electro-elastic cylindrical nanoshell. Eur. J. Mech. A/Solids 2023, 97, 104774. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).