Im2mesh: A Python Library to Reconstruct 3D Meshes from Scattered Data and 2D Segmentations, Application to Patient-Specific Neuroblastoma Tumour Image Sequences
Abstract
1. Introduction
2. Materials and Methods
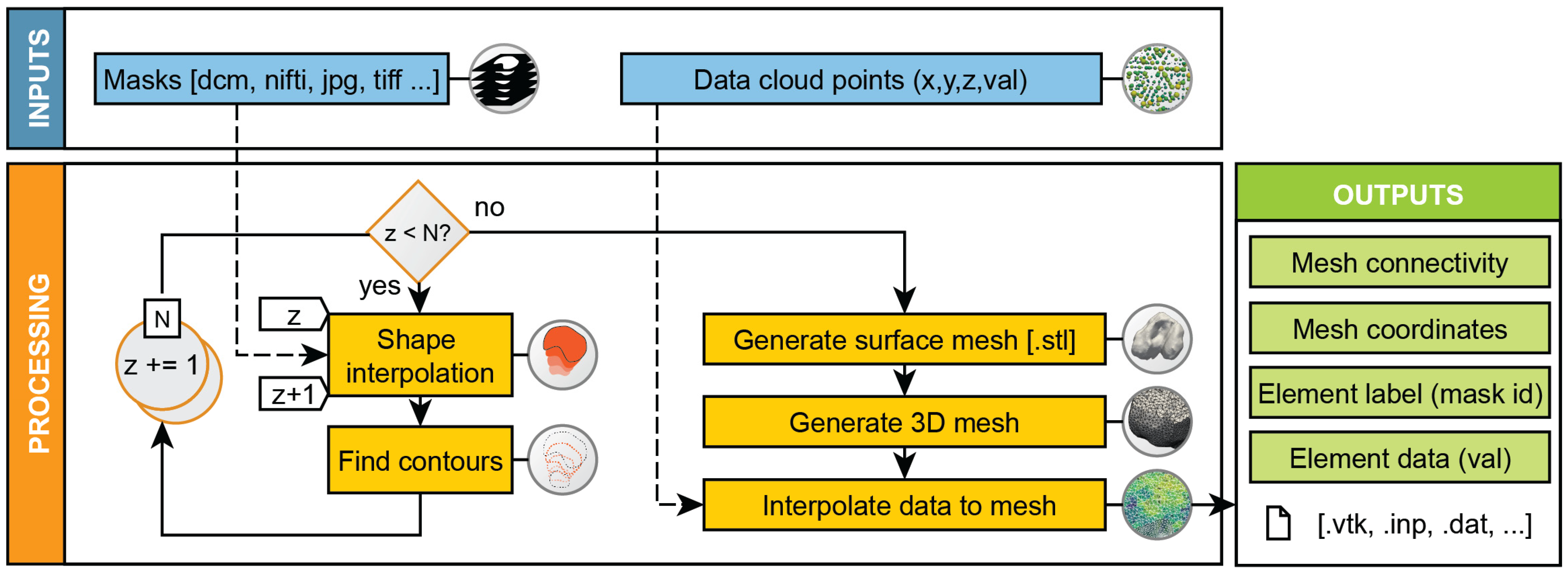
2.1. Workflow
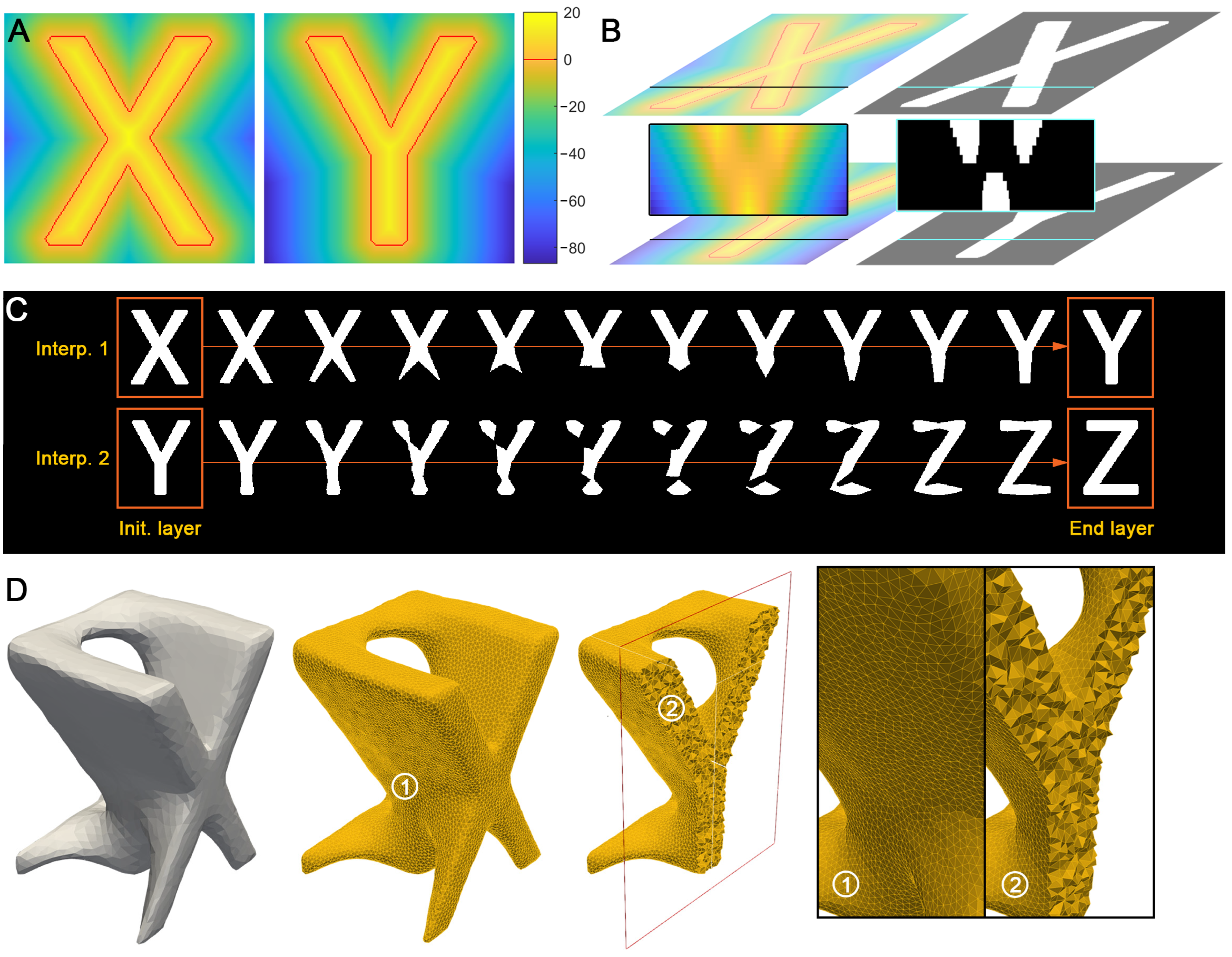
2.2. Shape Interpolation
2.3. Mesh Generation
2.4. Evaluation Metrics
2.5. Data Interpolation
3. Results
3.1. Volume Reconstruction
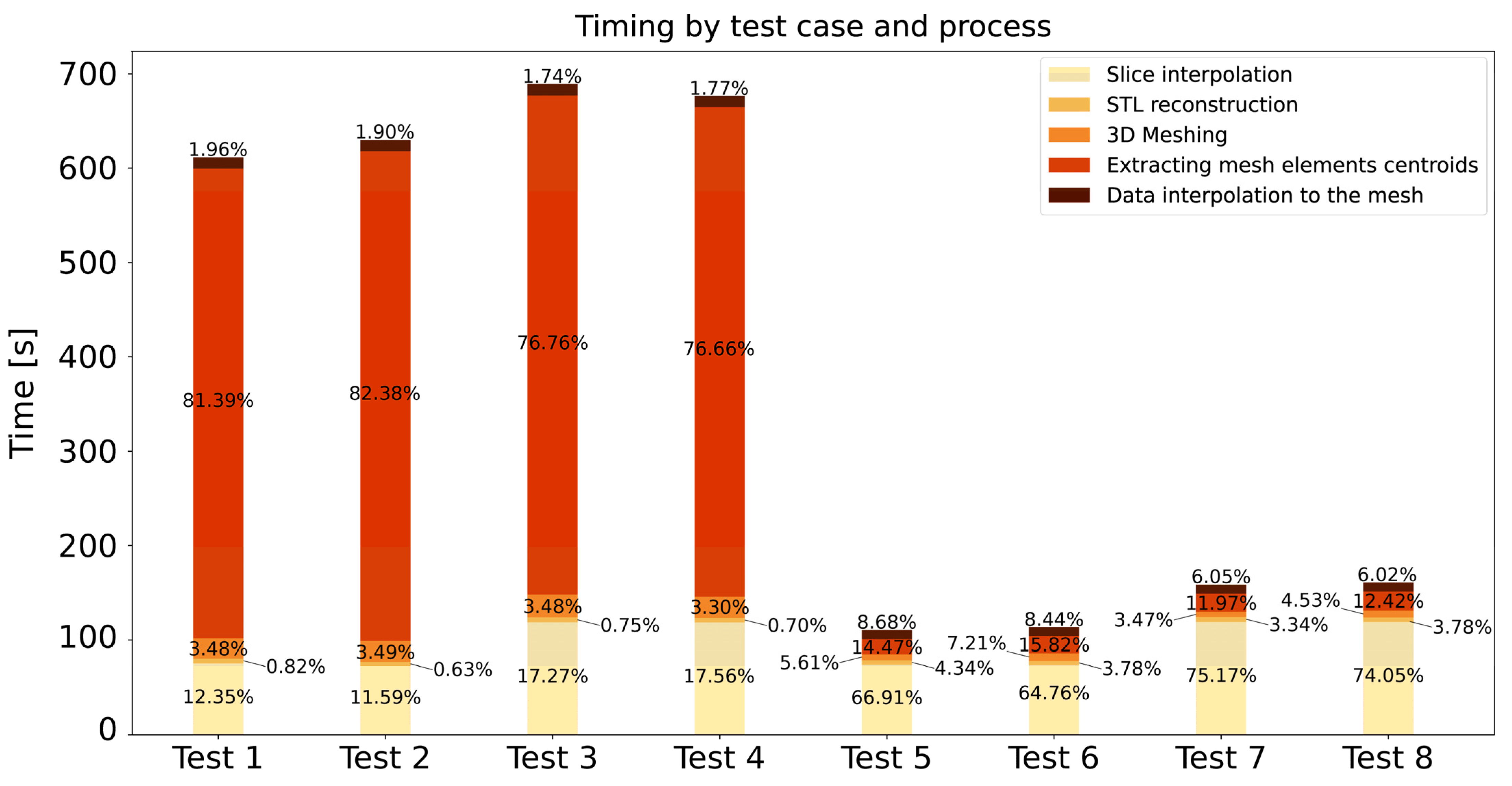
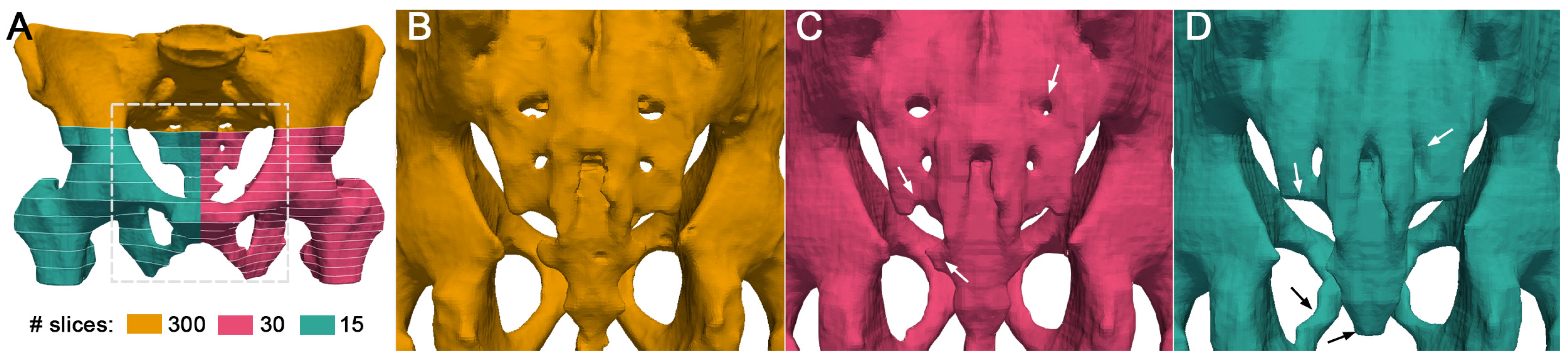
3.2. Effect of Downsampling
3.3. Application Case
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Metric | Mean | Std. Dev. | Median | p90 | p95 | p99 | Rec. Min. | Rec. Max. |
|---|---|---|---|---|---|---|---|---|
| Aspect Frobenius | 1.289 | 0.2338 | 1.225 | 1.566 | 1.76 | 2.216 | 1 | 1.3 |
| Aspect Gamma | 1.48 | 0.4319 | 1.356 | 1.96 | 2.335 | 3.298 | 1 | 3 |
| Aspect Ratio | 1.616 | 0.42 | 1.514 | 2.054 | 2.434 | 3.3397 | 1 | 3 |
| Condition | 1.323 | 0.3268 | 1.226 | 1.65 | 1.985 | 2.785 | 1 | 3 |
| Edge Ratio | 1.712 | 0.3086 | 1.647 | 2.141 | 2.293 | 2.595 | 1 | 3 |
| Jacobian | 131.8 | 53.75 | 125.4 | 205.1 | 230.4 | 279.6 | 1.00 × 10−30 | 1.00 × 1030 |
| Minimum Dihedral Angle | 49.11 | 12.12 | 50.36 | 63.63 | 67.04 | 73.56 | 40 | 70.53 |
| Aspect Beta | 1.381 | 0.3495 | 1.28 | 1.759 | 2.065 | 2.888 | 1 | 3 |
| Scaled Jacobian | 0.5656 | 0.1535 | 0.5736 | 0.7632 | 0.8064 | 0.8777 | 0.5 | 0.7071 |
| Shape | 0.7962 | 0.1156 | 0.8161 | 0.9273 | 0.9477 | 0.9744 | 0.3 | 1 |
Appendix B

Appendix C
| Test Case | Element Size | Number of Elements | STL Faces | Number of Interpolation Steps |
|---|---|---|---|---|
| Test 1 | 1.5 mm | 422,699 | 50,000 | 15 |
| Test 2 | 1.5 mm | 432,399 | 100,000 | 15 |
| Test 3 | 1.5 mm | 438,848 | 50,000 | 25 |
| Test 4 | 1.5 mm | 434,337 | 100,000 | 25 |
| Test 5 | 3 mm | 64,324 | 50,000 | 15 |
| Test 6 | 3 mm | 65,667 | 100,000 | 15 |
| Test 7 | 3 mm | 68,665 | 50,000 | 25 |
| Test 8 | 3 mm | 69,002 | 100,000 | 25 |
References
- Goetz, L.H.; Schork, N.J. Personalized medicine: Motivation, challenges, and progress. Fertil. Steril. 2018, 109, 952–963. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.K.; Júnior, J.R.F.; Wada, D.T.; Tenório, A.P.M.; Nogueira-Barbosa, M.H.; Marques, P.M.D.A. Artificial intelligence, machine learning, computer-aided diagnosis, and radiomics: Advances in imaging towards to precision medicine. Radiol. Bras. 2019, 52, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Grignon, B.; Mainard, L.; DeLion, M.; Hodez, C.; Oldrini, G. Recent advances in medical imaging: Anatomical and clinical applications. Surg. Radiol. Anat. 2012, 34, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Sturchio, A.; Marsili, L.; Mahajan, A.; Grimberg, B.; Kauffman, M.A.; Espay, A.J. How have advances in genetic technology modified movement disorder nosology? Eur. J. Neurol. 2020, 27, 1461–1470. [Google Scholar] [CrossRef] [PubMed]
- Merino-Casallo, F.; Gómez-Benito, M.J.; Juste-Lanas, Y.; Martinez-Cantin, R.; Garcia-Aznar, J.M. Integration of in vitro and in silico models using Bayesian optimization with an application to stochastic modeling of mesenchymal 3D cell migration. Front. Physiol. 2018, 9, 1246. [Google Scholar] [CrossRef] [PubMed]
- Hadjicharalambous, M.; Wijeratne, P.A.; Vavourakis, V. From tumour perfusion to drug delivery and clinical translation of in silico cancer models. Methods 2020, 185, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Hervas-Raluy, S.; Wirthl, B.; Guerrero, P.E.; Rei, G.R.; Nitzler, J.; Coronado, E.; de Mora, J.F.; Schrefler, B.A.; Gomez-Benito, M.J.; Garcia-Aznar, J.M.; et al. Tumour growth: Bayesian parameter calibration of a multiphase porous media model based on in vitro observations of Neuroblastoma spheroid growth in a hydrogel microenvironment. bioRxiv 2022. [Google Scholar] [CrossRef]
- Lima, E.A.B.F.; Faghihi, D.; Philley, R.; Yang, J.; Virostko, J.; Phillips, C.M.; Yankeelov, T.E. Bayesian calibration of a stochastic, multiscale agent-based model for predicting in vitro tumor growth. PLoS Comput. Biol. 2021, 17, e1008845. [Google Scholar] [CrossRef]
- World Health Organization. Cancer. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 6 October 2022).
- Angeli, S.; Emblem, K.E.; Due-Tonnessen, P.; Stylianopoulos, T. Towards patient-specific modeling of brain tumor growth and formation of secondary nodes guided by DTI-MRI. NeuroImage Clin. 2018, 20, 664–673. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Ii, D.A.H.; Barnes, S.L.; Feng, X.; Huang, W.; Yankeelov, T.E. Incorporating drug delivery into an imaging-driven, mechanics-coupled reaction diffusion model for predicting the response of breast cancer to neoadjuvant chemotherapy: Theory and preliminary clinical results. Phys. Med. Biol. 2018, 63, 105015. [Google Scholar] [CrossRef]
- Gabelloni, M.; Faggioni, L.; Borgheresi, R.; Restante, G.; Shortrede, J.; Tumminello, L.; Scapicchio, C.; Coppola, F.; Cioni, D.; Gómez-Rico, I.; et al. Bridging gaps between images and data: A systematic update on imaging biobanks. Eur. Radiol. 2022, 32, 3173–3186. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Erdt, M.; Janoos, F.; Chang, T.-C.; Egger, J. Medical image segmentation in oral-maxillofacial surgery. Comput.-Aided Oral Maxillofac. Surg. 2021, 1–27. [Google Scholar] [CrossRef]
- Wang, H.; Prasanna, P.; Syeda-Mahmood, T. Rapid annotation of 3D medical imaging datasets using registration-based interpolation and adaptive slice selection. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 1340–1343. [Google Scholar] [CrossRef]
- Ravikumar, S.; Wisse, L.; Gao, Y.; Gerig, G.; Yushkevich, P. Facilitating Manual Segmentation of 3D Datasets Using Contour And Intensity Guided Interpolation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 714–718. [Google Scholar] [CrossRef]
- Wang, R.; Lei, T.; Cui, R.; Zhang, B.; Meng, H.; Nandi, A.K. Medical image segmentation using deep learning: A survey. IET Image Process. 2020, 16, 1243–1267. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. IEEE Access 2015, 9, 16591–16603. [Google Scholar] [CrossRef]
- Albu, A.B.; Beugeling, T.; Laurendeau, D. A Morphology-Based Approach for Interslice Interpolation of Anatomical Slices from Volumetric Images. IEEE Trans. Biomed. Eng. 2008, 55, 2022–2038. [Google Scholar] [CrossRef]
- Zhao, C.; Duan, Y.; Yang, D. A Deep Learning Approach for Contour Interpolation. In Proceedings of the 2021 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 12–14 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Martí-Bonmatí, L.; Alberich-Bayarri, Á.; Ladenstein, R.; Blanquer, I.; Segrelles, J.D.; Cerdá-Alberich, L.; Gkontra, P.; Hero, B.; Garcia-Aznar, J.M.; Keim, D.; et al. PRIMAGE project: Predictive in silico multiscale analytics to support childhood cancer personalised evaluation empowered by imaging biomarkers. Eur. Radiol. Exp. 2020, 4, 1–11. [Google Scholar] [CrossRef]
- Scapicchio, C.; Gabelloni, M.; Forte, S.M.; Alberich, L.C.; Faggioni, L.; Borgheresi, R.; Erba, P.; Paiar, F.; Marti-Bonmati, L.; Neri, E. DICOM-MIABIS integration model for biobanks: A use case of the EU PRIMAGE project. Eur. Radiol. Exp. 2021, 5, 1–12. [Google Scholar] [CrossRef]
- Bradski, G. The OpenCV library. Dr. Dobb’s J. 2000, 25, 120–125. Available online: https://www.proquest.com/trade-journals/opencv-library/docview/202684726/se-2?accountid=14795 (accessed on 6 October 2022).
- Schenk, A.; Prause, G.; Peitgen, H.O. Efficient semiautomatic segmentation of 3D objects in medical images. Lect. Notes Comput. Sci. 2000, 1935, 186–195. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An Open-Source Mesh Processing Tool. In Proceedings of the Sixth Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar]
- Bridson, R. Fast Poisson disk sampling in arbitrary dimensions. In ACM SIGGRAPH 2007 Sketches, SIGGRAPH’07; Association for Computing Machinery: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Kazhdan, M.; Hoppe, H. Screened poisson surface reconstruction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Garland, M.; Heckbert, P.S. Surface simplification using quadric error metrics. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH’97), Anaheim, LA, USA, 3–8 August 1997; pp. 209–216. [Google Scholar]
- Vollmer, J.; Mencl, R.; Muller, H. Improved Laplacian Smoothing of Noisy Surface Meshes. Comput. Graph. Forum 1999, 18, 131–138. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Knupp, P.M.; Ernst, C.D.; Thompson, D.C.; Stimpson, C.J.; Pebay, P.P. The Verdict Geometric Quality Library; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Sandia National Laboratories (SNL): Livermore, CA, USA, 2006. [Google Scholar] [CrossRef]
- Atuegwu, N.C.; Arlinghaus, L.R.; Li, X.; Chakravarthy, A.B.; Abramson, V.G.; Sanders, M.E.; Yankeelov, T.E. Parameterizing the Logistic Model of Tumor Growth by DW-MRI and DCE-MRI Data to Predict Treatment Response and Changes in Breast Cancer Cellularity during Neoadjuvant Chemotherapy. Transl. Oncol. 2013, 6, 256–264. [Google Scholar] [CrossRef]
- Khalifa, F.; Soliman, A.; El-Baz, A.; El-Ghar, M.A.; El-Diasty, T.; Gimel’Farb, G.; Ouseph, R.; Dwyer, A.C. Models and methods for analyzing DCE-MRI: A review. Med. Phys. 2014, 41, 124301. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0 Contributors. SciPy 1.0 Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- de Moraes, T.F.; Amorim, P.H.J.; Azevedo, F.; da Silva, J.V.L. InVesalius—An open-sourceimaging application. World J. Urol. 2012, 30, 687–691. [Google Scholar]
- Scientific Computing and Imaging Institute (SCI). Seg3D: Volumetric Image Segmentation and Visualization. 2016. Available online: http://www.seg3d.org (accessed on 18 October 2022).
- Lukeš, V. dicom2fem. 2014. Available online: https://github.com/vlukes/dicom2fem (accessed on 17 October 2022).
- Lukeš, V.; Jiřík, M.; Jonášová, A.; Rohan, E.; Bublík, O.; Cimrman, R. Numerical simulation of liver perfusion: From CT scans to FE model. In Proceedings of the 7th European Conference on Python in Science, EuroSciPy 2014, Cambridge, UK, 27–30 August 2014; p. 79. [Google Scholar] [CrossRef]
- Rister, B.; Shivakumar, K.; Nobashi, T.; Rubin, D.L. CT-ORG: CT Volumes with Multiple Organ Segmentations [Dataset]. 2019. Available online: https://wiki.cancerimagingarchive.net/display/Public/CT-ORG%3A+CT+volumes+with+multiple+organ+segmentations (accessed on 6 October 2022).
- Clark, K.; Vendt, B.; Smith, K.; Freymann, J.; Kirby, J.; Koppel, P.; Moore, S.; Phillips, S.; Maffitt, D.; Pringle, M.; et al. The Cancer Imaging Archive (TCIA): Maintaining and Operating a Public Information Repository. J. Digit. Imaging 2013, 26, 1045–1057. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sainz-DeMena, D.; García-Aznar, J.M.; Pérez, M.Á.; Borau, C. Im2mesh: A Python Library to Reconstruct 3D Meshes from Scattered Data and 2D Segmentations, Application to Patient-Specific Neuroblastoma Tumour Image Sequences. Appl. Sci. 2022, 12, 11557. https://doi.org/10.3390/app122211557
Sainz-DeMena D, García-Aznar JM, Pérez MÁ, Borau C. Im2mesh: A Python Library to Reconstruct 3D Meshes from Scattered Data and 2D Segmentations, Application to Patient-Specific Neuroblastoma Tumour Image Sequences. Applied Sciences. 2022; 12(22):11557. https://doi.org/10.3390/app122211557
Chicago/Turabian StyleSainz-DeMena, Diego, José Manuel García-Aznar, María Ángeles Pérez, and Carlos Borau. 2022. "Im2mesh: A Python Library to Reconstruct 3D Meshes from Scattered Data and 2D Segmentations, Application to Patient-Specific Neuroblastoma Tumour Image Sequences" Applied Sciences 12, no. 22: 11557. https://doi.org/10.3390/app122211557
APA StyleSainz-DeMena, D., García-Aznar, J. M., Pérez, M. Á., & Borau, C. (2022). Im2mesh: A Python Library to Reconstruct 3D Meshes from Scattered Data and 2D Segmentations, Application to Patient-Specific Neuroblastoma Tumour Image Sequences. Applied Sciences, 12(22), 11557. https://doi.org/10.3390/app122211557







