A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models
Abstract
1. Introduction
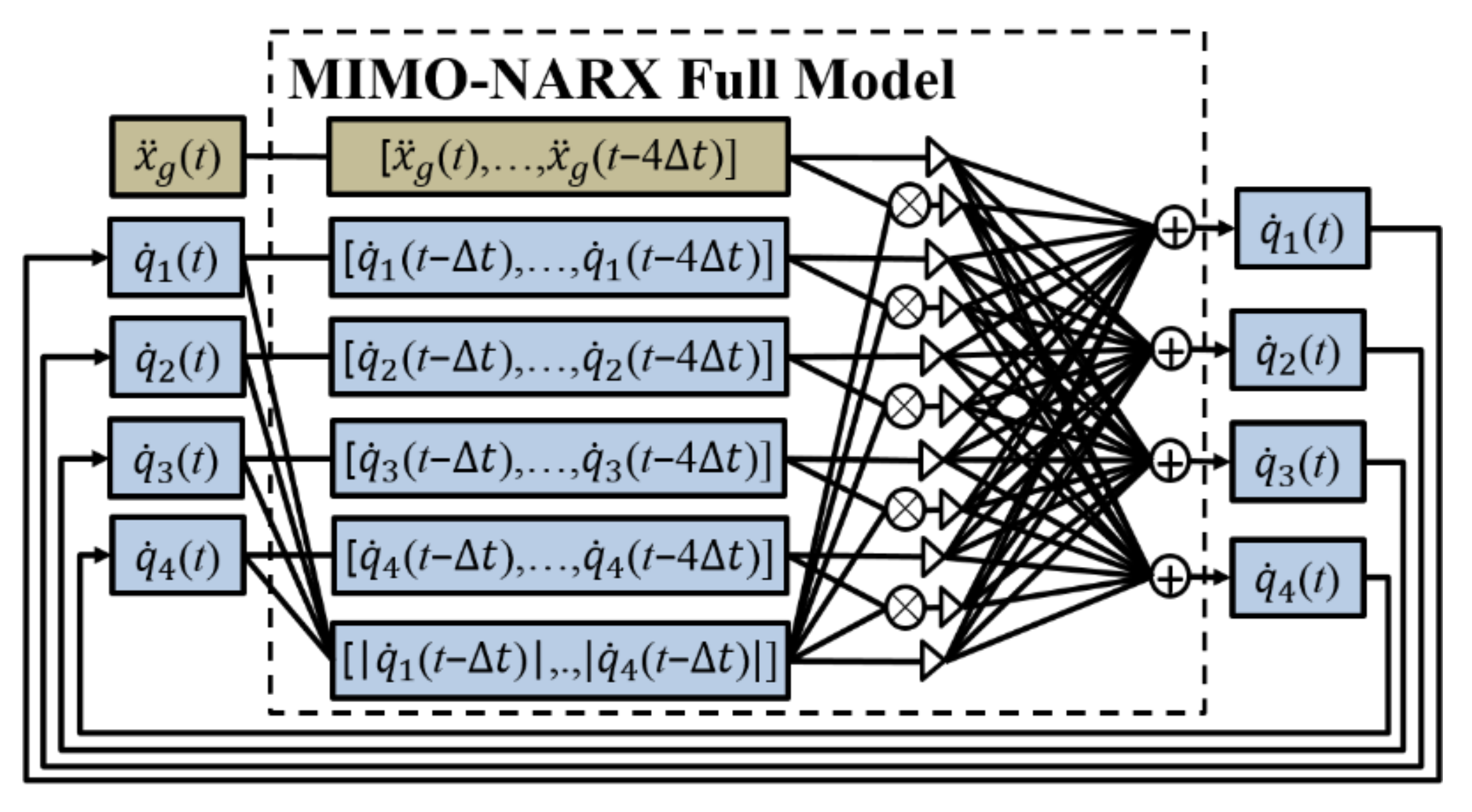
2. Brief Review of MIMO-NARX Modeling
2.1. MIMO-NARX Model for MDOF System
2.2. Model Order Reduction
2.3. NARX Model Pruning
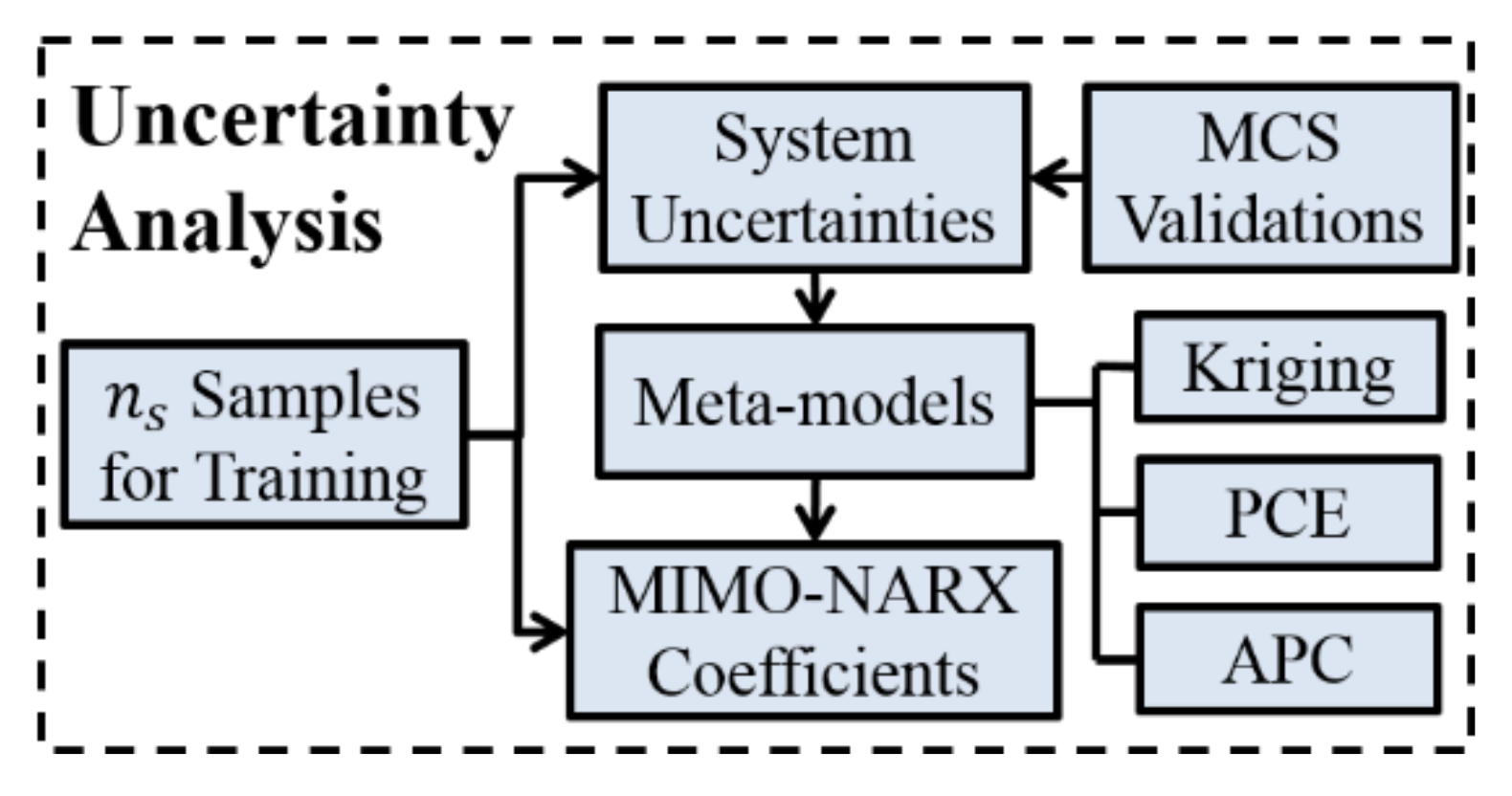
3. Meta-Modeling Techniques for Surrogating NARX Model Coefficients
3.1. Kriging Meta-Model
3.2. PCE Meta-Model
3.3. APC Meta-Model
4. Training of MIMO-NARX Meta-Models
4.1. Nine-DOF Shear Structure
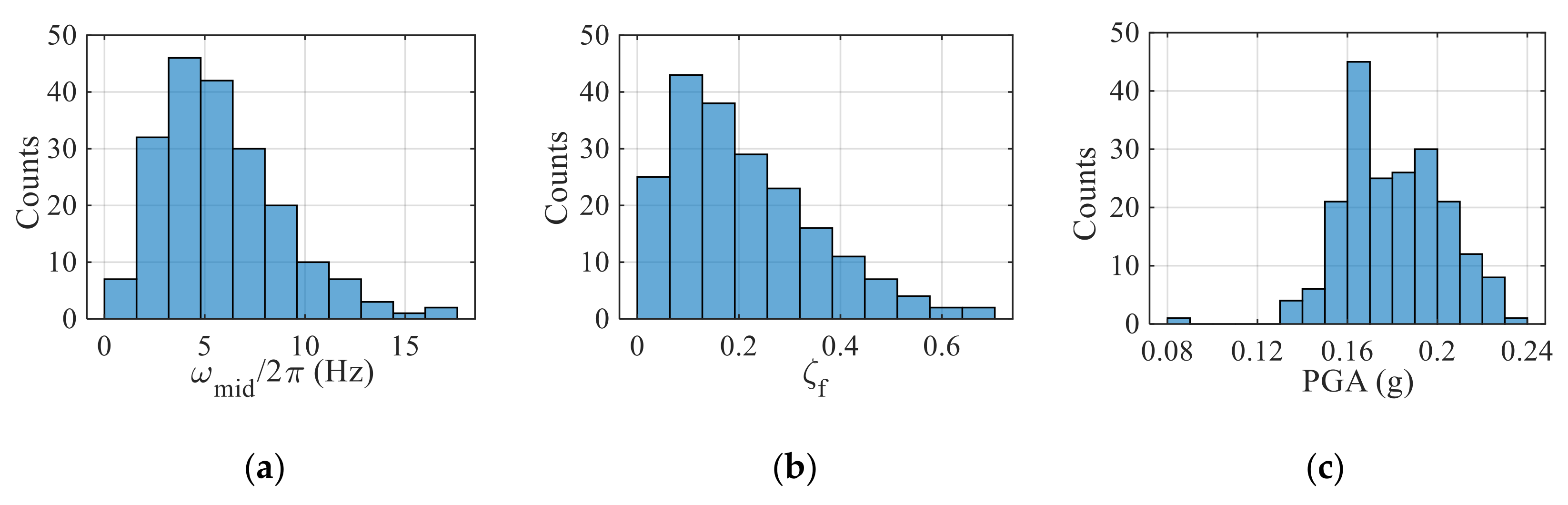
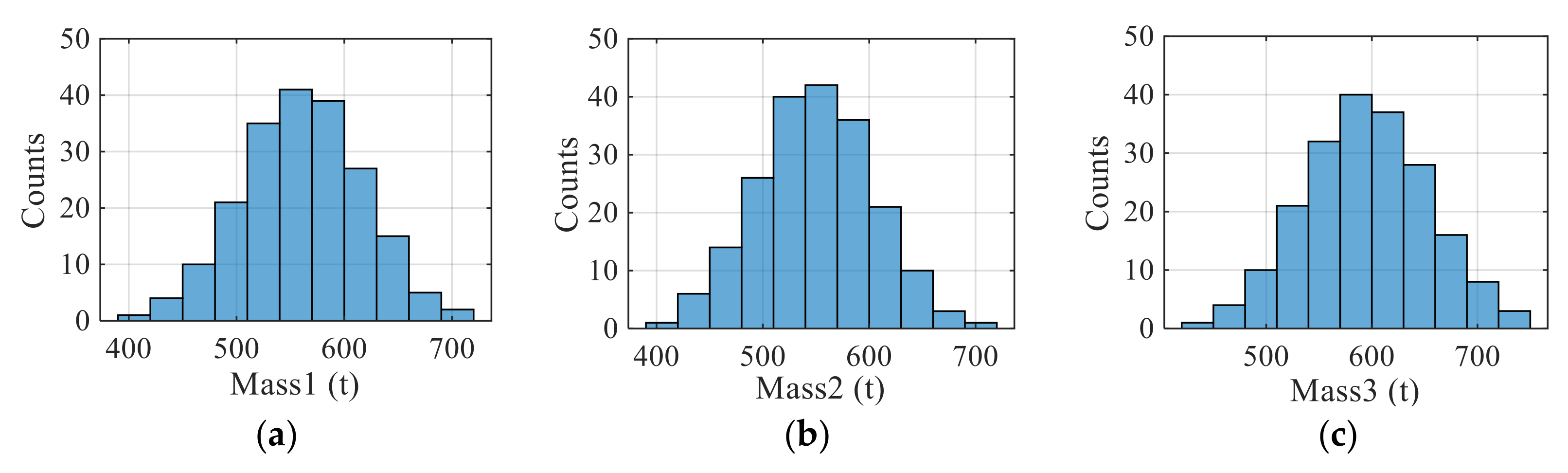
4.2. Uncertainties in Ground Motion and Structural Properties
4.3. MIMO-NARX Model Training
4.4. Surrogating NARX Coefficients by Meta-Models
5. Validation of Surrogated MIMO-NARX Model
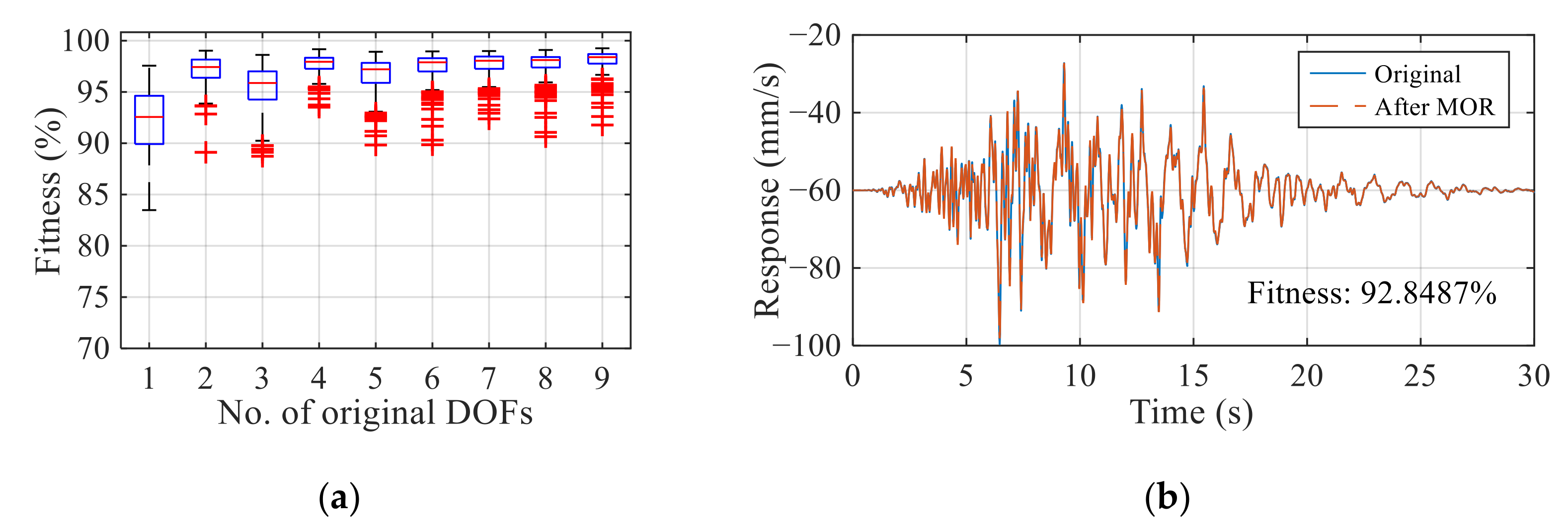
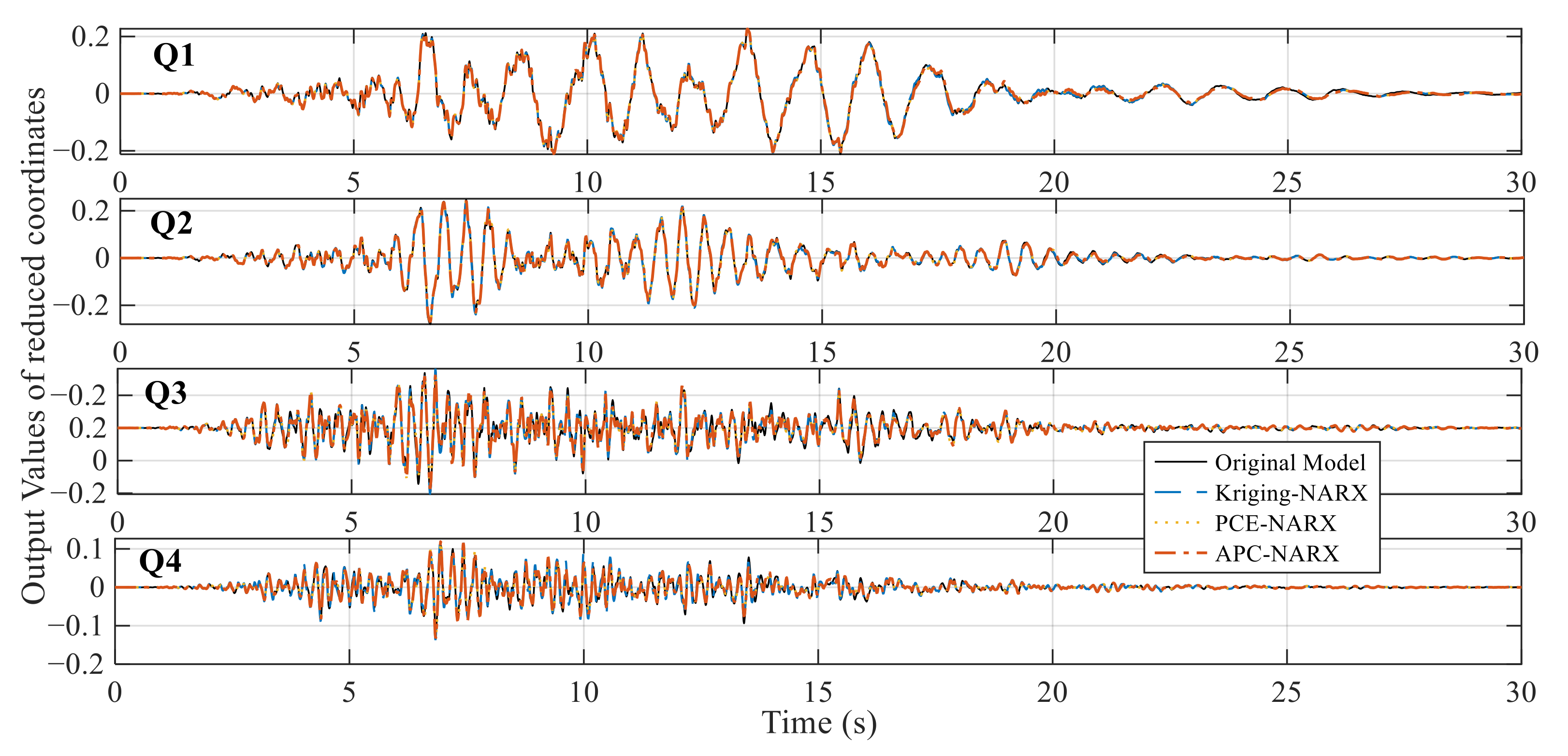
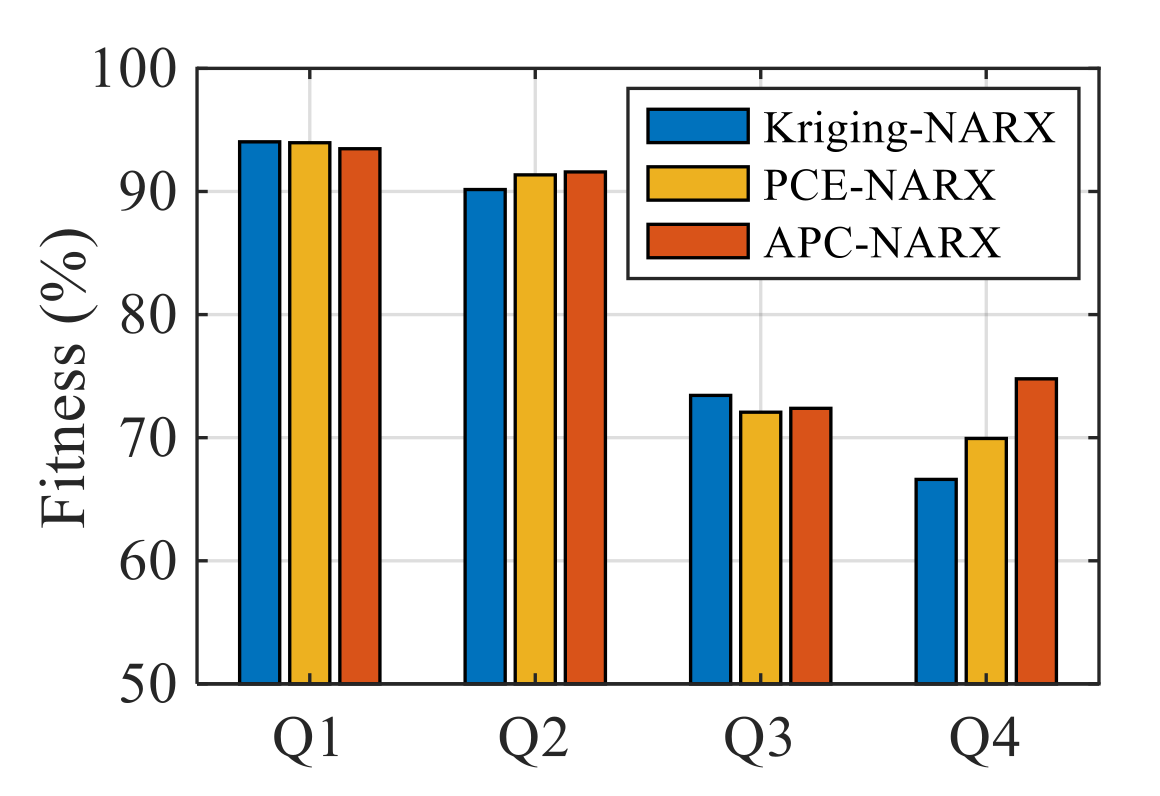
5.1. Accuracy Assessment of MIMO-NARX Outputs in Reduced Coordinates
5.2. Accuracy Assessment of Absolute Structural Responses
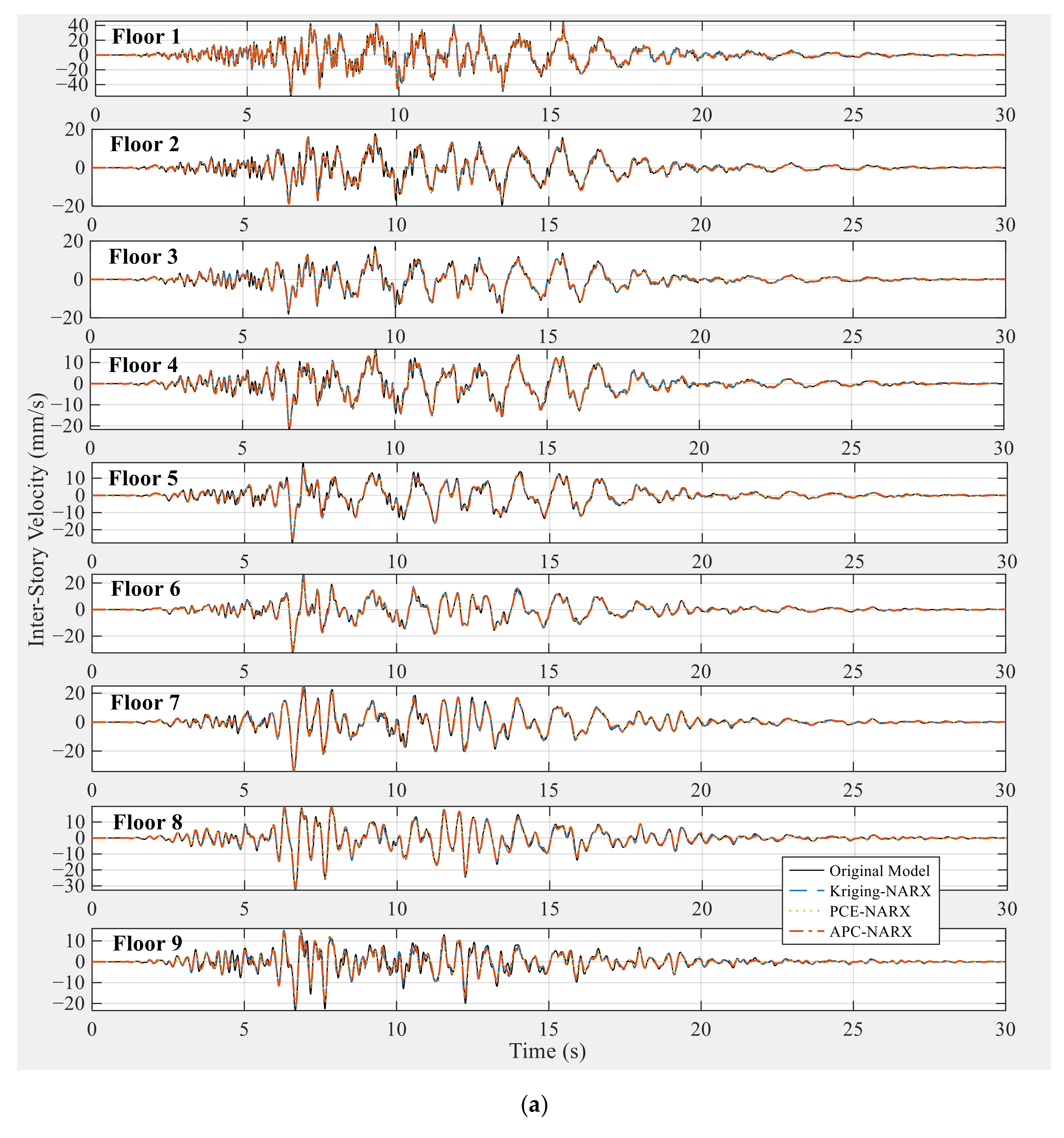
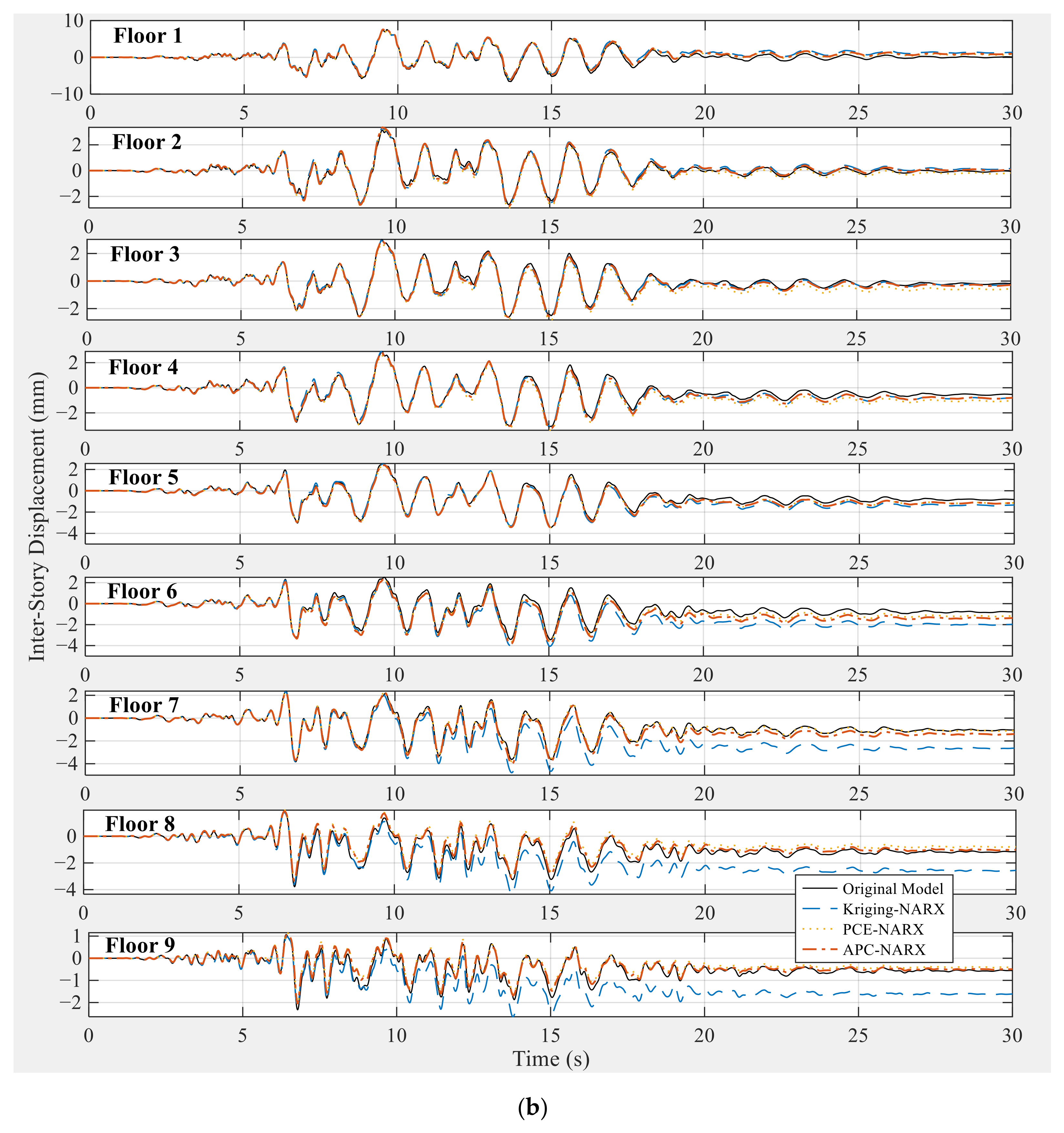
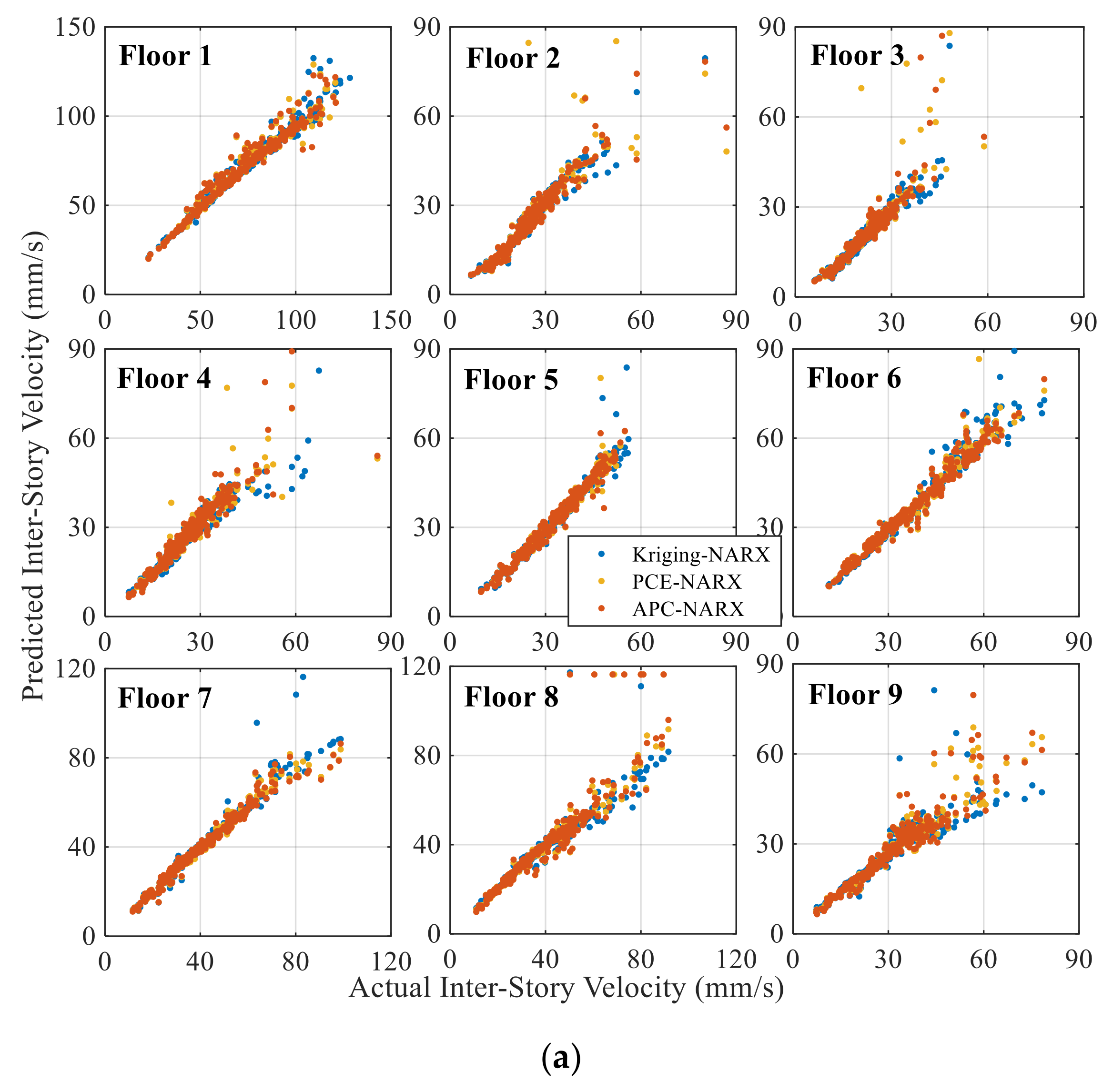
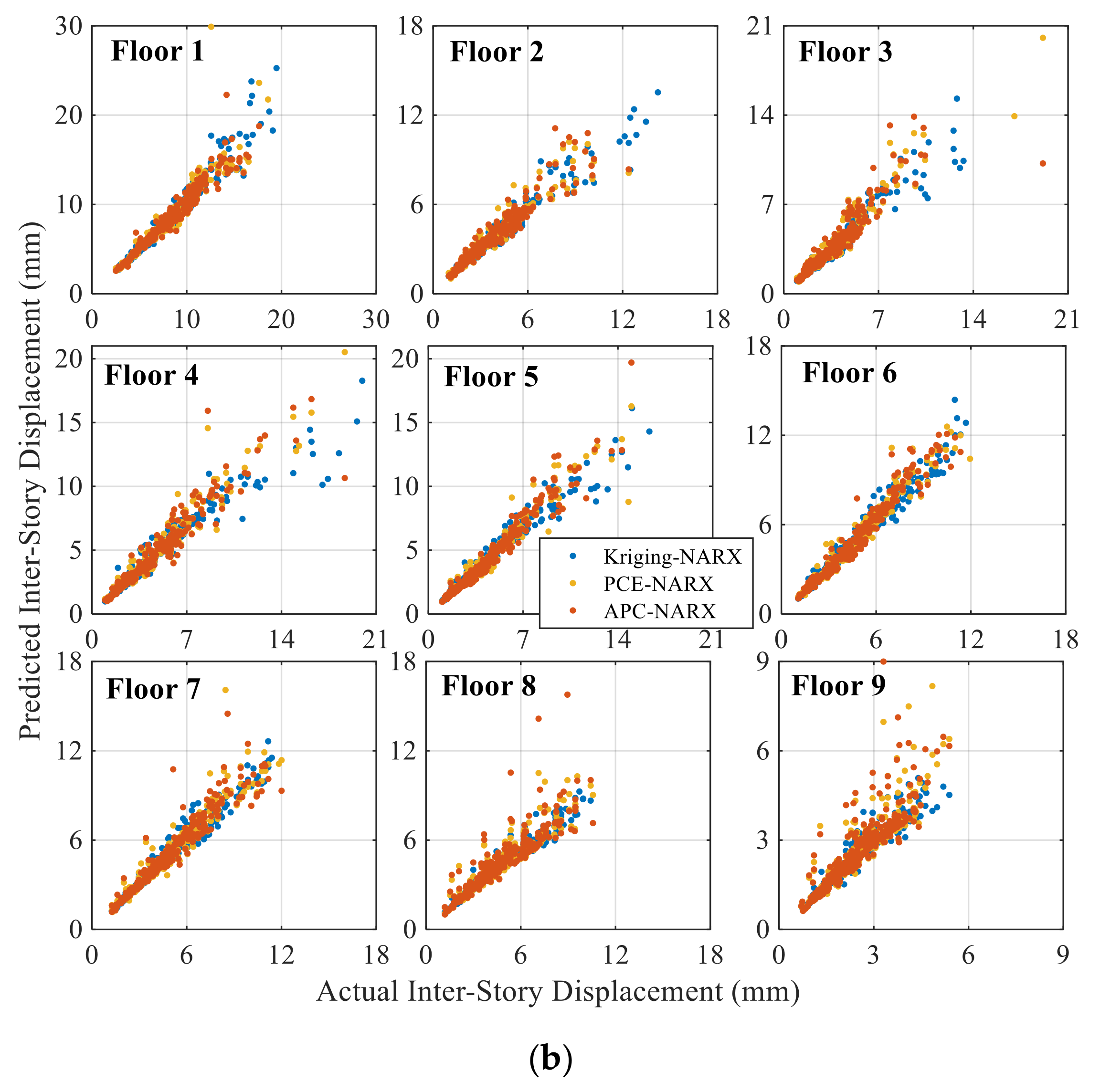
5.3. Accuracy Assessment of Inter-Story Structural Responses
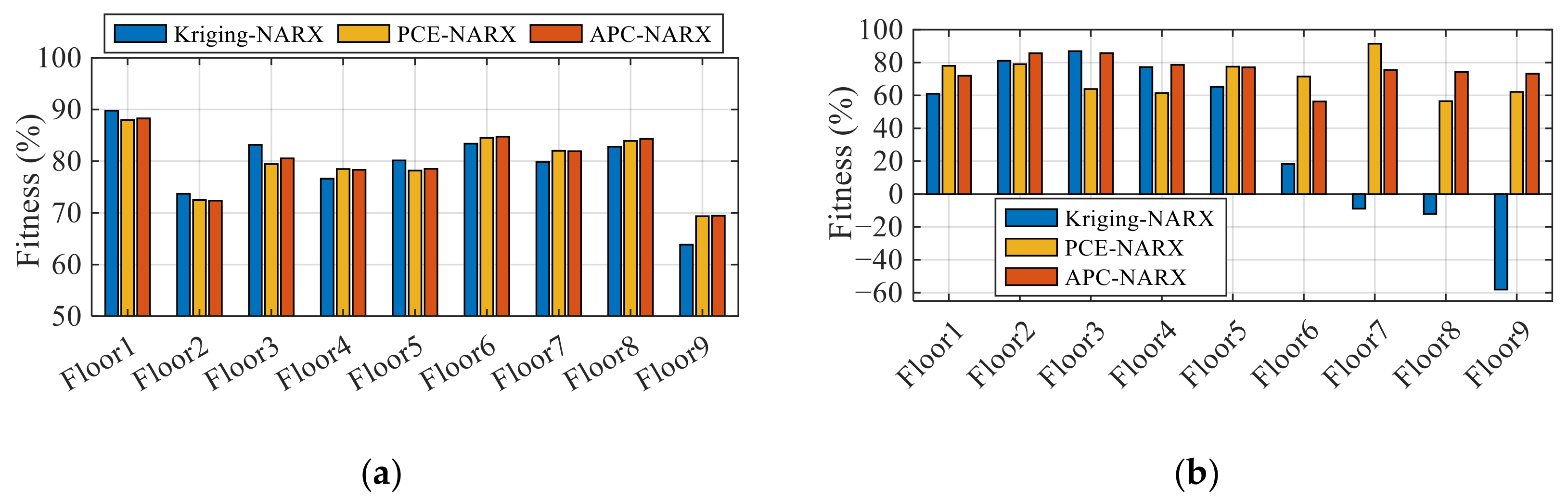
5.4. Comparison of Peak Story Responses
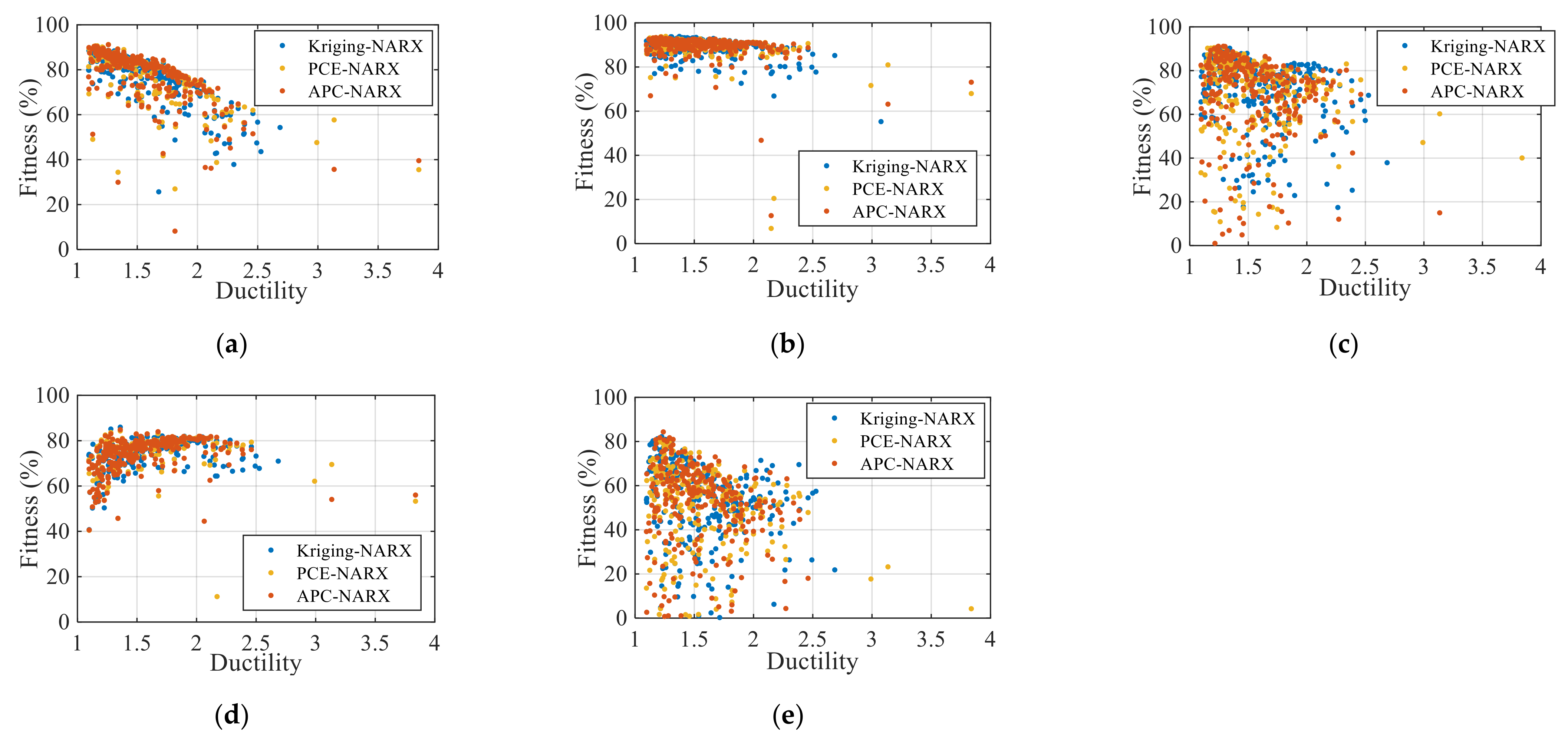
5.5. Statistics for All Validation Cases
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kundu, A.; Adhikari, S. Transient Response of Structural Dynamic Systems with Parametric Uncertainty. J. Eng. Mech. 2014, 140, 315–331. [Google Scholar] [CrossRef]
- Silva, F.M.A.; Goncalves, P.B. The influence of uncertainties and random noise on the dynamic integrity analysis of a system liable to unstable buckling. Nonlinear Dyn. 2015, 81, 707–724. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chowdhury, R. Polynomial Correlated Function Expansion for Nonlinear Stochastic Dynamic Analysis. J. Eng. Mech. 2015, 141, 04014132. [Google Scholar] [CrossRef]
- Mai, C.V.; Sudret, B. Surrogate Models for Oscillatory Systems Using Sparse Polynomial Chaos Expansions and Stochastic Time Warping. SIAM-ASA J. Uncertain. Quantif. 2017, 5, 540–571. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo Simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Hua, H.; Liang, X. Nonlinear stochastic dynamics of a rub-impact rotor system with probabilistic uncertainties. Nonlinear Dyn. 2020, 102, 2229–2246. [Google Scholar] [CrossRef]
- Gidaris, I.; Taflanidis, A.A.; Mavroeidis, G.P. Kriging metamodeling in seismic risk assessment based on stochastic ground motion models. Earthq. Eng. Struct. Dyn. 2015, 44, 2377–2399. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng. Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part I: Deterministic non-linear systems. Int. J. Control 1985, 41, 303–328. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Input-output parametric models for non-linear systems Part II: Stochastic non-linear systems. Int. J. Control 1985, 41, 329–344. [Google Scholar] [CrossRef]
- Gao, X.S.; Hou, H.T.; Huang, L.; Yu, G.Q.; Chen, C. Evaluation of Kriging-NARX modeling for uncertainty quantification of nonlinear SDOF systems with degradation. Int. J. Struct. Stab. Dyn. 2021, 21, 2150060. [Google Scholar] [CrossRef]
- Billings, S.A.; Chen, S.; Korenberg, M.J. Identification of MIMO non-linear systems using a forward-regression orthogonal estimator. Int. J. Control 1989, 49, 2157–2189. [Google Scholar] [CrossRef]
- Li, B.W.; Chuang, W.C.; Spence, S.M.J. Response Estimation of Multi-Degree-of-Freedom Nonlinear Stochastic Structural Systems through Metamodeling. J. Eng. Mech. 2021, 147, 04021082. [Google Scholar] [CrossRef]
- Grigoriu, M. Reduced order models for random functions. Application to stochastic problems. Appl. Math. Model. 2009, 33, 161–175. [Google Scholar] [CrossRef]
- Jensen, H.A.; Munoz, A.; Papadimitriou, C.; Millas, E. Model reduction techniques for reliability-based design problems of complex structural systems. Reliab. Eng. Syst. Saf. 2016, 149, 204–217. [Google Scholar] [CrossRef]
- Bamer, F.; Amiri, A.K.; Bucher, C. A new model order reduction strategy adapted to nonlinear problems in earthquake engineering. Earthq. Eng. Struct. Dyn. 2017, 46, 537–559. [Google Scholar] [CrossRef]
- Mai, C.V.; Spiridonakos, M.D.; Chatzi, E.N.; Sudret, B. Surrogate modeling for stochastic dynamical systems by combining nonlinear autoregressive with exogenous input models and polynomial chaos expansions. Int. J. Uncertain. Quantif. 2016, 6, 313–339. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Jacquelin, E.; Brizard, D. A Kriging-NARX model for uncertainty quantification of nonlinear stochastic dynamical systems in time domain. J. Eng. Mech. 2020, 146, 1–21. [Google Scholar] [CrossRef]
- Leontaritis, I.J.; Billings, S.A. Experimental design and identifiability for non-linear systems. Int. J. Syst. Sci. 1987, 18, 189–202. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–451. [Google Scholar] [CrossRef]
- Piroddi, L.; Spinelli, W. An identification algorithm for polynomial NARX models based on simulation error minimization. Int. J. Control 2003, 76, 1767–1781. [Google Scholar] [CrossRef]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; Wiley: Chichester, UK, 2013. [Google Scholar]
- Kerschen, G.; Golinval, J.C. Physical interpretation of the proper orthogonal modes using the singular value decomposition. J. Sound Vib. 2002, 249, 849–865. [Google Scholar] [CrossRef]
- Phalippou, P.; Bouabdallah, S.; Breitkopf, P.; Villon, P.; Zarroug, M. Sparse POD modal subsets for reduced-order nonlinear explicit dynamics. Int. J. Numer. Methods Eng. 2019, 121, 763–777. [Google Scholar] [CrossRef]
- Kaymaz, I. Application of kriging method to structural reliability problems. Struct. Saf. 2005, 27, 133–151. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I.; Williams, B.J. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2003. [Google Scholar]
- Schobi, R.; Sudret, B.; Wiart, J. Polynomial-chaos-based Kriging. Int. J. Uncertain. Quantif. 2015, 5, 171–193. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Lophaven, S.N.; Søndergaard, J. DACE, a MATLAB Kriging Toolbox, Informatics and Mathematical Modelling; Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in Matlab. In Proceedings of the 2nd International Conference on Vulnerability, Risk Analysis and Management (ICVRAM2014), Liverpool, UK, 13–16 July 2014. [Google Scholar]
- Chen, M.H.; Guo, T.; Chen, C.; Xu, W.J. Data-driven Arbitrary Polynomial Chaos Expansion on Uncertainty Quantification for Real-time Hybrid Simulation Under Stochastic Ground Motions. Exp. Tech. 2020, 44, 751–762. [Google Scholar] [CrossRef]
- Ohtori, Y.; Christenson, R.E.; Spencer, B.F.; Dyke, S.J. Benchmark control problems for seismically excited nonlinear buildings. J. Eng. Mech. 2004, 130, 366–385. [Google Scholar] [CrossRef]
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. ASCE 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Ikhouane, F.; Hurtado, J.E.; Rodellar, J. Variation of the hysteresis loop with the Bouc-Wen model parameters. Nonlinear Dyn. 2007, 48, 361–380. [Google Scholar] [CrossRef]
- Rezaeian, S.; Kiureghian, A.D. Simulation of synthetic ground motions for specified earthquake and site characteristics. Earthq. Eng. Struct. Dyn. 2010, 39, 1155–1180. [Google Scholar] [CrossRef]
- Chen, C.; Ricles, J.M. Development of Direct Integration Algorithms for Structural Dynamics Using Discrete Control Theory. J. Eng. Mech. 2008, 134, 676–683. [Google Scholar] [CrossRef]
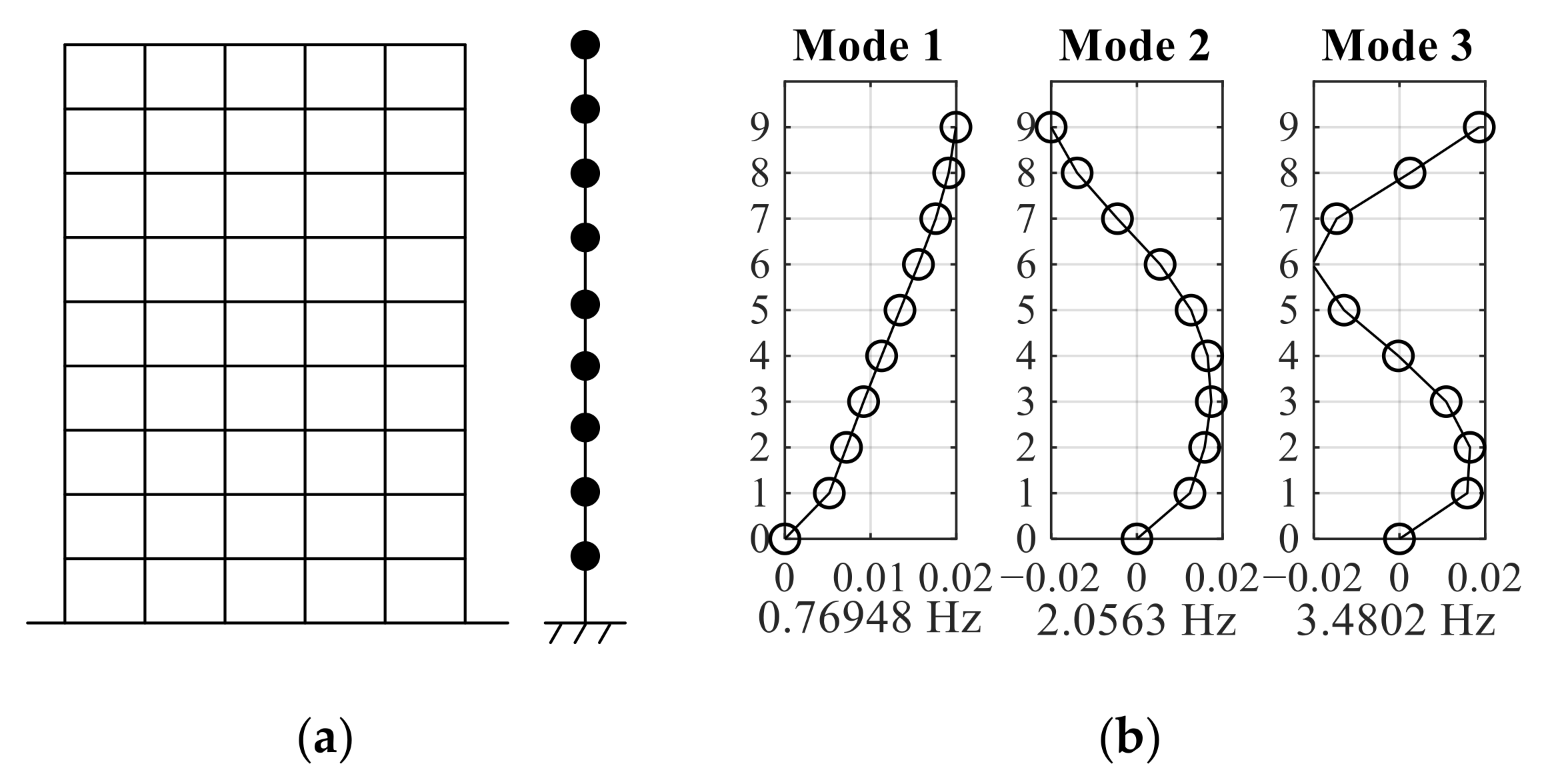









| Floor | ||||||
|---|---|---|---|---|---|---|
| 1 | 2.9793 × 105 | 0.01 | 1 | 0.02 | 0.02 | 0.01 |
| 2 | 7.3787 × 105 | 0.01 | 1 | 0.1 | 0.1 | 0.01 |
| 3 | 6.9252 × 105 | 0.01 | 1 | 0.1 | 0.1 | 0.01 |
| 4 | 6.0177 × 105 | 0.01 | 1 | 0.1 | 0.1 | 0.01 |
| 5 | 5.2397 × 105 | 0.01 | 1 | 0.08 | 0.08 | 0.01 |
| 6 | 4.4108 × 105 | 0.01 | 1 | 0.06 | 0.06 | 0.01 |
| 7 | 3.6986 × 105 | 0.01 | 1 | 0.06 | 0.06 | 0.01 |
| 8 | 3.4706 × 105 | 0.01 | 1 | 0.08 | 0.08 | 0.01 |
| 9 | 3.2748 × 105 | 0.01 | 1 | 0.1 | 0.1 | 0.01 |
| Variable | Distribution Type | Bounds | Mean | Standard Deviation |
|---|---|---|---|---|
| Gamma | [0, +∞] | 5.87 | 3.11 | |
| Beta | [0.02, 1] | 0.213 | 0.143 | |
| Mass 1 | Gaussian | [392.77, 729.43] | 561.1 | 56.11 |
| Mass 2 | Gaussian | [384.58, 714.22] | 549.4 | 54.94 |
| Mass 3 | Gaussian | [416.08, 772.72] | 594.4 | 59.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Gao, X.; Chen, C.; Guo, T.; Xu, W. A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models. Appl. Sci. 2022, 12, 11553. https://doi.org/10.3390/app122211553
Chen M, Gao X, Chen C, Guo T, Xu W. A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models. Applied Sciences. 2022; 12(22):11553. https://doi.org/10.3390/app122211553
Chicago/Turabian StyleChen, Menghui, Xiaoshu Gao, Cheng Chen, Tong Guo, and Weijie Xu. 2022. "A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models" Applied Sciences 12, no. 22: 11553. https://doi.org/10.3390/app122211553
APA StyleChen, M., Gao, X., Chen, C., Guo, T., & Xu, W. (2022). A Comparative Study of Meta-Modeling for Response Estimation of Stochastic Nonlinear MDOF Systems Using MIMO-NARX Models. Applied Sciences, 12(22), 11553. https://doi.org/10.3390/app122211553






