Complex Mathematical Modeling of the Well Drilling Process
Abstract
1. Introduction
- The main topic of the article is the construction, application, or experimental verification of a mathematical model of at least one of the processes taking place during the well drilling.
- The article should be devoted to modeling the processes occurring directly in the well during drilling. The studies devoted to modeling the processes occurring in the reservoir (for example, fluid filtration) and those devoted to the operation of surface equipment were excluded from consideration.
- The model considered in the paper is not specific to any particular equipment or material used in drilling. For example, studies devoted to the fatigue analysis of some particular type of drill pipes were not included in the review.
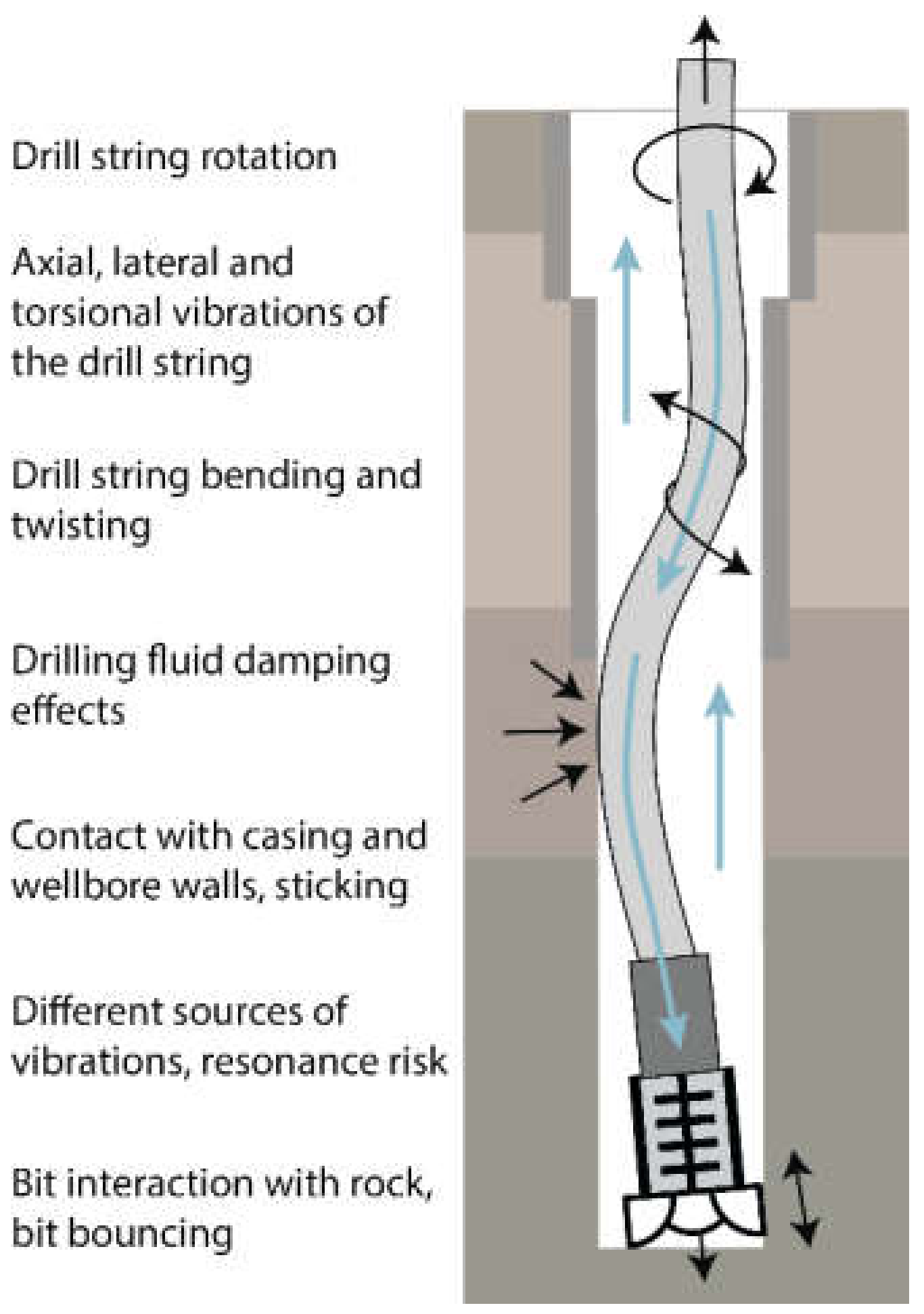
2. Drill String Dynamics
3. Drilling Fluid Circulation in the Wellbore
4. Rock Crushing with a Drill Bit
5. Mass Transfer between the Drilling Fluid and Soil in the Open Section of the Well
6. Heat Exchange between the Well and the Surrounding Soil Massive
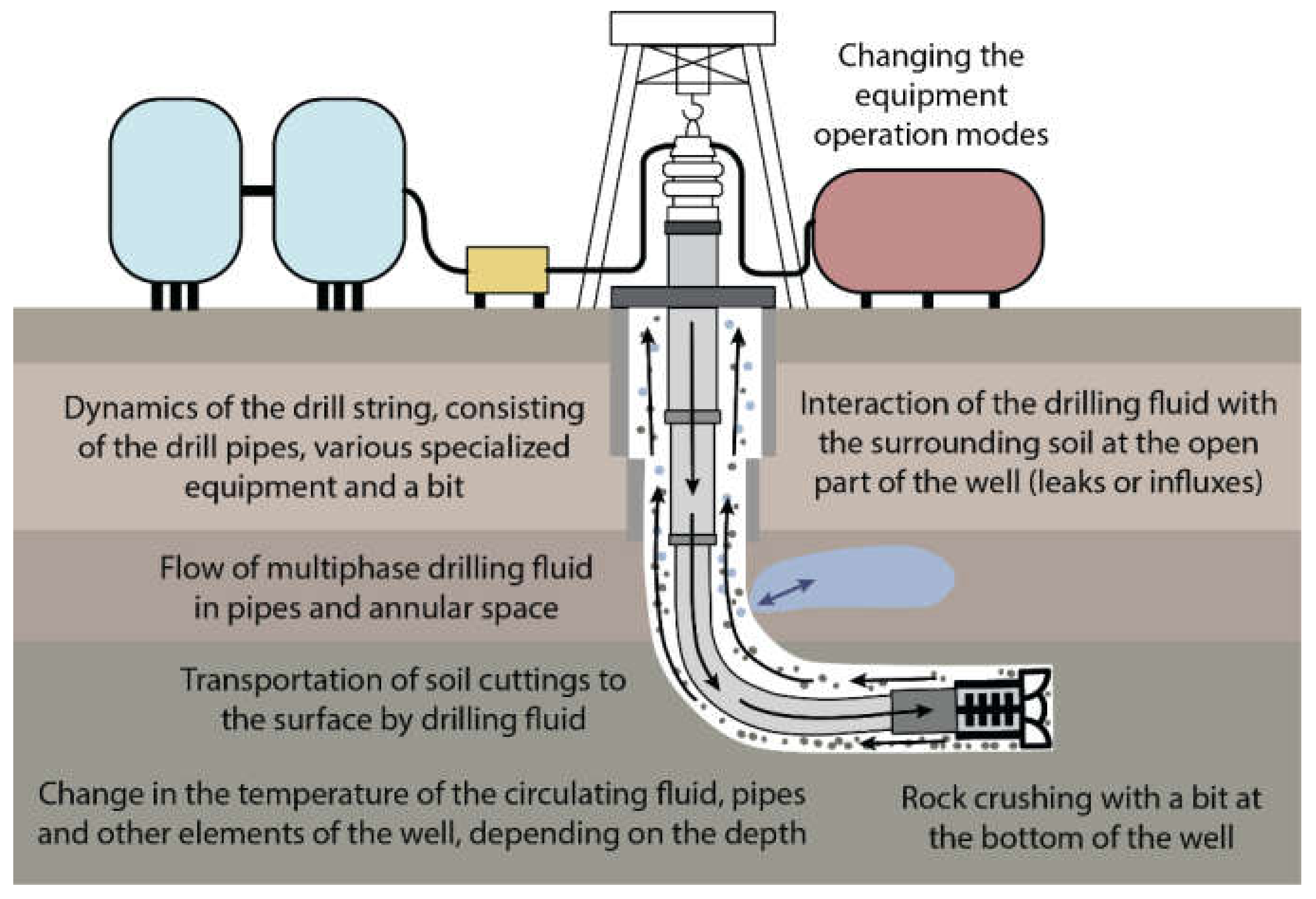
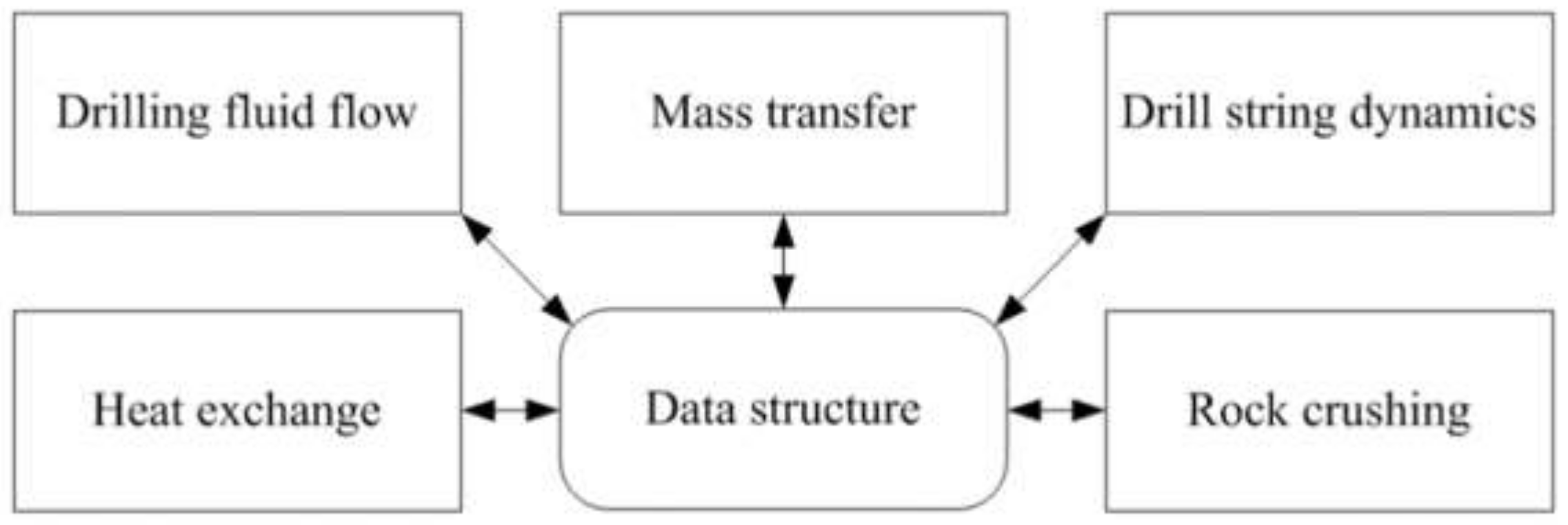
7. Multiphysical Model of the Drilling Process
8. Conclusions
- Expertise in each of the areas under consideration is needed for solving these problems. It is often difficult to find such expertise in one scientific group.
- The computation time of the numerical solution of each of the considered subproblems should be comparable. Otherwise, the simulation does not make practical sense, since in practice it is always required to carry out multiple calculations corresponding to the various scenarios under consideration.
- However, there is one important circumstance that facilitates the numerical solution of the problem under consideration. The mutual influence of the considered processes on each other is not so strong that special iterative procedures (e.g., Aitken’s method [137]) are required to ensure the convergence of the numerical process at each time step. It is enough to provide the data exchange between separate solvers at each time step.
- The suggested multiphysical model is a first step on a way to model the complex physical processes in the well and their impact on each other. This topic needs further research to include more specific physical aspects in the model, for example, the wear of the bit cutting tools while leaving the model applicable for engineering calculations that are not very time-consuming to perform.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitchell, R.F.; Miska, S.Z. Fundamentals of Drilling Engineering; SPE Textbook Series; Onepetro: Richardson, TX, USA, 2011; p. 696. [Google Scholar]
- Austin, E. Drilling Engineering Handbook; Springer: Dordrecht, The Netherlands, 2012; p. 301. [Google Scholar]
- Available online: https://www.oliasoft.com/ (accessed on 15 July 2022).
- Available online: https://www.pvisoftware.com/drilling-software.html (accessed on 15 July 2022).
- Available online: https://www.landmark.solutions/ (accessed on 15 July 2022).
- Available online: https://www.software.slb.com/ (accessed on 15 July 2022).
- Ghasemloonia, A.; Rideout, D.G.; Butt, S.D. A review of drillstring vibration modeling and suppression methods. J. Pet. Sci. Eng. 2015, 131, 150–164. [Google Scholar] [CrossRef]
- Livescu, S. Mathematical modeling of thixotropic drilling mud and crude oil flow in wells and pipelines—A review. J. Pet. Sci. Eng. 2012, 98–99, 174–184. [Google Scholar] [CrossRef]
- Spanos, P.D.; Chevalllier, A.M.; Politis, N.P. Nonlinear stochastic drillstring vibrations. ASME J. Vib. Acoust. 2002, 124, 512–519. [Google Scholar] [CrossRef]
- Chin, W.C. Wave Propagation in Petroleum Engineering; Gulf Publishing Co.: Houston, TX, USA, 1994; p. 396. [Google Scholar]
- Christoforou, A.P.; Yigit, A.S. Active control of stick-slip vibrations: The role of fully coupled dynamics. In Proceedings of the SPE#68093, SPE Middle East Oil Show, Manama, Bahrain, 17–20 March 2001. [Google Scholar]
- Márquez, M.B.S.; Boussaada, I.; Mounier, H.; Niculescu, S.I. Analysis and Control of Oilwell Drilling Vibrations—A Time-Delay Systems Approach; Springer: Berlin/Heidelberg, Germany, 2015; p. 282. [Google Scholar]
- Azar, J.J.; Samuel, G.R. Drilling Engineering; PennWell Books: Tulsa, OK, USA, 2007; p. 465. [Google Scholar]
- Kreisle, L.F.; Vance, J.M. Mathematical analysis of the effect of shock sub on the longitudinal vibrations of an oilwelldrillstring. SPE J. 1970, 10, 349–356. [Google Scholar]
- Li, Z.; Yanshan, U.; Guo, B. Analysis of longitudinal vibration of drillstring in air and gas drilling. In Proceedings of the SPE#107697, SPE Rocky Mountain Oil and Gas Technology Symposium, Denver, Colorado, 16–18 April 2007. [Google Scholar]
- Dunayevsky, V.A.; Abbassian, F.; Judzls, A. Dynamic stability of drillstrings under fluctuating weight on bit. SPE Drill. Complet. 1993, 8, 84–92. [Google Scholar] [CrossRef]
- Dareing, D.W. Guidelines for controlling drillstring vibrations. J. Energy Resour. Technol. 1984, 106, 272–277. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; John Whiley& Sons, Inc.: Hoboken, NJ, USA, 2007; p. 720. [Google Scholar]
- Ghasemloonia, A.; Rideout, D.G.; Butt, S.D. Coupled transverse vibration modeling of drillstrings subjected to torque and spatially varying axial load. J. Mech. Eng. Sci. 2012, 227, 946–960. [Google Scholar] [CrossRef]
- Gulyaev, V.I.; Lugovoi, P.Z.; Belova, M.A.; Solov’Ev, I.L. Stability of the equilibrium for rotating drillstrings. Int. Appl. Mech. 2006, 42, 692–698. [Google Scholar] [CrossRef]
- Gulyaev, V.I.; Lugovoi, P.Z.; Gaidaichuk, V.V.; Solov’ev, I.L. Effect of the length of a rotating drillstring on the stability of its quasistatic equilibrium. Int. Appl. Mech. 2007, 43, 1017–1023. [Google Scholar] [CrossRef]
- Gulyayev, V.I.; Gaidaichuk, V.V.; Solovjov, I.L. The buckling of elongated rotating drillstrings. J. Pet. Sci. Eng. 2009, 67, 140–148. [Google Scholar] [CrossRef]
- Gulyayev, V.I.; Borshch, O.I. Free vibrations of drillstrings in hyper deep bore- wells. J. Pet. Sci. Eng. 2011, 78, 759–764. [Google Scholar] [CrossRef]
- Beck, A.T.; da Silva, C.R.A., Jr. Timoshenko versus Euler beam theory: Pitfalls of a deterministic approach. Struct. Saf. 2010, 33, 19–25. [Google Scholar] [CrossRef]
- Jamal, Z.; Seyed, J.H.; Gholamreza, R. Finite element analysis of drillstring lateral vibration. Sci. Res. Essays 2011, 6, 2682–2694. [Google Scholar]
- Lin, Y.Q.; Wang, Y.H. Stick-slip vibration of drillstrings. ASME J. Eng. Ind. 1991, 113, 38–43. [Google Scholar] [CrossRef]
- Tucker, W.R.; Wang, C. An integrated model for drillstring dynamics. J. Sound Vib. 1999, 224, 123–165. [Google Scholar] [CrossRef]
- Palmov, V.A.; Bromundt, E.; Belyaev, A.K. Stability analysis of drillstring rotation. Dyn. Stab. Syst. Int. J. 1995, 10, 99–110. [Google Scholar] [CrossRef]
- Balanov, A.G.; Janson, N.B.; McClintock, P.V.; Tucker, R.W.; Wang, C.H.T. Bifurcation analysis of a neutral delay differential equation modeling the torsional motion of a driven drill-string. Chaos Solitons Fractals 2003, 15, 381–394. [Google Scholar] [CrossRef]
- Lima, L.C.C.; Aguiar, R.R.; Ritto, T.G.; Hbaieb, S. Analysis of the torsional stability of a simplified drillstring. In Proceedings of the DINAME 2015—Proceedings of the XVII International Symposium on Dynamic Problems of Mechanics, Natal, Brazil, 22–27 February 2015. [Google Scholar]
- Gulyaev, V.I.; Lugovoy, P.Z.; Borsch, E.I. Self-excitation of oscillations of the drill string bit. Appl. Mech. 2013, 49, 114–124. (In Russian) [Google Scholar]
- Besselink, B.; van de Wouw, N.; Nijmeijer, H. A semi-analytical of stick-slip oscillations in drilling systems. ASME J. Comput. Nonlinear Dyn. 2011, 6, 021006-1. [Google Scholar] [CrossRef]
- Barton, D.; Krauskopf, B.; Wilson, R.E. Nonlinear dynamics of torsional waves in a drill-string model with spatial extent. J. Vib. Control 2010, 16, 1049–1065. [Google Scholar] [CrossRef]
- Sampaio, R.; Piovan, M.T.; Lozano, G.V. Coupled axial torsional vibrations of drillstring by means of nonlinear model. J. Mech. Res. Commun. 2007, 34, 497–502. [Google Scholar] [CrossRef]
- Kamel, J.M.; Yigit, A. Modeling and Analysis of Axial and Torsional Vibrations of Drillstrings with Drag Bits. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 19–22 January 2014. [Google Scholar]
- Zamanian, M.; Khadem, S.E.; Ghazavi, M.R. Stick-slip oscillations of drag bits by considering damping of drilling mud and active damping system. J. Pet. Sci. Eng. 2007, 59, 289–299. [Google Scholar] [CrossRef]
- Elsayed, M.A.; Raymond, D.W. Analysis of coupling between axial and torsional vibration in a compliant model of a drillstring equipped with a PDC bit. In Proceedings of the ASME Engineering Technology Conference on Energy (ETCE), Houston, TX, USA, 4–5 February 2002. [Google Scholar]
- Yigit, A.S.; Christoforou, A.P. Coupled torsional and bending vibrations of drillstrings subject to impact with friction. J. Sound Vib. 1998, 215, 167–181. [Google Scholar] [CrossRef]
- Yigit, A.S.; Christoforou, A.P. Coupled torsional and bending vibrations of actively controlled drillstrings. J. Sound Vib. 2000, 234, 67–83. [Google Scholar] [CrossRef]
- Al-Hiddabi, S.A.; Samanta, B.; Seibi, A. Nonlinear control of torsional and bending vibrations of oil well drillstrings. J. Sound Vib. 2003, 265, 401–415. [Google Scholar] [CrossRef]
- Leine, R.I.; Van Campen, D.H.; Keultjes, W.J.G. Stick-slip whirl interaction in drillstring dynamics. ASME J. Vib. Acoust. 2002, 124, 209–220. [Google Scholar] [CrossRef]
- Yigit, A.S.; Christoforou, A.P. Coupled axial and transverse vibrations of oilwell drillstrings. J. Sound Vib. 1996, 195, 617–627. [Google Scholar] [CrossRef]
- Yigit, A.S.; Al-Ansary, M.D.; Khalid, M. Active control of drillstring vibrations by mode localization. J. Struct. Control 1997, 4, 47–63. [Google Scholar] [CrossRef]
- Hakimi, H.; Moradi, S. Drillstring vibration analysis using differential quadrature method. J. Pet. Sci. Eng. 2009, 70, 235–242. [Google Scholar] [CrossRef]
- Mahyari, M.F.; Behzad, M.; Rashed, G.R. Drillstring instability reduction by optimum positioning of stabilizers. Int. J. Mech. Eng. Sci. 2009, 224, 647–653. [Google Scholar]
- Trindade, M.A.; Wolter, C.; Sampaio, R. Karhunen–Loeve decomposition of coupled axial—Bending vibrations of beams subject to impacts. J. Sound Vib. 2005, 279, 1015–1036. [Google Scholar] [CrossRef]
- Christoforou, A.P.; Yigit, A.S. Fully coupled vibrations of actively controlled drillstrings. J. Sound Vib. 2003, 267, 1029–1045. [Google Scholar] [CrossRef]
- Baumgart, A. Stick-slip and bit-bounce of deep-hole drillstrings. ASME J. Energy Resour. Technol. 2000, 122, 78–82. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Al-Naser, H. Finite element dynamic analysis of drillstrings. J. Finite Elem. Anal. Des. 2005, 41, 1270–1288. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Al-Sulaiman, F.A.; Bashmal, S. Vibration analysis of drillstrings with string–borehole interaction. Int. J. Mech. Eng. Sci. 2008, 222, 2099–2110. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Al-Sulaiman, F.A. Laboratory investigation of drillstring vibrations. Int. J. Mech. Eng. Sci. 2009, 223, 2226–2249. [Google Scholar] [CrossRef]
- Wang, R.; Liu, X.; Song, G.; Zhou, S. Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction. Appl. Sci. 2021, 11, 9047. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Qin, X.; Dou, Z.; Feng, Z.; Yang, G. Investigating Drillstring Vibration and Stability in Coring Drilling. Energies 2022, 15, 5234. [Google Scholar] [CrossRef]
- Khajiyeva, L.A.; Andrianov, I.V.; Sabirova, Y.F.; Kudaibergenov, A.K. Analysis of Drill-String Nonlinear Dynamics Using the Lumped-Parameter Method. Symmetry 2022, 14, 1495. [Google Scholar] [CrossRef]
- Nouri, J.M.; Umur, H.; Whitelaw, J.H. Flow of Newtonian and non-Newtonian fluids in concentric and eccentric annuli. J. Fluid. Mech. 1993, 253, 617–641. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Han, S.-M.; Woo, N.-S. Flow of Newtonian and non-Newtonian fluids in a concentric annulus with a rotating inner cylinder. Korea-Aust. Rheol. J. 2013, 25, 77–85. [Google Scholar] [CrossRef]
- Scheid, C.M.; Calçada, L.A.; Braga, E.R.; Paraiso, E.C.H.; Martins, A.L. Hydraulic study of drilling fluid flow in circular and annular tubes. Braz. J. Pet. Gas 2011, 5, 239–253. [Google Scholar] [CrossRef]
- Platonov, D.V. Numerical modeling of non-Newtonian flows in annular channels. In Proceedings of the XVI International Scientific and Practical Conference “Modern Equipment and Technologies”, Tomsk, Russia, 12–16 April 2010. pp. 198–199. (In Russian).
- Wilkinson, W.L. Non-Newtonian Fluids; Mir: Moscow, Russia, 1964; 216p. (In Russian) [Google Scholar]
- Gnoevoy, A.V.; Klimov, D.M. Fundamentals of the Theory of Flows of Bingham Media; Fizmatlit: Moscow, Russia, 2004; p. 272. (In Russian) [Google Scholar]
- Beloglazov, I.; Morenov, V.; Leusheva, E.; Gudmestad, O.T. Modeling of heavy-oil flow with regard to their rheological properties. Energies 2021, 14, 359. [Google Scholar] [CrossRef]
- Bulatov, A.I.; Makarenko, P.P.; Proselkov Yu, M. Drilling Flushing and Grouting Solutions; Study Guide for Universities; Nedra: Moscow, Russia, 1999; 424p. (In Russian) [Google Scholar]
- Gukasov, N.A.; Bryukhovetsky, O.S.; Chikhotkin, V.F. Hydrodynamics in Exploration Drilling; Nedra-Businesscenter: Moscow, Russia, 2000; 304p. (In Russian) [Google Scholar]
- Skalle, P. Drilling Fluid Engineering; Bookboon: London, UK, 2011; p. 159. [Google Scholar]
- Makovei, N. Drilling Hydraulics: Per. from Romanian; Nedra: Moscow, Russia, 1986; 536p. (In Russian) [Google Scholar]
- Mirzajanzade, A.K.; Yentov, V. Hydrodynamics in Drilling; Nedra: Moscow, Russia, 1985; 196p. (In Russian) [Google Scholar]
- Whittaker, A. Theory and Applications of Drilling Fluid Hydraulics; Springer: Dordrecht, The Netherlands, 1985; Volume 1, 203p. [Google Scholar]
- Leonov, E.G.; Isaev, V.I. Complications and accidents while drilling oil and gas wells. In Hydroaeromechanics in Drilling; 2 Parts. Part 1; Nedra-Businesscenter: Moscow, Russia, 2006; p. 416. (In Russian) [Google Scholar]
- Wiśniowski, R.; Skrzypaszek, K.; Małachowski, T. Selection of a Suitable Rheological Model for Drilling Fluid Using Applied Numerical Methods. Energies 2020, 13, 3192. [Google Scholar] [CrossRef]
- Saasen, A.; Ytrehus, J.D. Viscosity Models for Drilling Fluids—Herschel-Bulkley Parameters and Their Use. Energies 2020, 13, 5271. [Google Scholar] [CrossRef]
- Isaev, V.I. Hydrodynamics of Two-Phase Mixtures in the Processes of Drilling Oil and Gas Wells. Ph.D. Dissertation, Russian State University of Oil and Gas named after I.M. Gubkin, Moscow, Russia, 8 December 2009. (In Russian). [Google Scholar]
- Kashevarov, A.A.; Eltsov, I.N.; Epov, M.I. Hydrodynamic model of the formation of penetration zones during well drilling. Appl. Mech. Tech. Phys. 2003, 44, 148–157. (In Russian) [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Han, S.; Yu, Z. A novel approach to modeling and simulating of underbalanced drilling process in oil and gas wells. Fuzzy Inf. Eng. 2009, 2, 413–421. [Google Scholar]
- Wang, Z.; Sun, B. Annular multiphase flow behavior during deep water drilling and the effect of hydrate phase transition. Pet. Sci. 2009, 6, 57–63. [Google Scholar] [CrossRef]
- Yeoh, G.H.; Tu, J. Computational Techniques for Multi-Phase Flows; Elsevier Ltd.: Amsterdam, The Netherlands, 2010; p. 644. [Google Scholar]
- Crowe, C.T. (Ed.) Multiphase Flow Handbook; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Brennen, C.E. Fundamentals of Multiphase Flows; Cambridge University Press: Cambridge, UK, 2006; p. 410. [Google Scholar]
- Gross, S.; Reusken, A. Numerical Methods for Two-Phase Incompressible Flows; Springer: Berlin/Heidelberg, Germany, 2011; p. 498. [Google Scholar]
- Balachandar, S.; Prosperetti, A. (Eds.) IUTAM Symposium on Computational Approaches to Multiphase Flow. In Proceedings of the IUTAM Symposium, Argonne National Laboratory, Argonne, France, 4–7 October 2004; p. 443. [Google Scholar]
- Wallis, G. One-Dimensional Two-Phase Flows; Courier Dover Publications: New York, NY, USA, 1972; p. 440. [Google Scholar]
- Brill, J.P.; Beggs, H.D. Two-Phase Flow in Pipes, 6th ed.; Universty of Tulsa: Tulsa, OK, USA, 1991; p. 640. [Google Scholar]
- Chhabra, R.P. Bubbles, Drops, and Particles in Non-Newtonian Fluids, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007; p. 743. [Google Scholar]
- Fang, Q.; Meng, Y.; Wei, N.; Xu, C.; Li, G. A Hydraulic Model for Multiphase Flow Based on the Drift Flux Model in Managed Pressure Drilling. Energies 2019, 12, 3930. [Google Scholar] [CrossRef]
- Richard, T.; Germay, C.; Detournay, E. A simplified model to explore the root cause of stick-slip vibrations in drilling systems with drag bits. J. Sound Vib. 2007, 305, 432–456. [Google Scholar] [CrossRef]
- Goicoechea, H.E.; Lima, R.; Buezas, F.S.; Sampaio, R. Drill-string with cutting dynamics: A mathematical assessment of two models. J. Sound Vib. 2022, 544, 117364. [Google Scholar] [CrossRef]
- Tengesdal, N.K.; Hovda, S.; Holden, C. A discussion on the decoupling assumption of axial and torsional dynamics in bit-rock models. J. Pet. Sci. Eng. 2021, 202, 108070. [Google Scholar] [CrossRef]
- Wang, W.; Liu, G.; Li, J.; Zha, C.; Lian, W. Numerical simulation study on rock-breaking process and mechanism of compound impact drilling. Energy Rep. 2021, 7, 3137–3148. [Google Scholar] [CrossRef]
- Sevastyanov, B.A. The theory of branching processes. In The Results of Science and Technology ; Series Theory of Probability; Math Statistics; Russian Institute of Scientific and Technical Information RAS: Moscow, Russia, 1968; pp. 5–46. (In Russian) [Google Scholar]
- Kolmogorov, A.N. On the logarithmically normal law of the distribution of particle sizes in crushing. Rep. Acad. Sci. USSR 1941, 31, 99–101. [Google Scholar]
- Filippov, A.F. On the distribution of particle sizes in crushing. TVP 1961, 3, 299–318. [Google Scholar]
- Cheng, Z.; Render, S. Kinetics of fragmentation. J. Phys. A. Math. 1990, 23, 1233–1258. [Google Scholar] [CrossRef]
- Fowler, A.C.; Scheu, B. A theoretical explanation of grain size distributions in explosive rock fragmentation. Proc. R. Soc. 2016, 472, 20150843. [Google Scholar] [CrossRef]
- Penkov, V.B.; Vedernikov, N.V. Kinetics of the process of grinding dispersed particles. DAS SSSR 1989, 307, 401–405. (In Russian) [Google Scholar]
- Korolev, V.Y. On the size distribution of particles during crushing. Inform. Its Appl. 2009, 3, 60–68. (In Russian) [Google Scholar]
- Korolev, L.V.; Bytev, D.O. Equation of grinding kinetics with an arbitrary law of waiting time distribution. Vestn. SGTU 2012, 64, 31–35. (In Russian) [Google Scholar] [CrossRef]
- Pryadko, N.S.; Saxonov, G.M.; Ternovaya, E.V. Simulation model of the kinetics of fine grinding of materials. Bull. Natl. Tech. Univ. 2014, 53, 89–98. (In Russian) [Google Scholar]
- Kozlovsky, E.A. (Ed.) Handbook for Drilling Exploration Wells; LLC “Nedra”: St. Petersburg, Russia, 2000. (In Russian) [Google Scholar]
- Kessai, I.; Benammar, S.; Doghmane, M.Z.; Tee, K.F. Drill Bit Deformations in Rotary Drilling Systems under Large-Amplitude Stick-Slip Vibrations. Appl. Sci. 2020, 10, 6523. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Guan, Z. Dynamic Characteristics of Downhole Bit Load and Analysis of Conversion Efficiency of Drill String Vibration Energy. Energies 2021, 14, 229. [Google Scholar] [CrossRef]
- Ivanova, T.N.; Biały, W.; Korshunov, A.I.; Jura, J.; Kaczmarczyk, K.; Turczyński, K. Increasing Energy Efficiency in Well Drilling. Energies 2022, 15, 1865. [Google Scholar] [CrossRef]
- Moisyshyn, V.; Voyevidko, I.; Tokaruk, V. Design of bottom hole assemblies with two rock cutting tools for drilling wells of large diameter. Min. Miner. Depos. 2020, 14, 128–133. [Google Scholar] [CrossRef]
- Ihnatov, A. Analyzing mechanics of rock breaking under conditions of hydromechanical drilling. Min. Miner. Depos. 2021, 15, 122–129. [Google Scholar] [CrossRef]
- Rabinovich, N.R. Engineering Problems of Continuum Mechanics in Drilling; Nedra: Moscow, Russia, 1989. [Google Scholar]
- Manikonda, K. Modeling Gas Kick Behavior in Water and Oil-Based Drilling Fluids. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2020. [Google Scholar]
- Policarpo, N.A. The study of mass transfer between phases in gas and organic drilling fluid mixtures. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012; Volume 6, pp. 4810–4820. [Google Scholar]
- Zhao, X.; Yan, X.; Sun, X.; Zhao, Q.; Jiang, H.; Gao, Y.; Yang, G. Modelling of Transient CO2/Water Flow in Wellbore considering Multiple Mass and Heat Transfer, Multiscale Flow and Optimal Production Control Techniques in Smart Unconventional Reservoirs. Geofluids 2021, 2021, 8879205. [Google Scholar]
- Bodwadkar, S.V.; Chenevert, M.E. Diffusion of Gas in Oil Based Drilling Fluids. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 9–11 March 1997. Paper Number: SPE-37475-MS. [Google Scholar]
- Chevalier, T.; Chevalier, C.; Clain, X.; Dupla, J.C.; Canou, J.; Rodts, S.; Coussot, P. Darcy’s law for yield stress fluid flowing through a porous medium. J. Non-Newton. Fluid Mech. 2013, 195, 57–66. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of Circulating Mud Temperatures. J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- Ramey, H.J., Jr. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Marshall, D.W.; Bentsen, R.G. A Computer Model to Determine the Temperature Distributions in a Wellbore. J. Can. Pet. Technol. 1982, 21, 63–75. [Google Scholar] [CrossRef]
- CemCADE 4.41. User Guide; Schlumberger: Houston, TX, USA, 2004; p. 217. [Google Scholar]
- Yang, M.; Meng, Y.; Li, G.; Li, Y.; Chen, Y.; Zhao, X.; Li, H. Estimation of Wellbore and Formation Temperatures during the Drilling Process under Lost Circulation Conditions. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Lupuleac, S.; Toropov, E.; Shabalin, A.; Kirillov, M. Prototype Model of Autonomous Offshore Drilling Complex. In Progress in Industrial Mathematics at ECMI 2016; Quintela, P., Barral, P., Gómez, D., Pena, F.J., Rodríguez, J., Salgado, P., Vázquez-Méndez, M.E., Eds.; Mathematics in Industry; Springer: Cham, Switzerland, 2017; Volume 26. [Google Scholar]
- Churilova, M.A.; Lupulyak, S.V.; Toropov, E.E.; Shabalin, A.A.; Kirillov, M.V.; Oganov, A.S. Integrated virtual simulation model of the well drilling process. Bull. Assoc. Drill. Contract. 2020, 3, 18–23. (In Russian) [Google Scholar]
- Ishii, M.; Hibiki, T. Thermo-Fluid Dynamics of Two-Phase Flow, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011; p. 537. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980; p. 205. [Google Scholar]
- Leonov, E.G.; Isaev, V.I. Hydroaeromechanics in Drilling; Nedra: Moscow, Russia, 1987; p. 304. (In Russian) [Google Scholar]
- Manninen, M.; Taivassalo, V.; Kallio, S. On the Mixture Model for Multiphase Flow; VTT Publications: Espoo, Finland, 1996; p. 67. [Google Scholar]
- Grigor’ev, B.S.; Eliseev, A.A. Narrow channel approximation in modeling the multiphase flows in pipes. In Fundamental and Applied Sciences Today X, Proceedings of the Conference, North Charleston, SC, USA, 26–27 December 2016; CreateSpace: North Charleston, SC, USA, 2016; Volume 2, pp. 141–143. [Google Scholar]
- Eliseev, A.A.; Grigoriev, B.S. Mixture Model of the Flow of Multiphase Fluids During Drilling of Oil Wells; Institute of Applied Mathematics and Mechanics. Publishing House of the Polytechnic. Univ.: St. Petersburg, Russia, 2016. (In Russian) [Google Scholar]
- Eliseev, A.A.; Grigoriev, B.S. Modification of the Mixture Model of the Flow of Multiphase Fluids to Account for Gas and Water Manifestations During Drilling; Institute of Applied Mathematics and Mechanics. Publishing House of the Polytechnic. Univ.: St. Petersburg, Russia, 2017; pp. 70–73. (In Russian) [Google Scholar]
- Beznea, L.; Deaconu, M.; Lupas, O. Branching processes for the fragmentation equation. Stoch. Process. Appl. 2015, 125, 1861–1885. [Google Scholar] [CrossRef]
- Andrade, E.D.C.; Randall, R.F.Y. The Rehbinder Effect. Proc. Roy. Soc. B 1950, 63, 990. [Google Scholar] [CrossRef]
- Grigoriev, B.S.; Eliseev, A.A.; Pogarskaya, T.A.; Toropov, E.E. Mathematical modeling of rock crushing and multiphase flow of drilling fluid in well drilling. J. Min. Inst. 2019, 235, 16–23. [Google Scholar] [CrossRef]
- Basniev, K.S.; Dmitriev, N.M.; Rozenberg, G.D. Oil and Gas Hydromechanics; Computer Research Institute: Moscow, Russia, 2005; p. 544. (In Russian) [Google Scholar]
- Faruk, C. Reservoir formation damage. In Fundamentals, Modeling, Assessment and Mitigation, 2nd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Partial Differential Equation Toolbox. User’s Guide MATLAB R2016a; MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
- Gulyaev, V.; Gaidaichuk, V.; Solov’ev, I.; Gorbunovicha, I. Quasistatic critical states of strings for deep dilling. Strength Mater. 2006, 38, 527–534. [Google Scholar] [CrossRef]
- Li, J.; Yan, T.; Sun, X.; Peng, S. Finite element analysis on drilling string axial vibration in a crooked hole. In Proceedings of the ICPTT-2012, Wuhan, China, 19–22 October 2012; pp. 1328–1334. [Google Scholar]
- Wu, A.; Hareland, G.; Fazaelizadeh, M. Torque and drag analysis using finite element method. Mod. Appl. Sci. 2011, 5, 13–27. [Google Scholar] [CrossRef][Green Version]
- Liao, Y.; Wang, Z.; Chao, M.; Sun, X.; Wang, J.; Zhou, B.; Sun, B. Coupled wellbore–reservoir heat and mass transfer model for horizontal drilling through hydrate reservoir and application in wellbore stability analysis. J. Nat. Gas Sci. Eng. 2021, 95, 104216. [Google Scholar] [CrossRef]
- Ritto, T.G.; Sampaio, R. Christian Soize. Drill-string nonlinear dynamics accounting for the drilling fluid. In Proceedings of the 30º CILAMCE-Iberian-Latin-American Congress on Computational Methods in Engineering, Armação dos Búzios, RJ, Brazil, 8–11 November 2009; pp. 1–25. [Google Scholar]
- Zhang, J.; Li, X.; Tang, X.; Luo, W. Establishment and Analysis of Temperature Field of Riserless Mud Recovery System. Oil Gas Sci. Technol. –Rev. D’ifp Energ. Nouv. 2019, 74, 19. [Google Scholar] [CrossRef]
- Guo, B.; Li, J.; Song, J.; Li, G. Mathematical modeling of heat transfer in counter-current multiphase flow found in gas-drilling systems with formation fluid influx. Pet. Sci. 2017, 14, 711–719. [Google Scholar] [CrossRef]
- Yang, A.; Zhu, Z.; Zhang, N.; Ye, Y. Solution and Analysis of Wellbore Temperature and Pressure Field Coupling Model under Lost Circulation. ACS Omega 2022, 7, 28675–28684. [Google Scholar] [CrossRef] [PubMed]
- Küttler, U.; Wall, W.A. Fixed-point fluid-structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]

| Article | Drill String Dynamics | Drilling Fluid Circulation | Drill Bit Interaction with Rock | Fluid Exchange with Soil (Mass Transfer) | Heat Exchange with Soil |
|---|---|---|---|---|---|
| Liao et al. [132], 2021 | − | + | − | + | + |
| Ritto et al. [133], 2009 | + | + | − | − | − |
| Zhang et al. [134], 2019 | − | + | − | − | + |
| Guo et al. [135], 2017 Yang et al. [136], 2022 | − | + | − | + | + |
| Tengesdal et al. [86], 2021 | + | − | + | − | − |
| Lupuleac et al. [114], 2017 Churilova et al. [115], 2020 | + | + | + | + | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Churilova, M.; Lupuleac, S.; Shaposhnikov, N. Complex Mathematical Modeling of the Well Drilling Process. Appl. Sci. 2022, 12, 11369. https://doi.org/10.3390/app122211369
Churilova M, Lupuleac S, Shaposhnikov N. Complex Mathematical Modeling of the Well Drilling Process. Applied Sciences. 2022; 12(22):11369. https://doi.org/10.3390/app122211369
Chicago/Turabian StyleChurilova, Maria, Sergey Lupuleac, and Nikita Shaposhnikov. 2022. "Complex Mathematical Modeling of the Well Drilling Process" Applied Sciences 12, no. 22: 11369. https://doi.org/10.3390/app122211369
APA StyleChurilova, M., Lupuleac, S., & Shaposhnikov, N. (2022). Complex Mathematical Modeling of the Well Drilling Process. Applied Sciences, 12(22), 11369. https://doi.org/10.3390/app122211369






