Nonlinear Model Predictive Control with Terminal Cost for Autonomous Vehicles Trajectory Follow
Abstract
1. Introduction
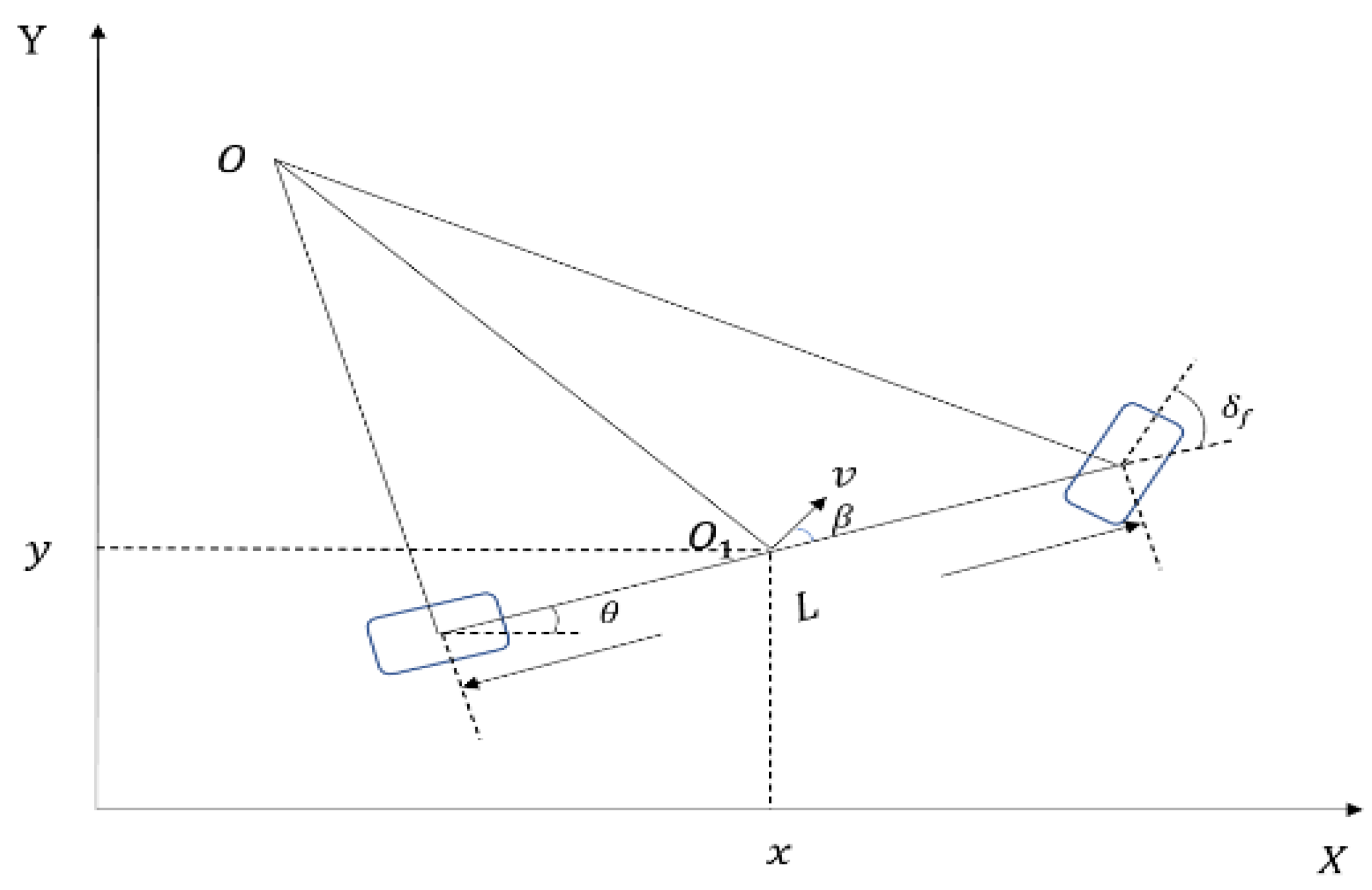
2. Kinematic Bicycle Model for Autonomous Vehicle
3. Controller Design and Numerical Simulation Verification
3.1. Controller Design
3.2. Algorithm Numerical Verification
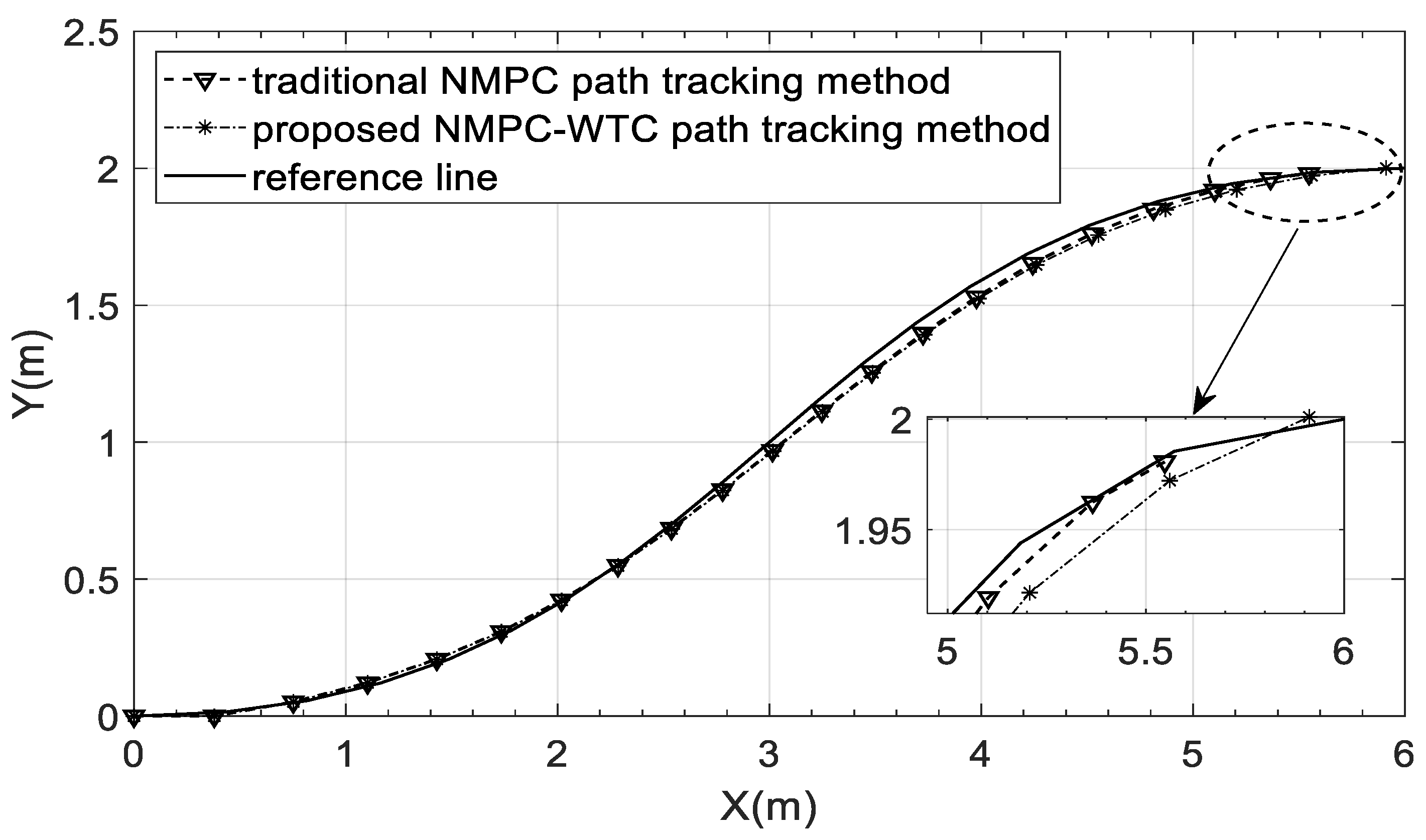
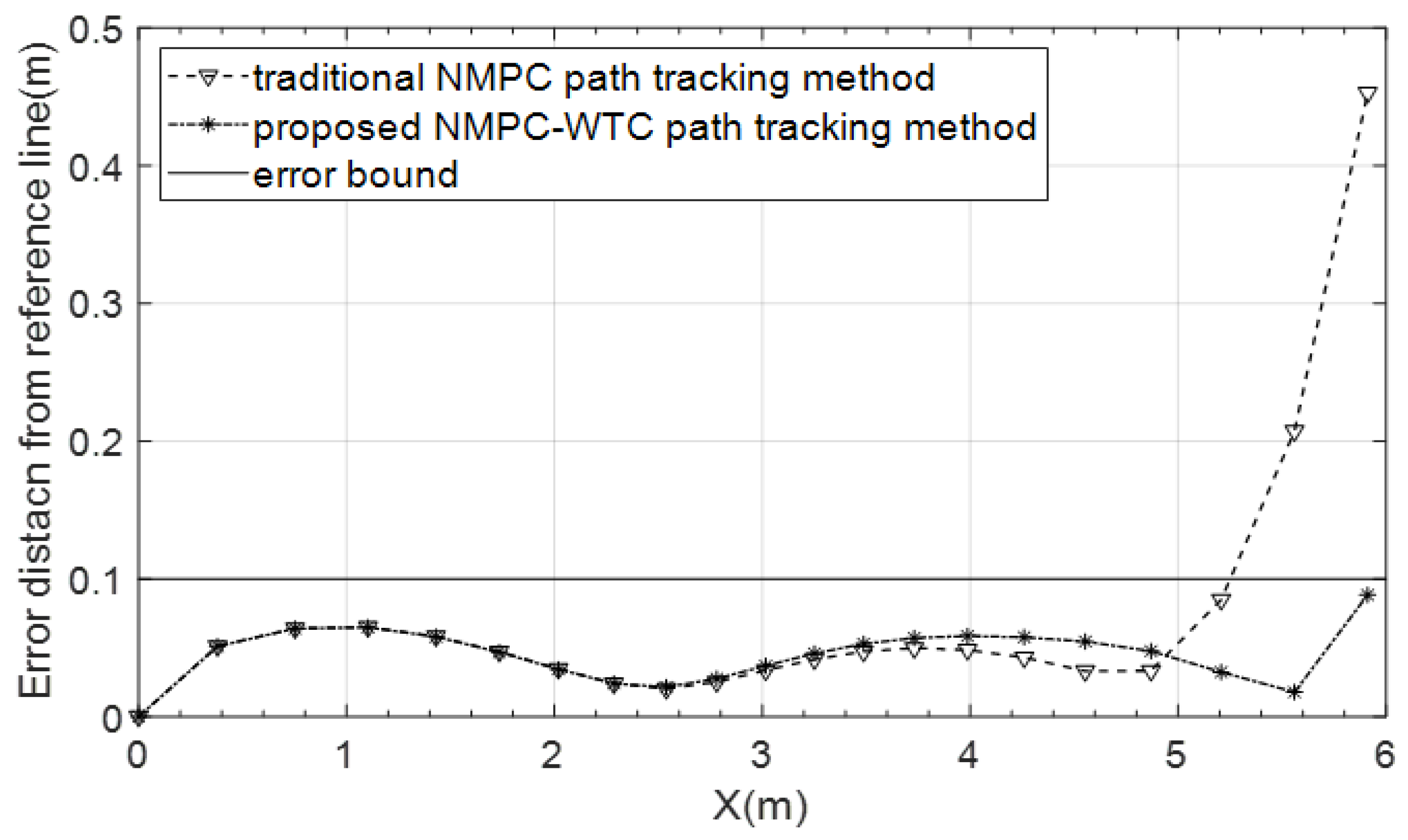
3.2.1. Control Open-Loop Simulation
3.2.2. The Influence of Terminal Cost Coefficient
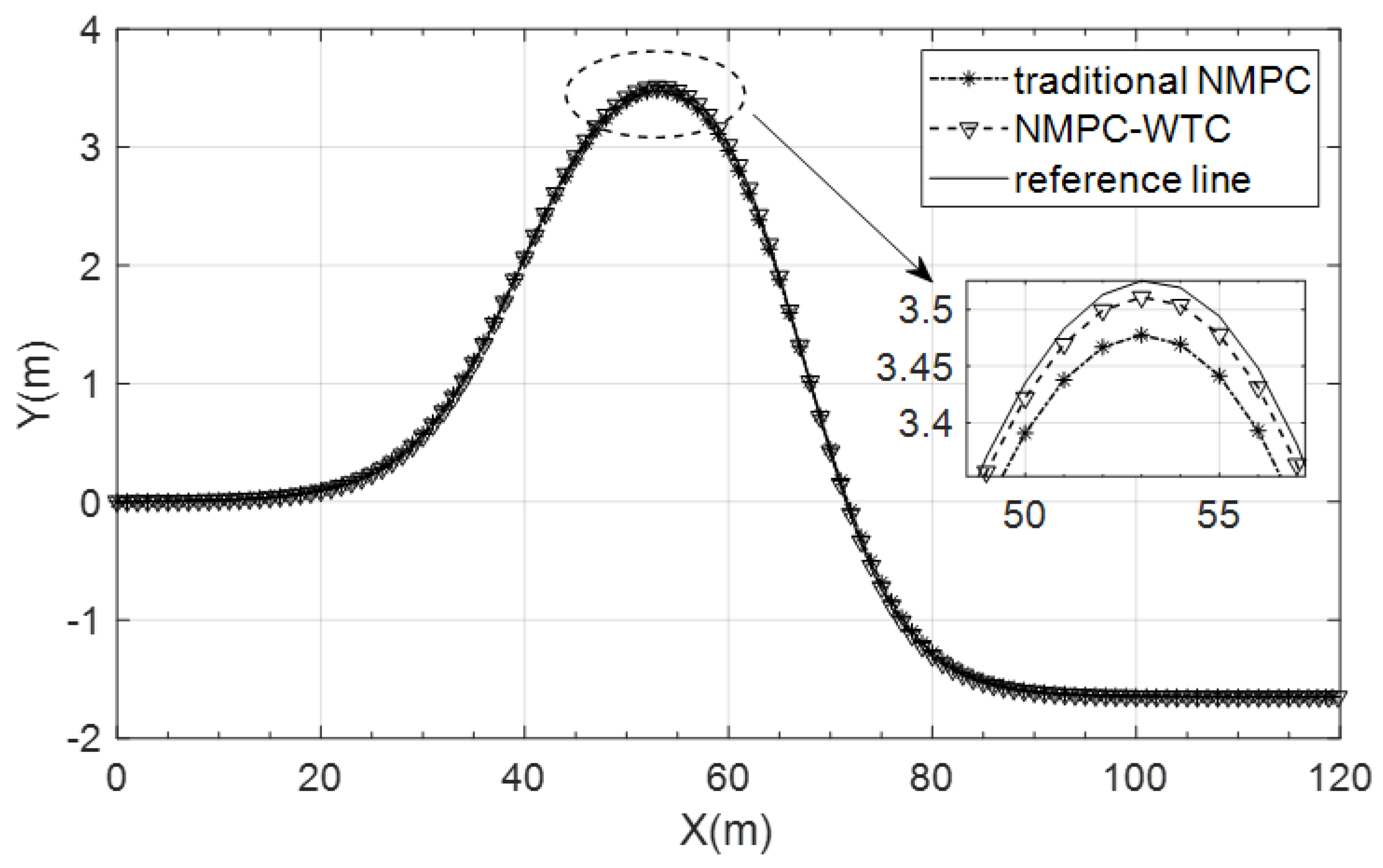
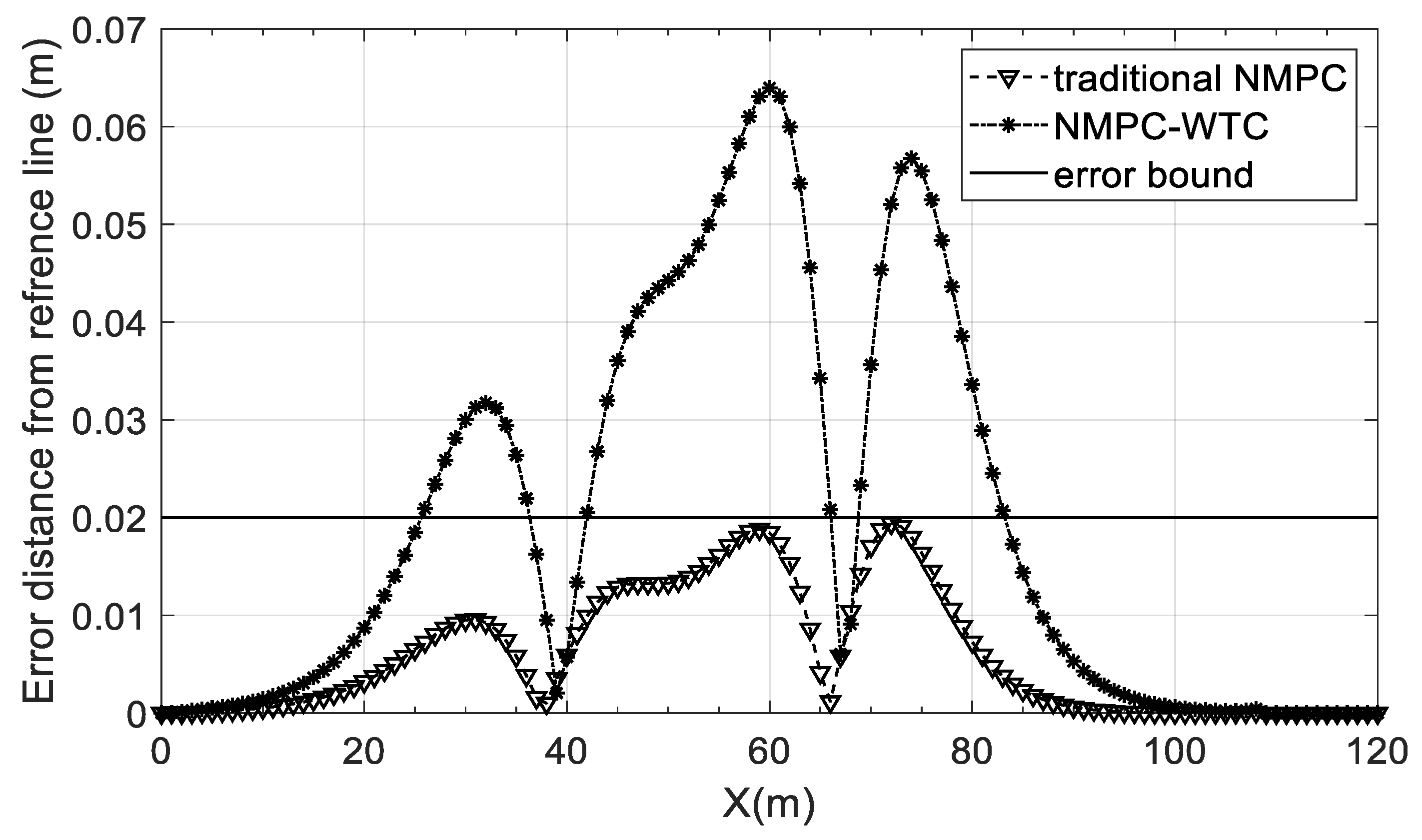
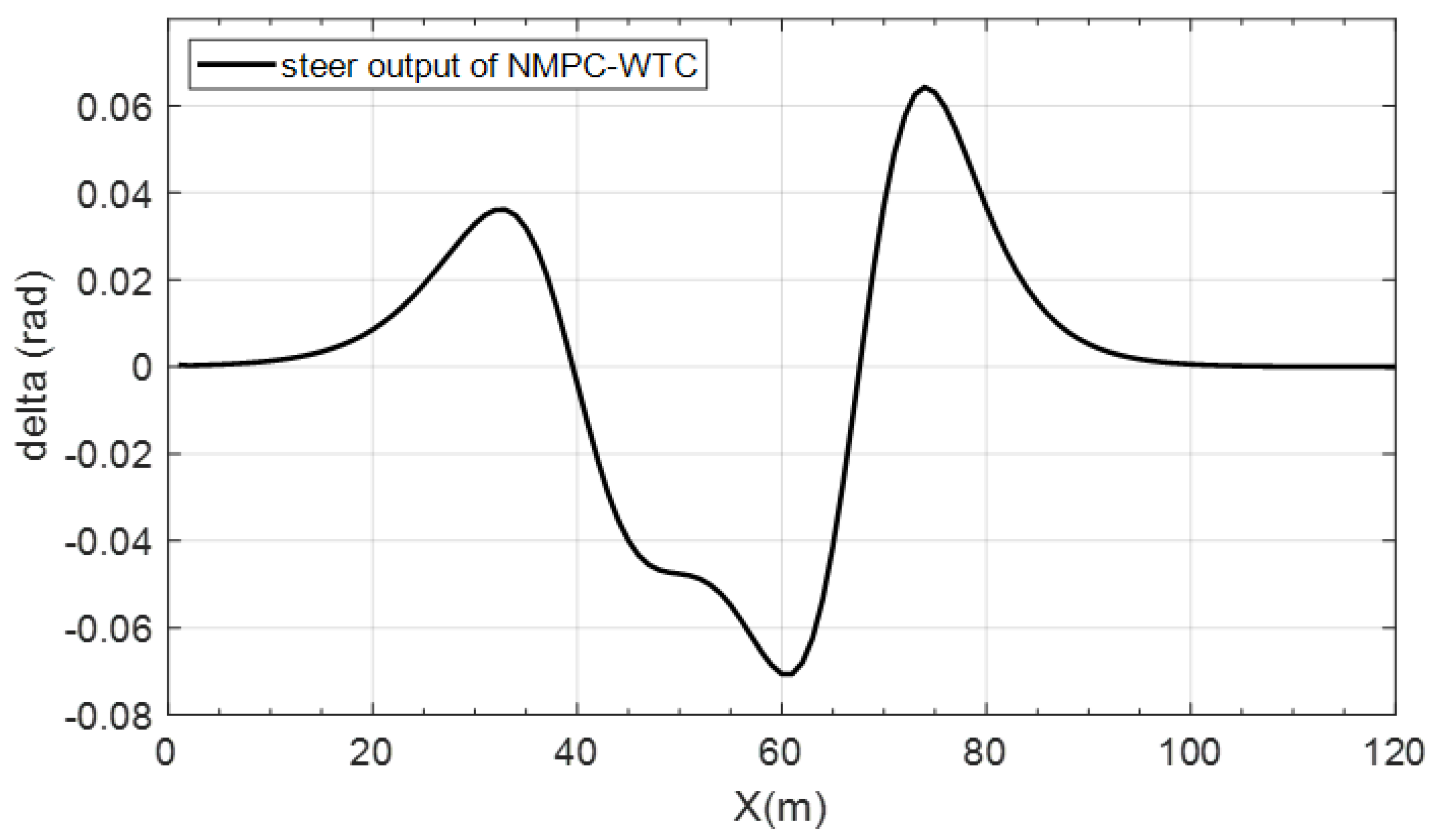
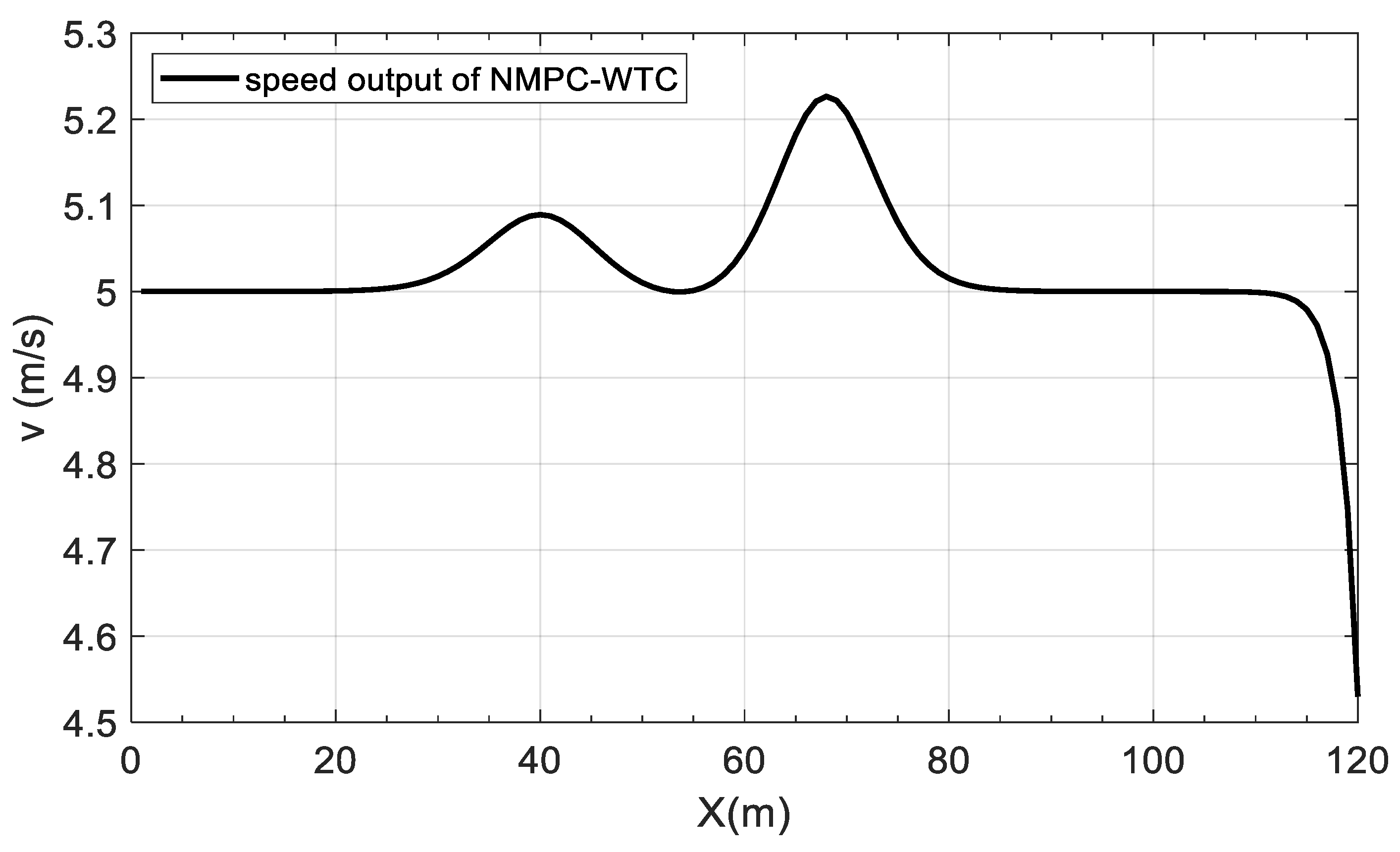
3.2.3. Control Closed-Loop Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alcala, E.; Puig, V.; Quevedo, J.; Cayuela, V.P.; Casin, J.Q. TS-MPC for Autonomous Vehicles Including a TS-MHE-UIO Estimator. IEEE Trans. Veh. Technol. 2019, 68, 6403–6413. [Google Scholar] [CrossRef]
- Paden, B.; Cap, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Kong, J.; Pfeiffer, M.; Schildbach, G.; Borrelli, F. Kinematic and dynamic vehicle models for autonomous driving control design. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 1094–1099. [Google Scholar] [CrossRef]
- Kühne, F.; Lages, W.F.; Silva, J.M. Model Predictive Control of a Mobile Robot Using Linearization. In Proceedings of the Mechatronics and Robotics 2004, Aachen, Germany, 13–15 September 2004. [Google Scholar]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path tracking control for autonomous vehicles based on an improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Shuai, Z.; Zhang, H.; Wang, J.; Li, J.; Ouyang, M. Combined AFS and DYC control of four-wheel-independent-drive electric vehicles over CAN network with time-varying delays. IEEE Trans. Veh. Technol. 2013, 63, 591–602. [Google Scholar] [CrossRef]
- Chen, X.; Bao, Q.; Zhang, B. Research on 4WIS Electric Vehicle Path Tracking Control Based on Adaptive Fuzzy PID Algorithm. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 6753–6760. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.; Xie, C.; Ye, Q. Investigation on adaptive preview distance path tracking control with directional error compensation. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 484–500. [Google Scholar] [CrossRef]
- Findeisen, R.; Allgöwer, F. An introduction to nonlinear model predictive control. In Proceedings of the 21st Benelux Meeting on Systems and Control, Veldhoven, The Netherlands, 19–21 March 2002; Volume 11, pp. 119–141. [Google Scholar]
- Rafaila, R.C.; Livint, G. Nonlinear model predictive control of autonomous vehicle steering. In Proceedings of the 2015 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015; pp. 466–471. [Google Scholar] [CrossRef]
- Falcone, P.; Eric Tseng, H.; Borrelli, F.; Asgari, J.; Hrovat, D. MPC-based yaw and lateral stabilization via active front steering and braking. Veh. Syst. Dyn. 2008, 46, 611–628. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Q.; Chen, W.; Zhao, L.; Tan, D. Path tracking based on model predictive control with variable predictive horizon. Trans. Inst. Meas. Control 2021, 43, 014233122110038. [Google Scholar] [CrossRef]
- Bai, G.; Liu, L.; Meng, Y.; Luo, W.; Gu, Q.; Ma, B. Path Tracking of Mining Vehicles Based on Nonlinear Model Predictive Control. Appl. Sci. 2019, 9, 1372. [Google Scholar] [CrossRef]
- Chu, D.; Li, H.; Zhao, C.; Zhou, T. Trajectory Tracking of Autonomous Vehicle Based on Model Predictive Control with PID Feedback. IEEE Trans. Intell. Transp. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. Constrained model predictive control: Stability and optimality. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Amrit, R.; Rawlings, J.B.; Angeli, D. Economic optimization using model predictive control with a terminal cost. Ann. Rev. Control 2011, 35, 178–186. [Google Scholar] [CrossRef]
- Koehler, J.; Muller, M.A.; Allgower, F. A nonlinear model predictive control framework using reference generic terminal ingredients. IEEE Trans. Autom. Control 2019, 65, 3576–3583. [Google Scholar] [CrossRef]
- Köhler, J.; Zeilinger, M.; Grüne, L. Stability and performance analysis of NMPC: Detectable stage costs and general terminal costs. arXiv 2021, arXiv:2110.11021. [Google Scholar]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Andersson, J.A.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Marruedo, D.L.; Alamo, T.; Camacho, E.F. Enlarging the domain of attraction of MPC controller using invariant sets. IFAC Proc. Vol. 2002, 35, 47–52. [Google Scholar] [CrossRef]
- Sawma, J.; Khatounian, F.; Monmasson, E.; Ghosn, R.; Idkhajine, L. The effect of prediction horizons in MPC for first order linear systems. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 316–321. [Google Scholar] [CrossRef]
- Ma, A.; Liu, K.; Zhang, Q.; Liu, T.; Xia, Y. Event-Triggered Distributed MPC With Variable Prediction Horizon. IEEE Trans. Autom. Control 2021, 66, 4873–4880. [Google Scholar] [CrossRef]

| The Parameter of Vehicle Model | Value |
|---|---|
| Wheelbase, L | 2.9 m |
| Value range of front wheel angle, | −0.26 rad~0.26 rad |
| Longitudinal speed of the vehicle, v | 0~33.3 m/s |
| Forward Euler discrete time, T | 200 ms |
| Predictive horizon, | 20 |
| The Value of Terminal Cost Coefficient (α) | Solution Time |
|---|---|
| 1 (without terminal cost) | 0.030 s |
| 2 | 0.032 s |
| 10 | 0.043 s |
| 100 | 0.058 s |
| 500 | 0.061 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, J.; Ye, X.; Cao, W. Nonlinear Model Predictive Control with Terminal Cost for Autonomous Vehicles Trajectory Follow. Appl. Sci. 2022, 12, 11359. https://doi.org/10.3390/app122211359
Nan J, Ye X, Cao W. Nonlinear Model Predictive Control with Terminal Cost for Autonomous Vehicles Trajectory Follow. Applied Sciences. 2022; 12(22):11359. https://doi.org/10.3390/app122211359
Chicago/Turabian StyleNan, Jinrui, Xucheng Ye, and Wanke Cao. 2022. "Nonlinear Model Predictive Control with Terminal Cost for Autonomous Vehicles Trajectory Follow" Applied Sciences 12, no. 22: 11359. https://doi.org/10.3390/app122211359
APA StyleNan, J., Ye, X., & Cao, W. (2022). Nonlinear Model Predictive Control with Terminal Cost for Autonomous Vehicles Trajectory Follow. Applied Sciences, 12(22), 11359. https://doi.org/10.3390/app122211359







