A Point Crack Source Location Method without Velocity Information in Anisotropic Plates
Abstract
1. Introduction
2. Methodology
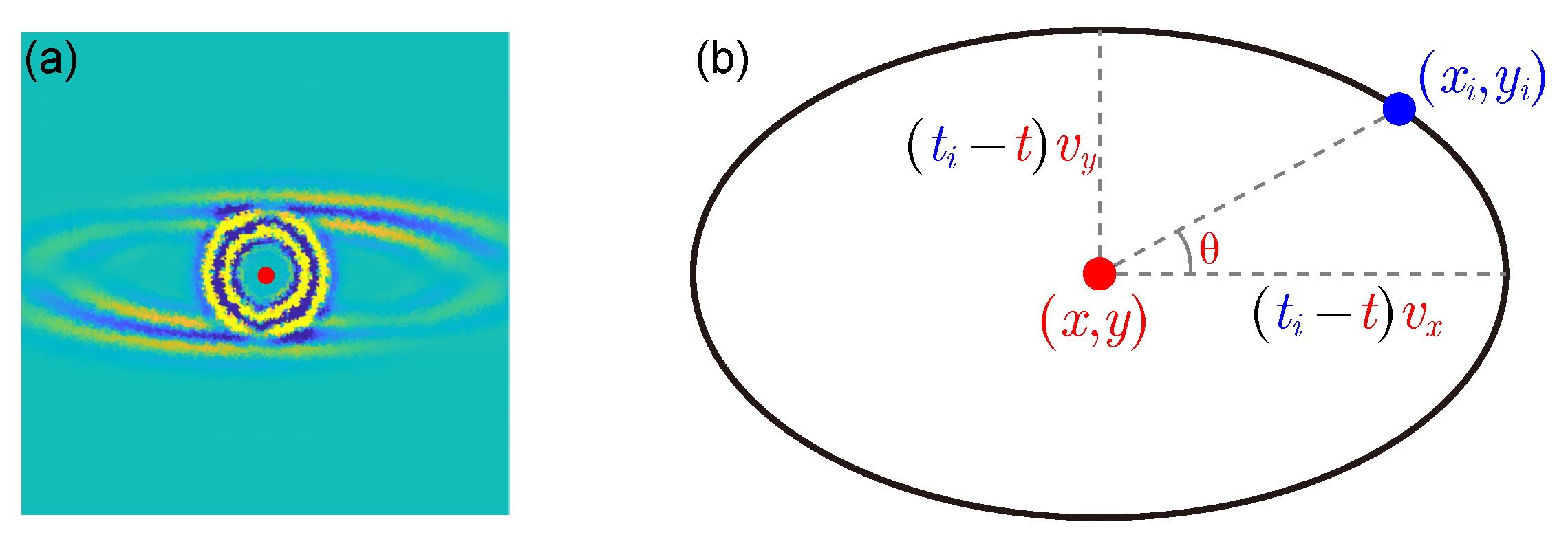
2.1. Elliptic Wavefront
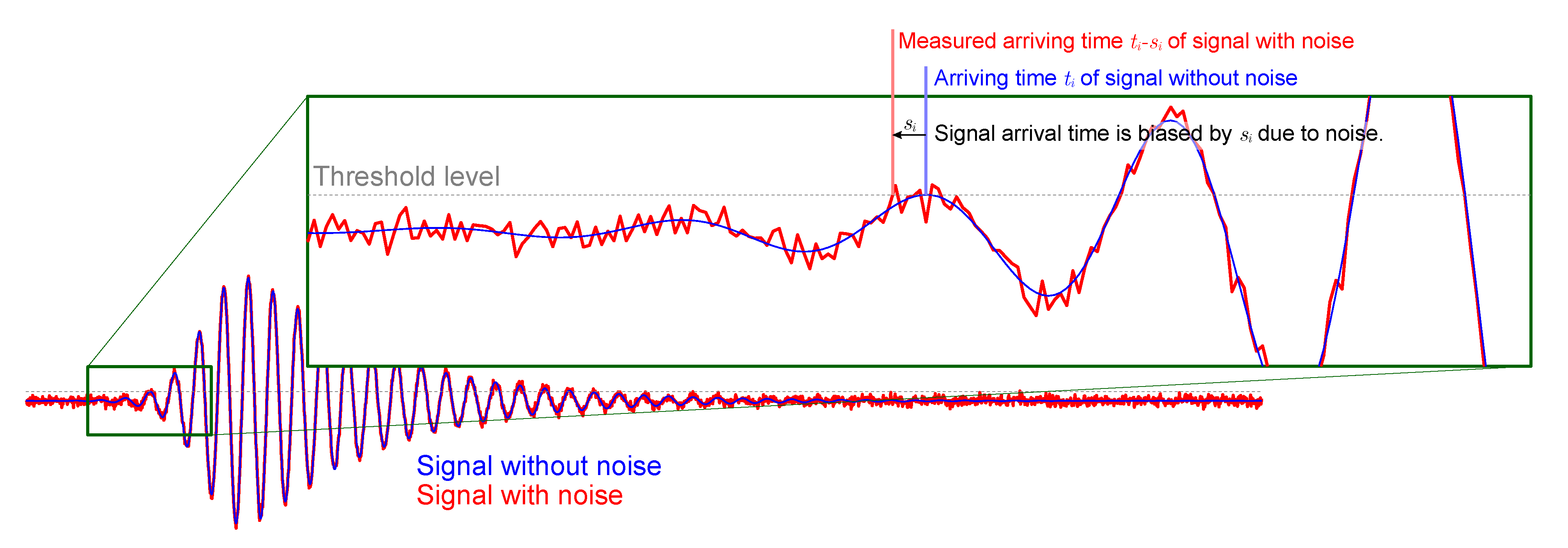
2.2. Signal Arrival Time Error Correction
2.3. Objective Function and Minimization
3. Experiments
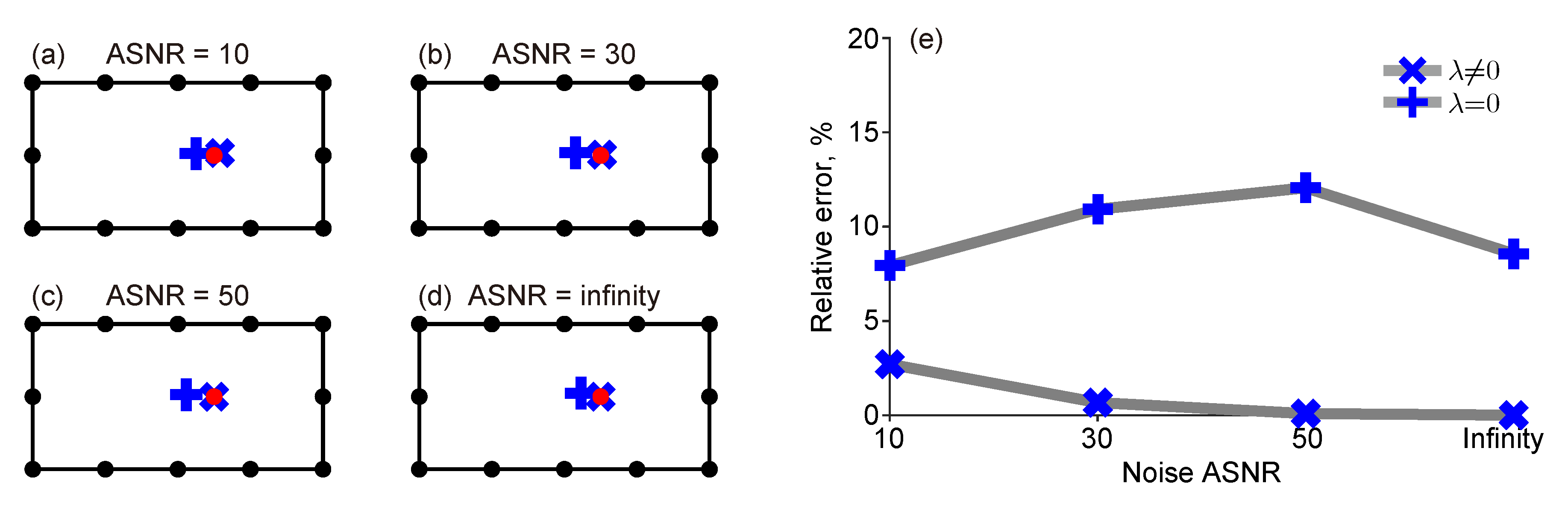
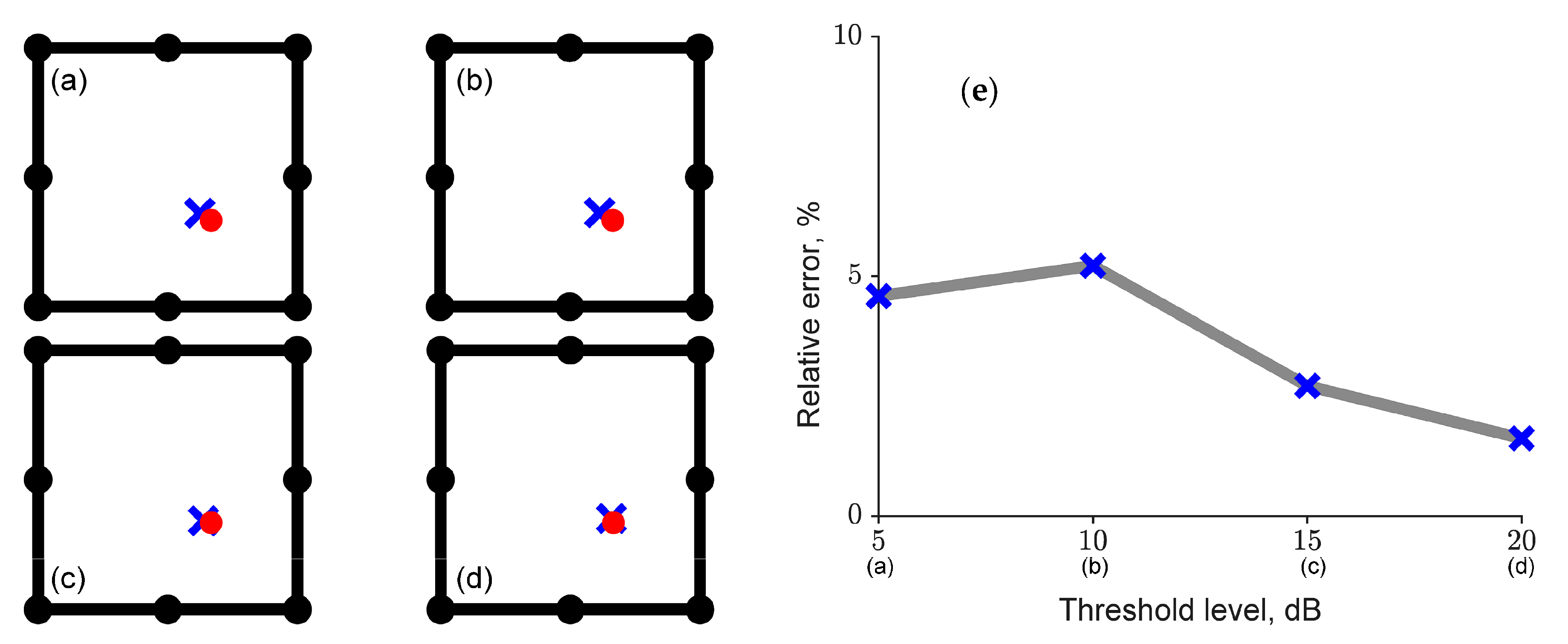
3.1. Robustness
3.2. Numerical Experiment Based on a Physical Model
3.3. Cfrp Phantom Experiment
4. Results
4.1. Robustness on Noise
4.2. Robustness on TOA Thresholds
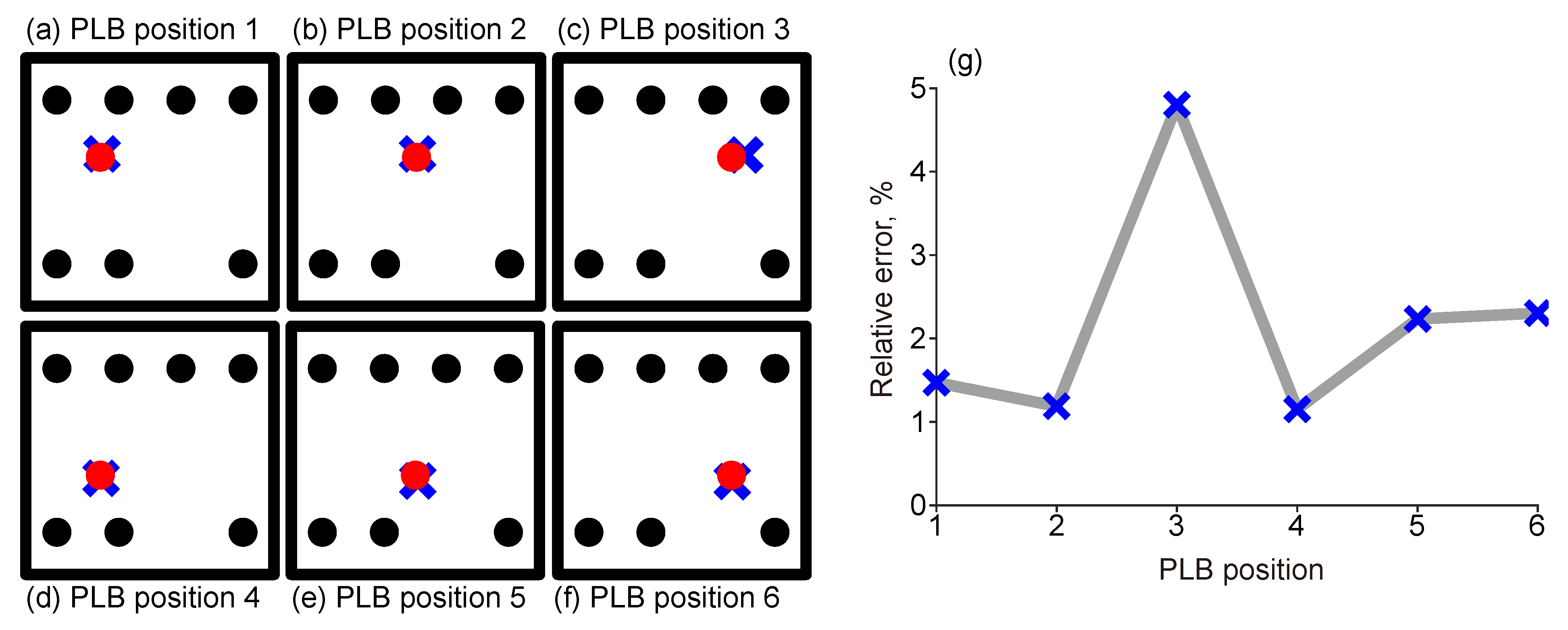
4.3. Plb Test on the CFRP Plate
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grosse, C.U.; Ohtsu, M. (Eds.) Acoustic Emission Testing; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Kocur, G.K.; Saenger, E.H.; Grosse, C.U.; Vogel, T. Time reverse modeling of acoustic emissions in a reinforced concrete beam. Ultrasonics 2016, 65, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Sagar, R.V.; Prasad, B.K.R.; Sharma, R. Evaluation of damage in reinforced concrete bridge beams using acoustic emission technique. Nondestruct. Test. Eval. 2012, 27, 95–108. [Google Scholar] [CrossRef]
- Shehadeh, M.F.; Elbatran, A.H.; Mehanna, A.; Steel, J.A.; Reuben, R.L. Evaluation of acoustic emission source location in long steel pipes for continuous and semi-continuous sources. J. Nondestruct. Eval. 2019, 38, 1–15. [Google Scholar] [CrossRef]
- Kim, K.H.; Kishi, T. Three dimensional AE source location in metals. Nondestruct. Test. Eval. 1987, 3, 75–88. [Google Scholar] [CrossRef]
- Buttle, D.J.; Scruby, C.B. Acoustic emission source location in fiber reinforced plastic composites. J. Acoust. Emiss. 1988, 7, 211–223. [Google Scholar]
- Miller, R.K.; Hill, E.v.K.; Moore, P.O. Nondestructive Testing Handbook, Third Edition: Volume 6, Acoustic Emission Testing, 3rd ed.; American Society for Nondestructive: Columbus, OH, USA, 2005. [Google Scholar]
- Saenger, E.H.; Kocur, G.K.; Jud, R.; Torrilhon, M. Application of time reverse modeling on ultrasonic non-destructive testing of concrete. Appl. Math. Model. 2011, 35, 807–816. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Wang, D.; Wang, J.; Zhang, W.; Hong, J.; Gao, L. AE source localization and imaging on cylindrical shell structures based on six-AE-sensor monitoring network and VTR focusing imaging. Nondestruct. Test. Eval. 2021, 36, 35–61. [Google Scholar] [CrossRef]
- Tobias, A. Acoustic-emission source location in two dimensions by an array of three sensors. Non-Destr. Test. 1976, 9, 9–12. [Google Scholar] [CrossRef]
- Li, N.; Wang, E.; Ge, M.; Sun, Z. A nonlinear microseismic source location method based on Simplex method and its residual analysis. Arab. J. Geosci. 2014, 7, 4477–4486. [Google Scholar] [CrossRef]
- Ge, M. Analysis of source location algorithms: Part I: Overview and non-iterative methods. J. Acoust. Emiss. 2003, 21, 14–28. [Google Scholar]
- Ge, M. Analysis of source location algorithms: Part II. Iterative methods. J. Acoust. Emiss. 2003, 21, 29–51. [Google Scholar]
- Kim, Y.-H.; Lee, S.-S. Simulation of elastic wave propagation in anisotropic materials. J. Korean Soc. Nondestruct. Test. 1997, 17, 227–236. [Google Scholar]
- Castagnede, B.; Sachse, W.; Kim, K.Y. Location of pointlike acoustic emission sources in anisotropic plates. J. Acoust. Soc. Am. 1989, 86, 1161–1171. [Google Scholar] [CrossRef]
- Kundu, T.; Das, S.; Martin, S.A.; Jata, K.V. Locating point of impact in anisotropic fiber reinforced composite plates. Ultrasonics 2008, 48, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Koabaz, M.; Hajzargarbashi, T.; Kundu, T.; Deschamps, M. Locating the acoustic source in an anisotropic plate. Struct. Health Monitor. 2011, 11, 315–323. [Google Scholar] [CrossRef]
- Kundu, T.; Das, S.; Jata, K.V. Point of impact prediction in isotropic and anisotropic plates from the acoustic emission data. J. Acoust. Soc. Am. 2007, 122.4, 2057–2066. [Google Scholar] [CrossRef]
- Sen, N.; Kundu, T. Acoustic source localization in a highly anisotropic plate with unknown orientation of its axes of symmetry and material properties with numerical verification. Ultrasonics 2020, 100, 105977. [Google Scholar] [CrossRef]
- Sen, N.; Kundu, T. A new wave front shape-based approach for acoustic source localization in an anisotropic plate without knowing its material properties. Ultrasonics 2018, 87, 20–32. [Google Scholar] [CrossRef]
- Yin, S.; Cui, Z.; Kundu, T. Acoustic source localization in anisotropic plates with “Z” shaped sensor clusters. Ultrasonics 2018, 84, 34–37. [Google Scholar] [CrossRef]
- Sen, N.; Gawroński, M.; Packo, P.; Uhl, T.; Kundu, T. Square-shaped sensor clusters for acoustic source localization in anisotropic plates by wave front shape-based approach. Mech. Syst. Signal Process. 2021, 153, 107489. [Google Scholar] [CrossRef]
- Kundu, T.; Nakatani, H.; Takeda, N. Acoustic source localization in anisotropic plates. Ultrasonics 2012, 52, 740–746. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer Science & Business Media: Berlin, Germany, 1995; Volume 328. [Google Scholar]
- Bai, F.; Gagar, D.; Foote, P.; Zhao, Y. Comparison of alternatives to amplitude thresholding for onset detection of acoustic emission signals. Mech. Syst. Signal Process. 2017, 84, 717–730. [Google Scholar] [CrossRef]
- Eaton, M.J.; Pullin, R.; Holford, K.M. Towards improved damage location using acoustic emission. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2141–2153. [Google Scholar] [CrossRef]
- Sedlak, P.; Hirose, Y.; Enoki, M. Acoustic emission localization in thin multi-layer plates using first-arrival determination. Mech. Syst. Signal Process. 2013, 36, 636–649. [Google Scholar] [CrossRef]
- Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Schroeder, D.J. Astronomical Optics; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Bushberg, J.T.; Boone, J.M. The Essential Physics of Medical Imaging; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2011. [Google Scholar]
- Kelly, P. Solid Mechanics Part I: An Introduction to Solid Mechanics; A Creative Commons Attributions: Mountain View, CA, USA, 2013. [Google Scholar]
- Tsvankin, I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media; Society of Exploration Geophysicists: Houston, TX, USA, 2012. [Google Scholar]
- Lee, H. Homogenization-based multiscale analysis for equivalent mechanical properties of nonwoven carbon-fiber fabric composites. J. Mech. Sci. Technol. 2019, 33, 411–4770. [Google Scholar] [CrossRef]
- Lowe, M.; Alleyne, D.; Cawley, P. Defect detection in pipes using guided waves. Ultrasonics 1998, 36, 147–154. [Google Scholar] [CrossRef]
- Falcetelli, F.; Romero, M.B.; Pant, S.; Troiani, E.; Martinez, M. Modelling of pencil-lead break acoustic emission sources using the time reversal technique. In Proceedings of the 9th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018; pp. 10–13. [Google Scholar]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]



| Sample Rate | Threshold | Digital Filter | PDT | HDT | HLT | Max Duration |
|---|---|---|---|---|---|---|
| (Microseconds) | (Milliseconds) | |||||
| 2 MSPS | 40 dB | 20 kHz–1 MHz | 60 | 150 | 10,000 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, D.G.; Lee, W.G.; Kim, J.; Kwon, H. A Point Crack Source Location Method without Velocity Information in Anisotropic Plates. Appl. Sci. 2022, 12, 11081. https://doi.org/10.3390/app122111081
Lim DG, Lee WG, Kim J, Kwon H. A Point Crack Source Location Method without Velocity Information in Anisotropic Plates. Applied Sciences. 2022; 12(21):11081. https://doi.org/10.3390/app122111081
Chicago/Turabian StyleLim, Dong Geon, Won Gi Lee, Jaeseong Kim, and Hyeuknam Kwon. 2022. "A Point Crack Source Location Method without Velocity Information in Anisotropic Plates" Applied Sciences 12, no. 21: 11081. https://doi.org/10.3390/app122111081
APA StyleLim, D. G., Lee, W. G., Kim, J., & Kwon, H. (2022). A Point Crack Source Location Method without Velocity Information in Anisotropic Plates. Applied Sciences, 12(21), 11081. https://doi.org/10.3390/app122111081






