Transfer Learning-Assisted Evolutionary Dynamic Optimisation for Dynamic Human-Robot Collaborative Disassembly Line Balancing
Abstract
1. Introduction
- (1)
- The D-HRDLB problem is introduced in this paper. This problem fully considers the characteristics of human-robot collaboration, and it can track and respond to the dynamic changes in the disassembly environment in real time. Compared with the traditional DLBPs, this problem is more applicable to the actual production environment in the remanufacturing enterprise.
- (2)
- A task-based dynamic disassembly process model is proposed. This model takes disassembly tasks as the basic elements instead of the traditional disassembly operations, and it can characterise the time-varying characteristics of the task, such as the task feasibility affected by the uncertain product quality.
- (3)
- A mathematical model for the D-HRDLB problem with three objectives is developed to optimise small-scale problem instances.
- (4)
- A feature-based transfer-assisted evolutionary dynamic optimisation algorithm is developed to obtain a dynamic Pareto-optimal solution set for the multiobjective optimisation of the D-HRDLB problem. The algorithm can transfer the knowledge of optimal solution sets between similar problems in different environments, thereby tracking and responding to environmental changes and obtaining the dynamic optimal solution set in a time-varying environment.
2. Literature Review
2.1. Disassembly Process Model
2.2. Disassembly Line Balancing under Uncertainty
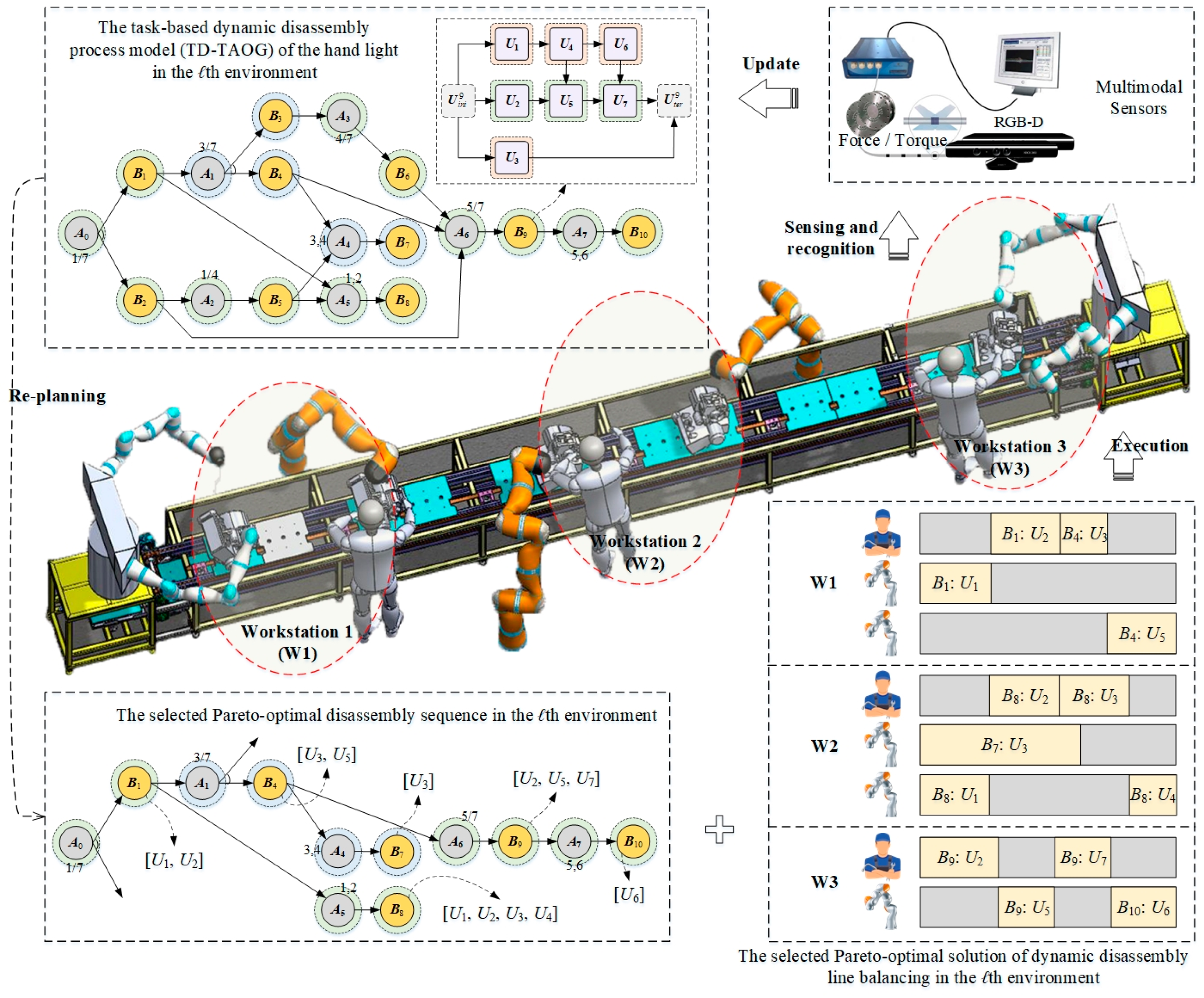
3. Task-Based Dynamic Disassembly Process Model
4. Dynamic Human-Robot Collaborative Disassembly Line Balancing
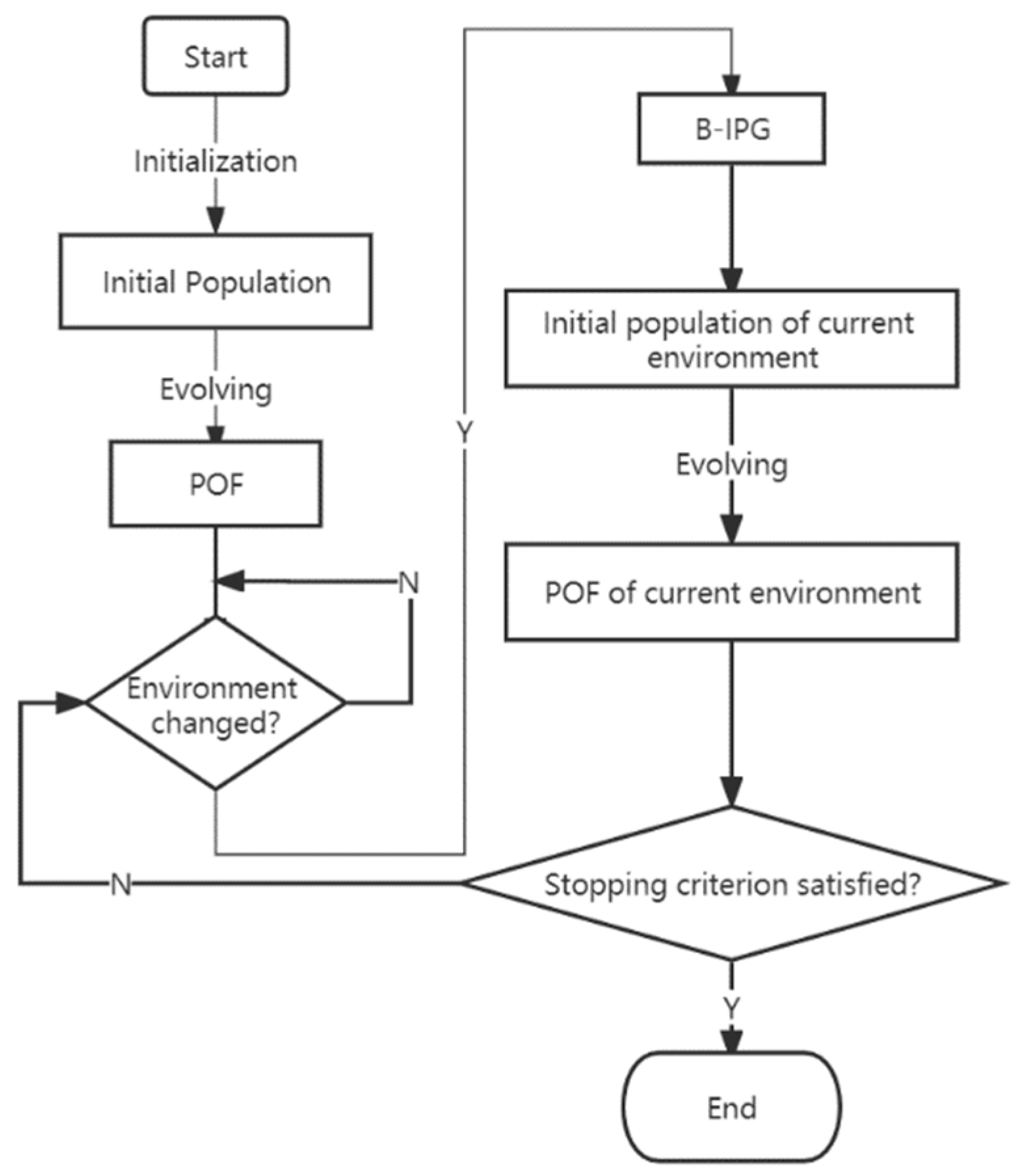
5. Transfer Learning-Assisted Dynamic Evolutionary Algorithm
| Algorithm 1 B-DMOEA |
| Input: D-HRDLB problem in the ℓth environment (FCℓ, ℓ = 0, 1 …); a MOEA; kernel function κ. Output: The POFs of the D-HRDLB problem. 1: Initialise the environment index ℓ = 0; 2: Initialise randomly a population init_pop with population size N; 3: Output POF0 ← MOEA(init_pop, FC0); 4: If (the environment has changed) Then 5: ℓ = ℓ + 1; 6: init_pop ← B-IPG(POF0, …, POFℓ−1, FC0, …, FCℓ, κ); 7: Output POFℓ ← MOEA(init_pop, FCℓ); 8: End If 9: If (the stopping criterion is satisfied) Then Stop; Else Go to Line 4; |
5.1. Transfer Learning-Assisted Initial Population Generation
| Algorithm 2 K-BDA |
| Input: Source and target sample set Ds and Dt; kernel function κ. Output: Feature transformation matrix W. 1: Obtain the class labels of the sampled data in Ds and Dt by using the hierarchical Pareto nondominated sorting method; 2: Construct K, M0, Mc, H, and I; 3: Build W by using the d smallest eigenvectors of R; 4: return W; |
| Algorithm 3 B-IPG |
| Input: The historical POFs of D-HRDLB problem POF0 …, POFℓ−1; D-HRDLB problem FC0 …, FCℓ; kernel function κ. Output: An initial population init_pop in the ℓth environment (ℓ = 1, 2 …). 1: Presearch to obtain a sample set D(ℓ) of the objective space in the ℓth environment; 2: Load the sample sets Dh = {D(0)…, D(ℓ−1)} of all historical objective spaces; 3: Select a sample set D(ℓ*) ∈ Dh with the smallest MMD from D(ℓ); 4: Ds ← D(ℓ*); Dt ← D(ℓ); Dh ← Dh∪{D(ℓ)}; 5: W ← K-BDA(Ds, Dt, κ); 6: Obtain the set of the mapped samples (M) of POFℓ* in the latent space by using W and κ; 7: For (m ∈ M) Do 8: Compute such a solution x in the objective space in the ℓth environment, which is the closest to m in the latent space; 9: init_pop ← init_pop∪{x}; 10: End For 11: Randomly pick the solutions in D(ℓ) to fill init_pop; 12: return init_pop; |
5.2. Solution for the D-HRDLB Problem
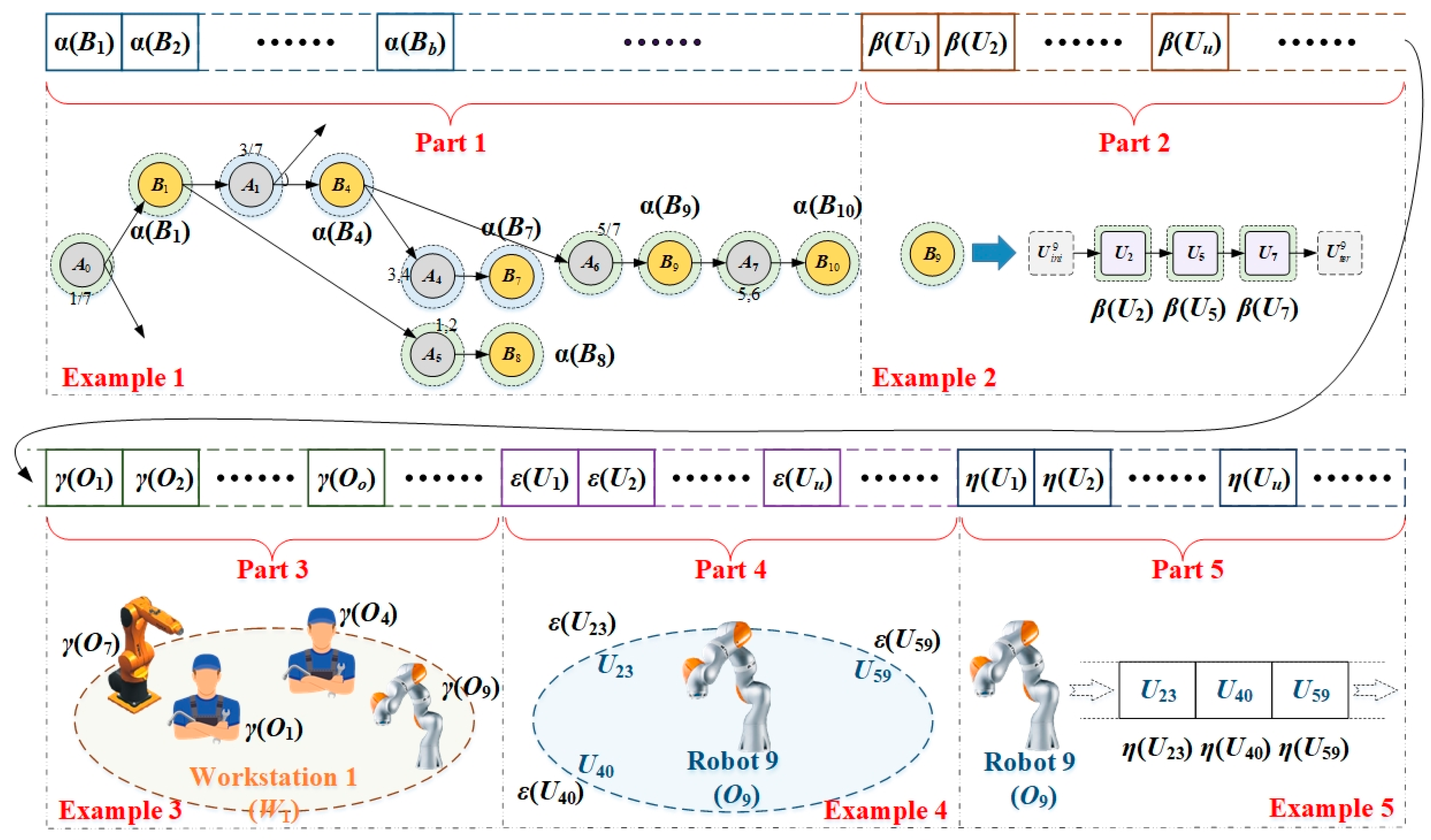
5.2.1. Solution Encoding and Decoding
5.2.2. Solution Initialisation and Variation
- (1)
- The values α of all succeeding normal nodes of each artificial node in a TD-TAOG are not equal.
- (2)
- The values β of all succeeding unit nodes in the same state of each initial node or unit node are not equal.
- (3)
- For any disassembly operation, at least one feasible task sequence can complete it in any state.
- (4)
- The range between the number of operators assigned to any workstation is [1, TO].
- (5)
- Each selected task can only be assigned to one operator in its feasible operation.
- (6)
- Operators needed to perform tasks must be assigned to workstations.
- (7)
- All selected tasks belonging to the same disassembly operation should be performed in the same workstation, and the operators performing these tasks should be assigned to the same workstation.
- (8)
- For any two selected tasks Uu and Uu′, if the disassembly operation to which Uu belongs is the predecessor of the disassembly operation to which Uu′ belongs, the operator performing Uu is either at the same workstation as the operator performing Uu’ or at the previous workstation of the workstation where the operator who performs Uu′ is located.
- (9)
- The values η of the tasks performed by the same operator without precedence constraint are not equal.
6. Computational Experiments
6.1. Experimental Settings
6.2. Experimental Results and Discussion
6.2.1. Parameter Sensitivity
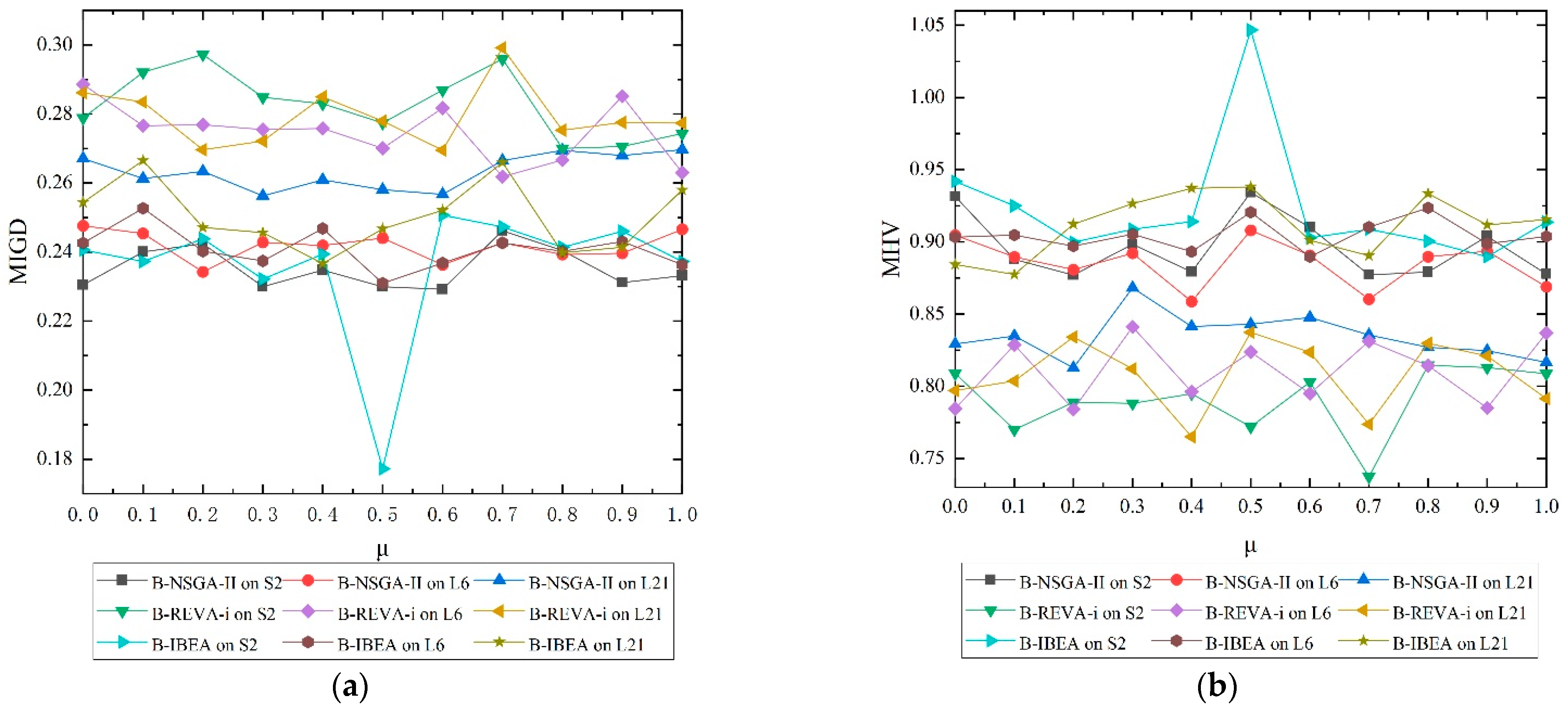
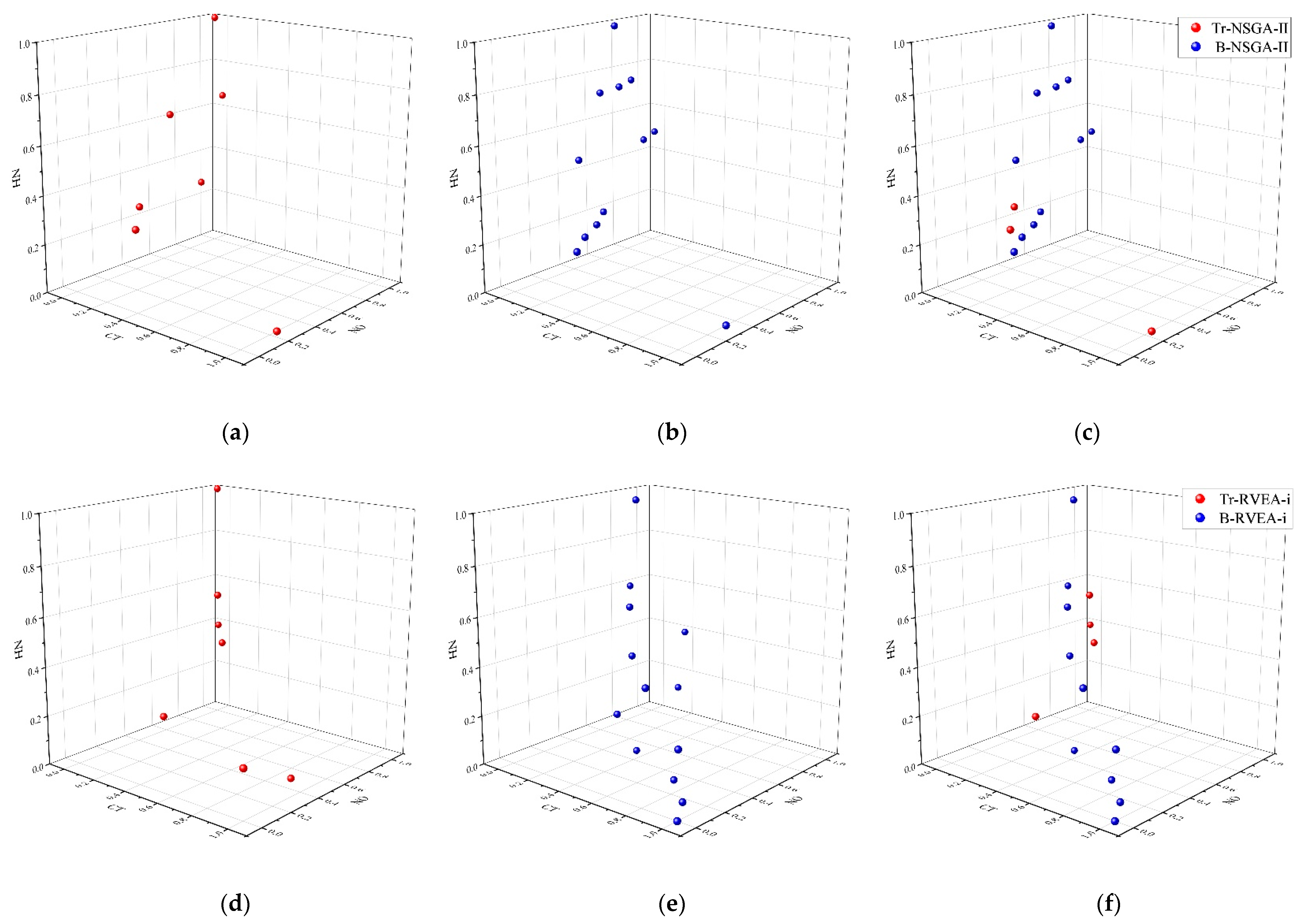
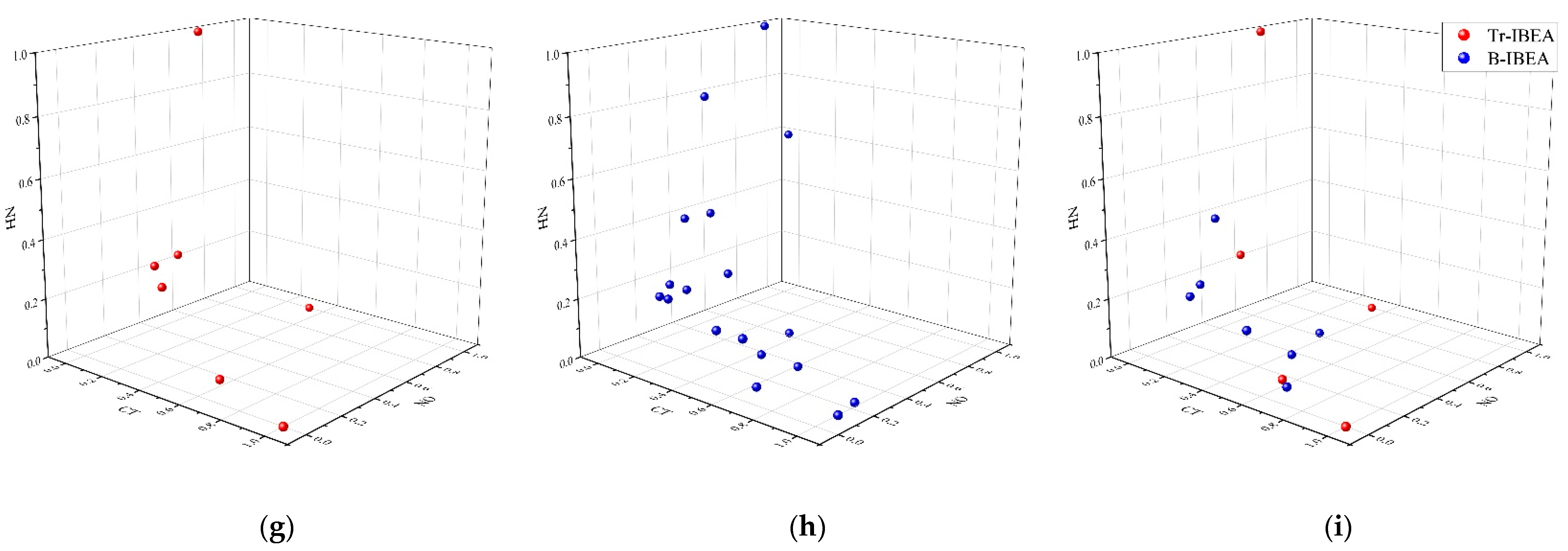
6.2.2. Performance Evaluation of B-DMOEA
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vongbunyong, S.; Kara, S.; Pagnucco, M. Basic behaviour control of the vision-based cognitive robotic disassembly automation. Assem. Autom. 2013, 33, 38–56. [Google Scholar] [CrossRef]
- Vongbunyong, S.; Pagnucco, M.; Kara, S. Vision-Based Execution Monitoring of State Transition in Disassembly Automation. Int. J. Autom. Technol. 2016, 10, 708–716. [Google Scholar] [CrossRef]
- Wang, L.; Gao, R.; Váncza, J.; Krüger, J.; Wang, X.; Makris, S.; Chryssolouris, G. Symbiotic human-robot collaborative assembly. CIRP Ann. 2019, 68, 701–726. [Google Scholar] [CrossRef]
- Cammarata, A.; Lacagnina, M.; Sinatra, R. Closed-form solutions for the inverse kinematics of the Agile Eye with constraint errors on the revolute joint axes. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 317–322. [Google Scholar]
- Fang, Y.; Liu, Q.; Li, M.; Laili, Y.; Pham, D.T. Evolutionary many-objective optimization for mixed-model disassembly line balancing with multi-robotic workstations. Eur. J. Oper. Res. 2019, 276, 160–174. [Google Scholar] [CrossRef]
- Boysen, N.; Fliedner, M.; Scholl, A. A classification of assembly line balancing problems. Eur. J. Oper. Res. 2007, 183, 674–693. [Google Scholar] [CrossRef]
- Koc, A.; Sabuncuoglu, I.; Erel, E. Two exact formulations for disassembly line balancing problems with task precedence diagram construction using an AND/OR graph. IIE Trans. 2009, 41, 866–881. [Google Scholar] [CrossRef]
- Bentaha, M.L.; Dolgui, A.; Battaïa, O.; Riggs, R.J.; Hu, J. Profit-oriented partial disassembly line design: Dealing with hazardous parts and task processing times uncertainty. Int. J. Prod. Res. 2018, 56, 7220–7242. [Google Scholar] [CrossRef]
- Özceylan, E.; Paksoy, T. Interactive fuzzy programming approaches to the strategic and tactical planning of a closed-loop supply chain under uncertainty. Int. J. Prod. Res. 2014, 52, 2363–2387. [Google Scholar] [CrossRef]
- Fang, Y.; Ming, H.; Li, M.; Liu, Q.; Pham, D.T. Multi-objective evolutionary simulated annealing optimisation for mixed-model multi-robotic disassembly line balancing with interval processing time. Int. J. Prod. Res. 2020, 58, 846–862. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades—Part A. IEEE Trans. Evol. Comput. 2021, 25, 609–629. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-Objective Evolutionary Algorithms: A Survey. ACM Comput. Surv. 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Feng, W.; Shen, Z. Balanced Distribution Adaptation for Transfer Learning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1129–1134. [Google Scholar]
- Mantripragada, R.; Whitney, D.E. The Datum Flow Chain: A systematic approach to assembly design and modeling. Res. Eng. Des. 1998, 10, 150–165. [Google Scholar] [CrossRef]
- Homem de Mello, L.S.; Sanderson, A.C. A correct and complete algorithm for the generation of mechanical assembly sequences. IEEE Trans. Robot. Autom. 1991, 7, 228–240. [Google Scholar] [CrossRef]
- Wilson, R.H.; Latombe, J.-C. Geometric reasoning about mechanical assembly. Artif. Intell. 1994, 71, 371–396. [Google Scholar] [CrossRef]
- Laili, Y.; Tao, F.; Pham, D.T.; Wang, Y.; Zhang, L. Robotic disassembly re-planning using a two-pointer detection strategy and a super-fast bees algorithm. Robot. Comput.-Integr. Manuf. 2019, 59, 130–142. [Google Scholar] [CrossRef]
- De Fazio, T.; Whitney, D. Simplified generation of all mechanical assembly sequences. IEEE J. Robot. Autom. 1987, 3, 640–658. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhang, S.Y. Product cooperative disassembly sequence planning based on branch-and-bound algorithm. Int. J. Adv. Manuf. Technol. 2010, 51, 1139–1147. [Google Scholar] [CrossRef]
- Pbioore, K.E.; Gungor, A.; Gupta, S.M. Disassembly process planning using Petri nets. In Proceedings of the 1998 IEEE International Symposium on Electronics and the Environment. ISEE–1998 (Cat. No.98CH36145), Oak Brook, IL, USA, 6 May 1998; pp. 88–93. [Google Scholar]
- Zhu, B.; Sarigecili, M.I.; Roy, U. Disassembly information model incorporating dynamic capabilities for disassembly sequence generation. Robot. Comput.-Integr. Manuf. 2013, 29, 396–409. [Google Scholar] [CrossRef]
- He, J.; Chu, F.; Dolgui, A.; Zheng, F.; Liu, M. Integrated stochastic disassembly line balancing and planning problem with machine specificity. Int. J. Prod. Res. 2022, 60, 1688–1708. [Google Scholar] [CrossRef]
- Hu, P.; Chu, F.; Fang, Y.; Wu, P. Novel distribution-free model and method for stochastic disassembly line balancing with limited distributional information. J. Comb. Optim. 2022, 43, 1423–1446. [Google Scholar] [CrossRef]
- Yin, T.; Zhang, Z.; Zhang, Y.; Wu, T.; Liang, W. Mixed-integer programming model and hybrid driving algorithm for multi-product partial disassembly line balancing problem with multi-robot workstations. Robot. Comput.-Integr. Manuf. 2022, 73, 102251. [Google Scholar] [CrossRef]
- Seidi, M.; Saghari, S. The Balancing of Disassembly Line of Automobile Engine Using Genetic Algorithm (GA) in Fuzzy Environment. Ind. Eng. Manag. Syst. 2016, 15, 364–373. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K.; Zhu, L.; Wang, Y. A Pareto improved artificial fish swarm algorithm for solving a multi-objective fuzzy disassembly line balancing problem. Expert Syst. Appl. 2017, 86, 165–176. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, C.; Zhao, F.; Triebe, M.J.; Meng, L. An MCDM-Based Multiobjective General Variable Neighborhood Search Approach for Disassembly Line Balancing Problem. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3770–3783. [Google Scholar] [CrossRef]
- He, J.; Chu, F.; Zheng, F.; Liu, M.; Chu, C. A multi-objective distribution-free model and method for stochastic disassembly line balancing problem. Int. J. Prod. Res. 2020, 58, 5721–5737. [Google Scholar] [CrossRef]
- Colledani, M.; Battaïa, O. A decision support system to manage the quality of End-of-Life products in disassembly systems. CIRP Ann. 2016, 65, 41–44. [Google Scholar] [CrossRef]
- Bentaha, M.-L.; Voisin, A.; Marangé, P. A decision tool for disassembly process planning under end-of-life product quality. Int. J. Prod. Econ. 2020, 219, 386–401. [Google Scholar] [CrossRef]
- Bentaha, M.-L.; Moalla, N.; Ouzrout, Y. A Disassembly Line Design Approach for Management of End-of-Life Product Quality. In Product Lifecycle Management Enabling Smart X; Nyffenegger, F., Ríos, J., Rivest, L., Bouras, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 594, pp. 460–472. [Google Scholar]
- Zhu, L.; Zhang, Z.; Wang, Y.; Cai, N. On the end-of-life state oriented multi-objective disassembly line balancing problem. J. Intell. Manuf. 2020, 31, 1403–1428. [Google Scholar] [CrossRef]
- Altekin, F.T.; Akkan, C. Task-failure-driven rebalancing of disassembly lines. Int. J. Prod. Res. 2012, 50, 4955–4976. [Google Scholar] [CrossRef]
- Mete, S.; Çil, Z.A.; Celik, E.; Ozceylan, E. Supply-driven rebalancing of disassembly lines: A novel mathematical model approach. J. Clean. Prod. 2019, 213, 1157–1164. [Google Scholar] [CrossRef]
- Xu, W.; Cui, J.; Liu, B.; Liu, J.; Yao, B.; Zhou, Z. Human-robot collaborative disassembly line balancing considering the safe strategy in remanufacturing. J. Clean. Prod. 2021, 324, 129158. [Google Scholar] [CrossRef]
- Gualtieri, L.; Rauch, E.; Vidoni, R. Development and validation of guidelines for safety in human-robot collaborative assembly systems. Comput. Ind. Eng. 2022, 163, 107801. [Google Scholar] [CrossRef]
- Zacharaki, N.; Dimitropoulos, N.; Makris, S. Challenges in human-robot collaborative assembly in shipbuilding and ship maintenance, repair and conversion (SMRC) industry. Procedia CIRP 2022, 106, 120–125. [Google Scholar] [CrossRef]
- Liu, B.; Xu, W.; Liu, J.; Yao, B.; Zhou, Z.; Pham, D.T. Human-Robot Collaboration for Disassembly Line Balancing Problem in Remanufacturing. In International Manufacturing Science and Engineering Conference; American Society of Mechanical Engineers: Erie, PA, USA, 2019; p. V001T02A037. [Google Scholar]
- Li, K.; Liu, Q.; Xu, W.; Liu, J.; Zhou, Z.; Feng, H. Sequence Planning Considering Human Fatigue for Human-Robot Collaboration in Disassembly. Procedia CIRP 2019, 83, 95–104. [Google Scholar] [CrossRef]
- Ouadfel, S.; Abd Elaziz, M. A multi-objective gradient optimizer approach-based weighted multi-view clustering. Eng. Appl. Artif. Intell. 2021, 106, 104480. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K.; Madadi, M.R. A new optimization algorithm to solve multi-objective problems. Sci. Rep. 2021, 11, 20326. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R. MOGBO: A new Multiobjective Gradient-Based Optimizer for real-world structural optimization problems. Knowl.-Based Syst. 2021, 218, 106856. [Google Scholar] [CrossRef]
- Fox, A.D.; Corne, D.W.; Adame, C.G.M.; Polton, J.A.; Henry, L.-A.; Roberts, J.M. An Efficient Multi-Objective Optimization Method for Use in the Design of Marine Protected Area Networks. Front. Mar. Sci. 2019, 6, 17. [Google Scholar] [CrossRef]
- Dhiman, G.; Singh, K.K.; Soni, M.; Nagar, A.; Dehghani, M.; Slowik, A.; Kaur, A.; Sharma, A.; Houssein, E.H.; Cengiz, K. MOSOA: A new multi-objective seagull optimization algorithm. Expert Syst. Appl. 2021, 167, 114150. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, M.; Zussman, E.; Caudill, R. Disassembly modeling, planning, and application. J. Manuf. Syst. 2002, 21, 200–217. [Google Scholar] [CrossRef]
- Jiang, M.; Huang, Z.; Qiu, L.; Huang, W.; Yen, G.G. Transfer Learning-Based Dynamic Multiobjective Optimization Algorithms. IEEE Trans. Evol. Comput. 2018, 22, 501–514. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, Z.; Guo, S.; Gao, X.; Tan, K.C. Individual-Based Transfer Learning for Dynamic Multiobjective Optimization. IEEE Trans. Cybern. 2021, 51, 4968–4981. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Lambert, A.J.D. Optimal disassembly of complex products. Int. J. Prod. Res. 1997, 35, 2509–2524. [Google Scholar] [CrossRef]
- Lambert, A.J.D. Optimizing disassembly processes subjected to sequence-dependent cost. Comput. Oper. Res. 2007, 34, 536–551. [Google Scholar] [CrossRef]
- Lambert, A.J.D. Linear programming in disassembly/clustering sequence generation. Comput. Ind. Eng. 1999, 36, 723–738. [Google Scholar] [CrossRef]
- Liu, Q.; Jin, Y.; Heiderich, M.; Rodemann, T.; Yu, G. An Adaptive Reference Vector-Guided Evolutionary Algorithm Using Growing Neural Gas for Many-Objective Optimization of Irregular Problems. IEEE Trans. Cybern. 2020, 1–14. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-Based Selection in Multiobjective Search. In Parallel Problem Solving from Nature—PPSN VIII; Yao, X., Burke, E.K., Lozano, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3242, pp. 832–842. [Google Scholar]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems With Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Reyes Sierra, M. A Study of the Parallelization of a Coevolutionary Multi-objective Evolutionary Algorithm. In MICAI 2004: Advances in Artificial Intelligence; Monroy, R., Arroyo-Figueroa, G., Sucar, L.E., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2972, pp. 688–697. [Google Scholar]

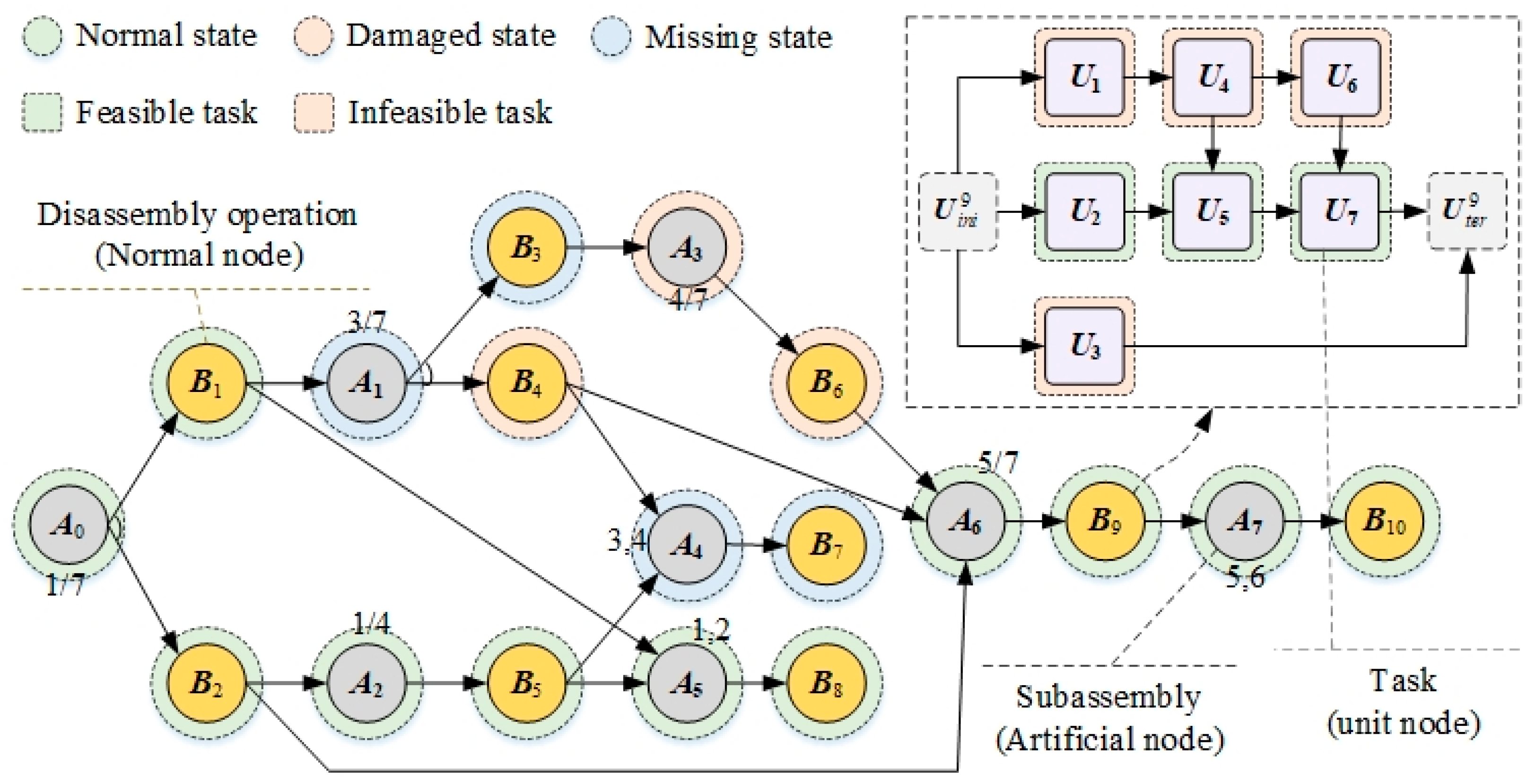
| Notation | Definition | Notation | Definition |
|---|---|---|---|
| a | Index of artificial nodes | b, b′ | Index of normal nodes |
| u, u′, υ, υ′, σ, ς | Index of unit nodes | w, w′ | Index of human-robot collaborative workstations |
| o, o′ | Index of operators | t, t′ | Index of time |
| ℓ | Index of environments |
| Notation | Definition | Notation | Definition |
|---|---|---|---|
| Set of workstations | Set of robots | ||
| Set of humans | Set of time | ||
| Set of all selected unit nodes in the ℓth environment | TO | Maximum number of operators at each workstation | |
| Set of artificial root nodes | Set of immediate successors of Aa | ||
| Set of immediate predecessors of Aa | Set of feasible immediate successors of Uu in the ℓth environment | ||
| Set of feasible immediate predecessors of Uu in the ℓth environment | Set of feasible operators for Uu in the ℓth environment | ||
| Set of immediate predecessors of Uu in | Set of all predecessors of Uu in | ||
| Set of all successors of Uu in | Ww | The wth workstation | |
| Oo | The oth operator | ψ | A big positive number |
| TCuo(ℓ) | The time required for the oth operator to process Uu in the ℓth environment | The number of unit nodes in | |
| Completion time of Uu in the ℓth environment |
| Notation | Definition | Notation | Definition |
|---|---|---|---|
| Zb | 1, if Bb is selected to perform; 0, otherwise | 1, if is selected to complete Bb; 0, otherwise | |
| Xuwot | 1, if Uu is assigned to the oth operator (e.g., a feasible robot or human for Uu) in the wth workstation and completes its processing at time t; 0, otherwise | Lwo | 1, if the oth operator is used in the wth workstation; 0, otherwise |
| Yuu’ | 1, if Uu is executed earlier than Uu’ by the same operator; 0, otherwise |
| Models | Uncertain Disassembly Operations |
|---|---|
| TD-TAOG 1 | 9 |
| TD-TAOG 2 | 20, 21, 22, 23 |
| TD-TAOG 3 | 6, 11 |
| TD-TAOG 4 | 7, 11 |
| TD-TAOG 5 | 9, 10, 11 |
| TD-TAOG 6 | 6, 7, 17, 18, 19, 30 |
| Problem | Scale | Products | Tasks | Problem | Scale | Products | Tasks |
|---|---|---|---|---|---|---|---|
| S1 | Small | 1, 2 | 241 | L6 | Large | 1, 3, 5 | 375 |
| S2 | Small | 1, 3 | 217 | L7 | Large | 1, 3, 6 | 435 |
| S3 | Small | 1, 4 | 164 | L8 | Large | 1, 4, 5 | 322 |
| S4 | Small | 1, 5 | 232 | L9 | Large | 1, 4, 6 | 382 |
| S5 | Small | 1, 6 | 292 | L10 | Large | 1, 5, 6 | 450 |
| S6 | Small | 2, 3 | 310 | L11 | Large | 2, 3, 4 | 400 |
| S7 | Small | 2, 4 | 257 | L12 | Large | 2, 3, 5 | 468 |
| S8 | Small | 2, 5 | 325 | L13 | Large | 2, 3, 6 | 528 |
| S9 | Small | 2, 6 | 385 | L14 | Large | 2, 4, 5 | 415 |
| S10 | Small | 3, 4 | 233 | L15 | Large | 2, 4, 6 | 475 |
| S11 | Small | 3, 5 | 301 | L16 | Large | 2, 5, 6 | 543 |
| S12 | Small | 3, 6 | 361 | L17 | Large | 3, 4, 5 | 391 |
| S13 | Small | 4, 5 | 248 | L18 | Large | 3, 4, 6 | 451 |
| S14 | Small | 4, 6 | 308 | L19 | Large | 3, 5, 6 | 519 |
| S15 | Small | 5, 6 | 376 | L20 | Large | 4, 5, 6 | 466 |
| L1 | Large | 1, 2, 3 | 384 | L21 | Large | 1, 2, 3, 4 | 474 |
| L2 | Large | 1, 2, 4 | 331 | L22 | Large | 1, 2, 3, 5 | 542 |
| L3 | Large | 1, 2, 5 | 399 | L23 | Large | 1, 2, 4, 5 | 489 |
| L4 | Large | 1, 2, 6 | 459 | L24 | Large | 1, 2, 4, 6 | 549 |
| L5 | Large | 1, 3, 4 | 307 |
| Problems | Tr-NSGA-II | B-NSGA-II | Tr-RVEA-i | B-RVEA-i | Tr-IBEA | B-IBEA |
|---|---|---|---|---|---|---|
| S1 | 2.4452 × 10−1 [1.4 × 10−2] | 1.8438 × 10−1[1.4 × 10−2] | 2.9134 × 10−1 [3.0 × 10−2] | 2.8346 × 10−1[3.5 × 10−2] | 2.4248 × 10−1[2.7 × 10−2] | 2.6209 × 10−1 [1.9 × 10−2] |
| S2 | 2.3724 × 10−1 [1.0 × 10−2] | 2.2995 × 10−1[1.9 × 10−2] | 3.0424 × 10−1 [3.2 × 10−2] | 2.7740 × 10−1[2.4 × 10−2] | 2.4383 × 10−1 [2.1 × 10−2] | 1.7722 × 10−1[1.1 × 10−2] |
| S3 | 2.2963 × 10−1 [2.4 × 10−2] | 2.1814 × 10−1[1.1 × 10−2] | 3.0019 × 10−1[2.7 × 10−2] | 3.0060 × 10−1 [3.3 × 10−2] | 2.3418 × 10−1 [3.8 × 10−2] | 2.2536 × 10−1[2.1 × 10−2] |
| S4 | 2.1752 × 10−1[1.1 × 10−2] | 2.1784 × 10−1 [1.3 × 10−2] | 2.7443 × 10−1[2.8 × 10−2] | 2.8932 × 10−1 [3.5 × 10−2] | 2.3339 × 10−1 [1.7 × 10−2] | 2.3077 × 10−1[1.8 × 10−2] |
| S5 | 2.3844 × 10−1 [1.1 × 10−2] | 2.3323 × 10−1[1.7 × 10−2] | 2.9138 × 10−1 [2.3 × 10−2] | 2.8994 × 10−1[1.4 × 10−2] | 2.6316 × 10−1 [3.1 × 10−2] | 2.5113 × 10−1[4.9 × 10−2] |
| S6 | 2.3010 × 10−1 [1.9 × 10−2] | 2.1976 × 10−1[1.4 × 10−2] | 2.8260 × 10−1 [3.2 × 10−2] | 2.5600 × 10−1[2.2 × 10−2] | 2.3648 × 10−1 [1.7 × 10−2] | 1.8782 × 10−1[9.1 × 10−3] |
| S7 | 2.2801 × 10−1 [2.3 × 10−2] | 2.1860 × 10−1[1.3 × 10−2] | 2.7257 × 10−1 [2.40 × 10−2] | 2.5558 × 10−1[2.3 × 10−2] | 2.3089 × 10−1 [1.4 × 10−2] | 2.1843 × 10−1[1.6 × 10−2] |
| S8 | 1.9563 × 10−1 [5.8 × 10−3] | 1.8677 × 10−1[1.8 × 10−2] | 2.5834 × 10−1 [2.2 × 10−2] | 2.5619 × 10−1[2.2 × 10−2] | 1.9090 × 10−1 [1.1 × 10−2] | 1.8166 × 10−1[7.5 × 10−3] |
| S9 | 2.3783 × 10−1 [2.2 × 10−2] | 2.2976 × 10−1[1.3 × 10−2] | 2.8184 × 10−1[2.1 × 10−2] | 2.8756 × 10−1 [1.7 × 10−2] | 2.4074 × 10−1 [1.4 × 10−2] | 2.2255 × 10−1[1.7 × 10−2] |
| S10 | 2.4093 × 10−1 [1.4 × 10−2] | 2.2855 × 10−1[1.4 × 10−2] | 2.8324 × 10−1[1.8 × 10−2] | 2.9758 × 10−1 [2.2 × 10−2] | 2.4034 × 10−1 [1.8 × 10−2] | 2.3150 × 10−1[1.1 × 10−2] |
| S11 | 2.1666 × 10−1[1.7 × 10−2] | 2.2573 × 10−1 [1.3 × 10−2] | 2.7445 × 10−1 [1.6 × 10−2] | 2.6756 × 10−1[1.6 × 10−2] | 2.2533 × 10−1 [2.1 × 10−2] | 2.2233 × 10−1[2.1 × 10−2] |
| S12 | 2.5712 × 10−1 [1.8 × 10−2] | 2.3898 × 10−1[1.5 × 10−2] | 2.8810 × 10−1[3.20 × 10−2] | 2.9191 × 10−1 [2.6 × 10−2] | 2.4306 × 10−1 [2.6 × 10−2] | 2.3886 × 10−1[1.5 × 10−2] |
| S13 | 2.2702 × 10−1 [1.8 × 10−2] | 2.1672 × 10−1[1.1 × 10−2] | 2.7059 × 10−1 [1.9 × 10−2] | 2.5719 × 10−1[1.8 × 10−2] | 2.3363 × 10−1 [1.7 × 10−2] | 2.2914 × 10−1[2.1 × 10−2] |
| S14 | 2.4190 × 10−1 [1.6 × 10−2] | 2.1207 × 10−1[1.2 × 10−2] | 2.9200 × 10−1[2.4 × 10−2] | 2.9462 × 10−1 [1.8 × 10−2] | 2.4505 × 10−1 [2.8 × 10−2] | 2.1807 × 10−1[2.4 × 10−2] |
| S15 | 2.5624 × 10−1 [2.0 × 10−2] | 2.4114 × 10−1[1.5 × 10−2] | 3.1559 × 10−1 [2.4 × 10−2] | 2.9914 × 10−1[2.7 × 10−2] | 2.3386 × 10−1 [1.9 × 10−2] | 2.3033 × 10−1[2.7 × 10−2] |
| Problems | Tr-NSGA-II | B-NSGA-II | Tr-RVEA-i | B-RVEA-i | Tr-IBEA | B-IBEA |
|---|---|---|---|---|---|---|
| L1 | 2.3935 × 10−1 [1.2 × 10−2] | 2.3063 × 10−1[6.2 × 10−3] | 2.9619 × 10−1 [3.0 × 10−2] | 2.7113 × 10−1[3.4 × 10−2] | 2.5128 × 10−1 [2.6 × 10−2] | 2.4689 × 10−1[1.9 × 10−2] |
| L2 | 2.3537 × 10−1[1.8 × 10−2] | 2.3924 × 10−1 [2.4 × 10−2] | 2.8540 × 10−1 [3.5 × 10−2] | 2.7994 × 10−1[2.5 × 10−2] | 2.5117 × 10−1 [3.8 × 10−2] | 2.3892 × 10−1[2.0 × 10−2] |
| L3 | 2.3213 × 10−1[1.8 × 10−2] | 2.4014 × 10−1 [2.4 × 10−2] | 2.8749 × 10−1 [3.5 × 10−2] | 2.7015 × 10−1[2.5 × 10−2] | 2.4205 × 10−1[3.8 × 10−2] | 2.6396 × 10−1 [2.0 × 10−2] |
| L4 | 2.4273 × 10−1 [1.3 × 10−2] | 2.3039 × 10−1[2.0 × 10−2] | 2.8185 × 10−1[2.2 × 10−2] | 2.9387 × 10−1 [4.2 × 10−2] | 2.6632 × 10−1 [2.8 × 10−2] | 2.4615 × 10−1[3.2 × 10−2] |
| L5 | 2.4366 × 10−1 [1.9 × 10−2] | 2.3203 × 10−1[1.9 × 10−2] | 2.7817 × 10−1 [2.0 × 10−2] | 2.7550 × 10−1[1.8 × 10−2] | 2.3752 × 10−1[2.8 × 10−2] | 2.4015 × 10−1 [1.5 × 10−2] |
| L6 | 2.4881 × 10−1 [2.5 × 10−2] | 2.4405 × 10−1[1.3 × 10−2] | 2.7308 × 10−1 [2.8 × 10−2] | 2.7005 × 10−1[1.3 × 10−2] | 2.4742 × 10−1 [2.0 × 10−2] | 2.3097 × 10−1[1.8 × 10−2] |
| L7 | 2.6642 × 10−1 [2.8 × 10−2] | 2.5105 × 10−1[1.6 × 10−2] | 2.8990 × 10−1 [3.2 × 10−2] | 2.8106 × 10−1[2.5 × 10−2] | 2.5246 × 10−1 [1.5 × 10−2] | 2.4094 × 10−1[1.8 × 10−2] |
| L8 | 2.3601 × 10−1 [1.9 × 10−2] | 2.2650 × 10−1[1.4 × 10−2] | 2.5279 × 10−1[2.1 × 10−2] | 2.6524 × 10−1 [3.2 × 10−2] | 2.4003 × 10−1 [2.9 × 10−2] | 2.3166 × 10−1[2.4 × 10−2] |
| L9 | 2.4765 × 10−1 [2.8 × 10−2] | 2.4503 × 10−1[3.2 × 10−2] | 2.8767 × 10−1 [3.1 × 10−2] | 2.7025 × 10−1[2.2 × 10−2] | 2.6361 × 10−1[3.2 × 10−2] | 2.6835 × 10−1 [4.9 × 10−2] |
| L10 | 2.7371 × 10−1 [2.8 × 10−2] | 2.5823 × 10−1[2.2 × 10−2] | 2.7792 × 10−1 [2.2 × 10−2] | 2.7048 × 10−1[2.5 × 10−2] | 2.6016 × 10−1 [2.2 × 10−2] | 2.5412 × 10−1[2.0 × 10−2] |
| L11 | 2.3321 × 10−1[1.9 × 10−2] | 2.4112 × 10−1 [3.2 × 10−2] | 2.6612 × 10−1[1.2 × 10−2] | 2.7659 × 10−1 [1.6 × 10−2] | 2.3368 × 10−1[3.0 × 10−2] | 2.3919 × 10−1 [3.0 × 10−2] |
| L12 | 2.4280 × 10−1 [1.8 × 10−2] | 2.3355 × 10−1[1.6 × 10−2] | 2.8230 × 10−1 [3.1 × 10−2] | 2.7953 × 10−1[1.2 × 10−2] | 2.5248 × 10−1 [1.3 × 10−2] | 2.4538 × 10−1[3.1 × 10−2] |
| L13 | 2.2932 × 10−1[2.6 × 10−2] | 2.4035 × 10−1 [1.5 × 10−2] | 2.7526 × 10−1 [3.1 × 10−2] | 2.7454 × 10−1[2.4 × 10−2] | 2.2399 × 10−1[1.9 × 10−2] | 2.2590 × 10−1 [1.4 × 10−2] |
| L14 | 2.3022 × 10−1 [2.7 × 10−2] | 2.2218 × 10−1[1.3 × 10−2] | 2.7224 × 10−1 [2.2 × 10−2] | 2.6957 × 10−1[2.2 × 10−2] | 2.4100 × 10−1 [2.9 × 10−2] | 2.2163 × 10−1[2.0 × 10−2] |
| L15 | 2.3626 × 10−1[2.0 × 10−2] | 2.4052 × 10−1 [2.9 × 10−2] | 2.9041 × 10−1 [2.4 × 10−2] | 2.8585 × 10−1[1.9 × 10−2] | 2.3801 × 10−1[1.3 × 10−2] | 2.4372 × 10−1 [2.4 × 10−2] |
| L16 | 2.4780 × 10−1 [2.7 × 10−2] | 2.3091 × 10−1[1.6 × 10−2] | 2.8216 × 10−1 [2.7 × 10−2] | 2.7861 × 10−1[1.8 × 10−2] | 2.4878 × 10−1[1.5 × 10−2] | 2.5932 × 10−1 [4.0 × 10−2] |
| L17 | 2.2096 × 10−1 [2.4 × 10−2] | 2.2051 × 10−1[1.7 × 10−2] | 2.5461 × 10−1[2.5 × 10−1] | 2.6527 × 10−1 [1.3 × 10−2] | 2.2753 × 10−1[2.3 × 10−1] | 2.3158 × 10−1 [2.3 × 10−1] |
| L18 | 2.3247 × 10−1 [2.7 × 10−2] | 2.3100 × 10−1[1.2 × 10−2] | 2.7617 × 10−1 [1.9 × 10−2] | 2.7364 × 10−1[2.3 × 10−2] | 2.4562 × 10−1 [2.2 × 10−2] | 2.2186 × 10−1[1.6 × 10−2] |
| L19 | 2.3837 × 10−1[2.4 × 10−2] | 2.4017 × 10−1 [2.1 × 10−2] | 2.8926 × 10−1[2.6 × 10−2] | 2.8989 × 10−1 [3.2 × 10−2] | 2.4037 × 10−1[2.3 × 10−2] | 2.5577 × 10−1 [3.8 × 10−2] |
| L20 | 2.5089 × 10−1 [2.0 × 10−2] | 2.4525 × 10−1[1.1 × 10−2] | 2.8957 × 10−1[2.5 × 10−2] | 2.9935 × 10−1 [2.8 × 10−2] | 2.6209 × 10−1 [4.3 × 10−2] | 2.5611 × 10−1[3.5 × 10−2] |
| L21 | 2.4511 × 10−1 [2.3 × 10−2] | 2.4499 × 10−1[2.1 × 10−2] | 2.6704 × 10−1 [1.8 × 10−2] | 2.5905 × 10−1[2.1 × 10−2] | 2.4263 × 10−1 [1.6 × 10−2] | 2.3891 × 10−1[2.0 × 10−2] |
| L22 | 2.7039 × 10−1 [2.8 × 10−2] | 2.5806 × 10−1[1.4 × 10−2] | 2.7736 × 10−1[2.3 × 10−2] | 2.7794 × 10−1 [2.0 × 10−2] | 2.5850 × 10−1 [2.0 × 10−2] | 2.4672 × 10−1[2.8 × 10−2] |
| L23 | 2.5855 × 10−1 [1.3 × 10−2] | 2.4295 × 10−1[2.0 × 10−2] | 2.7430 × 10−1 [1.9 × 10−2] | 2.6308 × 10−1[2.0 × 10−2] | 2.4715 × 10−1 [1.2 × 10−2] | 2.3413 × 10−1[1.4 × 10−2] |
| L24 | 2.4900 × 10−1 [1.5 × 10−2] | 2.4247 × 10−1[2.4 × 10−2] | 2.7597 × 10−1[1.8 × 10−2] | 2.9069 × 10−1 [1.9 × 10−2] | 2.4801 × 10−1[2.7 × 10−2] | 2.4963 × 10−1 [2.8 × 10−2] |
| Problems | Tr-NSGA-II | B-NSGA-II | Tr-RVEA-i | B-RVEA-i | Tr-IBEA | B-IBEA |
|---|---|---|---|---|---|---|
| S1 | 8.8137 × 10−1 [5.2 × 10−2] | 1.0172 × 10+00 [2.0 × 10−2] | 7.6992 × 10−1 [7.4 × 10−2] | 7.7664 × 10−1[7.3 × 10−2] | 9.1173 × 10−1[2.9 × 10−2] | 8.9558 × 10−1 [4.1 × 10−2] |
| S2 | 8.7458 × 10−1 [3.5 × 10−2] | 9.3420 × 10−1[3.0 × 10−2] | 7.5336 × 10−1 [6.7 × 10−2] | 7.7190 × 10−1[5.4 × 10−2] | 8.8512 × 10−1 [5.4 × 10−2] | 1.0468 × 10+00 [2.5 × 10−2] |
| S3 | 8.6021 × 10−1 [4.6 × 10−2] | 8.8963 × 10−1[2.4 × 10−2] | 7.7463 × 10−1 [6.0 × 10−2] | 7.8602 × 10−1[2.7 × 10−2] | 8.7914 × 10−1 [6.8 × 10−2] | 9.0052 × 10−1[4.2 × 10−2] |
| S4 | 9.0583 × 10−1[2.8 × 10−2] | 9.0107 × 10−1 [2.1 × 10−2] | 7.8558 × 10−1 [7.1 × 10−2] | 7.9593 × 10−1[4.9 × 10−2] | 9.0266 × 10−1 [3.6 × 10−2] | 9.1661 × 10−1[3.5 × 10−2] |
| S5 | 8.6359 × 10−1 [4.0 × 10−2] | 8.9617 × 10−1[3.8 × 10−2] | 7.8506 × 10−1 [4.9 × 10−2] | 8.3523 × 10−1[5.1 × 10−2] | 8.6735 × 10−1 [7.7 × 10−2] | 8.8879 × 10−1[5.5 × 10−2] |
| S6 | 8.9213 × 10−1 [4.8 × 10−2] | 9.2073 × 10−1[4.4 × 10−2] | 7.9493 × 10−1 [6.8 × 10−2] | 8.1352 × 10−1[5.9 × 10−2] | 9.5057 × 10−1 [3.9 × 10−2] | 1.0468 × 10+00 [2.5 × 10−2] |
| S7 | 8.4645 × 10−1 [6.3 × 10−2] | 8.5654 × 10−1[3.3 × 10−2] | 7.7372 × 10−1 [4.3 × 10−2] | 7.9620 × 10−1[4.9 × 10−2] | 8.5199 × 10−1 [5.6 × 10−2] | 8.5667 × 10−1[3.4 × 10−2] |
| S8 | 8.9229 × 10−1 [3.4 × 10−2] | 8.9895 × 10−1[3.3 × 10−2] | 7.7718 × 10−1 [4.6 × 10−2] | 7.8784 × 10−1[5.4 × 10−2] | 9.1101 × 10−1 [4.5 × 10−2] | 9.1815 × 10−1[2.7 × 10−2] |
| S9 | 9.0327 × 10−1 [3.8 × 10−2] | 9.6682 × 10−1[3.3 × 10−2] | 7.8916 × 10−1[4.4 × 10−2] | 7.7399 × 10−1 [5.9 × 10−2] | 9.3416 × 10−1 [3.1 × 10−2] | 9.6207 × 10−1[2.1 × 10−2] |
| S10 | 8.9399 × 10−1 [4.7 × 10−2] | 9.1839 × 10−1[3.8 × 10−2] | 8.1651 × 10−1[4.6 × 10−2] | 7.7583 × 10−1 [5.5 × 10−2] | 9.2889 × 10−1 [3.3 × 10−2] | 9.3775 × 10−1[3.2 × 10−2] |
| S11 | 9.1715 × 10−1[4.1 × 10−2] | 9.0983 × 10−1 [3.6 × 10−2] | 7.8974 × 10−1 [4.0 × 10−2] | 8.1380 × 10−1[5.4 × 10−2] | 9.3708 × 10−1 [2.6 × 10−2] | 9.4471 × 10−1[4.5 × 10−2] |
| S12 | 9.0279 × 10−1 [6.2 × 10−2] | 9.4832 × 10−1[3.9 × 10−2] | 8.0320 × 10−1 [5.4 × 10−2] | 8.0803 × 10−1[6.5 × 10−2] | 9.2235 × 10−1 [4.1 × 10−2] | 9.5697 × 10−1[4.6 × 10−2] |
| S13 | 9.0533 × 10−1 [4.4 × 10−2] | 9.2646 × 10−1[3.8 × 10−2] | 8.0787 × 10−1 [4.5 × 10−2] | 8.2723 × 10−1[2.9 × 10−2] | 8.7862 × 10−1 [4.8 × 10−2] | 9.0766 × 10−1[3.8 × 10−2] |
| S14 | 9.0159 × 10−1 [4.3 × 10−2] | 9.4480 × 10−1[4.3 × 10−2] | 7.8224 × 10−1 [5.2 × 10−2] | 7.9015 × 10−1[4.7 × 10−2] | 8.7288 × 10−1 [5.2 × 10−2] | 9.5582 × 10−1[3.3 × 10−2] |
| S15 | 9.0623 × 10−1 [5.2 × 10−2] | 9.4391 × 10−1[2.6 × 10−2] | 7.8049 × 10−1 [3.9 × 10−2] | 8.0042 × 10−1[3.8 × 10−2] | 9.4948 × 10−1 [4.4 × 10−2] | 9.6361 × 10−1[4.3 × 10−2] |
| Problems | Tr-NSGA-II | B-NSGA-II | Tr-RVEA-i | B-RVEA-i | Tr-IBEA | B-IBEA |
|---|---|---|---|---|---|---|
| L1 | 9.0036 × 10−1 [3.5 × 10−2] | 9.1018 × 10−1[2.2 × 10−2] | 7.6746 × 10−1 [6.0 × 10−2] | 8.2244 × 10−1[6.9 × 10−2] | 8.8050 × 10−1 [4.5 × 10−2] | 9.0750 × 10−1[3.7 × 10−2] |
| L2 | 9.0271 × 10−1[2.7 × 10−2] | 8.9514 × 10−1 [5.4 × 10−2] | 7.8644 × 10−1 [6.2 × 10−2] | 8.0711 × 10−1[5.6 × 10−2] | 8.8747 × 10−1 [7.9 × 10−2] | 9.0314 × 10−1[5.0 × 10−2] |
| L3 | 9.1960 × 10−1[3.4 × 10−2] | 8.7439 × 10−1 [4.2 × 10−2] | 8.1990 × 10−1[5.0 × 10−2] | 8.0815 × 10−1 [4.8 × 10−2] | 9.2754 × 10−1[4.9 × 10−2] | 8.9086 × 10−1 [5.8 × 10−2] |
| L4 | 9.0131 × 10−1 [5.1 × 10−2] | 9.0945 × 10−1[8.0 × 10−2] | 8.2961 × 10−1[2.5 × 10−2] | 8.0492 × 10−1 [6.5 × 10−2] | 8.9199 × 10−1 [5.6 × 10−2] | 8.9785 × 10−1[5.4 × 10−2] |
| L5 | 8.9207 × 10−1 [6.4 × 10−2] | 9.0436 × 10−1[5.1 × 10−2] | 8.0022 × 10−1 [6.5 × 10−2] | 8.0652 × 10−1[4.9 × 10−2] | 9.0361 × 10−1 [5.4 × 10−2] | 9.0530 × 10−1[3.5 × 10−2] |
| L6 | 8.8144 × 10−1 [6.5 × 10−2] | 9.0795 × 10−1[2.6 × 10−2] | 7.9694 × 10−1 [6.4 × 10−2] | 8.2378 × 10−1[4.0 × 10−2] | 8.9411 × 10−1 [5.1 × 10−2] | 9.2053 × 10−1[2.5 × 10−2] |
| L7 | 8.8145 × 10−1 [5.8 × 10−2] | 8.9781 × 10−1[3.4 × 10−2] | 7.8760 × 10−1 [1.1 × 10−1] | 8.2209 × 10−1[7.8 × 10−2] | 8.9717 × 10−1 [4.4 × 10−2] | 9.2491 × 10−1[3.0 × 10−2] |
| L8 | 8.5915 × 10−1 [4.1 × 10−2] | 8.8811 × 10−1[4.0 × 10−2] | 8.2064 × 10−1[5.1 × 10−2] | 8.0646 × 10−1 [5.9 × 10−2] | 8.7540 × 10−1 [5.0 × 10−2] | 8.9641 × 10−1[4.1 × 10−2] |
| L9 | 8.7632 × 10−1 [4.4 × 10−2] | 9.0017 × 10−1[1.9 × 10−2] | 7.9540 × 10−1 [7.8 × 10−2] | 8.2099 × 10−1[6.6 × 10−2] | 8.5812 × 10−1 [7.8 × 10−2] | 8.8288 × 10−1[7.0 × 10−2] |
| L10 | 8.6768 × 10−1 [5.8 × 10−2] | 8.7925 × 10−1[3.6 × 10−2] | 8.1317 × 10−1 [5.4 × 10−2] | 8.2274 × 10−1[4.6 × 10−2] | 9.0848 × 10−1 [5.8 × 10−2] | 9.0875 × 10−1[3.6 × 10−2] |
| L11 | 8.9713 × 10−1[2.5 × 10−2] | 8.8994 × 10−1 [4.9 × 10−2] | 8.2921 × 10−1[3.9 × 10−2] | 8.1423 × 10−1 [4.3 × 10−2] | 9.2999 × 10−1[5.5 × 10−2] | 9.0812 × 10−1 [6.5 × 10−2] |
| L12 | 9.0475 × 10−1 [4.7 × 10−2] | 9.0880 × 10−1[2.4 × 10−2] | 8.1330 × 10−1 [7.4 × 10−2] | 8.4537 × 10−1[3.3 × 10−2] | 8.9468 × 10−1 [4.2 × 10−2] | 9.2687 × 10−1[3.9 × 10−2] |
| L13 | 9.0550 × 10−1 [5.3 × 10−2] | 9.2308 × 10−1[3.0 × 10−2] | 8.2124 × 10−1 [7.1 × 10−2] | 8.2749 × 10−1[4.4 × 10−2] | 9.0963 × 10−1 [7.0 × 10−2] | 9.3389 × 10−1[3.5 × 10−2] |
| L14 | 8.9452 × 10−1 [3.1 × 10−2] | 9.0445 × 10−1[2.4 × 10−2] | 8.0014 × 10−1 [5.4 × 10−2] | 8.1013 × 10−1[5.8 × 10−2] | 9.0709 × 10−1 [4.3 × 10−2] | 9.4785 × 10−1[3.7 × 10−2] |
| L15 | 8.9159 × 10−1 [5.9 × 10−2] | 9.1480 × 10−1[3.9 × 10−2] | 7.8091 × 10−1 [5.0 × 10−2] | 8.1870 × 10−1[6.2 × 10−2] | 9.1601 × 10−1 [4.1 × 10−2] | 9.3450 × 10−1[3.2 × 10−2] |
| L16 | 8.8373 × 10−1 [5.3 × 10−2] | 9.2835 × 10−1[4.4 × 10−2] | 8.1387 × 10−1 [6.5 × 10−2] | 9.0778 × 10−1[4.8 × 10−2] | 9.0778 × 10−1[4.8 × 10−2] | 8.8873 × 10−1 [5.9 × 10−2] |
| L17 | 9.0005 × 10−1 [4.4 × 10−2] | 9.0100 × 10−1[4.1 × 10−2] | 8.0976 × 10−1 [4.4 × 10−2] | 8.1575 × 10−1[4.1 × 10−2] | 9.1786 × 10−1 [3.8 × 10−2] | 9.2020 × 10−1[4.0 × 10−2] |
| L18 | 9.0482 × 10−1 [4.7 × 10−2] | 9.3028 × 10−1[3.0 × 10−2] | 8.2526 × 10−1 [3.6 × 10−2] | 8.4592 × 10−1[5.4 × 10−2] | 9.3418 × 10−1 [4.2 × 10−2] | 9.5725 × 10−1[3.5 × 10−2] |
| L19 | 9.1043 × 10−1 [5.5 × 10−2] | 9.1367 × 10−1[4.0 × 10−2] | 8.0992 × 10−1 [4.9 × 10−2] | 8.2194 × 10−1[4.8 × 10−2] | 9.4361 × 10−1[3.5 × 10−2] | 8.9129 × 10−1 [5.7 × 10−2] |
| L20 | 8.8647 × 10−1 [4.4 × 10−2] | 9.0433 × 10−1[4.6 × 10−2] | 8.2320 × 10−1[4.2 × 10−2] | 8.0300 × 10−1 [5.7 × 10−2] | 8.9220 × 10−1 [8.4 × 10−2] | 9.1475 × 10−1[6.4 × 10−2] |
| L21 | 8.5629 × 10−1 [6.7 × 10−2] | 8.8725 × 10−1[5.1 × 10−2] | 8.1573 × 10−1 [8.2 × 10−2] | 8.2549 × 10−1[4.9 × 10−2] | 9.2198 × 10−1 [3.6 × 10−2] | 9.2877 × 10−1[3.8 × 10−2] |
| L22 | 8.0581 × 10−1 [6.0 × 10−2] | 8.4296 × 10−1[5.3 × 10−2] | 7.7601 × 10−1 [4.6 × 10−2] | 8.3737 × 10−1[6.5 × 10−2] | 9.1162 × 10−1 [5.7 × 10−2] | 9.3818 × 10−1[6.3 × 10−2] |
| L23 | 8.4144 × 10−1 [4.0 × 10−2] | 8.9131 × 10−1[3.9 × 10−2] | 7.8913 × 10−1 [4.4 × 10−2] | 8.1356 × 10−1[3.6 × 10−2] | 9.1316 × 10−1 [5.8 × 10−2] | 9.2955 × 10−1[4.5 × 10−2] |
| L24 | 8.6985 × 10−1 [5.5 × 10−2] | 8.8090 × 10−1[5.0 × 10−2] | 8.0074 × 10−1[5.2 × 10−2] | 7.3800 × 10−1 [5.3 × 10−2] | 8.9682 × 10−1 [5.5 × 10−2] | 8.9945 × 10−1[4.2 × 10−2] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Zhang, X.; Fang, Y.; Pham, D.T. Transfer Learning-Assisted Evolutionary Dynamic Optimisation for Dynamic Human-Robot Collaborative Disassembly Line Balancing. Appl. Sci. 2022, 12, 11008. https://doi.org/10.3390/app122111008
Jin L, Zhang X, Fang Y, Pham DT. Transfer Learning-Assisted Evolutionary Dynamic Optimisation for Dynamic Human-Robot Collaborative Disassembly Line Balancing. Applied Sciences. 2022; 12(21):11008. https://doi.org/10.3390/app122111008
Chicago/Turabian StyleJin, Liang, Xiao Zhang, Yilin Fang, and Duc Truong Pham. 2022. "Transfer Learning-Assisted Evolutionary Dynamic Optimisation for Dynamic Human-Robot Collaborative Disassembly Line Balancing" Applied Sciences 12, no. 21: 11008. https://doi.org/10.3390/app122111008
APA StyleJin, L., Zhang, X., Fang, Y., & Pham, D. T. (2022). Transfer Learning-Assisted Evolutionary Dynamic Optimisation for Dynamic Human-Robot Collaborative Disassembly Line Balancing. Applied Sciences, 12(21), 11008. https://doi.org/10.3390/app122111008







