Abstract
Coherent plane-wave compounding (CPWC) enables high-frame-rate ultrasound imaging, but the imaging quality is mainly determined by the beamforming method. Covariance-matrix-based statistical beamforming (CMSB) was previously proposed for synthetic aperture ultrasound imaging, which provides notable improvements in resolution and contrast over conventional delay-and-sum (DAS). However, the speckle quality is inadequate in the phantom experiment, and there exists a tradeoff between the contrast and speckle preservation of CMSB due to the constant diagonal reducing factor. In this paper, we applied CMSB in CPWC ultrasound imaging and propose an enhanced CMSB approach for CPWC to enhance the image quality. First, we introduced lag-one coherence (LOC) as an adaptive weighting factor for CMSB to suppress incoherent noise. Then, we propose adaptive diagonal reducing for CMSB using the coherence factor and amplitude standard deviation, with the aim to further improve the speckle quality. Finally, the combination of LOC weighting and adaptive diagonal reducing is proposed for CMSB to simultaneously improve the contrast and speckle quality. A simulation, experiments, and carotid studies were used to validate the imaging performance of the proposed methods. Results from the experiments show that LOC-weighted CMSB (LOCw-CMSB) with adaptive diagonal reducing improves the average contrast, generalized contrast-to-noise ratio (gCNR), and speckle signal-to-noise ratio (sSNR) by 59.9%, 53.6%, and 77.7%, respectively, in comparison with DMAS. The contrast and sSNR of the LOCw-CMSB with adaptive diagonal reducing were improved by 32.3% and 33.1%, respectively, compared to CMSB. In addition, LOCw-CMSB with adaptive diagonal reducing improves the contrast by 176.6% compared with SLSC in the in vivo carotid study, while it obtains a comparable gCNR. These results demonstrate that the proposed methods are effective in improving the image quality of CPWC imaging.
1. Introduction
Ultrasound plane-wave imaging (PWI) can significantly increase the frame rate and thus realize ultrafast imaging (>1000 frames per second) [1]. It has been widely studied because of the increasing need for high frame rates in medical ultrasound imaging over the past several decades [2,3]. Nevertheless, the absence of transmit focusing leads to a low signal-to-noise ratio (SNR) of echo signals and thus causes a poor image quality. To address this problem, Montaldo et al. [4] proposed coherent plane-wave compounding (CPWC) ultrasound imaging, which improves the resolution and contrast without compromising the high frame rate. It can achieve at least a similar image quality to conventional focused imaging with dynamic receive focusing [5,6,7,8], and it has been implemented in many advanced ultrasound applications, such as shear wave elastography [9], ultrafast micro-vessel imaging [10], and super-resolution ultrasound localization microscopy [11]. However, CPWC images reconstructed using data-independent delay-and-sum (DAS) suffer from a low quality due to broadened mainlobes and granting lobes [12].
In the past several decades, adaptive beamforming has been studied in depth to generate high-quality ultrasound images. Dual apodization with cross-correlation (DAX) [13] uses dual apodization, which is effective in removing clutter, to determine the contributions from the mainlobe and clutter in radio-frequency (RF) signals, and significantly improves the contrast-to-noise ratio (CNR). The minimum variance (MV) beamformer, which was first introduced by Capon [14], can significantly reduce the off-axis interference and sidelobes, and thus it can improve the resolution performance [15,16]. The eigenspace-based MV (ESBMV) [17] was then proposed by decomposing echo signals to desired signal and incoherent noise subspaces with the aim to improve the contrast of MV. In addition, short-lag spatial coherence (SLSC) imaging [18], the delay-multiply-and-sum (DMAS) beamformer [19], and the convolutional beamforming algorithm (COBA) [20] have enabled state-of-art image reconstruction with noisy data in ultrasound imaging [21,22,23,24]. Nevertheless, ESBMV, SLSC, DMAS, and COBA tend to introduce dark-region artifacts beside hyperechoic targets in ultrasound imaging [25]. Yan et al. [26] proposed regional-lag signed DMAS for CPWC imaging to overcome the tradeoff between speckle preservation and resolution.
In addition, pixel-based adaptive weighting, which enables an enhanced image quality, has also been investigated. The coherence-derived coherence factor (CF) [27] estimates the ratio of coherent energy to incoherent energy and directly weights the DAS beamformed data to reduce sidelobes. It can reduce the effects of phase aberration and reverberation and thus reduce artifacts from weakly coherent off-axis scatter and the granting lobe. However, a major problem of CF is the over-suppression of speckle signals, which leads to degraded speckle statistics with dark-region artifacts and a low speckle intensity. To this end, some promising solutions to overcome this problem have been developed, including generalized CF (GCF) using low-frequency energy [28], scaled CF (scCF) depending on the SNR [29], and spatio-temporally smoothed CF (StS-CF) [30]. These methods can preserve speckle signals to some extent, but possibly at the expense of the resolution advantage of CF. Long et al. [31] proposed lag-one coherence adaptive normalization (LoSCAN), which is derived from lag-one coherence (LOC) [32] and CF, to suppress incoherent clutter, leading to an improved contrast with no dark-region artifacts.
Recently, the amplitude standard deviation (ASD) of echo signals, which can differentiate clutter, has also been studied to suppress clutter. The signal mean-to-standard-deviation factor (SMSF) [33] estimates the ratio of mean and ASD to significantly improve the resolution and contrast. The signal-to-noise-ratio (SNR) factor [34] was then proposed using the variance, which is the power of ASD, to generate an ultrasound image with an improved resolution and contrast. The dynamic CF (DCF) based on the ASD [35] has been proposed for CPWC imaging, showing overall improvements in image quality over CF. The delay-multiply-and-standard-deviation (DMASD) factor based on the delay and standard deviation (DASD) beamforming [36], which uses the ASD of echo signals, was introduced to enhance the image contrast [37]. In addition, the ASD has also been studied to reduce the dark-region artifacts introduced by ESBMV in CPWC imaging [38].
Our previous work proposed a novel adaptive beamformer named the covariance-matrix statistical beamforming (CMSB) [39], which estimates adaptive weights based on the ratio between the mean and ASD [40] of a modified covariance matrix. It has been demonstrated that CMSB obtains an improved image resolution and contrast, as well as a maintained speckle quality. However, CMSB obtains a good speckle quality at the expense of contrast degradation. One possibility to improve the contrast is to apply an adaptive weighting technique. Another possibility to further improve the speckle quality of CMSB is to adaptively determine the diagonal reducing factor for different imaging targets.
Hereto, we propose enhanced CMSB methods based on LOC weighting and adaptive diagonal reducing in this study to enhance the resolution and contrast of CPWC imaging quality, as well as lesion detectability. To the best of our knowledge, LOC has not been studied as adaptive weighting for ultrasound beamforming. The goal of this paper is to enhance the noise reduction of CMSB by adaptive weighting and overcome the tradeoff between speckle statistics and contrast by adaptive diagonal reducing. The proposed methods were validated with simulation, phantom experiments, and in vivo experiments in CPWC ultrasound imaging, and compared with DAS, DMAS, SLSC, and CMSB. We also considered the effects of the channel noise level, kernel size, and number of transmit angles on the imaging performance when applying the proposed methods.
This paper is organized as follows. In Section 2, CPWC imaging, DMAS, SLSC, CMSB, and the proposed methods are introduced. Experimental setups as well as evaluating metrics are presented in Section 3. Section 4 presents the results, and Section 5 discusses the imaging performance of the proposed methods. A conclusion is drawn in Section 6.
2. Methods
2.1. Coherent Plane-Wave Compounding (CPWC)
In CPWC imaging, steered plane-waves at a number of angles are transmitted to improve SNR. Consider an M-elements linear array emitting plane waves with N different steering angles, and the sound of speed is c. When the n-th plane-wave steered at the angle of is emitted, the time-of-flight (TOF) consists of the time taken to propagate to an imaging point (i.e., image pixel) and the time taken to propagate back to the receive element located at . The TOF is given by:
The beamformed output for imaging point p at angle obtained by DAS is given as
where represents the signal received by the mth element located at , and = [, , …, ] represents the receive apodization window.
By compounding the beamformed outputs along N directions, the CPWC output obtained by DAS is expressed as the following:
To reconstruct CPWC images, ultrasound beamformers can be involved across different transmit angles, and it can also be involved in the receiving aperture through each transmit event. In this study, the proposed methods were implemented across different transmit apertures after the receive aperture data were synthesized using DAS.
2.2. Delay Multiply and Sum (DMAS)
The DMAS [19], which is a nonlinear beamforming method, can significantly improve the resolution and contrast over DAS. In DMAS, the signals are combinatorially coupled and multiplied before summing across the aperture. The unfiltered DMAS output is calculated as
where = . A bandpass filter centered at with a bandwidth of is then used to pass the second harmonic component and attenuate other components to generate the DMAS output, where is the center frequency of the emitted signals.
2.3. Short-Lag Spatial Coherence (SLSC)
The SLSC estimates spatial correlations of echo signals, and sums the spatial correlations estimated at various lags. Different from brightness mode, SLSC directly displays the image in [0, 1] without log-compression. The SLSC has demonstrated superior lesion detectability. The normalized spatial coherence calculated at lag m is
where is the kernel size.
By summing the normalized spatial coherence estimated at lags (i.e., 1,2, …, ) using (5), the SLSC output is obtained as
2.4. Covariance Matrix-Based Statistical Beamforming (CMSB)
The CMSB [39] is implemented by estimating adaptive weights using the ratio between the mean and standard deviation of a covariance matrix through rotary averaging and diagonal reducing. The normalized reciprocals of ASD from all imaging points are used to dynamically select the subarray length for each imaging point.
The normalized reciprocals of the ASD from all imaging points are , where is the ASD from all imaging points, and is the normalization operation. The ASD at imaging point p is , where .
The selected subarray length for imaging point p is
where is the rounding operation and is the maximum subarray length. When , the dynamic subarray length is set to 2.
The covariance matrix is then estimated based on as
where .
The rotary averaging and diagonal reducing are then applied on using the following (9) and (10), respectively, to form a modified covariance matrix,
where and are the reversal matrix and identity matrix of size , respectively, and the constant is the user-defined diagonal reducing factor.
Then, the weight vector of CMSB is obtained by calculating the mean-to-standard-deviation ratio (MSR) of each row vector , where is the row index. The adaptive weight is calculated as
The output of CMSB estimated with the weight vector is finally obtained as
CMSB has demonstrated a notably improved resolution and contrast over DAS. Additionally, CMSB can enhance the border visualization in rat mammary tumor imaging and human heart imaging with reduced off-axis clutter and smoothed tissue texture [39].
2.5. Proposed Methods
2.5.1. Lag-One Coherence Weighting for CMSB
For ultrasound beamforming methods, the speckle quality (i.e., smoothness and intensity) is an important characteristic of reconstructed images. CMSB obtains a good speckle quality when is large, but the contrast decreases notably. Nevertheless, pixel-based adaptive weighting (e.g., CF, GCF, and SLSC) can effectively improve the contrast, which inevitably causes degradation in speckle statistics in CPWC imaging [35,41].
The speckle texture generated by SLSC tends to be smoothed when the short-lag value is small [18]. As the normalized spatial coherence with a lag of one (i.e., single-lag spatial coherence in SLSC), lag-one coherence (LOC) estimates the correlation between backscattered echoes from pairs of neighboring array elements [32]. It has been studied to adaptively select frequency in real-time [42], as a metric to differentiate solid and fluid-filled mass [32], and to quantify the impact of breast density [43]. However, to the best of our knowledge, LOC has not been studied as adaptive weighting for ultrasound beamforming. Thus, we hypothesize that LOC weighting can enhance the contrast performance of CMSB while preserving the speckle statistics.
The LOC with a kernel size of is estimated as
Taking LOC as an adaptive weighting for CMSB, the LOC-weighted CMSB (LOCw-CMSB) output is obtained as
The LOCw-CMSB has the potential to enhance the noise reduction of CMSB while retaining speckle statistics to some extent. Note that the speckle quality of LOCw-CMSB will improve with the increasing kernel size, while the contrast might decrease.
2.5.2. Adaptive Diagonal Reducing for CMSB
The user-defined constant diagonal reducing factor in CMSB has an influence on the imaging performance. The contrast of CMSB improves with the decreasing while the speckle quality degrades [39]. The speckle quality of CMSB is insufficient in phantom experiments. In other words, a tradeoff exists between contrast and lesion detectability in CMSB due to the constant . Therefore, an accurate selection of for different imaging targets has the potential to overcome this problem. Here, we introduce adaptively choosing for diagonal reducing in CMSB by combining CF and the normalized reciprocal of ASD to maintain a balanced imaging performance with an improved speckle quality.
As an adaptive weighting, CF combined with synthetic aperture focusing has been applied in intravascular ultrasound imaging, showing an improved image quality [44,45]. The CF is calculated as the ratio of coherent to incoherent energy of echo signals,
When signals are perfectly coherent, the CF value equals 1, while, in the case of incoherent noise, it falls to 0. CF has the ability to reduce clutter and noise effectively; however, it often degrades the speckle statistics [25].
Nevertheless, the speckle statistics of CF can be improved by adjustment using the normalized reciprocal of ASD (i.e., ). The adaptive diagonal reducing factor selected using the aperture coherence (i.e., CF(p) and ) for imaging point p is defined as
where is the maximum diagonal reducing factor. According to (16), the value of is in the range from 0 to . The diagonal reducing factor selected for coherent signals is slightly larger than that for speckle signals, which is much larger than that for incoherent noise.
According to (10), the covariance matrix through the pixel-based adaptive diagonal reducing is obtained as
Then, the weight of CMSB with adaptive diagonal reducing is calculated according to (11) as
where is the row index.
The weights estimated from incoherent noise are always very low under different [39]. In addition, the weights estimated from speckle signals and coherent signals are more close due to the reason that the for speckle signals is slightly smaller than that for coherent signals. As a result, this will lead to an enhanced speckle intensity and smoothness in the CMSB image.
The output of CMSB with adaptive diagonal reducing factor , referred to as CMSB ( = ), is obtained as
where , and .
2.5.3. LOC-Weighted CMSB with Adaptive Diagonal Reducing
As mentioned above, LOC weighting and adaptive diagonal reducing have the potential to contribute to improvements in the contrast and speckle quality, respectively. We exploit the benefits of combining LOC weighting and adaptive diagonal reducing for CMSB, and propose LOC-weighted CMSB with adaptive diagonal reducing, referred to as LOCw-CMSB ( = ).
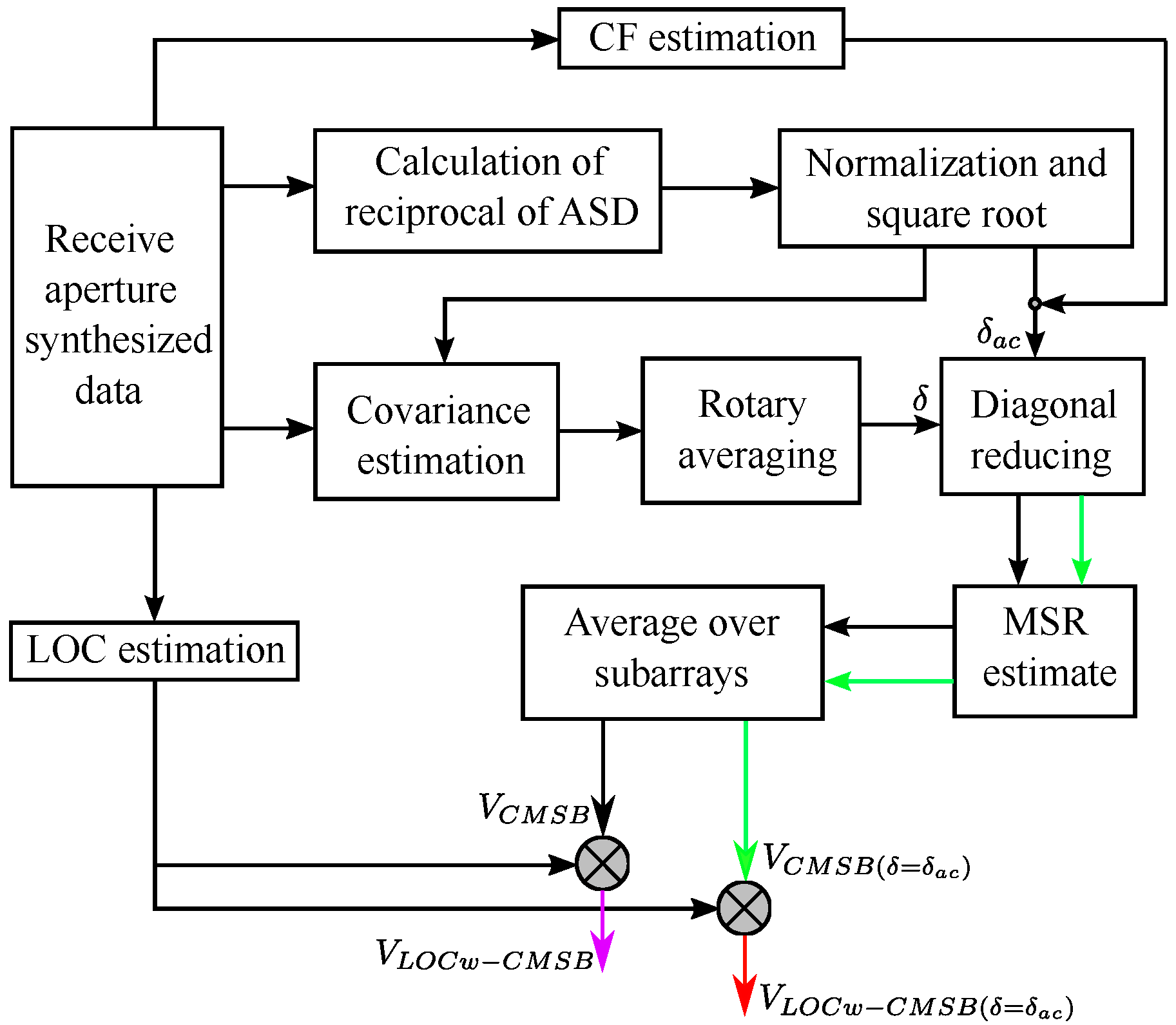
By combining LOC weighting and adaptive diagonal reducing, the image quality obtained by CMSB will be enhanced thoroughly. The workflow for CMSB-based methods is shown in Figure 1. First, the receive aperture synthesized data are used to calculate the CF, LOC, and the normalized reciprocal of ASD. Second, the data are used to estimate the covariance matrix, with the dynamic subarray length determined by the normalized reciprocal of ASD using (8). Third, the covariance matrix is rotary averaged and then diagonally reduced with adaptive diagonal reducing factor . Finally, the CMSB with adaptive diagonal reducing is obtained through MSR estimation and subarray averaging using (19), and the LOC-weighted CMSB with adaptive diagonal reducing is obtained using (14).
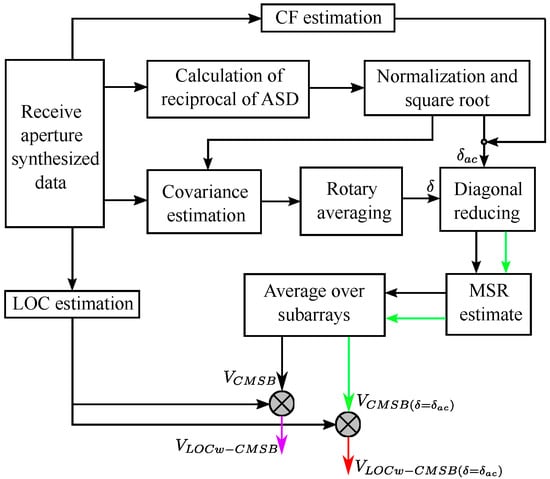
Figure 1.
Workflow for CMSB-based beamformers, including CMSB, and the proposed LOCw-CMSB, CMSB ( = ), and LOCw-CMSB ( = ).
3. Simulation and Experimental Setups
3.1. Simulated Tissue-Mimicking Phantom Study
We first used Field II [46,47] to generate the simulation data. The simulated phantom consists of a cyst target with a radius of 3.5 mm, and twelve point targets, including two laterally and two axially closely spaced points. The scatters used to simulate the phantom were randomly distributed and the amplitude was random. The density was 20 scatters in a resolution cell. The linear transducer had 128 elements and the pitch was 0.30 mm. The fractional bandwidth of the transducer was 67%, and the transmitted pulse had 2.5 cycles. The center frequency was 5.208 MHz and the sampling frequency was 20.832 MHz. In the simulation, 75 plane-waves were transmitted at angles of − to with an angle spacing of . The parameters were set the same as those used in experiments.
3.2. Experimental Phantom and In Vivo Carotid Studies
In addition to simulation, we tested our methods on the publicity available CPWC data [48]. The experimental datasets were collected using a Verasonics Vantage 256 research scanner and a L11-4v linear array probe (Verasonics Inc., Redmond, WA, USA). The specific parameters for the scanner and the acquisition system are listed in Table 1.

Table 1.
Parameter settings of acquisition system for simulation and experiment.
The proposed methods were compared with DAS, DMAS, SLSC, and CMSB. A tapered 25% Tukey window with an F-number of 1.75 was implemented in the receive aperture in DAS method. The was set to 23 in SLSC to obtain a high contrast performance, and the kernel size was set to . In simulation and phantom experimental studies, the was set to 1.3 in LOCw-CMSB, and was set to 1.3 in CMSB ( = ) and LOCw-CMSB ( = ). In the in vivo carotid study, was set to 0.5 in LOCw-CMSB, and was set to 0.5 in CMSB ( = ) and LOCw-CMSB ( = ). Additionally, the maximum subarray length was set to in all CMSB-based methods to achieve a balanced performance. The kernel size in LOC was set to to keep a good speckle, where is the wave length. We added a Gaussian distributed noise with an SNR of 20 dB to the in phase/quadrature (IQ) channel data prior to beamforming. All reconstructed ultrasound images are shown in a 60 dB dynamic range, except for SLSC images, which are displayed in [0, 1].
3.3. Image Quality Metrics
The lateral resolution was measured by the lateral full-width at half-maximum (FWHM, dB beam width) of a point target. The contrast ratio (CR) was calculated as
where and are mean values of pixel values before log-compression in selected cyst and background speckle regions, respectively.
The generalized contrast-to-noise ratio (gCNR) [49], which can evaluate the lesion detectability, is defined as
where and are the probability density functions of pixel intensity inside cyst and speckle regions, respectively.
The speckle signal-to-noise ratio (sSNR), which can evaluate the speckle quality, is estimated as
where is the standard deviation of pixel values in the selected background speckle region.
4. Results
4.1. Simulation
Figure 2 displays simulated images obtained by different methods. Regions indicated by the circle and box in Figure 2a were selected to calculate image quality metrics, the regions indicated by the cyan dashed lines were used to plot the lateral variations, and the point targets indicated by two cyan boxes were used to calculate FWHM values. The DMAS image shows an improved contrast over the DAS image; however, the background speckle brightness decreases. It can be seen from the SLSC image that the background speckle texture and the lesion detectability are enhanced; however, the point resolution is poor, and dark-region artifacts appears beside point targets. CMSB-based images show narrowed point targets compared with DMAS images. The CMSB ( = ) image shows a brighter speckle compared with the CMSB image. LOCw-CMSB reduces noise in the cyst target significantly in comparison with CMSB. In comparison with CMSB images, the LOCw-CMSB ( = ) image shows a smoothed speckle texture and higher brightness simultaneously. Note that the two axially closely spaced point targets cannot be distinguished by CMSB-based methods.

Figure 2.
Simulated images reconstructed by (a) DAS, (b) DMAS, (c) SLSC, (d) CMSB ( = 0.7), (e) CMSB ( = 1.3), (f) LOCw-CMSB, (g) CMSB ( = ), and (h) LOCw-CMSB ( = ).
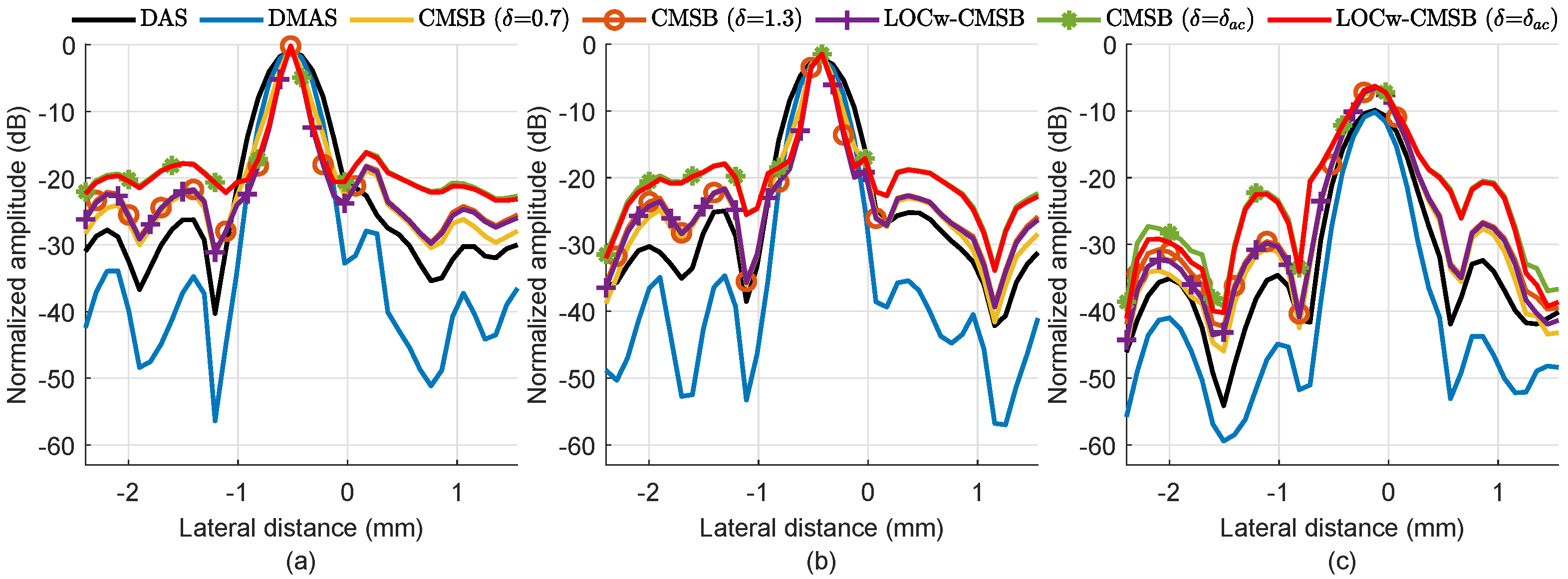
Figure 3 plots the lateral variations through point targets indicated by cyan boxes and the cyst target indicted by the cyan dashed line. As can be seen, CMSB-based methods all obtain a narrowed mainlobe compared with DAS and DMAS as seen from Figure 3a. In addition, CMSB methods can distinguish the two closely spaced point targets as seen from Figure 3b. From Figure 3c, we can see that CMSB-based methods, as well as DMAS, obtain the lowest noise level in the cyst target. Additionally, LOCw-CMSB and LOCw-CMSB ( = ) obtain the best cyst edge resolution.
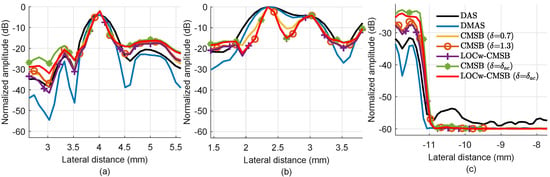
Figure 3.
Lateral variations through point targets at the depth of (a) 23.1 mm and (b) 27 mm, and (c) the cyst target in simulated tissue-mimicking images.
Table 2 lists image quality metrics of simulated tissue-mimicking images. Note that the resolution of the SLSC is not calculated because the image is not log-compressed. Compared with DAS, SLSC obtains a degradation of 9.1 dB in contrast, but it obtains the highest gCNR and sSNR. CMSB ( = 1.3) improves the resolution by 52.7% and 40.9% over DAS and DMAS, respectively. The proposed methods maintain the resolution performance of CMSB ( = 1.3). In addition, LOCw-CMSB improves the CR by 5.8% and 14.7% compared to CMSB ( = 0.7) and CMSB ( = 1.3), respectively, whereas the gCNR and sSNR are slightly higher than that of CMSB ( = 0.7). The gCNR and sSNR obtained by CMSB ( = ) are 4.3% and 40.6% larger than that of CMSB ( = 1.3), whereas CR decreases by 2.0%. Furthermore, LOCw-CMSB ( = ) leads to improvements of 12.4%, 4.3%, and 36.6% in CR, gCNR, and sSNR over CMSB ( = 1.3).

Table 2.
Image quality metrics in terms of full-width and half-maximum (FWHM), contrast ratio (CR), generalized contrast-to-noise ratio (gCNR), and speckle signal-to-noise ratio (sSNR) of simulated tissue-mimicking images formed using different methods.
4.2. Experimental Point Phantom
Figure 4 shows the experimental point phantom images. The three point targets indicated by cyan boxes in Figure 4a were used to calculate the FWHM. We can see that DMAS slightly narrows the point width compared to DAS and generates a darkened speckle pattern. The SLSC image shows a poor resolution and dark-region artifacts beside the point targets. CMSB-based images show visually narrowed points in comparison with the DAS image. The LOCw-CMSB ( = ) image shows a smoothed speckle pattern and improved overall speckle brightness compared with CMSB images. It is noted that the artifacts under the point at a 9.6 mm depth are amplified in LOCw-CMSB and LOCw-CMSB ( = ) images.

Figure 4.
Experimental point images reconstructed by (a) DAS, (b) DMAS, (c) SLSC, (d) CMSB ( = 0.7), (e) CMSB ( = 1.3), (f) LOCw-CMSB, (g) CMSB ( = ), and (h) LOCw-CMSB ( = ).
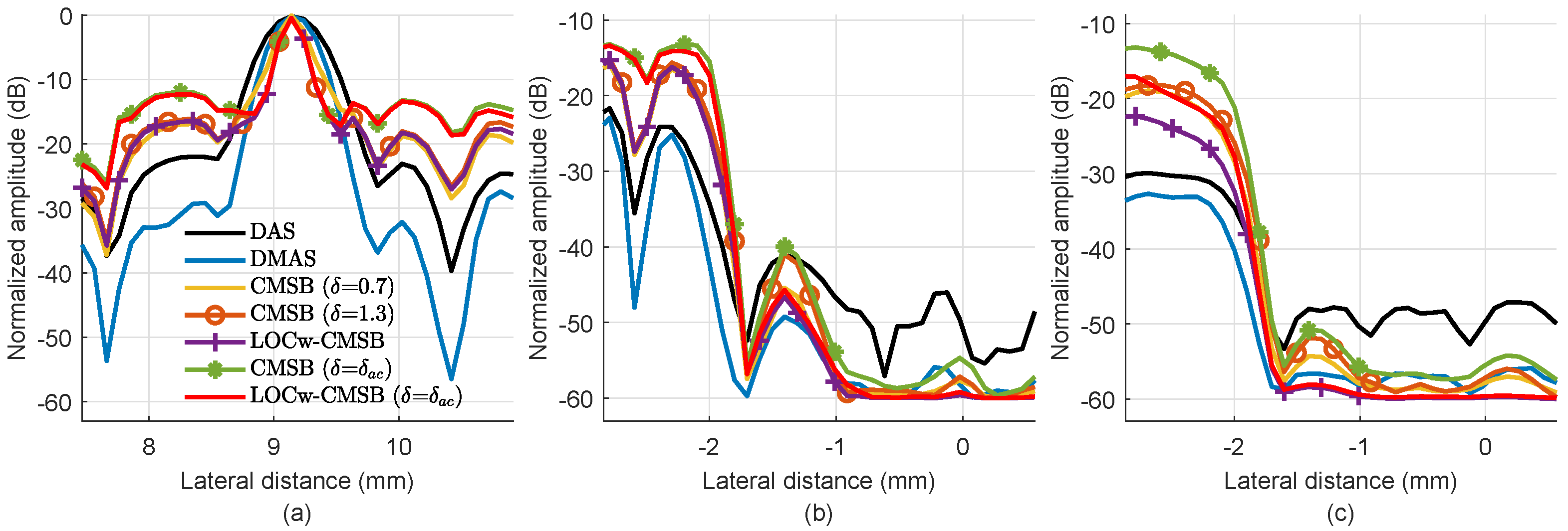
Figure 5 plots the lateral variations through three point targets at depths of 9.6 mm, 28.1 mm, and 47 mm indicated by cyan boxes, and Table 3 lists FWHM values at different depths. Note that the resolution of the SLSC is not calculated because the image is not log-compressed. We can see that DMAS narrows the mainlobe over DAS at different depths, resulting in an average resolution improvement of 20.2%. CMSB methods obtain an improved resolution over DMAS at depths of 9.6 mm and 28.1 mm, but a worse resolution at the depth of 47 mm. Specifically, CMSB ( = 0.7) and CMSB ( = 1.3) have average resolution improvements of 16.4% and 26.9% over DMAS, respectively. In addition, LOCw-CMSB preserves the resolution performance of CMSB at different depths. Although CMSB ( = ) and LOCw-CMSB ( = ) preserve the resolution of CMSB ( = 1.3) at depths of 9.6 mm and 28.1 mm, the obtained FWHM at the depth of 47 mm decreases by 14.3%.
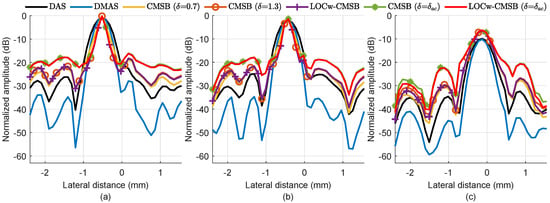
Figure 5.
Lateral variations through three points at the depth of (a) 9.6 mm, (b) 28.1 mm, and (c) 47 mm in the experimental point images.

Table 3.
Lateral FWHM at three different depths in the experimental point images.
4.3. Experimental Cyst Phantom
Figure 6 shows the experimental cyst images. Regions indicated by two circles and boxes were selected to calculate the image quality metrics, the regions indicated by the cyan dashed lines were used to plot the lateral variations, and the point target indicated by the cyan box was used to calculate the FWHM. DMAS obtains an improved contrast over DAS, but degrades the background intensity significantly. The SLSC image shows enhanced lesion detection, but the point resolution is poor and some dark-region artifacts appears beside the point. CMSB images show an improved contrast and improved background intensity. In addition, LOCw-CMSB suppresses noises in the cyst at 42.9 mm depth compared with CMSB ( = 1.3), and also removes noise in the cyst at 15 mm depth compared with CMSB, with equal to 0.7 and 1.3. This indicates that LOC weighting can effectively improve the contrast performance of CMSB. In addition, CMSB ( = ) improves the speckle smoothness and intensity over CMSB ( = 1.3).
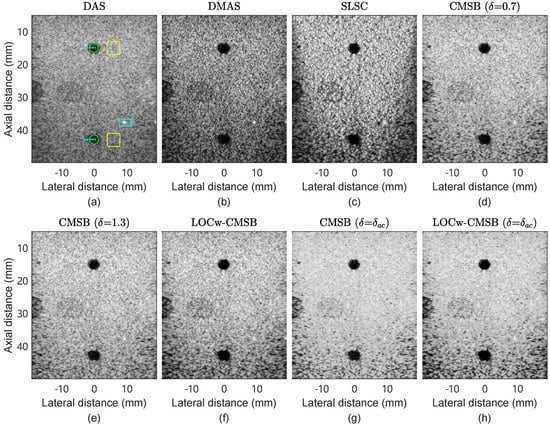
Figure 6.
Experimental cyst phantom images reconstructed by (a) DAS, (b) DMAS, (c) SLSC, (d) CMSB ( = 0.7), (e) CMSB ( = 1.3), (f) LOCw-CMSB, (g) CMSB ( = ), and (h) LOCw-CMSB ( = ).
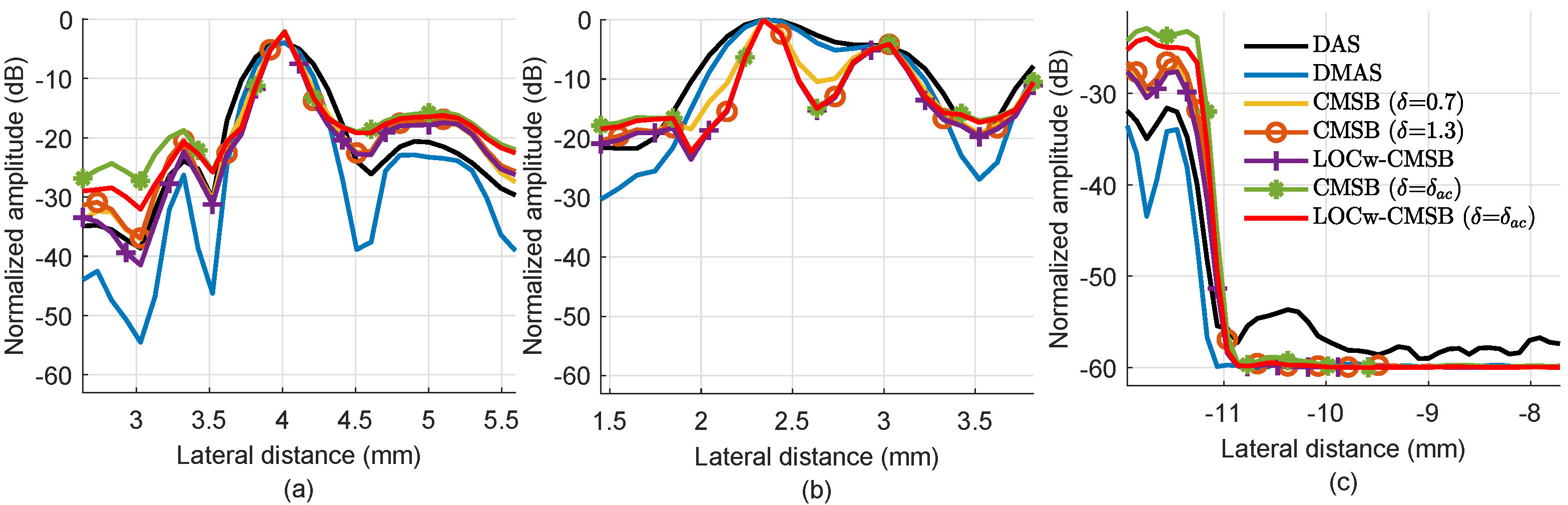
Figure 7 plots the lateral variations through the point target indicated by the cyan box, and the two cyst targets are indicated by cyan dashed lines in the experimental cyst images. As can be seen, CMSB ( = 0.7) obtains a narrower mainlobe compared with DMAS, and other CMSB-based methods all obtain the narrowest mainlobe. This indicates the maintained resolution performance of enhanced CMSB methods. In addition, LOCw-CMSB and LOCw-CMSB ( = ) obtain the lowest noise level in cyst targets, which is lower than that of DMAS, and have the best edge resolution according to Figure 7b,c.
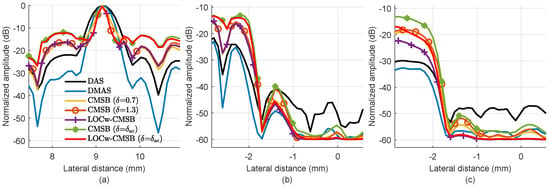
Figure 7.
Lateral variations through (a) the point target at (x,z) = (9.1 mm, 37.6 mm), and (b,c) two anechoic cysts in experimental cyst images.
Table 4 lists image quality metrics of experimental cyst phantom images. The point targets at (x,z) = (8 mm, 38 mm) were used to calculate FWHM. Note that the resolution of the SLSC is not calculated because the image is not log-compressed. SLSC obtains a lower contrast at a shallow depth but a higher contrast at a large depth compared with DAS, and SLSC obtains the highest gCNR and sSNR. The proposed methods preserve the resolution of CMSB ( = 1.3), which is a % improvement compared with DMAS. According to Table 4, CMSB obtains an improved CR, gCNR, and sSNR over DAS and DMAS. LOCw-CMSB improves the CR by 27.7% and 34.4% compared with CMSB ( = 0.7) and CMSB ( = 1.3), respectively. In addition, the gCNR and sSNR of LOCw-CMSB are almost equal to that of CMSB ( = 1.3) at the shallower depth, whereas they are 0.07 and 0.17 lower than that of ( = 1.3) in the deep region. CMSB ( = ) obtains improvements of 2.1% and 42.7% in gCNR and sSNR over that of CMSB ( = 1.3), while the CR decreases by 2.5%. In addition, LOCw-CMSB ( = ) leads to improvements of 32.3%, 0.5%, and 33.1% in CR, gCNR, and sSNR over CMSB ( = 1.3).

Table 4.
Image metrics of experimental cyst images.
4.4. In Vivo Carotid
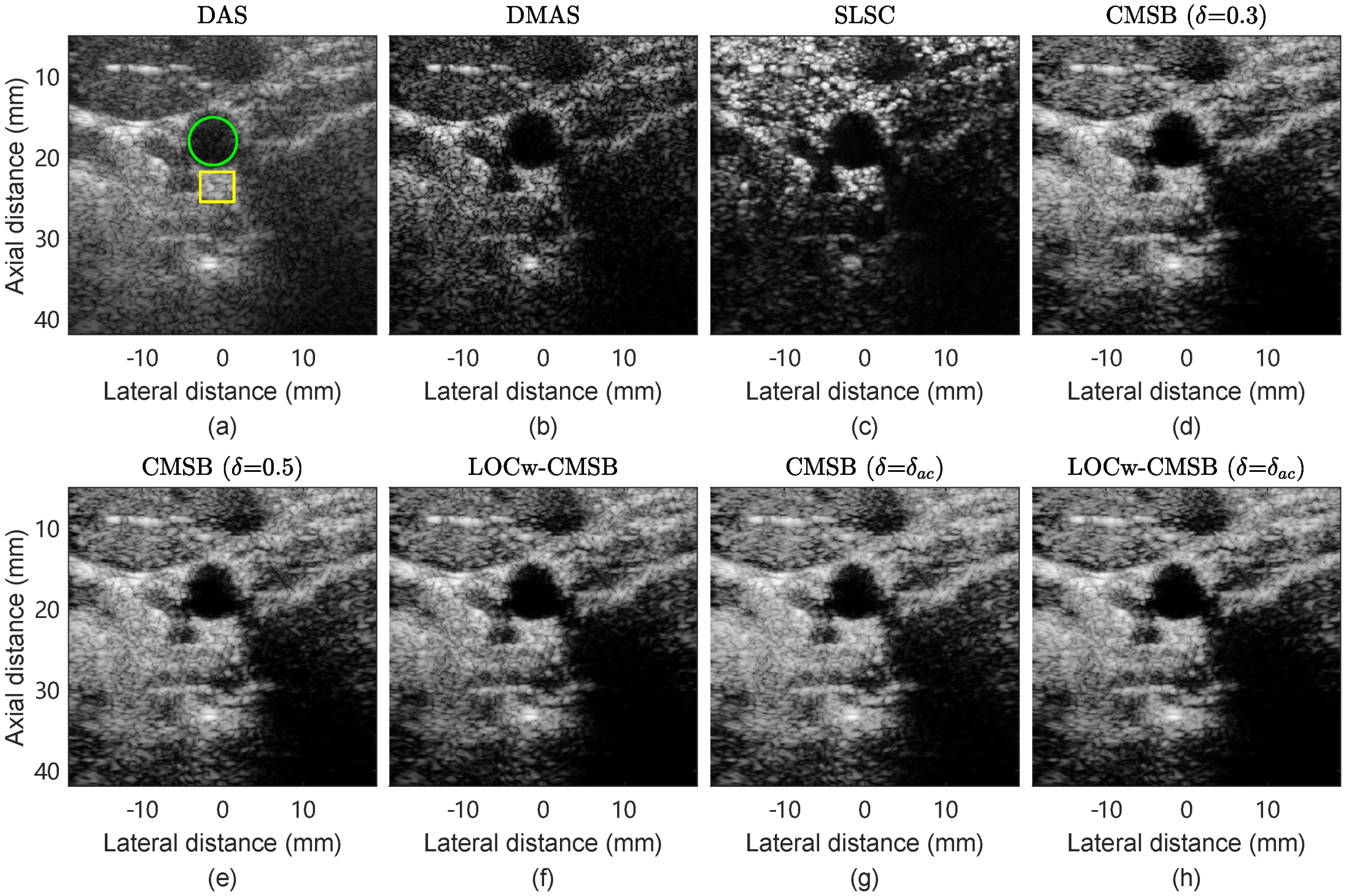
Figure 8 shows the in vivo cross section carotid images reconstructed by different methods. Regions indicated by the circle and box were selected to calculate image metrics. We can see that SLSC reduces clutter and noise; however, the tissue intensity degrades at a large depth. CMSB images show an improved contrast compared with the DAS image and an improved tissue intensity compared with DAS and DMAS images. In comparison with CMSB ( = 0.5), LOCw-CMSB reduces noise in the carotid artery and CMSB ( = ) improves the tissue smoothness, respectively. LOCw-CMSB ( = ) obtains a better performance inside the carotid artery and the anatomical structures are more distinguishable in comparison with CMSB ( = 0.5).
Table 5 lists image quality metrics of carotid images. Compared with DAS, DMAS and SLSC obtain an improvement and degradation of 51.9% and 23.0% in contrast, respectively. CMSB-based methods obtain an improved CR, gCNR, and sSNR over DAS and DMAS. LOCw-CMSB improves the CR by 9.0% and 15.7% compared with CMSB ( = 0.3) and CMSB ( = 0.5), respectively, and the gCNR and sSNR of LOCw-CMSB are slightly higher than that of CMSB ( = 0.5). The gCNR and sSNR of CMSB ( = ) are 7.2% and 17.3% larger than that of CMSB ( = 0.5), whereas CR is almost preserved. In addition, LOCw-CMSB ( = ) leads to improvements of 14.7%, 6.0%, and 13.3% in CR, gCNR, and sSNR over CMSB ( = 0.5). This demonstrates the high image quality of LOCw-CMSB ( = ) when imaging soft tissues.

Table 5.
Image quality metrics of in vivo carotid images obtained by different methods.
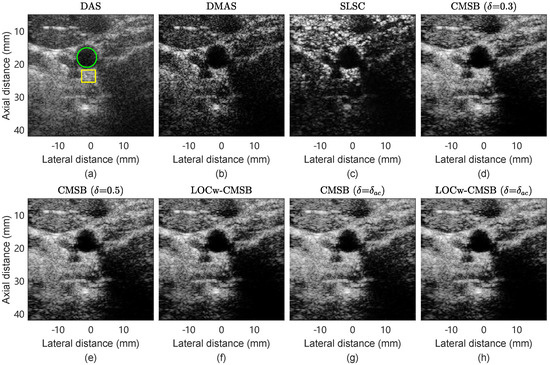
Figure 8.
In vivo cross section view of carotid images reconstructed by (a) DAS, (b) DMAS, (c) SLSC, (d) CMSB ( = 0.7), (e) CMSB ( = 1.3), (f) LOCw-CMSB, (g) CMSB ( = ), and (h) LOCw-CMSB ( = ).
Figure 8.
In vivo cross section view of carotid images reconstructed by (a) DAS, (b) DMAS, (c) SLSC, (d) CMSB ( = 0.7), (e) CMSB ( = 1.3), (f) LOCw-CMSB, (g) CMSB ( = ), and (h) LOCw-CMSB ( = ).
5. Discussion
5.1. Explanation of Results
From the results of all studies, it is clear that CMSB-based methods achieve improvements in resolution, contrast, and lesion detectability over DAS in CPWC ultrasound imaging. In addition, the proposed methods substantially increase the contrast and speckle quality over CMSB. The average contrast improvements obtained by LOCw-CMSB in the simulation and experiment over CMSB ( = 0.7) are 14.7% and 34.4%, respectively. The average gCNR and sSNR improvements obtained by CMSB ( = ) in the simulation and experiment over CMSB ( = 0.7) are 3.2% and 41.7%, respectively. Owing to the combination of LOC weighting and adaptive diagonal reducing, LOCw-CMSB ( = ) improves the average CR, gCNR, and sSNR by 22.3%, 2.4%, and 39.8% over CMSB ( = 1.3) in the simulation and experiment. This demonstrates the improvements in the contrast and speckle quality of the proposed methods over CMSB.
The preliminary study of CMSB did not consider the separability of closely spaced point targets and cyst edge resolution [39], which are also important metrics for adaptive beamformers [50]. In this study, the separability of closely spaced point targets and the cyst edge resolution of different methods were evaluated. As seen from Figure 3b, CMSB-based methods can distinguish the two laterally closely spaced point targets, while DAS and DMAS cannot distinguish the two point targets. In addition, CMSB ( = ) obtains the best cyst edge resolution as seen from Figure 3 and Figure 7. This demonstrates the resolution improvement of LOCw-CMSB and LOCw-CMSB ( = ). Note that LOC weighting and adaptive diagonal reducing scarcely have influence on the resolution performance of CMSB according to Table 2, Table 3 and Table 4.
In comparison with CMSB ( = 1.3), CMSB ( = ) generally has a slight contrast degradation as seen in Table 2 and Table 4. However, CMSB ( = ) obtains an improved contrast over CMSB ( = 1.3) at the deep region in the experimental cyst study according to Table 4. This is likely because the dynamic diagonal reducing preserves the speckle at larger depths.
5.2. Robustness to Channel Noise
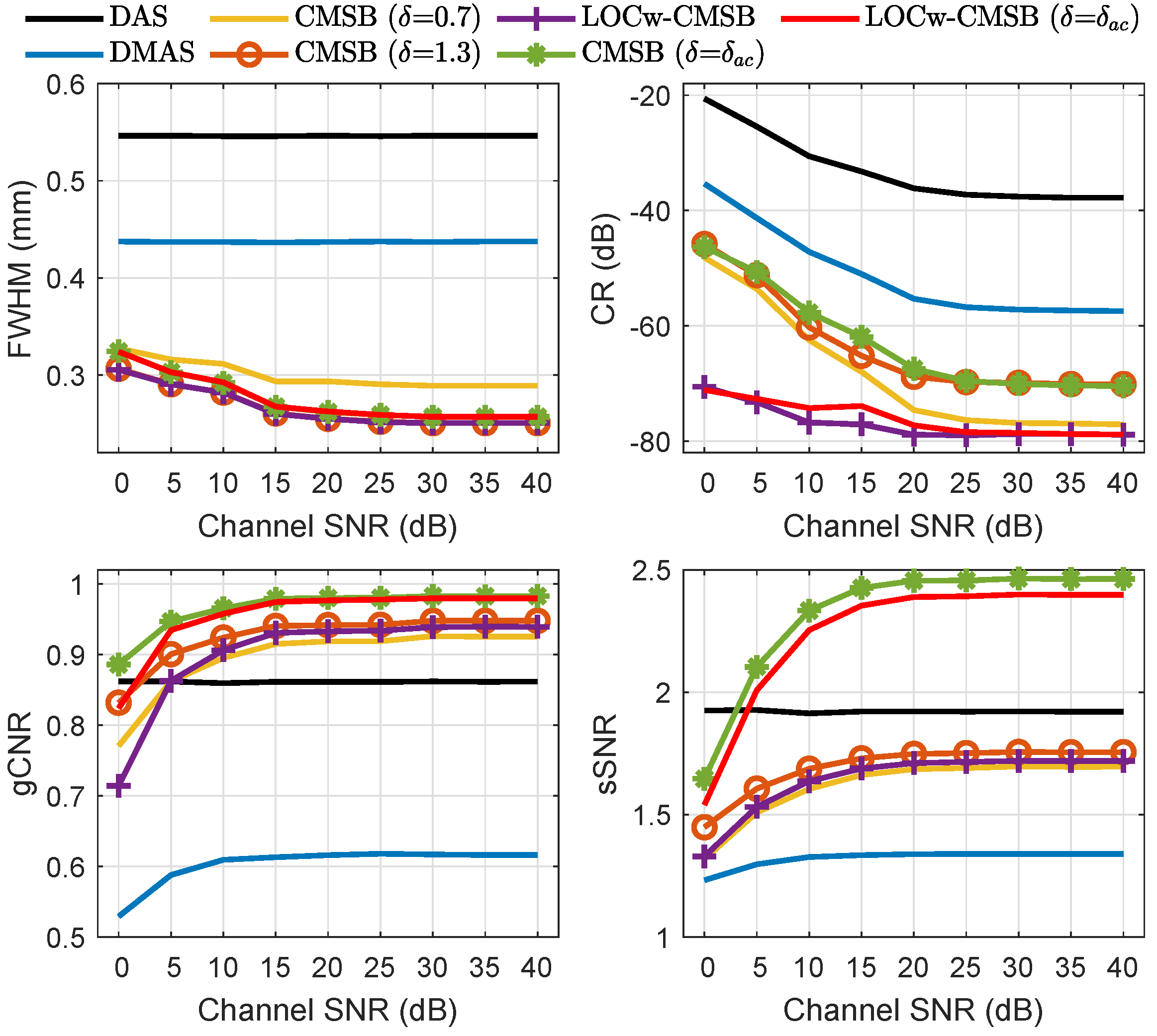
The imaging performance of all methods under different channel SNRs in the simulation was studied to evaluate the robustness to channel noise. As seen in Figure 9, CMSB-based methods all obtain an improved resolution, contrast, gCNR, and sSNR under different channel SNRs compared with DMAS. In addition, the contrast, gCNR, and sSNR obtained by CMSB-based methods degrade with the decreasing channel SNR, whereas the resolution increases. This is because the subarray lengths selected for speckle signals and clutter decrease as the channel SNR decreases, which results in contrast degradation and mainlobe interference rejection. Under the channel SNR of 5 dB, the contrast and sSNR obtained by LOCw-CMSB ( = ) are both much higher than that of DMAS and CMSB. This indicates that the contrast performance of LOCw-CMSB ( = ) is less susceptible to the channel noise, and the speckle quality can be preserved under a high level of channel noise.
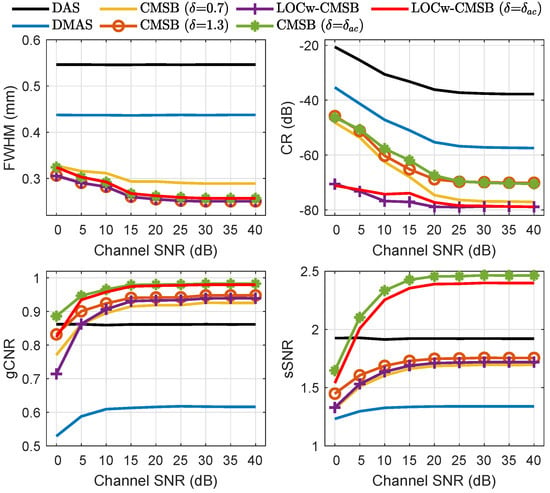
Figure 9.
Full-width and half-maximum (FWHM), contrast ratio (CR), generalized contrast-to-noise ratio (gCNR), and speckle signal-to-noise ratio (sSNR) of all methods under different channel SNRs in the simulation.
5.3. Impact of the Kernel Size
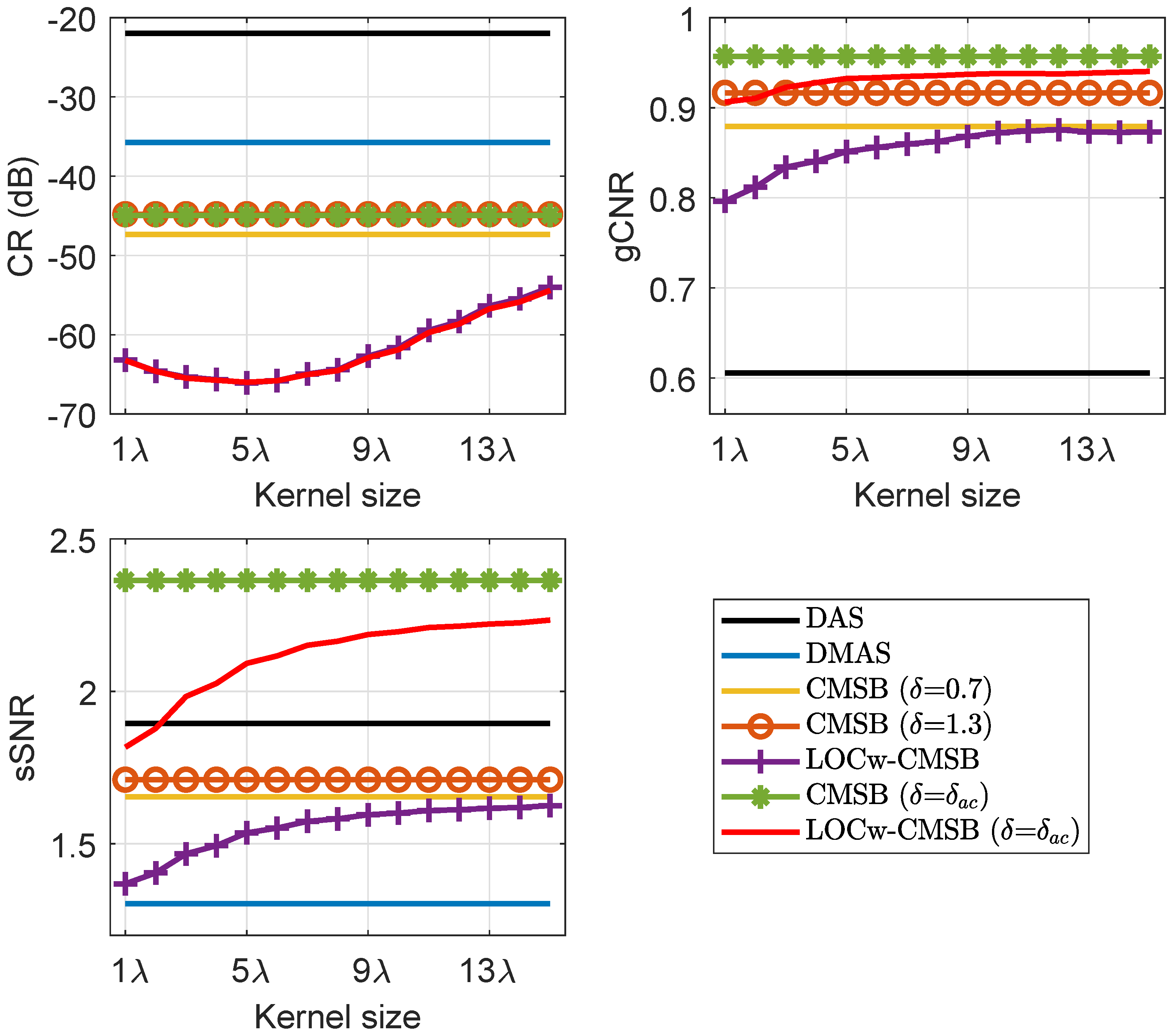
The kernel size for LOC estimation has an influence on the imaging performance of LOC-weighted methods. We evaluated the CR, gCNR, and sSNR obtained by LOCw-CMSB and LOCw-CMSB ( = ) in the cyst phantom experiment as a function of the kernel size. Note that the lateral resolution of LOC-weighted methods is not affected by the kernel size. The cyst target in the deeper region and the corresponding speckle region at the same depth were used to calculate the CR, gCNR, and sSNR. Figure 10 shows the measured CR, gCNR, and sSNR as a function of the kernel size. As can be seen, LOCw-CMSB and LOCw-CMSB ( = ) improve gCNR and sSNR as the kernel size increases, but the contrast degrades. In addition, the computational efficiency of LOC estimation decreases with the increasing kernel size. Hence, the kernel size in the range of 3 to 7 is appropriate for LOC weighting to obtain a high contrast while preserving the speckle quality to some extent, as well as avoiding a high computational load.
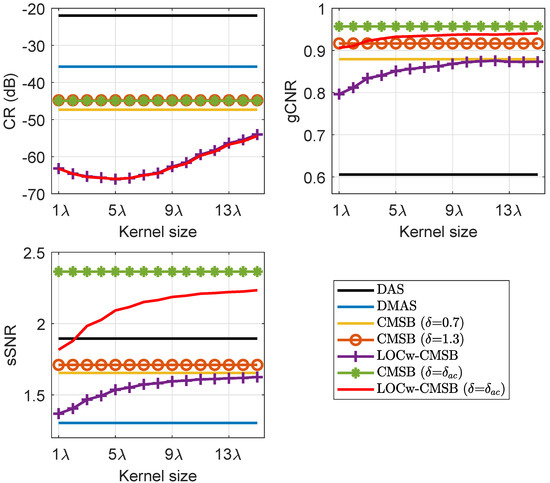
Figure 10.
CR, gCNR, and sSNR of LOC-weighted methods as a function of the kernel size in the cyst phantom experiment.
5.4. Influence of the Number of Transmit Angles
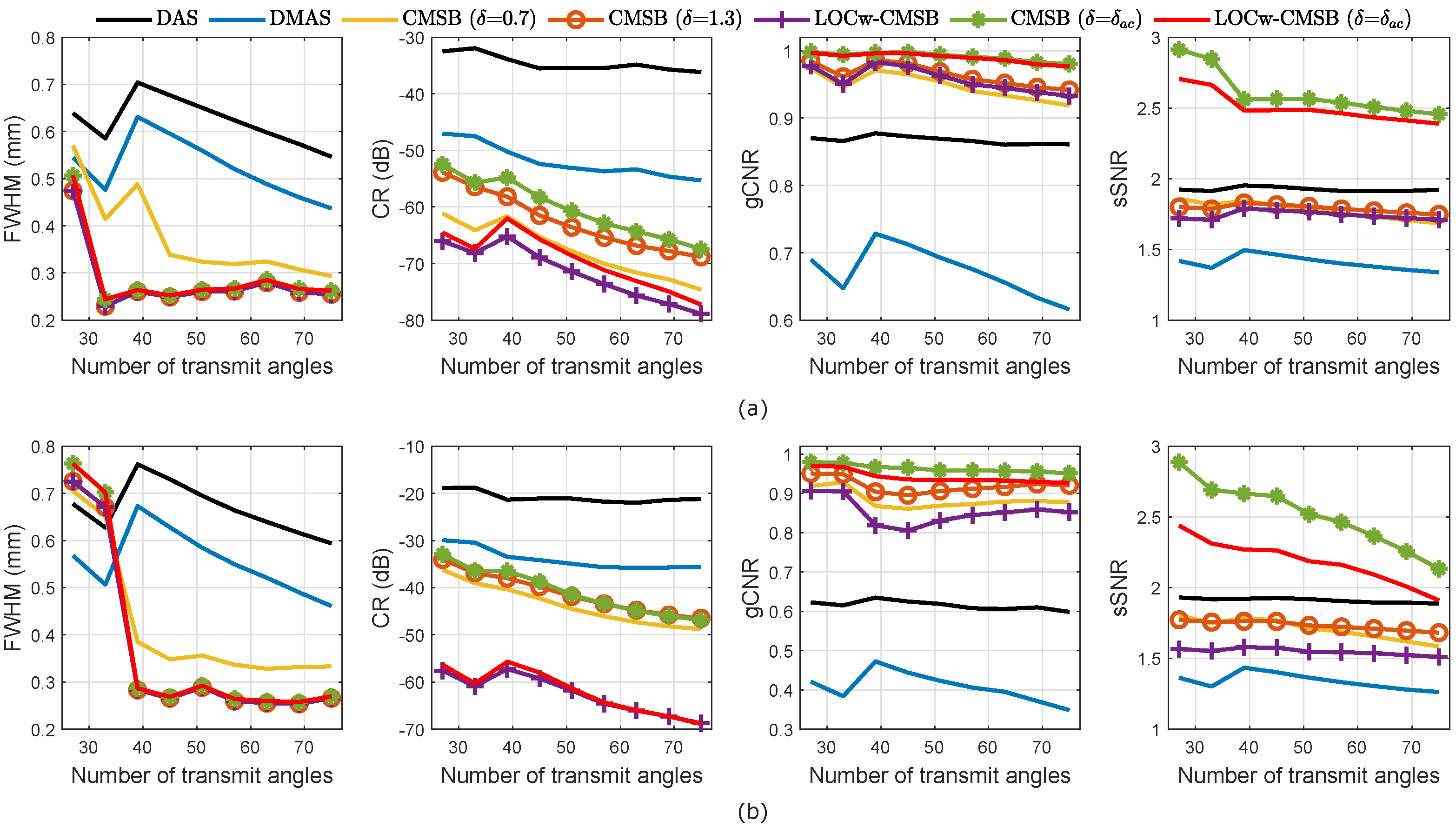
The imaging performance of different beamformers under different numbers of transmit angles was evaluated. Since the number of transmit angles determines the size of the covariance matrix in CMSB, the minimum number of transmit angles was set to 23 to evaluate the imaging performance. The selected transmit angles are symmetrical around 0. The corresponding results in the simulation and experiment are shown in Figure 11a,b, respectively.
As can be seen in Figure 11, the resolution of DAS and DMAS improves with an increasing number of angles when the number of angles is larger than 38. CMSB methods always achieve a higher resolution performance compared with DAS and DMAS. Additionally, the contrast of all methods improves as the number of angle increases. CMSB obtains an improved contrast compared with DMAS, and LOCw-CMSB ( = ) obtains an improved contrast over CMSB under different numbers of transmit angles in both the simulation and experiment. In addition, CMSB obtains an improved gCNR over DAS and DMAS under different numbers of transmit angles. Owing to adaptive diagonal reducing, CMSB ( = ) and LOCw-CMSB ( = ) both obtain an improved gCNR over CMSB. In addition, the sSNR obtained by CMSB is slightly lower than that of DAS, but higher than that of DMAS. Compared with CMSB, CMSB ( = ) and LOCw-CMSB ( = ) obtain a significantly improved sSNR under different numbers of transmit angles. This demonstrates that the proposed CMSB ( = ) and LOCw-CMSB ( = ) can be implemented with a lower number of transmissions to improve the image resolution and contrast, and to simultaneously improve the speckle quality and lesion detectability.
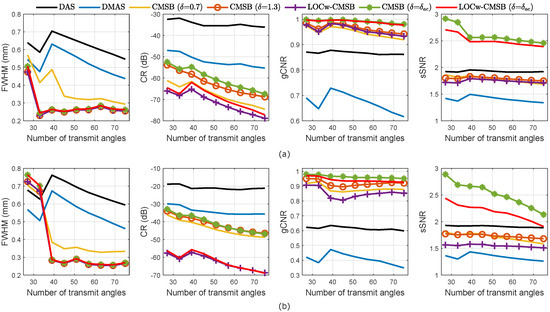
Figure 11.
Image quality metrics of different methods as a function of the number of transmit angles in (a) simulation, and (b) experiment.
Figure 11.
Image quality metrics of different methods as a function of the number of transmit angles in (a) simulation, and (b) experiment.
5.5. Limitations and Future Works
Despite a high resolution in the simulation, CMSB-based methods provide a poor resolution performance in the deeper region in the point phantom experiment compared with DMAS. This is mainly because of the low SNR in the deeper region, which results in undistinguishable strong off-axis clutter beside the point target. In addition, CMSB ( = ) obtains a worse resolution performance in the deeper region compared with CMSB ( = 1.3) as illustrated in Table 3. The resolution of CMSB in the deeper region is insufficient, and this is left for future work.
The speckle regions at the left and right bottom of CMSB-based methods show visually black-spot artifacts as seen from Figure 4 and Figure 6. One possible reason for this is that the speckle intensity in the shallow region is improved, and thus incoherent components-dominated speckle signals (bottom left and right) are suppressed. However, a smaller maximum subarray length might solve this problem at the expense of contrast. In addition, it can be seen from Figure 4 and Figure 6 that black-spot artifacts appear at the deeper region (bottom left and right) in LOC-weighted CMSB images. This is because LOC estimated from the channel signals of the homogeneous speckle region is sensitive to local SNR levels [31].
In addition, the resolution of CMSB-based methods is worse than DAS when the number of transmit angles decreases to 23 in the simulation and 37 in the experiment as illustrated in Figure 11. This is likely because the channel SNR decreases notably when transmitting a small number of plane-waves, and thus the amplitude standard deviations for desired targets and incoherent noise are close. This limits the imaging performance of CMSB-based methods in higher-frame-rate CPWC imaging with a smaller number of transmit angles. One possible way to address this problem is to set the maximum subarray length to the total number of transmit angles rather than half the total number of transmit angles in this study. This might improve the resolution performance of CMSB-based methods at the expense of the speckle quality. Furthermore, the signal sparse representation [51] and coded excitation technique [52] used to enhance SNR and the tensor completion (TC) to achieve the same image quality using 20% of a total angle of 75 [53] can be utilized to improve the imaging performance of CMSB-based methods when using a much lower number of transmit plane-waves.
6. Conclusions
In this paper, we applied CMSB in CPWC imaging and introduced LOC weighting and adaptive diagonal reducing to CMSB to further reduce spatially incoherent noise and preserve speckle signals. The proposed methods were validated through a simulation and experimental and carotid studies. The results from all studies show that LOCw-CMSB provides an obviously enhanced contrast without sacrificing the speckle quality of CMSB, and CMSB ( = ) effectively improves the speckle SNR of CMSB. In addition, LOCw-CMSB ( = ) provides an improved contrast, gCNR, and sSNR over CMSB. When applied to human carotid imaging, LOCw-CMSB ( = ) effectively enhances the contrast, lesion detectability, and tissue smoothness compared with CMSB, showing an improved diagnostic value. To summarize, the proposed beamformers can be useful image reconstruction methods for CPWC ultrasound imaging.
Author Contributions
Conceptualization, Y.W. (Yuanguo Wang), Y.W. (Yadan Wang) and H.P.; methodology, Y.W. (Yuanguo Wang) and Y.W. (Yadan Wang); validation, Y.W. (Yuanguo Wang), Y.W. (Yadan Wang) and H.P.; investigation, Y.W. (Yuanguo Wang), Y.W. (Yadan Wang), C.Z. and H.P.; writing—original draft preparation, Y.W. (Yuanguo Wang); writing—review and editing, Y.W. (Yuanguo Wang) and Y.W. (Yadan Wang); funding acquisition, Y.W. (Yuanguo Wang), Y.W. (Yadan Wang), C.Z. and H.P.; supervision, Y.W. (Yadan Wang), C.Z. and H.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 62101173 and 62071165), the China Postdoctoral Science Foundation (grant number 2021M690853), and the Fundamental Research Funds for the Central Universities of China (grant number JZ2021HGQB0275 and JZ2021HGTB0074).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CPWC | Coherent plane-wave compounding |
| CF | Coherence factor |
| DMAS | Delay-multiply-and-sum |
| ASD | Amplitude standard deviation |
| LOC | Lag-one coherence |
References
- Tanter, M.; Fink, M. Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 102–119. [Google Scholar] [CrossRef] [PubMed]
- Couture, O.; Fink, M.; Tanter, M. Ultrasound contrast plane wave imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2676–2683. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.; Stuart, M.B.; Jensen, J.A. Optimized plane wave imaging for fast and high-quality ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1922–1934. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, G.; Weijers, G.; Chen, C.; Hertel, M.; Lee, C.Y.; Dueppenbecker, P.; Radicke, M.; Milkowski, A.; Hansen, H.; de Korte, C.L. Ultrasound coherent plane-wave compound imaging: Image quality evaluation in phantoms and breast lesions. J. Acoust. Soc. Am. 2021, 150, A88. [Google Scholar] [CrossRef]
- Salles, S.; Liebgott, H.; Basset, O.; Cachard, C.; Vray, D.; Lavarello, R. Experimental evaluation of spectral-based quantitative ultrasound imaging using plane wave compounding. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1824–1834. [Google Scholar] [CrossRef]
- Porée, J.; Garcia, D.; Chayer, B.; Ohayon, J.; Cloutier, G. Noninvasive Vascular Elastography With Plane Strain Incompressibility Assumption Using Ultrafast Coherent Compound Plane Wave Imaging. IEEE Trans. Med. Imaging 2015, 34, 2618–2631. [Google Scholar] [CrossRef]
- Tang, J.; Zou, B.; Li, C.; Feng, S.; Peng, H. Plane-Wave Image Reconstruction via Generative Adversarial Network and Attention Mechanism. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Bercoff, J.; Tanter, M.; Fink, M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 396–409. [Google Scholar] [CrossRef]
- Demené, C.; Deffieux, T.; Pernot, M.; Osmanski, B.F.; Biran, V.; Gennisson, J.L.; Sieu, L.A.; Bergel, A.; Franqui, S.; Correas, J.M.; et al. Spatiotemporal Clutter Filtering of Ultrafast Ultrasound Data Highly Increases Doppler and fUltrasound Sensitivity. IEEE Trans. Med. Imaging 2015, 34, 2271–2285. [Google Scholar] [CrossRef]
- Errico, C.; Pierre, J.; Pezet, S.; Desailly, Y.; Lenkei, Z.; Couture, O.; Tanter, M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 2015, 527, 499–502. [Google Scholar] [CrossRef] [PubMed]
- You, Q.; Dong, Z.; Lowerison, M.R.; Song, P. Pixel-oriented Adaptive Apodization for Planewave Imaging Based on Recovery of the Complete Data Set. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 69, 512–522. [Google Scholar] [CrossRef] [PubMed]
- Seo, C.H.; Yen, J.T. Sidelobe suppression in ultrasound imaging using dual apodization with cross-correlation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2198–2210. [Google Scholar] [PubMed]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Synnevag, J.F.; Austeng, A.; Holm, S. Adaptive beamforming applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 1606–1613. [Google Scholar] [CrossRef]
- Synnevag, J.F.; Austeng, A.; Holm, S. Benefits of minimum-variance beamforming in medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1868–1879. [Google Scholar] [CrossRef]
- Asl, B.M.; Mahloojifar, A. Eigenspace-based minimum variance beamforming applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2381–2390. [Google Scholar] [CrossRef]
- Lediju, M.A.; Trahey, G.E.; Byram, B.C.; Dahl, J.J. Short-lag spatial coherence of backscattered echoes: Imaging characteristics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1377–1388. [Google Scholar] [CrossRef]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imaging 2015, 34, 940–949. [Google Scholar] [CrossRef]
- Cohen, R.; Eldar, Y.C. Sparse Convolutional Beamforming for Ultrasound Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 2390–2406. [Google Scholar] [CrossRef]
- Lediju Bell, M.A.; Goswami, R.; Kisslo, J.A.; Dahl, J.J.; Trahey, G.E. Short-Lag Spatial Coherence Imaging of Cardiac Ultrasound Data: Initial Clinical Results. Ultrasound Med. Biol. 2013, 39, 1861–1874. [Google Scholar] [CrossRef] [PubMed]
- Wiacek, A.; Rindal, O.M.H.; Falomo, E.; Myers, K.; Fabrega-Foster, K.; Harvey, S.; Lediju Bell, M.A. Robust Short-Lag Spatial Coherence Imaging of Breast Ultrasound Data: Initial Clinical Results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 527–540. [Google Scholar] [CrossRef] [PubMed]
- Moubark, A.M.; Alomari, Z.; Mohd Zaman, M.H.; Zulkifley, M.A.; Md Ali, S.H.; Nie, L.; Freear, S. Optimizing the lateral beamforming step for filtered-delay multiply and sum beamforming to improve active contour segmentation using ultrafast ultrasound imaging. Biomed. Signal Process. Control 2022, 71, 103267. [Google Scholar] [CrossRef]
- Cohen, R.; Fingerhut, N.; Varray, F.; Liebgott, H.; Eldar, Y.C. Sparse convolutional beamforming for 3-D ultrafast ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2444–2459. [Google Scholar] [CrossRef]
- Rindal, O.M.H.; Rodriguez-Molares, A.; Austeng, A. The dark region artifact in adaptive ultrasound beamforming. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Yan, X.; Qi, Y.; Wang, Y.; Wang, Y. Regional-lag Signed Delay Multiply and Sum Beamforming in Ultrafast Ultrasound Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 69, 580–591. [Google Scholar] [CrossRef]
- Hollman, K.; Rigby, K.; O’donnell, M. Coherence factor of speckle from a multi-row probe. In Proceedings of the 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No. 99CH37027), IEE, Tahoe, NV, USA, 17–20 October 1999; Volume 2, pp. 1257–1260. [Google Scholar]
- Li, P.C.; Li, M.L. Adaptive imaging using the generalized coherence factor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 128–141. [Google Scholar]
- Wang, Y.H.; Li, P.C. SNR-dependent coherence-based adaptive imaging for high-frame-rate ultrasonic and photoacoustic imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1419–1432. [Google Scholar] [CrossRef]
- Xu, M.; Yang, X.; Ding, M.; Yuchi, M. Spatio-temporally smoothed coherence factor for ultrasound imaging [Correspondence]. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 182–190. [Google Scholar] [CrossRef]
- Long, W.; Bottenus, N.; Trahey, G.E. Incoherent Clutter Suppression Using Lag-One Coherence. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1544–1557. [Google Scholar] [CrossRef]
- Long, W.; Bottenu, N.; Trahey, G.E. Lag-One Coherence as a Metric for Ultrasonic Image Quality. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1768–1780. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, C.; Peng, H.; Chen, Q. An adaptive beamforming method for ultrasound imaging based on the mean-to-standard-deviation factor. Ultrasonics 2018, 90, 32–41. [Google Scholar] [CrossRef]
- Hasegawa, H.; Nagaoka, R. Converting Coherence to Signal-to-noise Ratio for Enhancement of Adaptive Ultrasound Imaging. Ultrason. Imaging 2020, 42, 27–40. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zheng, C.; Peng, H. Dynamic coherence factor based on the standard deviation for coherent plane-wave compounding. Comput. Biol. Med. 2019, 108, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Bandaru, R.S.; Sornes, A.R.; Hermans, J.; Samset, E.; Dhooge, J. Delay and standard deviation beamforming to enhance specular reflections in ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 2057–2068. [Google Scholar] [CrossRef] [PubMed]
- Paridar, R.; Mozaffarzadeh, M.; Periyasamy, V.; Basij, M.; Mehrmohammadi, M.; Pramanik, M.; Orooji, M. Validation of delay-multiply-and-standard-deviation weighting factor for improved photoacoustic imaging of sentinel lymph node. J. Biophotonics 2019, 12, e201800292. [Google Scholar] [CrossRef] [PubMed]
- Lan, Z.; Zheng, C.; Wang, Y.; Peng, H.; Qiao, H. Adaptive threshold for eigenspace-based minimum variance beamformer for dark region artifacts elimination. IEEE Trans. Instrum. Meas. 2021, 70, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, C.; Liu, M.; Peng, H. Covariance Matrix-based Statistical Beamforming for Medical Ultrasound Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 69, 208–221. [Google Scholar] [CrossRef]
- Paul, S.; Mandal, S.; Singh, M.S. Noise Adaptive Beamforming for Linear Array Photoacoustic Imaging. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, C.; Peng, H.; Zhang, C. Coherent plane-wave compounding based on normalized autocorrelation factor. IEEE Access 2018, 6, 36927–36938. [Google Scholar] [CrossRef]
- Long, J.; Long, W.; Bottenus, N.; Pinton, G.F.; Trahey, G.E. Implications of Lag-One Coherence on Real-Time Adaptive Frequency Selection. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Wiacek, A.; Oluyemi, E.; Myers, K.; Ambinder, E.; Bell, M.A.L. Quantifying the impact of breast density on the lag-one coherence of hypoechoic masses. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Yu, M.; Li, Y.; Ma, T.; Shung, K.K.; Zhou, Q. Intravascular Ultrasound Imaging With Virtual Source Synthetic Aperture Focusing and Coherence Factor Weighting. IEEE Trans. Med. Imaging 2017, 36, 2171–2178. [Google Scholar] [CrossRef]
- Kang, S.; Lee, J.; Chang, J.H. Effectiveness of synthetic aperture focusing and coherence factor weighting for intravascular ultrasound imaging. Ultrasonics 2021, 113, 106364. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.A.; Svendsen, N.B. Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.A. FIELD: A Program for Simulating Ultrasound Systems. In Proceedings of the 10th Nordic-Baltic Conference on Biomedical Imaging, Tampere, Finland, 9–13 1996; Volume 34, pp. 351–353. [Google Scholar]
- Liebgott, H.; Rodriguez-Molares, A.; Cervenansky, F.; Jensen, J.; Bernard, O. Plane-Wave Imaging Challenge in Medical Ultrasound. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Rodriguez-Molares, A.; Rindal, O.M.H.; D’hooge, J.; Måsøy, S.; Austeng, A.; Bell, M.A.L.; Torp, H. The generalized contrast-to-noise ratio: A formal definition for lesion detectability. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 67, 745–759. [Google Scholar] [CrossRef] [PubMed]
- Hoel Rindal, O.M.; Austeng, A.; Rodriguez-Molares, A. Resolution Measured as Separability Compared to Full Width Half Maximum for Adaptive Beamformers. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Shen, M.; Zhang, Q.; Li, D.; Yang, J.; Li, B. Adaptive Sparse Representation Beamformer for High-Frame-Rate Ultrasound Imaging Instrument. IEEE Trans. Instrum. Meas. 2012, 61, 1323–1333. [Google Scholar] [CrossRef]
- Song, P.; Urban, M.W.; Manduca, A.; Greenleaf, J.F.; Chen, S. Coded excitation plane wave imaging for shear wave motion detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1356–1372. [Google Scholar] [CrossRef] [PubMed]
- Afrakhteh, S.; Behnam, H. Coherent Plane Wave Compounding Combined With Tensor Completion Applied for Ultrafast Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 3094–3103. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).