Abstract
This research investigates the texture influence of masonry walls’ lateral capacity by comparing analytical predictions performed via macro and micro limit analysis. In particular, the effect of regular and quasi-periodic bond types, namely Running, Flemish, and English, is investigated. A full factorial dataset involving 81 combinations is generated by varying geometrical (panel and block aspect ratio, bond type) and mechanical (friction coefficient) parameters. Analysis of variance (ANOVA) approach is used to investigate one-way and two-way factor interactions for each parameter in order to assess how it affects the horizontal load multiplier. Macro and micro limit analysis predictions are compared, and the differences in terms of mass-proportional horizontal load multiplier and failure mechanism are critically discussed. Macro and micro limit analysis provide close results, demonstrating the reliability of such approaches. Furthermore, results underline how the panel and block aspect ratio had the most significant effect on both the mean values and scatter of results, while no significant effect could be attributed to the bond types.
1. Introduction
Across the centuries, depending on the available materials, facilities, and skills of the workers, a great variety of different masonry typologies have been used to build structures. In Europe, bricks or stones were usually adopted to generate various assemblages, varying in terms of bond pattern, number of leaves, etc. Referring to brickworks, although a large variety of different-sized bricks were manufactured in the past, typically, they were rectangular, same-size, and arranged in periodic or quasi-periodic bond patterns [1,2,3,4,5]. To fully understand the influence of different bond patterns, comprehensive sensitivity analyses using advanced numerical or analytical strategies are required. The usage of one computational strategy rather than another is driven by the type of analysis, data quality, time availability, investigated phenomenon, etc. The taxonomies proposed in [6,7,8] identified four main approaches for the numerical modelling of masonry structures: (i) block-based models, (ii) continuum models, (iii) macroelement models, and (iv) geometry-based models.
Block-based models can account for the actual masonry texture since masonry is modelled following the unit-by-unit representation. Block-based approaches consider rigid or deformable blocks interacting according to a frictional or cohesive-frictional contact modelling [9,10,11,12,13]. Three main strategies can be grouped within this sub-class: (i) distinct element method (DEM) [14,15,16,17,18,19,20], which was introduced by Cundall [21], (ii) discontinuous deformation analysis (DDA), which takes into account the deformability of blocks and fulfils the assumption of no tension between blocks and no penetration of one block into another, (iii) non-smooth contact dynamics (NSCD) method [22,23,24,25,26,27,28,29], characterised by a direct contact formulation in its non-smooth form, implicit integrations schemes, and energy dissipation due to blocks impact.
Continuum models consider masonry as a deformable continuous medium. It requires less computational effort compared with the discontinous approaches because the mesh discretisation does not have to describe the actual block-by-block discretisation [30,31,32,33,34,35]. The most relevant issue in this approach is related to the mechanical modelling of the material properties, which may be performed with: (i) direct approaches, (ii) homogenisation procedures. Several authors proposed homogenisation procedures for quasi- or non-periodic masonry patterns in this context [36,37]. In some cases, authors coupled the procedure with a series of limit analyses to determine the limit load and failure mechanism for the homogenised model and to compare these results to the ones obtained with the heterogeneous model [38].
In macroelement models, the structure is idealised into rigid or deformable panel-scale structural components. In this case, the structure needs to be idealised a priori into piers and spandrels, and this could lead to the definition of a mechanical system that does not well represent the actual one, especially in the presence of very irregular opening layouts [39,40].
As an alternative to sophisticated numerical approaches, geometry-based models assume the structure’s geometry as the only input, in addition to the loading condition. The structure is modelled as a rigid body whose structural performance is assessed through limit-analysis theorems, i.e., static or kinematic. Static theorem-based computational approaches can provide very useful outcomes for the investigation of the equilibrium states in masonry vaulted structures and also appear especially suitable for predicting the collapse mechanism (and the collapse multiplier) in complex masonry structures [41,42,43,44,45]. Kinematic theorem-based limit analysis (LA) approaches have recently been widely used to assess existing masonry buildings [46].
In this context Rios et al. [47] investigated the effects of different geometrical (panel ratio, block ratio, and bond type) and mechanical (friction coefficient) parameters on the in-plane structural response of dry-stack masonry panels. The analytical simulation was performed using a kinematic upper bound micro LA model with an associative flow rule. The work demonstrates a negligible effect of the bond types. Malomo et al. [16] conducted parametric DEM analyses on masonry walls with different bond patterns (Flemish, English, Dutch cross-bond, Header, and Running bonds). The authors remarked how the walls’ initial stiffness and lateral capacity increased with the level of pre-compression and the decrease of wall aspect ratio. They also observed that the bond types significantly affected the results at high block aspect ratios.
However, few researchers investigated the influence of such geometrical and mechanical parameters by using more than one computational approach. In particular, studies comparing micro and macro strategies and assessing their pros and cons remain scarce. For example, Casapulla et al. [48,49] parametrically compared micro and macro LA formulations for IP and OOP failure mechanisms made with regular patterns by varying geometrical (panel aspect ratio, block aspect ratio), mechanical (friction coefficient) and overload levels.
This study performs a parametric analysis involving 81 combinations by varying geometrical (panel aspect ratio, block aspect ratio, bond type) and mechanical (friction coefficient) parameters. The ANOVA approach is used to investigate one-way and two-way factor interactions and assess how each parameter affects the horizontal load multiplier. Macro and micro limit analyses are compared, and the differences in terms of lateral load-carrying capacity and failure mechanism are critically discussed.
2. Limit Analysis Formulation
In this section, macro and micro LA formulations are briefly described. Macro LA is formulated according to the model proposed in [50], where the frictional resistance definition proposed in [51] for non-periodic masonry is generalised for quasi-periodic bond types. Micro LA formulation is formulated according to the pioneering work developed in [52]. Both approaches are implemented in a customised code in the Java programming language.
2.1. Macro LA Formulation
Several authors have used macro-block LA formulations to assess the structural behaviour of unreinforced masonry structures [50,53,54,55]. Typically, the failure mechanism is pre-defined (Figure 1), and the equilibrium equation is formulated using the virtual work principle, where the horizontal load multiplier is the only unknown variable. Regarding the in-plane sliding-rocking mechanism, the internal work is derived from the frictional resistance at the contact interfaces, whereas the external virtual work involves both the overturning and the stabilising works performed by the inertial forces:
where is the inertial force arising from the self-weight of the macro-block OBC, and are the virtual overturning and stabilising displacements of the centre of gravity of the macro-block, and is the frictional resistance generated by the wall. It is worth highlighting that the failure often includes mix- sliding-rocking failure mode, which might cause uplifting of the units and subsequent reduction of the contact surfaces. In order to consider this phenomenon, the solution proposed in Casapulla et al. [50] is adopted, where the frictional force is defined as a function of the crack inclination angle . This is given by:
where is the thickness of the in-plane wall, is the friction coefficient, is the specific weight of the masonry, is the actual crack inclination, and is the crack inclination upper threshold, which in the case of Running bond type is the function of the block aspect ratio:
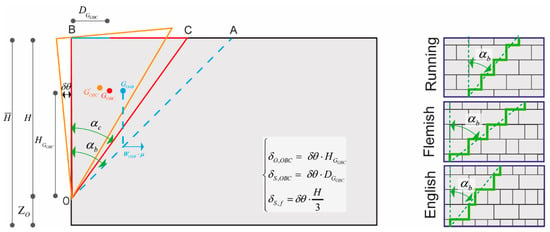
Figure 1.
Kinematic description of the sliding-rocking mechanism for an in-plane shear wall and definition of for quasi-periodic bond patterns.
Here, and are half-width and height of the units, respectively.
Since Equation (3) may only be adopted for Running patterns, an alternative solution to define for different quasi-periodic bond types is introduced next (Figure 1).
As proposed in [51], in order to compute the crack inclination upper thresholds, one can refer to a representative masonry pattern window (RMPW) and calculate according to (Figure 1):
It is worth remarking that, in this case, refers to the number of courses inside the RMPW, and is the i-th horizontal segments of the structured path UP-RIGHT-UP-RIGHT.
According to the analytical formulation proposed in [50], once the crack inclination upper threshold is defined, it is possible to apply the macro-block formulation, which allows the computation of the horizontal load multiplier and the geometry of the failure mechanism. In particular, the horizontal load multiplier can be obtained by equating the external and internal virtual works and solving for the load multiplier . Hence, the horizontal load multiplier can be computed through the solution of a constrained minimisation problem where geometrical parameters characterising the failure mechanism, i.e., and , are adopted as variables:
where is the height position of the pivot point and is the total height of the wall.
2.2. Micro LA Formulation
In the micro LA formulation, the dry-stack assemblage is represented by rigid blocks connected by frictional contact interfaces with a non-associative flow rule, with zero dilation (Figure 2).
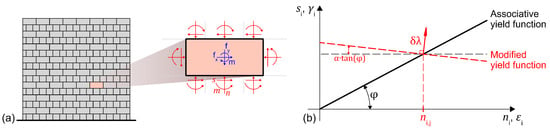
Figure 2.
(a) Dry-stack masonry wall, (b) yield function for the non-associative solution.
The solution scheme proposed in [52], involving a non-associative frictional flow rule consisting of sequential solutions of linear programs, is adopted (Figure 2b). At each iteration a static LA problem is defined in the form of a linear program (LP) as:
where is the load multiplier and the vector of unknown contact forces, and are the live and dead loads, is the cohesion vector, and are the equilibrium and yield constraint matrices. The first constraint represents the equilibrium of forces, whereas the second is the condition for yielding (failure) of the contact interfaces.
The yield conditions are updated at each iteration based on the normal forces at the previous iterations:
Here, and are the shear and normal forces of the i-th interface at the j-th iteration. and are algorithm parameters set to 0.01 and 0.6, respectively.
Finally, the steps of the iterative algorithm are the following [52]:
- Set up the micro LA problem, according to Equation (6) with associative-frictional yield condition.
- Solve the LP and save the load multiplier and the normal forces at each interface .
- Modify the shear failure condition based on the previous iteration, according to Equation (7).
- Solve the LP with the modified yield conditions in Step 3 and save the load multiplier and normal contact forces .
- If the exit condition is true, the algorithm terminates. Else, repeat from Step 3.
- Calculate the kinematic variables (displacement rates) from the dual linear program.
The algorithm has been implemented in a custom computer code in the JAVA programming language, and the interior point LP solver of the MOSEK optimisation software (https://www.mosek.com/ (accessed on 28 January 2021)) has been used for the subsequent numerical studies.
3. Parametric Analysis Design
As stated before, this work aims to understand the in-plane lateral capacity of single leaf masonry walls arranged with different bond types, namely Running, Flemish, and English, and subjected to horizontal mass proportional loading. According to [47], a full factorial dataset involving all 81 combinations of the input parameters is generated by varying geometrical (panel aspect ratio, block aspect ratio, bond type) and mechanical parameters (friction coefficient). One can note that the geometrical parameters are assumed to be consistent with [47], whereas more reasonable values of the frictional parameters have been assumed. Table 1 summarises the range of values adopted for each parameter.

Table 1.
Parametric analysis design: parameters’ values.
The 81 simulations have been performed with both micro and macro LA formulations, and the resulting horizontal load multipliers and failure mechanism have been stored within a database. The effect of input parameters on the results and the relation of the two approaches have been investigated with the ANOVA approach [47], where the average effect and its standard deviation are calculated for one (linear factor) or the joint effect of two or more parameters (two- or multiple-way factor) as:
where is the mean value of the load multiplier for all the cases, with the first input parameter having the value of i. is the mean value, where the first two input parameters have the values of i and j, respectively.
4. Results
Figure 3 shows parameters’ individual effects for both micro and macro LA models. The two formulations show good agreement in terms of both mean and standard deviation values.
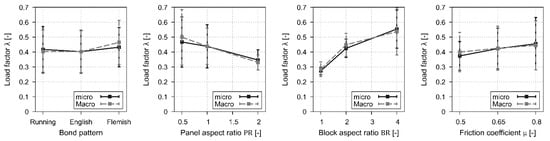
Figure 3.
Linear interaction: micro and macro LA.
Figure 3 remarks small differences in terms of horizontal load multiplier for the analysed bond patterns. As expected, the higher friction coefficient tends to increase the horizontal capacity of the in-plane walls but generates more scattered results. Panel aspect ratio () and the block aspect ratio () strongly influence the horizontal load multiplier. In both cases, the standard deviation is very sensitive to PR and BR. In particular, higher PR tends to reduce lateral capacity scattering, whereas a higher BR has the opposite effect since it tends to increase the noise in the prediction of both micro and macro LA formulations.
The macro and micro LA two-way factor interactions are reported in Figure 4 and Figure 5, respectively. Results are organised into a 4 × 4 matrix that is symmetric if one considers the data included in each cell, even though they are plotted by flipping the legends with the horizontal axis to provide broader information to the reader.
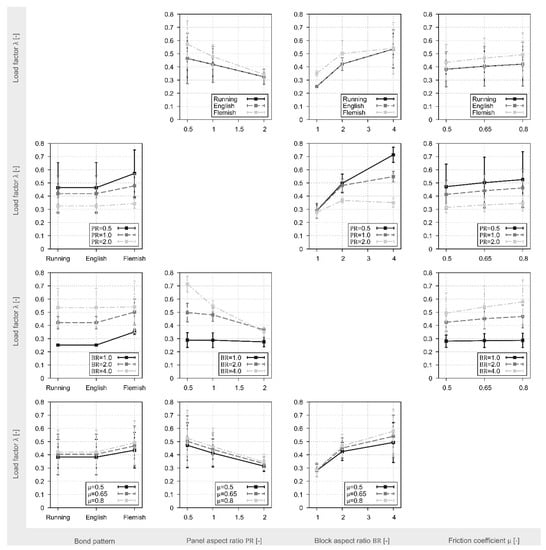
Figure 4.
Two-way interaction plots: macro LA.

Figure 5.
Two-way interaction plots: micro LA.
It is worth underlining the good agreement between macro and micro LA formulations is again confirmed. In macro LA, was set equal for Running and English bonds, so the corresponding mean and standard deviation values are the same. Conversely, the Flemish bond type is computed differently according to the graphical approach represented in Figure 1. Assuming micro LA results as more accurate, the overestimation of lateral capacity for Flemish bond type is generated by an inaccurate evaluation of . In fact, micro LA underlines slight differences among the bond types that could not be caught with macro LA. Referring to Figure 4, in macro LA simulations, the effect of the bond patterns tends to decrease by increasing PR and BR, whereas standard deviation values tend to decrease with higher values of PR and increase with higher values of BR, but stays constant with the change in friction coefficient. Micro LA shows a different influence of the bond types (Figure 5), where the two-way interaction with BR, PR, and friction coefficient does not provide remarkable differences, highlighting a relatively low influence of the bond type in predicting the lateral capacity of in-plane masonry walls. Referring to the second row of the matrices of both macro and micro LA formulations (Figure 4 and Figure 5), it is worth underlining that the bond type does not produce significant differences in terms of load multiplier predictions, whereas the two-way factors PR-BR and PR-friction coefficient produce remarkable differences, the latter yielding very scattered results.
The third row of the matrices shows a good agreement (Figure 4 and Figure 5). In particular, one can note how by increasing BR the prediction tends to be more scattered except in the case of a very slender wall, i.e., PR = 2, or very limited friction coefficient (e.g., ). Furthermore, analysing the data reported in the third row, one can note that the higher BR generates more friction resistance and produces an increment in terms of lateral capacity. The fourth row of the matrixes represents the two-way factor interactions with the friction coefficient. Overall, the friction coefficient has a much lower influence in terms of mean values; however, the high variation in the results underlines the importance of such a mechanical parameter for assessing the lateral capacity of dry-stack masonry walls.
Finally, to conclude the comparisons between the two computational procedures, one should note how macro LA result’s trend of varying the friction coefficient is not influenced by the value of PR, meaning the two parameters are not correlated. On the contrary, micro LA visualises an evident two-way friction-PR interaction. The friction-BR interaction shows excellent agreement between macro and micro LA models, where the mean values tend to increase with BR.
Micro LA failure mechanisms are collected into nine tables and reported in Appendix A, Appendix B, Appendix C, Appendix D, Appendix E, Appendix F, Appendix G, Appendix H and Appendix I, whereas a comprehensive summary of the parametric analysis performed is reported in Appendix J.
5. Conclusions
This research presents a comprehensive parametric analysis to assess the in-plane behaviour and capacity of unreinforced dry-joint masonry walls by varying geometrical (panel aspect ratio, block aspect ratio, bond type) and mechanical (friction coefficient) properties. Simulations were performed using two computational approaches based on micro and macro LA, respectively. The lateral capacity of the walls is represented by the mass-proportional horizontal load multiplier, i.e., the ratio of horizontal and vertical force on the masonry units. Subsequently, the load multipliers were examined via the ANOVA approach.
The following points summarise the main findings and contributions of the paper:
- The panel and block aspect ratios significantly affect the horizontal load multipliers, while the friction coefficient has less influence on the results.
- Significant variation in the results is noted for high friction coefficient values (e.g., 0.8), suggesting a careful selection of this parameter in LA.
- Running and quasi-periodic bond patterns only slightly influence the load multiplier prediction.
- Generally, a good agreement between macro and micro LA is observed in one- and two-way factor interactions. Specifically, the most significant difference between the two computational approaches (i.e., macro and micro LA) is obtained for the Flemish bond pattern.
Future developments will involve: (i) increasing the dataset generation by considering non-periodic masonry patterns, (ii) adoption of the proposed approach for the investigation of more complex masonry prototypes rather than an in-plane wall, (iii) developing an analytical equation based on mechanical assumptions or regression models.
Author Contributions
Conceptualisation, S.S. and M.F.F.; methodology, S.S., M.F.F. and B.P..; software, S.S. and M.F.F.; validation, S.S. and M.F.F. and B.P. formal analysis, S.S. and M.F.F.; investigation, S.S., M.F.F. and B.P.; resources, S.S., M.F.F. and B.P; data curation, S.S. and M.F.F.; writing—original draft preparation, S.S., M.F.F. and B.P.; writing—review and editing, M.F.F. and B.P.; visualisation, S.S., M.F.F. and B.P.; supervision, M.F.F. and P.B.L.; project administration, P.B.L.; funding acquisition, P.B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly financed by FCT/MCTES through national funds (PIDDAC) under the R&D Unit ISISE under reference UIDB/04029/2020. This study has been partly funded by the STAND4HERITAGE project that has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant agreement No. 833123), as an Advanced Grant.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the reported results in the present study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Failure Mechanisms for Running Bond with μ = 0.5.
Table A1.
Failure Mechanisms for Running Bond with μ = 0.5.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix B

Table A2.
Failure Mechanisms for Running bond with μ = 0.65.
Table A2.
Failure Mechanisms for Running bond with μ = 0.65.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix C

Table A3.
Failure Mechanisms for Running Bond with μ = 0.8.
Table A3.
Failure Mechanisms for Running Bond with μ = 0.8.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix D

Table A4.
Failure Mechanisms for Flemish Bond with μ = 0.50.
Table A4.
Failure Mechanisms for Flemish Bond with μ = 0.50.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix E

Table A5.
Failure Mechanisms for Flemish Bond with μ = 0.65.
Table A5.
Failure Mechanisms for Flemish Bond with μ = 0.65.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix F

Table A6.
Failure Mechanisms for Flemish Bond with μ = 0.80.
Table A6.
Failure Mechanisms for Flemish Bond with μ = 0.80.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix G

Table A7.
Failure Mechanisms for English Bond with μ = 0.50.
Table A7.
Failure Mechanisms for English Bond with μ = 0.50.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix H

Table A8.
Failure Mechanisms for English Bond with μ = 0.65.
Table A8.
Failure Mechanisms for English Bond with μ = 0.65.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix I

Table A9.
Failure Mechanisms for English Bond with μ = 0.80.
Table A9.
Failure Mechanisms for English Bond with μ = 0.80.
| Block Aspect Ratio BR | ||||
| 1.0 | 2.0 | 4.0 | ||
| Panel aspect ratio PR | 0.5 |  | ||
| 1.0 | ||||
| 2.0 | ||||
Appendix J. Comparison of Macro and Micro Load multiplier for All Dataset, with Difference (%) = (l micro − l Macro)/ l Micro × 100

Table A10.
Comparison of Macro and Micro Load multiplier for.
Table A10.
Comparison of Macro and Micro Load multiplier for.
| BOND | PR | BR | Friction Coeff. | l Micro | l Macro | Percentile Error |
|---|---|---|---|---|---|---|
| Running | 0.5 | 4 | 0.50 | 0.50 | 0.64 | 27.88 |
| Running | 0.5 | 4 | 0.65 | 0.65 | 0.69 | 6.22 |
| Running | 0.5 | 4 | 0.80 | 0.80 | 0.73 | 8.62 |
| Flemish | 0.5 | 4 | 0.50 | 0.50 | 0.71 | 41.18 |
| Flemish | 0.5 | 4 | 0.65 | 0.65 | 0.77 | 18.27 |
| Flemish | 0.5 | 4 | 0.80 | 0.77 | 0.82 | 6.32 |
| English | 0.5 | 4 | 0.50 | 0.50 | 0.64 | 27.88 |
| English | 0.5 | 4 | 0.65 | 0.65 | 0.69 | 6.22 |
| English | 0.5 | 4 | 0.80 | 0.77 | 0.73 | 5.6 |
| Running | 0.5 | 2 | 0.50 | 0.47 | 0.43 | 8.71 |
| Running | 0.5 | 2 | 0.65 | 0.50 | 0.45 | 8.38 |
| Running | 0.5 | 2 | 0.80 | 0.51 | 0.47 | 8.09 |
| Flemish | 0.5 | 2 | 0.50 | 0.43 | 0.55 | 27.72 |
| Flemish | 0.5 | 2 | 0.65 | 0.49 | 0.59 | 20.99 |
| Flemish | 0.5 | 2 | 0.80 | 0.53 | 0.62 | 16.07 |
| English | 0.5 | 2 | 0.50 | 0.42 | 0.43 | 2.44 |
| English | 0.5 | 2 | 0.65 | 0.46 | 0.45 | 0.6 |
| English | 0.5 | 2 | 0.80 | 0.49 | 0.47 | 4.43 |
| Running | 0.5 | 1 | 0.50 | 0.27 | 0.25 | 6.18 |
| Running | 0.5 | 1 | 0.65 | 0.27 | 0.25 | 5.89 |
| Running | 0.5 | 1 | 0.80 | 0.27 | 0.25 | 5.98 |
| Flemish | 0.5 | 1 | 0.50 | 0.30 | 0.35 | 18.68 |
| Flemish | 0.5 | 1 | 0.65 | 0.31 | 0.37 | 18.25 |
| Flemish | 0.5 | 1 | 0.80 | 0.31 | 0.37 | 19.41 |
| English | 0.5 | 1 | 0.50 | 0.26 | 0.25 | 2.57 |
| English | 0.5 | 1 | 0.65 | 0.26 | 0.25 | 4.84 |
| English | 0.5 | 1 | 0.80 | 0.27 | 0.25 | 5.42 |
| Running | 1 | 4 | 0.50 | 0.50 | 0.51 | 2.03 |
| Running | 1 | 4 | 0.65 | 0.65 | 0.56 | 14.25 |
| Running | 1 | 4 | 0.80 | 0.72 | 0.60 | 16.6 |
| Flemish | 1 | 4 | 0.50 | 0.50 | 0.49 | 3.03 |
| Flemish | 1 | 4 | 0.65 | 0.61 | 0.54 | 12.63 |
| Flemish | 1 | 4 | 0.80 | 0.69 | 0.58 | 15.87 |
| English | 1 | 4 | 0.50 | 0.50 | 0.51 | 2.03 |
| English | 1 | 4 | 0.65 | 0.58 | 0.56 | 4.33 |
| English | 1 | 4 | 0.80 | 0.64 | 0.60 | 7.27 |
| Running | 1 | 2 | 0.50 | 0.40 | 0.43 | 8.03 |
| Running | 1 | 2 | 0.65 | 0.44 | 0.45 | 3.38 |
| Running | 1 | 2 | 0.80 | 0.48 | 0.47 | 1.05 |
| Flemish | 1 | 2 | 0.50 | 0.40 | 0.50 | 24.59 |
| Flemish | 1 | 2 | 0.65 | 0.47 | 0.54 | 15.6 |
| Flemish | 1 | 2 | 0.80 | 0.52 | 0.57 | 10.55 |
| English | 1 | 2 | 0.50 | 0.37 | 0.43 | 16.75 |
| English | 1 | 2 | 0.65 | 0.42 | 0.45 | 8.14 |
| English | 1 | 2 | 0.80 | 0.46 | 0.47 | 3.44 |
| Running | 1 | 1 | 0.50 | 0.26 | 0.25 | 3.35 |
| Running | 1 | 1 | 0.65 | 0.27 | 0.25 | 5.78 |
| Running | 1 | 1 | 0.80 | 0.26 | 0.25 | 2.34 |
| Flemish | 1 | 1 | 0.50 | 0.30 | 0.35 | 18.66 |
| Flemish | 1 | 1 | 0.65 | 0.31 | 0.36 | 16.83 |
| Flemish | 1 | 1 | 0.80 | 0.32 | 0.37 | 14.73 |
| English | 1 | 1 | 0.50 | 0.24 | 0.25 | 3.73 |
| English | 1 | 1 | 0.65 | 0.27 | 0.25 | 6.64 |
| English | 1 | 1 | 0.80 | 0.27 | 0.25 | 7.98 |
| Running | 2 | 4 | 0.50 | 0.42 | 0.33 | 21.76 |
| Running | 2 | 4 | 0.65 | 0.42 | 0.37 | 14.03 |
| Running | 2 | 4 | 0.80 | 0.43 | 0.40 | 7.59 |
| Flemish | 2 | 4 | 0.50 | 0.41 | 0.29 | 29.48 |
| Flemish | 2 | 4 | 0.65 | 0.42 | 0.33 | 22.84 |
| Flemish | 2 | 4 | 0.80 | 0.43 | 0.36 | 17.19 |
| English | 2 | 4 | 0.50 | 0.40 | 0.33 | 17.8 |
| English | 2 | 4 | 0.65 | 0.41 | 0.37 | 11.2 |
| English | 2 | 4 | 0.80 | 0.42 | 0.40 | 6.21 |
| Running | 2 | 2 | 0.50 | 0.34 | 0.35 | 2.76 |
| Running | 2 | 2 | 0.65 | 0.36 | 0.36 | 1.55 |
| Running | 2 | 2 | 0.80 | 0.37 | 0.36 | 0.85 |
| Flemish | 2 | 2 | 0.50 | 0.35 | 0.35 | 0.21 |
| Flemish | 2 | 2 | 0.65 | 0.37 | 0.38 | 3.91 |
| Flemish | 2 | 2 | 0.80 | 0.38 | 0.40 | 5.77 |
| English | 2 | 2 | 0.50 | 0.33 | 0.35 | 6.17 |
| English | 2 | 2 | 0.65 | 0.35 | 0.36 | 4.31 |
| English | 2 | 2 | 0.80 | 0.36 | 0.36 | 0.41 |
| Running | 2 | 1 | 0.50 | 0.22 | 0.25 | 13.04 |
| Running | 2 | 1 | 0.65 | 0.26 | 0.25 | 3.94 |
| Running | 2 | 1 | 0.80 | 0.25 | 0.25 | 0.73 |
| Flemish | 2 | 1 | 0.50 | 0.28 | 0.33 | 15.73 |
| Flemish | 2 | 1 | 0.65 | 0.30 | 0.33 | 10.25 |
| Flemish | 2 | 1 | 0.80 | 0.31 | 0.33 | 5.83 |
| English | 2 | 1 | 0.50 | 0.23 | 0.25 | 6.63 |
| English | 2 | 1 | 0.65 | 0.26 | 0.25 | 2.41 |
| English | 2 | 1 | 0.80 | 0.26 | 0.25 | 2.68 |
References
- Sharma, S.; Silva, L.C.; Graziotti, F.; Magenes, G.; Milani, G. Modelling the Experimental Seismic Out-of-Plane Two-Way Bending Response of Unreinforced Periodic Masonry Panels Using a Non-Linear Discrete Homogenized Strategy. Eng. Struct. 2021, 242, 112524. [Google Scholar] [CrossRef]
- Zhang, S.; Beyer, K. Numerical Investigation of the Role of Masonry Typology on Shear Strength. Eng. Struct. 2019, 192, 86–102. [Google Scholar] [CrossRef]
- Stepinac, M.; Kisicek, T.; Renić, T.; Hafner, I.; Bedon, C. Methods for the Assessment of Critical Properties in Existing Masonry Structures under Seismic Loads—The ARES Project. Appl. Sci. 2020, 10, 1576. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gonen, S.; Parisi, F.; Erdogmus, E.; Tuncay, K.; Funari, M.F.; Lourenço, P.B. Probabilistic Approach to Assess URM Walls with Openings Using Discrete Rigid Block Analysis (D-RBA). J. Build. Eng. 2022, 61, 105269. [Google Scholar] [CrossRef]
- Stepinac, M.; Gašparović, M. A Review of Emerging Technologies for an Assessment of Safety and Seismic Vulnerability and Damage Detection of Existing Masonry Structures. Appl. Sci. 2020, 10, 5060. [Google Scholar] [CrossRef]
- Saloustros, S. Tracking Localized Cracks in the Computational Analysis of Masonry Structures. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2017. [Google Scholar]
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. Modeling Strategies for the Computational Analysis of Unreinforced Masonry Structures: Review and Classification. Arch. Comput. Methods Eng. 2020, 27, 1153–1185. [Google Scholar] [CrossRef]
- Roca, P.; Cervera, M.; Gariup, G.; Pela’, L. Structural Analysis of Masonry Historical Constructions. Classical and Advanced Approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
- Funari, M.F.; Silva, L.C.; Savalle, N.; Lourenço, P.B. A Concurrent Micro/Macro FE-Model Optimised with a Limit Analysis Tool for the Assessment of Dry-Joint Masonry Structures. Int. J. Multiscale Comput. Eng. 2021, 20, 65–85. [Google Scholar] [CrossRef]
- Guo, Y.T.; Bompa, D.V.; Elghazouli, A.Y. Nonlinear Numerical Assessments for the In-Plane Response of Historic Masonry Walls. Eng. Struct. 2022, 268, 114734. [Google Scholar] [CrossRef]
- Elghazouli, A.Y.; Bompa, D.V.; Mourad, S.A.; Elyamani, A. In-Plane Lateral Cyclic Behaviour of Lime-Mortar and Clay-Brick Masonry Walls in Dry and Wet Conditions. Bull. Earthq. Eng. 2021, 19, 5525–5563. [Google Scholar] [CrossRef]
- Pulatsu, B.; Bretas, E.M.; Lourenço, P.B. Discrete Element Modeling of Masonry Structures: Validation and Application. Earthq. Struct. 2016, 11, 563–582. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Lemos, J.V.; Hazzard, J. Discontinuum Analysis of the Fracture Mechanism in Masonry Prisms and Wallettes via Discrete Element Method. Meccanica 2020, 55, 505–523. [Google Scholar] [CrossRef]
- Sarhosis, V.; Bagi, K.; Lemos, J.; Milani, G. Computational Modeling of Masonry Structures Using the Discrete Element Method; IGI Global: Hershey, PA, USA, 2016. [Google Scholar]
- Malomo, D.; Mehrotra, A.; DeJong, M.J. Distinct Element Modeling of the Dynamic Response of a Rocking Podium Tested on a Shake Table. Earthq. Eng. Struct. Dyn. 2021, 50, 1469–1475. [Google Scholar] [CrossRef]
- Malomo, D.; DeJong, M.J.; Penna, A. Influence of Bond Pattern on the In-Plane Behavior of URM Piers. Int. J. Archit. Herit. 2019, 15, 1492–1511. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of Masonry Structures. Int. J. Archit. Herit. 2007, 1, 190–213. [Google Scholar] [CrossRef]
- Lemos, J.V. Discrete Element Modeling of the Seismic Behavior of Masonry Construction. Buildings 2019, 9, 43. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gonen, S.; Lourenço, P.B.; Lemos, J.V.; Hazzard, J. Computational Investigations on the Combined Shear-Torsion-Bending Behavior of Dry-Joint Masonry Using DEM. Comput. Part. Mech. 2022. [Google Scholar] [CrossRef]
- Pulatsu, B.; Gencer, F.; Erdogmus, E. Study of the Effect of Construction Techniques on the Seismic Capacity of Ancient Dry-Joint Masonry Towers through DEM. Eur. J. Environ. Civ. Eng. 2020, 26, 3913–3930. [Google Scholar] [CrossRef]
- Cundall, P.A. A Computer Model for Simulating Progressive, Large-Scale Movements in Blocky Rock Systems. In Proceedings of the Symposium of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Jean, M. The Non-Smooth Contact Dynamics Method. Comput. Methods Appl. Mech. Eng. 1999, 177, 235–257. [Google Scholar] [CrossRef]
- Moreau, J. Unilateral Contact and Dry Friction in Finite Freedom Dynamics. In Nonsmooth Mechanics and Applications; Springer: Vienna, Austria, 1988; pp. 1–82. [Google Scholar]
- Beatini, V.; Royer-Carfagni, G.; Tasora, A. A Regularized Non-Smooth Contact Dynamics Approach for Architectural Masonry Structures. Comput. Struct. 2017, 187, 88–100. [Google Scholar] [CrossRef]
- Clementi, F.; Ferrante, A.; Giordano, E.; Dubois, F.; Lenci, S. Damage Assessment of Ancient Masonry Churches Stroked by the Central Italy Earthquakes of 2016 by the Non-Smooth Contact Dynamics Method. Bull. Earthq. Eng. 2020, 18, 455–486. [Google Scholar] [CrossRef]
- Dubois, F.; Acary, V.; Jean, M. The Contact Dynamics Method: A Nonsmooth Story. Comptes Rendus Mécanique 2018, 346, 247–262. [Google Scholar] [CrossRef]
- Rafiee, A.; Vinches, M. Mechanical Behaviour of a Stone Masonry Bridge Assessed Using an Implicit Discrete Element Method. Eng. Struct. 2013, 48, 739–749. [Google Scholar] [CrossRef]
- Isfeld, A.; Shrive, N. Discrete Element Modeling of Stone Masonry Walls with Varying Core Conditions: Prince of Wales Fort Case Study. Int. J. Archit. Herit. 2015, 9, 564–580. [Google Scholar] [CrossRef]
- Ferrante, A.; Clementi, F.; Milani, G. Advanced Numerical Analyses by the Non-Smooth Contact Dynamics Method of an Ancient Masonry Bell Tower. Math. Methods Appl. Sci. 2020, 43, 7706–7725. [Google Scholar] [CrossRef]
- Degli Abbati, S.; D’Altri, A.M.; Ottonelli, D.; Castellazzi, G.; Cattari, S.; de Miranda, S.; Lagomarsino, S. Seismic Assessment of Interacting Structural Units in Complex Historic Masonry Constructions by Nonlinear Static Analyses. Comput. Struct. 2019, 213, 51–71. [Google Scholar] [CrossRef]
- Pelà, L.; Cervera, M.; Roca, P. An Orthotropic Damage Model for the Analysis of Masonry Structures. Constr. Build. Mater. 2013, 41, 957–967. [Google Scholar] [CrossRef]
- Berto, L.; Saetta, A.; Scotta, R.; Vitaliani, R. An Orthotropic Damage Model for Masonry Structures. Int. J. Numer. Methods Eng. 2002, 55, 127–157. [Google Scholar] [CrossRef]
- Szabó, S.; Kövesdi, A.; Vasáros, Z.; Csicsely, Á.; Hegyi, D. The Cause of Damage and Failure of the Mud-Brick Vault of the Khan in New-Gourna. Eng. Fail. Anal. 2021, 128, 105567. [Google Scholar] [CrossRef]
- Fortunato, G.; Funari, M.F.; Lonetti, P. Survey and Seismic Vulnerability Assessment of the Baptistery of San Giovanni in Tumba (Italy). J. Cult. Herit. 2017, 26, 64–78. [Google Scholar] [CrossRef]
- Funari, M.F.; Hajjat, A.E.; Masciotta, M.G.; Oliveira, D.V.; Lourenço, P.B. A Parametric Scan-to-FEM Framework for the Digital Twin Generation of Historic Masonry Structures. Sustainability 2021, 13, 11088. [Google Scholar] [CrossRef]
- Cluni, F.; Gusella, V. Homogenization of Non-Periodic Masonry Structures. Int. J. Solids Struct. 2004, 41, 1911–1923. [Google Scholar] [CrossRef]
- Sacco, E. A Nonlinear Homogenisation Procedure for Periodic Masonry. Eur. J. Mech. 2009, 28, 209–222. [Google Scholar] [CrossRef]
- Milani, G.; Esquivel, Y.W.; Lourenço, P.B.; Riveiro, B.; Oliveira, D.V. Characterization of the Response of Quasi-Periodic Masonry: Geometrical Investigation, Homogenization and Application to the Guimarães Castle, Portugal. Eng. Struct. 2013, 56, 621–641. [Google Scholar] [CrossRef]
- Dolatshahi, K.; Yekrangnia, M. Out-of-Plane Strength Reduction of Unreinforced Masonry Walls Because of in-Plane Damages. Earthq. Eng. Struct. Dyn. 2015, 44, 2157–2176. [Google Scholar] [CrossRef]
- Meriggi, P.; de Felice, G.; De Santis, S.; Gobbin, F.; Mordanova, A.; Pantò, B. Distinct Element Modelling of Masonry Walls under Out-Of-Plane Seismic Loading. Int. J. Archit. Herit. 2019, 13, 1110–1123. [Google Scholar] [CrossRef]
- Block, P.; Ciblac, T.; Ochsendorf, J. Real-Time Limit Analysis of Vaulted Masonry Buildings. Comput. Struct. 2006, 84, 1841–1852. [Google Scholar] [CrossRef]
- Fraternali, F. A Thrust Network Approach to the Equilibrium Problem of Unreinforced Masonry Vaults via Polyhedral Stress Functions. Mech. Res. Commun. 2010, 37, 198–204. [Google Scholar] [CrossRef]
- Marmo, F.; Masi, D.; Rosati, L. Thrust Network Analysis of Masonry Helical Staircases. Int. J. Archit. Herit. 2018, 12, 828–848. [Google Scholar] [CrossRef]
- Funari, M.F.; Silva, L.C.; Mousavian, E.; Lourenço, P.B. Real-Time Structural Stability of Domes through Limit Analysis: Application to St. Peter’s Dome. Int. J. Archit. Herit. 2021, 1–23. [Google Scholar] [CrossRef]
- Funari, M.F.; Mehrotra, A.; Lourenço, P.B. A Tool for the Rapid Seismic Assessment of Historic Masonry Structures Based on Limit Analysis Optimisation and Rocking Dynamics. Appl. Sci. 2021, 11, 942. [Google Scholar] [CrossRef]
- Giuffrè, A. Letture sulla Meccanica delle Murature Storiche; Kappa: Rome, Italy, 1990. [Google Scholar]
- Rios, A.J.; Pingaro, M.; Reccia, E.; Trovalusci, P. Statistical Assessment of In-Plane Masonry Panels Using Limit Analysis with Sliding Mechanism. J. Eng. Mech. 2022, 148, 04021158. [Google Scholar] [CrossRef]
- Casapulla, C.; Cascini, L.; Portioli, F.; Landolfo, R. 3D Macro and Micro-Block Models for Limit Analysis of out-of-Plane Loaded Masonry Walls with Non-Associative Coulomb Friction. Meccanica 2014, 49, 1653–1678. [Google Scholar] [CrossRef]
- Casapulla, C.; Portioli, F.; Maione, A.; Landolfo, R. A Macro-Block Model for in-Plane Loaded Masonry Walls with Non-Associative Coulomb Friction. Meccanica 2013, 48, 2107–2126. [Google Scholar] [CrossRef]
- Casapulla, C.; Argiento, L.U.; Maione, A.; Speranza, E. Upgraded Formulations for the Onset of Local Mechanisms in Multi-Storey Masonry Buildings Using Limit Analysis. Structures 2021, 31, 380–394. [Google Scholar] [CrossRef]
- Funari, M.F.; Pulatsu, B.; Szabó, S.; Lourenço, P.B. A Solution for the Frictional Resistance in Macro-Block Limit Analysis of Non-Periodic Masonry. Structures 2022, 43, 847–859. [Google Scholar] [CrossRef]
- Gilbert, M.; Casapulla, C.; Ahmed, H.M. Limit Analysis of Masonry Block Structures with Non-Associative Frictional Joints Using Linear Programming. Comput. Struct. 2006, 84, 873–887. [Google Scholar] [CrossRef]
- Casapulla, C.; Argiento, L.U. The Comparative Role of Friction in Local Out-of-Plane Mechanisms of Masonry Buildings. Pushover Analysis and Experimental Investigation. Eng. Struct. 2016, 126, 158–173. [Google Scholar] [CrossRef]
- Funari, M.F.; Spadea, S.; Lonetti, P.; Fabbrocino, F.; Luciano, R. Visual Programming for Structural Assessment of Out-of-Plane Mechanisms in Historic Masonry Structures. J. Build. Eng. 2020, 31, 101425. [Google Scholar] [CrossRef]
- Funari, M.F.; Spadea, S.; Ciantia, M.; Lonetti, P.; Greco, F. Visual Programming for the Structural Assessment of Historic Masonry Structures. In Proceedings of the REHABEND 2020, Granada, Spain, 24–27 March 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).