Free Vibration Analysis of Thick Annular Functionally Graded Plate Integrated with Piezo-Magneto-Electro-Elastic Layers in a Hygrothermal Environment

Abstract

The present work aims at investigating the hygrothermal effect on the natural frequencies of functionally graded (FG) annular plates integrated with piezo-magneto-electro-elastic layers resting on a Pasternak elastic foundation. The formulation is based on a layer-wise (LW) theory, where the Hamiltonian principle is used to obtain the governing equation of the problem involving temperature- and moisture-dependent material properties. The differential quadrature method (DQM) is applied here as a numerical strategy to solve the governing equations for different boundary conditions. The material properties of FG annular plates are varied along the thickness based on a power law function. The accuracy of the proposed method is, first, validated for a limit-case example. A sensitivity study of the free vibration response is, thus, performed for different input parameters, such as temperature and moisture variations, elastic foundation, boundary conditions, electric and magnetic potential of piezo-magneto-electro-elastic layers and geometrical ratios, with useful insights from a design standpoint.

1. Introduction

Functionally graded materials (FGMs) are well-known to be designed and produced for thermal protection of high-speed spacecrafts, ships and underwater vessels due to their outstanding mechanical properties. Nowadays, FGMs have been adopted in modern applications such as aircraft, civil engineering and other structures in thermal conditions with high temperatures. Hence, the investigation of their mechanical behavior, such as the vibration of FGM structures, is of great interest for structural designers even in a nonlocal sense. Reddy et al. [1] presented a nonlinear finite element approach to FG circular plates with a modified couple stress theory (MCST) and the first-order shear deformation theory (FSDT) to study their deflection response. Sofiyev et al. [2] analyzed the stability and vibration of three-layered conical shells with a FGM layer subjected to an axial compressive load. A novel sinusoidal shear deformation theory for bending, buckling and vibration of FG plates was developed by Thai and Vo [3], involving a sinusoidal distribution of transverse shear stresses, with only four unknowns, differently from conventional sinusoidal shear deformation theories. At the same time, Jooybar et al. [4] studied the thermal effect on the free vibration response of FG truncated conical shell panels while applying the Hamiltonian principle and FSDT to determine the governing equations of motion. Shaban and Alipour [5] proposed a semianalytical solution for the natural frequencies of thick FG plates resting on an elastic foundation. Jodaei et al. [6] studied the free vibration response of functionally graded piezoelectric (FGP) annular plates based on a 3D elasticity, where a reduced sensitivity of thinner plates to the FGM volume fraction index and boundary conditions was found. In another paper, Nateghi et al. [7] carried out a size-dependent buckling analysis of FG microbeams by means of a modified couple stress theory.

Sandwich constructions with thin facesheets and lightweight cores are largely applied in aircraft, aviation, satellites and naval applications because of their specific lightweight, stiffness and fatigue resistance. Recently, annular sandwich plates were used as structural elements in primary structures of an aircraft/helicopter, such as floor panels, wings, ailerons and rotor blades. To use them, a good knowledge of their constructional properties and dynamic behavior is crucial. Kheirkhah et al. [8] developed a biaxial buckling analysis of soft-core composite sandwich plates using an improved higher-order theory. In this work, a third-order plate theory was applied to model facesheets, whereas quadratic and cubic functions were considered for an accurate description of the transverse and in-plane displacements of the core. The governing equations and boundary conditions were derived by applying the principle of minimum potential energy. A refined zigzag theory was employed by Ghorbanpour Arani et al. [9] for the study of the vibration response of viscoelastic functionally graded carbon nanotube-reinforced composite (FG-CNTRC) microplates with piezoelectric layers. The Kelvin–Voigt model was used to present a realistic sandwich microplate immersed within a magnetic and electric field together with an orthotropic visco-Pasternak foundation. The governing equations of the problem were developed using the Hamiltonian principle, and they were solved using a Navier-type solution. The results showed a meaningful effect of the volume fraction on the natural frequency response of the structure, controlled by the electric and magnetic parameters. Allahverdizadeh et al. [10] discussed the structural modeling, vibration study and optimal viscoelastic layer characterization of adaptive sandwich beams with an electrorheological fluid (ERF) core, based on Timoshenko beam theory. Wang et al. [11] analyzed the aeroelastic dynamic stability of rotating annular sandwich plates with a viscoelastic core layer. The aerodynamic force acting on the plate was described by a rotating damping model, and the governing equations were solved based on the Galerkin method. Pandit et al. [12] applied an improved higher-order zigzag theory to investigate the buckling response of laminated sandwich plates with a soft core. The accuracy and range of applicability of the formulation proposed by the authors were established by comparing their results with 3D elasticity solutions. Romanoff and Reddy [13] presented an experimental validation of the modified couple stress Timoshenko beam theory for web-core sandwich panels. Among different refined theories for plate and shell structures, the layer-wise (LW) theory represents a valid strategy to account for the thickness effects with a minimum computational cost. Differently from the equivalent single layer formulations, the LW theory supposes a separate displacement field expansion within each subdivision and provides a kinematically correct representation of the strain field in discrete layers. In literature, Ranjbaran et al. [14] studied the buckling response of a sandwich plate using the LW theory, whose equations of motion were solved by means of the Rayleigh–Ritz approach. Malekzadeh et al. [15] developed a three-dimensional LW finite element for the free vibration analysis of thick laminated annular plates on an elastic foundation. In this work, the governing equations were obtained using the Hamiltonian principle. A zigzag-elasticity plate theory was applied, instead, by Alipour and Shariyat [16] to study the stress state of annular FGM sandwich plates with non-uniform normal and shear tractions, whose responses showed that the use of FGM facesheets or FGM cores could prevent failure. Ferreira et al. [17] presented a static and vibration analysis of composite sandwich plates by means of the LW theory and a novel numerical scheme, where a collocation by radial basis functions was capable of producing highly accurate results. Alipour and Shariyat [18] investigated an analytical LW free vibration response of circular annular composite sandwich plates with an auxetic core. In another work [19], the same authors applied the LW formulation to study the effect of elastic boundary constraints on the stress state of annular FG sandwich plates under a distributed loading condition. As stated before, FGMs were basically designed for thermal protection issues such that a large variety of works in literature has shown the effect of thermal environments on the mechanical behavior of FGM systems [20,21,22,23,24]. Akbarzadeh and Chen [25] analyzed the hygrothermal stresses in one-dimensional FG piezoelectric media under a constant magnetic field. In that paper, the moisture concentration and temperature distributions across the thickness of one-dimensional media were achieved by solving analytically the steady-state Fickian moisture diffusion and Fourier heat conduction equations. Lee and Kim [26] applied the FSDT to study the hygrothermal postbuckling behavior of FGM plates, as provided by classical finite elements and the Newton–Raphson iterative scheme. Based on the results, it was found that the frequency of the system decreases with an increasing moisture. Sobhy [27] developed an accurate shear deformation theory for the vibration and buckling of FGM sandwich plates in a hygrothermal environment. Mansouri and Shariyat [28] discussed the biaxial thermo-mechanical buckling of orthotropic auxetic FGM plates with moisture- and temperature-dependent material properties on an elastic foundation. The higher-order shear deformation governing differential equations were solved numerically accounting for the influence of moisture and temperature.

The main advantage of DQM-based numerical solutions over analytical predictions lies in the large flexibility of the selection of different boundary conditions. In this context, Ghorbanpour Arani et al. [29] analyzed the dynamic instability of visco-double-walled carbon nanotubes according to a sinusoidal strain gradient theory using the DQM and Bolotin method. Gurtin–Murdoch elasticity theory was also adopted in their research to include the surface stress effects while modeling the visco-Pasternak foundation as an elastic medium. Ke et al. [30] investigated the free vibration of nonlocal piezoelectric nanoplates, whose balance equations were solved numerically based on the DQM for different boundary conditions, temperatures, electric fields and mechanical loads. Accordingly, Eshraghi et al. [31] discussed the bending and free vibration response of FG annular and circular microplates under thermal loading. In another paper, Li et al. [32] analyzed the free vibration and buckling response of magneto-electro-elastic nanoplates with nonlocal models, accounting for the variation in both electric and magnetic potentials along the thickness direction of nanoplates while solving the equations of motion in an analytical sense. In Ref. [33], Akbarzadeh and Chen assessed the magneto-electro-elastic response of rotating cylinders resting on an elastic foundation under a hygrothermal loading. In their analyses, the authors considered the moisture and temperature dependence of the elastic coefficients for a uniform rise in moisture and temperature concentration. Wang and Zhang [34] also studied the postbuckling and thermal buckling response of temperature-dependent porous nanocomposite beams reinforced by graphene platelets as provided by a high-order shear deformation theory.

Based on the above-mentioned literature overview, however, it seems that the natural frequencies of thick annular FGM plate integrated with magneto-electro-elastic layers in a hygro-thermal environment have not been investigated to date. Thus, starting with limited information from the available literature, in the present work we focus on the free vibration of FG annular plates integrated with piezo-magneto-electro-elastic external skins. Meanwhile, the material properties of FG annular plates are supposed to vary in thickness according to the power law function. The selected sandwich structures are supposed to be immersed within an electric field and an elastic Pasternak foundation. The problem is studied according to the LW theory, whereby the equilibrium equations are obtained by means of the Hamiltonian principle. A numerical differential quadrature strategy is used, herein, to compute the frequency response according to different boundary conditions, along with different temperatures and moisture, foundation coefficients, external electric and magnetic potentials, as well as outer-inner radius ratios, power indexes and thickness ratios.

2. Theoretical Basics

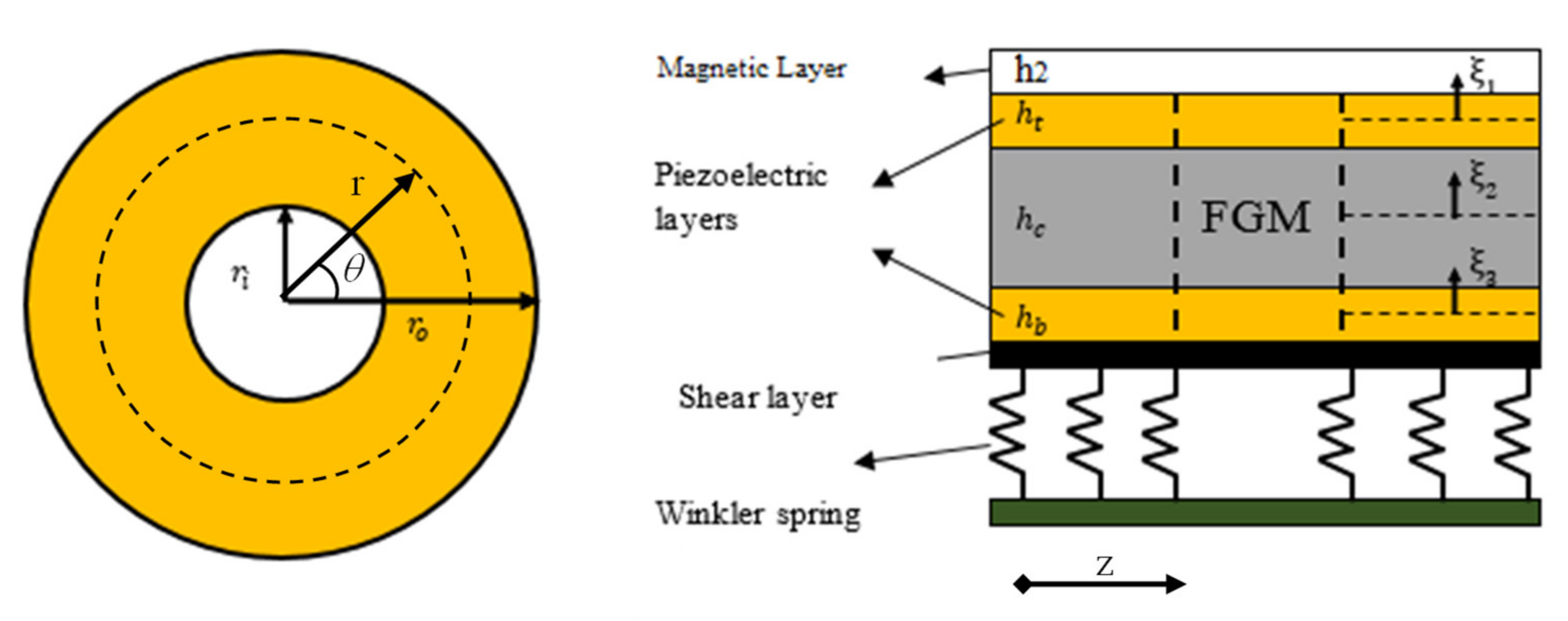
In this section, we determine the equilibrium equations of the problem, including the constitutive equations and a potential field for FG annular plates integrated with piezo-magneto-electric layers. The geometry of a FG annular sandwich plate polarized in the thickness direction in cylindrical $(r,\theta ,z)$ coordinates is depicted in Figure 1. The selected structure has inner and outer radii, $r_i$, $r_o$, respectively; an internal core of thickness, $h_c$; and external sheets with thicknesses, $h_t$ and $h_b$, at the top and bottom sides, respectively. This sandwich structure is subjected to both moisture and thermal variation, $\Delta C,$ and $\Delta T,$ together with an electric potential. It is worth mentioning that $\Delta T=T-T_0$ and $\Delta C=C-C_0$, in which $T$ and $C$ describe the absolute temperature and moisture concentration, respectively, and $C_0$, $T_0$ refer to the reference moisture concentration and temperature, respectively. The core layer of the sandwich plate is made of a FGM with material properties graded in the thickness direction, following the power law for the ceramic volume fraction $V_c$ of the following type [3]:

$$V_c={\left(\frac{z}{h_c}+\frac{1}{2}\right)}^g,\hspace{1em}\hspace{1em}g\ge 0$$

(1)

Based on Voigt’s rule, an arbitrary property, $P$, of a FG annular plate can be defined as a function of the constituent properties and volume fractions as follows:

$$P(z)=P_m+P_{cm}{\left(\frac{z}{h_c}+\frac{1}{2}\right)}^g,\hspace{1em}\hspace{1em}{P}_{cm}=P_c-P_m$$

(2)

in which $P_c$ and $P_m$ refer to the properties of the ceramic and metal phase, respectively, and $g$ is a non-negative constant, such as a power law index. In this paper, the modulus of elasticity ($E$), density, moisture and thermal expansion coefficient, $\beta$ and $\alpha$, are graded according to Equation (2), while Poisson’s ratio, $\upsilon$, is assumed constant in the thickness direction.

In line with the zigzag-sandwich plate theory, the radial displacement component can be considered as result of a superposition of global and local effects. Thus, by using linear global and local displacement fields and by enforcing the kinematic continuity conditions at the interfaces among layers, the LW displacement fields of the sandwich plate can be described as follows [16]:

$$U^t=u_0+{\zeta }^t{\theta }_r^t+\frac{h_t}{2}{\theta }_r^t+\frac{h_c}{2}{\theta }_r^c,\hspace{1em}\hspace{1em}-\frac{h_t}{2}\le {\zeta }^t\le \frac{h_t}{2}$$

(3)

$$U^c=u_0+{\zeta }^c{\theta }_r^c\hspace{1em}\hspace{1em}-\frac{h_c}{2}\le {\zeta }^c\le \frac{h_c}{2}$$

(4)

$$U^b=u_0+{\zeta }^b{\theta }_r^b-\frac{h_b}{2}{\theta }_r^b-\frac{h_c}{2}{\theta }_r^c,\hspace{1em}\hspace{1em}-\frac{h_b}{2}\le {\zeta }^b\le \frac{h_b}{2}$$

(5)

$$W=w_0$$

(6)

where $u_0$ and $w_0$ stand for the radial and transverse displacement of the mid-plane per each layer, respectively. Three transverse local coordinates are defined for the core $({\zeta }^c),$ top facesheet $({\zeta }^t)$ and bottom facesheet $({\zeta }^b),$ whereas ${\theta }_r^i\hspace{0.17em}(\mathrm{superscript}\hspace{0.17em}\hspace{0.17em}i=t,b\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}c)$ represents the local rotation for the ith layer. Therefore, the strain components are defined as follows:

$${\epsilon }_r^i=\frac{\partial U^i}{\partial r},\hspace{1em}{\epsilon }_{\theta }^i=\frac{U^i}{r},\hspace{1em}{\epsilon }_{rz}^i=\frac{\partial U^i}{\partial z}+\frac{\partial W}{\partial r}.$$

(7)

In a piezoelectric/piezomagnetic material, the application of an electric and magnetic field causes a strain field proportional to the mechanical strength, and vice versa. The constitutive equations for stresses $\left(\sigma \right)$, electric displacements $\left(D\right)$ and magnetic displacement $\left(B\right)$ for the piezoelectric facesheets obtain the following form:

$${\sigma }_r^{}=Q_{11}^{}{\epsilon }_r+Q_{12}^{}{\epsilon }_{\theta }-e_{31}^{}{E}_z-d_{31}^{}{H}_z-{\lambda }_{11}\Delta T-{\varsigma }_{11}\Delta C,$$

(8)

$${\sigma }_{\theta }^{}=Q_{12}^{}{\epsilon }_r+Q_{22}^{}{\epsilon }_{\theta }-e_{31}^{}{E}_z-d_{31}^{}{H}_z-{\lambda }_{22}\Delta T-{\varsigma }_{22}\Delta C,$$

(9)

$${\tau }_{rz}^{}=Q_{55}^{}{\epsilon }_{rz}+e_{15}^{}{E}_r+d_{15}^{}{H}_r,$$

(10)

$$D_r=e_{15}{\epsilon }_{rz}+{\in }_{11}{E}_r+g_{11}{H}_r+{\gamma }_1\Delta T+{\chi }_1\Delta C,$$

(11)

$$D_z=e_{31}({\epsilon }_{rz}+{\epsilon }_{\theta })+{\in }_{33}{E}_z+g_{33}{H}_z+{\gamma }_3\Delta T+{\chi }_3\Delta C,$$

(12)

$$B_r=d_{15}{\epsilon }_{rz}+g_{11}{E}_r+{\mu }_{11}{H}_r+{\tau }_1\Delta T+{\nu }_1\Delta C,$$

(13)

$$B_z=d_{15}({\epsilon }_{rz}+{\epsilon }_{\theta })+g_{33}{E}_z+{\mu }_{33}{H}_z+{\tau }_3\Delta T+{\nu }_3\Delta C,$$

(14)

where $Q_{11}^{}$ and $Q_{12}^{}$ describe the elastic stiffness; $Q_{55}^{}$ is the shear moduli of the piezoelectric layers; ${\in }_{11}$ and ${\in }_{33}$ are the dielectric constants; $e_{15}^{}$ and $e_{31}^{}$ are the piezoelectric coefficient; $d_{15}^{}$ and $d_{31}^{}$ describe the piezomagnetic coefficients; $g_{11}^{}$ and $g_{33}^{}$ are the electromagnetic coefficients; ${\mu }_{11}^{}$ and ${\mu }_{33}^{}$ are the magnetic permeability coefficients; ${\tau }_1$ and ${\tau }_3$ are the pyromagnetic coefficients; ${\nu }_1$ and ${\nu }_3$ are the hygromagnetic coefficients; ${\varsigma }_{11}$ and ${\lambda }_{11}$ represent the hygroscopic stress and thermal stress coefficients; and $p_q$ and ${\chi }_q(q=1,2)$ are the pyroelectric and hygroelectric coefficients, respectively. It should be noted that the thermal stress and hygroscopic stress coefficients are related to the elastic coefficient, thermal expansion coefficient $\alpha$ and moisture expansion coefficient $\beta$ as follows:

$${\lambda }_{qp}=Q_{kl}{\alpha }_{qp},\hspace{1em}\hspace{1em}(p=1,2),(k,l=1,2,5)$$

(15)

$${\varsigma }_{qp}=Q_{kl}{\beta }_{qp}$$

(16)

Meanwhile, the electric and magnetic fields $E_j,H_j(j=r,z)$ in terms of electric potential $(\Phi )$ and magnetic potential $(\Psi )$ can be written as follows [6]:

$$E_j=-\nabla {\Phi }_j$$

(17)

$$H_j=-\nabla {\Psi }_j$$

(18)

The electric and magnetic potential distributions $\Phi (r,\theta ,t)$, $\Psi (r,\theta ,t)$ in the thickness direction of the piezoelectric layer, at time, $t$, are defined as a combination of a half-cosine and linear variation, which satisfies the Maxwell equation [31]:

$${\Phi }^t(r,\theta ,z,t)=-\cos \left(\frac{\pi {\zeta }^t}{h_t}\right){\phi }^t(r,\theta ,t)+\frac{2{\zeta }^t{V}_0}{h_t},$$

(19)

$${\Phi }^b(r,\theta ,z,t)=-\cos \left(\frac{\pi {\zeta }^b}{h_b}\right){\phi }^b(r,\theta ,t),$$

(20)

$${\Psi }^t(r,\theta ,z,t)=-\cos \left(\frac{\pi {\zeta }^t}{h_t}\right){\psi }^t(r,\theta ,t)+\frac{2{\zeta }^t{\lambda }_0}{h_t},$$

(21)

$${\Psi }^b(r,\theta ,z,t)=-\cos \left(\frac{\pi {\zeta }^b}{h_b}\right){\psi }^b(r,\theta ,t),$$

(22)

where ${\Phi }^t$ and ${\Phi }^b$ represent the electric potential at the top and bottom layers of the sandwich structure, respectively, whereas ${\Psi }^t$ and ${\Psi }^b$ refer to the magnetic potential at the top and bottom layers, respectively. The same considerations can be repeated for the magnetic potential. Additionally, $V_0$ and ${\lambda }_0$ represent the external electric and magnetic potentials, respectively. The stress components in the core layer are assumed to be graded as follows:

$${\sigma }_r^c=\frac{E(z)}{1-{\upsilon }^2}({\epsilon }_r+\upsilon {\epsilon }_{\theta })-{\beta }_{11}\Delta T-{\varsigma }_{11}\Delta C,$$

(23)

$${\sigma }_{\theta }^c=\frac{E(z)}{1-{\upsilon }^2}({\epsilon }_{\theta }+\upsilon {\epsilon }_r)-{\beta }_{22}\Delta T-{\varsigma }_{22}\Delta C,$$

(24)

$${\tau }_{rz}^c=\frac{E(z)}{2(1+\upsilon )}{\epsilon }_{rz},$$

(25)

3. Governing Equations of the Problem

The governing equations of the problem are determined by applying the Hamiltonian principle within the time interval $\left[t_0,t_1\right]$ as follows:

$${\displaystyle {\int }_{t_0}^{t_1}\left[\delta U-\delta K-\delta W\right]}=0,$$

(26)

where $\delta U$, $\delta W$ and $\delta K$ are the variations in the strain energy, external work and kinetic energy, respectively. More specifically, the strain energy of the piezoelectric plate is defined as follows:

$$\begin{array}{cc}U=& \frac{1}{2}({\displaystyle {\int }_{r_i}^{r_o}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{-\frac{h_t}{2}}^{\frac{h_t}{2}}\left({\sigma }_r^t{\epsilon }_r^t+\right.{\sigma }_{\theta }^t{\epsilon }_{\theta }^t+2{\tau }_{rz}^t{\epsilon }_{rz}^t-D_r^t{E}_r^t-\left.D_z^t{E}_z^t-B_r^t{H}_r^t-B_z^t{H}_z^t\right)rd\theta drd{\zeta }^t}}}\hfill \\ & +{\displaystyle {\int }_{r_i}^{r_o}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{-\frac{h_c}{2}}^{\frac{h_c}{2}}\left({\sigma }_r^c{\epsilon }_r^c+\right.{\sigma }_{\theta }^c{\epsilon }_{\theta }^c+\left.2{\tau }_{rz}^c{\epsilon }_{rz}^c\right)rd\theta drd{\zeta }^c}}}\hfill \\ & {\displaystyle {\int }_{r_i}^{r_o}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{-\frac{h_b}{2}}^{\frac{h_b}{2}}\left({\sigma }_r^b{\epsilon }_r^b+\right.{\sigma }_{\theta }^b{\epsilon }_{\theta }^b+2{\tau }_{rz}^b{\epsilon }_{rz}^b-D_r^b{E}_r^b-\left.D_z^b{E}_z^b-B_r^b{H}_r^b-B_z^b{H}_z^b\right)rd\theta drd{\zeta }^b}}})\hfill \end{array}$$

(27)

The total kinetic energy of the annular sandwich plate is expressed as follows:

$$K=\frac{1}{2}\left({\displaystyle {\int }_{r_i}^{r_o}{\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\rho }_{}^i\left\{\left({\left({\dot{U}}_{}^i\right)}^2+{\left({\dot{W}}_{}^i\right)}^2\right)\right\}}rdrd\theta d{\zeta }^i}}\right.$$

(28)

where $h$ is the total thickness of structure. Moreover, the work conducted by the external forces is defined as follows:

$$W=\frac{1}{2}{\displaystyle {\int }_{r_i}^{r_o}{\displaystyle {\int }_0^{2\pi }\left(\left(N_t+N_e+N_m\right)\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)+k_{w}w-k_g\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)\right)}}rdrd\theta ,$$

(29)

where $k_w$ and $k_g$ define the Winkler and Pasternak stiffnesses, respectively; $N_t$, $N_c$, $N_e$ and $N_m$ refer to the normal forces induced by the temperature variation, $\Delta T$, moisture change, $\Delta C$, and external electric and magnetic potentials, which are, in turn, defined as follows:

$$N_e=2e_{31}^{}{V}_0,\hspace{1em}{N}_t=\lambda h_i\Delta T,\hspace{1em}{N}_c=\varsigma h_i\Delta C\hspace{1em}\hspace{1em}{N}_m=2d_{31}^{}{\lambda }_0.$$

(30)

By substituting Equations (27)–(29) into Equation (26), we obtain the following governing equations of motion:

$$\begin{array}{l}\frac{N_r^b-N_{\theta }^b}{r}+\frac{\partial N_r^b}{\partial r}+\frac{N_r^c-N_{\theta }^c}{r}+\frac{\partial N_r^c}{\partial r}+\frac{N_r^t-N_{\theta }^t}{r}+\frac{\partial N_r^t}{\partial r}=\left(I_0^b+I_0^c+I_0^t\right){\ddot{u}}_0\\ +\left(I_0^t\frac{h_t}{2}+I_1^t\right){\ddot{\theta }}_r^t+I_1^b{\ddot{\theta }}_r^c+\left(I_1^b-I_0^b\frac{h_b}{2}\right){\ddot{\theta }}_r^b,\end{array}$$

(31)

$$\begin{array}{c}\frac{h_t}{2}\left(\frac{N_r^t-N_{\theta }^t}{r}+\frac{\partial N_r^t}{\partial r}\right)+\frac{M_r^t-M_{\theta }^t}{r}+\frac{\partial M_r^t}{\partial r}-Q_{rz}^t=\left(I_0^t\frac{h_t}{2}+I_1^t\right){\ddot{u}}_0\hfill \\ +\frac{h_b}{2}\left(\frac{h_t}{2}{I}_0^t+I_1^t\right){\ddot{\theta }}_r^b+\left[I_2^t+h_t{I}_1^t+{\left(\frac{h_t}{2}\right)}^2{I}_0^t\right]{\ddot{\theta }}_r^t,\hfill \end{array}$$

(32)

$$\begin{array}{l}\frac{h_c}{2}\left(\frac{N_r^t-N_{\theta }^t}{r}+\frac{\partial N_r^t}{\partial r}\right)-\frac{h_c}{2}\left(\frac{N_r^b-N_{\theta }^b}{r}+\frac{\partial N_r^b}{\partial r}\right)+\frac{M_r^c-M_{\theta }^c}{r}+\frac{\partial M_r^c}{\partial r}-Q_{rz}^c=\\ \left(\frac{h_c}{2}{I}_0^t+I_1^c-\frac{h_2}{2}{I}_0^b\right){\ddot{u}}_0+\frac{h_c}{2}\left(I_1^t+\frac{h_t}{2}{I}_0^t\right){\ddot{\theta }}_r^t+\left[{\left(\frac{h_c}{2}\right)}^2\left(I_0^t+I_0^b\right)+I_2^c\right]{\ddot{\theta }}_r^c\\ -\frac{h_c}{2}\left(I_1^b-\frac{h_b}{2}{I}_0^b\right){\ddot{\theta }}_r^b,\end{array}$$

(33)

$$\begin{array}{l}-\frac{h_b}{2}\left(\frac{N_r^b-N_{\theta }^b}{r}+\frac{\partial N_r^b}{\partial r}\right)+\frac{M_r^b-M_{\theta }^b}{r}+\frac{\partial M_r^c}{\partial r}-Q_{rz}^b=\left(I_1^b-\frac{h_b}{2}{I}_0^b\right){\ddot{u}}_0\\ +\left[I_2^b-h_b{I}_1^b+{\left(\frac{h_b}{2}\right)}^2{I}_0^b\right]{\ddot{\theta }}_r^b+\frac{h_c}{2}\left(\frac{h_b}{2}{I}_0^b-I_1^b\right){\ddot{\theta }}_r^c,\end{array}$$

(34)

$$\begin{array}{l}\frac{\partial Q_r^b}{\partial r}+\frac{Q_r^b}{r}+\frac{\partial Q_r^c}{\partial r}+\frac{Q_r^c}{r}+\frac{\partial Q_r^t}{\partial r}+\frac{Q_r^t}{r}-\left(N_t+N_m+N_e+N_c\right)\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)\\ \left.+k_{w}w-k_g\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{\partial w}{r\partial r}\right)\right)=\left(I_0^t+I_0^b+I_0^c\right){\ddot{w}}_0,\end{array}$$

(35)

$${\displaystyle {\int }_{-\frac{h_b}{2}}^{\frac{h_b}{2}}\left[\cos \left(\frac{\pi {\zeta }^b}{h_b}\right)\frac{\partial D_r}{\partial r}+\frac{\pi }{h_b}\sin \left(\frac{\pi {\zeta }^b}{h_b}\right)D_z\right]}d{\zeta }^b=0,$$

(36)

$${\displaystyle {\int }_{-\frac{h_t}{2}}^{\frac{h_t}{2}}\left[\cos \left(\frac{\pi {\zeta }^t}{h_t}\right)\frac{\partial D_r}{\partial r}-\frac{\pi }{h_t}\sin \left(\frac{\pi {\zeta }^t}{h_t}\right)D_z\right]}d{\zeta }^t=0,$$

(37)

$${\displaystyle {\int }_{-\frac{h_b}{2}}^{\frac{h_b}{2}}\left[\cos \left(\frac{\pi {\zeta }^b}{h_b}\right)\frac{\partial B_r}{\partial r}+\frac{\pi }{h_b}\sin \left(\frac{\pi {\zeta }^b}{h_b}\right)B_z\right]}d{\zeta }^b=0,$$

(38)

$${\displaystyle {\int }_{-\frac{h_t}{2}}^{\frac{h_t}{2}}\left[\cos \left(\frac{\pi {\zeta }^t}{h_t}\right)\frac{\partial B_r}{\partial r}-\frac{\pi }{h_t}\sin \left(\frac{\pi {\zeta }^t}{h_t}\right)B_z\right]}d{\zeta }^t=0,$$

(39)

The stress resultants $M$, $N$ and $Q$ can be described as follows:

$${\displaystyle {\int }_{-\frac{h_t}{2}}^{\frac{h_t}{2}}\left[\cos \left(\frac{\pi {\zeta }^t}{h_t}\right)\frac{\partial B_r}{\partial r}-\frac{\pi }{h_t}\sin \left(\frac{\pi {\zeta }^t}{h_t}\right)B_z\right]}d{\zeta }^t=0,$$

(40)

$$Q_r^i={\displaystyle {\int }_{-\frac{h_i}{2}}^{\frac{h_i}{2}}{\tau }_{rz}^{i}d{\zeta }^i,}\hspace{1em}\hspace{1em}\hspace{1em}i=t,c,b\hspace{1em}\hspace{1em}j=r,\theta$$

(41)

and

$$I_f^i={\displaystyle {\int }_{-\frac{h_i}{2}}^{\frac{h_i}{2}}{\rho }^i}{\zeta }^{ik}d{\zeta }^i,\hspace{1em}\hspace{1em}f=0,1,2$$

(42)

More details about these terms can be found in Appendix A.

Various boundary conditions at both edges of the sandwich plate are, thus, assumed as follows [18]:

• Clamped edge:

$$\left\{\begin{array}{l}{u}_0=0\\ {\theta }_r^t=0\\ {\theta }_r^c=0\\ {\theta }_r^b=0\\ w_0=0\end{array}\right.,$$

(43)

• Simply supported edge:

$$\left\{\begin{array}{l}{u}_0=0\\ \frac{h_t}{2}{N}_r^t+M_r^t=0\\ \frac{h_c}{2}{N}_r^t+M_r^c-\frac{h_c}{2}{N}_r^b=0\\ -\frac{h_b}{2}{N}_r^b+M_r^b=0\\ w=0\end{array}\right.,$$

(44)

• Free edge:

$$\left\{\begin{array}{l}{N}_r^t+N_r^c+N_r^b=0\\ \frac{h_t}{2}{N}_r^t+M_r^t=0\\ \frac{h_c}{2}{N}_r^t+M_r^c-\frac{h_c}{2}{N}_r^b=0\\ -\frac{h_b}{2}{N}_r^b+M_r^b=0\\ Q_r^t+Q_r^c+Q_r^b=0\end{array}\right.,$$

(45)

The DQM is now adopted to solve the equilibrium equations. In this numerical method, the partial derivative of a function with respect to the spatial variables at a given discrete point is approximated as a weighted linear sum of the function values at all discrete points chosen in the solution domain. According to the DQM, the nth order partial derivative of a function $F\left(r\right)$ can be approximated as follow [31]:

$$\frac{{\partial }^{n}F(r_j)}{\partial r^n}={\displaystyle \sum _{k=1}^N{A}_{jk}^{(n)}F(r_k),}\hspace{1em}\hspace{1em}\hspace{1em}n=1,\dots ,N-1$$

(46)

in which $N$ is the total number of grid points and $A_{jk}^{(n)}$ represents the weighting coefficients. The Chebyshev–Gauss–Lobatto polynomials are here adopted to determine the spaced position of the grid points [31], namely:

$$r_j=r_i+\frac{r_o-r_i}{2}\left(1-\cos \left(\frac{2j-1}{N-1}\right)\pi \right).$$

(47)

where $r_i$ and $r_o$ are the inner and external radii, respectively. At the end, based on Equation (46), the motion equations can be written in matrix form as:

$$[K_D]+[M]{\omega }^2\left\{\begin{array}{l}{Y}_b\\ Y_d\end{array}\right\}=\left\{\begin{array}{l}0\\ 0\end{array}\right\},$$

(48)

in which $\left[K_D\right]$ is the stiffness matrix, $\left[M\right]$ is the mass matrix and $\omega$ refers to the circular natural frequencies of the system. The dynamic displacement vector $\left[Y\right]$ for both boundary and domain points is expressed as follows:

$$\left[Y\right]=\left[{\left\{u_0\right\}}^T,{\left\{{\theta }_r^t\right\}}^T,{\left\{{\theta }_r^c\right\}}^T,{\left\{{\theta }_r^b\right\}}^T,{\left\{w_0\right\}}^T,{\left\{{\Phi }^t\right\}}^T,{\left\{{\Phi }^b\right\}}^T,{\left\{{\Psi }^t\right\}}^T,{\left\{{\Psi }^b\right\}}^T\right].$$

(49)

4. Numerical Results

A large parametric investigation was performed to check for the sensitivity of the vibration response for the FG annular plates covered by magneto-electro-elastic layers, and surrounded by a Pasternak foundation, for different input parameters, primarily, temperature, moisture, external voltage, different boundary conditions, elastic foundations, thickness ratio, power index and number of grid points. The properties of ${\mathrm{BaTiO}}_3{/\mathrm{CoFeO}}_4$, ceramic (alumina) and metal (aluminum) are presented in

Table 1. Material properties of ${\mathrm{BaTiO}}_3{/\mathrm{CoFeO}}_4$ [33].

Properties
$Q_{11}(\mathrm{Pa})$	$2.86\times {10}^{11}$
$Q_{12}(\mathrm{Pa})$	$1.73\times {10}^{11}$
$Q_{55}(\mathrm{Pa})$	$0.453\times {10}^{11}$
$e_{31}(\mathrm{C}/{\mathrm{m}}^2)$	$-4.4$
$e_{33}(\mathrm{C}/{\mathrm{m}}^2)$	$18.6$
$d_{31}(\mathrm{N}/\mathrm{Am})$	$580.3$
$d_{33}(\mathrm{N}/\mathrm{Am})$	$699.7$
${\in }_{11}({\mathrm{C}}^2/{\mathrm{Nm}}^2)$	$8.0\times {10}^{-11}$
${\in }_{33}({\mathrm{C}}^2/{\mathrm{Nm}}^2)$	$9.3\times {10}^{-11}$
$g_{11}=g_{33}$	$3.0\times {10}^{-12}$
${\mu }_{11}\left({\mathrm{Ns}}^2/{\mathrm{C}}^2\right)$	$-590\times {10}^{-6}$
${\mu }_{33}\left({\mathrm{Ns}}^2/{\mathrm{C}}^2\right)$	$157\times {10}^{-6}$
${\alpha }_{11}={\alpha }_{22}(/\mathrm{K})$	$1\times {10}^{-6}$
${\beta }_{11}\left({\mathrm{m}}^3/\mathrm{kg}\right)$	$0$
${\beta }_{33}\left({\mathrm{m}}^3/\mathrm{kg}\right)$	$1.1\times {10}^{-4}$
${\chi }_1={\chi }_3(\mathrm{Cm}/\mathrm{Kg})$	$0$
${\tau }_1={\tau }_3\left(\mathrm{N}/\mathrm{AmK}\right)$	$6.0\times {10}^{-3}$
${\gamma }_1={\gamma }_3(\mathrm{C}/{\mathrm{m}}^2\mathrm{K})$	$-13.0\times {10}^{-5}$
${\nu }_1={\nu }_3\left(\mathrm{N}/{\mathrm{Am}}^2\mathrm{Kg}\right)$	$0$

and

Table 2. Material properties of ceramic and metal [27].

Properties
$E_c(\mathrm{Pa})$	$380\times {10}^9$
${\rho }_c(\mathrm{kg}/{\mathrm{m}}^3)$	$3800$
${\alpha }_c(/\mathrm{K})$	$7\times {10}^{-6}$
${\beta }_c{({\mathrm{wt}\%\mathrm{H}}_2\mathrm{O})}^{-1}$	$0.001$
${\upsilon }_c={\upsilon }_m$	$0.3$
$E_m(\mathrm{Pa})$	$70$
${\rho }_m(\mathrm{kg}/{\mathrm{m}}^3)$	$2707$
${\alpha }_m(/\mathrm{K})$	$23\times {10}^{-6}$
${\beta }_m{({\mathrm{wt}\%\mathrm{H}}_2\mathrm{O})}^{-1}$	$0.44$

, in line with Refs. [33] and [27], respectively.

At the same time, in the attempt to validate the proposed formulation, a simplified analysis was carried out, first, without considering the external facesheets, the hygrothermal environment and the LW theory, in line with Refs. [6,35]. The dimensionless frequency ${\omega }^{\ast }=\omega h\sqrt{{\rho }_{}/C_{11}}$ was, thus, determined, for different grid point discretization, as reported in

Table 3. Validation of present work with respect to Refs. [6,35].

Frequencies	Reference			$\mathit{N}$
		5	7	8	9	10
${\omega }_1^{\ast }$	Jodaei et al. [6]	0.081	0.08	0.0798	0.0797	0.0796
	Nie and Zhang [35]	0.0798	0.0812	0.0814	0.0802	0.0807
	Present	0.0805	0.0797	0.0795	0.0795	0.0795
${\omega }_2^{\ast }$	Jodaei et al. [6]	0.0834	0.083	0.0827	0.0827	0.0826
	Nie and Zhang [35]	0.0829	0.0843	0.0843	0.0832	0.0837
	Present	0.0828	0.0827	0.0822	0.0822	0.0822
${\omega }_3^{\ast }$	Jodaei et al. [6]	0.0954	0.0957	0.0953	0.0953	0.0952
	Nie and Zhang [35]	0.0956	0.0969	0.0968	0.0958	0.0961
	Present	0.0948	0.0952	0.095	0.095	0.095

, being $C_{11}=E(1-\upsilon )/(1+\upsilon )(1-2\upsilon )$.

The accuracy and convergence of the DQM-based results are summarized in

Table 4. Convergence behavior and accuracy of the DQM.

$\mathit{g}$	Grid Points (N)	${\mathit{\omega }}^{\ast }$	${\mathit{\omega }}^{\ast }$	${\mathit{\omega }}^{\ast }$
		$\Delta \mathit{T}=0\left[°\mathbf{C}\right]$	$\Delta \mathit{T}=100\left[°\mathbf{C}\right]$	$\Delta \mathit{T}=200\left[°\mathbf{C}\right]$
1	5	12.4713	12.3882	12.3046
	7	13.3089	13.2251	13.1407
	8	13.3076	13.2238	13.1394
	10	13.3076	13.2238	13.1394
2	5	12.0093	11.9403	11.8710
	7	12.7439	12.6747	12.6051
	8	12.7437	12.6745	12.6049
	10	12.7437	12.6745	12.6049
3	5	11.7305	11.6691	11.6074
	7	12.4071	12.3456	12.2838
	8	12.4070	12.3455	12.2837
	10	12.4070	12.3455	12.2837

in terms of dimensionless frequency for the selected sandwich annular plate, with clamped supports at both edges under different variations in temperature. More specifically, the dimensionless frequency is computed as

$${\omega }^{\ast }=\omega r_i^2\sqrt{{\rho }_t{h}_t/D}$$

(50)

in which

$$D=E_m{h}_t^3/12(1-{\upsilon }_m^2)$$

(51)

Moreover, in order to verify the free vibration of the annular plate by considering the electromagnetic layer, it is sufficient to consider the material property and geometry used in Ref. [36]. A comparison between the present results and Ref. [36] is shown in

Table 5. Validation of present work with respect to Ref. [36].

${\mathit{\omega }}^{\ast }{}_{{}_1}$	VE	Dimensionless Frequency (ω)
		${\mathit{\Omega }}_{\mathit{h}}=-{10}^6$	${\mathit{\Omega }}_{\mathit{h}}=0$	${\mathit{\Omega }}_{\mathit{h}}={10}^6$
Reference	−108	2.88	3.08	3.25
	0	2.85	3.06	3.23
	108	2.83	3.02	3.21
Present	−108	2.91	3.16	3.33
	0	2.94	3.16	3.31
	108	2.87	3.10	3.30

. As can be seen from this table, there is excellent agreement between them.

The results are derived for different values of DQM grid points, with a fast rate of convergence, even with a reduced number of grid points equal to eight. Thus, the systematic investigation accounts for the effects of the Winkler and Pasternak coefficients on the dimensionless frequency, as plotted in Figure 2 and Figure 3 vs. the radial ratio of the annular sandwich plates. The thickness and radial ratios are set here as $h_t/h_c=0.5$ and $r_i/r_o=0.2$, whereas temperature and moisture variations are assumed to be null, i.e., $\Delta T=0$ and $\Delta C=0$, respectively. As visible in Figure 2 and Figure 3, an increasing radial ratio gradually reduces the value of the frequency. As the Winkler and Pasternak coefficients increase, the dimensionless frequency also increases due to an increased stiffness and stability in the structure for the same radial ratio $r_i/r_o$. At the same time, the effect of the Pasternak coefficient is more effective than the Winkler one. This is due to the presence of both normal and transverse shear loads, as considered in the Pasternak foundation but not in the Winkler one, which is described in the normal direction. Figure 4 shows the variation in the dimensionless frequency with the thickness ratio under different external electric potentials while assuming $k_w=0$, $k_g=0$, $\Delta T=0$ and $\Delta C=0$. Note that the application of an electric potential can vary the frequency response of the sandwich structure, whereby a negative electric potential decreases the dimensionless frequency, and a positive voltage can yield the opposite effect. The enforcement of negative/positive voltages, indeed, seems to generate an axial compressive/tensile force in the top layer, with a consecutive variation in the overall structural stiffness. This means that the application of an external electric potential is an effective controlling parameter for the behavior of the structure. Figure 5 describes the variation in the dimensionless frequency with the thickness ratios under different external magnetic potentials, $\lambda$. Based on the plots in this figure, it is clear that a negative magnetic potential decreases the dimensionless frequency under the same thickness ratio assumption, where the contrary occurs under the application of a positive voltage. The influence of a power law index, $g$, on the dimensionless frequency is illustrated in Figure 6 for different $r_i/r_o$ ratios while keeping a null value for $k_w,k_g$ in the clamped structure. As visible from the plots in the figures below, the dimensionless frequency decreases monotonically for an increased power index under a fixed $r_i/r_o$ ratio, with a clear upward shift of curves, for an increased rational value of $r_i/r_o$.

Another parameter that can be changed to control the stability of a system, however, is represented by moisture. As plotted in Figure 7, the frequency features a monotone decrease for an increasing $r_i/r_o$ ratio under the same assumption for $\Delta C$, whereas an increase in moisture can provide a slight reduction in the frequency response under the same assumption for $r_i/r_o$. A more pronounced sensitivity of the frequency response is noticed in temperature. As plotted in Figure 8, an increased temperature variation seems to reduce the frequency response of the structure with a fixed geometry due to an overall reduction in its stiffness. The highest sensitivity, in any case, is observed for different structural constraints, as depicted comparatively in Figure 9 for clamped–clamped, clamped–simply and simply–simply supports, as well as different radial ratios, while keeping $g=0$ and $\left(h_c/h_t\right)=2.5$ fixed. Note that the use of clamped supports makes the structure stiffer and more stable such that it could support higher loads than simply supported structures.

5. Conclusions

This paper investigated the vibration of FG annular plates integrated with magneto-electro-elastic layers subjected to a hygrothermal environment and resting on an elastic foundation. The LW theory is proposed to define the problem, whose governing equations are derived from the Hamiltonian principle. Thus, the DQM is successfully applied as an efficient numerical tool to solve the problem for the different enforcements of boundary conditions. A large numerical campaign investigated the effect of varying Pasternak and Winkler coefficients, external voltage, temperature and moisture, thickness ratio, radial ratio and boundary conditions. Based on a comparative evaluation of results, it seems that an increased temperature or moisture yields a decrease in frequency and stability of the annular structure. At the same time, increased external electric and magnetic potentials, enable an overall increase in the natural frequency of the annular sandwich plate. In any case, we noticed that there exists an inverse relationship between radial ratio and frequency response of the annular sandwich plates, such that higher radial ratios can significantly reduce the structural stiffness and dimensionless frequency. Finally, it was found that increased values of the Pasternak and Winkler coefficients can enable an overall increase in the structural stiffness, with a consequent increase in natural frequencies.