Discretization of the Urban and Non-Urban Shape: Unsupervised Machine Learning Techniques for Territorial Planning
Abstract
1. Introduction
2. Materials and Methods
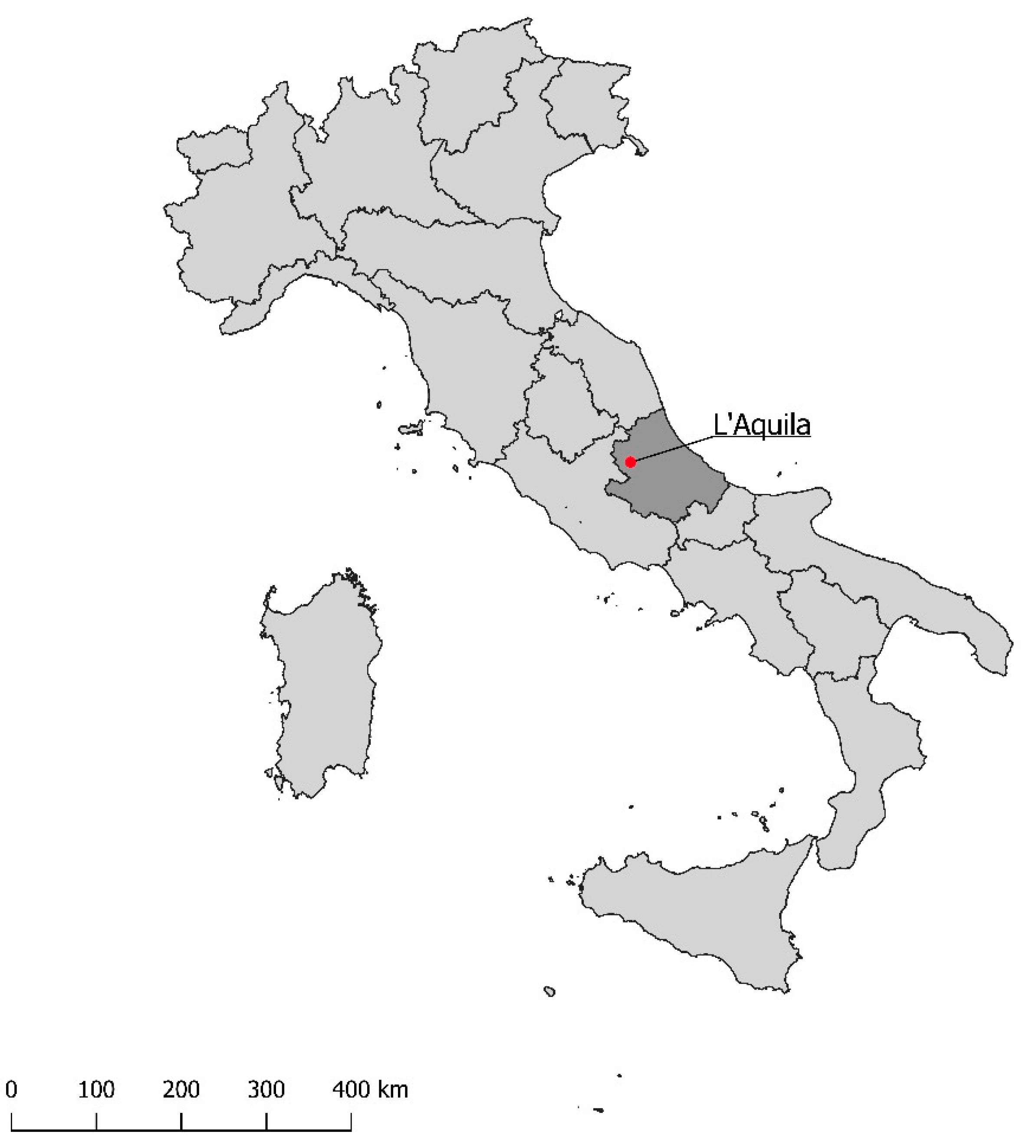
2.1. Study Area and Dataset
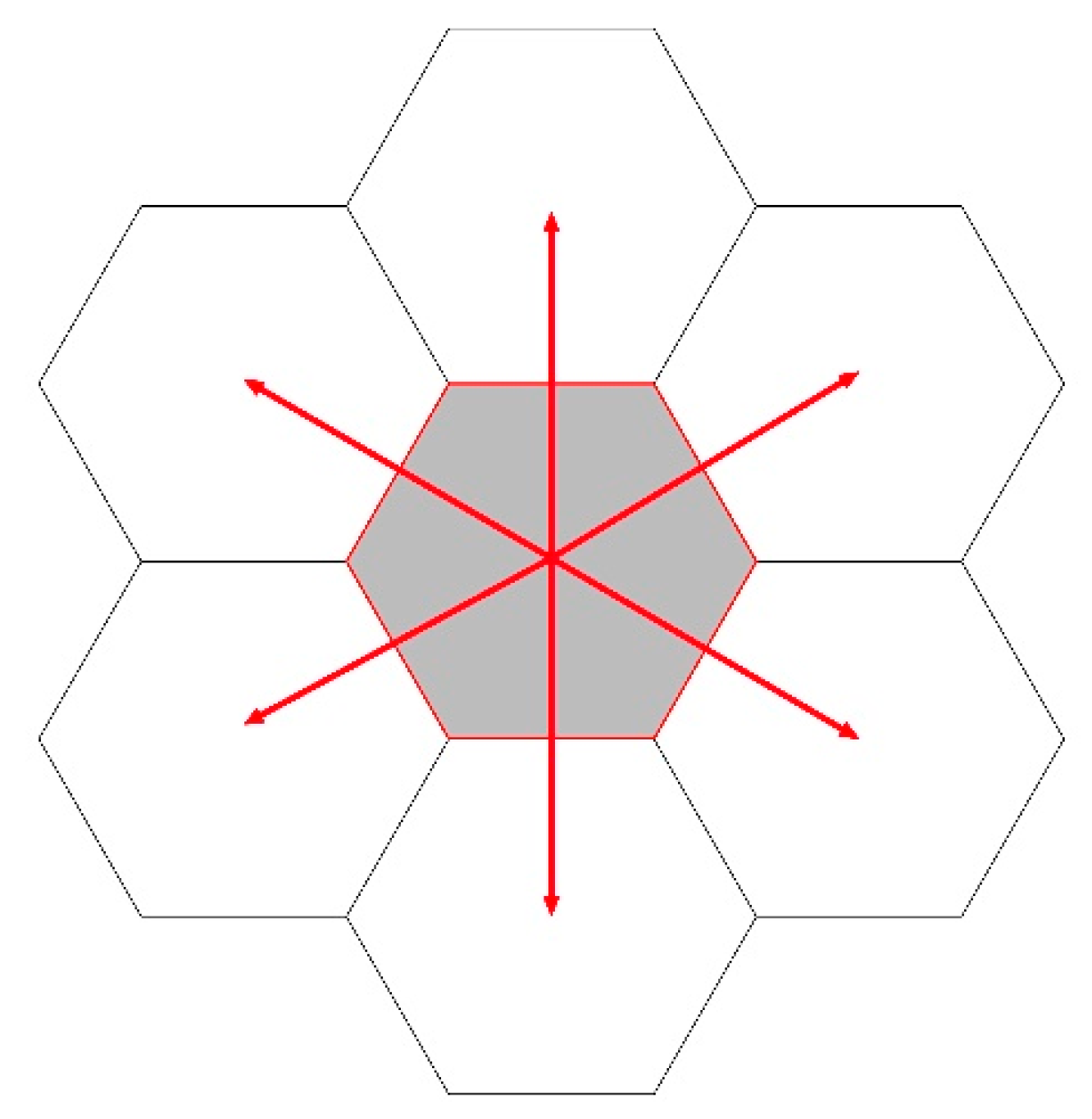
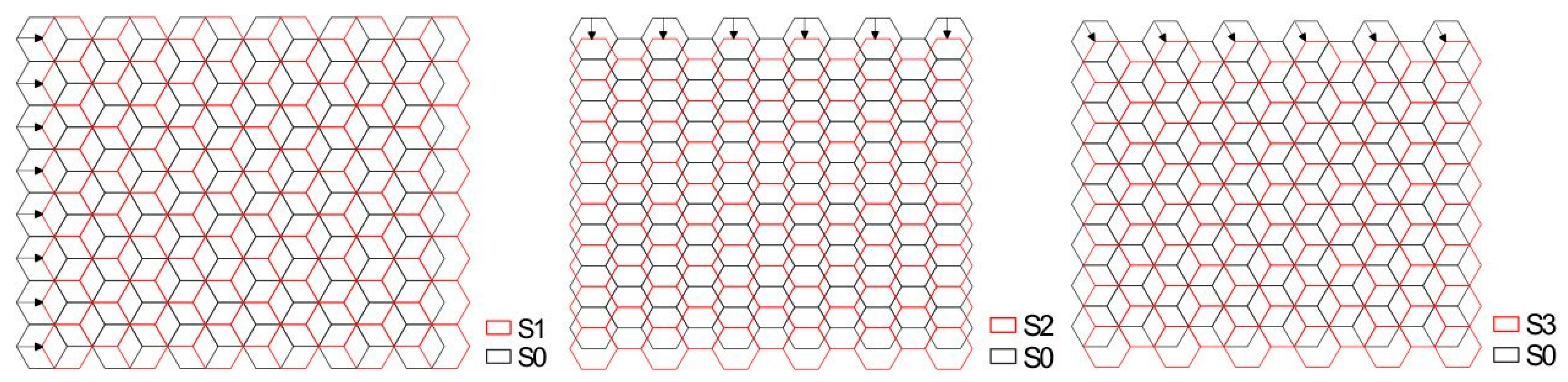
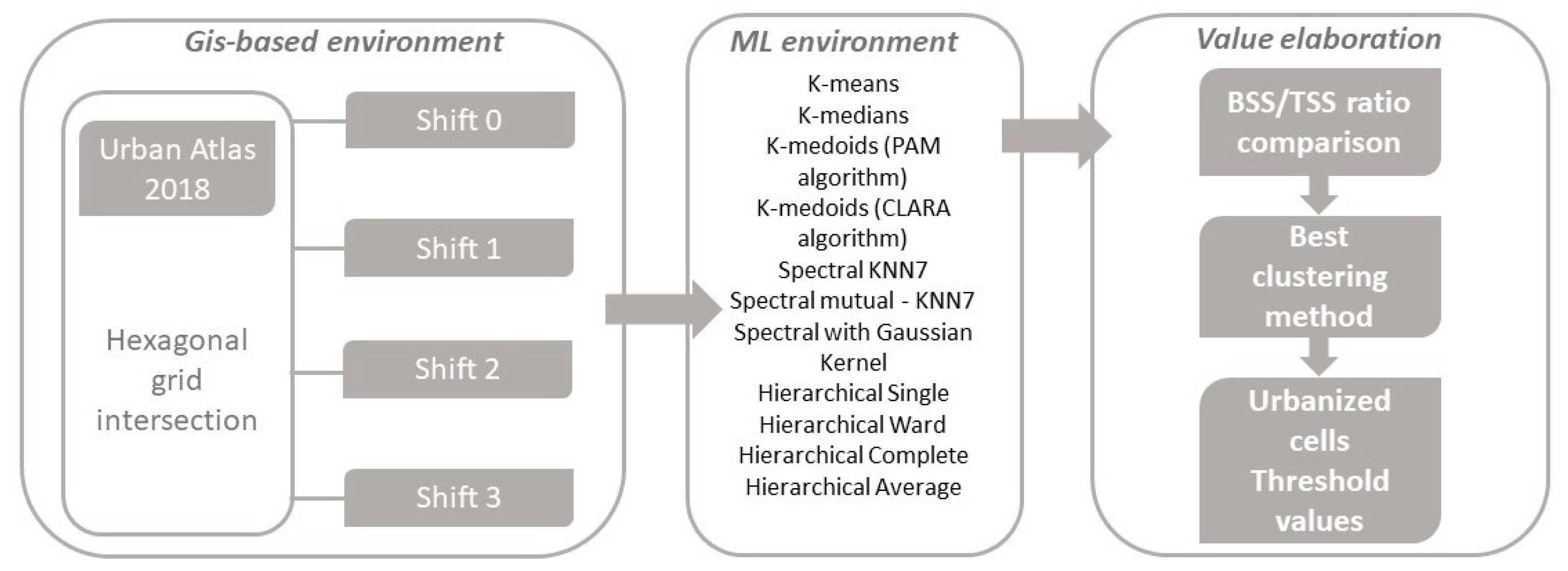
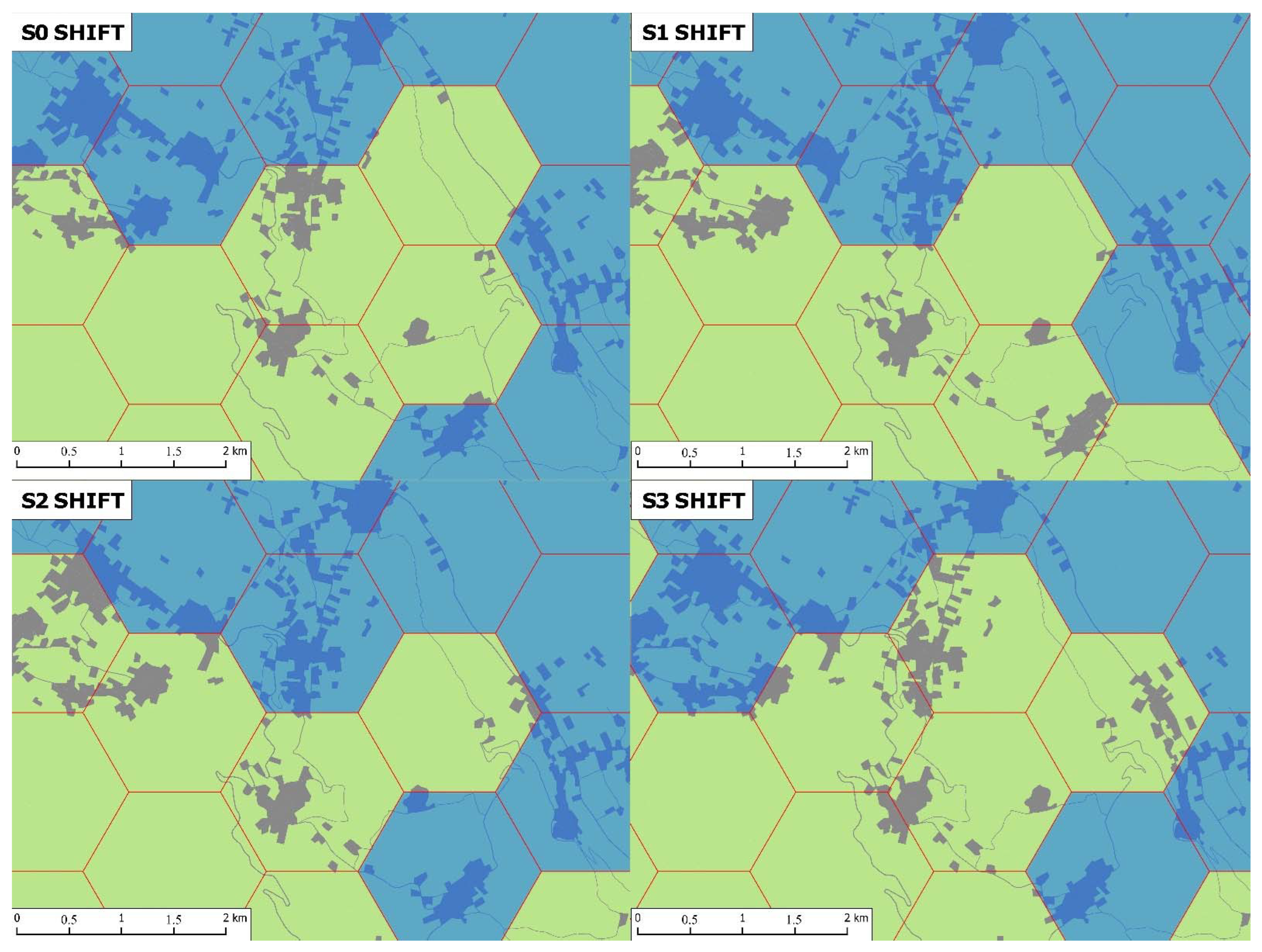
2.2. Grid Generation Procedures
2.3. Unsupervised Machine Learning Procedures
3. Results
3.1. BSS/TSS Metric Results
3.2. Graphic Elaborations and Cell Recognition Ability Comparison
3.3. Final Elaboration and Implications
3.4. Urban Area Threshold Values
4. Discussion
5. Conclusions
- The design of indicators aimed at highlighting the relationships between the sustainable development of urban transformations, the resilience of settlement systems and their potential to adapt to different economic and environmental stresses;
- Machine and deep learning have increasingly been used in urban studies; neural networks were introduced in the 1950s, but only recently they have reached advanced processing power and data storage capabilities to the point that deep learning algorithms can be used to create new applications, including satellite imagery analysis. Therefore, experimentation with ML and DL can only increase the interpretive capabilities of the urban mosaic and generate sustainable city configurations;
- New applications and innovative geospatial services are at the basis of an interdisciplinary development of disciplines, with particular reference to tools for spatial analysis and fast monitoring for urban resilience, the redevelopment of sensitive areas for the contrast of hydraulic and hydrogeological risk, for the mitigation of climate-altering effects, for the improvement of/increase in ecosystem services and for the evaluation of carbon balance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, L.Y.; Jorge Ochoa, J.; Shah, M.N.; Zhang, X. The Application of Urban Sustainability Indicators—A Comparison between Various Practices. Habitat Int. 2011, 35, 17–29. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Kainz, W.; Rahman, M.M.; Szabó, G. Geo-Information Sustainable Urban Land-Use Optimization Using GIS-Based Multicriteria Decision-Making (GIS-MCDM) Approach. ISPRS Int. J. Geo-Inf. 2022, 11, 313. [Google Scholar] [CrossRef]
- OGC Standards and Resources|OGC. Available online: https://www.ogc.org/standards/ (accessed on 14 June 2022).
- Castro, C.V.; Rifai, H.S.; Jones, B.G.; Al-Nasrawi, A.K.M.; Fuentes, I. Development and Assessment of a Web-Based National Spatial Data Infrastructure for Nature-Based Solutions and Their Social, Hydrological, Ecological, and Environmental Co-Benefits. Sustainability 2021, 13, 11018. [Google Scholar] [CrossRef]
- Borzacchiello, M.T.; Craglia, M. Estimating Benefits of Spatial Data Infrastructures: A Case Study on e-Cadastres. Comput. Environ. Urban Syst. 2013, 41, 276–288. [Google Scholar] [CrossRef]
- Farrugia, S.; Hudson, M.D.; McCulloch, L. An Evaluation of Flood Control and Urban Cooling Ecosystem Services Delivered by Urban Green Infrastructure. Int. J. Biodivers Sci. Ecosyst. Serv. Manag. 2013, 9, 782342. [Google Scholar] [CrossRef]
- Salata, S.; Grillenzoni, C. A Spatial Evaluation of Multifunctional Ecosystem Service Networks Using Principal Component Analysis: A Case of Study in Turin, Italy. Ecol. Indic. 2021, 127, 107758. [Google Scholar] [CrossRef]
- LIU, L.; WU, J. Scenario Analysis in Urban Ecosystem Services Research: Progress, Prospects, and Implications for Urban Planning and Management. Landsc. Urban Plan. 2022, 224, 104433. [Google Scholar] [CrossRef]
- Luiza Petroni, M.; Siqueira-Gay, J.; Lucia Casteli Figueiredo Gallardo, A. Understanding Land Use Change Impacts on Ecosystem Services within Urban Protected Areas. Landsc. Urban Plan. 2022, 223, 104404. [Google Scholar] [CrossRef]
- Vidal, D.G.; Dias, R.C.; Teixeira, C.P.; Fernandes, C.O.; Filho, W.L.; Barros, N.; Maia, R.L. Clustering Public Urban Green Spaces through Ecosystem Services Potential: A Typology Proposal for Place-Based Interventions. Environ. Sci. Policy 2022, 132, 262–272. [Google Scholar] [CrossRef]
- Angold, P.G.; Sadler, J.P.; Hill, M.O.; Pullin, A.; Rushton, S.; Austin, K.; Small, E.; Wood, B.; Wadsworth, R.; Sanderson, R.; et al. Biodiversity in Urban Habitat Patches. Sci. Total Environ. 2006, 360, 196–204. [Google Scholar] [CrossRef] [PubMed]
- Hendel, M.; Bobée, C.; Karam, G.; Parison, S.; Berthe, A.; Bordin, P. Developing a GIS Tool for Emergency Urban Cooling in Case of Heat-Waves. Urban Clim. 2020, 33, 100646. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, X.; Xu, H.; Jing, Q.; Pan, X.; Liu, T.; Wang, H.; Hou, H. A GIS-Based Spatial Multi-Index Model for Flood Risk Assessment in the Yangtze River Basin, China. Environ. Impact Assess. Rev. 2020, 83, 106397. [Google Scholar] [CrossRef]
- Alvarez León, L.F. A Blueprint for Market Construction? Spatial Data Infrastructure(s), Interoperability, and the EU Digital Single Market. Geoforum 2018, 92, 45–57. [Google Scholar] [CrossRef]
- Nijhum, F.; Westbrook, C.; Noble, B.; Belcher, K.; Lloyd-Smith, P. Evaluation of Alternative Land-Use Scenarios Using an Ecosystem Services-Based Strategic Environmental Assessment Approach. Land Use Policy 2021, 108, 105540. [Google Scholar] [CrossRef]
- Ledda, A.; di Cesare, E.A.; Satta, G.; Cocco, G.; de Montis, A. Integrating Adaptation to Climate Change in Regional Plans and Programmes: The Role of Strategic Environmental Assessment. Environ. Impact Assess. Rev. 2021, 91, 106655. [Google Scholar] [CrossRef]
- Wende, W.; Bond, A.; Bobylev, N.; Stratmann, L. Climate Change Mitigation and Adaptation in Strategic Environmental Assessment. Environ. Impact Assess. Rev. 2012, 32, 88–93. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Asghari, A.; Tayyebi, A.; Taleai, M. Coupling Machine Learning, Tree-Based and Statistical Models with Cellular Automata to Simulate Urban Growth. Comput. Environ. Urban Syst. 2017, 64, 297–308. [Google Scholar] [CrossRef]
- Saganeiti, L.; Mustafa, A.; Teller, J.; Murgante, B. Modeling Urban Sprinkling with Cellular Automata. Sustain. Cities Soc. 2021, 65, 102586. [Google Scholar] [CrossRef]
- Mustafa, A.; Rienow, A.; Saadi, I.; Cools, M.; Teller, J. Comparing Support Vector Machines with Logistic Regression for Calibrating Cellular Automata Land Use Change Models. Eur. J. Remote Sens. 2018, 51, 391–401. [Google Scholar] [CrossRef]
- Rienow, A.; Goetzke, R. Supporting SLEUTH—Enhancing a Cellular Automaton with Support Vector Machines for Urban Growth Modeling. Comput. Environ. Urban Syst. 2015, 49, 66–81. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Kim, Y.; Safikhani, A.; Tepe, E. Machine Learning Application to Spatio-Temporal Modeling of Urban Growth. Comput. Environ. Urban Syst. 2022, 94, 101801. [Google Scholar] [CrossRef]
- Xing, W.; Qian, Y.; Guan, X.; Yang, T.; Wu, H. A Novel Cellular Automata Model Integrated with Deep Learning for Dynamic Spatio-Temporal Land Use Change Simulation. Comput. Geosci. 2020, 137, 104430. [Google Scholar] [CrossRef]
- Romano, B.; Zullo, F.; Fiorini, L.; Ciabò, S.; Marucci, A. Sprinkling: An Approach to Describe Urbanization Dynamics in Italy. Sustainability 2017, 9, 97. [Google Scholar] [CrossRef]
- LIFE—Centro Planeco. Available online: https://www.centroplaneco.it/life/ (accessed on 20 June 2022).
- SOSTEN&RE—Centro Planeco. Available online: https://www.centroplaneco.it/sostenere-2/ (accessed on 20 June 2022).
- Transforming Our World: The 2030 Agenda for Sustainable Development|Department of Economic and Social Affairs. Available online: https://sdgs.un.org/2030agenda (accessed on 24 June 2022).
- REACT-EU|European Commission. Available online: https://ec.europa.eu/info/funding-tenders/find-funding/eu-funding-programmes/react-eu_en (accessed on 24 June 2022).
- PIANO NAZIONALE DI RIPRESA E RESILIENZA #NEXTGENERATIONITALIA. Available online: https://www.governo.it/sites/governo.it/files/PNRR.pdf (accessed on 10 October 2022).
- Urban Atlas—Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/local/urban-atlas (accessed on 16 June 2022).
- Novovi´cnovovi´c, O.; Brdar, S.; Mesaroš, M.; Crnojevi´c, V.C.; Papadopoulos, A.N. Geo-Information Uncovering the Relationship between Human Connectivity Dynamics and Land Use. ISPRS Int. J. Geo-Inf. 2020, 9, 140. [Google Scholar] [CrossRef]
- Rusche, K.; Reimer, M.; Stichmann, R. Mapping and Assessing Green Infrastructure Connectivity in European City Regions. Sustainability 2019, 11, 1819. [Google Scholar] [CrossRef]
- Zambon, I.; Serra, P.; Pili, S.; Bernardini, V.; Ferrara, C.; Salvati, L. A New Approach to Land-Use Structure: Patch Perimeter Metrics as a Spatial Analysis Tool. Sustainability 2018, 10, 2147. [Google Scholar] [CrossRef]
- Birch, C.P.D. Diagonal and Orthogonal Neighbours in Grid-Based Simulations: Buffon’s Stick after 200 Years. Ecol. Modell. 2006, 192, 637–644. [Google Scholar] [CrossRef]
- Birch, C.P.D.; Oom, S.P.; Beecham, J.A. Rectangular and Hexagonal Grids Used for Observation, Experiment and Simulation in Ecology. Ecol. Modell. 2007, 206, 347–359. [Google Scholar] [CrossRef]
- Overton, W.S.; White, D.; Stevens, D.L., Jr. Environmental Monitoring and Assessment Program: Design Report; EMaAP Environmental Protection Agency: Washington, DC, USA, 1990; Volume 52.
- Coppola, D.M.; Purves, H.R.; Mccoy, A.N.; Purves, D. The Distribution of Oriented Contours in the Real World. Proc. Natl. Acad. Sci. USA 1998, 95, 4003–4006. [Google Scholar] [CrossRef]
- Yeh, A.G.O.; Li, X.; Xia, C. Cellular Automata Modeling for Urban and Regional Planning. Urban Book Ser. 2021, 865–883. [Google Scholar] [CrossRef]
- Zhou, Y.; Tu, M.; Wang, S.; Liu, W. Geo-Information A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect. ISPRS Int. J. Geo-Inf. 2018, 7, 135. [Google Scholar] [CrossRef]
- Nugraha, A.T.; Waterson, B.J.; Blainey, S.P.; Nash, F.J. Unravelling the Dynamics behind the Urban Morphology of Port-Cities Using a LUTI Model Based on Cellular Automata. Comput. Environ. Urban Syst. 2022, 92, 101733. [Google Scholar] [CrossRef]
- Welcome to the QGIS Project! Available online: https://www.qgis.org/en/site/ (accessed on 29 September 2022).
- GeoDa on Github. Available online: https://geodacenter.github.io/ (accessed on 29 September 2022).
- de Hoon, M.; Imoto, S.; Miyano, S. The C Clustering Library; Institute of Medical Science, Human Genome Center, University of Tokyo: Tokyo, Japan, 2003; Volume 11. [Google Scholar]
- Ezugwu, A.E.; Ikotun, A.M.; Oyelade, O.O.; Abualigah, L.; Agushaka, J.O.; Eke, C.I.; Akinyelu, A.A. A Comprehensive Survey of Clustering Algorithms: State-of-the-Art Machine Learning Applications, Taxonomy, Challenges, and Future Research Prospects. Eng. Appl. Artif. Intell. 2022, 110, 104743. [Google Scholar] [CrossRef]
- Bienvenido-Huertas, D.; Farinha, F.; Oliveira, M.J.; Silva, E.M.J.; Lança, R. Challenge for Planning by Using Cluster Methodology: The Case Study of the Algarve Region. Sustainability 2020, 12, 1536. [Google Scholar] [CrossRef]
- Liu, Y.; Kilby, P.; Frankcombe, T.J.; Schmidt, T.W. The Electronic Structure of Benzene from a Tiling of the Correlated 126-Dimensional Wavefunction. Nat. Commun. 2020, 11, 1210. [Google Scholar] [CrossRef] [PubMed]
- López-Goyburu, P.; García-Montero, L.G. The Urban-Rural Interface as an Area with Characteristics of Its Own in Urban Planning: A Review. Sustain. Cities Soc. 2018, 43, 157–165. [Google Scholar] [CrossRef]
- Shaw, B.J.; van Vliet, J.; Verburg, P.H. The Peri-Urbanization of Europe: A Systematic Review of a Multifaceted Process. Landsc. Urban Plan. 2020, 196, 103733. [Google Scholar] [CrossRef]
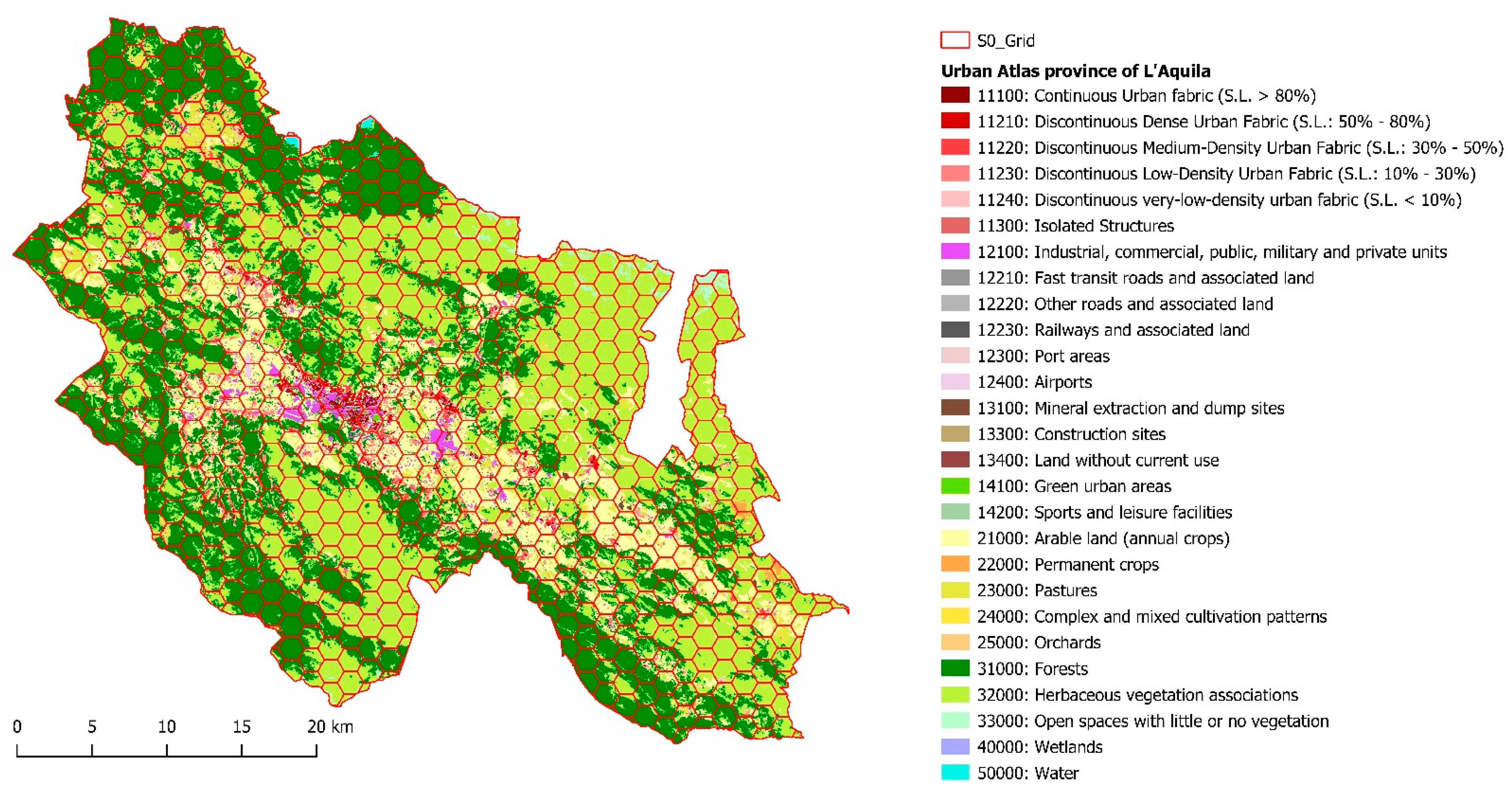
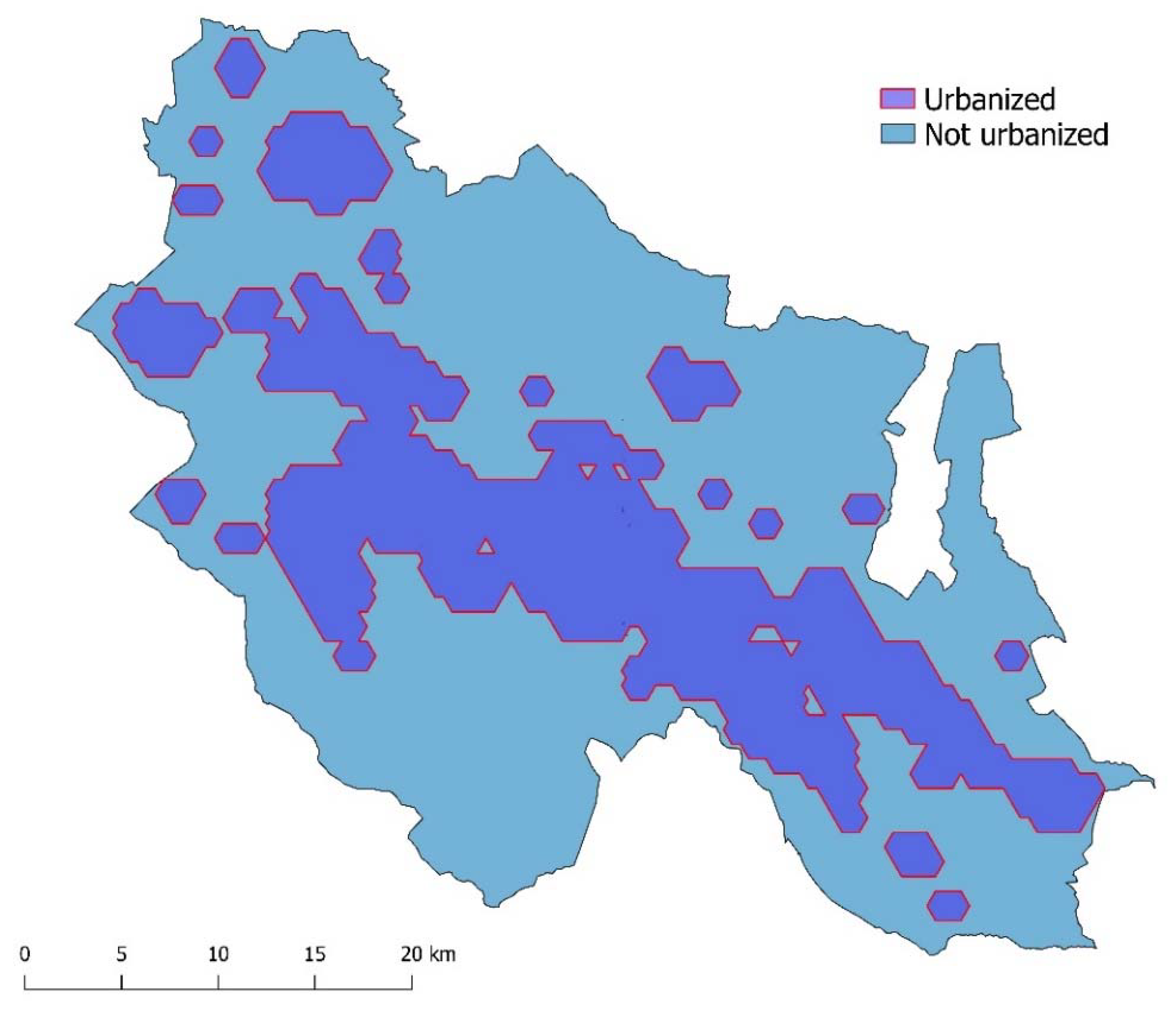
| 2 UA CLASSES | 5 UA CLASSES |
|---|---|
| 1 Artificial areas | 1 Artificial areas |
| 2 Non-artificial areas | 2 Agricultural areas 3 Natural areas 4 Wetlands 5 Water bodies |
| METHOD | CRITERIA | |||||||
|---|---|---|---|---|---|---|---|---|
| Transformation | Initialization Method | Initialization Re-Runs | Max. Iterations | Dist. Function | N. of Samples/ Iterations | Sample Size/Rate | Affinity | |
| K—Means | Raw | Random | 150 | 1000 | Euclidean | / | / | / |
| K—Medians | Raw | Random | 150 | 1000 | Manhattan | / | / | / |
| K—Medoids (CLARA Algorithm) | Raw | LAB | / | / | Manhattan | 10 | 200 | / |
| K—Medoids (PAM Algorithm) | Raw | LAB | / | / | Manhattan | / | / | / |
| Spectral K-NN | Raw | Random | 150 | 300 | Manhattan | / | / | K—NN #Neighors = ln(n) + 1 |
| Spectral Mutual K-NN | Raw | Random | 150 | 300 | Manhattan | / | / | Mutual K—NN #Neighors = second ln(n) +1 |
| Spectral Gaussian | Raw | Random | 150 | 300 | Manhattan | / | / | Sigma = |
| Hierarchical Single linkage | Raw | / | / | / | Manhattan | / | / | / |
| Hierarchical Ward’s linkage | Raw | / | / | / | Euclidean | / | / | / |
| Hierarchical Complete linkage | Raw | / | / | / | Manhattan | / | / | / |
| Hierarchical Average linkage | Raw | / | / | / | Manhattan | / | / | / |
| METHOD | RATIO OF BETWEEN TO TOTAL SUM OF SQUARES (BSS/TSS) | |||
|---|---|---|---|---|
| TWO UA CLASSES | ||||
| S0 | S1 | S2 | S3 | |
| K—Means | 0.655676 | 0.660526 | 0.659399 | 0.625655 |
| K—Medians | 0.457219 | 0.466214 | 0.507931 | 0.51609 |
| K—Medoids (PAM and CLARA algorithms) | 0.450213 (CLARA) 0.450213 (PAM) | 0.450298 (CLARA) 0.450298 (PAM) | 0.503916 (CLARA) 0.503916 (PAM) | 0.530062 (CLARA) 0.531839 (PAM) |
| Spectral KNN7 | 0.0431401 | 0.301221 | 0.285217 | 0.369646 |
| Spectral mutual—KNN7 | 0.0172236 | 0.0654304 | 0.025808 | 0.00357514 |
| Spectral with Gaussian Kernel | 0.00069968 | 0.000470756 | 0.103149 | 0.0215007 |
| Hierarchical Single | 0.242457 | 0.170793 | 0.0865453 | 0.37389 |
| Hierarchical Ward | 0.654512 | 0.63072 | 0.656826 | 0.623812 |
| Hierarchical Complete | 0.414637 | 0.564536 | 0.606873 | 0.37389 |
| Hierarchical Average | 0.414637 | 0.564536 | 0.499687 | 0.37389 |
| FIVE UA CLASSES | ||||
| S0 | S1 | S2 | S3 | |
| K—Means | 0.72593 | 0.71977 | 0.7165 | 0.720882 |
| K—Medians | 0.678369 | 0.66402 | 0.670743 | 0.689813 |
| K—Medoids (PAM and CLARA algorithms) | 0.667808 (CLARA) 0.670513 (PAM) | 0.670126 (CLARA) 0.670126 (PAM) | 0.697807 (CLARA) 0.697807 (PAM) | 0.689813 (CLARA) 0.683157 (PAM) |
| Spectral KNN7 | 0.319202 | 0.349396 | 0.17429 | 0.334059 |
| Spectral mutual—KNN7 | 0.0142809 | 0.164442 | 0.116453 | 0.0970793 |
| Spectral with Gaussian Kernel | 0.0175808 | 0.0339564 | 0.0249459 | 0.0296962 |
| Hierarchical Single | 0.0389586 | 0.0268354 | 0.00450728 | 0.0825486 |
| Hierarchical Ward | 0.662854 | 0.646998 | 0.7101 | 0.715121 |
| Hierarchical Complete | 0.542857 | 0.533737 | 0.707919 | 0.622929 |
| Hierarchical Average | 0.0563574 | 0.719427 | 0.700252 | 0.617819 |
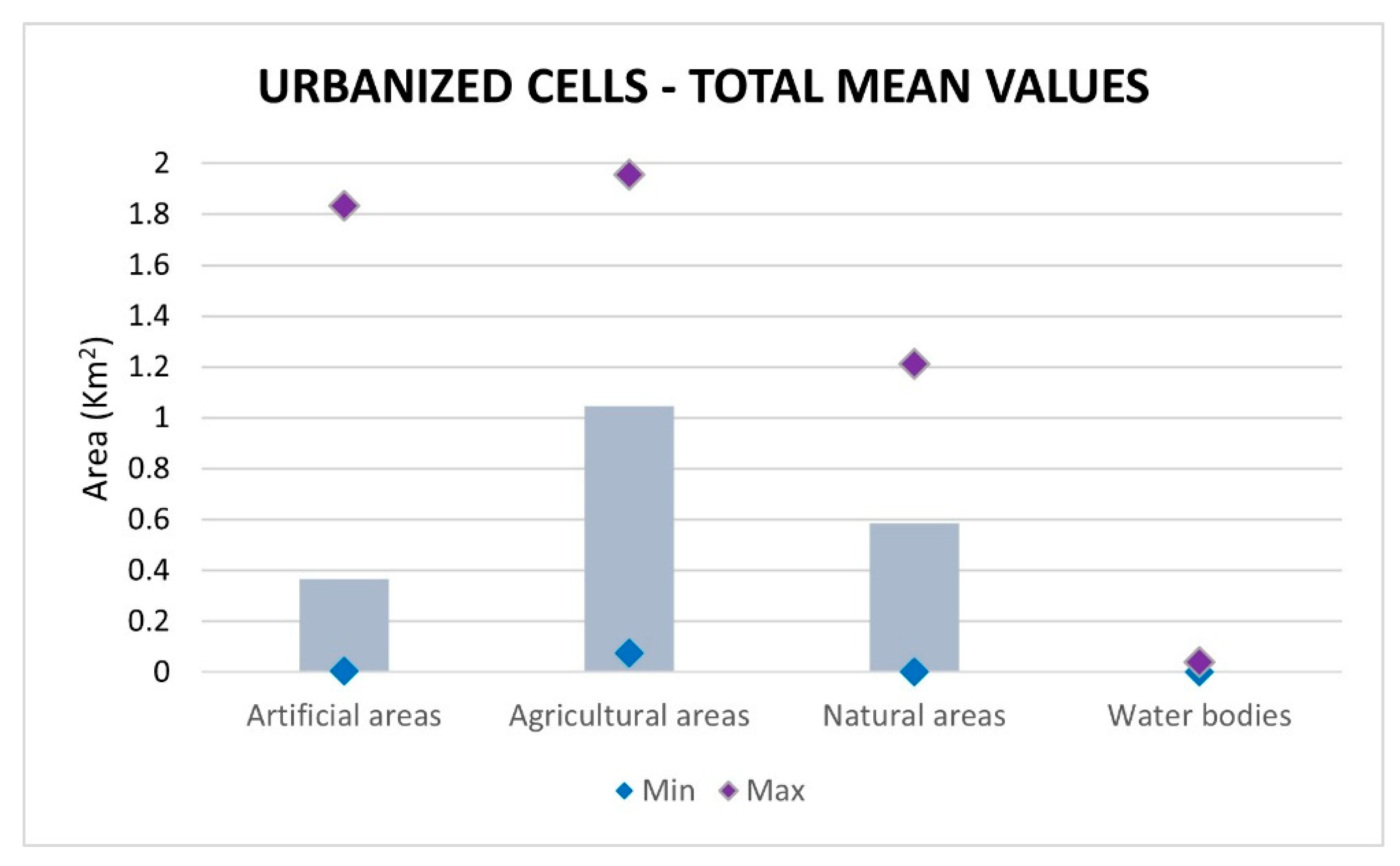
| K—MEANS METHOD, FIVE CLASSES OF URBANIZED CELLS | S0 (km2) | S1 (km2) | S2 (km2) | S3 (km2) | Total Mean (km2) | |
|---|---|---|---|---|---|---|
| Artificial areas | Mean | 0.366799 | 0.373849 | 0.381433 | 0.365336 | 0.36606753 |
| Min | 0 | 0 | 0 | 0.007381 | 0.003690363 | |
| Max | 1.900423 | 1.945933 | 1.915146 | 1.769396 | 1.834909834 | |
| Agricultural areas | Mean | 1.024998 | 1.027607 | 1.053506 | 1.064393 | 1.044695669 |
| Min | 0.05609 | 0.026234 | 0.080825 | 0.094188 | 0.075138679 | |
| Max | 1.936165 | 1.954988 | 1.974852 | 1.975681 | 1.955923058 | |
| Natural areas | Mean | 0.604997 | 0.595129 | 0.561606 | 0.567071 | 0.586034235 |
| Min | 0 | 0.000774 | 0.003879 | 0 | 0 | |
| Max | 1.219838 | 1.230902 | 1.224494 | 1.201435 | 1.210636192 | |
| Water bodies | Mean | 0.003124 | 0.003333 | 0.003372 | 0.003115 | 0.003119508 |
| Min | 0 | 0 | 0 | 0 | 0 | |
| Max | 0.042653 | 0.046287 | 0.046287 | 0.038076 | 0.040364711 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiorini, L.; Falasca, F.; Marucci, A.; Saganeiti, L. Discretization of the Urban and Non-Urban Shape: Unsupervised Machine Learning Techniques for Territorial Planning. Appl. Sci. 2022, 12, 10439. https://doi.org/10.3390/app122010439
Fiorini L, Falasca F, Marucci A, Saganeiti L. Discretization of the Urban and Non-Urban Shape: Unsupervised Machine Learning Techniques for Territorial Planning. Applied Sciences. 2022; 12(20):10439. https://doi.org/10.3390/app122010439
Chicago/Turabian StyleFiorini, Lorena, Federico Falasca, Alessandro Marucci, and Lucia Saganeiti. 2022. "Discretization of the Urban and Non-Urban Shape: Unsupervised Machine Learning Techniques for Territorial Planning" Applied Sciences 12, no. 20: 10439. https://doi.org/10.3390/app122010439
APA StyleFiorini, L., Falasca, F., Marucci, A., & Saganeiti, L. (2022). Discretization of the Urban and Non-Urban Shape: Unsupervised Machine Learning Techniques for Territorial Planning. Applied Sciences, 12(20), 10439. https://doi.org/10.3390/app122010439











