1. Introduction
Since Arthur Ashkin first proposed the optical trap in 1970 [
1], it has become a versatile tool for the micromanipulation of biological objects [
2,
3] without physical contact. The optical trap has been widely used from basic research on light to manipulation of microspheres [
4,
5]. The dual-fiber optical trap relies on two laser beams transmitting toward each other to realize the powerful control of the microsphere. In 1993, Constable et al. first used two counter-propagating beams emanating from two cleaved fibers to “clamp” particles [
6]. It captured particles at a low light intensity, and could effectively reduce damage to the captured particles, especially biological cells. At the same time, compared with the single-beam optical trap, the dual-fiber optical trap has a longer working distance and a wider lateral range, and has applications, such as optical wrench [
7] and optical stretching [
8]. However, axial trapping efficiencies in the dual-beam optical fiber were low, and the phenomenon of multiple captured stable positions was frequently encountered [
9]. Attempts to improve axial stability have been realized by the use of a spherical-tapered ended fiber to focus the beams to a spot [
10,
11,
12].
In this paper, the dual-fiber optical trap system was integrated into a chip. Two spherical-tapered ended fibers were designed to replace traditional flat ended fibers. The spherical-tapered ended fiber is more conducive to beam focusing. The use of spherical-tapered ended fiber in a dual-fiber optical trap provides greater accessibility to improve the stability of the optical trap. It was proved by simulation and experiment that the dual spherical-tapered ended fiber optical trap had higher optical trap stiffness than the dual flat ended fiber optical trap. Furthermore, the integrated chip-scale platform makes this system stable and more convenient to debug and reuse. This structure can be effectively applied in physics, biology [
13], chemistry [
14], and medical research [
15], such as optical wrench [
16], optical orbital rotation [
17], cell screening [
18], and optical stretching [
19]. This research on optical trapping by the dual spherical-tapered ended fiber optical trap shows the great potential of micro-structured optical fibers that can be used for optical trapping and micro-manipulation.
2. Simulation
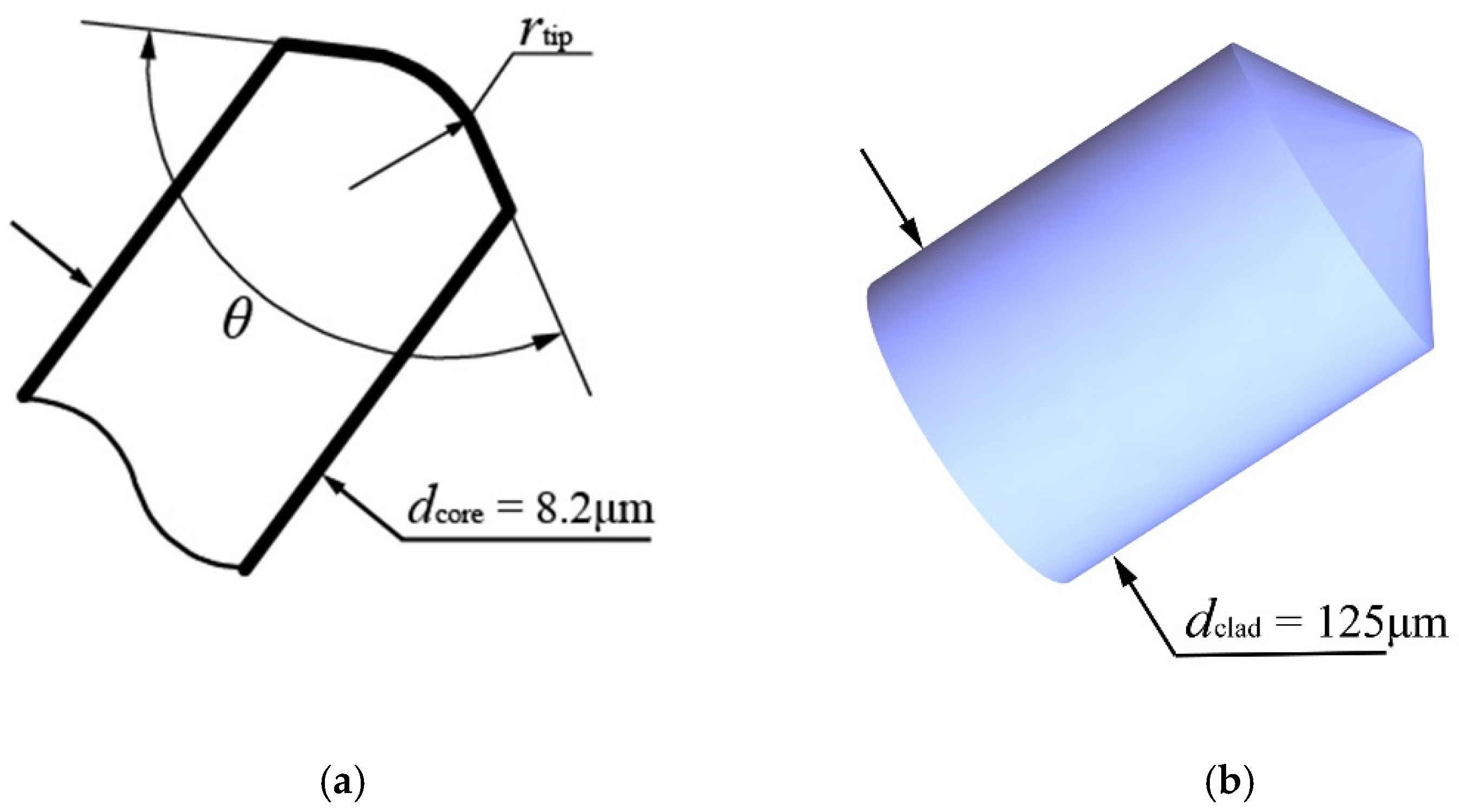
We set a cone angle
θ = 120°, a fiber cladding refractive index of 1.446, a core refractive index of 1.452, core radius
dcore = 8.2 μm, clad diameter
dclad = 125 μm, and the radius of cone tip
rtip = 2 μm. The schematic of a spherical-tapered ended fiber is shown in
Figure 1.
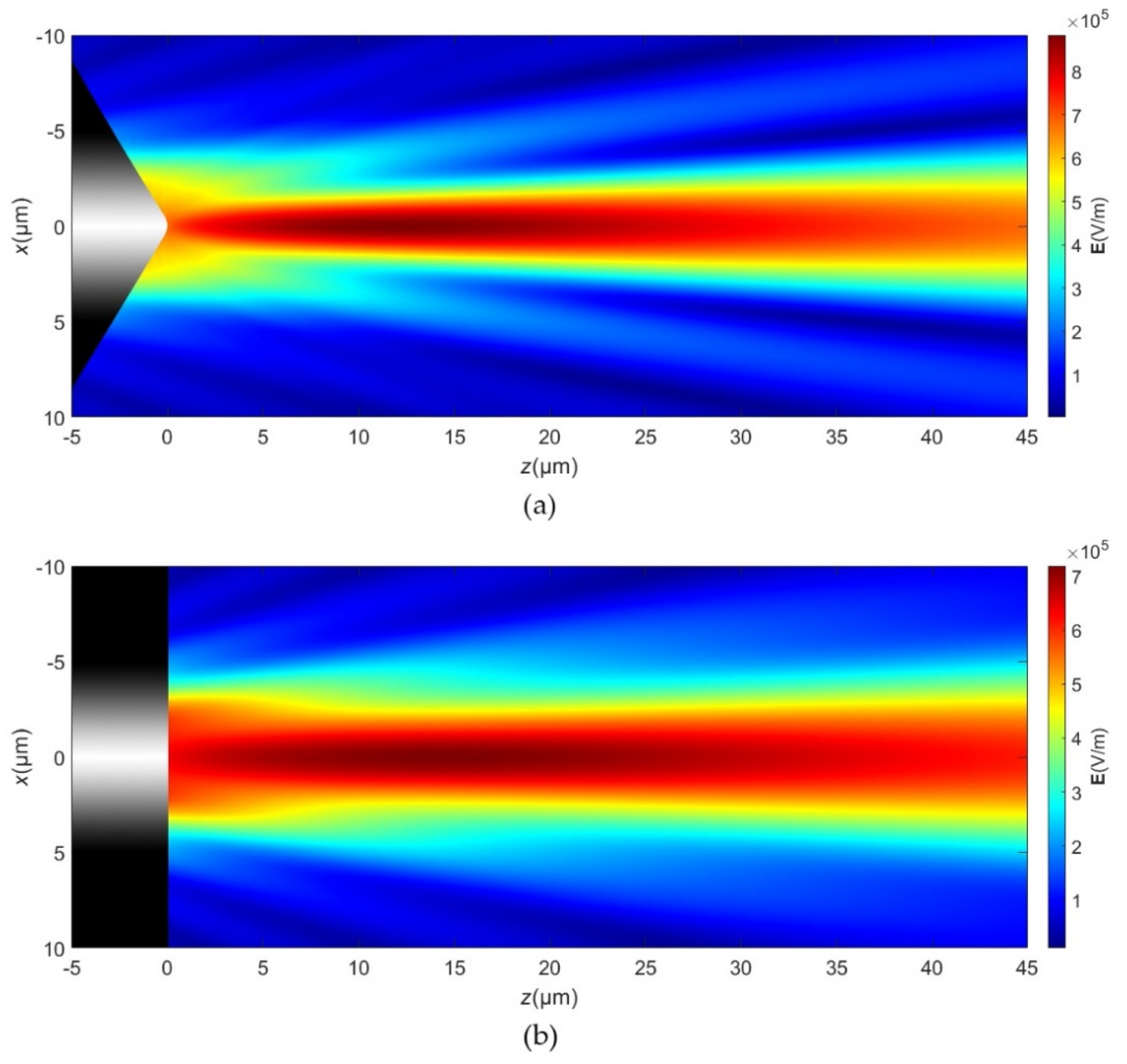
Compared with flat ended fiber, the light intensity distribution of spherical-tapered ended fiber can form a more focused spot.
Figure 2 shows the light intensity distribution of the output light field by using a spherical-tapered ended fiber with a tip angle of 120° and flat ended fibers. The mode field emitted from the fiber has the characteristics of a small beam divergence angle, which lays the foundation for the high stiffness of the dual spherical-tapered ended fiber optical trap.
In this paper, Finite-difference time-domain (FDTD) was used to calculate the optical trapping force of microspheres in a dual spherical-tapered ended fiber optical trap and a dual flat ended fibers optical trap. FDTD is a numerical calculation method of electromagnetic field, first put forward by K.S. Yee in 1966 [
20]. It is based on the differential form of the Maxwell curl equation, and the computational domain is divided into grids containing electric and magnetic fields. This method has a wide range of applications, especially in the field of physics.
When the electromagnetic field acts on the particles and changes the momentum of the particles, the momentum of the electromagnetic field also changes to some extent. Among the changes, the Lorentz force on the charge is expressed as:
where
f is the density of Lorentz force,
ρ is the charge density,
J is current density,
E is electric field intensity, and
B is magnetic induction intensity. For the steady-state distribution of the electromagnetic field, the time change rate of the total amount of motion of the electromagnetic field is zero. The total momentum of the charging system in the region changes. The total force of the electromagnetic field in the volume is equal to the area of Maxwell’s stress tension
on the interface. By substituting Maxwell equations into Equation (1), Maxwell’s stress tension
and the total force
F can be obtained, expressed as:
where
ε0 is vacuum capacitance,
μ0 is vacuum magnetic permeability, and
H is magnetic field intensity. Considering the continuous wave of the two-dimensional TM model frequency, there are three field (
Hy,
Ex,
Ez) components, which can be used to derive the force [
21]:
where
S is the outer boundary of the target space in the two-dimensional XOZ plane,
ε1 is the relative capacitance of the medium, and
μ is the relative magnetic permeability of the medium.
Due to the symmetry of the optical trap, the force distribution of the microspheres along the y-axis is similar to the x-axis. Therefore, only the x-axis and z-axis directions were analyzed in this paper. The z-axis direction is defined as the axial direction, and the x-axis direction is defined as the lateral direction. Near the center of the optical trap, the optical trapping force
Fx and
Fz acting on particles is a recovery force, which is proportional to the displacement of the microsphere offset from the center of the optical tweezers, expressed as:
where
kx and
kz are the trapping stiffness on x-axis and z-axis, and
x and
z are the displacement deviating from the capture location on x-axis and z-axis. Additionally, a spherical particle has no torque in a dual-beam optical trap. When the two optical fibers experience misalignment [
22,
23], the captured microsphere realizes optical rotation or optical orbital rotation. In the simulation, we set a polystyrene microsphere (refractive index
n2 = 1.59, radius
r0 = 3 µm) to be captured in water (refractive index
n1 = 1.33). The output power of each fiber in the optical trap was
PL =
PR = 18 mW.
Figure 3 shows the difference of force which acted on the microsphere between dual spherical-tapered ended fiber optical trap and flat ended dual-fiber optical trap along
x and
z axes. The distance between the two fibers was set as 25 µm. According to Equations (6) and (7), in the spherical-tapered ended fiber optical trap, the trapping stiffness was 0.43 pN/µm on the z-axis and 11.46 pN/µm on the x-axis. In the flat ended fibers optical trap, the trapping stiffness was 0.15 pN/µm on the z-axis and 3.61 pN/µm on the x-axis. This showed that the polystyrene microsphere, with a radius of 3 µm, could be captured more stably in the dual spherical-tapered ended fiber optical trap. Both the axial and transverse optical trap stiffnesses of the dual spherical-tapered ended fiber optical trap were greater than those of the dual flat ended fibers optical trap.
The distance between two fiber ends is a key factor contributing to the trapping force.
Figure 4 shows the trapping force acting on the microsphere for different distances between the two fiber ends. Due to the focus of the output optical field of the spherical-tapered ended fiber being near 12.5 µm from the fiber end, the distance between the two fibers was set as 25 µm. In addition, when the distance between the two ends was too close, the effective capture area became too small, so it would make capturing difficult in the experiment. Therefore, we discuss the impact of the distance between two ends on the optical trap from 25 µm or greater distance. With the increase of the distance between the two fiber ends, the stiffness of the lateral optical trap changed little, and the stiffness of the axial optical trap decreased. When two points with a force of 0 and a negative slope of the tangent were found in the diagram, the microsphere could not be captured at the center of the optical trap. Instead, a bistable result appeared in the optical trap. The microsphere had two capture points symmetrically about the central position in the optical trap. This discovery could be applied to the study of bistable structures in the optical trap [
24].
3. Experiment
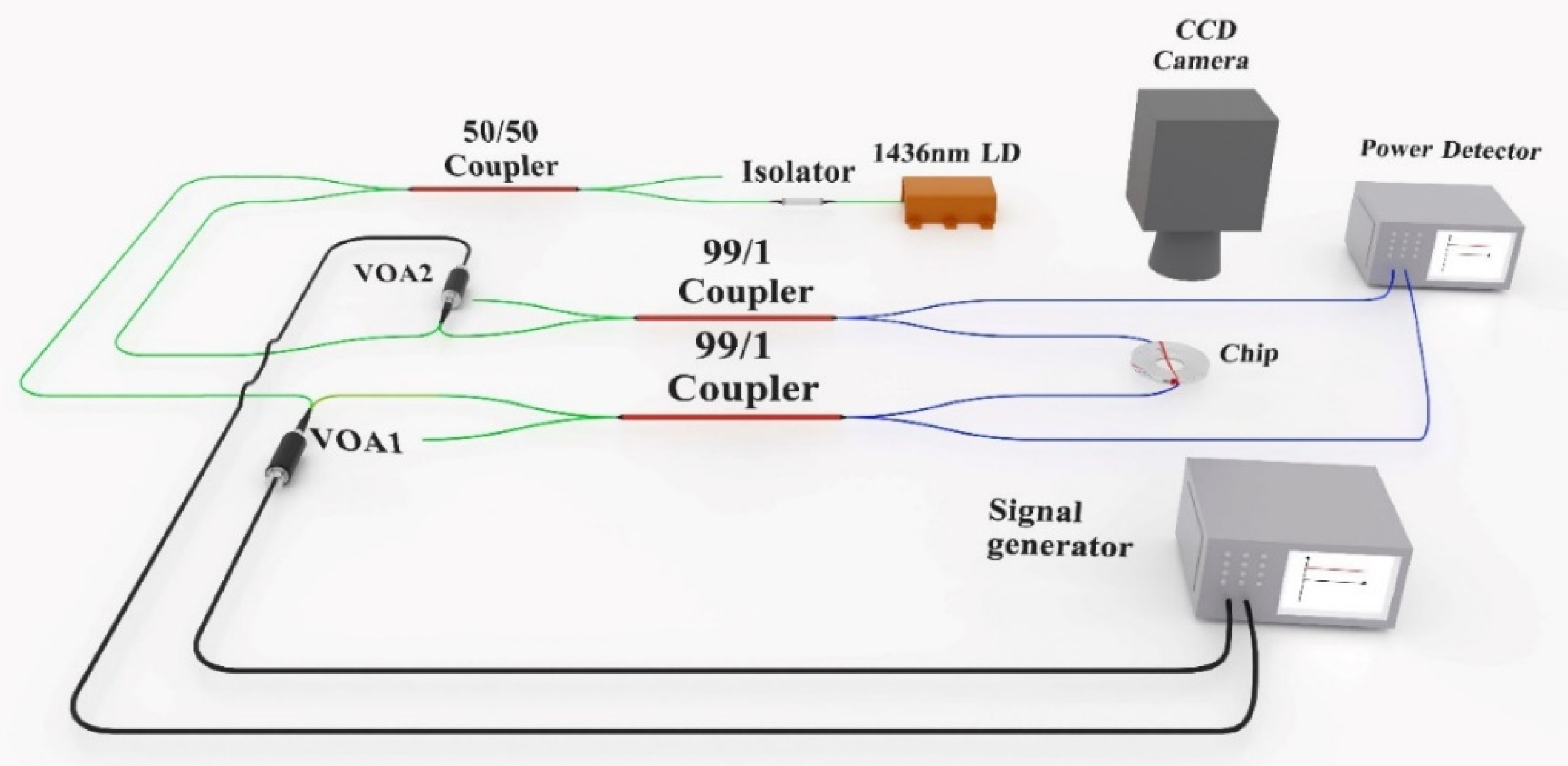
The optical layout for the dual spherical-tapered ended fiber optical trap is shown in
Figure 5. A laser with a wavelength of 1436 nm was divided into two trapping beams by a 50/50 coupler. In each optical path, a variable optical attenuator (VOA) was used to ensure that the two beams incident on the trap had the same power. The trapping beams were ultimately transmitted to the dual spherical-tapered ended fiber optical trap chip to capture microspheres. The power input into the optical trap was precisely monitored by two power detectors (LD) in real-time. The phenomena were imaged by using a CCD camera.
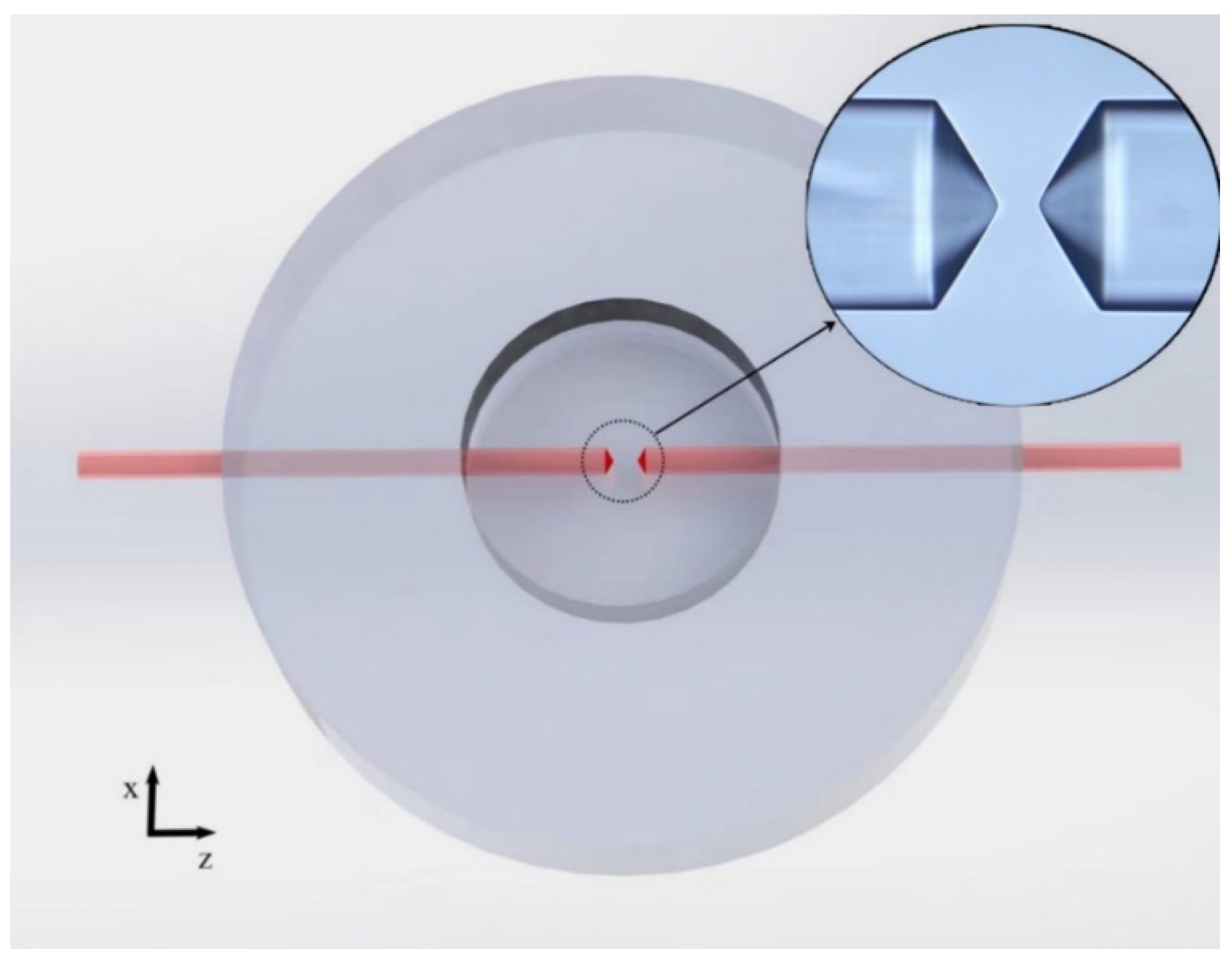
The schematic of the dual spherical-tapered ended fiber optical trap chip is shown in
Figure 6. The particle could be trapped by counter-propagating beams emanating from the two spherical-tapered ended fibers. The diameter and depth of the columniform capturing room were 1 mm and 500 µm, respectively. On the chip, the dual spherical-tapered ended fiber optical trap required high coupling accuracy of the two fibers. Therefore, the two fibers were fixed to V-grooves to increase coupling accuracy and stability.
In the experiment, a polystyrene microsphere with a radius of 3 µm was trapped using the simulation’s configuration, see images in
Figure 7. A polystyrene microsphere was trapped near the center of the dual spherical-tapered ended fiber trap as expected. The microsphere could be captured for a long time in the dual spherical-tapered ended fiber optical trap.
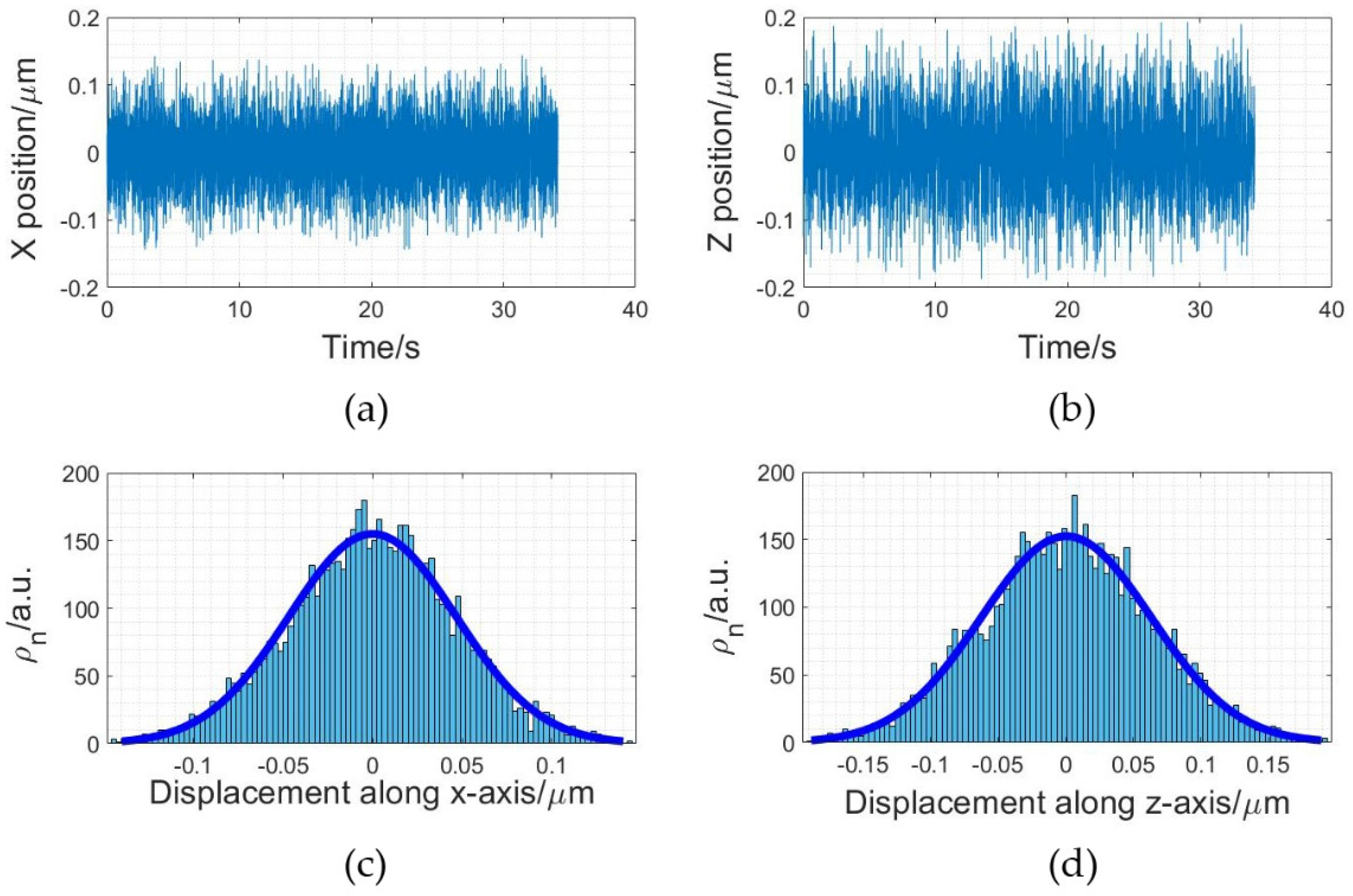
The particle trapping videos were recorded, and a particle tracking algorithm was used to extract the time-dependent particle positions from trapping videos. The displacement of the microspheres in the xz plane was collected from each video frame. The corresponding experimental results on the dual spherical-tapered ended fiber optical trap are shown in
Figure 8. The axial and lateral displacements of the captured microspheres changed with time, shown, respectively, in
Figure 8a,b. The probability distribution on the x-axis and the z-axis are shown in
Figure 8c,d.
The thermal displacement of the captured microsphere in the optical trap conformed to the Boltzmann distribution. The probability distribution of the x-axis displacement of the microsphere can be expressed as follows [
25]:
where
E(
x) is the potential energy,
kBT is thermal energy (
T is the temperature,
kB is the Boltzmann constant), and
C is the normalizing constant of the probability distribution. According to the energy equipartition method, the stiffness of the optical trap can be directly expressed as [
16]:
where <
x2> is the mean square deviation of the displacement,
κB is the Boltzmann constant. The stiffness was calculated according to Equation (9). The stiffness along the x-axis was 1.76 pN/µm, and along the z-axis it was 0.99 pN/µm in the dual spherical-tapered ended fiber optical trap.
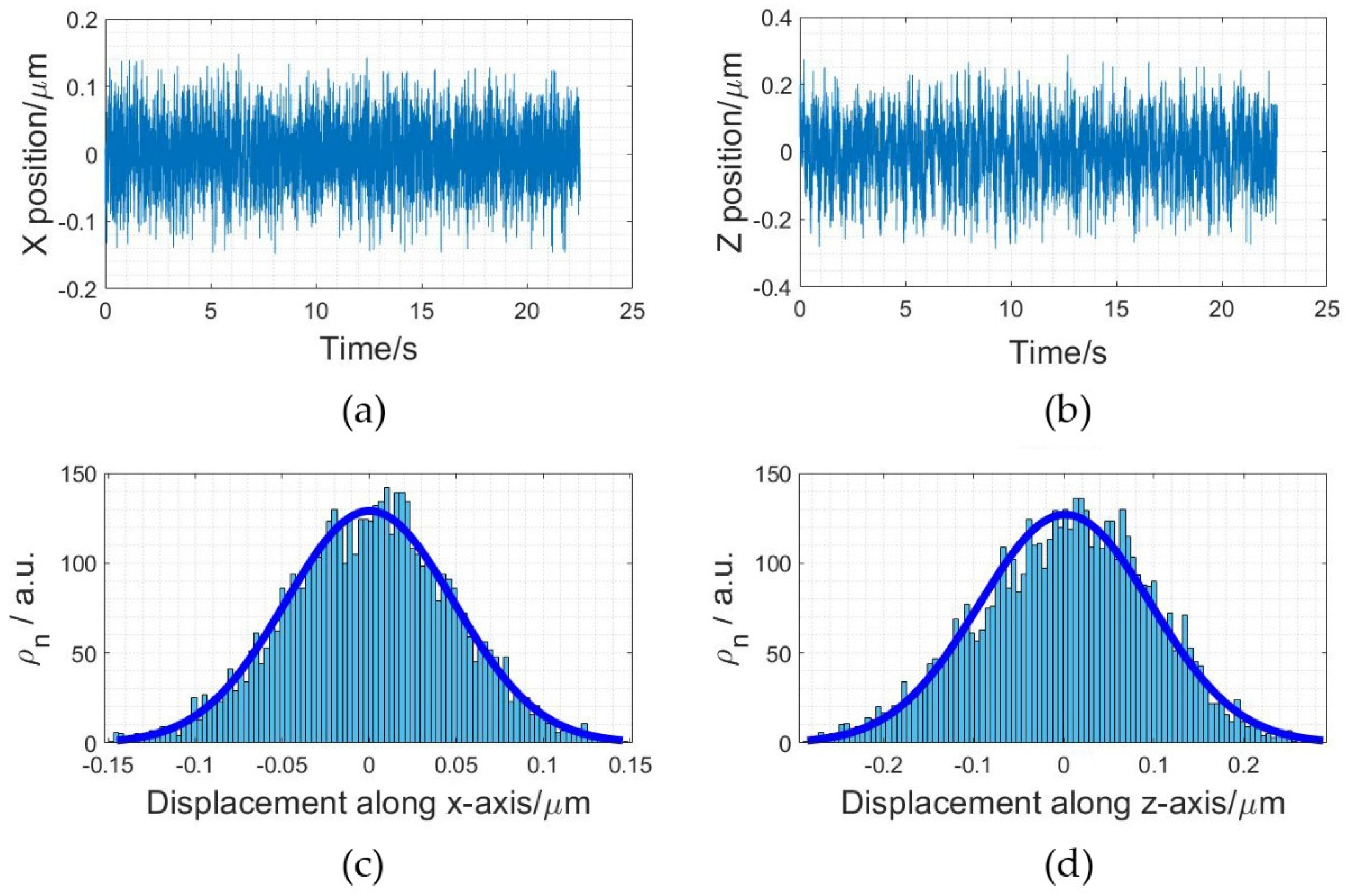
Figure 9 shows the experimental results for the dual flat ended fibers optical trap. The stiffness along the x-axis was 1.68 pN/µm, and along the z-axis it was 0.44 pN/µm in the dual spherical-tapered ended fiber optical trap. Compared with the dual flat ended fibers optical trap, the dual spherical-tapered ended fiber optical trap effectively enhanced the stiffness of the dual-beam optical trap, which was consistent with the results of the simulation. The improvement of the stiffness of the optical trap plays a positive role in improving the capture stability of the system.
4. Conclusions
In this paper, we demonstrated highly efficient optical trapping in a counter-propagating fiber arrangement by using a dual spherical-tapered ended fiber optical trap instead of a dual flat ended fiber optical trap. A design of a low-cost, robust chip of a dual-fiber optical trap, using spherical-tapered ended fiber for optical trapping of particles, was presented and produced.
The output light field when using spherical-tapered ended fiber and flat ended fibers was calculated. Compared with flat ended fiber, the light intensity distribution of spherical-tapered ended fiber could form a more focused spot. A polystyrene microsphere with a radius 3 µm was captured in water in the dual-fiber optical trap. In this scenario, the force acting on the particle and the stiffness of the optical trap were simulated and the results were checked in an experiment. In the simulation, compared with flat ended fiber optical trap, the dual spherical-tapered ended fiber optical trap increased the axial stiffness from 0.15 pN/µm to 0.43 pN/µm, and increased the lateral stiffness from 3.61 pN/µm to 11.46 pN/µm. This meant particles could be captured more stably in the dual spherical-tapered ended fiber optical trap. We were able to gain the lateral and axial displacements change with time by a particle tracking algorithm in the experiment. Compared with the flat ended fiber optical trap, the dual spherical-tapered ended fiber optical trap increased the axial stiffness from 1.68 pN/µm to 1.76 pN/µm, and increased the lateral stiffness from 0.44 pN/µm to 0.99 pN/µm in the experiment. It was proved by simulation and experiment that spherical-tapered ended fiber can obviously increase the stiffness in lateral and axial axis of the dual-fiber optical trap.
In this work, we demonstrated the possibility of using the dual spherical-tapered ended fiber optical trap chip to realize stable particle capturing. It shows the great potential of micro-structured optical fibers for use in optical trapping and micro-manipulation. Both the cone angle and the radius of the top affect the stiffness of the lateral and axial optical trap, and investigation into this is to be carried out in the follow-up study. Furthermore, other optical fiber end structures can also change the optical trap stiffness, which is also the focus of follow-up research. By changing the micro-structure of the fiber, different optical traps can be customized according to requirements. This paves the way toward high stiffness optical trap chips for fiber optical trapping.