CFD Analysis on the Heat Dissipation of a Dry-Lubricated Gear Stage
Abstract
1. Introduction
2. Methods and Materials
2.1. Object of Investigation
2.2. Operating Conditions
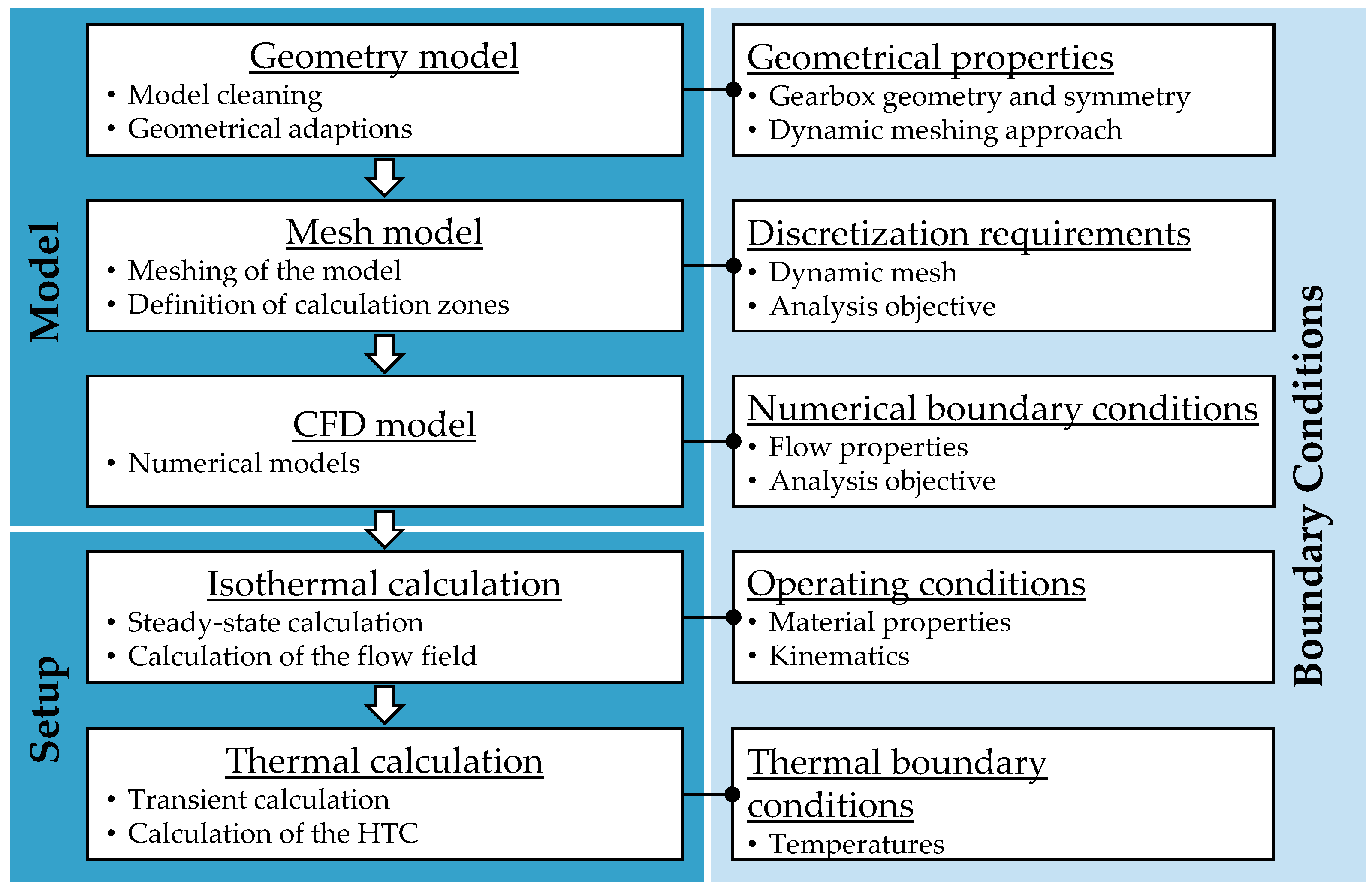
2.3. Numerical Modeling and Calculation
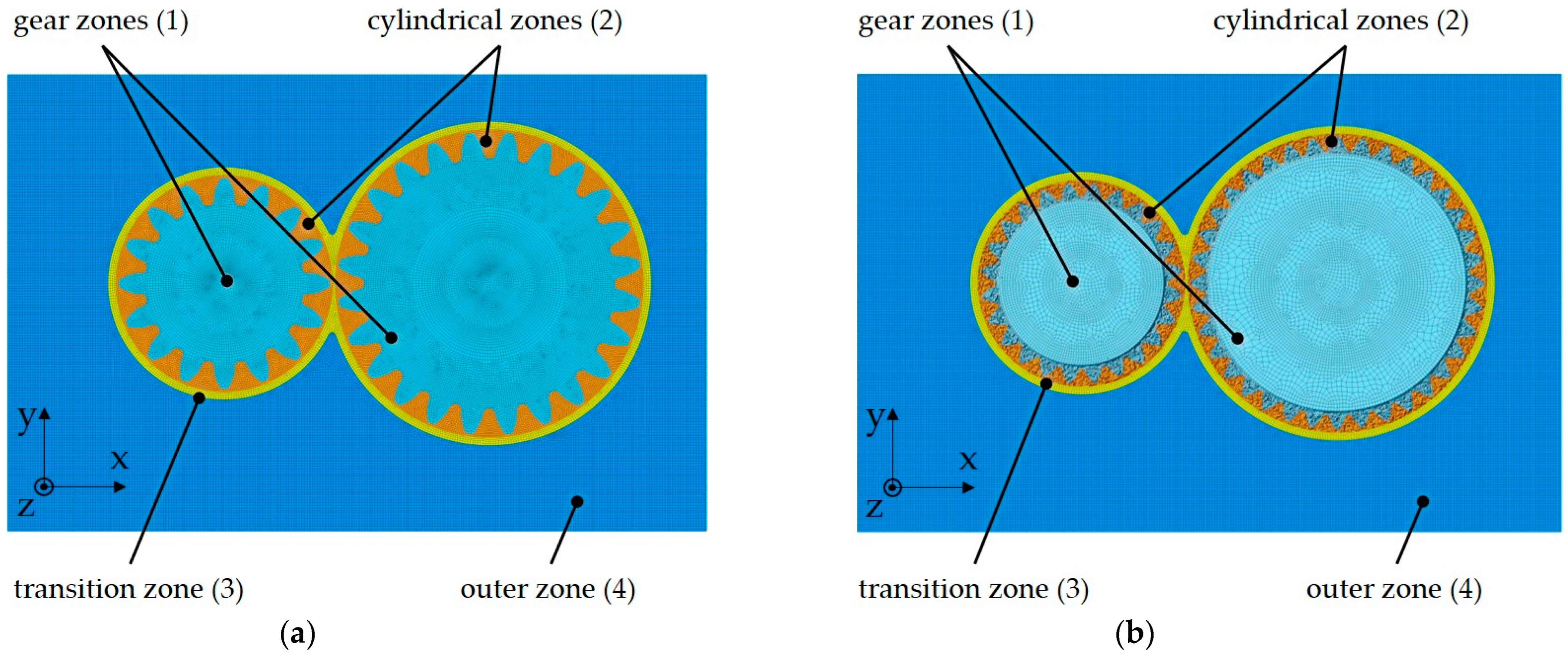
2.3.1. Geometry and Mesh Models
2.3.2. Governing Equations
2.3.3. Finite Volume Method
2.3.4. Turbulence Model
2.3.5. Wall Modeling
2.3.6. Heat Transfer
2.3.7. Simulation Procedure
3. Results
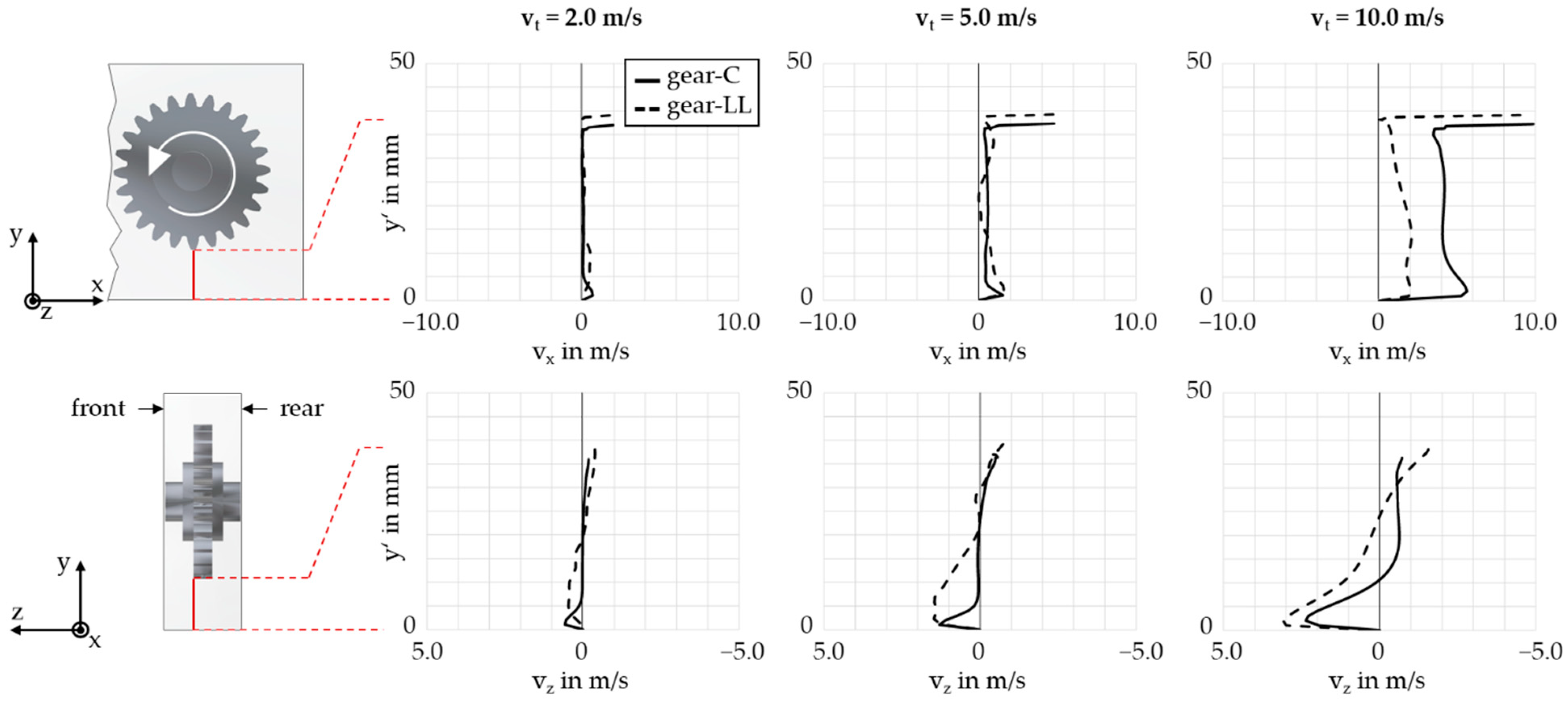
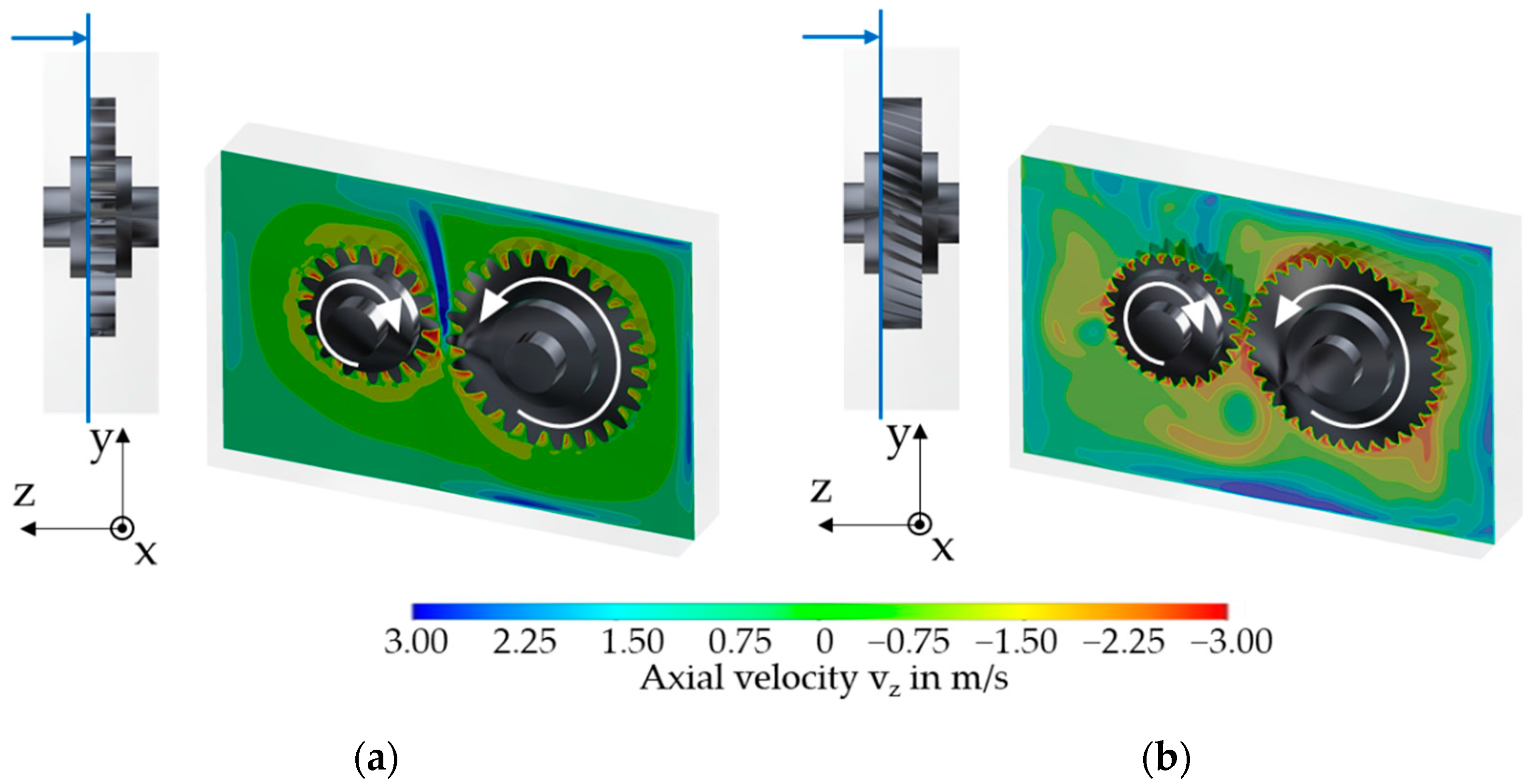
3.1. Analysis of the Isothermal Flow Field
3.2. Analysis of the Heat Transfer Coefficient
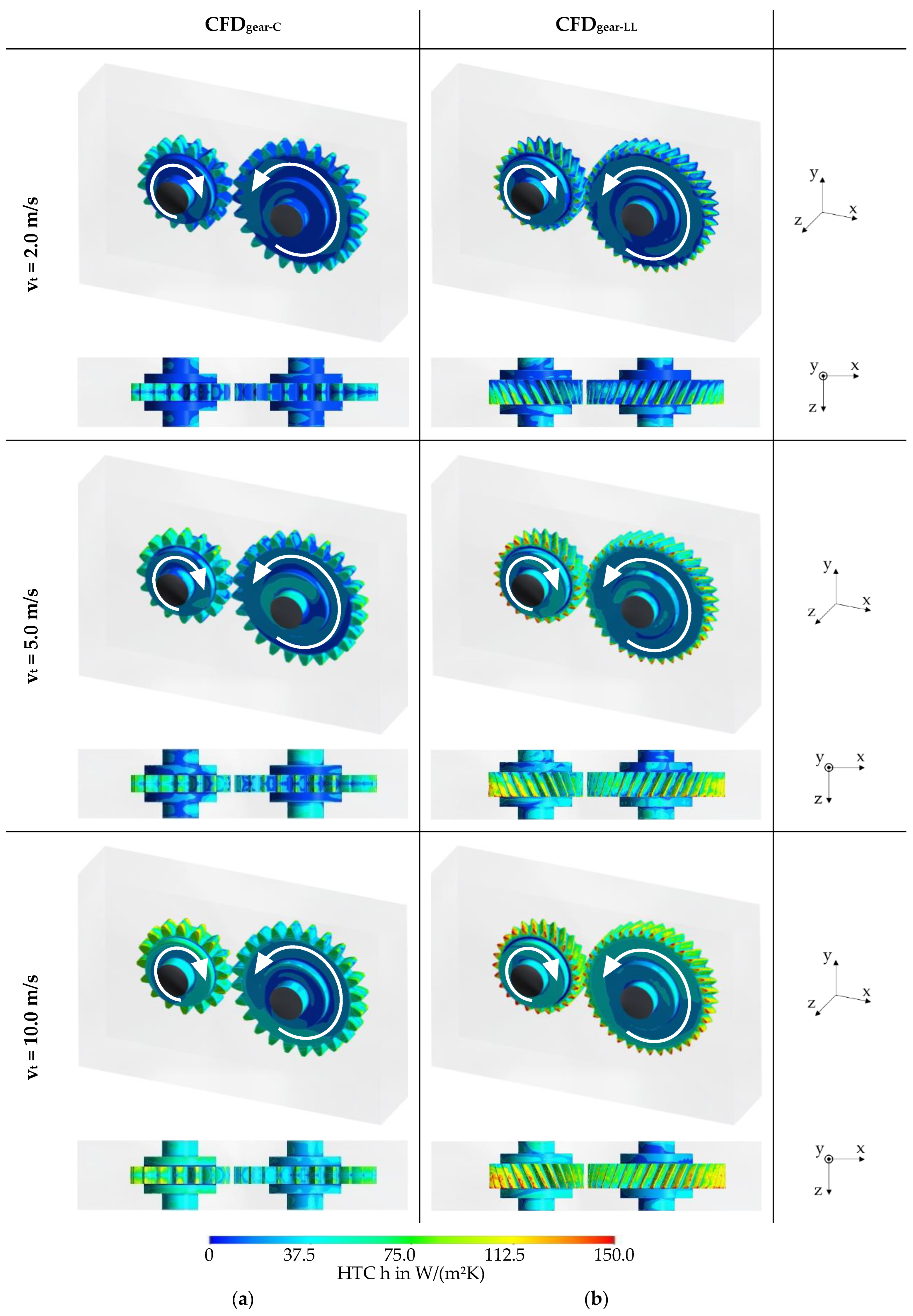
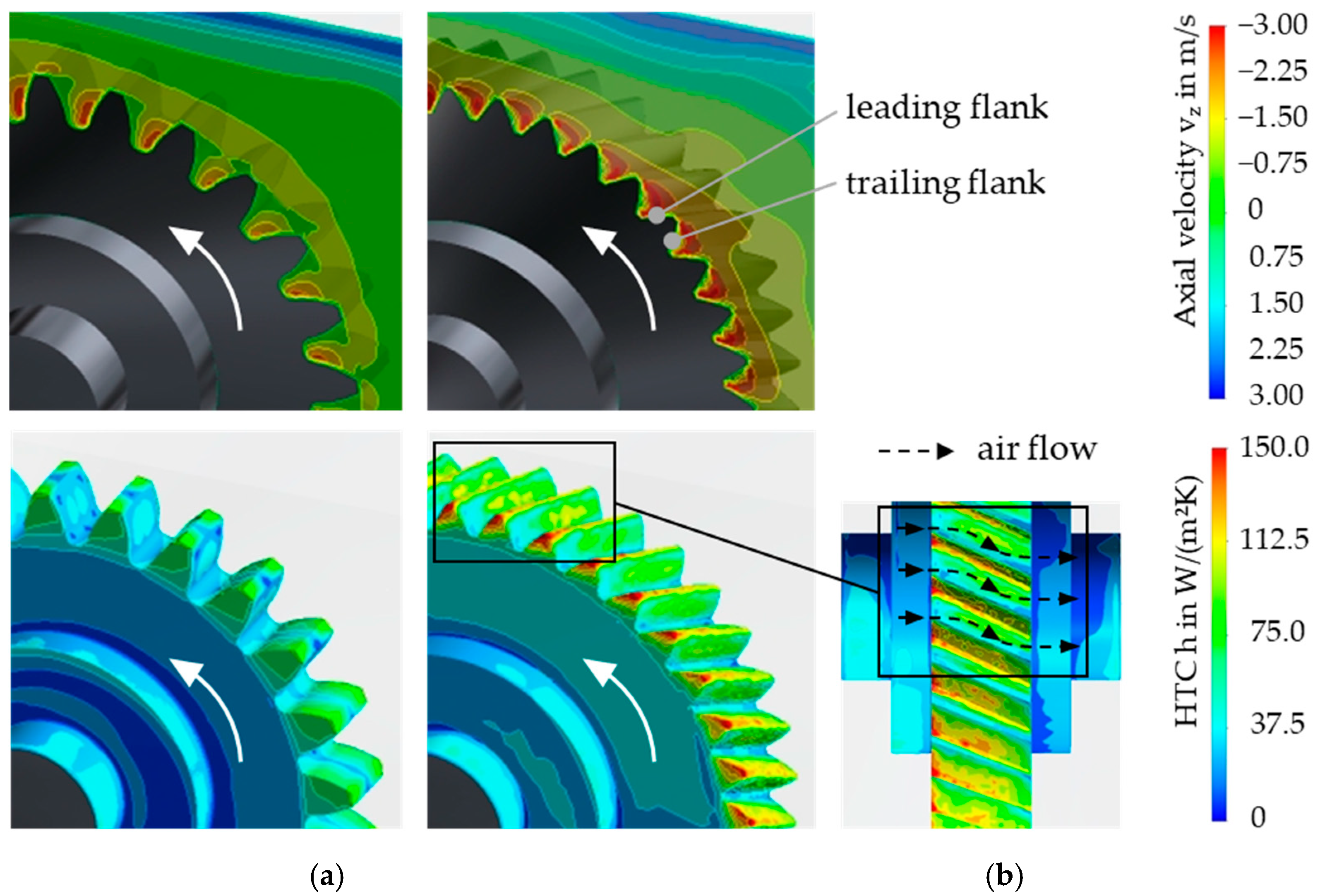
3.2.1. Local Heat Transfer Coefficient
3.2.2. Influence of Flow Characteristics
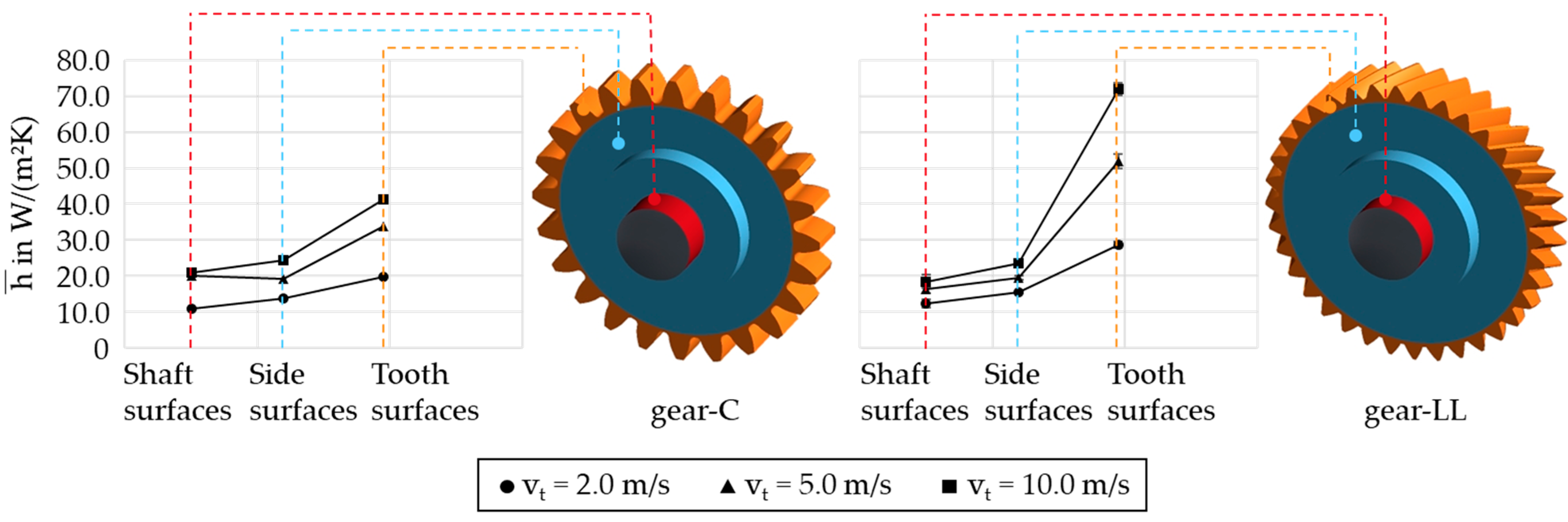
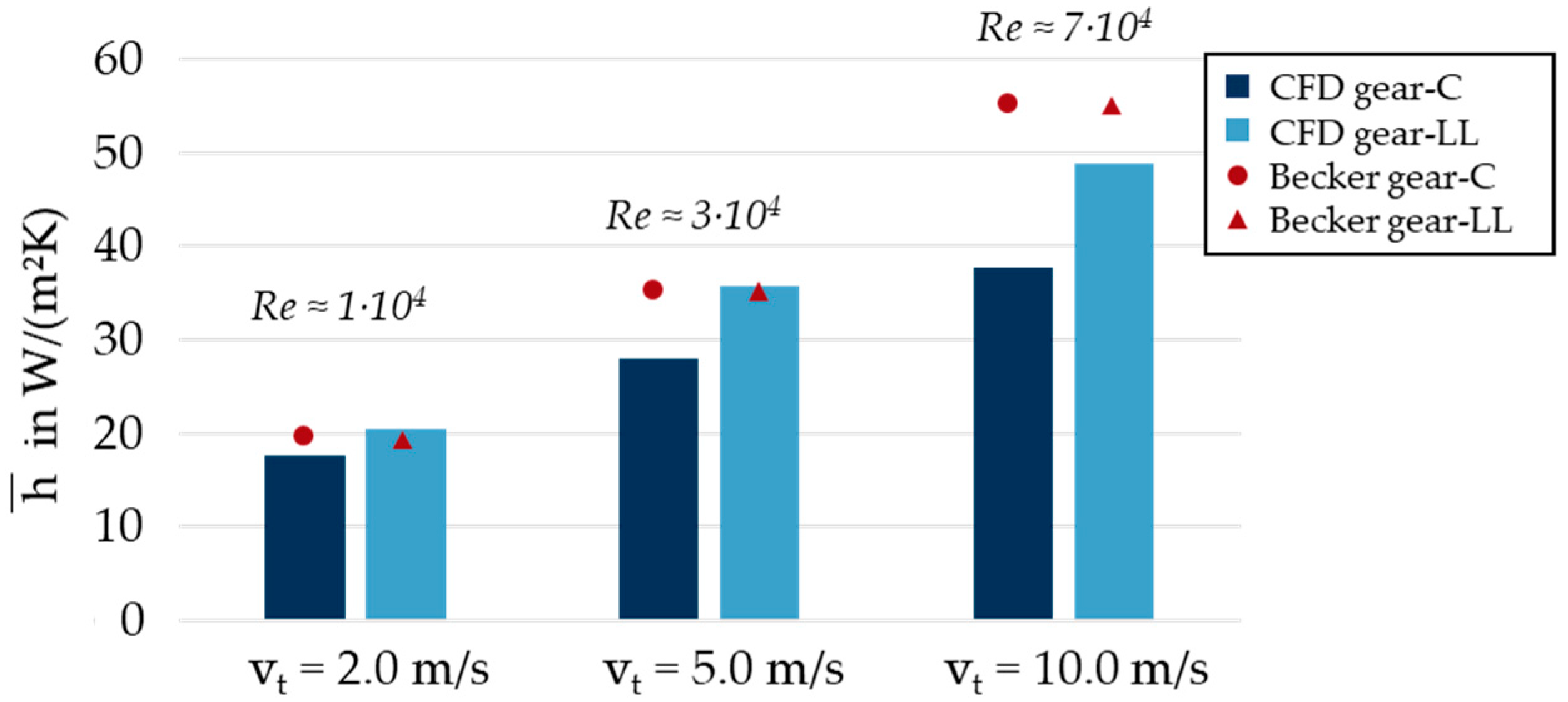
3.2.3. Surface-Averaged Heat Transfer Coefficient
4. Conclusions
- A circulating flow is formed in the gearbox due to the displacement of air by the gears and backflow to the gears.
- Spur gears show a distinct radial displacement and a symmetrical axial backflow of air to the teeth. Helical gears show a distinct axial air flow due to conveying effects.
- High heat transfer coefficients are particularly present on surfaces that interact strongly with air, e.g., on the leading tooth flanks.
- Surface-averaged heat transfer coefficients show higher values for helical gears compared to spur gears.
- The simplified Nusselt correlation can predict the order of magnitude of the simulated heat transfer coefficient as well as its trend over the circumferential speed.
- The specific influence of gear geometry and the fluid flow on the heat transfer coefficient cannot be addressed by simple correlation analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Notation | ||
| Forces | N | |
| Vector orthogonal to surface | - | |
| Source or sink of | - | |
| Fluid velocity | m/s | |
| a | Center distance | mm |
| b | Tooth width | mm |
| D | Reference length | m |
| da | Tip diameter | mm |
| h | Heat transfer coefficient│Energy | W/(m²K)│J |
| mn | Normal module | mm |
| Nu | Nusselt number | - |
| Pr | Prantl number | - |
| Re | Reynolds number | - |
| S | Surface | m2 |
| t | Time | s |
| T | Temperature | K |
| TM | Bulk temperature | K |
| u* | Dimensionless velocity | - |
| uτ | Friction velocity | m/s |
| V | Volume | m3 |
| vt | Circumferential speed | m/s |
| x | Coordinate axis | m |
| y | Distance from wall│Coordinate axis | m│m |
| y+ | Dimensionless distance | - |
| z | Tooth number│Coordinate axis | -│m |
| α | Pressure angle | ° |
| β | Helix angle | ° |
| λ | Thermal conductivity | W/(mK) |
| ν | Kinematic viscosity | mm2/s |
| ρ | Density | kg/m3 |
| Generic quantity | - | |
| Indices | ||
| wall | Wall | |
| ref | Reference | |
| oil | Oil | |
| x | Direction of x coordinate axis | |
| y | Direction of y coordinate axis | |
| z | Direction of z coordinate axis | |
| sim | Simulation | |
| 1 | Pinion | |
| 2 | Wheel | |
References
- Lince, J.R. Effective Application of Solid Lubricants in Spacecraft Mechanisms. Lubricants 2020, 8, 74. [Google Scholar] [CrossRef]
- Quiban, R.; Changenet, C.; Marchesse, Y.; Ville, F. Experimental Investigations About the Power Loss Transition between Churning and Windage for Spur Gears. J. Tribol. 2021, 143, 205. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method. Lubricants 2018, 6, 47. [Google Scholar] [CrossRef]
- Höhn, B.-R.; Stahl, K.; Michaelis, K.; Otto, H.-P. Possibilities and Limitations for an Oil-Free Powertrain. In Proceedings of the 18th International Colloquium Tribology-Industrial and Automotive Lubrication, Ostfildern, Germany, 10–12 January 2012. [Google Scholar]
- Yilmaz, M.; Kratzer, D.; Lohner, T.; Michaelis, K.; Stahl, K. A study on highly-loaded contacts under dry lubrication for gear applications. Tribol. Int. 2018, 128, 410–420. [Google Scholar] [CrossRef]
- Sklenak, S.; Brimmers, J.; Brecher, C. Analyse der Wirkmechanismen im fluidfreien Wälzkontakt mit beschichteten Oberflächen. Forsch. Ing. 2022, 86, 357–366. [Google Scholar] [CrossRef]
- Simo Kamga, L.; Nguyen, T.-D.; Emrich, S.; Oehler, M.; Schmidt, T.; Gedan-Smolka, M.; Kopnarski, M.; Sauer, B. The effect of irradiated PTFE on the friction and wear behavior of chemically bonded PA46-PTFE-cb and PA66-PTFE-cb compounds. Wear 2022, 502–503, 204380. [Google Scholar] [CrossRef]
- Hofmann, S.; Yilmaz, M.; Maier, E.; Lohner, T.; Stahl, K. Friction and contact temperature in dry rolling-sliding contacts with MoS2-bonded and a-C:H:Zr DLC coatings. Int. J. Mech. Mater. Eng. 2021, 16, 9. [Google Scholar] [CrossRef]
- Bobzin, K.; Kalscheuer, C.; Thiex, M.; Stahl, K.; Lohner, T.; Maier, E.; Yilmaz, M. Adaptive (Cr,Al)N+Mo:Sg Coating for Highly-Stressed Contacts under Dry Rolling-Sliding Conditions. Tribol. Int. 2022, 174, 107761. [Google Scholar] [CrossRef]
- Handschuh, R.F. Test Facility Simulation Results for Aerospace Loss-of-Lubrication of Spur Gears; 2014. Available online: https://ntrs.nasa.gov/citations/20140017465 (accessed on 8 September 2022).
- Höhn, B.-R.; Michaelis, K.; Otto, H.-P. Flank load carrying capacity and power loss reduction by Minimized Lubrication. In Proceedings of the American Gear Manufacturers Association Fall Technical Meeting, Milwaukee, WI, USA, 17–19 October 2010. [Google Scholar]
- Yilmaz, M.; Önüt, A.; Lohner, T.; Stahl, K. Gear and bearing power losses: From dip to minimum quantity lubrication. ILT 2022. [Google Scholar] [CrossRef]
- Höhn, B.-R.; Michaelis, K.; Otto, H.-P. Minimised gear lubrication by a minimum oil/air flow rate. Wear 2009, 266, 461–467. [Google Scholar] [CrossRef]
- Lu, F.; Wang, M.; Pan, W.; Bao, H.; Ge, W. CFD-Based Investigation of Lubrication and Temperature Characteristics of an Intermediate Gearbox with Splash Lubrication. Appl. Sci. 2021, 11, 352. [Google Scholar] [CrossRef]
- Becker, K.M. Measurements of convective heat transfer from a horizontal cylinder rotating in a tank of water. Int. J. Heat Mass Transf. 1963, 6, 1053–1062. [Google Scholar] [CrossRef]
- Lebeck, A.O. Principles and Design of Mechanical Face Seals; Wiley: New York, NY, USA, 1991; ISBN 978-0-471-51533-3. [Google Scholar]
- Changenet, C.; Oviedo-Marlot, X.; Velex, P. Power Loss Predictions in Geared Transmissions Using Thermal Networks-Applications to a Six-Speed Manual Gearbox. J. Mech. Des. 2006, 128, 618–625. [Google Scholar] [CrossRef]
- Ayan, E.; von Plehwe, F.C.; Keller, M.C.; Kromer, C.; Schwitzke, C.; Bauer, H.-J. Experimental Determination of Heat Transfer Coefficient on Impingement Cooled Gear Flanks: Validation of the Evaluation Method. J. Turbomach. 2022, 144, 081008. [Google Scholar] [CrossRef]
- Paschold, C.; Sedlmair, M.; Lohner, T.; Stahl, K. Efficiency and heat balance calculation of worm gears. Forsch. Ing. 2020, 84, 115–125. [Google Scholar] [CrossRef]
- Paschold, C.; Sedlmair, M.; Lohner, T.; Stahl, K. Calculating component temperatures in gearboxes for transient operation conditions. Forsch. Ing. 2022, 86, 521–534. [Google Scholar] [CrossRef]
- Geiger, J.S. Wirkungsgrad und Wärmehaushalt von Zahnradgetrieben bei Instationären Betriebszuständen. Ph.D. Thesis, Verlag Dr. Hut, München, Germany, 2015. [Google Scholar]
- Hildebrand, L.; Dangl, F.; Sedlmair, M.; Lohner, T.; Stahl, K. CFD analysis on the oil flow of a gear stage with guide plate. Forsch. Ing. 2021, 30, 285. [Google Scholar] [CrossRef]
- Morhard, B.; Schweigert, D.; Mileti, M.; Sedlmair, M.; Lohner, T.; Stahl, K. Efficient lubrication of a high-speed electromechanical powertrain with holistic thermal managament. Forsch. Ing. 2020, 85, 443–456. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F. Computational Fluid Dynamics Applied to Lubricated Mechanical Components: Review of the Approaches to Simulate Gears, Bearings, and Pumps. Appl. Sci. 2020, 10, 8810. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Korsukova, E.; Morvan, H. Preliminary CFD Simulations of Lubrication and Heat Transfer in a Gearbox. In Volume 5B: Heat Transfer, Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; ISBN 978-0-7918-5088-6. [Google Scholar]
- Uerlich, R.; Koch, T.; Theising, H.; Eckstein, L. Method for thermal evaluation of automotive gearbox packages taking into account load point-dependent oil distribution. Automot. Engine Technol. 2022. [Google Scholar] [CrossRef]
- Fürstenberger, M.D. Betriebsverhalten Verlustoptimierter Kunststoffzahnräder: Verzahnungsverluste, Temperaturen, Tragfähigkeit und dynamisches Betriebsverhalten. Ph.D. Thesis, Techn. Univ., München, Germany, 2013. ISBN 978-3-8439-1228-0. [Google Scholar]
- Gersten, K. Einführung in Die Strömungsmechanik; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1981. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-319-99691-2. [Google Scholar]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Determination of oil distribution and churning power loss of gearboxes by finite volume CFD method. Tribol. Int. 2017, 109, 346–354. [Google Scholar] [CrossRef]
- Liu, H.; Link, F.; Lohner, T.; Stahl, K. Computational fluid dynamics simulation of geared transmissions with injection lubrication. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7412–7422. [Google Scholar] [CrossRef]
- Schwarze, R. Mathematische Modelle einer Strömung. In CFD-Modellierung; Schwarze, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 53–58. ISBN 978-3-642-24377-6. [Google Scholar]
- Gorla, C.; Concli, F.; Stahl, K.; Höhn, B.-R.; Klaus, M.; Schultheiss, H.; Stemplinger, J.-P. CFD Simulations of Splash Losses of a Gearbox. Adv. Tribol. 2012, 2012, 616923. [Google Scholar] [CrossRef]
- Yakhot, V.; Smith, L.M. The renormalization group, the ε-expansion and derivation of turbulence models. J. Sci. Comput. 1992, 7, 35–61. [Google Scholar] [CrossRef]
- Ansys. Fluent Theory Guide: Release 2020; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Polifke, W. Wärmeübertragung: Grundlagen, Analytische und Numerische Methoden, 2nd ed.; aktualisierte Auflage; Pearson Studium: München, Germnay, 2009; ISBN 9783827373496. [Google Scholar]
- VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen. VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
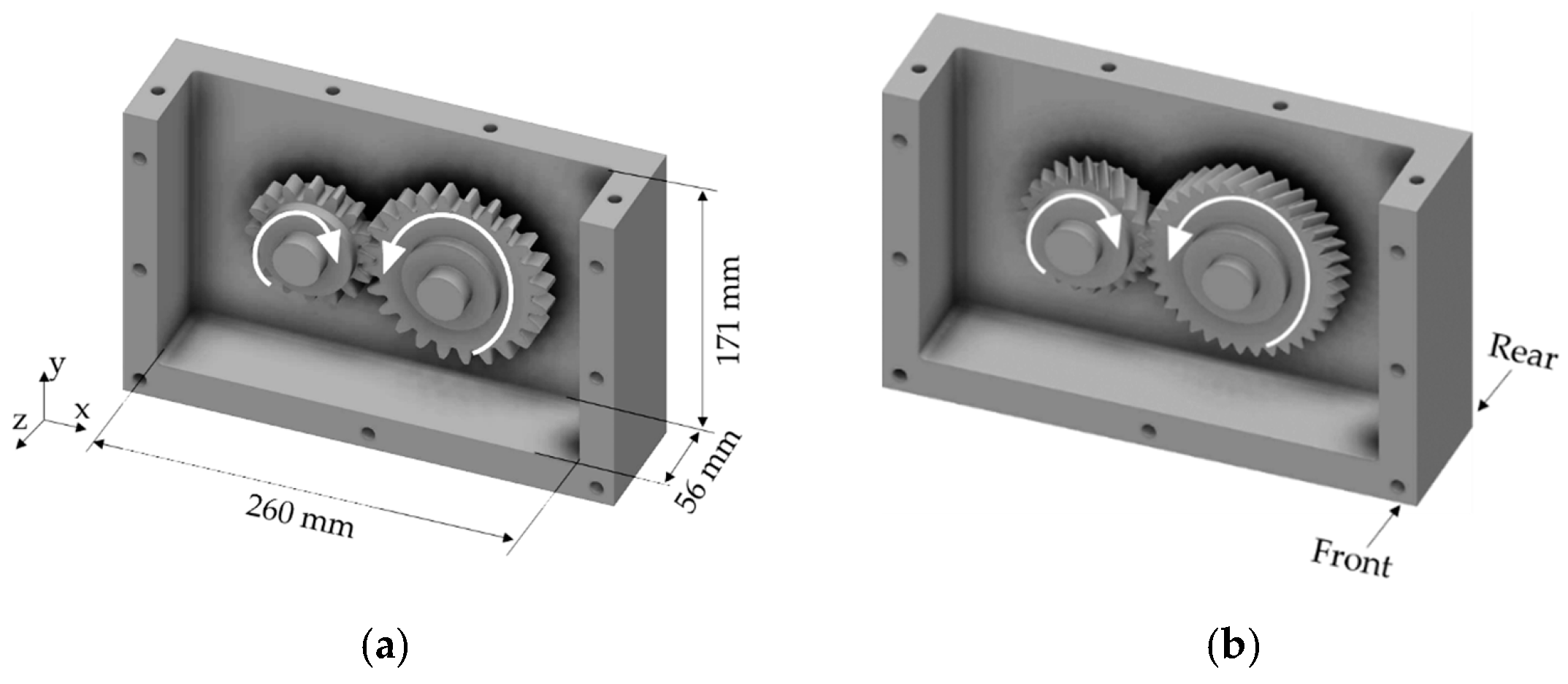


| gear-C | |||||||
|---|---|---|---|---|---|---|---|
| a in mm | z1|2 | mn in mm | αn in ° | β in ° | b1|2 in mm | da1|2 in mm | |
| Pinion (1) | 91.5 | 16 | 4.5 | 20.0 | 0 | 14 | 82.5 |
| Wheel (2) | 24 | 118.4 | |||||
| gear-LL | |||||||
| a in mm | z1|2 | mn in mm | αn in ° | β in ° | b1|2 in mm | da1|2 in mm | |
| Pinion (1) | 91.5 | 24 | 2.75 | 30.0 | 26 | 20 | 78.2 |
| Wheel (2) | 36 | 114.1 | |||||
| vt in m/s | Toil in K | TM1 in K | TM2 in K |
|---|---|---|---|
| 2.0 | 303.25 | 304.75 | 304.85 |
| 5.0 | 306.35 | 309.05 | 308.85 |
| 10.0 | 313.55 | 318.15 | 317.55 |
| Mesh Model | Zones | Element Size in mm | Element Number in M | Density in Elements per mm³ |
|---|---|---|---|---|
| Meshgear-C | (1) Gear zones | 0.75 (prism./hex.) | 222,373 | 1.47 |
| (2) Cylindrical zones | 1.00 (prism./hex.) | 784,795 | 2.56 | |
| (3) Transition zones | 1.00 (hex.) | 79,016 | 1.52 | |
| (4) Outer zone | 1.00 (hex.) | 810,488 | 1.01 | |
| Overall Model | 0.92 | 1.89 | 1.33 | |
| Meshgear-LL | (1) Gear zones | 0.75 (tet.) | 1,078,204 | 6.17 |
| (2) Cylindrical zones | 1.00 (prism./hex.) | 2,291,204 | 2.42 | |
| (3) Transition zones | 1.00 (hex.) | 102,866 | 1.52 | |
| (4) Outer zone | 1.00 (hex.) | 1,744,630 | 1.01 | |
| Overall Model | 0.92 | 5.21 | 2.45 |
| Equation | |||
|---|---|---|---|
| Mass | 1 | 0 | 0 |
| Impulse | |||
| Energy | h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hildebrand, L.; Dangl, F.; Paschold, C.; Lohner, T.; Stahl, K. CFD Analysis on the Heat Dissipation of a Dry-Lubricated Gear Stage. Appl. Sci. 2022, 12, 10386. https://doi.org/10.3390/app122010386
Hildebrand L, Dangl F, Paschold C, Lohner T, Stahl K. CFD Analysis on the Heat Dissipation of a Dry-Lubricated Gear Stage. Applied Sciences. 2022; 12(20):10386. https://doi.org/10.3390/app122010386
Chicago/Turabian StyleHildebrand, Lucas, Florian Dangl, Constantin Paschold, Thomas Lohner, and Karsten Stahl. 2022. "CFD Analysis on the Heat Dissipation of a Dry-Lubricated Gear Stage" Applied Sciences 12, no. 20: 10386. https://doi.org/10.3390/app122010386
APA StyleHildebrand, L., Dangl, F., Paschold, C., Lohner, T., & Stahl, K. (2022). CFD Analysis on the Heat Dissipation of a Dry-Lubricated Gear Stage. Applied Sciences, 12(20), 10386. https://doi.org/10.3390/app122010386









