Freedom in Osteoarthritis of the Knee

Abstract

The first peak of the external knee abduction moment (KAM) is often used as a surrogate measure of the medial compartment loading and has been correlated with pain and progression of knee osteoarthritis (OA). As a result, reducing the KAM is often the target of conservative interventions. OA should be considered as a “Whole Person” disease, including ecological psychosocial aspects. Scientists have developed gait alteration strategies to reduce the KAM. They attempted to force into a new position any particular part without reference to the pattern of the whole. We propose an alternative approach: in the vicinity of a special configuration of the knee, some or all of the components of the knee become overloaded. This study has shown that when six lines ${\$}_1^{\prime },{\$}_2^{\prime },{\$}_3^{\prime },{\$}_4^{\prime },{\$}_5^{\prime },{\$}_6^{\prime }$ are so situated that forces acting along them equilibrate when applied to one degree of freedom, 1$°$ F knee, a certain determinant vanishes. We wish to define the six lines as the knee complex in involution by virtue of some constraint upon the knee.

1. Introduction

Andriacchi (2020) argued that “To advance new osteoarthritis (OA) treatments that are safe and effective, OA should be considered as a whole person disease and require interaction across the whole body, including psychological aspects [1]”. To make good on this claim, Shull et al. attempted to develop gait retraining programs to reduce the knee adduction moment (KAM) and improve symptoms for medial compartment knee osteoarthritis and knee pain [2]. In addition, gait modification by wedged insoles was used to treat the medial compartment [3].

The first peak of the external KAM is often used as a surrogate measure of medial compartment loading. It has been correlated with pain and the presence, severity, and progression of medial compartment knee OA-conservative treatments that reduce the KAM hold potential for treating symptoms and slowing OA progression. This improvement reduced the adduction moment more than other nonsurgical treatments, such as braces or insoles. In addition, decreasing the foot progression angle shifted the knee joint center medially and the center of pressure laterally, both of which reduced the moment arm of the ground reaction force (GRF) at the knee [4].

Those studies generally take the KAM as the primary means to control overloaded joints. Therefore, the overloaded medial component must exert a force of correspondingly large intensity so that the sum of the ‘projections’ on the component’s force is large enough to equilibrate the GRF. In contrast, our study shows that the excessively large forces required on the medial compartment can be mediated theoretically. It follows that if the GRF is part of the reciprocal screw system of one degree-of-freedom of the knee (1$°$ F knee) defined by virtue of some constraint, these forces may be finite, for the reactions of the constraints are only manifested by the success with which they resist the efforts of certain force to disturb the equilibrium of the knee. The perceptual psychologist J. J. Gibson proposes gait control lies in the mutuality of animal–environment system, that is, the living object is surrounded in a special way, that the surface of gait is supporting differently from the way that a set of objects is supporting for a physical object [5].

Moreover, by virtue of positioning the 1$°$ F knee in the global frame [6], those 1$°$ F knees could be reciprocally connected with the ground reaction force (GRF) vector and functionally located at the associated COPs (Center of Pressure) during gait trials [7]. The COP is the point on the ground through which a single resultant force appears to act.

The purpose of this study was to propose the alternative approach that the only way to avoid overloading is by keeping the joint properly aligned relative to the surface by the use of a special configuration, knee complex in involution.

2. Materials and Methods

There are two main advantages to using screws, twists, and wrenches for describing rigid body kinematics: The first is that they allow a global description of rigid body motion that does not suffer from singularities due to local coordinates. Such singularities are inevitable when one represents rotation via Euler angles [8]. The second advantage is that the screw theory provides a very geometric description of rigid motion which significantly simplifies the analysis of biomechanisms. A given system of impressed forces will generally not be in equilibrium. This requires the fulfillment of special conditions. The total virtual work of the impressed forces will usually be different from zero in case the system’s motion makes up for the deficiency. The body moves so that the additional inertial forces produced by the motion bring the balance up to zero [9]. In this way, d’Alembert’s principle gives the equations of motion of an arbitrary mechanical system for reducing a problem of dynamics at a chosen instant to one of statics, allowing screws to be applied to a wide range of problems in biomechanics [7]. There will be extensive use of the geometry of screws throughout the paper, particularly in the results section, when studying the kinematics and special configuration of biomechanisms.

At the knee joint between a single pair of links—femur and tibia—there are at an instant the following two screws: (a) the common action screw of the pair of equal and opposite wrenches acting at the joint, a representative instance of these two wrenches are made up of all of the forces acting from one of the links upon the other at the point of contact and tension in ligaments at the joint, and (b) the common motion screws of the pair of equal and opposite rates of twisting screws at the joint; this latter, of course, is the screw of the relative instantaneous screw axis of the knee (ISA) [10]. If the joint is merely a transmitting joint, transferring their weights as directly as possible to the base, and if the transmission joint is held to be frictionless, the two screws should be seen to be reciprocal [11].

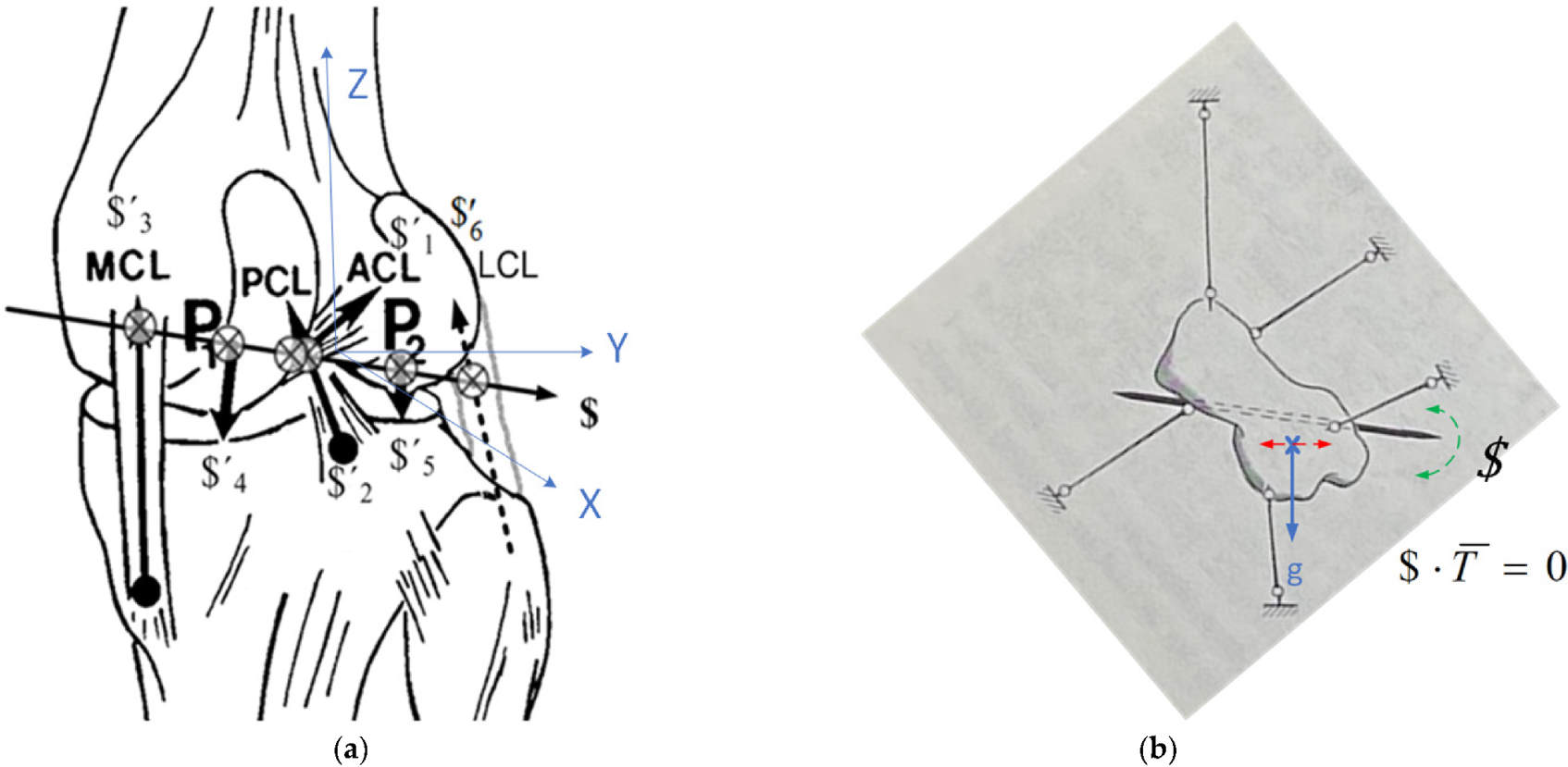
A linear complex is determined from the linear combination of five linearly independent lines; likewise, the knee complex is determined by the action screw five-system from six constraints representing the intra-articular structures of 1$°$ F knee [12]. Thus, the knee complex includes forces acting along with anterior cruciate ligaments (ACL), posterior cruciate ligament (PCL), medial collateral ligament (MCL), lateral collateral ligament (LCL), and articular cartilage contact in the medial (P1) and lateral (P2) compartments [13] (Figure 1a).

The knee synergy approach proposed herein was recently validated experimentally by Conconi et al. [14]. The authors calculated if all the lines of action intersect at the ISA or $ following natural knee motion to describe the knee complex invariant. The results show the mean distances between each constraint line of action, and the ISA or $ stayed below 3.4 mm and 4.5 mm for ex vivo and in vivo assessments, respectively (The results are used with the permission of Professor Michele Conconi. The video is available: https://drive.google.com/file/d/18_YtszzT3_IvNIken5uxObj4jmSd0Zs_/view?usp=sharing (accessed on 26 December 2021)).

It must always be possible to find a motion screw, the green line that is reciprocal to the six forces: two red lines in compression and the four blue lines in tension. For example, suppose the knee was only free to twist about the motion screw, then the six forces would not only collectively be in equilibrium, but severally would be unable to stir the knee only free to twist about the motion screw. In a tensegrity–truss model, the loads distribute through the system only in tension or compression. As in all truss systems, there are no levers and no moments at the joints [15]. The knee tensegrity structure is distinguished in that the compressed components must be disconnected, and the tensioned components should be connected to create an “ocean” of continuous tension with discontinuous compression floating in it.

The six screws of expression can be written as column vectors in a six-by-six tensor:

$$\left[\begin{array}{l}{L}^{\prime }\\ M^{\prime }\\ N^{\prime }\\ P^{\prime }\\ Q^{\prime }\\ R^{\prime }\end{array}\right]=\left[\begin{array}{cccccc}{\$}_1^{\prime }& {\$}_2^{\prime }& {\$}_3^{\prime }& {\$}_4^{\prime }& {\$}_5^{\prime }& {\$}_6^{\prime }\end{array}\right]\left[\begin{array}{l}{F}_1\\ F_2\\ F_3\\ F_4\\ F_5\\ F_6\end{array}\right]$$

(1)

The column on the left represents the external wrench created by applying the external forces, and the $F_j$ column represents the force intensities associated with the corresponding reciprocal force in the knee complex. In this case, the $F_j$ corresponding to the magnitudes of ligament tensile forces, the tibiofemoral compressive contact forces. The six-by-six $\left[{\$}_{ij}^{\prime }\right]$ tensor of the normalized screw is defined as the Jacobian [11]. The reciprocal connection manifests that if a knee joint is only free to twist about a screw $\$$ while in equilibrium, despite the impulsive reaction of the constraints ${\$}_1^{\prime },{\$}_2^{\prime },{\$}_3^{\prime },{\$}_4^{\prime },{\$}_5^{\prime },{\$}_6^{\prime }$, the mechanical work during a small displacement against the reaction forces in the $\left[{\$}_{ij}^{\prime }\right]$ must be zero, according to the following relationship [16]:

$${\$}^T\cdot \left[{\$}_{ij}^{\prime }\right]=0.$$

(2)

Ball has shown that when six lines ${\$}_1^{\prime },{\$}_2^{\prime },{\$}_3^{\prime },{\$}_4^{\prime },{\$}_5^{\prime },{\$}_6^{\prime }$ are so situated that forces acting along them equilibrate when applied to, for example, 1$°$F knee, a certain determinant vanishes. He speaks of the six lines so related as being in involution. Using the ideas and languages of the Theory of Screws, Ball verified that this determinant is the sexiant of the six screws, the pitches, of course, being zero. Therefore, a system of lines thus related consists of the screws of equal pitch belonging to a reciprocal screw five-system. In the language of Plűcker, a system of lines in involution forms a linear complex [17] (Ball 1900). In the language of freedom in osteoarthritis of the knee, the 1$°$F knee, surrounded by its reciprocal action screw five-system in a special way, forms a knee complex in involution. The knee complex in involution is calculated by equating the determinant $\left[{\$}_{ij}^{\prime }\right]$ to zero.

It must always be possible to find a single motion screw $\$$ that is reciprocal to the six screws or action screw five-system. For example, suppose the knee were only free to twist about $\$$. The six forces would not only collectively be in equilibrium but severally would be unable to stir the knee, only free to twist about $\$$ [18]. Thus, the six screws are members of a screw five-system and 1$°$ F knee. To visualize the linear complex and its reciprocal connections, one might consider the statics of a rigid body suspended—in stable equilibrium and in a parallel gravity field—by five taut strings (Figure 1b). It follows that, in the event of a small displacement, the five points at the points of attachment of the string upon the body and a sixth point at the center of mass will all move in directions perpendicular to the force acting there (T). Thus, the six linear velocities will be consistent with the unique instantaneous screw axis (ISA or $), which must exist, and the lines of action for the six forces—the five tensions in the five strings and the force of gravity—will reside as generators of the complex of tensional networks that surround the $. In other words, this gravity force must belong to the linear complex defined by the other five lines of actions (strings) [12].

Given the axis $ (with its pitch h) of a linear complex, there is no difficulty in finding the helices and any lines of the complex desired, expressing them in Plűcker coordinates or some other form. However, the inverse problem is much more complicated, given five lines, to find the linear complex to which they belong and find the instantaneous screw axis.

3. Results

Having introduced a special configuration in terms of the knee complex in involution, the situation will be examined more closely in order to determine where the six lines either lose linear independence or are close to losing it. Finally, to validate this modeling approach, current results are compared with the simulation of two cases: the knee complex in involution and the OA knee. We hypothesized that in the case of the healthy knee, the GRF becomes a member of the knee complex in involution, that is, a projective combination of the six lines of action. However, the OA knee shows the GRF is not dependent on the above six forces.

The normalized screw coordinates of six constraint lines were chosen in the tibial reference frame, obtained from a set of anatomical landmark location data taken from the literature [19,20] (Figure 1a).

There are six constraints ${\$}_i^{\prime },i=1,2,\dots ,6.$ like those of Equation (1): The Jacobian can be written by inspection as

$$\begin{array}{l}{\$}_1^{\prime }\equiv (0.52,0.46,0.72;0,0,0),\\ {\$}_2^{\prime }\equiv (-0.10,-0.54,0.84;0.37,-15.12,-9.67),\\ {\$}_3^{\prime }\equiv (0.28,-0.42,0.90;-24.78,-5.43,5.51),\\ {\$}_4^{\prime }\equiv (-0.09,-0.25,0.96;-10.30,-3.13,0.19),\\ {\$}_5^{\prime }\equiv (0.21,0.16,0.96;29.86,2.75,-6.90),\\ {\$}_6^{\prime }\equiv (0.21,-0.08,0.97;-3.95,-3.90,-1.75)\end{array}$$

(3)

Thus, for every screw five-system, there is one screw that is reciprocal to all the screws within the system [21].

The algorithm for calculating reciprocal screws using the nullspace operation was originally developed by Konkar and Cutkosky [22] and later presented in detail using MATLAB functions (Mathworks, Inc., Natick, MA, USA) by Adams and Whitney [23] (The Matlab script is presented in Appendix A). When written in ray-coordinate order, $, the ISA, is located at

$$\$\equiv (0.19,-0.54,0.82;-8.43,5.74,2.41).$$

(4)

It may be perceived that a given GRF may always be replaced by a wrench on any other screw, which itself is reciprocal to the 1$°$F knee. Active touch and movement refer to what is ordinarily called touching—variations in skin stimulation caused by surfaces are altered together by motor activity variations. This fact is worth noting because it is often neglected that locomotion and its surfaces form an inseparable pair [24].

This unit wrench ${{\$}^{\prime }}_{}$ was delivered to the knee body by the six forces $F_i$ on their respective constraints screw ${\$}_i^{\prime }$. These six equations can be solved for the six $F_i$ using the Equation (1).

$${\$}^{\prime }=(L^{\prime },M^{\prime },N^{\prime };P^{\prime },Q^{\prime },R^{\prime })\equiv (0.21,-0.08,0.97;-3.95,-3.90,-1.75)$$

(5)

The configuration is now modified by rotating the femur through an angle $\theta$ ($-\frac{\pi }{16}$) about the X-axis. By the angle theta, we tried to create the condition that GRF is not a member of the linear complex in involution. The knee complex in involution transitorily loses a degree of freedom since they are projectively independent of one another, resulting in an overconstrained condition. After this displacement, the configuration is no longer special, and having modified the column, the following results may be obtained:

$$\begin{array}{l}{\$}_1^{\prime }\equiv (0.52,0.59,0.62;0,0,0),\\ {\$}_2^{\prime }\equiv (-0.10,-0.36,0.92;0.37,-16.72,-6.54),\\ {\$}_3^{\prime }\equiv (0.28,-0.25,0.93;-24.78,-4.25,6.47),\\ {\$}_4^{\prime }\equiv (-0.09,-0.06,0.99;-10.30,-3.03,0.80),\\ {\$}_5^{\prime }\equiv (0.21,0.35,0.91;29.86,1.35,-7.31),\\ {\$}_6^{\prime }\equiv (0.21,0.11,0.97;-3.95,-4.17,-0.95)\end{array}$$

(6)

In the vicinity of a special configuration of a 1° F knee, after being modified, some or all of the constraints have to operate overloaded. Physically, the external wrench ${{\$}^{\prime }}_{}$ applied to the knee has a substantial component that is nearly reciprocal to (has a minimal ‘projection’ on) the screws of the overloaded interarticular members. However, none of the other members projects on to the substantial components of ${{\$}^{\prime }}_{}$. Therefore, each overloaded member must exert a force of correspondingly large intensity so that the sum of the ‘projections’ on ${{\$}^{\prime }}_{}$ of the members is large enough to equilibrate ${{\$}^{\prime }}_{}$. The excessively large forces required ${\$}_i^{\prime }$ are infinite when the angle $\theta$ = 0 theoretically, but if it is part of the screw system defined by them when the coordinates ${{\$}^{\prime }}_{}$ meet the condition, these forces may be finite [25].

The force values are presented in non-dimensional forms, like ligaments and contact force per unit applied load. To illustrate, the knee complex in involution shows finite values of forces, which manifests that given GRF is perceived to be replaced by a wrench of the appropriate intensity of any other screw belonging in the knee complex defined by the other five constraints. However, OA knee shows excessively large forces manifesting that a given GRF is not perceived as a member of the knee complex (

Table 1. Forces applied to the constraint components.

$\mathbf{Constraint}\mathbf{Components}{\mathbf{\$}}_{\mathit{i}}^{\prime }$	Force per Unit Applied Load
	The Knee Complex in Involution	The OA Knee
ACL	0.30	−2.10 × 1014
PCL	0.15	−1.05 × 1014
MCL	0.02	−1.38 × 1013
P1	0.57	−4.02 × 1014 −5.48 × 1013
P2	0.08
Q	N/A	7.11 × 1014

).

4. Discussion

The main finding of this study is that OA patients are likely to develop overloaded medial compartments during walking due to the slight projection of the external load onto the constraints at the knee. The peak of KAM is often used as a surrogate measure of medial compartment loading. However, this study puts an alternative measure on how OA patients perceive that a given external force may be actively replaced by a force whose line of action will be a member of the same knee complex in involution. We showed that in the case of the healthy knee, the GRF becomes a member of the knee complex in involution, that is, a projective combination of the six lines of action. However, the OA knee shows the GRF is not dependent on the above six forces.

The lower proprioceptive system [26] at the knee controls posture and equilibrium such as the given muscle forces and the external GRF may always be replaced by the forces of appropriate intensities in the screw five-system, the knee complex, in so far as the effect on the knee only free to twist about 1$°$ F knee is concerned. High loads incur from the impaired condition of this lower proprioceptive system in the knee. It may not be out of place to notice the analogy in which proprioception bears to the simple lower problem of the determination of the condition that a pair of antagonistic muscle forces should be unable to disturb the equilibrium of the 1$°$ F of the joint. One muscle of the pair contracts to move the body part, the other muscle in the pair then contracts to return the body part back to the original position. Muscles that work like this are called antagonistic pairs. The delicate play of this tonus in all muscles is what enables the animals to keep it balanced. Equilibrium is a process of continuous compensation. Sherrington’s contribution to the study of behavior was to experimentally show how animals’ posture and locomotion were governed by auto-stimulation or the circular action of the nervous system [26].

Suppose muscles are called upon to lift and to hold weights unnecessarily instead of to move bones in a balanced relationship. In that case, such action violates their relationship with the nervous system, as the reflex circle that arises is not designed to induce the appropriate reflexes. The holding of parts in fixed and strained relations impedes the circular action of the nervous system, and the resultant congestion of one part and the defrauding of another can work havoc throughout the system, operating overloaded in the medial compartment. Conscious direction of a moving function rather than a holding function should emphasize where bones, muscles, and ligaments are concerned since man presents a dynamic problem.

The lower proprioceptive system states this result in a somewhat different manner. Throughout the 1$°$ F knee complex run two forces: the one is mechanically operated by the 1° freedom in equilibrium, working on all parts of the body in the same way that it acts on any similar combination of weights, levers, and supports [9] (Lanczos 2012), and the other is the living force exerted by the neuromuscular mechanism. The muscle task is to move the bones, balance them at constraints in the joint such that no work results along the axis of 1$°$ F knee, and transfer their weights as directly as possible. They should be used for this purpose and not the work assigned to the bones.

5. Conclusions

To secure conscious control of balance in the bony structure of the human knee, it would be better to understand its mechanical design and then trust the long-established automatic machinery of the neuromuscular system to make the necessary space-time adjustments. The knee’s movements are neither triggered nor commanded but controlled. Moreover, they are controlled not by the brain but by information, that is, by touching oneself on the surface. The current neuromuscular modeling approach for knee OA seems to lead to the idea of a human object as an extremely complex object of the physical world. This way of thinking neglects the fact that the human–object is surrounded in a special way, that control lies in the human–surface system, but this automatic process is interfered with whenever we attempt to force into a new position any particular part without reference to the pattern of the whole, ignoring the mutuality of animal and surface [1]. The idea that inanimate objects offer action possibilities in an organism is a foundational concept known since Gibson’s work in ecological psychology. The ecological approach demonstrates how animal (including human) perception and action is continuous with interactions between inanimate physical systems or the world in general.