Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function
Abstract
:1. Introduction
2. Synchronized Assessment Method
2.1. Forward Problem
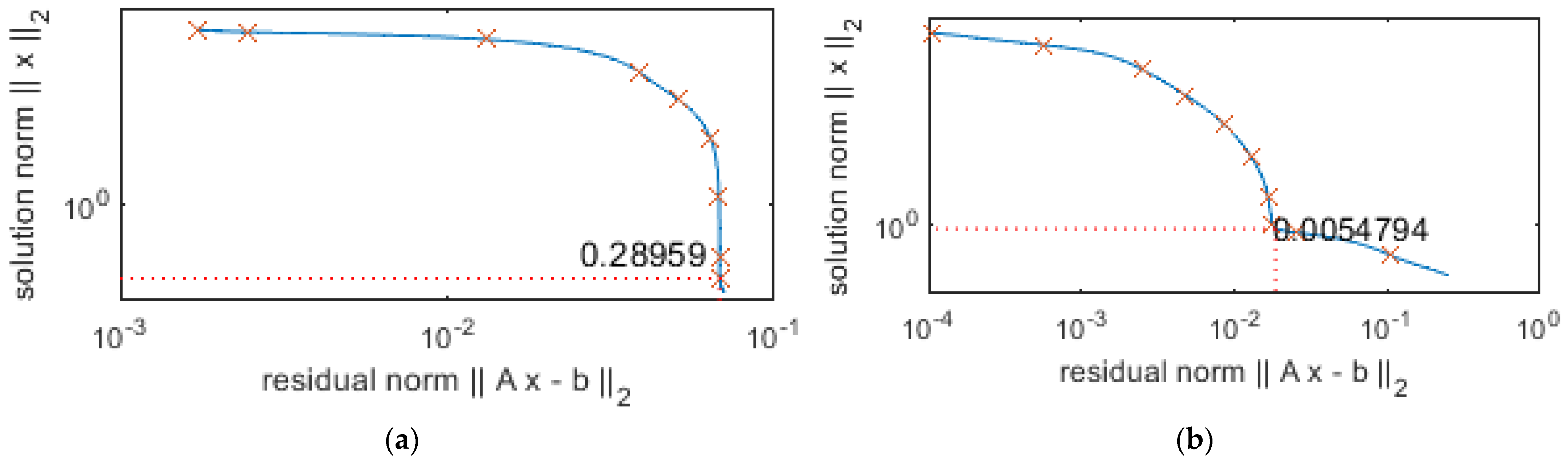
2.2. Inverse Problem
2.3. Reconstruction of Moving Force and Structural Damage
3. Numerical Validations
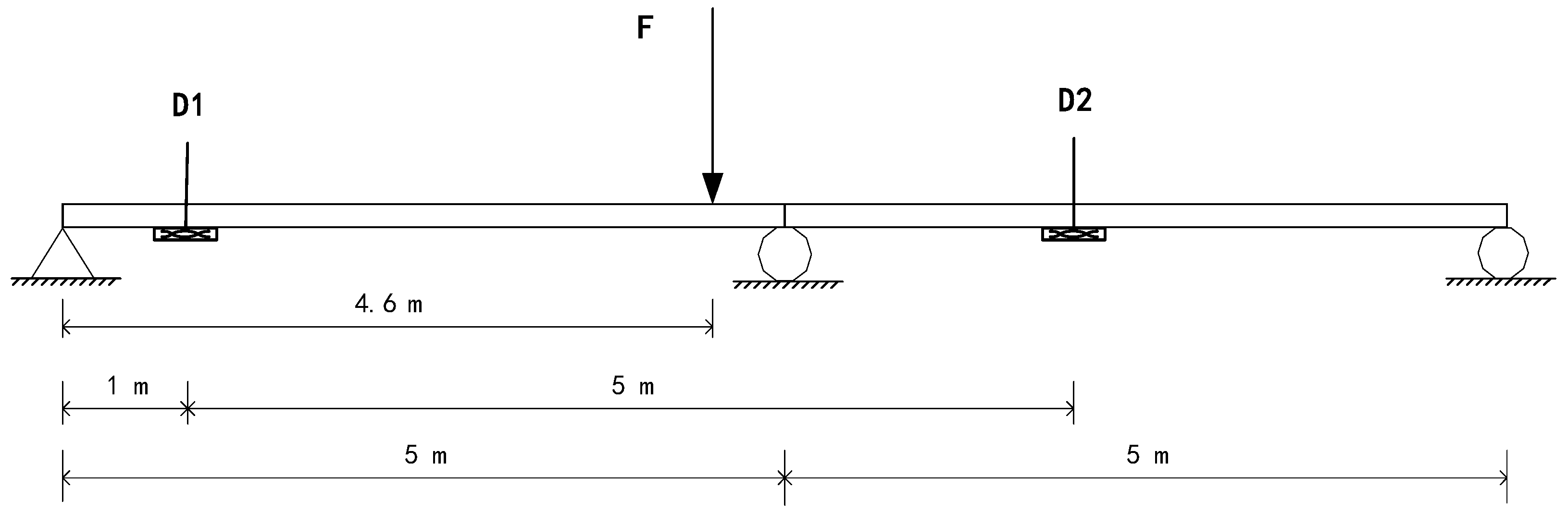
3.1. Continuous Beam Example
- (1)
- The relative position of the response
- (2)
- The type of the excitation force
- (3)
- The measurement noises
3.2. Truss Bridge Example
- (1)
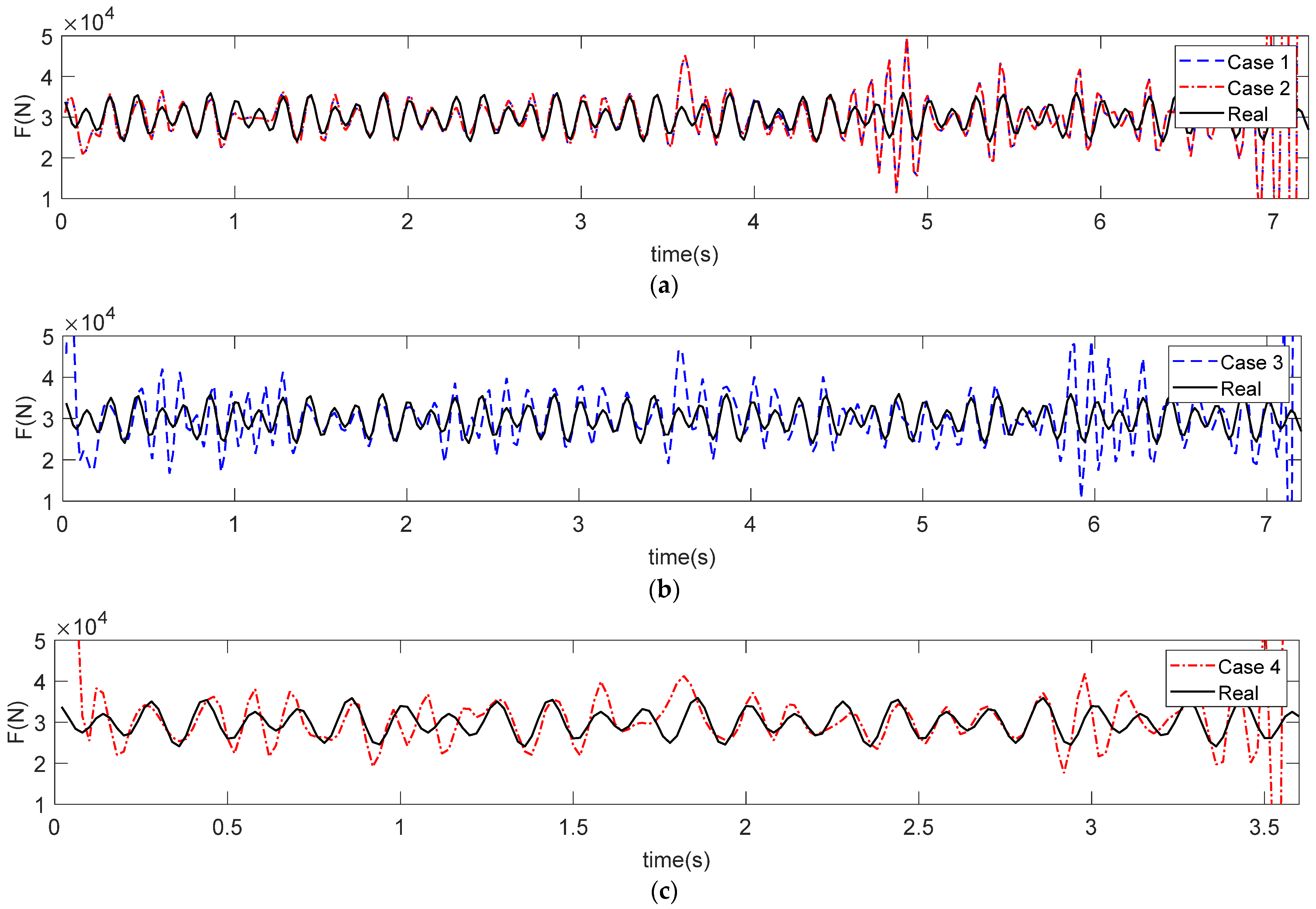
- Result discussion for MFI
- Influence of damage severity and location
- Effects of force speed and number
- Influence of measurement noise and sensor location
- (2)
- Result discussion for SDI
- Influence of damage severity and measurement noise
- Influence of moving force
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brouste, A. Testing the accuracy of WIM systems: Application to a B-WIM case. Measurement 2021, 185, 110068. [Google Scholar] [CrossRef]
- Yu, Y.; Cai, C.S.; Deng, L. Vehicle axle identification using wavelet analysis of bridge global responses. J. Vib. Control 2017, 23, 2830–2840. [Google Scholar] [CrossRef]
- Outay, F.; Mengash, H.A.; Adnan, M. Applications of unmanned aerial vehicle (UAV) in road safety, traffic and highway infrastructure management: Recent advances and challenges. Transp. Res. Part A Policy Pract. 2020, 141, 116–129. [Google Scholar] [CrossRef]
- Pitkänen, T.P.; Piri, T.; Lehtonen, A.; Peltoniemi, M. Detecting structural changes induced by Heterobasidion root rot on Scots pines using terrestrial laser scanning. For. Ecol. Manag. 2021, 492, 119239. [Google Scholar] [CrossRef]
- Lee, H.; Koo, B.; Chattopadhyay, A.; Neerukatti, R.K.; Liu, K.C. Damage detection technique using ultrasonic guided waves and outlier detection: Application to interface delamination diagnosis of integrated circuit package. Mech. Syst. Signal Process. 2021, 160, 107884. [Google Scholar] [CrossRef]
- Chan, T.H.T.; Yu, L.; Law, S.S.; Yung, T.H. Moving force identification studies, I: Theory. J. Sound Vib. 2001, 247, 59–76. [Google Scholar] [CrossRef]
- Law, S.S.; Chan, T.H.T.; Zhu, Q.X.; Zeng, Q.H. Regularization in Moving Force Identification. J. Eng. Mech. 2001, 127, 136–148. [Google Scholar] [CrossRef]
- Pan, C.D.; Yu, L.; Liu, H.L.; Chen, Z.P.; Luo, W.F.J.M.S.; Processing, S. Moving force identification based on redundant concatenated dictionary and weighted l1-norm regularization. Mech. Syst. Signal Process. 2018, 98, 32–49. [Google Scholar] [CrossRef]
- Ren, Y.; Cheng, W.; Wang, Y.; Wang, B. Analysis of flexural behavior of a simple supported thin beam under concentrated multiloads using trigonometric series method. Thin-Walled Struct. 2017, 120, 124–137. [Google Scholar] [CrossRef]
- Huang, C.; Ji, H.; Qiu, J.; Wang, L.; Wang, X. TwIST sparse regularization method using cubic B-spline dual scaling functions for impact force identification. Mech. Syst. Signal Process. 2022, 167, 108451. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Vuong, L.C.; Le, C.M.; Ngo, N.K.; Nguyen- Xuan, H. A data-driven approach based on wavelet analysis and deep learning for identification of multiple-cracked beam structures under moving load. Measurement 2020, 162, 107862. [Google Scholar] [CrossRef]
- Liu, J.; Sun, X.; Han, X.; Jiang, C.; Yu, D. A novel computational inverse technique for load identification using the shape function method of moving least square fitting. Comput. Struct. 2014, 144, 127–137. [Google Scholar] [CrossRef]
- Pan, C.D.; Yu, L. Moving Force Identification Based on Firefly Algorithm. J. Adv. Mater. Res. 2014, 3149, 329–333. [Google Scholar] [CrossRef]
- Boubaker, S. Identification of monthly municipal water demand system based on autoregressive integrated moving average model tuned by particle swarm optimization. J. Hydroinform. 2017, 19, 261–281. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Roy, K.; Ray-Chaudhuri, S. Fundamental mode shape and its derivatives in structural damage localization. J. Sound Vib. 2013, 332, 5584–5593. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, Z.; Gu, Z.; Zhu, C.; Qian, W. Damage Detection in Different Types of 3D Asymmetric Buildings Using Vibration Characteristics. Shock. Vib. 2021, 2021, 6004283. [Google Scholar] [CrossRef]
- Farahani, R.V.; Penumadu, D. Damage identification of a full-scale five-girder bridge using time-series analysis of vibration data. J. Eng. Struct. 2016, 115, 129–139. [Google Scholar] [CrossRef]
- Lee, E.-T.; Eun, H.-C.; Elahinia, M. Structural Damage Detection by Power Spectral Density Estimation Using Output-Only Measurement. J. Shock. Vib. 2016, 2016, 8761249. [Google Scholar] [CrossRef] [Green Version]
- Andrzej, K.; Viriato, A.d.S.J.; Hernâni, L. Damage identification by wavelet analysis of modal rotation differences. J. Struct. 2021, 30, 1–10. [Google Scholar]
- Minshui, H.; Wei, Z.; Jianfeng, G.; Yongzhi, L. Damage Identification of a Steel Frame Based on Integration of Time Series and Neural Network under Varying Temperatures. J. Adv. Civ. Eng. 2020, 2020, 4284381. [Google Scholar]
- Zhu, X.; Law, S. Damage detection in simply supported concrete bridge structure under moving vehicular loads. J. Vib. Acoust. 2007, 129, 58–65. [Google Scholar] [CrossRef]
- Zhang, K.; Law, S.; Duan, Z. Condition assessment of structures under unknown support excitation. Earthq. Eng. Eng. Vib. 2009, 8, 103–114. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous identification of moving masses and structural damage. Struct. Multidiscip. Optim. 2010, 42, 907–922. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Chan, T.H.; Thambiratnam, D.P.; Nguyen, A. Prestress and excitation force identification in a prestressed concrete box-girder bridge. Comput. Concr. 2017, 20, 617–625. [Google Scholar]
- Kołakowski, P.; Wikło, M.; Holnicki-Szulc, J. The virtual distortion method—A versatile reanalysis tool for structures and systems. Struct. Multidiscip. Optim. 2008, 36, 217–234. [Google Scholar] [CrossRef]
- Clough, R.; Penzien, J. Dynamics of Structures, 1st ed.; McGraw-Hill Companies: New York, NY, USA, 1975; pp. 87–89. [Google Scholar]
- Chen, Z.; Chan, T.H.T. A truncated generalized singular value decomposition algorithm for moving force identification with ill-posed problems. J. Sound Vib. 2017, 401, 297–310. [Google Scholar] [CrossRef]
- Chan, T.H.T.; Yu, L.; Law, S.S.; Yung, T.H. Moving force identification studies, II: Comparative studies. J. Sound Vib. 2001, 247, 77–95. [Google Scholar] [CrossRef]
- Huang, M.S.; Cheng, X.; Lei, Y.Z. Structural Damage Identification Based on Substructure Method and Improved Whale Optimization Algorithm. J. Civil. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar] [CrossRef]
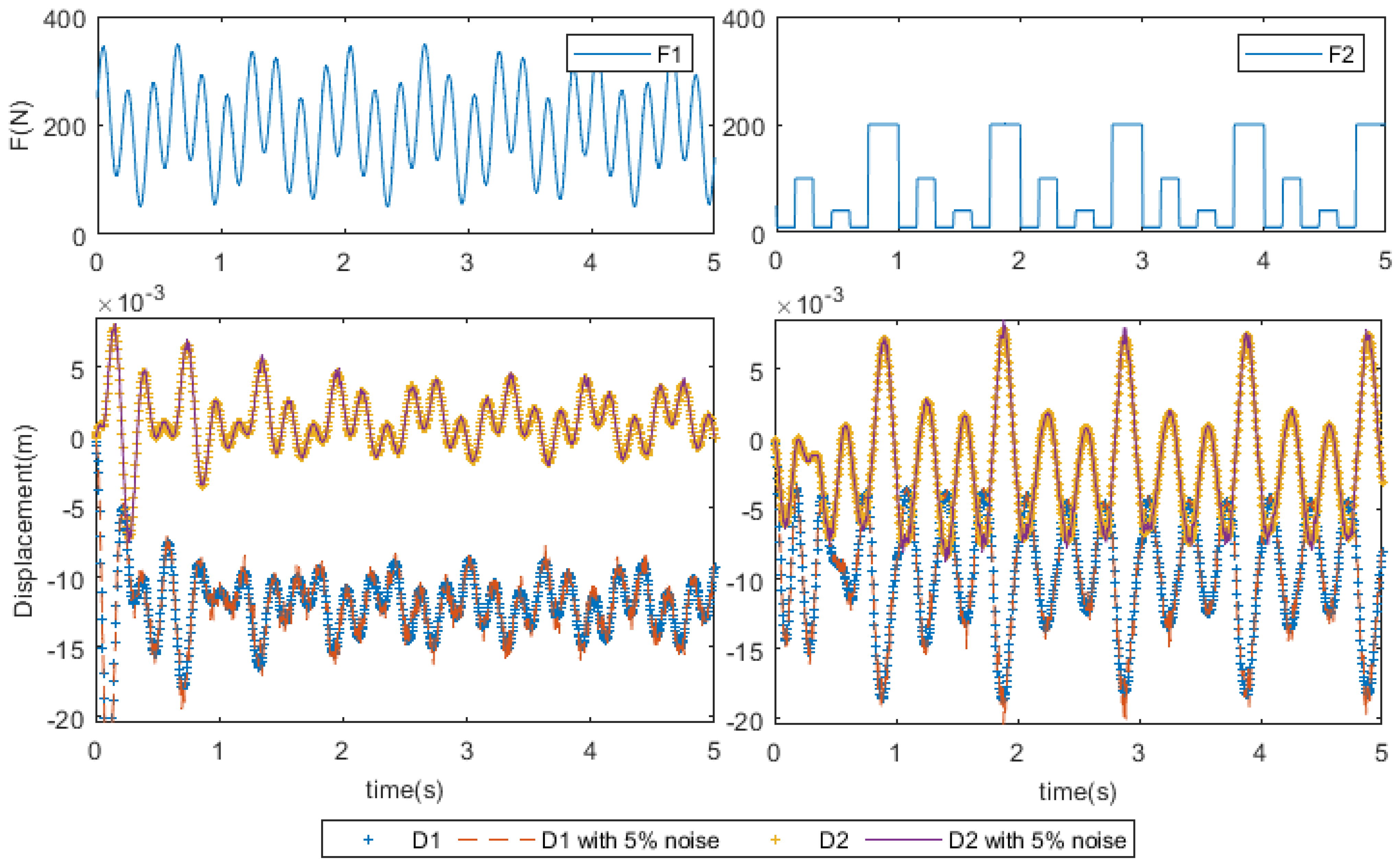



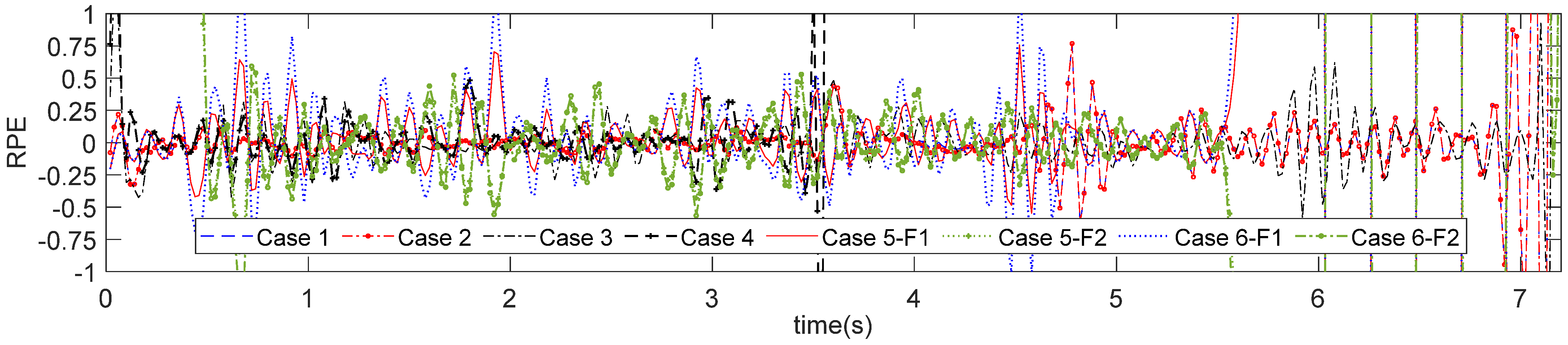
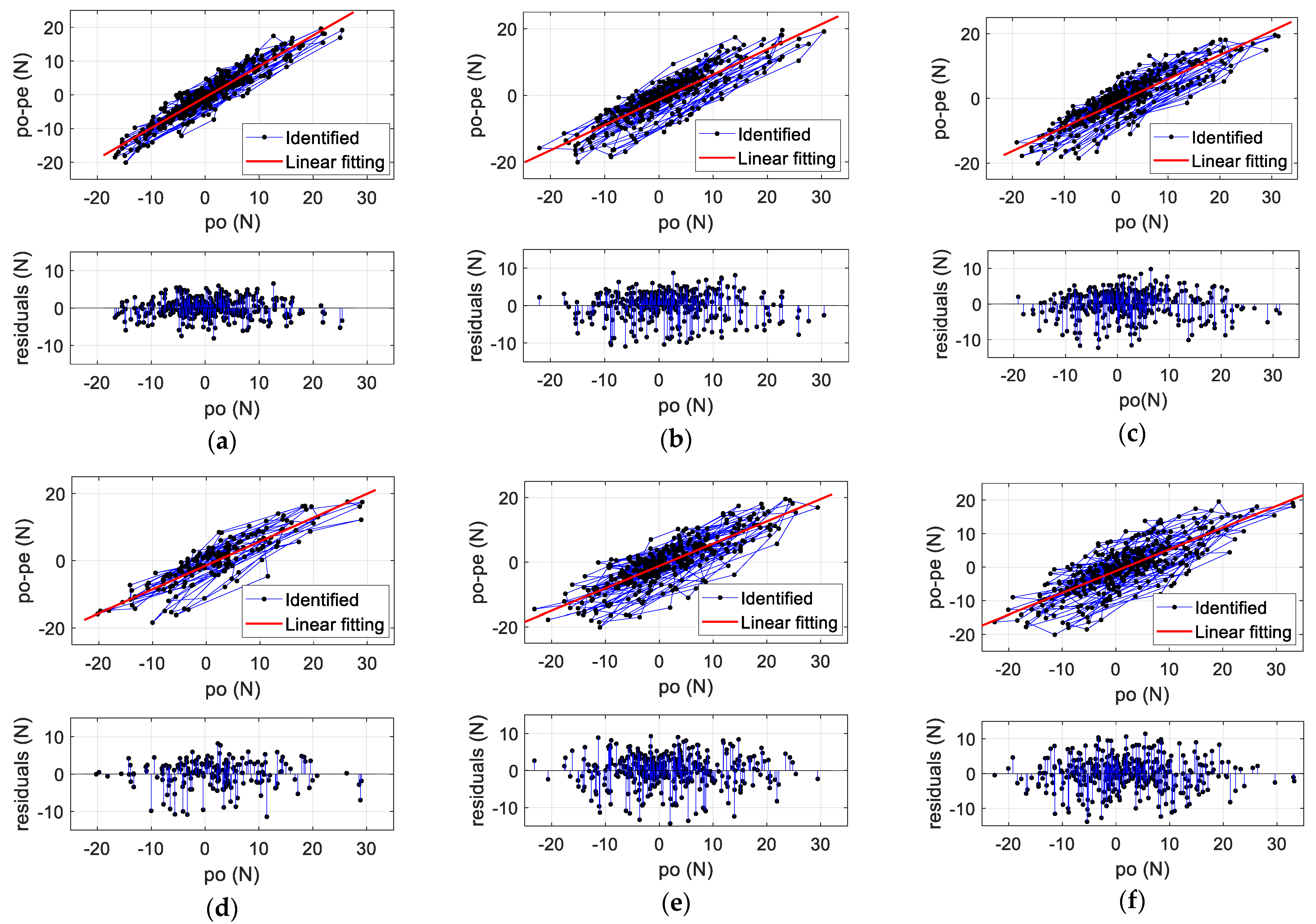
| RPE (%) | Harmonic Force | Square Wave Force |
|---|---|---|
| via D1 response | 1.5 | 6.72 |
| via D1 response with 5% noise | 5.73 | 9.42 |
| via D2 response | −48.1 | 13.41 |
| via D2 response with 5% noise | −49.1 | 22.85 |
| Case No. | Velocity (m/s) | Damage Severity | Damage Location | Force No. | Noise Level | Used Sensor |
|---|---|---|---|---|---|---|
| 1 | 10 | 5% | Damage 1 | F1 | 5% | S1 and S2 |
| 2 | 20% | |||||
| 3 | 10 | 20% | Damage 1 | F1 | 10% | S1 and S3 |
| 4 | 20 | S2 and S3 | ||||
| 5 | 10 | 20% | Damage 2 | F1 and F2 | 5% | S1, S2 and S3 |
| 6 | 10% |
| Case No. | Damage Severity | R-Squared Value | Case No. | Damage Severity | R-Squared Value |
|---|---|---|---|---|---|
| 1 | 9.73% | 0.8692 | 4 | 28.72% | 0.7556 |
| 2 | 24.25% | 0.7938 | 5 | 30.96% | 0.6723 |
| 3 | 25.83% | 0.7429 | 6 | 34.28% | 0.6311 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, J.; Xiang, Z.; Li, C. Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function. Appl. Sci. 2022, 12, 691. https://doi.org/10.3390/app12020691
Zhong J, Xiang Z, Li C. Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function. Applied Sciences. 2022; 12(2):691. https://doi.org/10.3390/app12020691
Chicago/Turabian StyleZhong, Jiwei, Ziru Xiang, and Cheng Li. 2022. "Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function" Applied Sciences 12, no. 2: 691. https://doi.org/10.3390/app12020691
APA StyleZhong, J., Xiang, Z., & Li, C. (2022). Synchronized Assessment of Bridge Structural Damage and Moving Force via Truncated Load Shape Function. Applied Sciences, 12(2), 691. https://doi.org/10.3390/app12020691





