Abstract
Topology optimization (TO) has been a popular design method among CAD designers in the last decades. This method optimizes the given design domain by minimizing/maximizing one or more objective functions, such as the structure’s stiffness, and at the same time, respecting the given constraints like the volume or the weight reduction. For this reason, the companies providing the commercial CAD/FEM platforms have taken this design trend into account and, thus, have included TO in their products over the last years. However, it is not clear which features, algorithms, or, in other words, possibilities the CAD designers do have using these software platforms. A comparative study among the most applied topology optimization software was conducted for this research paper. First, the authors developed an online database of the identified TO software in the form of a table. Interested CAD designers can access and edit its content, contributing in this way to the creation of an updated library of the available TO software. In addition, a deeper comparison among three commercial software platforms—SolidWorks, ANSYS Mechanical, and ABAQUS—was implemented using three common case studies—(1) a bell crank lever, (2) a pillow bracket, and (3) a small bridge. These models were designed, optimized, and validated numerically, as well as compared for their strength. Finally, the above software was evaluated with respect to optimization time, optimized designs, and TO possibilities and features.
1. Introduction
Topology optimization (TO) is an optimization technique where the material distribution of a structure is spatially optimized by minimizing or maximizing one or more objective function(s), such as stiffness and cost with respect to given constraints, for example, a specific weight reduction [1]. Structural optimization (SO), in general, has been well described over the previous decades in the literature [2,3,4]. In these works, the theoretical background, as well as the different types of SO, are presented in detail. According to Bendsøe and Sigmund [1], the SO consists of size, shape, and topology optimization. A more analytic representation of these optimization categories, together with their sub-categories that were introduced in the following years, is depicted in Figure 1.
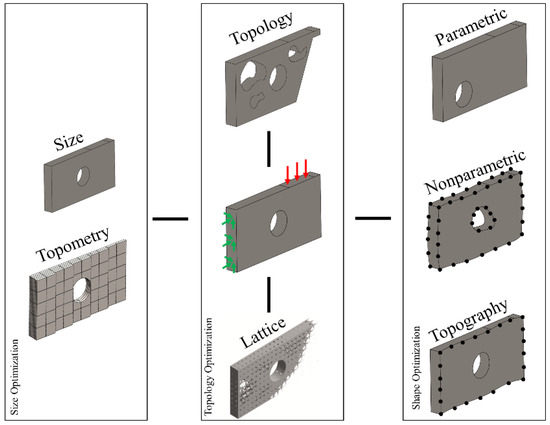
Figure 1.
The different types of SO adapted from [5].
In Figure 1, each of the three main categories of SO, which are size, shape, and topology, are further divided into sub-categories. The size optimization consists of global size optimization and local size optimization, which can be also referred to as topometry optimization. In topometry optimization, each element of the structure can be optimized independently [6]. At the topology optimization category, there is both the traditional TO at the macroscale level and the lattice optimization at the meso- and microscale levels of the structure [7,8,9]. Generative design, with its flexibility, could be added to this category [10]. Finally, the shape optimization can be either parametric, non-parametric (free form), or topographic, also named bead optimization. The latter can be considered a special case of shape optimization where the surface of a structure can be optimized independently [6].
A practical representation of the TO workflow in a TO software platform is shown in Figure 2.
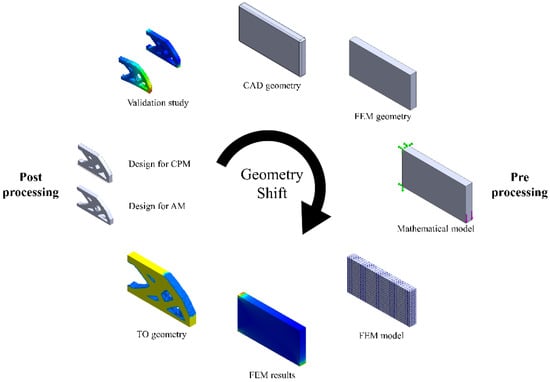
Figure 2.
A common TO workflow adapted from [11].
In Figure 2, the TO is divided into two main tasks—pre-processing and post-processing. On the one hand, the pre-processing of the design consists of the design phase, the implementation of the finite element method (FEM) with the definition of the mathematical model, and the discretization of the design space into finite elements. This task is concluded with the presentation and evaluation of the results. At this point, the computer-aided design (CAD) designer has to decide if there is room for optimization, which optimization method should be followed, and which TO software can satisfy his/her needs. On the other hand, post-processing is the second task where the optimized designs are prepared for production either by conventional production methods (CPM) or additive manufacturing (AM).
Thus, during the TO workflow, there are many decisions that have to be taken, referred to as the CAD designer’s inputs. These inputs can be classified into four clusters—the design constraints, the supports and connections, the loads, and the geometric restrictions due to manufacturing constraints [12]. The design constraints are all the geometrical dimensions that form the size and shape of the CAD model. The supports and connections restrain the degrees of freedom of the model. In other words, they define the relationship between the model and its environment, such as its interaction with other components. The loads are all the load cases that a CAD designer has to take into account in the optimization task. Finally, the geometric restrictions due to manufacturing constraints can be considered a subcase of the design constraints with a focus on the manufacturability of the CAD model. Different restrictions should be taken into account in the case of CPM compared to AM. In addition to these four clusters, a fifth cluster could be added regarding the properties and features of the TO software.
The first numerical method of TO was a 99-line script by Sigmund [13]. This can be considered the first form of a TO software platform and the kernel of many optimization platforms. The script was written in MATLAB and is based on the solid isotropic material with penalization method (SIMP) [2,14]. On the one hand, there is a plethora of open source software/scripts based on the 99-line script and SIMP, such as the top88 [15] and the top3D125 [16]. In addition, there are some scripts that implement different optimization methods, such as the CalculiX [17], which uses the bi-directional evolutionary structural optimization (BESO) [18], or the Allaire_Scilab [19], which applies the level set method [20]. Furthermore, there are a few open source platforms that offer a toolbox of TO scripts, such as the FreeFem [21] and the Firedrake [22]. On the other hand, the commercial CAD/FEM platforms have integrated TO over the last years due to the lack of computational power. The majority of them use the traditional compliance TO with SIMP, such as SolidWorks [23], ABAQUS [24], Siemens NX [25], and Altair Optistruct [26], while some others use different algorithms, such as AMEBA [27], which is BESO-based, or ANSYS Mechanical [28], which includes the level set method in addition to SIMP.
TO in commercial software is in its development since new design values that can be chosen both as objective functions and constraints, such as frequency and buckling, are gradually included in their TO modules. However, the authors could find only a few relevant TO studies in the literature. Zhou et al. [29] presented the casting and extrusion manufacturing constraints in TO software, newly introduced in 2002. In 2006, Schramm and Zhou [30] discussed the developments in the implementation of TO in commercial software. Reddy K et al. [31] compared and categorized twenty different commercial and educational (open source) TO software platforms for AM, based on their capabilities in 2016. It seems that literature is missing a recent library of the available TO software platforms, including their capabilities and limitations. Furthermore, a common CAD designer’s problem is the time spent, before optimization, looking for the ideal CAD/FEM platform that can support his/her optimization problem.
Hence, this research paper closes this scientific gap by the development of an online library of the most implemented TO software platforms (70 software platforms) in the form of a table. The library encompasses the name, company, availability (commercial/open source), and optimization types and methods that the software uses together with the available objective functions and constraints. In addition, when it was possible to identify, references and representative literature using the presented software were included. This TO library constitutes a useful tool for CAD designers interested in TO. In addition, it is accessible online for reading, editing, and updating its content. In Section 4, Section 5 and Section 6 of this paper, the authors present an in-depth comparison among a few of the TO software platforms found previously in the created library. This comparative study was limited to the commercial software. The choice of the software was made based on the authors’ accessibility to the software’s TO modules via the student licenses provided by their affiliated university. Thus, three commercial software platforms were picked—SolidWorks, ANSYS Mechanical, and ABAQUS. The utilized software platforms were compared with respect to their optimization time, optimized designs, pre- and post-processing of the results, as well as their features and optimization capabilities. For this reason, three common geometries found in the literature, including a bell crank lever, a pillow bracket, and a small bridge, were used as optimization case studies. Each of these models represents a separate example category. The bell crank lever has limited design space, the pillow bracket can lead to design solutions with an increased number of components, and the small bridge has significantly increased design space. The optimization of these structures was focused on simplicity, and thus, it was limited to the traditional compliance TO based on the SIMP method. The lessons learned from the used case studies and the applied research work within this comparative study offer useful insights to CAD designers.
The rest of the paper is structured as follows. In Section 2, the general SO problem is described together with some popular optimization methods. Section 3 presents the identified TO software and its features and capabilities. Section 4 describes the used case studies and their optimization workflow in this research work, and Section 5 presents the results. A comparison of the used commercial software is presented in Section 6. The results of the conducted research work are discussed in Section 7. Finally, Section 8 and Section 9 constitute the conclusion and the future research, respectively.
2. Theory
According to Christensen and Klarbring [32], a general SO problem can be expressed mathematically by an objective function , a design variable (), and a state variable (). The objective function is a function that is used to classify the designs and can usually measure compliance, weight, and displacement. On the one hand, the design variables are related to the geometry of the structure or the chosen material. On the other hand, the state variables represent the response of the structure, such as stress and strain. In addition, Christensen and Klarbring [32] categorize the design constraints into behavioral, design, and equilibrium. The behavioral constraints are related to the state variable, while the design constraints concern the design variables. Finally, the discretization of the design space Ω creates the need for equilibrium constraints, which, in a linear problem, have the following representation:
where K(x), u, and F(x) are the stiffness matrix, the displacement vector, and the force vector, respectively. In the traditional compliance TO, also described by Bendsøe and Sigmund [4], the objective function measures the stiffness of the structure via compliance (), and the design variable is a pseudo-density of the elements (), where means material and is the void. In addition, a volume constraint, , is used to express the maximum amount of the distributed material (). A nested representation of the compliance TO problem is as follows:
However, the discrete formulation faces many problems, such as the checkerboard problem and computational limitations. Thus, continuous variables are used instead of binary ones. The elements’ densities can now attain values between zero and one [4], as follows:
The solution of this problem can be conducted by either gradient-based optimization techniques (GTO), such as the optimality criteria (OC) and the method of moving asymptotes (MMA), and non-gradient topology optimization techniques (NGTO), such as genetic algorithms [33]. Interpolation is used for the expression of the material properties in a continuous setting. One of the most popular interpolation methodologies is the solid isotropic material with penalization (SIMP). SIMP interpolates Young’s modulus of the material () using the following power law [4]:
where is a penalization parameter for the elements with intermediate densities, which usually takes a value between 1 and 3 [34]. Usually, the traditional density-based TO is called simply SIMP in the literature. Other notable TO methods are the level set [20], the evolutionary structural optimization (ESO) [35], the topological derivatives [36], and the phase field [37].
3. Different TO Software Platforms
At this point, a thorough literature search was conducted for the identification of the available software that can be used for the implementation of SO with a special focus on TO. The result of this research was the creation of a library in a table form that contains 70 different TO software platforms. This library encompasses the name, company, availability (commercial/open source), the optimization type (size, shape, topology), and methods ((parametric (P)/non-parametric (NP), TO (SIMP, RAMP, level set), lattice)) that the software uses, as well as the objective functions and constraints of TO. The constraints are categorized based on the four clusters of the CAD designers’ input presented in Section 1. In addition, it is shortly described how TO results are presented in the software’s interface. Furthermore, relative references and representative literature for each software platform are included, if they are available. Table 1 presents a section of the developed TO library. In this table, only the software platforms used in the comparative study presented later in this paper are included, which are SolidWorks, ANSYS Mechanical, and ABAQUS. Interested readers can access and edit the library online at the following links: https://docs.google.com/document/d/1CnQOA492EkOdX1gi59EWaPnrJBL-fOQs/edit?usp=sharing&ouid=110678641076107916949&rtpof=true&sd=true (accessed on 15 December 2021 ) or Supplementary Material [13,15,16,22,23,24,26,27,28,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173]. The authors’ intention was to create an updated database of the existing TO software where every CAD designer could add new or missing TO software.

Table 1.
A section of the table containing the TO software.
Figure 3a shows that only 31% of the software is open source, and the rest is commercial. However, 44% of the commercial software gives access to students to their TO module by offering a free student license. Concerning the SO categories, the majority of the software offers both size, shape, and topology optimization. It is worth mentioning that 17% of the software offers generative design, and 30% gives the possibility of designing and optimizing lattice structures. The most popular TO method is the SIMP, with 83%, while the level set and ESO methods are found in 20% and 17% of the software, respectively (see Figure 3b). In addition, the authors could not identify any software that supports the methods of phase field and topological derivatives.
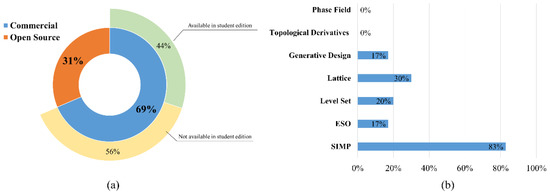
Figure 3.
(a) Commercial vs. open source software, and (b) the availability of the different TO methods in software.
The compliance/stiffness/strain energy is the most common objective function. However, some software platforms, such as ABAQUS and Altair Optistruct, offer a plethora of objective functions. Another category that differentiates the SO software is the manufacturing constraints. A gradual increase in the manufacturing constraints in software shows the trend in the companies of focusing on the post-processing of the results by bridging the optimized designs with the manufacturing methods and CAM. Furthermore, the majority of the software allows the user to create a plot of the distribution of the elements’ density, while some generate stress, strain, and displacement plots of the optimized models. However, based on the authors’ experience, these results are only some estimations and not the actual values. Only numerical validations can offer a good approximation of the stresses, strains, and displacements of the structures found through experiments.
As mentioned in Section 1, an in-depth comparison was conducted in this paper among three TO commercial software platforms—Solidworks, ANSYS Mechanical, and ABAQUS.
Solidworks offers size, parametric shape, and topology optimization in the student edition. Regarding the TO, it uses the traditional compliance TO with the SIMP method when mass, stiffness, and displacement can be used as objective functions. Furthermore, it offers member size, mold (pull direction), and planar symmetry in addition to the standard manufacturing constraints. The optimized models consist of faceted geometries. Stress and displacement plots can be created together with the plot of element density distribution.
ANSYS Mechanical supports the same optimization categories as SolidWorks. However, it also contains lattice and non-parametric shape optimization. Concerning the TO, it applies both the SIMP and the level set methods. Compliance, mass, and volume are the three available values that can be used as objective functions. Extrusion, cyclic symmetry, overhang angle, and 3D printing direction are the four additional manufacturing constraints. The optimized models are also faceted geometries here, but the only available plot is the element density distribution.
Finally, ABAQUS offers additional topography optimization. Furthermore, it contains a plethora of objective functions and constraints that can be also used in combinations. A faceted geometry represents the optimized designs again, while stress, strain, and displacement estimations are available here. The optimization time, optimized designs, and pre-and post-processing of these three software platforms are compared further in this paper using the case studies presented in Section 4.
4. Case Studies and Methodology
Three well-known structures found in the literature were used in this paper as case studies—a bell crank lever, a pillow bracket, and a small bridge.
A bell crank lever is a crank that is used in aircraft, automotive, and bicycles for transmitting motion between two parts meeting at an angle [174]. The arms of the used bell crank lever were 150 mm in length and 15 mm thick. A pair of 500 N bearing forces were applied at the end of each arm while the crank lever was fixed on its 60 mm/80 mm fulcrum, as shown in Figure 4a. This case study is an ordinary TO with limited design space. In other words, the main design of the product was known from the beginning, but a material reduction was needed.
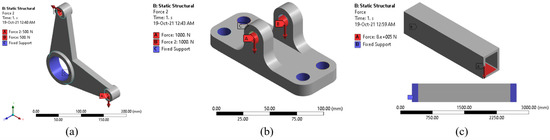
Figure 4.
The three case studies: (a) bell crank lever, (b) pillow bracket, and (c) small bridge.
A pillow bracket, 130 × 52 × 52 mm, was used as the second case study. The pillow bracket is a mechanical part designed to resist high bending forces [8]. The four holes of the bracket are fixed while a pair of 1000 N forces is applied to the hole on its top, as is depicted in Figure 4b. In this optimization case, the main design of the structure was also known; however, the number of the components in the final solution can be differentiated, as is presented in the results section.
Finally, the last case study was a small bridge (2500 × 500 × 600 mm). The authors intended to use a bigger structure here for comparison reasons. The initial CAD of the bridge was a hollow box, which was fixed at two sections to the left and right, as presented in Figure 4c. Furthermore, a vertical force of 800 KN was applied at the inner bottom surface of the box. This example was an optimization problem where the structure’s design space was increased significantly to let the optimization algorithm decide the final design. The expanded design space increased the flexibility of the algorithm, leading to new and better-optimized solutions, but also dramatically increased the optimization time [11].
The CAD models were first designed in SolidWorks. ANSYS Mechanical was used for both FEA at the pre-processing and post-processing steps with the validation of the optimized designs. It was crucial to use the same FEA software for comparison reasons. The TO was conducted in three different software platforms—SolidWorks, ANSYS Mechanical, and ABAQUS, with the same settings. The assigned material in all cases was a structural steel with the following properties: elastic modulus (E) = 210,000 MPa, Poisson’s ratio (ν) = 0.28, mass density (ρ) = 7700 Kg/m3, and yield strength (σy) = 724 MPa. Both the bell crank lever and the pillow bracket were discretized to 3 mm tetrahedral elements, while 30 mm tetrahedral elements were used for the bridge. The element sizes were identified using mesh convergence studies in each CAD model. Figure 5 shows the results of the conducted studies by presenting No. of Elements–Max Von Mises Stress diagrams of five FEA with different element sizes for each model. The tested element sizes are written near the data points inside the diagrams.
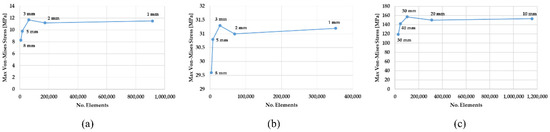
Figure 5.
The conducted mesh convergence studies: (a) bell crank lever, (b) pillow bracket, and (c) small bridge.
The used TO method was the traditional compliance optimization with SIMP. A 50% weight reduction was used as a constraint for the first optimization case, while the lightest designs were identified for the second one for a factor of safety (FOS) ≥ 1.2. Specific manufacturing constraints were used in each case study. An XY planar symmetry was used for the bell crank lever. Both XY and YX planar symmetries were used for the pillow bracket. The same planar symmetries were also used for the bridge together with a minimum size member of 100 mm. The areas where the BC and loads were applied were preserved from the optimization region in all case studies. The designs were optimized for AM; thus, they were not redesigned but were accordingly prepared for 3D printing. Hence, smoothing tools in each software platform were applied in order to fix sharp edges and overhangs and to eliminate stress singularities. The prepared models from SolidWorks and ABAQUS were imported as STEP files to ANSYS Mechanical for numerical validation. The software platforms were compared in both optimization cases with respect to the optimization time, the used design cycles, the pre-and post-processing, as well as the weight and strength of their optimized designs in all case studies.
5. Results
As mentioned before, three case studies, a bell crank lever, a pillow bracket, and a small bridge, were optimized in this paper. The results of the optimizations, conducted in SolidWorks, ANSYS Mechanical, and ABAQUS, are presented in this section for both optimization cases—compliance TO with 50% weight reduction and compliance TO with maximum weight reduction. Table 2 contains the number of the design cycles, the optimization times, the weights after TO and after 3D preparation in percentages of the initial weight (IW), the maximum Von Mises stresses, and the minimum FOS against yield.

Table 2.
The results of the optimizations and validation studies for 50%/maximum weight reduction.
In general, it was observed that in both optimization cases, ANSYS Mechanical used the lowest number of design cycles in all CAD models, except for the maximum weight reduction of the bell crank lever where Solidworks had fewer design cycles. The optimization time is dependent on the executed design cycles. Therefore, the more design cycles used, the more optimization time is required. However, SolidWorks optimized the designs in less time compared to the other software, except for the 50% weight reduction of the bell crank lever where ANSYS Mechanical had the best optimization time.
Concerning the weight reduction of the models, it was noticed that there was a difference between the weight of the optimized designs and their weight after the 3D preparation with the utilization of smoothing tools. In the first optimization case, the conducted 3D preparation in SolidWorks and ABAQUS increased the weight of their optimized designs from 0.3% for the bridge to 18.2% for the bell crank lever. On the other hand, the 3D preparation in ANSYS SpaceClaim decreased the weight of the optimized designs at a range of 0.4% of the bell crank lever to 9.8% of the bridge. It is important to take into account these weight fluctuations with the choice of the weight constraint at the optimization step. For example, for a 50% weight reduction of the bell crank lever, 56%, 47%, and 57.5% were the chosen weight constraints in SolidWorks, ANSYS Mechanical, and ABAQUS, respectively. In the second optimization case, the 3D preparation in ANSYS SpaceClaim decreased the weight of the designs in addition to. In the pursuit of the lightest design, the smoothing tools in ANSYS SpaceClaim gave the opportunity for higher reduction, ranging from 13.9% for the bridge to 34.7% for the pillow bracket. The designs in SolidWorks had higher weight again after the 3D preparation (0.13–10%). Finally, the 3D preparation in ABAQUS increased the weight of the bridge by 7%, while it decreased the weight of the bell crank lever and the pillow bracket by 7% and 4.3%, respectively.
The maximum Von Mises stresses, found with the FEA before TO, were 11.7 MPa for the bell crank lever, 31.3 MPa for the pillow bracket, and 157 MPa for the bridge. In general, the designs with 50% weight reduction had maximum stress at the same level or even less than their initial designs, as was found in the validation studies. The maximum stress for the lightest designs was higher, as expected, but always smaller than the yield strength of their material. In the following sections, the results of each case study are presented in detail.
5.1. Optimization of a Bell Crank Lever
Figure 6 shows the optimized designs of the bell crank lever for 50% and maximum weight reduction. The general design of the model was not changed. However, holes were created in the structure by removing useless material. The initial weight of the model was 1.965 Kg. It can be observed that the design solutions taken from SolidWorks and ABAQUS are quite similar in both optimization cases, while the optimization in ANSYS Mechanical resulted in different designs. In addition, ABAQUS could create the lightest design with an 88.3% weight reduction compared to 81.9% and 87.5% maximum reductions in SolidWorks and ANSYS Mechanical, respectively. However, SolidWorks optimized the model approximately five to ten times faster than ANSYS Mechanical and ABAQUS.
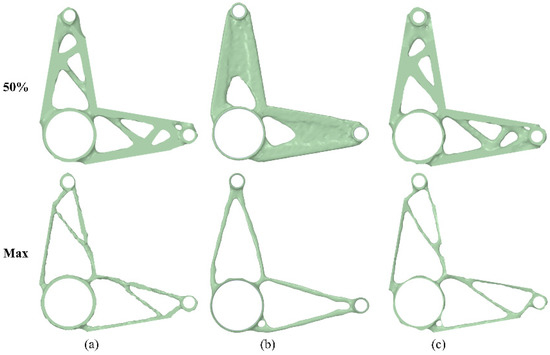
Figure 6.
The optimized designs of bell crank lever for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
The FEA of the bell crank lever was conducted in ANSYS Mechanical with 3 mm tetrahedral elements, resulting in 61,666 elements in total. The maximum identified stress of the model was 11.7 MPa. Figure 7 depicts the maximum Von Mises stresses taken from the validation studies in both optimization cases. The maximum stresses for the optimization case with 50% mass reduction ranged from 17.2 to 18.6 MPa. It seems that the weight of the chosen bell crank lever could be easily reduced by half without compromising its strength. For the optimization case with maximum weight reduction, SolidWorks resulted in the design with the lowest maximum stress, 395.2 MPa, compared to ANSYS Mechanical and ABAQUS with maximum stresses of 526.7 and 487.5, respectively. However, ABAQUS gave the best solution for the combination of weight and strength against yield.
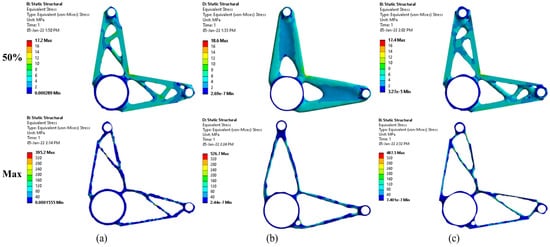
Figure 7.
The results of the validation studies of bell crank lever for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
5.2. Optimization of a Pillow Bracket
As is shown in Figure 8, the optimization of the pillow bracket resulted again in almost identical designs in SolidWorks and ABAQUS, while the designs in ANSYS Mechanical differentiated a little bit from them. The main observed difference in the first optimization case, with the 50% weight reduction, was that ANSYS Mechanical resulted in one optimized part, while the other two software platforms created two optimized parts based on the initial design. That was not the case in the optimization with maximum weight reduction, where all software resulted in design solutions with two parts. The initial weight of the model was 0.785 Kg. ABAQUS again resulted in the lightest design equal to 0.111 Kg, which corresponds to a weight reduction of 85.9%. The second best design in terms of weight was the optimized design by ANSYS Mechanical, with an 85.6% weight reduction, and finally, SolidWorks could reduce the weight of the pillow bracket by 84.7%. The optimization time in this case study was almost the same in SolidWorks and ANSYS Mechanical, while in ABAQUS, it was approximately nine times more.
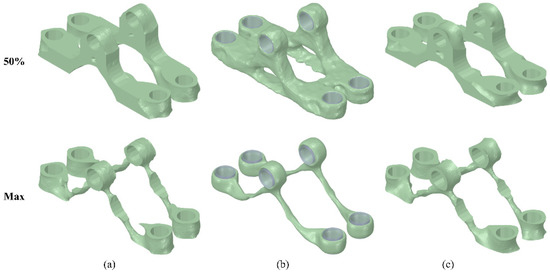
Figure 8.
The optimized designs of pillow bracket for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
The FEA in this case study was also conducted with the same finite elements, 3 mm tetrahedral, resulting in 27,649 elements. The plots of the Von Mises stress in both optimization cases are shown in Figure 9. It was observed that the optimized designs taken from SolidWorks and ABAQUS for 50% weight reduction had smaller maximum stresses (29 MPa and 29.3 MPa) compared to the original design (31.3 MPa). The lowest maximum stress for the second optimization case was 307.8 MPa and was found in the validation study of the optimized design created by ANSYS Mechanical. The maximum stresses of the optimized designs in SolidWorks and ABAQUS were 348.4 MPa and 314 MPa, respectively. It seems that ABAQUS again offered the best design solution in terms of weight and acceptable yield strength.
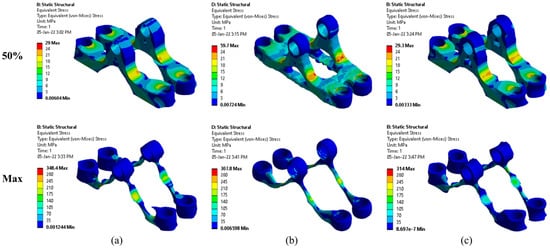
Figure 9.
The validation results of the pillow bracket for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
5.3. Optimization of a Small Bridge
The intention of the authors here was to optimize a bigger structure. In addition, they used an increased design space in order to increase the algorithm’s flexibility. The weight of the initial design was 2274.1 Kg, which is higher compared to the weight of the previous case studies. The design solutions of SolidWorks and ABAQUS were alike, as is shown in Figure 10. However, some differences can be observed in this case study. For example, in the optimization case with a 50% weight reduction, SolidWorks’ design contains six beam-like geometries on each side of the bridge, while the ABAQUS design has eight. In addition, both designs have the same weight, but their beams have different diameters. It seems that the software’s TO algorithm removed material from different regions of the structure despite the fact that they are both using the SIMP method. Furthermore, their designs in the second optimization case are also quite different. ANSYS Mechanical again resulted in different design solutions, especially in the first optimization case. ABAQUS came up with the heaviest bridge, 633 Kg, which corresponds to a 72.2% weight reduction, while SolidWorks created the lightest design with 477.2 Kg (79%) and ANSYS Mechanical with 500.6 Kg (78%).
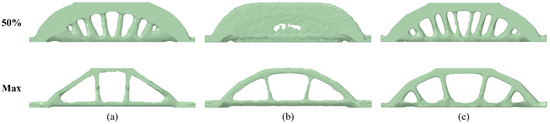
Figure 10.
The optimized designs of the bridge for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
At the FEA, the CAD model has been discretized into 30 mm tetrahedral elements, resulting in 101,108 finite elements in total. The maximum identified Von Mises stress was 157 MPa. In the first optimization case with a 50% weight reduction, all the designs had smaller maximum stresses, as shown in Figure 11. Among them, SolidWorks resulted in the strongest design solution. In addition, the derived SolidWorks solution in the second optimization case had the higher maximum stress, 571.9 MPa. ANSYS Mechanical and ABAQUS came up with stronger solutions with maximum stresses of 527.3 and 414.2 MPa, respectively, but much heavier designs (see Figure 11). Thus, SolidWorks’ design is preferred in terms of weight and acceptable yield strength.
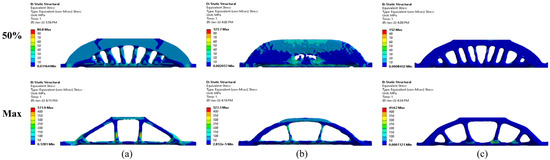
Figure 11.
The results of the validation studies for the bridge for 50% and maximum weight reduction in (a) SolidWorks, (b) ANSYS Mechanical, and (c) ABAQUS.
6. Comparison of the Used Commercial Software
The three chosen software platforms, SolidWorks, ANSYS Mechanical, and ABAQUS, were compared for their optimization capabilities and limitations during the TO workflow. In addition, three case studies, a bell crank lever, a pillow bracket, and a small bridge, were optimized using the above software and their results were compared with respect to the number of used design cycles, the optimization time, their weight after TO, and 3D preparation, as well as their maximum Von Mises stresses and FOS against yield.
6.1. SolidWorks
SolidWorks was chosen for the design of the models due to its user-friendly CAD interface. The software provides a plethora of exporting methods of the 3D models, such as the widely supported, standardized formats, IGES and STEP. The SolidWorks FEM module for the pre-processing task is quite capable and includes any possible analysis. However, ANSYS Mechanical was used for both the finite element analysis of the initial designs and the numerical validation studies of their optimized designs. It was crucial to use the same software for all FEA studies for comparison reasons. In addition, ANSYS has different mesh capabilities and can easily repair bad geometries in a faceted geometry that could possibly be created by TO.
The TO in SolidWorks is quite easy, but its TO module offers limited capabilities and options. The supported objective functions are stiffness, mass, and displacement, while displacement, mass, frequency, stress, and FOS can be used as constraints. Furthermore, it offers member size, mold (pull direction), and planar symmetry in addition to the standard manufacturing constraints. The TO module creates stress, displacement, strain, and FOS plots for the optimized designs. However, the software platform claims that these are only rough estimates and recommends redesigning the model for a validation study. In addition, the TO module gives the possibility to change the isosurface values (isovalues) and, thus, remove/add more material from the optimized design by using elements with a relative density higher than a specific number (element density distribution plot). The isovalue is, by default, equal to 0.3. The optimized models in SolidWorks are faceted geometries that can be exported as STL files or transferred to a validation study.
Concerning the post-processing of the optimized designs, SolidWorks focuses mostly on the design for CPM and not so much on the design for AM. It contains an automatic smoothing tool with 11 cycles from coarse to smooth quality. The smoothed geometry can be exported either as an STL file ready for 3D printing or as a graphics, solid, or surface file for further editing. The optimized design can easily be imported to the CAD module for redesigning. However, a complete 3D preparation module with manual smoothing and facets editing tools is missing.
SolidWorks optimized the models in less time compared to ANSYS Mechanical and ABAQUS. In addition, it gave the heaviest designs of the bell crank lever and pillow bracket but created the lightest bridge with a big difference from the other two software platforms. It seems that the TO module of SolidWorks is more effective for large structures.
6.2. ANSYS
ANSYS SpaceClaim, which is the ANSYS 3D modeling tool, has a user-friendly interface with many capabilities. The created 3D models can be easily exported to different file types or further analyzed in several ANSYS tools. ANSYS Mechanical is the primary ANSYS FEM tool, which also contains the TO module. ANSYS Mechanical offers a complete set of options that can be used in the pre-processing of the models.
The TO module in ANSYS Mechanical offers level set and lattice optimization in addition to the standard SIMP method. However, the available objective functions are limited to compliance, mass, and volume. On the other hand, multiple manufacturing constraints can be applied, focusing on design for both CPM and AM. Pull direction in mold, extrusion direction, and symmetry are some examples of constraints related to design for CPM, while the overhang angle and 3D building direction support the 3D preparation and, thus, the design for AM. The optimized geometries also consist of facets here. The TO module cannot create any type of plot for the optimized design. Thus, a proper validation study is needed in order to check and validate the design solutions. However, it offers a plot for the topology density (element density distribution plot). The derived density is divided into three density categories, as follows: 0.0−0.4 (elements that have to be removed), 0.4−0.6 (elements with intermediate densities), and 0.6−1.0 (elements that are crucial for the design and should be kept). The threshold of the elements with intermediate densities (isovalues) can be manually changed, creating alternative designs.
The post-processing of the optimized results is the main benefit of ANSYS. The redesign of the optimized design in SpaceClaim is user-friendly. Furthermore, SpaceClaim contains a plethora of tools that support the 3D preparation by checking, repairing, and smoothing, both manually and automatically, the organic faceted geometries created by TO. The smoothing tools are mainly applied for flattening the sharp areas that could be potential areas for stress concentrations and singularities. However, they can be also used for additional weight reduction. The smoothed designs can be either exported as STL files for 3D printing or further transferred to a validation study. ANSYS creates an automatic validation study in Mechanical where all the inputs of the initial FEA (BCs, load cases, mesh properties) are copied in the validation study.
ANSYS Mechanical, in general, used the lowest number of design cycles for the optimization of the case studies. The derived optimized designs were close to the lightest designs. Furthermore, its optimization time was reasonable. It can be stated that ANSYS Mechanical offered balanced optimized designs in terms of weight reduction, optimization time, and strength.
6.3. ABAQUS
The CAD module of ABAQUS is quite complex and demands many inputs from the CAD designer. The created 3D models can be easily exported to different file types or transferred to the FEM module for pre-processing. The FEM module here is also complex and quite demanding. However, it contains any possible type of analysis, load case, and boundary condition. In addition, it offers different finite elements as well as meshing properties.
The TO module of ABAQUS is its strongest part. A plethora of design values, called design responses, can be used for either objective functions or constraints, making the ABAQUS TO module a powerful optimization tool that can solve complex multi-optimization problems. However, the available manufacturing constraints in the TO module are only focused on the design for CPM and not for AM. The optimized designs are faceted geometries and can be exported as STL files. Stress, displacement, and strain plots of the optimized designs are available. However, as in the case of SolidWorks, these are estimations and not the actual values found from a validation study. However, ABAQUS does not have the appropriate tools to support either the redesign or the 3D preparation of the optimized geometries. Thus, the post-processing of the results is not possible in ABAQUS, making it dependent on other software for the implementation of the validation study.
ABAQUS created the lightest designs in all case studies except the bridge, where its optimization solution was the worst in terms of weight reduction compared to the other two software platforms. Furthermore, the TO in ABAQUS is time demanding since the optimization of the models lasted five to eight times more than the other software.
The authors’ intention with this comparison was not to promote one software platform above another but to present the capabilities and limitations of their TO modules. All three of these software platforms are competent and provide the CAD designer with useful design, analysis, and optimization tools. As general guidance, it could be claimed that ABAQUS is more of a TO software platform due to its plethora of available options. Complex multi-optimization problems can be solved here. However, the solution of the optimization tasks is time demanding in ABAQUS. On the other hand, ANSYS is a simulation platform with many capabilities. The ANSYS TO module contains level set and lattice optimization, which are not available in the other two platforms. ANSYS creates balanced designs in terms of weight and optimization time. Furthermore, it offers remarkable post-processing tools for the optimized designs for both CPM and AM. Finally, SolidWorks is more of a CAD/FEM platform. The SolidWorks TO module is quite new and is limited to a few optimization options. However, it is quite efficient in terms of time and is recommended for big structures, such as the optimized bridge in this paper, where SolidWorks created the lightest design.
7. Discussion
The goal of this paper was two-fold—first, to develop a novel library of the most applied open source and commercial TO software, and secondly, to focus on the practical implementation of TO via a comparative study of three commercial software platforms using three well-known CAD models as case studies. The results of this research work provide CAD designers with a better understanding of TO and advise them through recommendations to avoid common pitfalls.
On the one hand, the developed TO library consists of 70 software platforms, 22 open source and 48 commercial, that encompass TO in their modules. This novel library could be considered an updated version of the library developed by Reddy K, Ferguson, Frecker, Simpson, and Dickman [30]. However, its content is broader, including more software packages and additional information. The identified software platforms were investigated and categorized based on their capabilities in a table together with their name, company, availability, and optimization types and methods, as well as the objective functions and constraints that they provide. In addition, a column in the table contains all the available designer inputs categorized into four clusters—design constraints, supports and connections, loads, and geometric restrictions due to manufacturing constraints. Furthermore, information about the presentation of the TO results in the software interface, as well as representative literature, was included. Moreover, it was the authors’ intention to create an updated online database of TO software. Thus, the library can be accessed online where interested readers can both read and edit its contents, contributing in this way to the creation of an updated library of the available TO software. This database could be a practical manual for CAD designers interested in TO and can conserve valuable time in their pursuit of the ideal software that can support their optimization case.
Comparing the developed TO library in this paper with the relevant identified TO studies conducted in 2002 [29], 2006 [30], and 2016 [31], it seems that new objective functions and design constraints have been introduced in the TO software over the last years, with a particular focus on the manufacturing constraints. The authors observed that there are continuous introductions of new manufacturing constraints in the commercial software. The software companies try to provide adequate manufacturing constraints that can support the manufacturability of the topologically optimized designs from both CPM and AM. However, the derived design solutions cannot be directly manufactured. There is still a need for manual interpretation of them by the CAD designers, as also stated by Reddy K, Ferguson, Frecker, Simpson, and Dickman [31] in 2016. In the comparison study conducted by the authors, all case studies, including a bell crank lever, a pillow bracket, and a small bridge, were oriented to AM. In this way, the redesign of the optimized solutions demanded by the CPM, in order to mitigate the created organic shapes by TO, could be omitted. However, manual checks and repairs of the faceted geometries were inevitable in order to address the mesh discontinuities in the validation studies.
On the other hand, three different commercial software platforms, SolidWorks, ABAQUS, and ANSYS, were used in the comparative study in order to compare their user interfaces and TO outputs. Despite the fact that each of the aforementioned CAD models was optimized in the above software using the same TO method, mesh quality, as well as designer inputs and constraints, the derived optimized designs were not identical. SolidWorks and ABAQUS resulted in a similar optimized bell crank lever and pillow bracket, but their design solutions in the small bridge displayed differences. Furthermore, tetrahedral finite elements of the same size were used in all simulations; however, the number of the discretized finite elements differentiated among the software packages. It seems that the discretization of the CAD models was conducted in different ways. That could be a reason for the different optimized designs. Regardless of the fact that all software platforms use the same TO method, their TO algorithms and implementation are different, as it was shown both from the different derived solutions and their optimization times. In addition, each software applies different smoothing tools to fix sharp edges and overhangs and to eliminate stress singularities of the faceted geometries. In spite of this, these tools changed both the shape and the weight of the optimized designs; in the case of SolidWorks and ABAQUS, they increased their weight, while in ANSYS, they decreased them. CAD designers should take into account these parameters at the beginning of the TO implementation. It is known that the TO results are sensitive to designers’ inputs; however, in some cases, the optimization can lead to unintended designs, such as the design solution of the pillow bracket by ANSYS, which comprised two parts instead of one, while the other software resulted in one optimized part. An additional design constraint could easily avoid the separation of the component. For example, adding the faces between the holes of the pillow bracket to the ‘frozen areas’ could preserve the removal of material from them and thus prevent the part split. Despite the fact that all these issues can be avoided using proper design and manufacturing constraints it seems that the commercial software can sometimes still be a ‘black box’ for CAD designers. Moreover, all these additional constraints demand manual input by the CAD designers and decrease the available design space for optimization, and thus, algorithms’ flexibility.
8. Conclusions
A comparative study of the application of different TO software was conducted in this research work, and, thus, a table containing 70 existing TO software platforms was created. The table is available online and was developed in a way that could be changed and edited by readers interested in TO. In this way, an updated library of the available TO software platforms was developed, offering useful information about them, such as their availability, optimization types and methods, objective functions, constraints, and representation of the results. A search of the literature showed that the most applied TO method is the compliance optimization with the SIMP method at 80%.
Three commercial software were chosen for further comparison—Solidworks, ANSYS Mechanical, and ABAQUS. The software was compared for its TO workflow and results using three commercial models—a bell crank lever, a pillow becket, and a small bridge. The small differences in their workflows, such as the 3D preparation, led to different optimized designs despite the fact that the same TO method (SIMP) and properties, as well as CAD designer inputs, were used in all of them. The software could reduce the models’ weight in remarkable percentages, 88.3% for the bell crank lever, 85.9% for the pillow bracket, and 79% for the bridge without compromising their strength. ABAQUS gave the best designs in terms of the weight of the bell crank lever and the pillow bracket, while SolidWorks created the lightest bridge. In addition, SolidWorks was the most efficient software in terms of optimization time.
The existing TO software provides the CAD designer with many different options for both optimization type, objective function, constraints, and representation and analysis of the results. In this way, the software supports the CAD designer in all steps that constitute the TO workflow. However, each platform has its capabilities and limitations that differentiate it from the other. Both the CAD designer’s inputs and the small details in a TO software platform could affect the geometry, the weight, and the strength of the final designs. Thus, these have to be taken into account during all the steps of the TO workflow. Finally, the lack of an ideal TO platform causes CAD designers to work with different software in order to get a design that fulfills the desired requirements.
9. Future Research
The comparative study in this paper was limited to commercial software, and, thus, it will be of high interest to implement an analogous study among the open source software platforms. In addition, differences and similarities could be studied between the commercial and open source software platforms. Furthermore, in order to check the optimization limits of the software, other case studies could be investigated using alternative and multiple objective functions except for compliance, such as frequency and buckling.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app12020611/s1, Table S1: Library of TO software.
Author Contributions
Conceptualization; methodology; software; writing—original draft preparation, E.T.; writing—review and editing, E.T; supervision, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heildeberg, Germany, 2013; p. 370. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. Topology and Parametric Optimization-Based Design Processes for Lightweight Structures. Appl. Sci. 2020, 10, 4496. [Google Scholar] [CrossRef]
- Leiva, J.P. Structural optimization methods and techniques to design efficient car bodies. In Proceedings of the International Automotive Body Congress, Troy, MI, USA, 9–10 November 2011. [Google Scholar]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization of multi-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, P.; Biyikli, E.; Bai, J.; Robbins, J.; To, A. Efficient design optimization of variable-density cellular structures for additive manufacturing: Theory and experimental validation. Rapid Prototyp. J. 2017, 23, 660–677. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. A comparative study between traditional topology optimization and lattice optimization for additive manufacturing. Mater. Des. Processing Commun. 2020, 2, e128. [Google Scholar] [CrossRef] [Green Version]
- Krish, S. A practical generative design method. Comput. Aided Des. 2011, 43, 88–100. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Haskins, C.; Steinert, M. Topology-Optimization-Based Learning: A Powerful Teaching and Learning Framework under the Prism of the CDIO Approach. Educ. Sci. 2021, 11, 348. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. Messing with boundaries-quantifying the potential loss by pre-set parameters in topology optimization. Procedia CIRP 2019, 84, 979–985. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, F.; Sigmund, O. A new generation 99 line Matlab code for compliance topology optimization and its extension to 3D. Struct. Multidiscip. Optim. 2020, 62, 2211–2228. [Google Scholar] [CrossRef]
- Dhondt, G. CalculiX CrunchiX User’s Manual Version 2.12. Munich, Germany, accessed September, 2017; 21, 2017. [Google Scholar]
- Querin, O.; Young, V.; Steven, G.; Xie, Y. Computational efficiency and validation of bi-directional evolutionary structural optimisation. Comput. Methods Appl. Mech. Eng. 2000, 189, 559–573. [Google Scholar] [CrossRef]
- Allaire, G.; Karrman, A.; Michailidis, G. Scilab Code Manual. 2012. Available online: http://www.cmap.polytechnique.fr/~allaire/levelset/manual.pdf (accessed on 29 November 2021).
- Allaire, G.; Jouve, F.; Toader, A.-M. A level-set method for shape optimization. Comptes Rendus Math. 2002, 334, 1125–1130. [Google Scholar] [CrossRef]
- Bernardi, D.; Hecht, F.; Ohtsuka, K.; Pironneau, O. FREEFEM; Universite Pierre et Marie Curie: Paris, France, 1999. [Google Scholar]
- Gibson, T.H.; McRae, A.T.; Cotter, C.J.; Mitchell, L.; Ham, D.A. Firedrake. In Compatible Finite Element Methods for Geophysical Flows; Springer Nature: Basingstoke, UK, 2019; pp. 39–54. [Google Scholar] [CrossRef]
- 3DS. SOLIDWORKS. Available online: https://www.solidworks.com/ (accessed on 29 November 2021).
- 3DS. ABAQUS. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 29 November 2021).
- Siemens. Siemens NX. Available online: https://www.plm.automation.siemens.com/global/en/products/nx/ (accessed on 29 November 2021).
- ALTAIR. OptiStruct. Available online: https://www.altair.com/optistruct/ (accessed on 29 November 2021).
- XIE_Technologies. Ameba. Available online: https://ameba.xieym.com/ (accessed on 29 November 2021).
- ANSYS. ANSYS Mechanical. Available online: https://www.ansys.com/products/structures/ansys-mechanical (accessed on 29 November 2021).
- Zhou, M.; Fleury, R.; Shyy, Y.-K.; Thomas, H.; Brennan, J. Progress in topology optimization with manufacturing constraints. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002; p. 5614. [Google Scholar]
- Schramm, U.; Zhou, M. Recent developments in the commercial implementation of topology optimization. In Proceedings of the IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials, Copenhagen, Denmark, 26–29 October 2005; pp. 239–248. [Google Scholar]
- Reddy Kantareddy, S.N.; Ferguson, I.; Frecker, M.; Simpson, T.W.; Dickman, C.J. Topology optimization software for additive manufacturing: A review of current capabilities and a real-world example. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; p. V02AT03A029. [Google Scholar]
- Christensen, P.W.; Klarbring, A. An Introduction to Structural Optimization; Springer Science & Business Media: Berlin/Heildeberg, Germany, 2008; Volume 153. [Google Scholar]
- Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [Google Scholar] [CrossRef]
- Zhou, M.; Pagaldipti, N.; Thomas, H.; Shyy, Y. An integrated approach to topology, sizing, and shape optimization. Struct. Multidiscip. Optim. 2004, 26, 308–317. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Eschenauer, H.A.; Kobelev, V.V.; Schumacher, A. Bubble Method for Topology and Shape Optimization of Structures. Struct. Optim. 1994, 8, 42–51. [Google Scholar] [CrossRef]
- Bourdin, B.; Chambolle, A. Design-dependent loads in topology optimization. Esaim Control. Optim. Calc. Var. 2003, 9, 19–48. [Google Scholar] [CrossRef]
- 3D_SYSTEMS. 3DXpert. Available online: https://www.3dsystems.com/software/3dxpert (accessed on 29 November 2021).
- Lopez, C.; Stroobants, J. Lattice topology optimization and additive manufacturing of a 316l control arm. In Proceedings of the Sim-AM 2019: II International Conference on Simulation for Additive Manufacturing, Pavia, Italy, 11–13 September 2019; pp. 186–192. [Google Scholar]
- Tyflopoulos, E.; Hofset, T.A.; Olsen, A.; Steinert, M. Simulation-based design: A case study in combining optimization methodologies for angle-ply composite laminates. Procedia CIRP 2021, 100, 607–612. [Google Scholar] [CrossRef]
- BETA. ACP OpDesign. Available online: https://www.beta-cae.com/opdesign.htm (accessed on 29 November 2021).
- Burbulla, F.; Hallquist, J.; L‘Eplattenier, P.; Stander, N.; Huang, Y.; Bala, S.; Del Pin, F. Modelling of Adhesively Bonded Joints in CAE-Models at Porsche–Look behind the Scenes. In Proceedings of the 11th European LS-DYNA Conference, Salzburg, Austria, 9–11 May 2017; p. 37. [Google Scholar]
- Allaire, G. Allaire_Scilab. Available online: http://www.cmap.polytechnique.fr/~allaire/levelset_en.html (accessed on 29 November 2021).
- Karrman, A.M.B.; Allaire, G. Structural optimization using sensitivity analysis and a level-set method, in Scilab and Matlab. Techn. Rep. Ec. Polytech. 2009, 194, 1–13. [Google Scholar]
- Zhou, M.; Shyy, Y.; Thomas, H. Checkerboard and minimum member size control in topology optimization. Struct. Multidiscip. Optim. 2001, 21, 152–158. [Google Scholar] [CrossRef]
- Kontovourkis, O.; Tryfonos, G.; Georgiou, C. Robotic additive manufacturing (RAM) with clay using topology optimization principles for toolpath planning: The example of a building element. Archit. Sci. Rev. 2020, 63, 105–118. [Google Scholar] [CrossRef]
- BETA. ANSA. Available online: https://www.beta-cae.com/ansa.htm (accessed on 29 November 2021).
- Salway, D.; Zeguer, T. Multi-disciplinary Topology Optimization for Vehicle Bonnet Design. In Proceedings of the 9th European LS-DYNA Conference, Manchester, UK, 2–4 June 2013. [Google Scholar]
- ANSYS. ANSYS Discovery. Available online: https://www.ansys.com/products/3d-design/ansys-discovery (accessed on 29 November 2021).
- Tyflopoulos, E.; Lien, M.; Steinert, M. Optimization of Brake Calipers Using Topology Optimization for Additive Manufacturing. Appl. Sci. 2021, 11, 1437. [Google Scholar] [CrossRef]
- Gunwant, D.; Misra, A. Topology Optimization of sheet metal brackets using ANSYS. MIT Int. J. Mech. Eng. 2012, 2, 120–126. [Google Scholar]
- Autodesk. Autodesk Fusion 360. Available online: https://www.autodesk.com/products/fusion-360/overview (accessed on 29 November 2021).
- Salaimanimagudam, M.P.; Suribabu, C.R.; Murali, G.; Abid, S.R. Impact response of hammerhead pier fibrous concrete beams designed with topology optimization. Period. Polytech. Civ. Eng. 2020, 64, 1244–1258. [Google Scholar] [CrossRef]
- Autodesk. Autodesk Inventor. Available online: https://www.autodesk.com/products/inventor/overview?term=1-YEAR&tab=subscription (accessed on 29 November 2021).
- Barnes, J.B.; Camisa, J.A. Additive Manufacturing for Oil and Gas-Potential of Topology Optimization for Offshore Applications. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Autodesk. Autodesk Netfabb. Available online: https://www.autodesk.com/products/netfabb/overview (accessed on 29 November 2021).
- Samarkin, A.; Samarkina, E.; Mikushev, V.; Plohov, I. Simulation of the strength properties of lattice structures, produced by the method of three-dimensional printing. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2188, p. 040004. [Google Scholar]
- Autodesk. Autodesk Within Medical. Available online: https://www.autodesk.eu/products/within-medical/overview?wcmmode=disabled (accessed on 29 November 2021).
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for additive manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- LMS_Samtech. BOSS-Quattro. Available online: https://www.lmsintl.com/samtech-boss-quattro (accessed on 29 November 2021).
- Santer, M.; Pellegrino, S. Topology optimization of adaptive compliant aircraft wing leading edge. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1714. [Google Scholar]
- Fidesys. CAE Fidesys. Available online: https://cae-fidesys.com/products/desktop/?hl=en (accessed on 29 November 2021).
- Nikishkov, G.; Vershinin, A.; Nikishkov, Y. Mesh-independent equivalent domain integral method for J-integral evaluation. Adv. Eng. Softw. 2016, 100, 308–318. [Google Scholar] [CrossRef]
- FRIENDSHIP_SYSTEMS. CAESES. Available online: https://www.caeses.com/ (accessed on 29 November 2021).
- Harries, S.; Abt, C. CAESES—The HOLISHIP Platform for Process Integration and Design Optimization. In A Holistic Approach to Ship Design; Springer: Berlin/Heildeberg, Germany, 2019; pp. 247–293. [Google Scholar] [CrossRef]
- Dhondt, G.; Wittig, K. CalculiX. Available online: http://www.calculix.de/ (accessed on 29 November 2021).
- Löffelmann, F. Calculix/Beso. Available online: https://github.com/calculix/beso (accessed on 29 November 2021).
- Löffelmann, F. Failure Index Based Topology Optimization for Multiple Properties. In Proceedings of the 23rd International Conference on Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; pp. 15–18. [Google Scholar]
- 3DS. CATIA. Available online: https://www.3ds.com/products-services/catia/ (accessed on 29 November 2021).
- Chang, J.W.; Lee, Y.S. Topology optimization of compressor bracket. J. Mech. Sci. Technol. 2008, 22, 1668–1676. [Google Scholar] [CrossRef]
- CES-Eckard_GmbH. CATOPO. Available online: http://ces-eckard.de/ (accessed on 29 November 2021).
- Faskhutdinov, R.; Dubrovskaya, A.; Dongauzer, K.; Maksimov, P.; Trufanov, N. Topology optimization of a gas-turbine engine part. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 177, p. 012077. [Google Scholar]
- COMSOL_Inc. COMSOL. Available online: https://www.comsol.com/ (accessed on 29 November 2021).
- Srinivas, V.; Ananthasuresh, G. Analysis and topology optimization of heat sinks with a phase-change material on COMSOL multiphysics™ platform. In Proceedings of the COMSOL Users Conference, Paris, France, 7 November 2006. [Google Scholar]
- Ptc. Creo. Available online: https://www.ptc.com/en/products/creo (accessed on 29 November 2021).
- Shilpa, K.; Subbarao, D.; SAI, P.S.T. Design Evaluation and Optimization of Helical Gears using CREO. Int. J. Sci. Eng. Technol. Res. 2015, 4, 3967–3970. [Google Scholar]
- Diabatix. Diabatix. Available online: https://www.diabatix.com/ (accessed on 29 November 2021).
- Cuypers, C.; Sanders, N.; Vantieghem, L. Cooling, Battery and Suspension System of the Umicore Eclipse. ATZextra Worldw. 2019, 24, 30–33. [Google Scholar] [CrossRef]
- BETA. Epilysis. Available online: https://www.beta-cae.com/epilysis.htm (accessed on 29 November 2021).
- Park, I.; Papadimitriou, D. Efficient Surrogate-Based NVH Optimization of a Full Vehicle Using FRF Based Substructuring. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 1429–1442. [Google Scholar] [CrossRef]
- DevDept. Eyeshot. Available online: https://www.devdept.com/eyeshot (accessed on 29 November 2021).
- Martini, G. CAD Aspects on Isogeometric Analysis and Hybrid Domains. Ph.D. Thesis, Alma Mater Studiorum Università di Bologna, Bologna, Italy, May 2016. [Google Scholar]
- König, O.; Wintermantel, M.; Zehnder, N.; Giger, M.; Roos, R.; Barandun, G.A.; Keller, D. FELyX. Available online: http://felyx.sourceforge.net/idea.html (accessed on 29 November 2021).
- Giger, M.; Ermanni, P. Evolutionary truss topology optimization using a graph-based parameterization concept. Struct. Multidiscip. Optim. 2006, 32, 313–326. [Google Scholar] [CrossRef] [Green Version]
- DDS. FEMTools. Available online: https://www.femtools.com/products/ftopt.htm (accessed on 29 November 2021).
- Shook, B.W.; Nizam, A.; Gong, Z.; Francis, A.M.; Mantooth, H.A. Multi-objective layout optimization for multi-chip power modules considering electrical parasitics and thermal performance. In Proceedings of the 2013 IEEE 14th Workshop on Control and Modeling for Power Electronics (COMPEL), Salt Lake City, UT, USA, 23–26 June 2013; pp. 1–4. [Google Scholar]
- Firedrake. Firedrake. Available online: https://www.firedrakeproject.org/ (accessed on 29 November 2021).
- Salazar De Troya, M.; Beck, V.A. Level Set Topology Optimization in Firedrake; Lawrence Livermore National Lab.(LLNL): Livermore, CA, USA, 2020. [Google Scholar]
- Lindemann, J.; Olsson, K.-G. ForcePAD. Available online: http://forcepad.sourceforge.net/ (accessed on 29 November 2021).
- Beger, A.-L.; Brezing, A.; Feldhusen, J. The potential of low cost topology optimization. In Proceedings of the 15th International Conference on Engineering and Product Design Education, Dublin, Ireland, 5–6 September 2013. [Google Scholar]
- Pironneau, O. FreeFEM. Available online: https://freefem.org/ (accessed on 29 November 2021).
- Zhan, Y.; Zhuang, C.; Xiong, Z.; Ding, H. Structural Topology Optimization Based on the Level Set Method and FreeFEM. China Mech. Eng. 2009, 20, 0-1292. [Google Scholar]
- VR&D. GENESIS. Available online: http://www.vrand.com/products/genesis/ (accessed on 29 November 2021).
- Leiva, J.P.; Wang, L.; Recek, S.; Watson, B.C. Automobile design using the GENESIS structural optimization program. In Proceedings of the Nafems Seminar: Advances in Optimization Tecnologies for Product Design, Chicago, IL, USA, 6–7 June 2017. [Google Scholar]
- Renard, Y.; Pommier, J. GetFEM++. Available online: https://getfem.org/index.html (accessed on 29 November 2021).
- Bluhm, G.L.; Sigmund, O.; Poulios, K. Internal contact modeling for finite strain topology optimization. Comput. Mech. 2021, 67, 1099–1114. [Google Scholar] [CrossRef]
- Rutten, D. Grasshopper. Available online: https://www.rhino3d.com/6/new/grasshopper/ (accessed on 29 November 2021).
- McNeel, R. Rhino. Available online: https://www.rhino3d.com/ (accessed on 29 November 2021).
- McNeel, R. Food4Rhino. Available online: https://www.food4rhino.com/en (accessed on 29 November 2021).
- Søndergaard, A.; Amir, O.; Knauss, M. Topology Optimization and Digital Assembly of Advanced Space-Frame Structures; Aarhus School of Architecture: Aarhus, Denmark, 2013. [Google Scholar]
- Engys. HELYX. Available online: https://engys.com/products/helyx (accessed on 29 November 2021).
- Agarwal, D.; Kapellos, C.; Robinson, T.; Armstrong, C. Using parametric effectiveness for efficient CAD-based adjoint optimization. Comput. Aided Des. Appl. 2019, 16, 703–719. [Google Scholar] [CrossRef]
- ALTAIR. Inspire. Available online: https://www.altair.com/resource/altair-inspire-accelerate-simulation-driven-design (accessed on 29 November 2021).
- Ferede, N. Topology Optimization of Automotive sheet metal part using Altair Inspire. Int. J. Eng. Manag. Sci. 2020, 5, 143–150. [Google Scholar] [CrossRef]
- LimitState_Ltd. LimitState:FORM. Available online: https://limitstate3d.com/limitstateform (accessed on 29 November 2021).
- He, L.; Gilbert, M.; Johnson, T.; Pritchard, T. Conceptual design of AM components using layout and geometry optimization. Comput. Math. Appl. 2019, 78, 2308–2324. [Google Scholar] [CrossRef]
- Metal, D. Live Parts. Available online: https://www.desktopmetal.com/products/live-parts (accessed on 29 November 2021).
- Simpson, T.W. Designing for Additive Manufacturing. In Additive Manufacturing; CRC Press: Boca Raton, FL, USA, 2019; pp. 233–268. [Google Scholar]
- DYNAmore. LS-DYNA. Available online: https://www.lsoptsupport.com/ (accessed on 29 November 2021).
- Roux, W. Topology Design using LS-TaSC™ Version 2 and LS-DYNA®; Livermore Software Technology Corporation: Livermore, CA, USA, 2011. [Google Scholar]
- Materialise. Materialise 3-Matic. Available online: https://www.materialise.com/en/software/3-matic (accessed on 29 November 2021).
- Klaus, M.; Holtzhausen, S.; Schöne, C.; Stelzer, R. Topology-Oriented Deformation of FE-Meshes in Iterative Reverse Engineering Processes. In Engineering Systems Design and Analysis; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44878, pp. 505–509. [Google Scholar]
- MathWorks. Matlab. Available online: https://www.mathworks.com/ (accessed on 29 November 2021).
- Ferrari, F.; Sigmund, O.; Guest, J.K. Topology optimization with linearized buckling criteria in 250 lines of Matlab. Struct. Multidiscip. Optim. 2021, 63, 3045–3066. [Google Scholar] [CrossRef]
- Andreasen, C.S.; Elingaard, M.O.; Aage, N. Level set topology and shape optimization by density methods using cut elements with length scale control. Struct. Multidiscip. Optim. 2020, 62, 685–707. [Google Scholar] [CrossRef]
- Kamardina, N.V.; Guseynov, R.M.; Danilov, I.K.; Konoplev, V.N.; Ivanov, K.A.; Zharko, A.S.; Polishchuk, G.M. Topological optimization of the “Earring” element. RUDN J. Eng. Res. 2020, 21, 20–26. [Google Scholar] [CrossRef]
- Huang, X.; Xie, M. Evolutionary Topology Optimization of Continuum Structures: Methods and Applications; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- MFEM_Team. MFEM. Available online: https://mfem.org/ (accessed on 29 November 2021).
- Carstensen, C.; Liu, D. Nonconforming FEMs for an optimal design problem. SIAM J. Numer. Anal. 2015, 53, 874–894. [Google Scholar] [CrossRef] [Green Version]
- MIDAS. midasNFX. Available online: https://www.midasoft.com/mechanical/products/midasnfx (accessed on 29 November 2021).
- Sahithi, N.; Chandrasekhar, K. Isogeometric topology optimization of continuum structures using an evolutionary algorithm. J. Appl. Comput. Mech. 2019, 5, 414–440. [Google Scholar] [CrossRef]
- MoFEM_Team. MoFEM. Available online: http://mofem.eng.gla.ac.uk/mofem/html/ (accessed on 29 November 2021).
- Kaczmarczyk, Ł.; Ullah, Z.; Lewandowski, K.; Meng, X.; Zhou, X.-Y.; Athanasiadis, I.; Nguyen, H.; Chalons-Mouriesse, C.-A.; Richardson, E.J.; Miur, E. MoFEM: An open source, parallel finite element library. J. Open Source Softw. 2020, 5, 1441. [Google Scholar] [CrossRef]
- HEXAGON; MSC. MSC Apex. Available online: https://www.mscsoftware.com/product/msc-apex (accessed on 29 November 2021).
- Klippstein, H.; Duchting, A.; Reiher, T.; Hengsbach, F.; Menge, D.; Schmid, H.-J. Development, Production And Post-Processing Of A Topology Optimized Aircraft Bracket. In Proceedings of the 30th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2019. [Google Scholar]
- HEXAGON; MSC. MSC Nastran. Available online: https://www.mscsoftware.com/product/msc-nastran (accessed on 29 November 2021).
- Bakhtiary, N.; Allinger, P.; Friedrich, M.; Mulfinger, F.; Sauter, J.; Müller, O.; Puchinger, M. A new approach for sizing, shape and topology optimization. SAE Trans. 1996, 745–761. [Google Scholar] [CrossRef] [Green Version]
- NTopology. nTopology. Available online: https://ntopology.com/ (accessed on 29 November 2021).
- Groen, J.; Thomsen, C.; Sigmund, O. Multi-scale topology optimization for stiffness and de-homogenization using implicit geometry modeling. Struct. Multidiscip. Optim. 2021, 1–16. [Google Scholar] [CrossRef]
- OpenCFD. OpenFOAM. Available online: https://www.openfoam.com/ (accessed on 29 November 2021).
- Othmer, C.; de Villiers, E.; Weller, H. Implementation of a continuous adjoint for topology optimization of ducted flows. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 3947. [Google Scholar]
- M2DO. OpenLSTO. Available online: http://m2do.ucsd.edu/software/ (accessed on 29 November 2021).
- Hyun, J.; Kim, H.A. Transient level-set topology optimization of a planar acoustic lens working with short-duration pulse. J. Acoust. Soc. Am. 2021, 149, 3010–3026. [Google Scholar] [CrossRef]
- Gray, J.S.; Hwang, J.T.; Martins, J.R.; Moore, K.T.; Naylor, B.A. OpenMDAO. Available online: https://openmdao.org/ (accessed on 29 November 2021).
- Gray, J.S.; Hwang, J.T.; Martins, J.R.; Moore, K.T.; Naylor, B.A. OpenMDAO: An open-source framework for multidisciplinary design, analysis, and optimization. Struct. Multidiscip. Optim. 2019, 59, 1075–1104. [Google Scholar] [CrossRef]
- Quint_Corporation. OPTISHAPE-TS. Available online: https://www.quint.co.jp/eng/pro/ots/index.htm (accessed on 29 November 2021).
- Choi, J. An Analysis of Femoral Bone Remodeling Using Topology Optimization Method. J. Biomed. Eng. Res. 2005, 26, 365–372. [Google Scholar]
- Paramatters. Paramatters. Available online: https://paramatters.com/ (accessed on 29 November 2021).
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- SciArt. ParetoWorks. Available online: https://www.sciartsoft.com/pareto (accessed on 29 November 2021).
- Ali, M.H.; Yerbolat, G.; Amangeldi, S. Material optimization method in 3D printing. In Proceedings of the 2018 IEEE International Conference on Advanced Manufacturing (ICAM), Yunlin, Taiwan, 16–18 November 2018; pp. 365–368. [Google Scholar]
- HEXAGON; MSC. Patran. Available online: https://www.mscsoftware.com/product/patran (accessed on 29 November 2021).
- Shaari, M.; Rahman, M.; Noor, M.; Kadirgama, K.; Amirruddin, A. Design of connecting rod of internal combustion engine: A topology optimization approach. In Proceedings of the National Conference in Mechanical Engineering Research and Postgraduate Studies (2nd NCMER 2010), Pekan, Malaysia, 3–4 December 2010; pp. 3–4. [Google Scholar]
- INTES. PERMAS. Available online: https://www.intes.de/kategorie_permas/einfuehrung (accessed on 29 November 2021).
- Helfrich, R.; Schünemann, A. Topology Optimization of an Engine Bracket Under Harmonic Loads. In Proceedings of the SIA International Conference “Automotive NVH Comfort”, Le Mans, France, 13–14 October 2021; pp. 19–20. [Google Scholar]
- CAESS. ProTOp. Available online: https://www.caess.eu/ (accessed on 29 November 2021).
- Ramadani, R.; Belsak, A.; Kegl, M.; Predan, J.; Pehan, S. Topology optimization based design of lightweight and low vibration gear bodies. Int. J. Simul. Model. 2018, 17, 92–104. [Google Scholar] [CrossRef]
- PSF. Python. Available online: https://www.python.org/ (accessed on 29 November 2021).
- Zuo, Z.H.; Xie, Y.M. A simple and compact Python code for complex 3D topology optimization. Adv. Eng. Softw. 2015, 85, 1–11. [Google Scholar] [CrossRef]
- CSI. SAP2000. Available online: https://www.csiamerica.com/products/sap2000 (accessed on 29 November 2021).
- Lagaros, N.D.; Vasileiou, N.; Kazakis, G. AC# code for solving 3D topology optimization problems using SAP2000. Optim. Eng. 2019, 20, 1–35. [Google Scholar]
- Siemens. Simcenter Nastran/Femap. Available online: https://www.plm.automation.siemens.com/global/en/products/simcenter/femap.html (accessed on 29 November 2021).
- Păcurar, R.; Păcurar, A. Topology Optimization of an Airplane Component to Be Made by Selective Laser Melting Technology. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2015; Volume 808, pp. 181–186. [Google Scholar]
- Simright. Simright Toptimizer. Available online: https://www.simright.com/apps/simright-toptimizer (accessed on 29 November 2021).
- Siemens. Solid Edge. Available online: https://solidedge.siemens.com/en/ (accessed on 29 November 2021).
- Shanmugasundar, G.; Dharanidharan, M.; Vishwa, D.; Kumar, A.S. Design, analysis and topology optimization of connecting rod. Mater. Today Proc. 2021, 46, 3430–3438. [Google Scholar] [CrossRef]
- Lakshmi Srinivas, G.; Jaya Aadityaa, G.; Pratap Singh, S.; Javed, A. Energy efficiency enhancement of SCORBOT ER-4U manipulator using topology optimization method. Mech. Based Des. Struct. Mach. 2021, 1–20. [Google Scholar] [CrossRef]
- TOffeeAM. TOffeeAM. Available online: https://www.toffeeam.co.uk/ (accessed on 29 November 2021).
- Montomoli, F.; Antorkas, S.; Pietropaoli, M.; Gaymann, A.; Hammond, J.; Marioni, Y.F.; Isaksson, N.; Massini, M.; Vazquez-Diaz, R.; Adami, P. Towards digital design of gas turbines. J. Glob. Power Propuls. Soc. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Denk, M.; Prescott, D. ToOptix. Available online: https://github.com/Foxelmanian/ToOptixUpdate (accessed on 29 November 2021).
- Strömberg, N. TopoBox and MetaBox. Available online: https://www.fema.se/index.html (accessed on 29 November 2021).
- Strömberg, N. A Two-Variable Topology Optimization Approach for Simultaneously Macro Layout and Local Grading of Periodic Lattice Structures; Orebro University: Orebro, Sweden, 2020. [Google Scholar]
- TopOpt_group. TopOpt. Available online: https://www.topopt.mek.dtu.dk/?q=node/11 (accessed on 29 November 2021).
- Aage, N.; Nobel-Jørgensen, M.; Andreasen, C.S.; Sigmund, O. Interactive topology optimization on hand-held devices. Struct. Multidiscip. Optim. 2013, 47, 1–6. [Google Scholar] [CrossRef]
- OMEVA. Toptimiz3D. Available online: https://matematicas.uclm.es/omeva/?page_id=2104 (accessed on 29 November 2021).
- Aranda, E.; Bellido, J.C.; Donoso, A. Toptimiz3D: A topology optimization software using unstructured meshes. Adv. Eng. Softw. 2020, 148, 102875. [Google Scholar] [CrossRef]
- Hunter, W. ToPy—Topology Optimization with Python. Available online: https://github.com/williamhunter/topy (accessed on 29 November 2021).
- Sosnovik, I.; Oseledets, I. Neural networks for topology optimization. Russ. J. Numer. Anal. Math. Model. 2019, 34, 215–223. [Google Scholar] [CrossRef] [Green Version]
- Trinitas_team. Trinitas. Available online: http://www.solid.iei.liu.se/Offered_services/Trinitas/index.html (accessed on 29 November 2021).
- Suresh, S.; Thore, C.-J.; Torstenfelt, B.; Klarbring, A. Topology optimization accounting for surface layer effects. Struct. Multidiscip. Optim. 2020, 62, 3009–3019. [Google Scholar] [CrossRef]
- Virtual.PYXIS. Virtual.PYXIS. Available online: https://virtualpyxis.com.br/ (accessed on 29 November 2021).
- Z88. Z88Arion. Available online: https://z88.de/ (accessed on 29 November 2021).
- Mukherjee, S.K. Product Design with Form, Strength, and Function for Undergraduate Product Design Students—A Case Study. In Design for Tomorrow; Springer: Berlin/Heildeberg, Germany, 2021; Volume 2, pp. 229–241. [Google Scholar] [CrossRef]
- Sowjanya, C.; Nagabhushana Rao, V.; Pavani Sri Kavya, B. Optimum Design and Analysis of Bell Crank Lever for an Automobile. In Advanced Manufacturing Systems and Innovative Product Design; Springer: Berlin/Heildeberg, Germany, 2021; pp. 189–208. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).