Modified Coral Reef Optimization Methods for Job Shop Scheduling Problems

Abstract

The job shop scheduling problem (JSSP) is a fundamental operational research topic with numerous applications in the real world. Since the JSSP is an NP-hard (nondeterministic polynomial time) problem, approximation approaches are frequently used to rectify it. This study proposes a novel biologically-inspired metaheuristic method named Coral Reef Optimization in conjunction with two local search techniques, Simulated Annealing (SA) and Variable Neighborhood Search (VNS), with significant performance and finding-solutions speed enhancement. The two-hybrid algorithms’ performance is evaluated by solving JSSP of various sizes. The findings demonstrate that local search strategies significantly enhance the search efficiency of the two hybrid algorithms compared to the original algorithm. Furthermore, the comparison results with two other metaheuristic algorithms that also use the local search feature and five state-of-the-art algorithms found in the literature reveal the superior search capability of the two proposed hybrid algorithms.

1. Introduction

Scheduling production is crucial in product manufacturing since it directly influences system performance and overall manufacturing process efficiency [1]. In various enterprises, production scheduling has become a significant issue. Dozens of innovative techniques are being scrutinized to increase manufacturing efficiency, emphasizing schedule optimization [2]. Accordingly, optimizing production scheduling problems is attracting attention in both research and manufacturing realms [3].

Industrialization has regarded production schedules as a crucial issue since the 1950s, and the job shop scheduling problem (JSSP) is a quintessential production scheduling model [4]. Since Johnson’s (1954) first methodology of scheduling with two machines [5], the complexity of the JSSP has grown in correlation with the number of devices and jobs. Due to its immense complexity, the JSSP is categorized as NP-hard (nondeterministic polynomial time) [6]. Solving large-scale JSSP in a reasonable time is a challenge that has been researched for decades. In addition to increasing workload, JSSP is taking on numerous new forms with distinct properties and characteristics. It responds in diverse approaches to solving variations of the fundamental JSSP [7]. JSSP is a typical resource allocation problem in manufacturing production scheduling. It has innumerable applications in many different industrial fields requiring high levels of automation and mass production. Among the most successful applications of JSSP are semiconductor and electronic component manufacturing, which need mass production and increased automation to improve production efficiency, reduce production cycle time, and optimize resources. According to a survey by Xiong et al. [8], within five years from 2016 to 2021, hundreds of studies and optimization models of various aspects of JSSP and its applications in the mentioned fields were conducted and presented.

Due to significant repercussions on the productivity of the production line, the JSSP has never been eradicated from combinatorial optimization. JSSP is categorized as a multi-stage, static, deterministic job scheduling problem in computer science and operations research and its solving strategies evolve at each stage of research development [8]. The fundamental JSSP includes:

• A set of $n$ jobs $J=\{ J_i|i=1, 2, \dots n \}$, where $J_i$ denotes ith job $\left(1 \le i \le n\right)$.
• A set of $m$ machines $M=\{ M_j|j=1, 2, \dots m \}$, and $Mj$ denotes jth machine.
• Each job $Ji$ has a specific set of operations $O=\left\{O_{i1},O_{i2}, \dots , O_{ik}\right\}$, where $k$ is the total number of operations in job $Ji$. Note that operation $O_{ij}$ will be processed only once the operation $O_{ij-1}$ has been completed in job $Ji$.

The primary goal of scheduling is to assign shared resources to concurrent tasks as efficiently as possible throughout the processing period. The scheme necessitates allocating and organizing limited resources pursuant to the problem’s constraints, such as the order of activities and processing time, and providing a plan to achieve the optimization objectives. The following conditions are the fundamental JSSP requirements [9]:

• Each operation is performed independently of the others.
• One job operation cannot begin until all previous operations have been completed.
• Once a processing operation has begun, it will not be interrupted until the procedure is completed.
• It is impossible to handle multiple operations of the same job simultaneously.
• Job operations must wait in line until the next suitable machine is available.
• One machine can only perform one operation at a time.
• During the unallocated period, the machine will remain idle.

Notably, the set of constraints in real-world problems is more complex, such as multiple objective scheduling challenges in a job shop, processing times can be either deterministic (constant) or probabilistic (variable), limit idle time requests to no more than two consecutive machines, or no idle time. Any change to the problem’s limitations can create a new variation of the problem. Consequently, JSSP solving approaches evolve with each research development phase [10].

Metaheuristic optimization is one of the practical approaches to JSSP with the ability to provide a satisfactory optimization solution in a reasonable time [11]. Metaheuristic algorithms employ innovative search strategies to explore the solution space and avoid getting stuck in local optima by steering the feasible solution with a bias, enabling the rapid generation of high-quality solutions. Contemporary metaheuristic algorithms also combine with different mathematical models [12] and analytical operating procedures [13] to enhance performance.

The coral reef optimization approach (CRO) is one of the complex bio-inspired computation methods used to solve engineering and science problems by simulating the “formation” and “reproduction” of corals in coral reefs. The approach was first envisioned by Salcedo-Sanz et al. in 2014 [14]. Since then, it has been utilized in various relevant topics, including optimal mobile network deployment [15], enhanced battery scheduling of microgrids [16], and wind speed prediction systems with success in renewable energy in “Offshore Wind Farm Design” [17]. This article contributes by proposing modified coral reef optimization methods with local search techniques for the JSSP feature. Two hybrid algorithms have been developed and presented based on the original coral reef optimization (CRO) method. CROLS1 integrates CRO with the Simulated Annealing (SA) strategy, whereas CROLS2 combines CRO with the Variable Neighborhood Search (VNS) technique. This article focuses on the optimizing effect of local search techniques on the CRO algorithm. The experiments demonstrate that local search strategies significantly enhance the search efficiency of the two hybrid algorithms compared to the original algorithm. Furthermore, the comparison results with two other metaheuristic algorithms that also use the local search feature and five state-of-the-art algorithms found in the literature reveal the superior search capability of the two proposed hybrid algorithms.

The remaining of this article is structured into several parts: Section 2 summarizes prior work and CRO. Section 3 outlines the basis for the suggested strategy. Then, in Section 4, the experimental results are reported. Finally, Section 5 concludes this study.

2. Related Work

Since its inception, operation research has focused on exact algorithms for solving combinatorial problems involving multiple variables. Exact algorithms are defined as guaranteeing accurate solutions to an optimization problem. Utilizing exact algorithms could achieve the best solution to almost any bounded combinatorial optimization problem by identifying all possible solutions in a short timeframe [18]. However, it has been asserted that when exact algorithms are employed to handle combinatorial optimization issues, the amount of time required to identify the best strategy grows exponentially with the complexity of the problem. Branch and bound algorithms and mixed integer programming are the most frequently adopted exact algorithms for JSSP solving [19]. Small-scale JSSP rarely represents production environments in actual production, so it is crucial to evaluate more complex concerns involving various works and resources. Nevertheless, the exact methods are barely applied to large-scale situations due to resource limits and lengthy execution times.

In the context that exact algorithms cannot match the requirements of addressing large-scale optimization issues, numerous methods based on artificial intelligence were initially proposed and opened a new direction in the research of problem-solving strategies [20], and approximation algorithms are one of the most explored solutions to large-scale combinatorial optimization issues. Although approximation algorithms are not guaranteed to locate an optimal solution but assured of identifying a near-optimal solution in a decent and realistic amount of computation time. As a result, it has evolved into a new research subject for resolving complex and large-scale problems. Approximation algorithms may be divided into two categories: heuristic algorithms and metaheuristic algorithms [21].

Heuristic approaches could be divided into two parts: constructive search methods and local search methods [22]. In typical constructive algorithms, solutions are built up piece by piece until they are entirely dependent on the problem’s initial constraints or pre-determined priorities; in the case of scheduling problems, solutions are frequently developed through operations. These algorithms may “build” processes individually using “Dispatching Rules,” for example, programming to find a feasible solution within the constraints of a priority hierarchy. Following that, solutions are speedily developed while preserving the integrity of solution quality. While with local search methods, the initially generated keys are gradually replaced by features learned on a set of neighboring solutions, whether they begin with a random collection of initial solutions or use construction algorithms [23]. These methods allow the investigation of neighbor solutions more efficiently in a dilemma space. The disadvantage of these algorithms is that they cannot find and utilize global solutions. Consequently, they may become trapped in the local optima region.

Meta-heuristics combines heuristic techniques commonly adopted to handle combinatorial optimization issues. Meta-heuristic algorithms employ innovative search strategies to unravel the global optimum and avoid getting entangled in local optima by steering solution searching with a bias to gain higher viable alternatives more quickly. Some bias mechanisms include bias derived from the objective function, bias based on previous decisions, the bias of experience, etc. [21]. In this study, diverse and intensified search tactics are employed. The diversification strategy’s fundamental objective is to efficiently explore all potential solution space neighborhoods by utilizing a metaheuristic method. On the other hand, the intensification technique involves using previously gained search abilities and exploring through a more local solution subspace. Meta-heuristic algorithms are classified into two categories: population-based algorithms and single-point search algorithms. Among population-based algorithms, nature-inspired optimization algorithms are ubiquitous in terms of ease of implementation and superior searchability [24]. For instance, the GA (genetic algorithm—inspired by evolution) [25,26], PSO (particle swarm optimization—influenced by swarm intelligence) [27], and SA (simulated annealing—inspired by metal cooling behavior) [28] are among the most reliable and effective algorithms accessible.

Significantly, meta-heuristic algorithms differ from blindly random search algorithms in that randomness is used intelligently and biasedly, making them the current research trend for solving difficult and complex issues. In addition, combination metaheuristic approaches have been established to leverage the capabilities within each method to obtain more robust and exhaustive optimization strategies. Modern metaheuristic algorithms also incorporate various mathematical models and analytical operational techniques to deliver greater performance. Guzman et al. propose a metaheuristic algorithm that combines GA with a disjunctive mathematical model and employs the open-source solution Coin-OR Branch and Cut to optimize the JSSP [12]. By combining an open-source solver with genetic algorithm, the metaheuristic approach enables the development of efficient solutions and reduces computation time. Viana et al. suggested employing a guidance operator assigned to changing ill-adapted individuals utilizing genetic material from well-adapted individuals to enhance the GA population [13]. The results indicate the new algorithm achieves a result 45.88% better than the old approach. Wang et al. introduce a novel metaheuristic algorithm capable of guiding the search process to promising regions based on the expected value affected by the performance of applicant samples and the growth rate of the candidate solutions region, called search economics for the job shop scheduling problem (SEJSP) [29]. SEJSP also produced positive experimental findings when attempting to resolve JSSP.

In recent years, solving a fundamental problem such as JSSP has been approached in the direction of enhancing classical metaheuristic algorithms or combining them with other methodologies. Yu et al. [30] improve PSO to NGPSO by incorporating nonlinear inertia weight and Gaussian mutation to handle JSSP. Mohamed Kurdi proposed the GA-CPG-GT method using the GA algorithm with uniform crossover paired with the Giffler and Thompson algorithm and yielded positive results when addressing JSSP [31]. T.Jiang and C.Zang utilized Gray Wolf Optimization (GWO) algorithm, inspired by the gray wolves’ social hierarchy and hunting behaviors, to solve JSSP [32], and Feng Wang et al. developed them with some modifications to establish the Discrete Wolf Pack Algorithm (DWPA) and achieved numerous exciting results in investigating JSSP [33]. In another direction, Alper Hamzaday et al. deployed a novel meta-heuristic technique called Single Seekers Society (SSS) to manage JSSP effectively [34].

The coral reef optimization approach (CRO) is one of the complex bio-inspired computation methods used to solve engineering and science problems by simulating the “formation” and “reproduction” of corals in coral reefs. The approach was first envisioned by Salcedo-Sanz et al. in 2014 [14]. Since then, it has been utilized in various relevant topics, including optimal mobile network deployment [15], enhanced battery scheduling of microgrids [16], and wind speed prediction systems with success in renewable energy in “Off-shore Wind Farm Design” [17]. Various hybrid algorithms based on the original version have evolved to facilitate better performance while diminishing computing time. For example, in 2016, a combination of CRO and a variable neighborhood search method was applied to unequal area facility layout problems [35]. Alternatively, another hybrid CRO technique takes advantage of Spark’s MapReduce programming paradigm to reduce the system’s overall response time and numerous other fascinating applications [36].

3. Materials and Methods

To properly depict the problem’s reality and make encoding and decoding more efficient, selecting the most suitable form of methodology is necessary. This choice substantially impacts the success or failure of problem-solving.

3.1. Representation of Job-Shop Scheduling Problem

When the coral reef optimization (CRO) technique is used to solve JSSP issues, the operation solutions are encoded as sequences of decimal integers. Several other approaches describe the resolution of JSSP based on the problem’s specific characteristics, such as operation-based representation, rule-based priority representation, machine-based representation, etc. [37,38]. Direct and indirect encoding techniques are the two fundamental divisions of these representations.

Our strategy for describing the solution is based on implementing “random keys.” This technique has the advantage of providing a detailed summary of the circumstance. Each number in the sequence indicates the number of the individual jobs, and the number of occurrences of each position in sequences defines the number of machines the job must pass through before completion. In this research, a “random key” technique exposes a solution to a problem satisfying the specified criteria below:

• Each element appearing in a solution represents the job to be processed;
• The number of appearing jobs correlates to the number of machines they must pass through;
• The order of the element in the solution follows the machine sequence that the job must pass through.

Figure 1 depicts a “random key” in the case of two machines and three jobs:

Figure 1. An example JSSP solution is created by a random key technique.

The CRO algorithm divides into two main stages: “reef formation” and “coral reproduction”:

Initially, a “reef” is constructed from a square grid of size MxN. Individual corals are selected from a population and then randomly placed in any available empty square on the reef according to the free/occupation ratio r0 (zero value representing no occupation), with the remaining available. Each coral represents a different solution in the solution space and will be given a health function; the higher the health function, the greater the likelihood that the corals would survive the algorithm’s later generations. The value of coral health is calculated using the fitness function, which depends on the objective functions of the problem.

During the second stage, the CRO performs coral reproduction with five main mechanisms being repeated to produce new coral generation (called larvae). Including External sexual “Broadcast Spawning”, Internal sexual “Brooding”, “Larvae setting”, Asexual “Budding”, and the “Depredation” phase, which are all described in detail below:

External sexual Broadcast Spawning: in nature, this process is also known as “cross-reproduction”. Two individuals produce every larva in a population model’s evolution by simulating natural selection. This process combines the attributes of each parent to create generations of offspring that inherit their positive characteristics to develop better individuals.

Internal sexual Brooding: this process simulates an individual’s mutation in a population during evolution. Each coral in the selected population can change its genetic code to create a new individual with the original individual’s characteristics and unique “mutation” attributes.

Larvae setting: this process simulates the “fighting of the coral” for space in a finite space environment. Only stronger individuals can survive and reproduce to create new generations, while weaker individuals are removed from the reef. The larvae are generated by the above sexual reproduction process and have repeatedly fought with other reef corals. Individuals with higher health values will be given more opportunities to develop in the reef.

Asexual budding: this process simulates the asexual reproduction of corals. When corals grow to a particular stage, they can separate into new individuals and disperse throughout the reef. Usually, healthy corals can produce better, more viable offspring, thus gaining preference in this spawning process. So, a select number of individuals with excellent health statistics are permitted to reproduce and spread over the reef, but only in limited numbers.

Depredation phase: this process simulates the elimination of corals. To create free space for the next generation of corals but without losing the diversity of the population, this mechanism only eliminates a part of the weak corals. After the maximum number of allowed corals is reached, any remaining similar corals in the reef are eliminated. It keeps the reef from growing too many identical corals at once and makes room for the next generation of corals. It also enhances population diversity to prevent the process from falling into a local optimum.

Figure 2 illustrates the operation of the CRO algorithm on reef size $5\times 5$ with a random key implementation corresponding to JSSP, including two machines and three jobs with an individual tracked by a red circle.

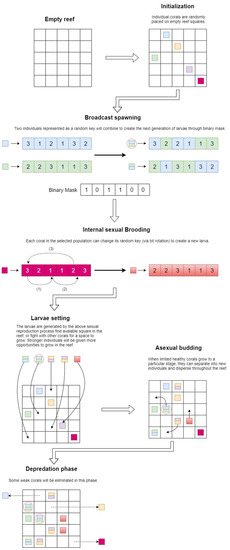
Figure 2. The phase of CRO algorithm with random key implementation and an individual coral tracked by the red circle.

The implementation of the CRO algorithm is described in Algorithm 1 as below:

Algorithm 1: Coral Reef Optimization (CRO).

Input: $M\times N$: reef size, ${\rho }_0$: occupation rate, $F_B$: fraction of broadcast spawners, $F_A$: fraction of asexual reproduction, ${\mathrm{F}}_D$: fraction of the worse fitness corals, ${\mathrm{P}}_D$: the deprecated probability of the worse fitness corals. Output: reasonable solution with best fitness #Initialization—Reef formation phase: 1. $M\times N\leftarrow$ reef size 2. Generate initial coral population 2. Calculate the fitness value of each coral 2. Deploy randomly on the reef with occupied rate ${\rho }_0$ 2. #Main loop—Coral reproduction phase: 2. Repeat 2. Reproduce coral fraction $F_B$ by external sexual broadcast spawning 2. Reproduce coral fraction $1-F_B$ by internal sexual brooding 9. Larvae setting 9. Reproduce best corals fraction $F_A$ by asexual budding 9. Predation of ${\mathrm{F}}_D$ worst reef corals with ${\mathrm{P}}_D$ probability 9. Untilstop_condition 9. Return best_resonable_solution

3.2. Objective Function

In this study, we use “minimize the makespan” as the objective function for solving the JSSP. This is the time between starting the first job and completing the last one. For a fundamental JSSP with a set of n jobs and a set of m machines: O_ij is operation of jth job that executed on ith machine; p_ij defines the processing time of jth job that executed on ith machine with the starting time (r_ij) of operation O_ij; following that, the time required to complete operation O_ij can be calculated as follows:

$$C_{ij}=r_{ij}+p_{ij}$$

(1)

Because machines and jobs have specific and different completion times, c_in and c_jm are defined as the completion time of the last (nth) operation on ith machine and the completion time of the last (mth) operation of jth job, respectively. The starting time r_ij can be calculated as below:

$$r_{ij}=max(c_{in}, c_{jm})$$

(2)

Finally, makespan can be calculated as the time to complete the last operation on the last machine:

$$makespan=C_{max}=max\left(C_{im}\right)$$

(3)

The scheduler’s scheduling efficiency can be evaluated by comparing the entire idle time spent by the machine to the total processing time spent by the system:

$$C^{\prime }=1+\frac{{{\displaystyle \sum }}_i{l}_i}{{{\displaystyle \sum }}_{j,k}{p}_{jk}}=\frac{C.m}{{{\displaystyle \sum }}_{j,k}{p}_{jk}}$$

(4)

where $li$ denotes the machine’s idle time of machine i; C means of makespan; m denotes the total number of machines; p_jk denotes the processing time of job i on machine k.

When applied to the JSSP, the algorithm evaluates the solution quality using the Objective and Fitness functions derived as Equations (5) and (6). Where the Objective function indicates how “excellent” the solution is in terms of the performance of the optimized function, the Fitness function directs the optimization process by expressing how inextricably the proposed solution meets the defined goal.

$$f=\frac{1}{C_{max}}$$

(5)

$$F_{\left(i\right)}=\frac{f_{\left(i\right)}}{{{\displaystyle \sum }}_1^n{f}_{\left(i\right)}}$$

(6)

where $C_{max}$ (or makespan) is the time between starting the first job and completing the last one e, $f_{\left(i\right)}$ is the fitness function, n is the population size.

3.3. Local Search: Simulated Annealing (SA)

The first of two local search algorithms mentioned is the SA approach [39]. It is a method used to simulate the cooling behavior of metals when exposed to extreme heat. The metal is rapidly heated to a high temperature and then progressively cooled according to a “cooling schedule” to obtain the ideal crystal structure with the lowest possible internal energy. High temperature causes the crystal grains to have a high energy level, which allows them to “jump” freely and quickly to their proper locations in the crystal structure. During the cooling procedure, the temperature steadily decreases, and the crystals are anticipated to be in their optimal locations once the temperature has been appropriately dropped [28].

Avoiding local optimization traps is one of the primary differences between SA and conventional gradient-based approaches. In other words, each algorithm step uses a probabilistic value to determine whether to transition the system from its current state to an adjacent state s* (this state can be better or worse). When this probability is high, the system can easily switch to another state regardless of whether that state is better or worse than the previous state. Meanwhile, when this probability is low, the current state is maintained if a better state cannot be found. This probability will gradually decrease through each loop based on the decrease in system temperature controlled by the “cooling schedule.” This process is repeated until the system reaches a state that is acceptable to the application or until the given computation resource has been exhausted [40].

The SA is described by Algorithm 2 as follows:

Algorithm 2: Simulated Annealing

Input: $t$: temperature, $t_{min}$: min temperature,$\alpha$: cooling rate, $F$: fitness function, $S$: solution, $maxIter$: maximum iteration Output: Best_solution #Initialization: 1. $t\leftarrow$ initial temperature 2. $\mathrm{Best}\_\mathrm{solution}\leftarrow$ $S$ #Main loop: While$t>t_{min}$ do 3. $\mathrm{iter}\leftarrow$ 0 4. While $\mathrm{iter}<maxIter$ do 5. Select a random solution $S’$ 6. $∆\leftarrow F\left(S^{\prime }\right)-F\left(S\right)$ 7. If $∆<0$ do 8. $\mathrm{S}\leftarrow$S’ 9. If $F\left(S^{\prime }\right)<F\left(\mathrm{Best}\_\mathrm{solution}\right)$ do 10. $\mathrm{Best}\_\mathrm{solution}\leftarrow$S’ 11. Else if $rand\left(0,1\right)<e^{\raisebox{1ex}{$-∆$}\!\left/ \!\raisebox{-1ex}{$t$}\right.}$ do 12. $\mathrm{S}\leftarrow$S’ 13. $\mathrm{iter}\leftarrow \mathrm{iter}+1$ 14. $\mathrm{t}\leftarrow \mathrm{t}\ast \mathsf{\alpha }$ 15. Return $\mathrm{Best}\_\mathrm{solution}$

3.4. Local Search: Variable Neighborhood Search (VNS)

Variable Neighborhood Search (VNS) is another ancillary local search technique [41]. This approach executes the search process by altering the solution’s neighborhood structure to identify the optimal solution, using a combination of two nested loops: shake and local search. The VNS algorithm’s fundamental design is simple and sometimes needs no additional parameters. It is primarily accomplished by transforming solutions from one state to another across the whole solution space using neighborhood structures (NS). Each neighborhood in the VNS solution space is considered a subset of the overall solution space, so it is possible to retrieve a trapped solution in one structure by using it in another structure. VNS systematically adjusts the neighborhood by moving from one NS to another while searching via nested loops, which are referred to as shake and local search Inside the algorithm, the shaking loop enables the algorithm to move to a different NS; meanwhile, the local search loop is responsible for finding the best solution in the current neighborhood structure. The cycle of local search is repeated until a more acceptable solution is discovered. The allowed loop will control the shaking loop. As a result, the algorithm expands the search space and improves the ability to locate the optimal solution [42]. Algorithm 3 describes the VNS as follows:

Algorithm 3: Variable Neighborhood Search

Input: $k$: index denoting the neighborhood structure, $k_{max}$: total number of neighborhood structures,$x$: solution, $F$: fitness function, $N_k$: solution set in $k$-th neighborhood structure, $t$: computation time Output: Best_solution #Initialization: 1. $\mathrm{Best}\_\mathrm{solution}\leftarrow$ initial solution $x$ #Main loop: While$t<t_{max}$ do 2. k$\leftarrow$ 1 3. While k$<k_{max}$ do 4. $x’\leftarrow Shake\left(N_k,x\right)$ 5. $x’’\leftarrow Local\_search\left(x’\right)$ 6. If $F\left(x^{\prime }’\right)<F\left(x\right)$ do 7. $x\leftarrow x’’$ 8. k$\leftarrow$ 1 9. Else 10. k$\leftarrow$k+1 11. $\mathrm{t}\leftarrow \mathrm{Cpu}\_\mathrm{Time}()$ 12. Return $\mathrm{Best}\_\mathrm{solution}$

3.5. Proposal Approaches

With the two local search techniques mentioned above, we propose two hybrid algorithms named CROLS1 and CROLS2 based on the CRO algorithm described in the following flow chart in Figure 3:

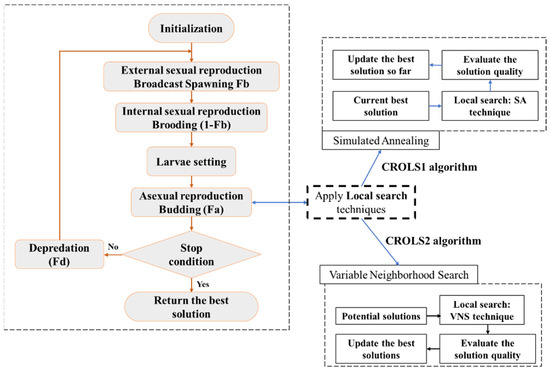
Figure 3. CRO applied local search techniques.

Typically, algorithms that identify the optimal solution from a random initial solution, such as the CRO, take significant time to obtain an optimal result. Occasionally, the search process becomes trapped in the local optimum and cannot converge to the optimal answer. Combining local search approaches is recommended to reduce the convergence time to the optimal solution, avoid needless local optimal, and enhance search efficiency. The process is performed by searching for answers in the neighborhood of the input solution, modifying the structure, and locating the optimal solutions in the solution space; or discovering the ideal solution when the search process is close to the optimal solution, while preventing other mechanisms from altering the solution’s structure. We found that employing local search strategies on all current problem solutions is time-consuming and unnecessary. So, two distinct search strategies were employed to optimize computation time and enhance algorithm performance:

With CROLS1, applied only with the current best solution, the probability of implementation is small at the beginning and increases until the end of the search. The idea is to increase the local search when the found solution is close to the optimal solution.

With CROLS2, apply the local search on several best solutions selected through the budding process above. The idea here is to find the optimal solution through all the neighborhoods of the potential solutions.

Algorithm 4 describes the CROLS1 and CROLS2 algorithms as follows:

Algorithm 4: Hybrid Coral Reef Optimization Algorithms (CROLS1 and CROLS2)

Input: $M\times N$: reef size, ${\rho }_0$: occupation rate, $F_B$: fraction of broadcast spawners, $F_A$: fraction of asexual reproduction, ${\mathrm{F}}_D$: fraction of the worse fitness corals, ${\mathrm{P}}_D$: the deprecated probability of the worse fitness corals. Output: Reasonable solution with best fitness #Initialization—Reef formation phase: 1. Choose running CROLS1 or CROLS2 2. $M\times N\leftarrow$ reef size 3. Generate initial coral population 4. Calculate the fitness value of each coral 5. Deploy randomly on the reef with occupied rate ${\rho }_0$ 6. #Main loop—Coral reproduction phase: 7. Repeat 8. Reproduce coral fraction $F_B$ by external sexual broadcast spawning 9. Reproduce coral fraction $1-F_B$ by internal sexual brooding 10. Larvae evaluation 11. Larvae setting 12. If running CROLS1 then apply “Local search strategy: SA” 13. else running CROLS2 apply “Local search strategy: VNS” 14. end if 15. Reproduce best corals fraction $F_A$ by asexual budding 16. Predation of ${\mathrm{F}}_D$ worst reef corals with ${\mathrm{P}}_D$ probability 17. Untilstop_condition 17. Return best _solution

3.6. Time Complexity

Without any loss of generality, let $f$ be the optimization problem by CRO, $f_{SA}$ and $f_{VNS}$ be the local search problems by SA and VNS approach, respectively. Assume that the computational time complexity of evaluating the problem’s function value is $O\left(f\right)$. Accordingly, the computational time complexity of CRO is defined as $O\left(f\times ite{r}_{max}\times n_{coral}\right)$ and the computational time complexity of two hybrid algorithms CROLS1 and CROLS2 are $O\left(\left(f+f_{SA}\times n_{SA}\right)\times ite{r}_{max}\times n_{coral}\right)$ and $O\left(\left(f+f_{VNS}\times n_{VNS}\right)\times ite{r}_{max}\times n_{coral}\right)$, respectively, where $ite{r}_{max}$ is the maximum number of iterations, $n_{coral}$ is the number of corals (population size), $n_{SA}$ is the number of corals that performed SA technique on and $n_{VNS}$ is the number of corals that performed VNS technique on.

4. Experiment Results and Discussion

This section provides a brief and accurate description of the experimental data, their interpretation, and the discussion derived from the investigation.

4.1. Dataset

In this study, we employ a subset of JSSP from Lawrence (1984) (LA) [43], one of the typical instances for addressing JSSP to evaluate the algorithm’s efficiency. The two primary components of input data are machine sequence and processing time. Where machine sequence reflects the execution order on the machines for each specific job, processing time represents the time consumption for each operation above. The most significant difference between LA instances is their complexity and the number of possible solutions to the problem, which grows exponentially with the number of jobs and machines. These are all feasible (n!m) solutions to problems involving n jobs and m machines. LA is also a well-known instance group in JSSP commonly used with a significant level of normalization and convergence. LA contains groups of sizes 10 × 5, 15 × 5, 20 × 5, 10 × 10, 15 × 10, 20 × 10, 30 × 10 and 15 × 15. Due to the similarity of the problem posed within each size group, we chose two sample examples from each size group to conduct the experiments and related comparisons so that the experimental method is not spread.

4.2. Parameters Used in the Algorithm

A plurality of metaheuristic optimization algorithms use randomly generated parameters to direct their search for the optimal solution. Consequently, establishing the criteria is among the most critical procedures. These settings stipulate the algorithm’s exploration and mining capabilities and substantially impact the algorithm’s performance. We chose suitable parameters for the hybrid algorithm based on the theory of general evolutionary algorithms and JSSP experiments. These parameters are shown in Table 1 below:

Table 1. Parameters used in the hybrid algorithms.

Parameter	Technique	Definition	Range
$M\times N$	CRO	Reef size	$[10\times 10$$, 30\times 30$]
Iter	CRO	Number of iterations (generations)	$\left[50, 200\right]$
Fb	CRO	Probability of Broadcast spawning process	$\left[0.8, 0.9\right]$
Fa	CRO	Probability of Budding process	$\left[0.05, 0.15\right]$
r0	CRO	Initial free/occupied ratio	$\left[0.6, 0.8\right]$
Fd	CRO	Probability of selecting weak individuals from the population	$\left[0.01, 0.1\right]$
Pd	CRO	Probability of removing weak individuals from the population	$\left[0.01, 0.1\right]$
k	CRO	Number of chances for a new coral to colonize a reef	$\left[2, 4\right]$
ke	CRO	Maximum number of allowed equal corals	$\left[0.1, 0.3\right]$
$t_{min}$	SA	Min temperature	[0.0001, 1]
$\alpha$	SA	Cooling rate	[0.7, 0.99]
$N_k$	VNS	Solution set in neighborhood structure	[1, L]

Where L = number of jobs × number of machines.

Based on the experimental findings, we believe that the algorithm’s parameters may fluctuate based on the complexity and size of the problem. It should be emphasized that even though the setup parameters are identical, the outcomes in different situations are not equivalent. It is necessary to experiment with alternative setup settings to discover the ideal solution in a reasonable time for problems of varying sizes. We conducted the trial-and-error methodology for tuning parameters through a series of experiments to acquire a suitable parameter set. Table 2 summarizes parameter setting recommendations for two hybrid proposal algorithms with different problem sizes.

Table 2. Suggested parameters set for different sizes of problem.

Size	$\mathit{M}\times \mathit{N}$	r0	Fb	Fa	Fd	Pd	k	tmin	α	Nk
Small	$10\times 10$	0.6	0.9	0.05	0.01	0.1	3	0.5	0.85	L
Medium	$20\times 20$	0.7	0.85	0.05	0.05	0.1	3	0.5	0.85	L
Large	$30\times 30$	0.7	0.85	0.1	0.1	0.1	3	0.5	0.85	L

4.3. Experiment Results

The experimental approach is conducted in two steps: first, we will evaluate the impact of local search on CRO via an aggregated outcomes table of CRO and two hybrid algorithms. Friedman’s test and Wilcoxon’s signed-rank test were also performed later based on the discovered table to evaluate the results statistically. Second, we evaluate the effectiveness of local search approaches applied to CRO by comparing the best search results of CROLS1, CROLS2, and two algorithms that also employ local search techniques: HGA [44] (hybrid genetic algorithm integrated with local search and some novel genetic operators) and MA [45] (memetic algorithm combines global search and local search, exchanging and inserting depending on the critical route). The proposed algorithm is coded in Python on a computer with 3.1 GHz Intel (R) Core i5 CPU and 24 GB of RAM.

4.3.1. Search Performance on CRO-Based Algorithm with Different Reef Sizes

We will evaluate the impact of local search on CRO via an aggregated outcomes table of CRO and two hybrid algorithms. Table 3 depicts the best, the worst, the mean, and the standard deviation (SD) of the makespan values derived from 30 independent executions of each method on 16 JSSP instances.

Table 3. CRO-based algorithms statistics for 16 LA instances.

Instance	Size	Reef Size	Method	Opt	Best	Worst	Mean	SD	Time (s)
LA01	$10\times 5$	10 × 10	CRO	666	666	674	668.91	2.4	128.45
			CROLS1	666	666	666	666	0	39.91
			CROLS2	666	666	666	666	0	33.18
		20 × 20	CRO	666	666	671	667.73	1.58	45.09
			CROLS1	666	666	671	668.45	1.79	20.45
			CROLS2	666	666	666	666	0	15.64
		30 × 30	CRO	666	666	674	669.55	2.7	44.27
			CROLS1	666	666	671	668.09	2	20.27
			CROLS2	666	666	671	667.45	1.91	14.64
LA02	$10\times 5$	10 × 10	CRO	655	655	676	664.91	6.41	118.73
			CROLS1	655	655	655	655	0	40.91
			CROLS2	655	655	655	655	0	33.91
		20 × 20	CRO	655	655	671	663.73	5.68	43.82
			CROLS1	655	655	671	662.27	5.57	18.55
			CROLS2	655	655	655	655	0	15.27
		30 × 30	CRO	655	655	676	665.36	6.62	44.55
			CROLS1	655	655	671	663.18	6.02	18.55
			CROLS2	655	655	670	661.09	6.21	14.09
LA06	$15\times 5$	10 × 10	CRO	926	926	946	935.45	7.54	169.09
			CROLS1	926	926	926	926	0	151.82
			CROLS2	926	926	926	926	0	149.73
		20 × 20	CRO	926	926	940	931.73	4.73	125.91
			CROLS1	926	926	940	932.36	5.46	100.73
			CROLS2	926	926	926	926	0	92.45
		30 × 30	CRO	926	926	946	935	7.82	76.36
			CROLS1	926	926	940	931.18	5.04	46.55
			CROLS2	926	926	940	933.18	5.09	41.09
LA07	$15\times 5$	10 × 10	CRO	890	899	922	906.45	6.24	175.73
			CROLS1	890	890	895	890.73	1.54	148.18
			CROLS2	890	890	892	890.45	0.81	133.55
		20 × 20	CRO	890	895	916	905.73	5.8	117.91
			CROLS1	890	890	916	907	5.04	94.82
			CROLS2	890	890	890	890	0	88.73
		30 × 30	CRO	890	890	922	908.18	7.38	78.09
			CROLS1	890	890	916	906.91	5.29	45.91
			CROLS2	890	890	916	905.09	5.92	33.64
LA11	$20\times 5$	10 × 10	CRO	1222	1222	1257	1235.64	13.41	237.36
			CROLS1	1222	1222	1222	1222	0	224.09
			CROLS2	1222	1222	1222	1222	0	229.73
		20 × 20	CRO	1222	1222	1244	1228.55	7.15	166.91
			CROLS1	1222	1222	1244	1229.64	7.13	147.91
			CROLS2	1222	1222	1222	1222	0	136.55
		30 × 30	CRO	1222	1222	1257	1233.45	12.58	128.82
			CROLS1	1222	1222	1244	1230.73	8.52	100.18
			CROLS2	1222	1222	1244	1229.91	7.89	95.72
LA12	$20\times 5$	10 × 10	CRO	1039	1039	1062	1049.55	6.96	241.45
			CROLS1	1039	1039	1042	1039.36	0.92	228.55
			CROLS2	1039	1039	1039	1039	0	217.64
		20 × 20	CRO	1039	1039	1062	1049.55	6.87	164.27
			CROLS1	1039	1039	1062	1051.91	6.62	157.91
			CROLS2	1039	1039	1039	1039	0	149.91
		30 × 30	CRO	1039	1039	1060	1048.27	7.96	120.09
			CROLS1	1039	1039	1043	1047.45	7.27	103.45
			CROLS2	1039	1039	1039	1050.91	7.01	89.91
LA16	$10\times 10$	10 × 10	CRO	945	971	1024	979.27	22.73	349.64
			CROLS1	945	945	979	958.91	10.69	317.73
			CROLS2	945	945	980	959.36	12.44	315.64
		20 × 20	CRO	945	948	1011	981.91	17.11	239.73
			CROLS1	945	945	956	949.64	4.37	212.55
			CROLS2	945	945	955	948.91	4	198.64
		30 × 30	CRO	945	948	1011	976.55	19.06	177.64
			CROLS1	945	945	955	947.73	2.93	125.91
			CROLS2	945	945	955	948.73	4.13	132.55
LA17	$10\times 10$	10 × 10	CRO	784	799	888	833.55	31.06	337.09
			CROLS1	784	787	807	795.18	7.55	309.73
			CROLS2	784	788	807	797.91	7.79	297.55
		20 × 20	CRO	784	788	832	811.91	13.08	252.64
			CROLS1	784	784	788	785.36	1.69	198.55
			CROLS2	784	784	799	790.36	5.71	222.91
		30 × 30	CRO	784	788	832	808.27	13.51	183.18
			CROLS1	784	784	799	788.55	4.88	128.82
			CROLS2	784	784	799	787.09	4.43	130.09
LA21	$15\times 10$	10 × 10	CRO	1046	1069	1146	1105.73	79.28	553.64
			CROLS1	1046	1056	1117	1100.64	10.07	487.18
			CROLS2	1046	1055	1115	1099	8.29	473.09
		20 × 20	CRO	1046	1069	1100	1071.45	49.41	345.91
			CROLS1	1046	1046	1054	1048.82	3.27	269.36
			CROLS2	1046	1046	1066	1053.09	6.34	274.27
		30 × 30	CRO	1046	1106	1250	1172.64	51.47	256.64
			CROLS1	1046	1046	1066	1052.55	7.76	164.36
			CROLS2	1046	1046	1066	1052.55	6.88	165.55
LA22	$15\times 10$	10 × 10	CRO	927	978	1220	1178.36	30.51	538.45
			CROLS1	927	930	1011	983.45	16.83	479.73
			CROLS2	927	934	988	976.09	8.32	464.09
		20 × 20	CRO	927	944	1150	1030.64	57.45	356.27
			CROLS1	927	927	974	944.18	16.83	267.91
			CROLS2	927	927	944	932.18	4.8	265.55
		30 × 30	CRO	927	935	1150	1030.09	53.54	248.27
			CROLS1	927	927	944	932.73	5.69	185.18
			CROLS2	927	927	944	934.27	6.21	174.27
LA26	$20\times 10$	10 × 10	CRO	1218	1333	1358	1349.64	22.89	759.64
			CROLS1	1218	1246	1316	1297.09	10.72	655.82
			CROLS2	1218	1242	1323	1305.82	12.36	651.91
		20 × 20	CRO	1218	1256	1280	1263.27	45.98	536.64
			CROLS1	1218	1218	1253	1235.91	12.07	456.91
			CROLS2	1218	1218	1246	1230.27	8.97	440.36
		30 × 30	CRO	1218	1226	1275	1255.82	44.37	359.91
			CROLS1	1218	1218	1246	1229.91	10.75	281.73
			CROLS2	1218	1218	1246	1231.09	9.12	246.27
LA27	$20\times 10$	10 × 10	CRO	1235	1323	1495	1446.55	30.3	748.09
			CROLS1	1235	1255	1310	1275.36	8.51	688.91
			CROLS2	1235	1256	1304	1261.09	8.29	650.64
		20 × 20	CRO	1235	1305	1415	1461.09	22.57	541.09
			CROLS1	1235	1235	1305	1260.55	28.95	459.45
			CROLS2	1235	1235	1246	1239.18	4.1	447.36
		30 × 30	CRO	1235	1255	1375	1359.55	25.96	336.18
			CROLS1	1235	1235	1246	1239.09	4.2	260.18
			CROLS2	1235	1235	1246	1240.27	4.09	239.27
LA32	$30\times 10$	10 × 10	CRO	1850	1934	2328	2254.91	96.2	827.91
			CROLS1	1850	1852	1896	1862.73	13.75	713.55
			CROLS2	1850	1850	1888	1866.73	9.77	693.09
		20 × 20	CRO	1850	1932	2126	2074.85	30.69	740.73
			CROLS1	1850	1850	1865	1855.36	5.77	646.64
			CROLS2	1850	1850	1856	1852.18	2.29	630.18
		30 × 30	CRO	1850	1912	2105	1998.52	30.26	566.64
			CROLS1	1850	1850	1856	1853	2.05	453.45
			CROLS2	1850	1850	1856	1852.18	2.33	418.45
LA33	$30\times 10$	10 × 10	CRO	1719	1865	2131	2014.73	65	824.18
			CROLS1	1719	1720	1752	1732.27	12.43	726.09
			CROLS2	1719	1722	1752	1730.27	11.39	692.82
		20 × 20	CRO	1719	1818	2056	1955.73	55.54	737.91
			CROLS1	1719	1719	1723	1720.45	1.56	643.09
			CROLS2	1719	1719	1732	1723.91	5.48	617.27
		30 × 30	CRO	1719	1805	2034	1934.91	60.59	557.82
			CROLS1	1719	1719	1732	1723.45	4.97	441.73
			CROLS2	1719	1719	1732	1724.18	5.14	438.82
LA39	$15\times 15$	10 × 10	CRO	1233	1388	1466	1498.82	42.44	869.09
			CROLS1	1233	1238	1316	1278.73	16.66	725.73
			CROLS2	1233	1274	1318	1279.82	13.48	624.45
		20 × 20	CRO	1233	1368	1428	1419.36	7.61	834.09
			CROLS1	1233	1238	1264	1241.64	27.32	675.45
			CROLS2	1233	1239	1264	1244.91	29.39	568.73
		30 × 30	CRO	1233	1332	1403	1397.21	24.37	752.09
			CROLS1	1233	1233	1255	1243.09	34.44	592.64
			CROLS2	1233	1233	1255	1237.55	13.78	502.82
LA40	$15\times 15$	10 × 10	CRO	1222	1396	1506	1451.25	49.25	875
			CROLS1	1222	1240	1336	1313.27	11.24	728.45
			CROLS2	1222	1269	1305	1288.45	35.41	625.36
		20 × 20	CRO	1222	1364	1455	1390.35	58.7	826.82
			CROLS1	1222	1240	1299	1270.27	35.09	674.73
			CROLS2	1222	1239	1299	1273.09	30.93	568.82
		30 × 30	CRO	1222	1342	1424	1374.33	24.88	739.82
			CROLS1	1222	1228	1264	1238.25	15.89	585.45
			CROLS2	1222	1232	1279	1248.45	23.22	495.55

Table 3 shows that the local search strategies have made the CRO algorithm more stable, as the amplitude of the mean between the best to the worst and the standard deviation in all cases have improved. CROLS2 demonstrates greater stability with smaller standard deviations than CRO and CROLS1 in most instances. Additionally, local search methods assist in reducing the worst-case of CROLS1 and CROLS2 compared to CRO. Similar to the best value acquired by each hybrid algorithm, the local search technique helps CROLS1 and CROLS2 reach the best-known optimal values for the situations examined. In most instances, CROLS1 and CROLS2 can get the best-known outcomes with reef sizes of 10 × 10 and 20 × 20. However, for instances of high complexity, such as LA39 and LA40, the best results can only be reached with reef sizes of 30 × 30.

CROLS1 and CROLS2 significantly reduce the search duration compared to the original method. This is more noticeable when the complexity of the instance is greater; the computational time can be reduced by up to 30% for LA40. In addition, for complex cases such as LA39 and LA40, the CROLS2 algorithm surpasses CROLS1 when outcomes are similar, but the execution time is reduced by more than 10%. Technically, CROLS1 and CROLS2 have 20% and 100% more fitness function calls than the original algorithm since they employ local search techniques. Even though this increases the amount of computational work, it helps the algorithm converge quickly and experimentally shows that CROLS1 and CROLS2 are still more rapid at searching than the original CRO.

To evaluate the improvement of the two hybrid algorithms compared to CRO statistically, we performed Friedman’s test on the data in Table 3. Friedman’s test, based on the ranking, will be utilized to determine the difference between three CRO-based algorithms using experimental findings collected from 16 LA instances and categorized by three reef sizes 10 × 10, 20 × 20, and 30 × 30. The “mean rank” and Friedman’s test statistic results of three algorithms participating in the evaluation will be described in Table 4 and Table 5, respectively.

Table 4. Mean rank of three CRO-based algorithms.

Algorithm	Mean Rank
	Reef Size 10 × 10	Reef Size 20 × 20	Reef Size 30 × 30
CRO	3.00	2.69	2.94
CROLS1	1.56	2.06	1.47
CROLS2	1.44	1.25	1.59

Table 5. Friedman’s test statistic of three CRO-based algorithm.

	Χ2	ρ
Reef Size 10 × 10	25.733	0.000003
Reef Size 20 × 20	16.625	0.000245
Reef Size 30 × 30	21.556	0.000021

According to Table 4, there is little difference in the mean rank of the CRO algorithm between reef sizes. The mean rank of CROLS1 and CROLS2 are significantly different from CRO, indicating that local search techniques substantially impact these two algorithms. Table 5 provides the test statistics for Friedman’s test with a significance level of α = 0.05. All ${\chi }^2$ values are larger than the critical value ${\chi }_0^2=5.991,$ and all ρ values are less than 0.05, demonstrating statistically significant differences in the performance of three CRO-based algorithms.

Following Friedman’s test made a significant result, we performed Wilcoxon’s signed-rank test as a posthoc analysis to determine the difference between three CRO-based algorithms in pairwise group. The search findings of three reef sizes will be averaged to feed the Wilcoxon’s test with a statistical significance of 0.05. Table 6 provides the statistical results of the Wilcoxon’s test.

Table 6. Wilcoxon’s test statistic of three CRO-based algorithms.

	CRO-CROLS1	CRO-CROLS2	CROLS1-CROLS2
Z	−3.516	−3.516	−1.533
p	0.000438	0.000438	0.125153

Using the Z distribution table, we can find the critical value of Z is 1.96 at a statistical significance of 0.05. According to Table 6, the statistical findings of two pairs of algorithms, CRO-CROLS1 and CRO-CROLS2, are nearly equivalent as Z = −3.516 (|Z| > 1.96) and p = 0.000438 < 0.05. So, the null hypothesis is rejected at statistical significance of 0.05; the advantage of local search approaches on CROLS1 and CROLS2 compared to the original CRO algorithm is statistically significant. In contrast, the values Z = −1.533 (|Z|< 1.96), and p = 0.125153 > 0.05 indicate no significant performance difference between the CROLS1 and CROLS2 hybrid algorithms.

4.3.2. Comparison of the Computational Result of CRO-Based Algorithms with Other Implemented Local Search Technique Algorithms

This experiment aims to test the algorithm’s efficiency in finding the optimal value of the problem. We choose MA and HGA as two algorithms employing local search strategies to compare the performance of algorithms that use such techniques. Five algorithms are mentioned in Table 7, including the original algorithm CRO and two proposed hybrid algorithms CROLS1 and CROLS2. Each CRO algorithm is executed 30 times with three different reef sizes and takes the best value obtained in Table 7. The results of HGA and MA were consulted from the research of Y. Wang et al. [44] and L. Gao et al. [45], respectively.

Table 7. Experiment results of five metaheuristic algorithms employing local search techniques.

Ins.	Size.	Opt.	CRO			CROLS1			CROLS2			HGA	MA
			10 × 10	20 × 20	30 × 30	10 × 10	20 × 20	30 × 30	10 × 10	20 × 20	30 × 30
LA01	$10\times 5$	666	666	666	666	666	666	666	666	666	666	666	666
LA02	$10\times 5$	655	655	655	655	655	655	655	655	655	655	655	655
LA06	$15\times 5$	926	926	926	926	926	926	926	926	926	926	926	926
LA07	$15\times 5$	890	899	895	890	890	890	890	890	890	890	890	890
LA11	$20\times 5$	1222	1228	1222	1222	1222	1222	1222	1222	1222	1222	1222	1222
LA12	$20\times 5$	1039	1042	1039	1039	1039	1039	1039	1039	1039	1039	1039	1039
LA16	$10\times 10$	945	956	955	955	945	945	945	945	945	945	945	945
LA17	$10\times 10$	784	799	788	788	787	784	784	788	784	784	784	784
LA21	$15\times 10$	1046	1069	1069.9	1056	1046	1046	1046	1055	1046	1046	1046	1055
LA22	$15\times 10$	927	978	944	935	930	927	927	934	928	927	935	927
LA26	$20\times 10$	1218	1333	1256	1226	1246	1218	1218	1242	1218	1218	1218	1218
LA27	$20\times 10$	1235	1323	1305	1255	1255	1235	1235	1256	1246	1246	1236	1261
LA32	$30\times 10$	1850	1934	1932	1912	1852	1850	1850	1850	1850	1850	1850	1850
LA33	$30\times 10$	1719	1865	1818	1805	1720	1719	1719	1722	1719	1719	1719	1719
LA39	$15\times 15$	1233	1388	1368	1332	1238	1238	1233	1274	1239	1233	1233	1241
LA40	$15\times 15$	1222	1396	1364	1342	1240	1240	1228	1269	1239	1232	1229	1233

It can be seen that the two-hybrid algorithms CROLS1 and CROLS2 can discover the optimal solution in the majority of instances with the reef size set to 20 × 20 and 30 × 30. However, the original algorithm CRO can only find the optimal solution in a few cases with a small number of jobs and machines. Compared with the other two metaheuristics, the performance of the two-proposed hybrid algorithm is superior when the reef size is 20 × 20 or 30 × 30 in some instances of the problem.

4.3.3. Comparison of the Computational Result of CRO-Based Algorithms with Other Contemporary Algorithms

To further verify the effectiveness of CRO and two proposed hybrid algorithms, we performed extensive experiments on the 12 LA instances mentioned before, Fisher and Thompson instances [46]: FT06, FT10, FT20; Applegate and Cook instances [47]: ORB01–ORB09; and five of Adams et al. instances [48] denoted as ABZ05 to ABZ09. Three CRO-based algorithms were compared with the results of five state-of-the-art algorithms found in the literature: Multi-Crossover Local Search Genetic Algorithm (mXLSGA) [49], hybrid PSO enhanced with nonlinear inertia weight, and Gaussian mutation (NGPSO) [30], single seekers society (SSS) algorithm [34], genetic algorithm with a critical-path-guided Giffler and Thompson crossover operator (GA-CPG-GT) [31], discrete wolf pack algorithm (DWPA) [33]. The best makespan produced by the CRO-based algorithms with reef size 30 × 30 from 10 independent runs was utilized as a performance criterion. Table 8 presents the experimental results for the 34 instances, listing the instance name, problem size (number of tasks × number of machines), best-known solution (BKS), and best solution achieved by each of the compared algorithms.

Table 8. Comparison of experimental results between CRO-based algorithms and other state-of-the-art algorithms for 34 instances. The symbol “-” means “not evaluated in that instance.”.

Instance	Size	BKS	CRO	CROLS1	CROLS2	mXLSGA (2020)	NGPSO (2020)	SSS (2020)	GA-CPG-GT (2019)	DWPA (2019)
LA01	10 × 5	666	666	666	666	666	666	666	666	666
LA02	10 × 5	655	655	655	655	655	655	655	655	655
LA06	15 × 5	926	926	926	926	926	926	926	926	926
LA07	15 × 5	890	890	890	890	890	890	890	890	890
LA11	20 × 5	1222	1222	1222	1222	1222	1222	1222	1222	1222
LA12	20 × 5	1039	1039	1039	1039	1039	1039	-	1039	1039
LA16	10 × 10	945	955	945	945	945	945	947	946	993
LA17	10 × 10	784	788	784	784	784	794	-	784	793
LA21	15 × 10	1046	1056	1046	1046	1059	1183	1076	1090	1105
LA22	15 × 10	927	935	927	927	935	927	-	954	989
LA26	20 × 10	1218	1226	1218	1218	1218	1218	-	1237	1303
LA27	20 × 10	1235	1255	1235	1246	1269	1394	-	1313	1346
LA32	30 × 10	1850	1912	1850	1850	1850	1850	-	1850	1850
LA33	30 × 10	1719	1805	1719	1719	1719	1719	-	1719	1719
LA39	15 × 15	1233	1332	1233	1233	1258	1662	-	1290	1334
LA40	15 × 15	1222	1342	1228	1232	1243	1222	1252	1252	1347
FT06	6 × 6	55	55	55	55	55	55	55	55	-
FT10	10 × 10	930	934	930	930	930	930	936	935	-
FT20	20 × 5	1165	1197	1174	1170	1165	1210	1165	1180	-
ABZ05	10 × 10	1234	1255	1234	1234	1234	1234	-	1238	-
ABZ06	10 × 10	943	988	943	943	943	943	-	947	-
ABZ07	20 × 15	656	755	731	727	695	713	-	-	-
ABZ08	20 × 15	665	720	709	705	713	729	-	-	-
ABZ09	20 × 15	679	817	707	711	721	930	-	-	-
ORB01	10 × 10	1059	1120	1070	1072	1068	1174	-	1084	-
ORB02	10 × 10	888	927	899	895	889	913	-	890	-
ORB03	10 × 10	1005	1097	1021	1023	1023	1104	-	1037	-
ORB04	10 × 10	1005	1121	1005	1005	1005	1005	-	1028	-
ORB05	10 × 10	887	904	890	894	889	887	-	894	-
ORB06	10 × 10	1010	1085	1020	1023	1019	1124	-	1035	-
ORB07	10 × 10	397	418	397	397	397	397	-	404	-
ORB08	10 × 10	899	988	912	907	907	1020	-	937	-
ORB09	10 × 10	934	955	938	940	940	980	-	943	-
ORB10	10 × 10	944	1010	967	950	944	1027	-	967	-

We can observe that the original CRO algorithm can only discover the optimal value in a few basic cases, such as LA01, LA02, LA06, LA07, LA11, LA12, and FT06, but the rest of the CRO results are relatively decent and equivalent to GA-CPG-GT. While both the CROLS1 and CROLS2 hybrid algorithms demonstrated efficiency, CROLS1 obtained the best comparative value in 11/12 LA cases, 2/3 FT instances, 3/5 ABZ instances, and 5/10 ORB instances. CROLS2 produced comparable results, with 11/12 LA instances, 2/3 FT instances, 3/5 ABZ instances, and 5/10 ORB instances better or equal to the compared results of five state-of-the-art algorithms. The findings of two algorithms, CROLS1 and CROLS2, outperform SSS, GA-CPG-GT, DWPA algorithms, and competitive comparison with mXLSGA and NGPSO, even outperforming NGPSO in ABZ instances and some instances as ORB01, ORB03, ORB08, ORB10.

4.3.4. Improvement of Search Efficiency

We utilize the mean deviation from the optimal makespan of the two hybrid algorithms CROLS1 and CROLS2 that surpass the original approach CRO in terms of search performance to evaluate the two hybrid algorithms’ performance enhancement. The progression of search effectiveness is calculated using the following formula:

$$P{I}_{\left(CROLS/CRO\right)}=\frac{S_{\left(CRO\right)}-S_{\left(CROLS\right)} }{S_{\left(Opt\right)}}$$

(7)

where $P{I}_{\left(CROLS/CRO\right)}$ is the percentage of improvement, $S_{\left(CROLS\right)}$ is the minuscule makespan by CROLS, $S_{\left(CRO\right)}$ is the minuscule makespan by CRO and $S_{\left(Opt\right)}$ is the minuscule makespan in comparison between CROLS and CRO.

Table 9 represents the percentage performance increase in CROLS1 and CROLS2 over the original CRO.

Table 9. Improve performance of two hybrid algorithms.

Instance	Size	CROLS1			CROLS2
		10 × 10	20 × 20	30 × 30	10 × 10	20 × 20	30 × 30
LA01	$10\times 5$	0	0	0	0	0	0
LA02	$10\times 5$	1.68	0.46	0.15	1.68	0.46	0.15
LA06	$15\times 5$	0	0	0	0	0	0
LA07	$15\times 5$	1.01	0.56	0	1.01	0.56	0
LA11	$20\times 5$	0.49	0	0	0.49	0	0
LA12	$20\times 5$	0.29	0	0	0.29	0	0
LA16	$10\times 10$	2.43	0.32	0.32	2.75	0.32	0.32
LA17	$10\times 10$	1.53	0.51	0.51	1.4	0.51	0.51
LA21	$15\times 10$	2.2	2.28	0.96	1.34	2.28	0.96
LA22	$15\times 10$	5.18	1.83	0.86	4.75	1.73	0.86
LA26	$20\times 10$	7.14	3.12	0.66	7.47	3.12	0.66
LA27	$20\times 10$	5.51	5.67	1.62	5.43	4.78	0.73
LA32	$30\times 10$	4.43	4.43	3.35	4.54	4.43	3.35
LA33	$30\times 10$	8.44	5.76	5	8.32	5.76	5
LA39	$15\times 15$	12.17	10.54	8.03	9.25	10.46	8.03
LA40	$15\times 15$	12.77	10.15	9.33	10.39	10.23	9

Analyzing Table 9 reveals that the local search approaches have enhanced the original CRO algorithm’s search performance. The improvement is not too obvious in the simple instances (LA01–LA22), with most PI metrics below 3%. Nonetheless, when the problem complexity increased, both CROLS1 and CROLS2 performed significantly more effectively than the original CRO. In LA26 and LA27, CROLS1 and CROLS2 outperform CRO when working on small reef sizes such as 10 × 10 and 20 × 20 with a PI of approximately 5%. However, when operating on reef sizes 30 × 30, CRO is as efficient as two hybrid algorithms with a PI of less than 2%; since when the population size increases, the searchability of CRO will increase, and even the original CRO can find a good solution. Even in LA40, where it is difficult for the CRO to discover the best-known solution, the PI reaches a peak of approximately 10%, which occurs in all reef sizes. This demonstrates the positive impact of local search algorithms on search performance.

4.3.5. Convergence Ability

The algorithm’s ability to converge to the optimal solution is a second criterion for comparison. The collection of data is dependent on the experimental outcomes of the LA01 instance. Table 10 displays the average number of generations required to discover the optimal solution for three CRO algorithms with three different reef sizes.

Table 10. Average objective function evaluations test needed to find the optimal solution.

Reef Size	10 × 10	20 × 20	30 × 30
CRO	150.5	42.2	30.4
CROLS1	13.4	10.6	10.4
CROLS2	12.2	8	6.4

First, as the reef size parameter increases, the number of generations conducted to explore the optimal solution for the three algorithms decreases most noticeably for the original CRO. Second, the two hybrid algorithms have significantly fewer generations than the original. In this scenario, the CROLS2 algorithm exhibits the quickest convergence capability. Experimental results proved that local search strategies significantly enhanced the search process and expedited finding optimal answers. For optimal performance, it is preferable to utilize local search approaches later in the algorithm because they have little impact in the early stages and waste time. Figure 4, Figure 5 and Figure 6 depict the convergence graph of three CRO, CROLS1, and CROLS2 methods for three reef sizes (10 × 10, 20 × 20, and 30 × 30) in five instances LA01, LA16, LA26, LA32, and LA40.

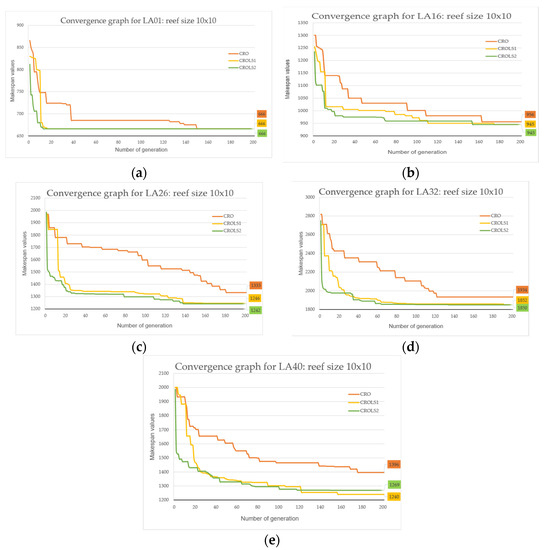
Figure 4. Convergence graph of CRO-based with reef size 10 × 10: (a) LA01, (b) LA16, (c) LA26, (d) LA32, (e) LA40.

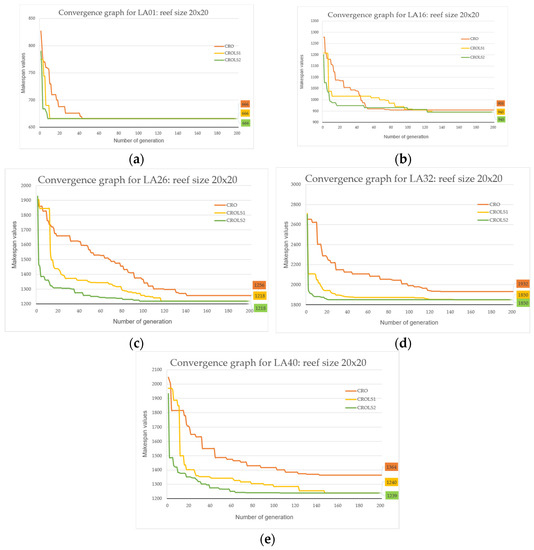
Figure 5. Convergence graph of CRO-based with reef size 20 × 20: (a) LA01, (b) LA16, (c) LA26, (d) LA32, (e) LA40.

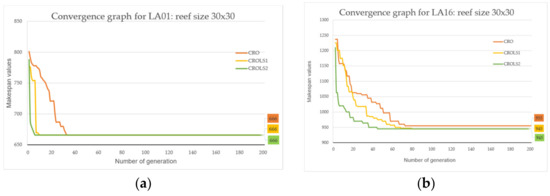
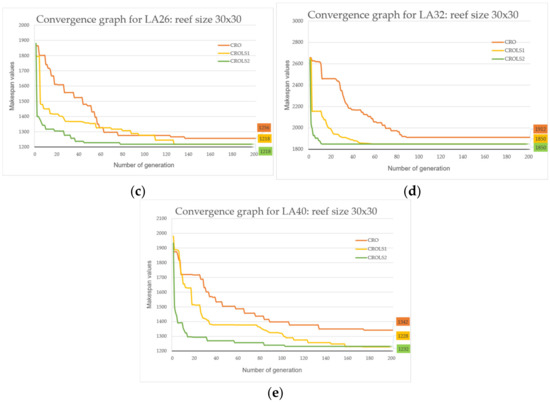
Figure 6. Convergence graph of CRO-based with reef size 30 × 30: (a) LA01, (b) LA16, (c) LA26, (d) LA32, (e) LA40.

The optimal solution (corresponding to the makespan value 666) of the LA01 instance is shown in Figure 7 through Gantt-chart, including ten jobs (J1–J10) and five machines (M0–M4), with each color representing a job.

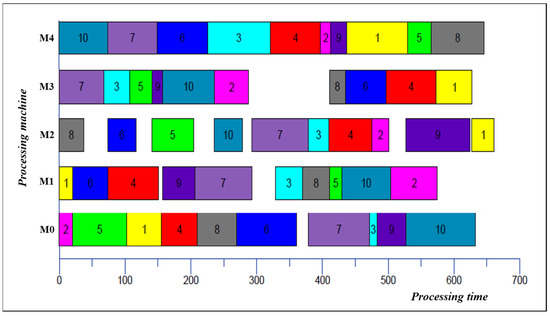
Figure 7. Representing optimal solution of LA01 instance by Gantt-chart.

5. Conclusions

This paper presents two novel hybrid algorithms, CROLS1 and CROLS2, that utilize distinct search strategies. The CROLS1 algorithm employs simulated annealing (SA) to find the global optimal solution and avoid the local optimum. This technique increases the likelihood of obtaining the optimal response while decreasing execution time. In the second model, VNS is applied to the most significant number of probable solutions in CROLS2. This search strategy aims to create new, superior individuals by utilizing the reef-wide potential and increasing its convergence.

The experiment presented that local search tactics have made the CRO algorithm more stable, as the mean amplitude and standard deviation have improved. Local search approaches also reduce CROLS1 and CROLS2 worst-case compared to CRO and let them find the best-known optimal values for each case more conveniently. CROLS1 and CROLS2 considerably shorten search time compared to the original CRO, even saving computational time by up to 30% for the LA40 instance. For complicated scenarios such as LA39 and LA40, CROLS2 surpassed CROLS1 when results are similar, but the execution time is 10% faster. Statistical analyses such as Friedman’s and Wilcoxon’s tests also confirm that the improvement of CROLS1 and CROLS2 compared to the original algorithm is significant. Comparing the best search results with two metaheuristic algorithms that employ other local search strategies, MA and HGA, CROLS1 and CROLS2 demonstrate their superiority in complex problem scenarios. To further verify the effectiveness of CRO and two proposed hybrid algorithms, we conducted extensive experiments on the 34 instances of varying complexity as LA, FT, ABZ, and ORB. The achieved results were compared with five state-of-the-art algorithms in related works: mXLSGA, NGPSO, SSS, GA-CPG-GT, and DWPA. By analyzing the results, we can conclude that the two proposed hybrid algorithms get competitive results in JSSP instances and can obtain good makespan results.

This research focuses on investigating the improvement of the local search approach on the CRO algorithm, which is demonstrated through positive experimental evidence. The efficiency of the two hybrid algorithms is further seen when their best search outcomes are comparable with the best-known results. Numerous multi-objective optimization techniques and various JSSP have been suggested for more challenging issues. In the upcoming plan, we aim to develop the optimal algorithm for multi-objectives and optimize the processing time. Developing algorithms to handle multi-objective optimization problems is an exciting future research path to increase the relevance of JSSP in manufacturing.