Parametric Optimization of Nozzle Turbine Vane Modal Characteristics by Means of Artificial System
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Modal Analysis
2.2. Formulation of the Optimization Problem
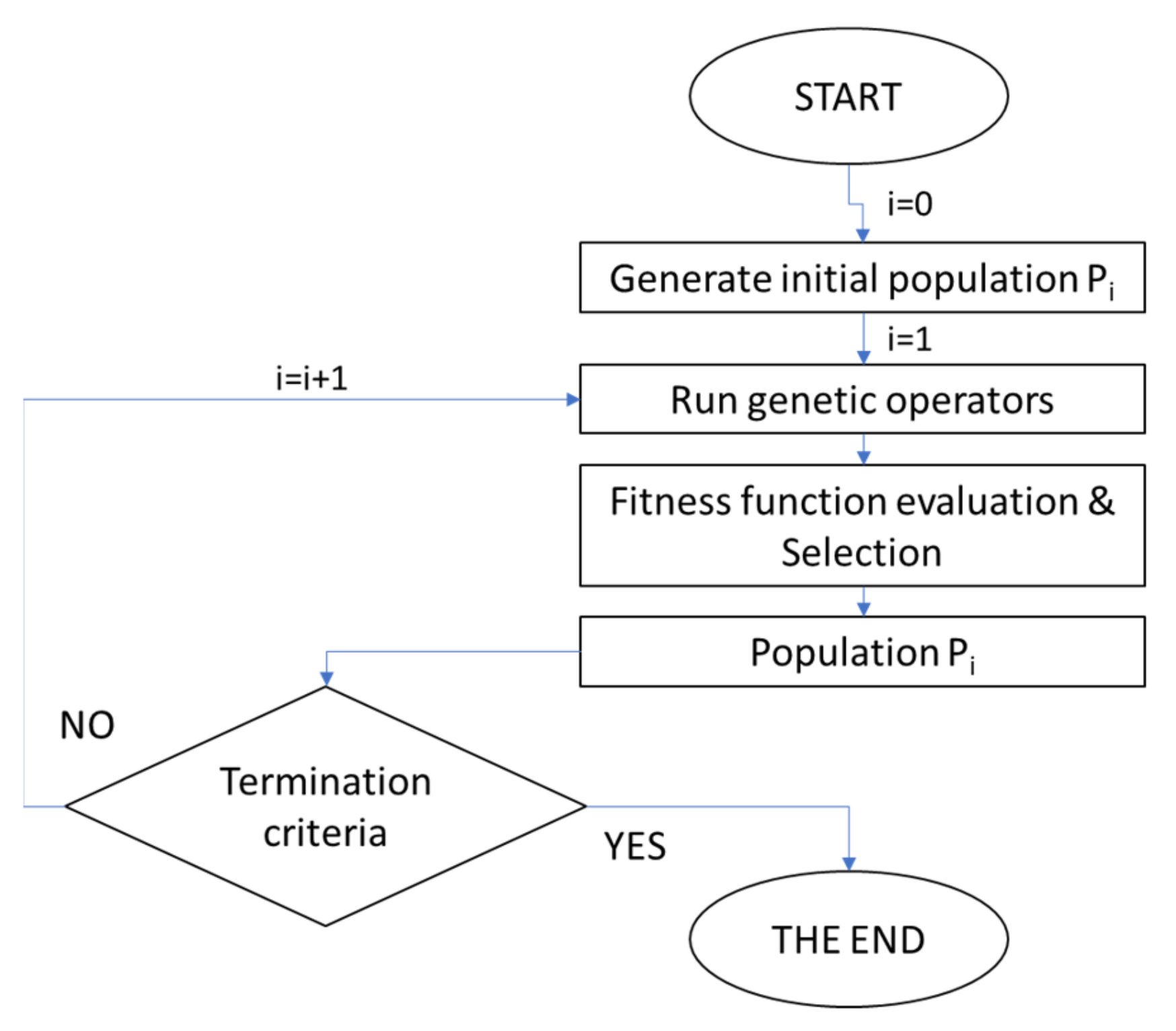
2.3. Genetic Algorithm (GA)
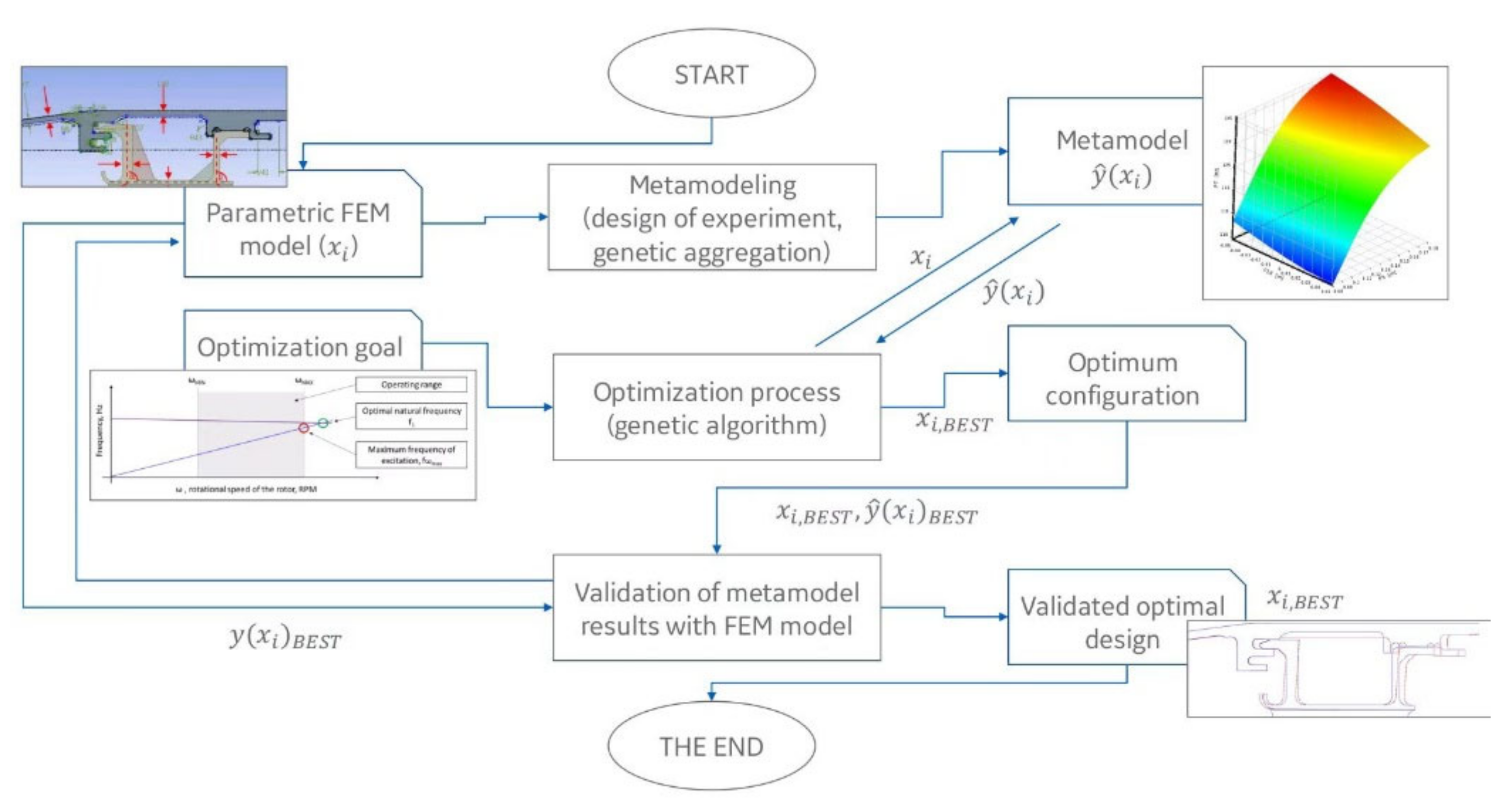
2.4. Metamodeling with Genetic Aggregation
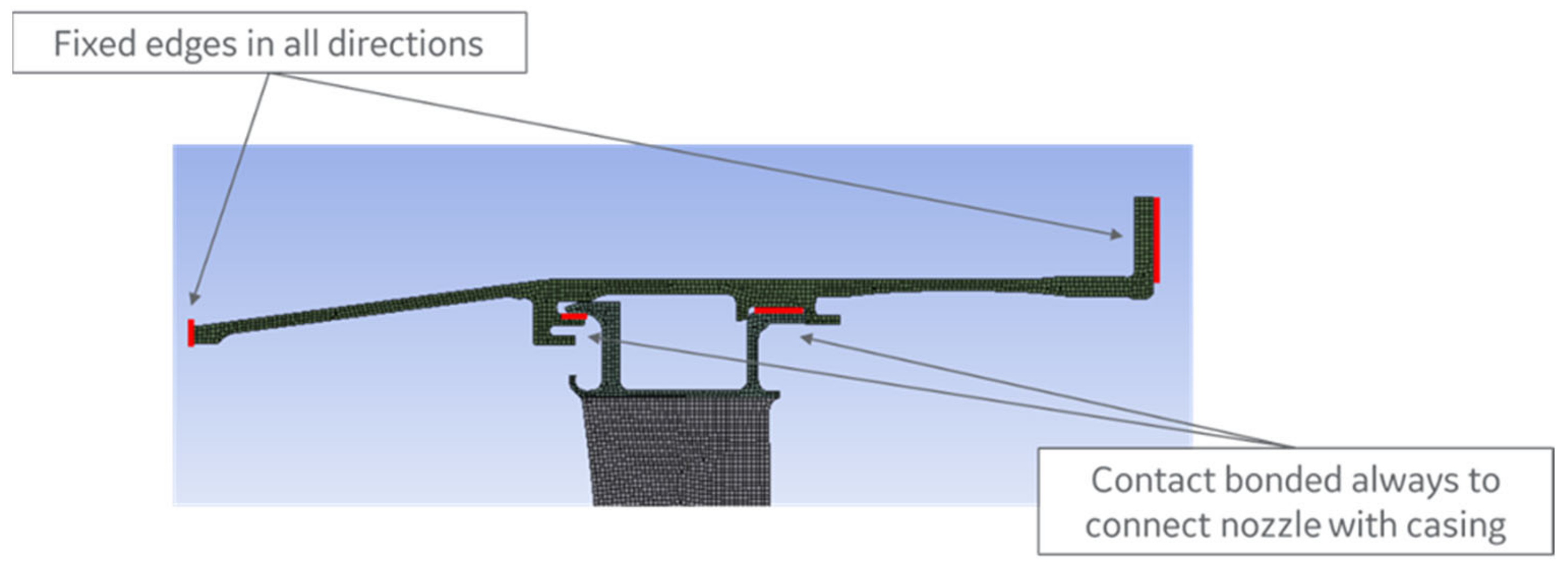
2.5. FEM Model Description
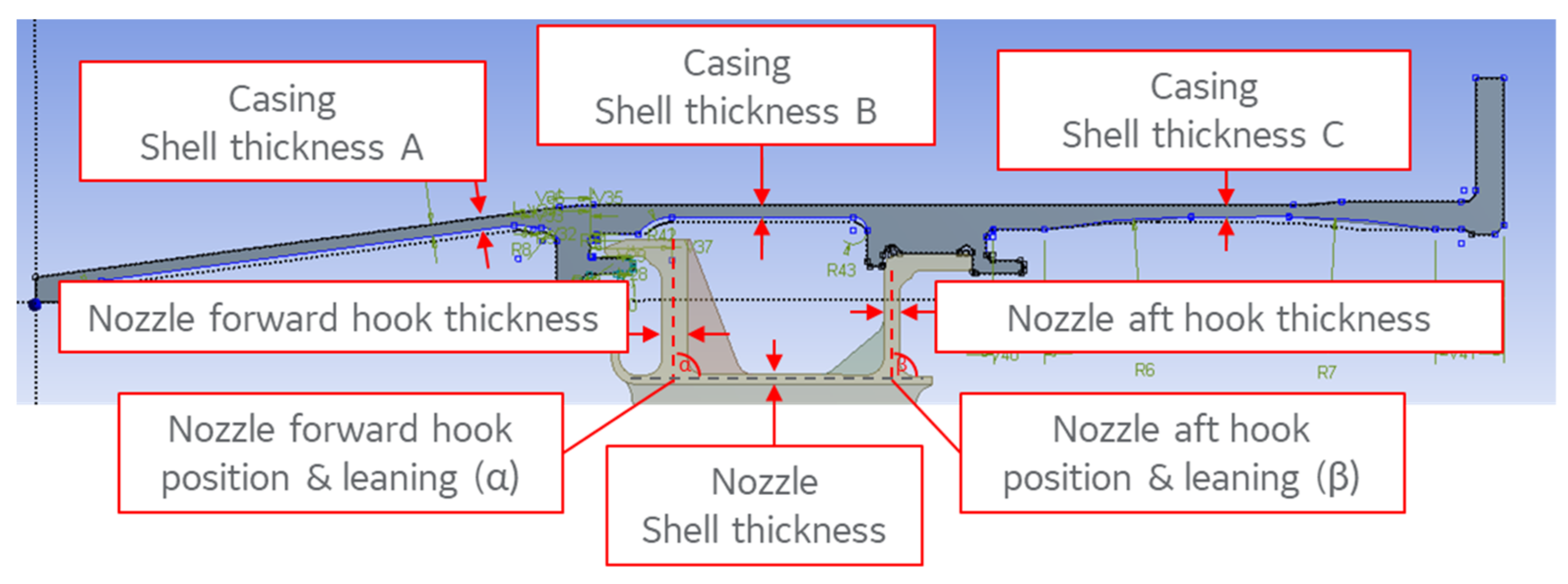
2.6. Parametric Model Definition
3. Results
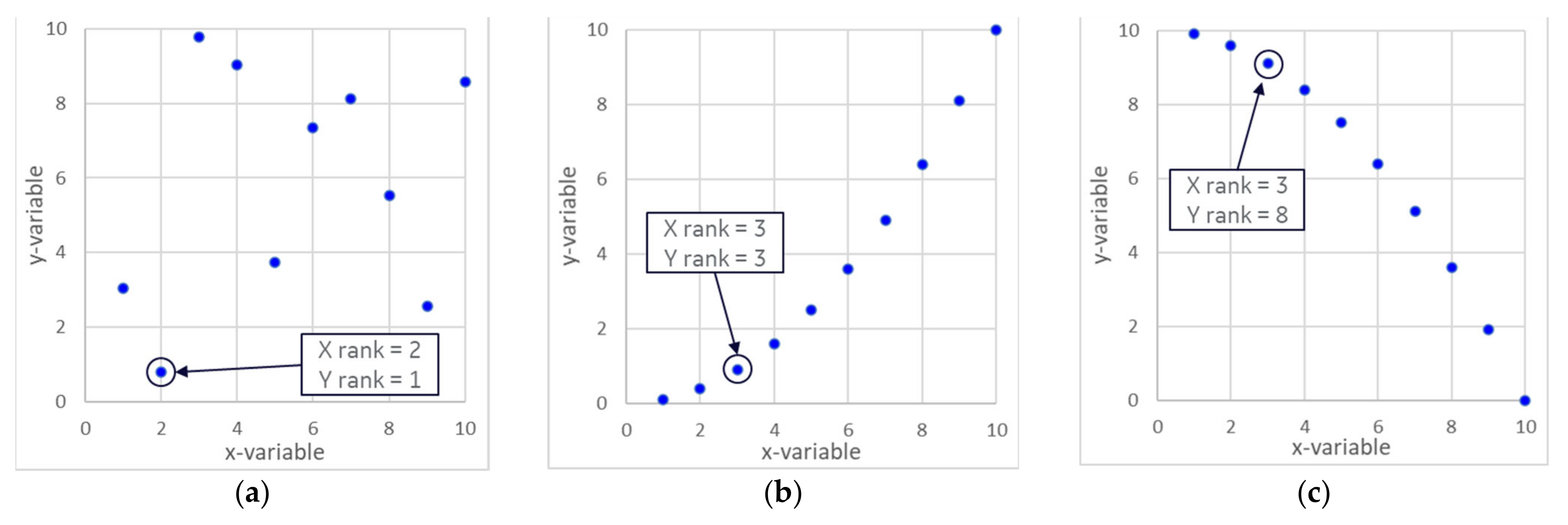
3.1. Sensitivity Analysis
3.2. Optimization Results
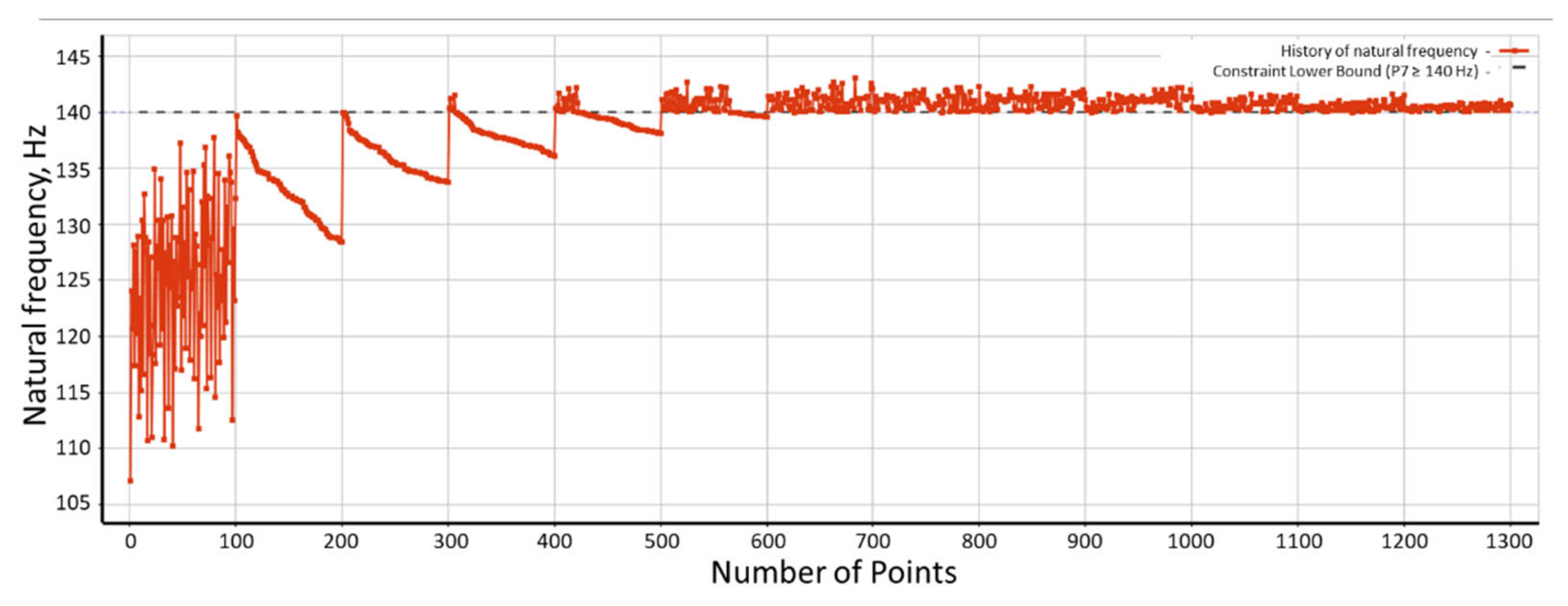
3.2.1. Optimization with Genetic Algorithm—Objective Function J1
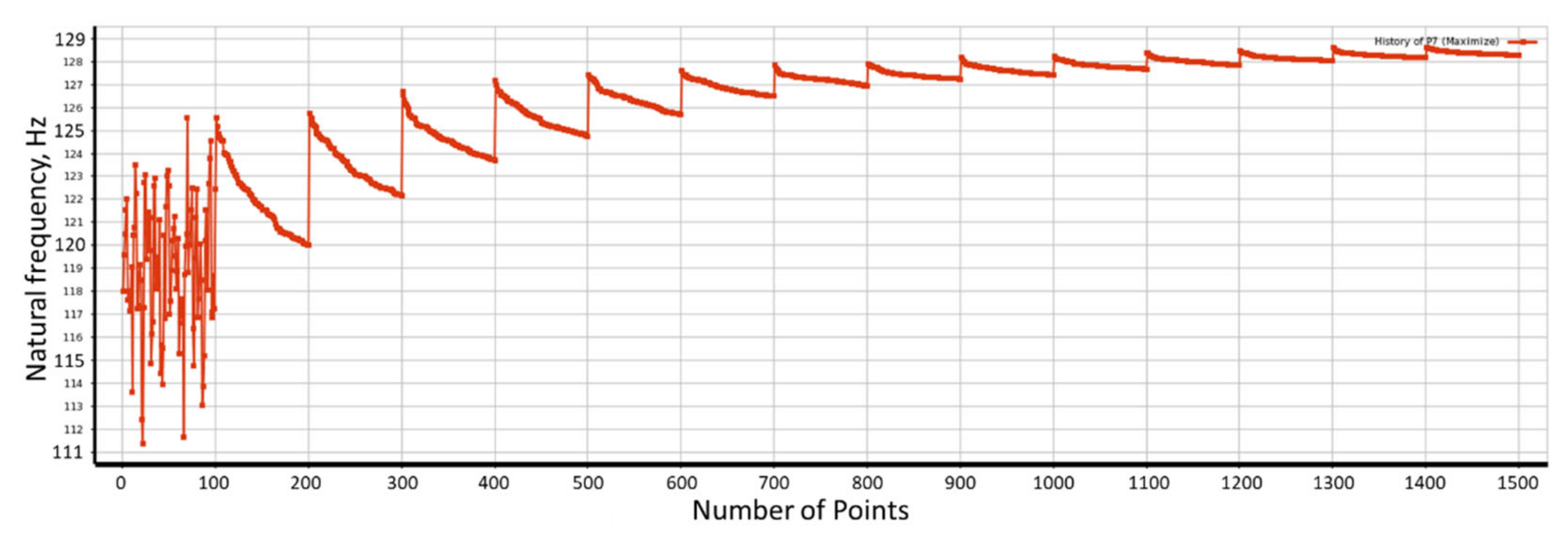
3.2.2. Optimization with Genetic Algorithm—Objective Function J2A
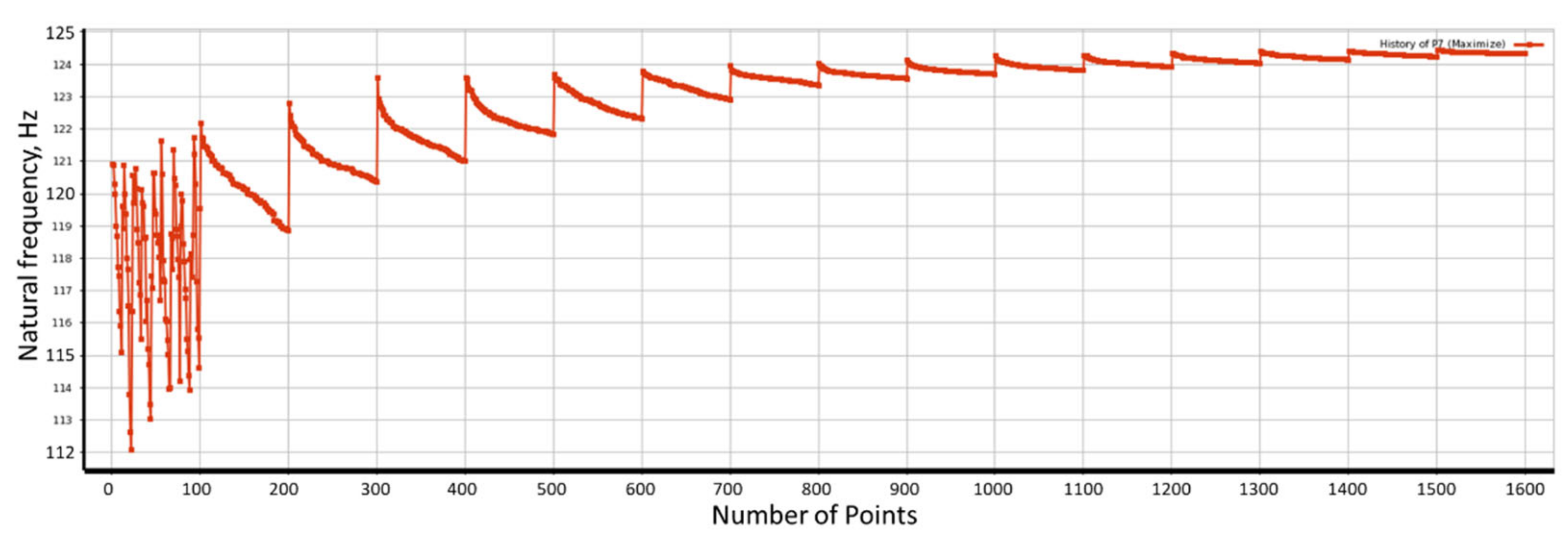
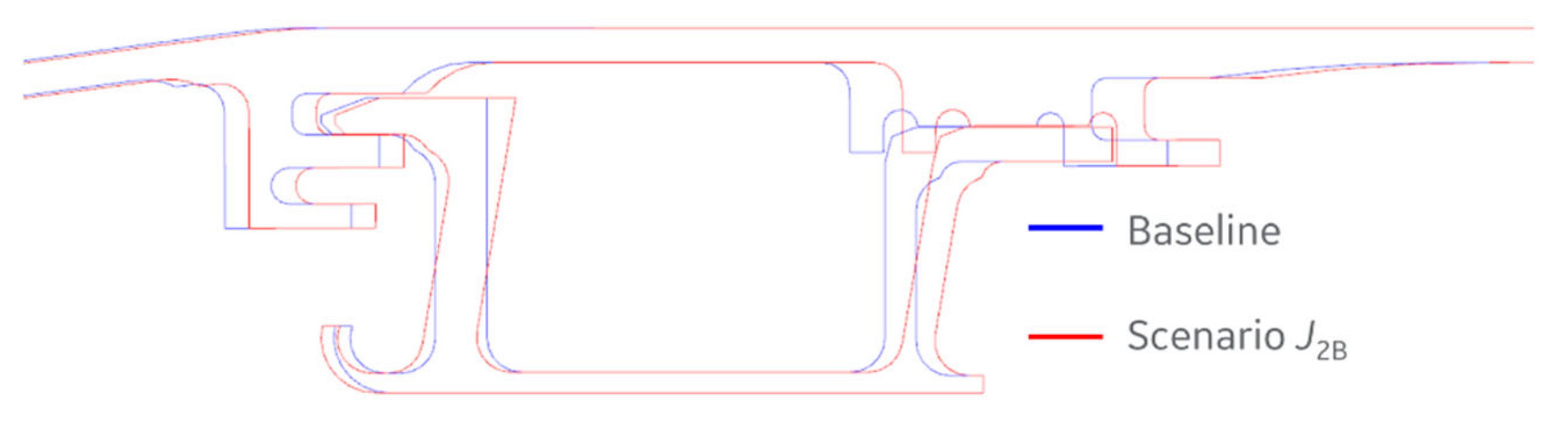
3.2.3. Optimization with Genetic Algorithm—Objective Function J2B
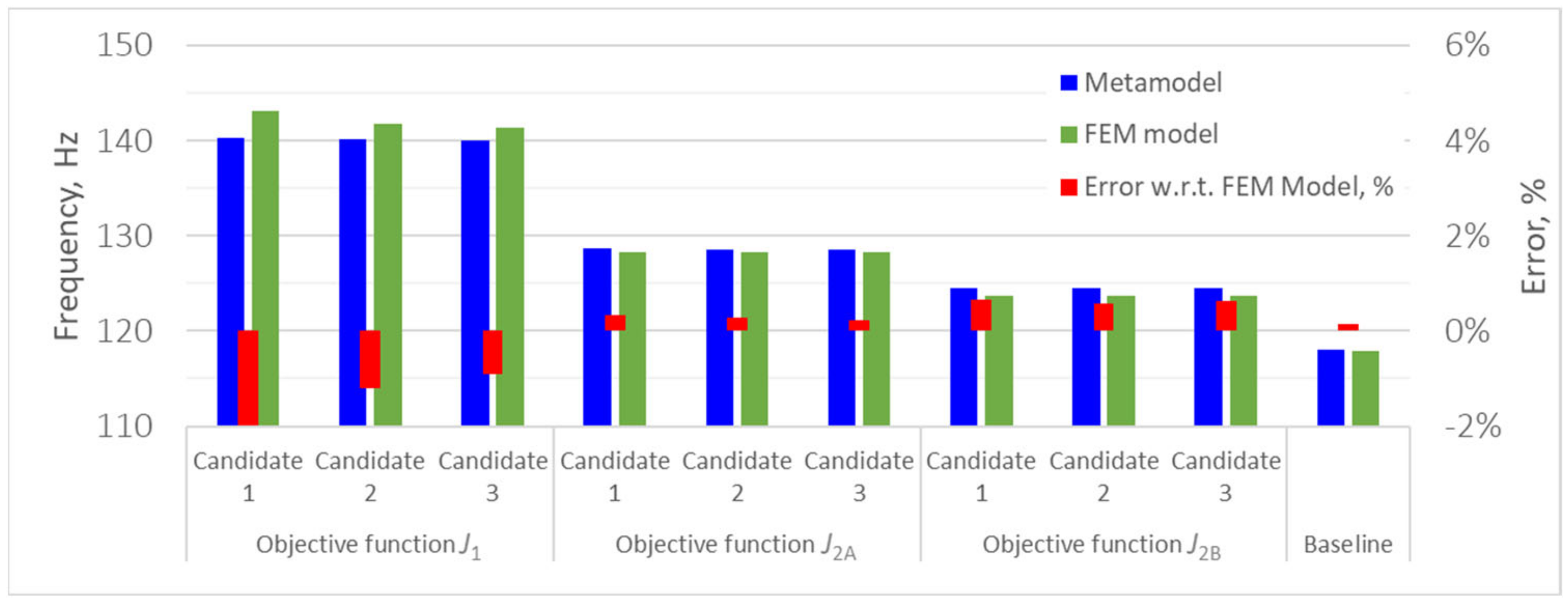
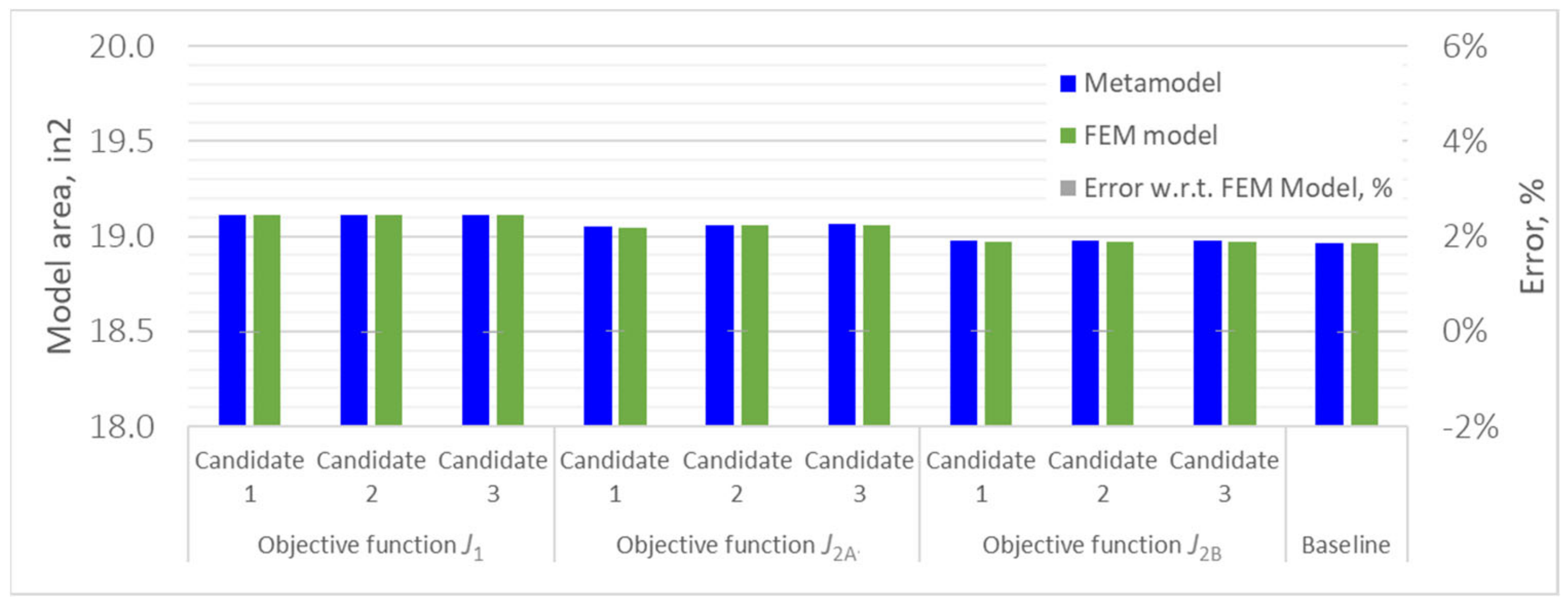
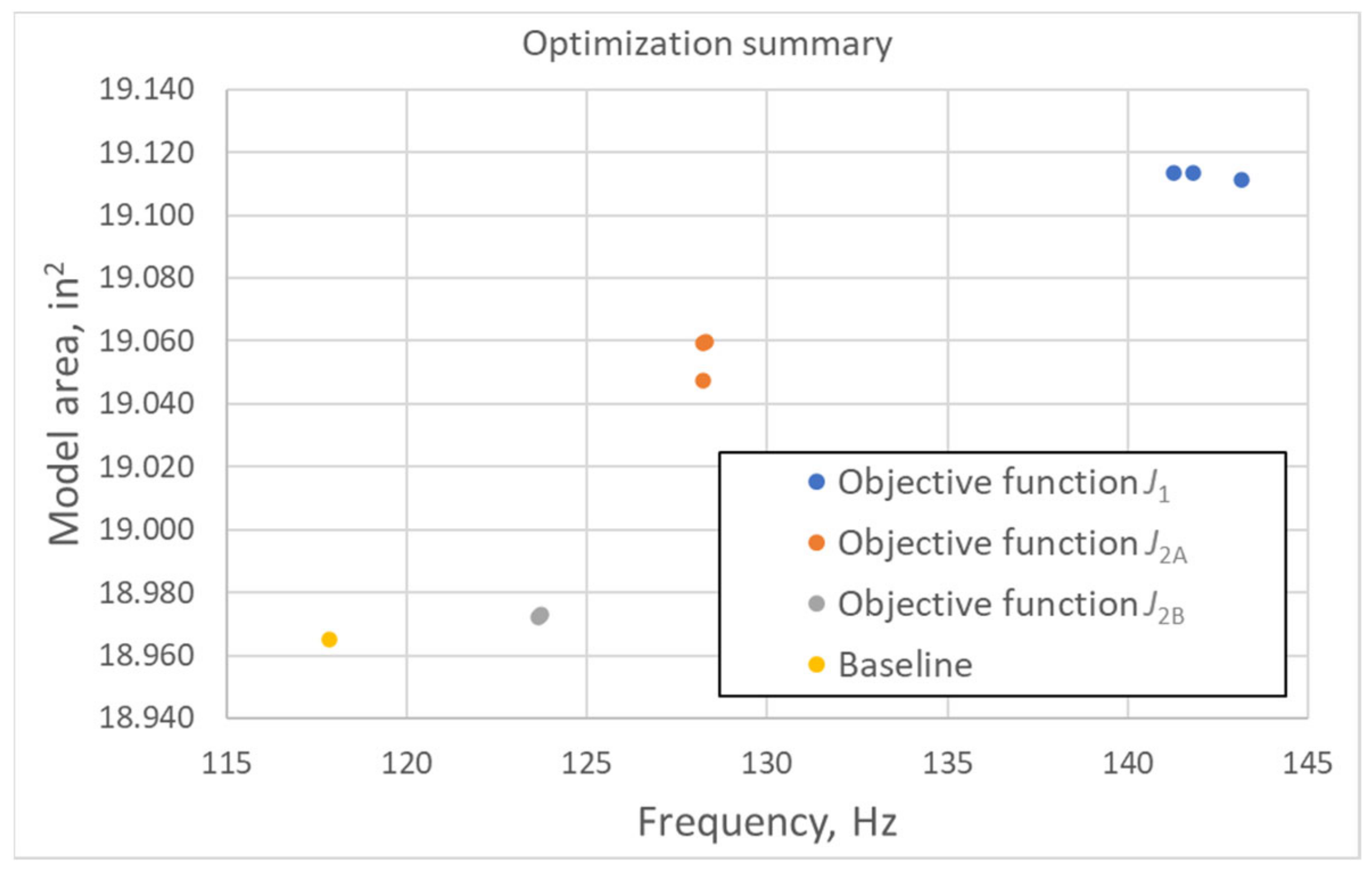
3.3. Optimization Summary
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geradin, M.; Rixen, D.J. Mechanical Vibrations; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Case, J.; Chilver, A.H. Strength of Materials and Structures; Edward Arnold: Baltimore, MD, USA, 1986. [Google Scholar]
- Zienkiewicz, O.C. The Finite Element Method in Structural and Continuum Mechanics; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Flemming, S. Performance optimization of gas turbine engines using STUDGA. In Proceedings of the 14th Triennial World Congress, Beijing, China, 5–9 July 1999. [Google Scholar]
- Davari, A.R.; Hasheminejad, M.; Boorboor, A. Shape Optimization of Wind Turbine Airfoils by Genetic Algorithm. IACSIT Int. J. Eng. Technol. 2013, 5, 206. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Umar, B.M.; Wang, W.; Wang, Z. Influence of structural parameters on the modal characteristics of a Francis runner. Eng. Fail. Anal. 2022, 131, 105853. [Google Scholar] [CrossRef]
- Soares, C. Gas Turbines: A Handbook of Air, Land and Sea Applications; Chapter 1: Gas Turbines: An Introduction and Applications; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Soares, C. Gas Turbines: A Handbook of Air, Land and Sea Applications; Chapter 10: Performance, Performance Testing, and Performance Optimization; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Rakowski, G.; Kacprzyk, Z. Metoda Elementów Skończonych w Mechanice Konstrukcji; Oficyna Wydawnicza Politechniki Warszawskiej: Warsaw, Poland, 1993. [Google Scholar]
- Holland, J.H. Outline for biological theory of adaptive systems. J. ACM 1962, 3, 297–314. [Google Scholar] [CrossRef]
- Arbor, A.; Holland, J.H. Adaptation in Natural and Artificial Systems; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Holland, J.H.; Reitman, J.S. Cognitive Systems Based on Adaptive Algorithms, Pattern-Directed Inference Systems; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Darwin, C.; Smith, S.; Rachootin, S.P. Charles Darwin’s Natural Selection; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Goldberg, D.E. Algorytmy Genetyczne i ich Zastosowania; Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 1995. [Google Scholar]
- Viana, F.A.C.; Haftka, R.T.; Steffen, V. Multiple Surrogates: How Cross-Validation Errors Can Help Us to Obtain the Best Predictor. Struct. Multidiscip. Optim. 2009, 39, 439–457. [Google Scholar] [CrossRef]
- Salem, B.; Roustant, O.; Gamboa, F.; Tomaso, L. Universal prediction distribution for surrogate models. SIAM/ASA J. Uncertain. Quantif. 2017, 5, 1086–1109. [Google Scholar] [CrossRef]
- Acar, E. Various Approaches for Constructing an Ensemble of Metamodels Using Local Measures. Struct. Multidiscip. Optim. 2010, 42, 879–896. [Google Scholar] [CrossRef]
- Available online: https://www.ansys.com/ (accessed on 9 May 2022).
- Gill, P.E.; Murray, W.; Saunders, M.A.; Wright, M.H. Sequential Quadratic Programming Methods for Nonlinear Programming. In Computer Aided Analysis and Optimization of Mechanical System Dynamics; NATO ASI Series (Series F: Computer and Systems Sciences); Haug, E.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 9. [Google Scholar]
- Exler, O.; Schittkowski, K.; Lehmann, T. A comparative study of numerical algorithms for nonlinear and nonconvex mixed-integer optimization. Math. Program. Comput. 2012, 1, 383–412. [Google Scholar] [CrossRef]
- Exler, O.; Schittkowski, K. A trust region SQP algorithm for mixed-integer nonlinear programming. Optim. Lett 2007, 1, 269–280. [Google Scholar] [CrossRef]
- Exler, O.; Lehmann, T.; Schittkowski, K. MISQP: A Fortran Subroutine of a Trust Region SQP Algorithm for Mixed-Integer Nonlinear Programming—User’s Guide Report; Department of Computer Science, University of Bayreuth: Bayreuth, Germany, 2012. [Google Scholar]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]










| Metamodel | A | B | C | D | E | Ensemble |
|---|---|---|---|---|---|---|
| R2 | 89.3% | 94.7% | 99.0% | 96.1% | 59.3% | 99.1% |
| Parameter | Lower Bound, in | Upper Bound, in |
|---|---|---|
| Casing shell A | 0.080 | 0.120 |
| Casing shell B | 0.080 | 0.180 |
| Casing shell C | 0.080 | 0.120 |
| Forward hook thickness | 0.100 | 0.200 |
| Rear hook thickness | 0.090 | 0.120 |
| Nozzle shell thickness | 0.060 | 0.120 |
| Forward hook position | −0.050 | 0.050 |
| Rear hook position | −0.050 | 0.050 |
| Parameter | Lower Bound, deg. | Upper Bound, deg. |
|---|---|---|
| Forward hook leaning | 80 | 100 |
| Rear hook leaning | 80 | 100 |
| Parameter Name | Value |
|---|---|
| Number of chromosomes in population | 100 |
| Convergence Stability Percentage | 2 |
| Mutation probability | 0.01 |
| Crossover probability | 0.98 |
| Maximum Number of Iterations | 20 |
| Maximum Number of Candidates | 3 (best first 3 chromosomes) |
| Name | Baseline | Candidate 1 | Candidate 2 | Candidate 3 |
|---|---|---|---|---|
| Shell_1_THCK (in) | 0.100 | 0.105 | 0.106 | 0.105 |
| Shell_2_THCK (in) | 0.100 | 0.169 | 0.169 | 0.169 |
| Shell_3_THCK (in) | 0.100 | 0.114 | 0.115 | 0.114 |
| FWD Hook THCK (in) | 0.150 | 0.164 | 0.163 | 0.162 |
| AFT Hook THCK (in) | 0.090 | 0.101 | 0.102 | 0.107 |
| FWD Hook Lean (degree) | 90 | 85.007 | 84.742 | 87.618 |
| AFT Hook Lean (degree) | 90 | 80.949 | 82.309 | 82.062 |
| Nozzle Shell THCK (in) | 0.060 | 0.067 | 0.067 | 0.068 |
| FWD Hook Pos (in) | 0 | 0.013 | 0.013 | 0.014 |
| AFT Hook Pos (in) | 0 | −0.046 | −0.045 | −0.042 |
| 1st System mode Frequency (Hz) | 118.0 | 140.3 | 140.1 | 140.0 |
| Geometry Surface Area (in2) | 18.965 | 19.109 | 19.112 | 19.113 |
| Name | Baseline | Candidate 1 | Candidate 2 | Candidate 3 |
|---|---|---|---|---|
| Shell_1_THCK (in) | 0.100 | |||
| Shell_2_THCK (in) | 0.100 | |||
| Shell_3_THCK (in) | 0.100 | |||
| FWD Hook THCK (in) | 0.150 | 0.198 | 0.200 | 0.198 |
| AFT Hook THCK (in) | 0.090 | 0.118 | 0.119 | 0.118 |
| FWD Hook Lean (degree) | 90 | 80.637 | 82.204 | 81.153 |
| AFT Hook Lean (degree) | 90 | 80.064 | 80.060 | 80.253 |
| Nozzle Shell THCK (in) | 0.060 | 0.076 | 0.086 | 0.087 |
| FWD Hook Pos (in) | 0 | 0.038 | 0.038 | 0.040 |
| AFT Hook Pos (in) | 0 | −0.049 | −0.047 | −0.049 |
| 1st System mode Frequency (Hz) | 118.0 | 128.6 | 128.6 | 128.6 |
| Geometry Surface Area (in2) | 18.965 | 19.049 | 19.061 | 19.062 |
| Name | Baseline | Candidate 1 | Candidate 2 | Candidate 3 |
|---|---|---|---|---|
| Shell_1_THCK (in) | 0.100 | |||
| Shell_2_THCK (in) | 0.100 | |||
| Shell_3_THCK (in) | 0.100 | |||
| FWD Hook THCK (in) | 0.150 | |||
| AFT Hook THCK (in) | 0.090 | |||
| FWD Hook Lean (degree) | 90 | 80.577 | 80.013 | 80.122 |
| AFT Hook Lean (degree) | 90 | 80.329 | 80.343 | 80.446 |
| Nozzle Shell THCK (in) | 0.060 | |||
| FWD Hook Pos (in) | 0 | 0.037 | 0.038 | 0.036 |
| AFT Hook Pos (in) | 0 | −0.050 | −0.050 | −0.050 |
| 1st System mode Frequency (Hz) | 118.0 | 124.4 | 124.4 | 124.4 |
| Geometry Surface Area (in2) | 18.965 | 18.978 | 18.978 | 18.979 |
| Baseline | Objective Function | |||
|---|---|---|---|---|
| J1 | J2A | J2B | ||
| Frequency, Hz | 118.03 | 143.2 | 128.2 | 123.6 |
| Model area, in2 | 18.965 | 19.111 | 19.047 | 18.972 |
| Frequency shift, % | 21% | 9% | 5% | |
| Effectiveness Area/Freq shift (Area cost per 1 Hz) | 0.006 | 0.008 | 0.001 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robak, R.; Szczepanik, M.; Rulik, S. Parametric Optimization of Nozzle Turbine Vane Modal Characteristics by Means of Artificial System. Appl. Sci. 2022, 12, 9724. https://doi.org/10.3390/app12199724
Robak R, Szczepanik M, Rulik S. Parametric Optimization of Nozzle Turbine Vane Modal Characteristics by Means of Artificial System. Applied Sciences. 2022; 12(19):9724. https://doi.org/10.3390/app12199724
Chicago/Turabian StyleRobak, Rafał, Mirosław Szczepanik, and Sebastian Rulik. 2022. "Parametric Optimization of Nozzle Turbine Vane Modal Characteristics by Means of Artificial System" Applied Sciences 12, no. 19: 9724. https://doi.org/10.3390/app12199724
APA StyleRobak, R., Szczepanik, M., & Rulik, S. (2022). Parametric Optimization of Nozzle Turbine Vane Modal Characteristics by Means of Artificial System. Applied Sciences, 12(19), 9724. https://doi.org/10.3390/app12199724


_Yang.png)



