Electromagnetic Wave Scattering by a Multiple Core Model of Composite Cylindrical Wires at Oblique Incidence

Abstract

A complex cylindrical structure consisting of a group of parallel stratified circular lossy dielectric cylinders, embedded in a dielectric circular cylindrical region and surrounded by unbounded dielectric space, is considered in this paper. The scattering of electromagnetic (EM) plane waves by the aforementioned configuration was studied; the EM waves impinged obliquely upon the structure and were arbitrarily polarized. The formulation used was based on the boundary-value approach coupled with the generalized separation of variables method. The EM field in each region of space was expanded in cylindrical wave-functions. Furthermore, the translational addition theorem of these functions was applied in order to match the EM field components on any cylindrical interface and enforce the boundary conditions. The end result of the analysis is an infinite set of linear algebraic equations with the wave amplitudes as unknowns. The system is solved by the truncation of series and unknowns and then matrix inversion; thus, we provide a semi-analytical solution for the scattered far-field and, as a consequence, for the scattering cross section of the complex cylindrical structure. The numerical results focus on calculations of the electric- and magnetic-field intensity of the far-field as well as of the total scattering cross section of several geometric configurations that fall within the aforementioned general structure. The effect of the geometrical and electrical characteristics of the structure on the scattered field was investigated. Specifically, the cylinders’ size and spacing, their conductivity and permittivity as well as the incidence direction were modified in order to probe how these variations are imprinted on scattering. Moreover, comparisons with previously published results, as well as convergence tests, were performed; all tests and comparisons proved to be successful.

1. Introduction

Although the scattering of electromagnetic waves by cylindrical structures has been broadly investigated for many decades, it still draws interest nowadays because of the variety of scientific areas it is associated with, such as microwave engineering, electromagnetic compatibility, mobile and satellite communications, geophysical and mineral exploration, space and military technologies, defense and the security sector. It’s applications include simulating complicated structures, analyzing modes in waveguides, simulating communication lines and space wires, controlling the radar cross section of various targets, communicating within tunnels and underground constructions, detecting and monitoring pipelines and subsurface resources.

Plane-wave scattering by two stand-alone parallel circular cylinders at normal incidence is one of the simplest pertinent problems and it was treated some decades ago [1,2,3,4], whereas oblique incidence at the same structure has also been examined [5,6]. Another, relatively simple, geometric configuration that has drawn strong interest consists of a circular conductive or dielectric cylinder embedded in a host cylinder either concentrically or eccentrically [7,8,9,10]. The case of scattering by inhomogeneous cylinders has also been studied [11], while arbitrary polarization and oblique incidence on either dielectric cylinders loaded by strips [12] or dielectric semi-cylinders loaded by ground plane slots [13] have been considered. More recently, scattering by dielectric cylinders eccentrically coated by cylindrical metamaterial shells has been investigated [14].

The most popular method to treat such problems is the expansion of the electromagnetic (EM) field expressions in cylindrical wavefunctions with unknown coefficients, which are found by applying the corresponding boundary conditions and solving the consequent infinite set of linear equations by truncation and matrix inversion [15]. However, various analytical formulations and numerical techniques have been proposed to deal with scattering from cylindrical structures; the latter may be far more complex than the ones mentioned in the previous paragraph. Indicative works are cited below.

The computational method of moments has been used to study electromagnetic scattering by perfect electric conductor (PEC) cylinders with arbitrary cross sections and several dielectric layers [16,17], and an impedance boundary condition of 2nd order has been employed to examine the effects of different dielectric coverings on PEC cylinders [18], while fictitious filamentary sources have been used to imitate the EM field scattered from a coated cylinder [19]. Scattering from eccentrically stratified cylinders has been addressed by enforcing the boundary conditions directly upon cylindrical surfaces at normal [20] and oblique incidence [21], while a new technique based on an indirect mode matching and 2nd Green’s vector theorem has been introduced to solve problems of EM-wave scattering from complex cylindrical structures such as eccentrically stratified cylindrical inclusions embedded in a host cylinder [22,23]. The rigorous coupled wave analysis in bipolar coordinates has been used to investigate scattering from eccentric multi-cylinder configurations [24] and the T-matrix method has been employed to study scattering by a cylinder with eccentric cylindrical inclusions [25]. The more complicated case of bianisotropic cylindrical inclusions in a host cylinder which is embedded in a bianisotropic space, at oblique incidence, has also been treated [26].

The scattering of electromagnetic waves by structures that involve several parallel cylindrical rods has been considered by many researchers; a common geometric configuration comprises cylinders with a circular [27] or arbitrary cross section [28,29] at normal incidence, while obliquely incident plane waves have been also examined [30]. More complicated problems/geometries include scattering from multiple dielectric and metallic objects studied by using the T-matrix method [31], oblique incidence at multilayered crossed arrays of circular cylinders [32], an S-matrix solution to scattering from periodic arrays of metallic cylinders with an arbitrary cross section [33], an iterative scattering procedure applied to parallel anisotropic chiral cylinders [34] and scattering from various periodic arrays of cylinders [35,36,37].

Over the last few years, interest in problems of scattering by cylindrical structures remains vivid, albeit the geometries/problems treated become even more sophisticated [38]. A series solution based on continuity has been presented for scattering from multilayer cylinders of arbitrary shapes [39,40], a Voltera integral equation formulation has been proposed for scattering by radially inhomogeneous cylinders in the case of oblique incidence [41], the spectral integral method (SIM) has been employed in the case of scattering by multilayer magnetodielectric cylinders [42], a hybrid integral equation method has been investigated in the case of scattering from doubly connected cylinders at oblique incidence [43] and a generalized vector cylinder harmonics (VCH) expansion has been applied for the scattering of an inhomogeneous plane wave by various cylindrical structures, such as a multilayer cylinder and an ensemble of stratified cylinders [44,45,46]. Recently, multilayered cylindrical geometries have been adopted to simulate photonic crystals [47,48]. The absorption and reflection of EM-waves by such crystals has been examined by using the transfer matrix method [47], while a multiphysics sensor consisting of magnetized plasma and isotropic dielectric layers with a periodic cylindrical structure has been proposed by Zhang et al. [48].

In this paper, we extend the method applied in [26] as a means to address and efficiently solve the problem of electromagnetic scattering of plane waves with arbitrary polarization, as they are obliquely incident upon a complex cylindrical structure of infinite length consisting of a group of parallel stratified circular lossy dielectric cylinders, embedded in a dielectric circular cylindrical housing surrounded by dielectric space. To the best of our knowledge, except [49] where scattering from a similar configuration is addressed as an engineering electromagnetics exercise from an educational point of view, this cylindrical structure is one of the most complicated configurations considered so far at oblique incidence. Admittedly, even more complex geometries may be found in the literature [23,24]; however, the EM wave is assumed to impinge normally on these structures. Thus, the main contribution of this paper is a solution to EM-wave scattering by combining a rather complicated cylindrical configuration with EM waves at obliquely incidence, which, in addition, are arbitrarily polarized. Furthermore, a semi-analytical method is used to address the problem, the only approximation being the truncation of the infinite series and the (numerical) matrix inversion.

The composite cylindrical wire considered in this work offers great flexibility in complex cylindrical object modeling because the analysis does not impose any restrictions on the physical properties (its multitude, size, position) and the electrical characteristics of the multi-layered cylindrical rods enclosed in the outer cylinder, provided that they are not overlapped. The multiple core model presented herein may be used for the simulation of space wires with applications in EM compatibility problems.

This paper is organized as follows. A description of the geometric configuration is given in Section 2. Additionally, the semi-analytical solution is developed in the same section. The end-result of the analysis is the calculation of the scattered electric and magnetic field intensity as well as the total scattering cross section of the structure. The indicative results are included in Section 3; the convergence of the solution is also examined therein. A discussion of the results is provided in Section 4, together with comparisons with previously published works. Finally, our conclusions are presented in Section 5.

2. Materials and Methods

A geometric configuration of our problem is depicted in Figure 1; Figure 1a displays the cross section of the general structure, while Figure 1b offers a 3D view of a simpler configuration that may serve as an example. The general configuration consists of a circular dielectric cylinder (affiliated to region 1) which is placed within the boundless free space (affiliated to region 0) and comprises L − 1 parallel circular stratified cylinders (each with two lossy dielectric layers, affiliated to regions $2, 3, 4, 5, \dots , 2L-2, 2L-1$). Each cylindrical region of space is identified by the index, i $(i=0, 1, 2, 3, 4, 5, \dots , 2L-2, 2L-1)$, and is characterized by its dielectric permittivity, ${\epsilon }_i$, magnetic permeability, ${\mu }_i$, electric conductivity, ${\sigma }_i$, and radius, ${\alpha }_i$. All L cylinders (the external as well as the embedded ones) are parallel to each other, with their axis-to-axis distances symbolized by $D_{pq}$ ($p, q=1, 2,\dots ,L$). We define L − 1 local cylindrical coordinate systems, ${\mathrm{O}}_p({\rho }_p,{\phi }_p,z)$, with $p=1, 2,\dots ,L$ and each one attached to the axis of the corresponding p-th cylinder, while the ${\mathrm{O}}_1 ({\rho }_1,{\phi }_1,z)$ system devoted to the outer cylinder’s axis is used as reference.

The primary excitation is provided by an EM plane wave with arbitrary polarization, impinging on the configuration of Figure 1a from the external region (0), where it propagates. The vector wavenumber of the aforementioned EM wave is given by

$${\overline{\mathrm{k}}}^{inc}({\mathsf{\theta }}^{\prime },{\mathsf{\phi }}^{\prime })={\mathrm{k}}_{\mathsf{\rho }}{\stackrel{⌢}{\mathrm{k}}}_{\mathsf{\rho }}^{inc}+\mathsf{\beta }\stackrel{⌢}{z}={\mathrm{k}}_0\sin {\mathsf{\theta }}^{\prime } (\cos {\mathsf{\phi }}^{\prime } \stackrel{⌢}{x}+\sin {\mathsf{\phi }}^{\prime } \stackrel{⌢}{y})+{\mathrm{k}}_0\cos {\mathsf{\theta }}^{\prime } \stackrel{⌢}{z},$$

(1)

where ${\mathsf{\theta }}^{\prime }$ and ${\mathsf{\phi }}^{\prime }$ are the angles of plane wave oblique incidence shown in Figure 2, $\mathsf{\beta }=\mathrm{k}\cos {\mathsf{\theta }}^{\prime }$ is the propagation constant, ${\mathrm{k}}_{\mathsf{\rho }}={\mathrm{k}}_0\sin {\mathsf{\theta }}^{\prime }$ and ${\mathrm{k}}_0=\mathsf{\omega }\sqrt{{\mathsf{\epsilon }}_0{\mathsf{\mu }}_0}$ is the wavenumber of free space when ω implies the circular frequency. Henceforth, the EM field $[{\overline{\mathrm{E}}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }}), {\overline{\mathrm{H}}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})] e^{-\mathrm{j}\mathsf{\beta }z}=[ \stackrel{⌢}{z} {\mathrm{E}}_{\mathrm{z}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})+{\overline{\mathrm{E}}}_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }}), \stackrel{⌢}{z} {\mathrm{H}}_{\mathrm{z}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})+{\overline{\mathrm{H}}}_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }}) ] e^{-\mathrm{j}\mathsf{\beta }\mathrm{z}}$ with arbitrary polarization, which is excited at $\overline{\mathsf{\rho }}\in (0)$ of the cylindrical structure, is referred to as the incident field. The harmonic $\exp [\mathrm{j}(\mathsf{\omega }t-\mathsf{\beta }z)]$ dependence on time and z is suppressed throughout the analysis for brevity.

Using the coordinate system (${\mathrm{O}}_1$) of the outer cylinder, the longitudinal components of the incident electromagnetic field may be written [50] as follows:

$$\left[\begin{array}{c}{\mathrm{E}}_z^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_z^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]=\left[\begin{array}{c}{\mathrm{E}}_0\\ {\mathrm{H}}_0\end{array}\right] \exp (-\mathrm{j} {\overline{\mathrm{k}}}_{\mathsf{\rho }}^{\mathrm{i}\mathrm{n}\mathrm{c}}\cdot \overline{\mathsf{\rho }})=\left[\begin{array}{c}{\mathrm{E}}_0\\ {\mathrm{H}}_0\end{array}\right] {\displaystyle \sum _{n=-\infty }^{\infty }{\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}0}{\mathsf{\rho }}_1) {\mathrm{j}}^n {\mathrm{e}}^{\mathrm{j}n({\mathsf{\phi }}_1-{\mathsf{\phi }}^{\prime })}}.$$

(2)

${\mathrm{E}}_0$ and ${\mathrm{H}}_0$, in Equation (2), are the magnitudes of the incident electric and magnetic fields, whereas ${\mathsf{\rho }}_1$ and ${\mathsf{\phi }}_1$ are the polar coordinates of $\overline{\mathsf{\rho }}$ in (${\mathrm{O}}_1$), ${\mathrm{k}}_{\mathrm{c}0}=\sqrt{{\mathrm{k}}_0^2-{\mathsf{\beta }}^2}$ and ${\mathrm{J}}_n(x)$ stands for the Bessel function of order n and argument x [51]. Τhe φ-components of the incident field can be expressed as

$$\left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]=\left[\begin{array}{c}{\mathrm{E}}_0\\ {\mathrm{H}}_0\end{array}\right] {\displaystyle \sum _{n=-\infty }^{\infty }{}^n\overline{\overline{\mathrm{G}}}{}_0^{\mathrm{J}}({\mathsf{\rho }}_1) {\mathrm{j}}^n {\mathrm{e}}^{\mathrm{j}n({\mathsf{\phi }}_1-{\mathsf{\phi }}^{\prime })}},$$

(3)

where ${}^n\overline{\overline{\mathrm{G}}}{}_i^{\mathrm{J}}(\mathsf{\rho })$ is the abbreviation for

$${}^n\overline{\overline{\mathrm{G}}}{}_i^{\mathrm{J}}(\mathsf{\rho })=\left[\begin{array}{cc}\frac{\mathsf{\beta }n}{{\mathrm{k}}_{\mathrm{c}i}^2 \mathsf{\rho }}{\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })& \frac{\mathrm{j}\mathsf{\omega }{\mathsf{\mu }}_i}{{\mathrm{k}}_{\mathrm{c}i}}{\mathrm{J}}_n^{\prime }({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })\\ -\frac{\mathrm{j}\mathsf{\omega }{\epsilon }_i+{\mathsf{\sigma }}_i}{{\mathrm{k}}_{\mathrm{c}i}}{J}_n^{\prime }({\mathrm{k}}_{ci} \mathsf{\rho })& \frac{\mathsf{\beta }n}{{\mathrm{k}}_{\mathrm{c}i}^2 \mathsf{\rho }}{\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })\end{array}\right],$$

(4)

and ${\mathrm{J}}_n^{\prime }(x)$ is the first derivative of the Bessel function of order n with respect to its argument, x.

The EM field $[{\overline{\mathrm{E}}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }}), {\overline{\mathrm{H}}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})] {\mathrm{e}}^{-\mathrm{j}\mathsf{\beta }z}=[ \stackrel{⌢}{\mathrm{z}}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})+{\overline{\mathrm{E}}}_{\mathrm{t}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }}) , \stackrel{⌢}{\mathrm{z}}{\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})+{\overline{\mathrm{H}}}_{\mathrm{t}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }}) ] {\mathrm{e}}^{-\mathrm{j}\mathsf{\beta }z}$ excited at any observation point $\overline{\mathsf{\rho }}$ of the cylindrical region $(i)$, with $i=0, 1, 2, 3, \dots , 2L-1$, is referred to as the scattered field due to the existence of the L dielectric stratified cylinders of Figure 1. It should be noted that regions (i) with $i=2, 4, \dots , 2(s-1),\dots , 2(L-1)$ and $i= 3, 5, \dots , 2(s-1)+1, \dots , 2(L-1)+1$ designate the cladding and the core regions for the s-th cylinder ($s=2, 3, \dots , L$), respectively. Regarding the local coordinate system of the q-th cylinder (${\mathrm{O}}_q$), the longitudinal components ${\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}$ and ${\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}$ of the scattered field may be written in compact form as

$$\begin{array}{l}\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]={\displaystyle \sum _{n=-\infty }^{\infty }\{(1-{\mathsf{\delta }}_{i,0}) {\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}i} {\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{a}_n^i\\ b_n^i\end{array}\right]+{\mathsf{\delta }}_{i,2(q-1)}{\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} {\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{c}_n^{i+1}\\ d_n^{i+1}\end{array}\right]}\\ +{\mathsf{\delta }}_{i,1} {\displaystyle \sum _{s=2}^L{\mathrm{H}}_n^{(2)}({\mathrm{k}}_{c1} {\mathsf{\rho }}_s) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_s} \left[\begin{array}{c}{c}_n^{2(s-1)}\\ d_n^{2(s-1)}\end{array}\right]}+{\mathsf{\delta }}_{i,0} {\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}0} {\mathsf{\rho }}_1) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_1}\left[\begin{array}{c}{c}_n^1\\ d_n^1\end{array}\right]\}\end{array},$$

(5)

where i indicates the cylindrical region of the corresponding q cylinder, ${\mathsf{\rho }}_q$ and ${\mathsf{\phi }}_q$ signify the polar coordinates of the observation point $\overline{\mathsf{\rho }}$ regarding the cylindrical coordinate system (${\mathrm{O}}_q$), $a_n^i$, $c_n^i$ and $b_n^i$, $d_n^i$ denote the unknown coefficients of the series expansions for the electric and magnetic field intensity, respectively, ${\mathrm{k}}_{\mathrm{c}i}=\sqrt{{\mathrm{k}}_i^2-{\mathsf{\beta }}^2}$, ${\mathrm{k}}_i=\sqrt{{\mathsf{\epsilon }}_i {\mathsf{\mu }}_i {\mathsf{\omega }}^2-\mathrm{j}\mathsf{\omega } {\mathsf{\mu }}_i {\mathsf{\sigma }}_i}$, ${\mathsf{\delta }}_{i,\ell }$ stands for the Kronecker delta piecewise function of i and ℓ and ${\mathrm{H}}_n^{(2)}(x)$ is the Hankel function of the 2nd kind, order n and argument x [51].

The infinite sum at the right-hand side of Equation (5) represents the scattered EM field in every region of space according to the values of the Kronecker delta functions, as explained below. The scattered wave in the unbounded external empty space (region 0) is expressed in terms of ${\mathrm{H}}_n^{\left(2\right)}\left({\mathrm{k}}_{\mathrm{c}0}{\mathsf{\rho }}_1\right)$, as indicated by the fourth term in the sum of Equation (5), since this term exists only for i = 0; the aforementioned Hankel function of the second kind acquires the form of a diverging cylindrical wave far from the axis of the structure (i.e., for ${\mathrm{k}}_{\mathrm{c}0}{\mathsf{\rho }}_1\gg 1$). The EM field inside the host cylinder (region 1) comprises the contribution of each internal (stratified) cylinder in the form of a diverging cylindrical wave; the latter is expressed in terms of ${\mathrm{H}}_n^{\left(2\right)}\left({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\rho }}_{\mathrm{s}}\right)$, as denoted by the third term in the sum of Equation (5), which exists only for i = 1. An additional term, regular at ${\mathsf{\rho }}_1\to 0$ (since it contains Bessel functions of the first kind), is included in the modal expansion of the EM field in region 1 to account for the contribution of the outer boundary of the cladding; this term is actually the first term in the sum of Equation (5) for i = 1. The EM field inside the core of each cylindrical inclusion is represented by the first term in the sum of Equation (5) for $i=3, 5, \dots , 2(L-1)+1$; the modal expansion contains only Bessel functions of the first kind since the EM field should be regular at the local origin ${\mathrm{O}}_{\mathrm{q}}$ (i.e., for ${\mathsf{\rho }}_{\mathrm{q}}\to 0$). The expansion of the EM field inside the cylindrical layer of each inclusion should comprise both Bessel and Hankel functions since the (local) origin is not included in these regions. The Bessel functions of the first kind appear in the first term at the right-hand side of Equation (5), for $i=2, 4, \dots , 2(L-1)$, whereas the third term represents the expansion in Hankel functions of the second kind.

By applying the Bessel and Hankel functions translational addition theorems, one may prove that [26,51]

$${\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_1) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_1}={\displaystyle \sum _{m=-\infty }^{\infty }{\mathrm{J}}_{n-m}\left({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{1q}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_{1q}} {\mathrm{J}}_m\left({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\rho }}_q\right) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_q}},$$

(6a)

$${\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_s) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_s}={\displaystyle \sum _{m=-\infty }^{\infty }{\mathrm{H}}_{n-m}^{(2)}\left({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_{q,s}^{>}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_{q,s}^{>}} {\mathrm{J}}_m\left({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_{q,s}^{<}\right) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_{q,s}^{<}}},$$

(6b)

where

$$\begin{array}{cc}\hfill {\mathsf{\rho }}_{q,s}^{>}=\max \{{\mathsf{\rho }}_q, {\mathrm{D}}_{sq}\}, & {\mathsf{\rho }}_{q,s}^{<}=\min \{{\mathsf{\rho }}_q, {\mathrm{D}}_{sq}\},\hfill \\ \hfill {\mathsf{\phi }}_{q,s}^{<}=\{\begin{array}{c}{\mathsf{\phi }}_q, \mathrm{if} {\mathsf{\rho }}_{q,s}^{<}={\mathsf{\rho }}_q\\ {\mathsf{\phi }}_{sq}, \mathrm{if} {\mathsf{\rho }}_{q,s}^{<}={\mathrm{D}}_{sq}\end{array}, & {\mathsf{\phi }}_{q,s}^{>}=\{\begin{array}{c}{\mathsf{\phi }}_q, \mathrm{if} {\mathsf{\rho }}_{q,s}^{>}={\mathsf{\rho }}_q\\ {\mathsf{\phi }}_{sq}, \mathrm{if} {\mathsf{\rho }}_{q,s}^{>}={\mathrm{D}}_{sq}\end{array},\hfill \end{array}$$

(6c)

and (${\mathrm{O}}_s$) and (${\mathrm{O}}_q$) are the coordinate systems attached to the axis of the s-th and q-th cylinder, respectively.

Substituting (5) in (4), the compact general expressions of Equation (7) for the excitation electromagnetic field in any region (i) are obtained:

$$\begin{array}{r}\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]={\displaystyle \sum _{n=-\infty }^{\infty }\{(1-{\mathsf{\delta }}_{i,0})(1-{\mathsf{\delta }}_{i,1}) {\mathrm{J}}_n({\mathrm{k}}_{\mathrm{c}i} {\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{a}_n^i\\ b_n^i\end{array}\right]+{\mathsf{\delta }}_{i,2(q-1)} {\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} {\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{c}_n^{i+1}\\ d_n^{i+1}\end{array}\right]}\\ +{\mathsf{\delta }}_{i,0} {\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}0} {\mathsf{\rho }}_1) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_1}\left[\begin{array}{c}{c}_n^1\\ d_n^1\end{array}\right]+{\mathsf{\delta }}_{i,1}[{\displaystyle \sum _{m=-\infty }^{\infty }{\mathrm{J}}_{n-m}\left({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{1q}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\phi }_{1q}} {\mathrm{J}}_m\left({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_q\right) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_q}} \left[\begin{array}{c}{a}_n^1\\ b_n^1\end{array}\right]\\ +{\displaystyle \sum _{s=2}^L{\displaystyle \sum _{m=-\infty }^{\infty }{\mathrm{H}}_{n-m}^{(2)}\left({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_{q,s}^{>}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_{q,s}^{>}} {\mathrm{J}}_m\left({\mathrm{k}}_{\mathrm{c}1} {\mathsf{\rho }}_{q,s}^{<}\right) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_{q,s}^{<}}} \left[\begin{array}{c}{c}_n^{2(s-1)}\\ d_n^{2(s-1)}\end{array}\right]}]\}\end{array}.$$

(7)

By expressing the ${\mathsf{\phi }}_q$-components of the scattered field at $\overline{\mathsf{\rho }}\in (i)$, the analysis yields

$$\begin{array}{r}\left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]={\displaystyle \sum _{n=-\infty }^{\infty }\{(1-{\mathsf{\delta }}_{i,0})(1-{\mathsf{\delta }}_{i,1}) {}^n\overline{\overline{\mathrm{G}}}_i^{\mathrm{J}}({\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{a}_n^i\\ b_n^i\end{array}\right]+{\mathsf{\delta }}_{i,2(q-1)} {}^n\overline{\overline{\mathrm{G}}}{}_i^{\mathrm{H}}({\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_q}\left[\begin{array}{c}{c}_n^{i+1}\\ d_n^{i+1}\end{array}\right]}\\ +{\mathsf{\delta }}_{i,0} {}^n\overline{\overline{\mathrm{G}}}{}_0^{\mathrm{H}}({\mathsf{\rho }}_1) {\mathrm{e}}^{\mathrm{j}n{\mathsf{\phi }}_1}\left[\begin{array}{c}{c}_n^1\\ d_n^1\end{array}\right]+{\mathsf{\delta }}_{i,1}{\displaystyle \sum _{m=-\infty }^{\infty }{}^m\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{J}}({\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_q} {\mathrm{J}}_{n-m}\left({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{1q}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_{1q}}} \left[\begin{array}{c}{a}_n^1\\ b_n^1\end{array}\right]\\ +{\mathsf{\delta }}_{i,1} [{\displaystyle \sum _{s=2}^L{\displaystyle \sum _{m=-\infty }^{\infty } [ {\mathsf{\delta }}_{qs}^{\prime }{}^{n-m}\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{H}}({\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_q} {\mathrm{J}}_m\left({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{sq}\right) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_{sq}}}}\\ +(1-{\mathsf{\delta }}_{qs}^{\prime }) {\mathrm{H}}_{n-m}^{(2)}\left({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{sq}\right) {\mathrm{e}}^{\mathrm{j}(n-m){\mathsf{\phi }}_{sq}} {}^m\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{J}}({\mathsf{\rho }}_q) {\mathrm{e}}^{\mathrm{j}m{\mathsf{\phi }}_q}] \left[\begin{array}{c}{c}_n^{2(s-1)}\\ d_n^{2(s-1)}\end{array}\right]]\}\end{array},$$

(8)

where ${\delta }_{qs}^{\prime }=1 ( \mathrm{if} {\mathsf{\rho }}_{q,s}^{>}={\mathsf{\rho }}_q)$, or $0 (\mathrm{if} {\mathsf{\rho }}_{q,s}^{<}={\mathsf{\rho }}_q)$, ${}^n\overline{\overline{\mathrm{G}}}{}_i^{\mathrm{H}}(\mathsf{\rho })$ stands for the abbreviation

$${}^n\overline{\overline{G}}{}_i^{\mathrm{H}}(\mathsf{\rho })=\left[\begin{array}{cc}\frac{\mathsf{\beta }n}{{\mathrm{k}}_{\mathrm{c}i}^2 \mathsf{\rho }}{\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })& \frac{\mathrm{j}\mathsf{\omega }{\mathsf{\mu }}_i}{{\mathrm{k}}_{\mathrm{c}i}}{{\mathrm{H}}^{\prime }}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })\\ -\frac{\mathrm{j}\mathsf{\omega }{\mathsf{\epsilon }}_i+{\mathsf{\sigma }}_i}{{\mathrm{k}}_{\mathrm{c}i}}{{\mathrm{H}}^{\prime }}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })& \frac{\mathsf{\beta }n}{{\mathrm{k}}_{\mathrm{c}i}^2 \mathsf{\rho }}{\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}i} \mathsf{\rho })\end{array}\right],$$

(9)

and ${{\mathrm{H}}^{\prime }}_n^{(2)}(x)$ is the Hankel function’s first derivative with respect to its argument, x.

The total EM field $[{\overline{\mathrm{E}}}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }}), {\overline{\mathrm{H}}}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }})] {\mathrm{e}}^{-\mathrm{j}\mathsf{\beta }z}$ at $\overline{\mathsf{\rho }}\in (i)$ may be expressed, by using Equations (2), (3), (7) and (8), as follows:

$$\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }})\end{array}\right]=\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]+{\mathsf{\delta }}_{i,0} \left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right], \left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{t}\mathrm{o}\mathrm{t}}(\overline{\mathsf{\rho }})\end{array}\right]=\left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]+{\mathsf{\delta }}_{i,0} \left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right].$$

(10)

Subsequently, we apply the appropriate boundary conditions, imposing the continuity of the total EM field’s components ${\mathrm{E}}_{\mathrm{z}}^{\mathrm{t}\mathrm{o}\mathrm{t}}$, ${\mathrm{H}}_{\mathrm{z}}^{\mathrm{t}\mathrm{o}\mathrm{t}}$, ${\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{t}\mathrm{o}\mathrm{t}}$ and ${\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{t}\mathrm{o}\mathrm{t}}$ over each cylindrical boundary (${\mathsf{\rho }}_1={\alpha }_1$, ${\mathsf{\rho }}_p={\alpha }_{2(p-1)}$ and ${\mathsf{\rho }}_p={\alpha }_{2(p-1)+1}$; $p=2,\dots ,L$) of the complex configuration. Then, we multiply both sides of each of the resulting equations by $\exp (-\mathrm{j}M{\mathsf{\phi }}_p)$ and integrate from ${\mathsf{\phi }}_p=0$ to ${\mathsf{\phi }}_p=2\pi$. Thus, we obtain an infinite set of linear, algebraic equations for the unknown expansion coefficients, which is written in the following compact form:

$$\begin{array}{c}[{\mathsf{\delta }}_{q,2(p-1)}\left[\begin{array}{cc}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}q}{\mathsf{\alpha }}_q)\overline{\overline{\mathrm{I}}}& -{\mathrm{H}}_M^{(2)}({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\alpha }}_q) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_q^{\mathrm{J}}({\mathsf{\alpha }}_q)& -{}^M\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{H}}({\mathsf{\alpha }}_q)\end{array}\right] \\ +\left({\mathsf{\delta }}_{q,1}+ {\mathsf{\delta }}_{q,2(p-1)+1}\right) \left[\begin{array}{cc}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}q}{\mathsf{\alpha }}_q)\overline{\overline{\mathrm{I}}}& -{\mathrm{H}}_M^{(2)}({\mathrm{k}}_{\mathrm{c}(q-1)}{\mathsf{\alpha }}_q) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_q^{\mathrm{J}}({\mathsf{\alpha }}_q)& -{}^M\overline{\overline{\mathrm{G}}}{}_{(q-1)}^{\mathrm{H}}({\mathsf{\alpha }}_q)\end{array}\right]] \left[\begin{array}{c}\left(\begin{array}{c}{a}_M^q\\ b_M^q\end{array}\right)\\ \left(\begin{array}{c}{c}_M^q\\ d_M^q\end{array}\right)\end{array}\right]\\ +{\mathsf{\delta }}_{q,2(p-1)} \left[\begin{array}{c}{\mathrm{H}}_M^{(2)}({\mathrm{k}}_{\mathrm{c}q}{\mathsf{\alpha }}_q) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_q^{\mathrm{H}}({\mathsf{\alpha }}_q)\end{array}\right] \left(\begin{array}{c}{c}_M^{q+1}\\ d_M^{q+1}\end{array}\right)-{\mathsf{\delta }}_{q,2(p-1)+1} \left[\begin{array}{c}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}(q-1)}{\mathsf{\alpha }}_q)\overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_{(q-1)}^{\mathrm{J}}({\mathsf{\alpha }}_q)\end{array}\right] \left(\begin{array}{c}{a}_M^{q-1}\\ b_M^{q-1}\end{array}\right)\\ -{\mathsf{\delta }}_{q,2(p-1)} {\displaystyle \sum _{n=-\infty }^{\infty }[{\mathrm{J}}_{n-M}({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{1p}) {\mathrm{e}}^{\mathrm{j}(n-M){\mathsf{\phi }}_{1p}}\left[\begin{array}{c}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\alpha }}_q) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{J}}({\mathsf{\alpha }}_q)\end{array}\right] \left(\begin{array}{c}{a}_n^1\\ b_n^1\end{array}\right)}\\ +{\displaystyle \sum _{\begin{array}{l}s=2\\ s\ne p\end{array}}^L{\mathrm{H}}_{n-M}^{(2)}({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{sp}) {\mathrm{e}}^{\mathrm{j}(n-M){\mathsf{\phi }}_{sp}}\left[\begin{array}{c}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\alpha }}_q) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{J}}({\mathsf{\alpha }}_q)\end{array}\right] \left(\begin{array}{c}{c}_n^{2(s-1)}\\ d_n^{2(s-1)}\end{array}\right)}]\\ +{\mathsf{\delta }}_{q,1}{\displaystyle \sum _{n=-\infty }^{\infty } {\displaystyle \sum _{s=2}^L{\mathrm{J}}_{n-M}({\mathrm{k}}_{\mathrm{c}1}{\mathrm{D}}_{s1}) {\mathrm{e}}^{\mathrm{j}(n-M){\mathsf{\phi }}_{s1}}\left[\begin{array}{c}{\mathrm{H}}_M^{(2)}({\mathrm{k}}_{\mathrm{c}1}{\mathsf{\alpha }}_1) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_1^{\mathrm{H}}({\mathsf{\alpha }}_1)\end{array}\right] \left(\begin{array}{c}{c}_n^{2(s-1)}\\ d_n^{2(s-1)}\end{array}\right)}}\\ ={\mathsf{\delta }}_{q,1} {\mathrm{j}}^M {\mathrm{e}}^{-\mathrm{j}M{\mathsf{\phi }}^{\prime }} \left[\begin{array}{c}{\mathrm{J}}_M({\mathrm{k}}_{\mathrm{c}0}{\mathsf{\alpha }}_1) \overline{\overline{\mathrm{I}}}\\ {}^M\overline{\overline{\mathrm{G}}}{}_0^{\mathrm{J}}({\mathsf{\alpha }}_1)\end{array}\right] \left[\begin{array}{c}{\mathrm{E}}_0\\ {\mathrm{H}}_0\end{array}\right].\end{array}$$

(11)

Equation (11) represents an infinite number of linear, algebraic equations since the index M may take the values $M=0, \pm 1, \pm 2, \dots , \pm \infty$. Moreover, in Equation (11), $p=1, \dots , L$; $q=1, 2, 3, 4, \dots , 2(L-1), 2(L-1)+1$; $s=2, 3, \dots , L$, $\overline{\overline{\mathrm{I}}}$ is the identity matrix of order $2\times 2$, ${\mathrm{D}}_{sp}$ denotes the axis-to-axis distance separating the (${\mathrm{O}}_s$) and (${\mathrm{O}}_p$) cylindrical coordinate systems, ${\mathsf{\phi }}_{sp}$ stands for the location angle of the (${\mathrm{O}}_p$) cylindrical coordinate system with reference to the (${\mathrm{O}}_s$) one, while ${\mathsf{\alpha }}_{2(p-1)+1}$ and ${\mathsf{\alpha }}_{2(p-1)}$ are the radii of the core and the cladding regions of the p-th cylinder.

The multitude of the unknown expansion coefficients in the equation set of (11) may be considerably reduced by truncating the summations over n as well as the values of M; the truncation number is denoted as $N_r$. Thus, Equation (11) result in a set of $20 (2N_r+1)\times 20 (2N_r+1)$ linear, algebraic equations. It is worth mentioning that the matrix elements and the constant terms consist mainly of sole-term Bessel and Hankel functions and are given by simple analytical expressions; thus, they may be considered in closed form. The square coefficient matrix is non-singular, its determinant is non-zero and its inverse can be calculated straightforwardly. For this purpose, a custom computer code was developed in Fortran 90. Addressing the equation set of (11) results in the fast, accurate and efficient evaluation of the field expansion coefficients $a_n^i$, $c_n^i$, $b_n^i$ and $d_n^i$ $(i=0, 1, 2,\dots ,2L-1)$ that appear in Equations (7) and (8).

The scattered far-field may be obtained from Equation (5) by letting $\overline{\mathsf{\rho }}({\mathsf{\rho }}_1, {\phi }_1)\in (0)$ and ${\rho }_1\to \infty$. Through the large argument asymptotic approximation of the ${\mathrm{H}}_n^{(2)}({\mathrm{k}}_{\mathrm{c}0}{\rho }_1)$ Hankel function [51], the z- and φ-components of the electromagnetic far-field are given by the analytical expressions of Equation (12)

$$\left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]={\mathrm{e}}^{-\mathrm{j} ({\mathrm{k}}_{\mathrm{c}0} {\rho }_1-\mathsf{\pi }/4)}\sqrt{\frac{2}{\mathsf{\pi }{\mathrm{k}}_{\mathrm{c}0}{\rho }_1}}{\displaystyle \sum _{n=-\infty }^{\infty }{\mathrm{e}}^{\mathrm{j}n({\phi }_1+\mathsf{\pi }/2)} \left[\begin{array}{c}{c}_n^1\\ d_n^1\end{array}\right]}$$

(12a)

$$\left[\begin{array}{c}{\mathrm{E}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\\ {\mathrm{H}}_{\mathsf{\phi }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\end{array}\right]=\left[\begin{array}{cc}0& {\mathrm{Z}}_0{\left(\sin {\theta }^{\prime }\right)}^{-1}\\ -{\left({\mathrm{Z}}_0\sin {\theta }^{\prime }\right)}^{-1}& 0\end{array}\right] \left[\begin{array}{c}{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\rho })\\ {\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\rho })\end{array}\right],$$

(12b)

where ${\mathrm{k}}_{\mathrm{c}0}=\sqrt{{\mathrm{k}}_0^2-{\mathsf{\beta }}^2}={\mathrm{k}}_0\sin {\theta }^{\prime }$ and ${\mathrm{Z}}_0=\sqrt{{\mathsf{\mu }}_0/{\mathsf{\epsilon }}_0}$.

The radial component of the Poynting vector is given by:

$${\mathrm{S}}_{\mathsf{\rho }}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})=\frac{1}{2{\mathrm{Z}}_0\sin {\theta }^{\prime }} \left[{\left|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\right|}^2+{\mathrm{Z}}_0^2 {\left|{\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}(\overline{\mathsf{\rho }})\right|}^2\right].$$

(13)

The total radial scattered power, ${\mathrm{P}}_{\mathsf{\rho }}^{\mathrm{s}\mathrm{c}}$, may be found by integrating ${\mathrm{S}}_{\mathsf{\rho }}^{\mathrm{sc}}(\overline{\mathsf{\rho }})$ on the surface of a cylinder of infinite radius, ${\alpha }_1\to \infty$, and finite length, $\mathrm{dz}$. Consequently, the total scattering cross section, ${\mathsf{\sigma }}_{\mathrm{t}}$, of the structure is obtained by [50]

$${\mathsf{\sigma }}_t=\frac{{\mathrm{P}}_{\mathsf{\rho }}^{\mathrm{s}\mathrm{c}}}{|{\mathrm{S}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})| \mathrm{dz}} \Rightarrow {\mathsf{\sigma }}_t=\frac{1}{{\mathrm{k}}_0} {\left[\frac{2}{\sin {\theta }^{\prime }}\right]}^2 \frac{1}{{\mathrm{E}}_0^2+{\mathrm{Z}}_0^2{\mathrm{H}}_0^2} {\displaystyle \sum _{\mathrm{n}=-\infty }^{\infty }\left({\left| c_n^1\right|}^2+{\left|{\mathrm{Z}}_0 d_n^1\right|}^2\right)},$$

(14)

where ${\mathrm{S}}^{\mathrm{i}\mathrm{n}\mathrm{c}}(\overline{\mathsf{\rho }})$ is the Poynting vector of the incident plane wave.

3. Numerical Results and Convergence

Indicative numerical results, derived from the analysis presented in Section 2, are given in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The scattered far-field, as well as the total scattering cross section, are presented for specific configurations of the general structure of Figure 1, considering both polarizations. Each configuration considered herein is depicted as a small inset in the corresponding Figure, for the sake of clarity. All details that concern the configurations examined, such as the geometric characteristics of the cylinders and the electrical characteristics of each region of space, are given in the captions; they are omitted from the text for the sake of brevity.

Moreover, the analysis presented herein and the corresponding computer codes were verified using reciprocity and energy conservation internal tests. The reciprocity was examined for multiple duets of scattering and incidence directions. Energy conservation was tested using the optical theorem, according to which the scattering cross section should be identical to the extinction cross section when all materials constituting the complex cylindrical structure are lossless [50]. All these tests were successful, and the corresponding results are omitted for brevity.

Figure 3 and Figure 4 correspond to a pair ($L=3$) of dissimilar dielectric cylindrical rods, Figure 5, Figure 6, Figure 7 and Figure 8 correspond to a pair ($L=3$) of similar lossy dielectric doubly-layered cylinders, while Figure 9 and Figure 10 refer to a quadruplet ($L=5$) of similar dielectric cylindrical rods. Regions 0 and 1, in all cases, are considered as vacuum.

In order to check the convergence of the algorithm, we calculated the scattered electric field intensity, for several configurations, by sequentially increasing the truncation number, $N_r$, until the achievement of accuracy with seven digits. An indicative example is presented in

Table 1. $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\rho }_1\to \infty , {\phi }_1={45}^{°})|$ when increasing truncation number ${\mathrm{N}}_{\mathrm{r}}$ for the structure shown in the inset of Figure 5.

${\mathbf{N}}_{\mathbf{r}}$	$|{\mathbf{E}}_{\mathbf{z}}^{\mathbf{s}\mathbf{c}}({\mathit{\rho }}_1\to \mathit{\infty },{\mathit{\phi }}_1={45}^{°})|$
7	56.99990
8	57.30295
9	57.24285
10	57.24623
11	57.23580
12	57.23515
13	57. 23517
14	57. 23517
15	57. 23517

, where the values of $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\rho }_1\to \infty , {\phi }_1={45}^{°})|$ are shown for an increasing ${\mathrm{N}}_{\mathrm{r}}$. The geometric configuration used for the production of Table 1 corresponds to the inset of Figure 5 with ${\theta }^{\prime }={\phi }^{\prime }={45}^{°}$, ${\mathrm{E}}_0={\mathrm{H}}_0=1$, $L=3$, ${\mathrm{D}}_{23}=0.7{\mathsf{\lambda }}_0$, ${\mathsf{\epsilon }}_1={\mathsf{\epsilon }}_0$, ${\mathsf{\epsilon }}_2={\mathsf{\epsilon }}_4=2.32{\mathsf{\epsilon }}_0$, ${\mathsf{\alpha }}_2={\mathsf{\alpha }}_4=0.3{\mathsf{\lambda }}_0$, ${\mathsf{\epsilon }}_3={\mathsf{\epsilon }}_5=4.34{\mathsf{\epsilon }}_0$, ${\mathsf{\alpha }}_3={\mathsf{\alpha }}_5=0.2{\mathsf{\lambda }}_0$, ${\mathsf{\mu }}_i={\mathsf{\mu }}_0$ and ${\mathsf{\sigma }}_1={\mathsf{\sigma }}_2={\mathsf{\sigma }}_3={\mathsf{\sigma }}_4={\mathsf{\sigma }}_5=0$. Evidently, the algorithm converges very rapidly and steadily, since an ${\mathrm{N}}_{\mathrm{r}}$ as low as 12 is sufficient to determine the far-field value within six significant decimal digits.

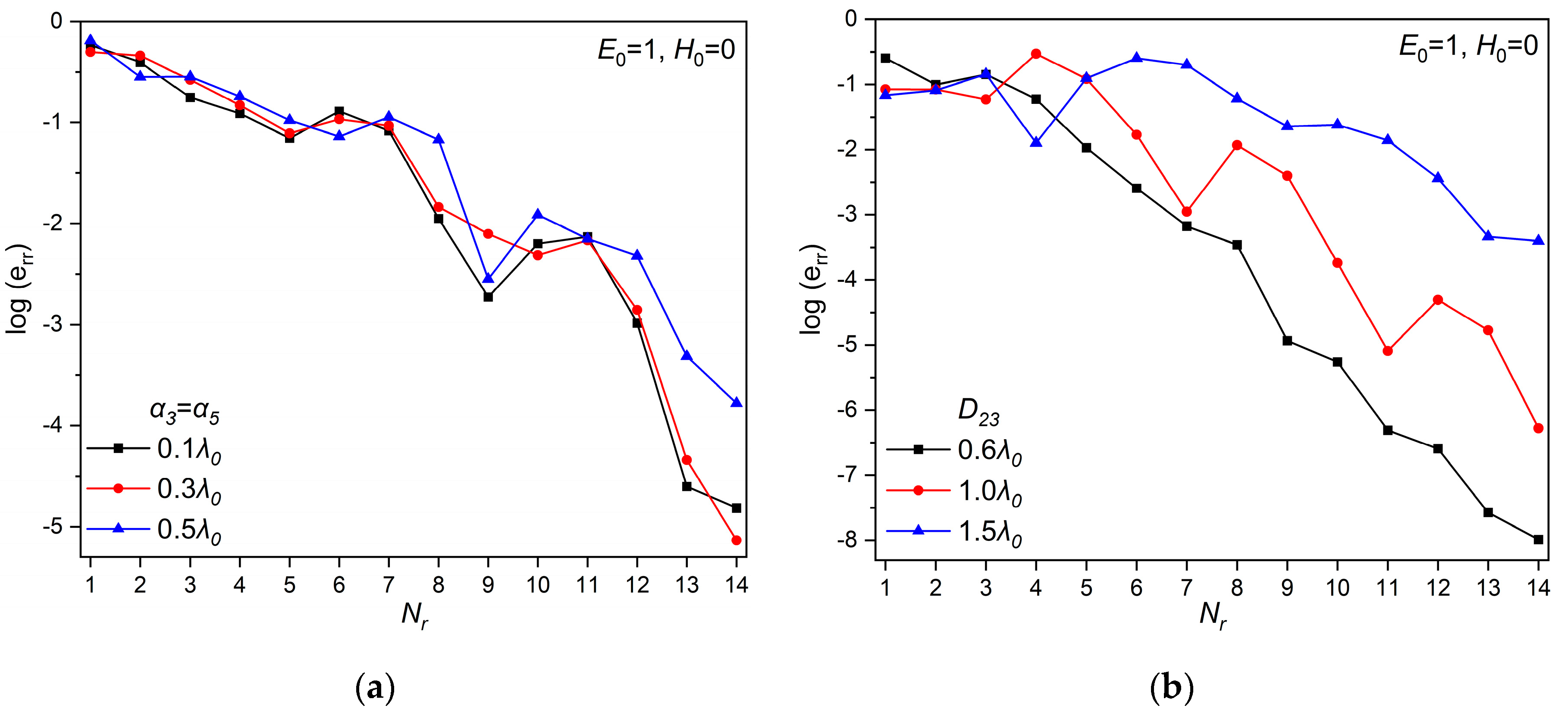
The convergence of our semi-analytical solution was further investigated through Figure 11 and Figure 12. We calculated the error from the following relationship [52]:

$${\mathrm{e}}_{rr}=\frac{\left|{\mathsf{\sigma }}_t^{\mathrm{N}+1}-{\mathsf{\sigma }}_t^{\mathrm{N}}\right|}{\left|{\mathsf{\sigma }}_t^{\mathrm{N}}\right|},\mathrm{N}=1,2,3,\dots ,{\mathrm{N}}_{\mathrm{r}}$$

(15)

where ${\mathsf{\sigma }}_{\mathrm{t}}^{\mathrm{N}}$ and ${\mathsf{\sigma }}_{\mathrm{t}}^{\mathrm{N}+1}$ stand for the total scattering cross section of the structure, computed from Equation (14), after truncating the infinite sum to N and N + 1 terms, respectively. Figure 11 refers to the E-polarized incident plane wave, while in Figure 12 the incident wave is arbitrarily polarized. The main remark to be made about Figure 11 and Figure 12 is that all curves follow the same trend: the error function decreases as the truncation number increases. This is an expected outcome, which is necessary to guarantee the convergence of the solution and has also been reported by other researchers, albeit for different configurations [52].

In addition, Figure 11a suggests that the truncation number does not depend strongly on the size of the inner cylinders, especially when they are rather small; the black and red curves almost coincide. However, by inspecting the curves of Figure 11b, one might conclude that the truncation number is strongly affected by the distance between the inner cylinders. For example, for $D_{23}=0.6{\lambda }_0$ (black curve), 3-digit accuracy may be achieved with ${\mathrm{N}}_r\approx 7$, while 13 terms are necessary for the same accuracy if ${\mathrm{D}}_{23}=1.5{\mathsf{\lambda }}_0$ (blue curve). The rather strong dependence of the truncation number on the separation between the inner cylinders may also be verified for the arbitrary polarization of the incident wave (Figure 12). It is evident from Figure 12 that the greater the distance between the rods, the greater the truncation number required in order to achieve a specific accuracy.

4. Discussion and Comparisons

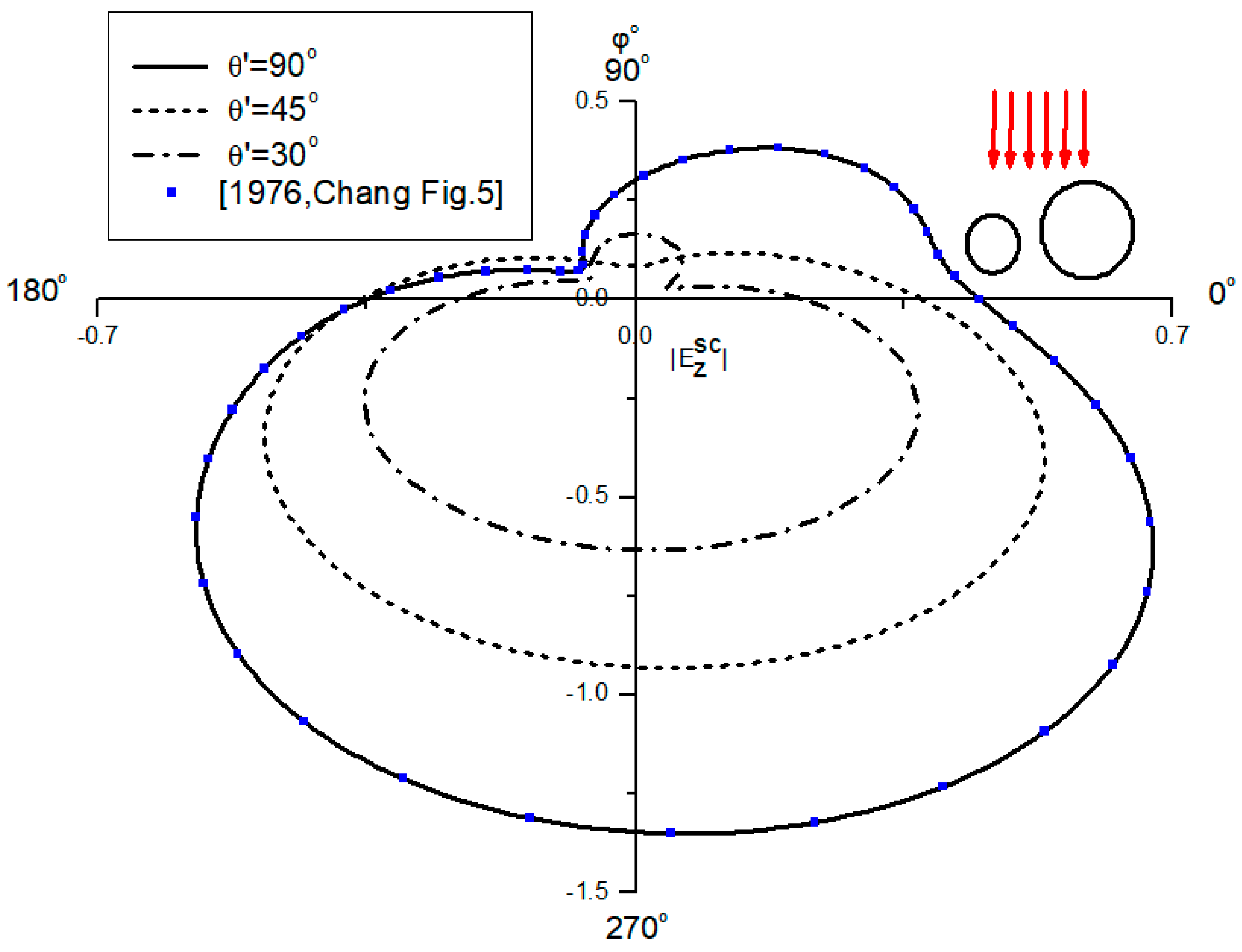
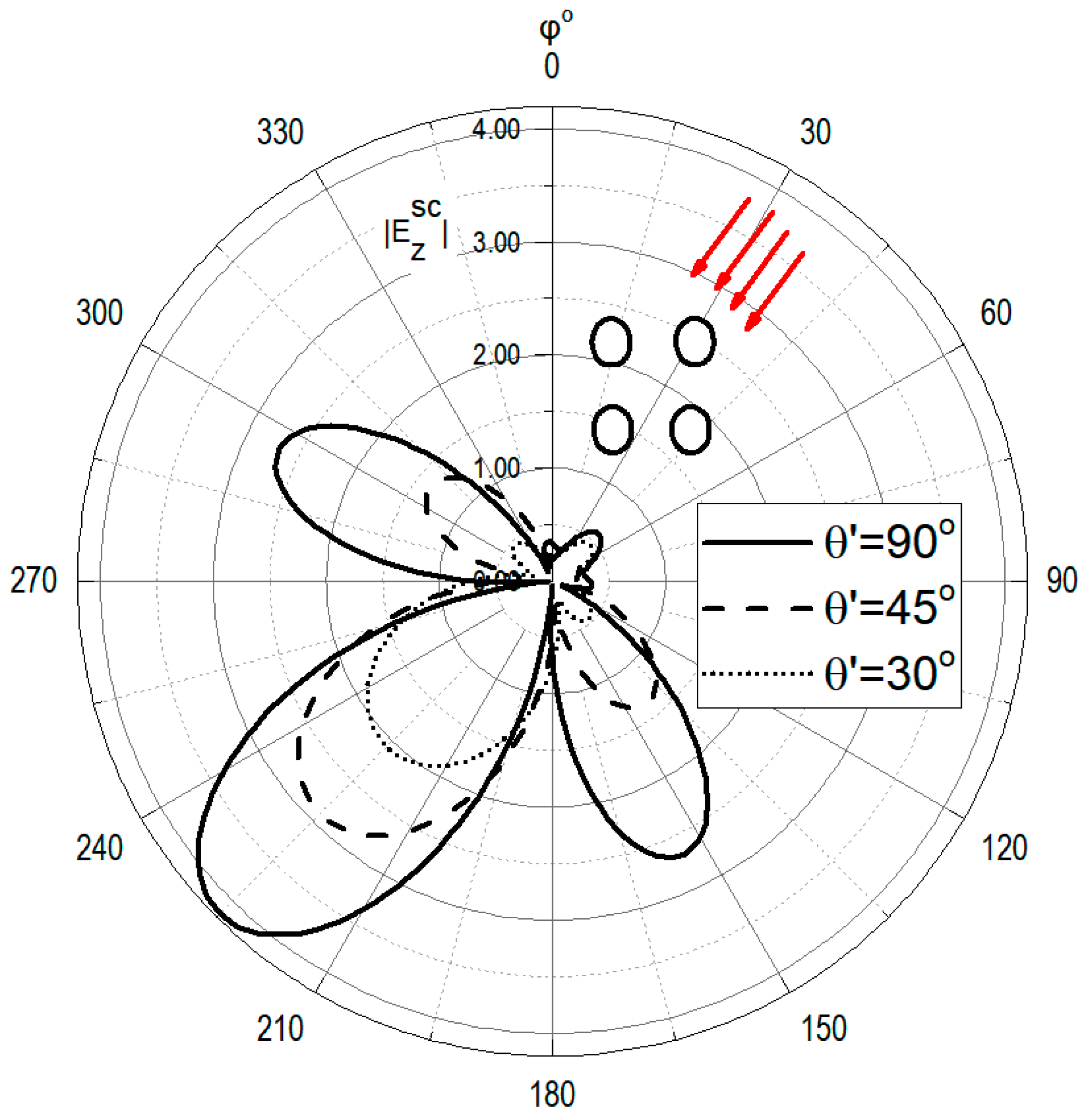
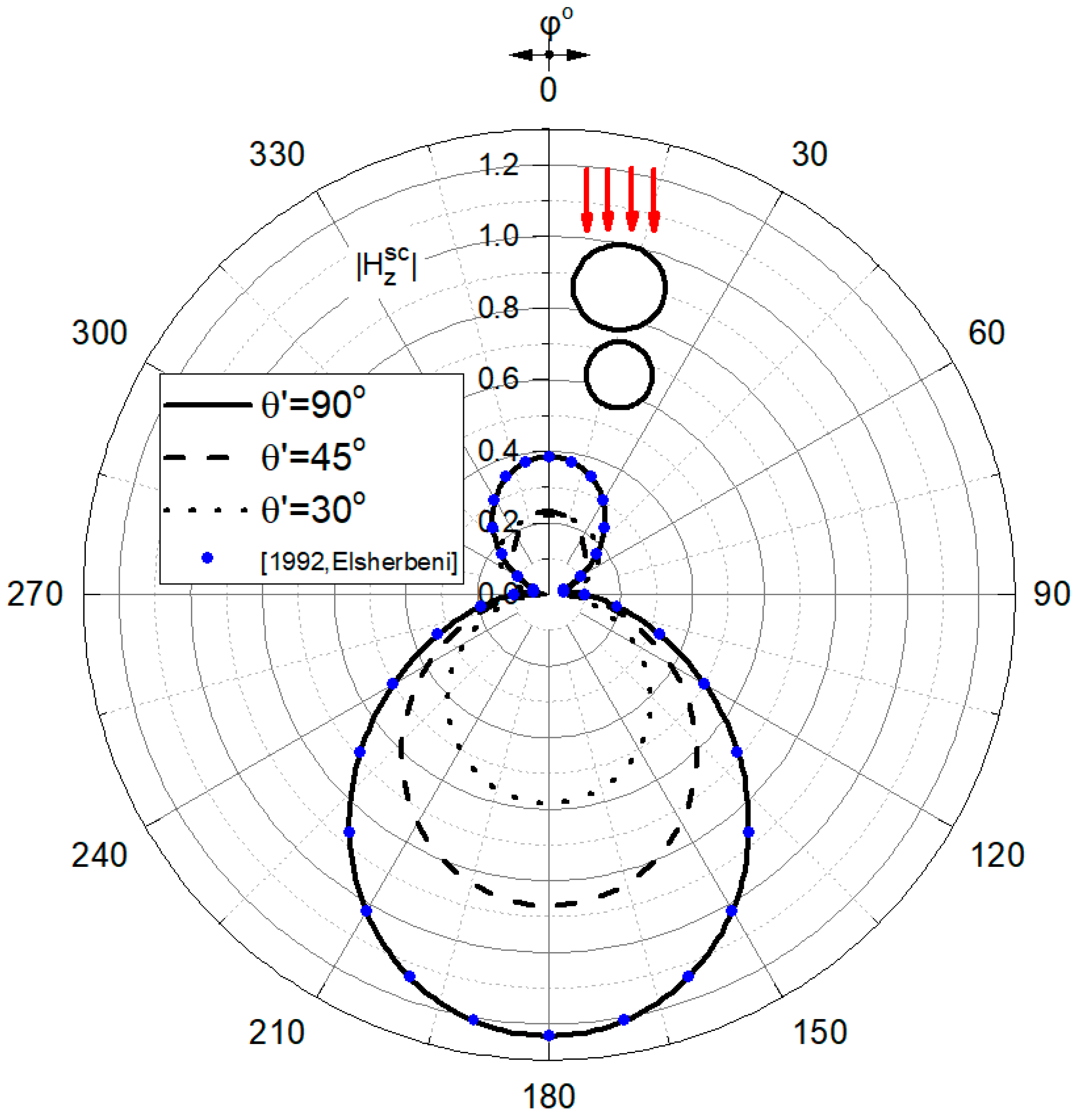
Figure 3 illustrates the scattered electric far-field polar pattern $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ of the structure shown in the inset, for ${\phi }^{\prime }={90}^{°}$ and for several values of ${\theta }^{\prime }$. The structure is stimulated by an E-polarized plane wave which is obliquely incident. In Figure 4, we present the scattered magnetic far-field polar pattern $|{\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ of the inset structure, in the excitation case of an obliquely incident H-polarized plane wave with ${\phi }^{\prime }=0^{°}$ and ${\theta }^{\prime }=30^{°}, {45}^{°}, {90}^{°}$. The occasion of normal incidence, i.e., ${\theta }^{\prime }={90}^{°}$, is included in both figures for reference.

Moreover, exhaustive comparisons with previously published results that correspond to much simpler, marginal cases of the complex geometric structure treated herein were performed. Two examples are provided in Figure 3 and Figure 4 by plotting the corresponding numerical results, for normal incidence, given in Figure 5 of [11] and Figure 3 of [27], respectively, as indicated in the insets. It is evident that our results coincide with the published ones. Other results, not presented herein for the sake of brevity, indicate that our general solution is capable of reproducing Figures 3–10 of [22]; all these plots refer to normal incidence and the corresponding configurations fall within the geometry illustrated in Figure 1.

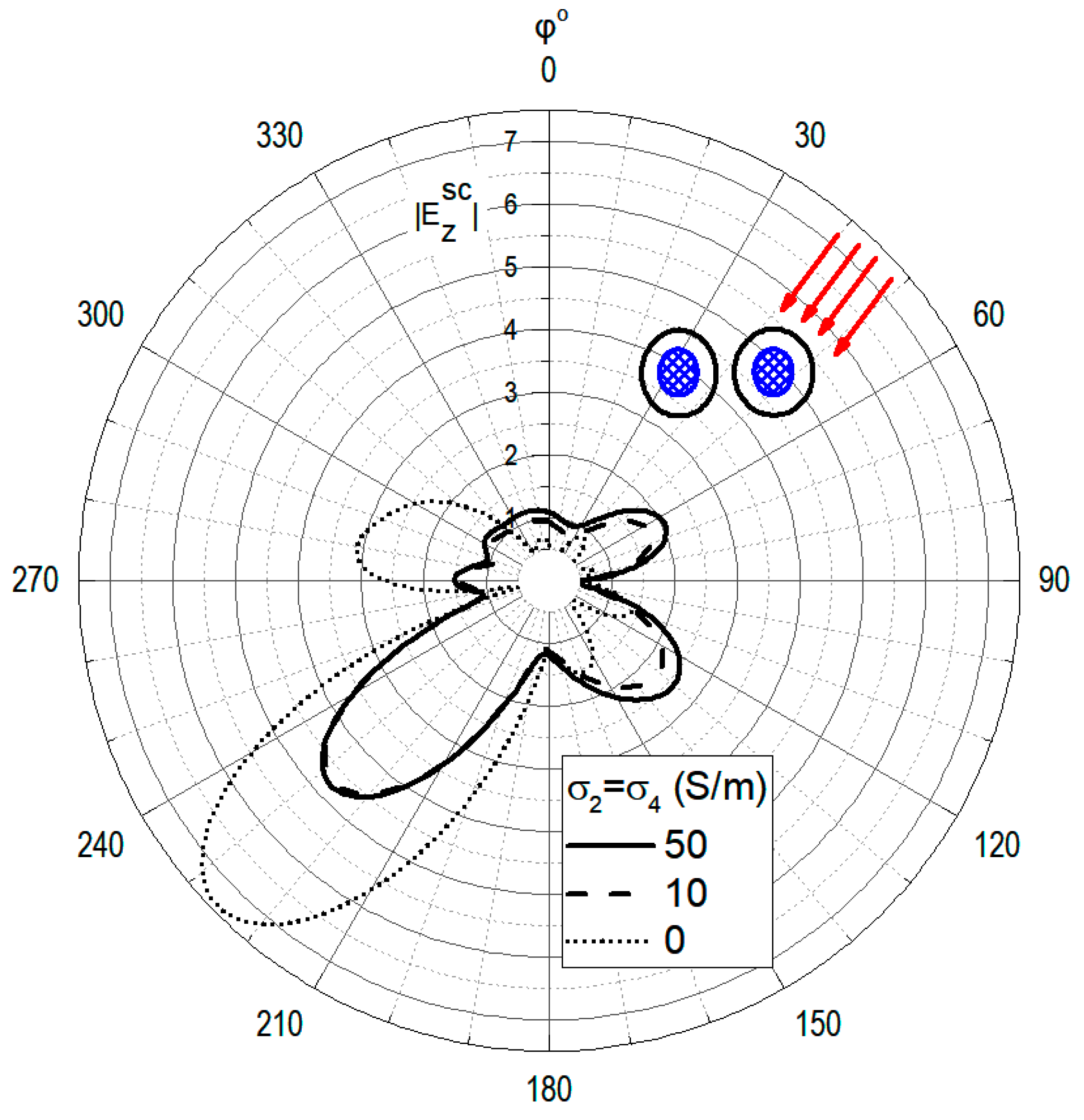
The scattered far-field pattern $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ of two stratified cylinders for oblique incidence (as shown in the inset) is depicted in Figure 5 and Figure 6. The former is produced by setting ${\theta }^{\prime }={60}^{°}$ and ${\phi }^{\prime }={45}^{°}$, while ${\theta }^{\prime }={70}^{°}$ and ${\phi }^{\prime }={45}^{°}$ were assumed for the latter. Several values of the dielectric constant of the cladding regions, with ${\mathsf{\epsilon }}_2={\mathsf{\epsilon }}_4$, are tested in Figure 5, whereas the effect of the electric conductivity of the cladding regions $({\mathsf{\sigma }}_2={\mathsf{\sigma }}_4)$ on $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ is investigated through Figure 6. The main remark to be made about Figure 5 and Figure 6 is the presence of several lobes, with the main one at ${\phi }_1\approx {229}^{°}$ for the case ${\mathsf{\epsilon }}_2={\mathsf{\epsilon }}_4\ne {\mathsf{\epsilon }}_0$ (Figure 5) or at ${\phi }_1\approx {227}^{°}$ for the case ${\mathsf{\sigma }}_2={\mathsf{\sigma }}_4$ (Figure 6). Figure 5 and Figure 6 suggest that the position of the main lobe does not depend strongly on the electrical characteristics of the cladding regions. Moreover, it should be noted that a further increase in the cladding regions’ conductivities ${\mathsf{\sigma }}_2$ and ${\mathsf{\sigma }}_4$ has practically no effect on the solid curve field pattern that corresponds to ${\mathsf{\sigma }}_2={\mathsf{\sigma }}_4=50 \mathrm{S}/\mathrm{m}$.

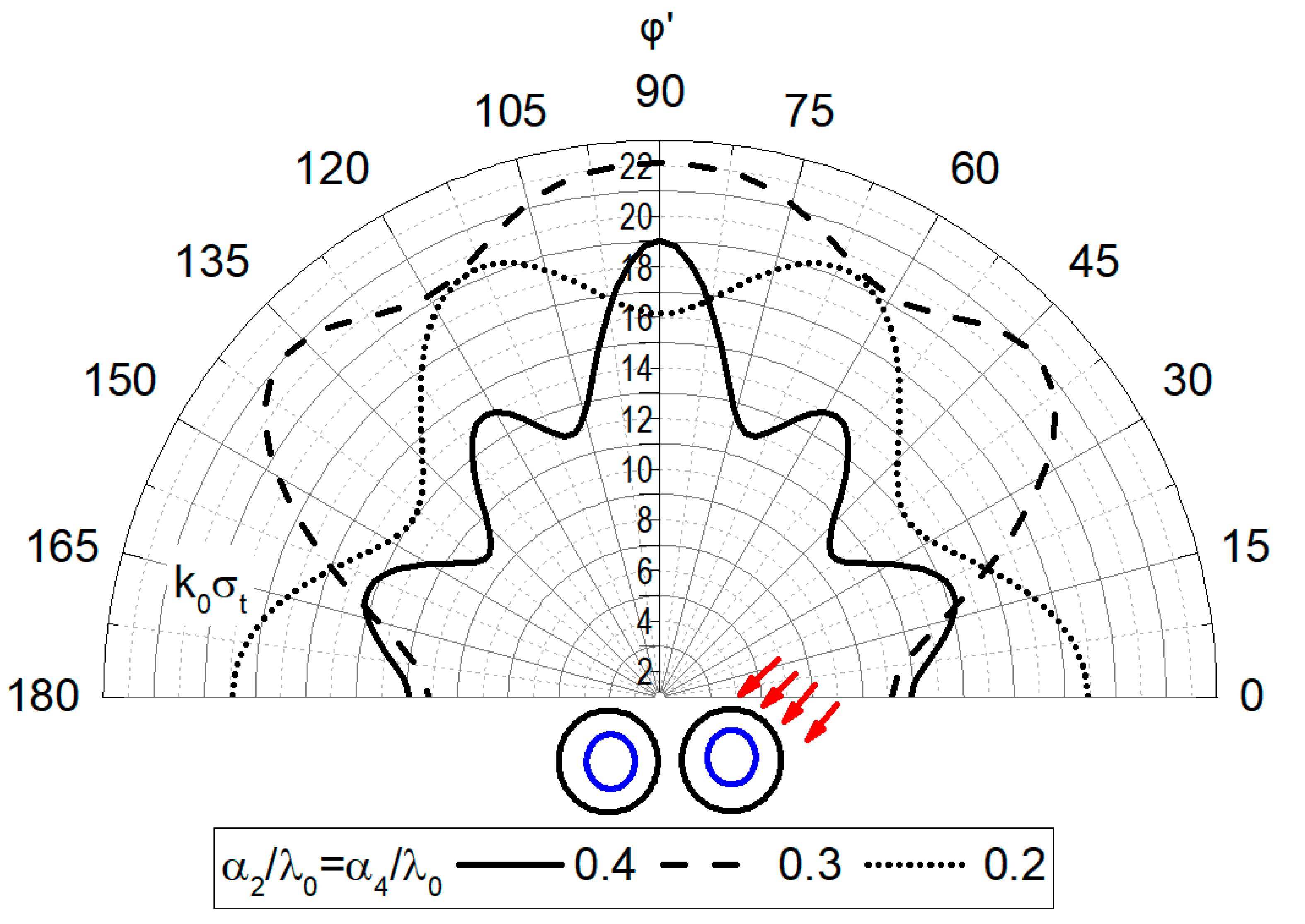
Figure 7 and Figure 8 present the total scattering cross section normalized to the free space wavenumber (${\mathrm{k}}_0{\mathsf{\sigma }}_{\mathrm{t}}$) versus the incidence angle ${\phi }^{\prime }$ for the configuration shown in the insets; several values for the off-axis distance, ${\mathrm{D}}_{23}$ (Figure 7), or the cladding regions’ radii, ${\mathsf{\alpha }}_2$ and ${\mathsf{\alpha }}_4$ (Figure 8), were considered. Due to the symmetrical scatterer geometry, the ${\mathrm{k}}_0{\mathsf{\sigma }}_{\mathrm{t}}$ values are also symmetrical about the vertical xz-plane (${\phi }^{\prime }={90}^{°}$). Figure 7 indicates that ${\mathsf{\sigma }}_t$ is strongly dependent on ${\mathrm{D}}_{23}$, provided that ${54}^{°}<{\mathsf{\phi }}^{\prime }<{126}^{°}$, while the dependence of the total scattering cross section ${\mathsf{\sigma }}_{\mathrm{t}}$ on the cylinders’ radius (size) is rather strong for most values for the angle ${\phi }^{\prime }$. Thus, changing ${\mathrm{D}}_{23}$ and/or ${\mathsf{\alpha }}_2$,${\mathsf{\alpha }}_4$ properly may offer the feasibility to handle the scattering cross section of the cylindrical structure.

The scattered far-field patterns $|{\mathrm{E}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ and $|{\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ are depicted in Figure 9 and Figure 10, respectively, for the dielectric cylinders’ quadruplet shown in the insets. E-polarization and several values of ${\theta }^{\prime }$, for ${\phi }^{\prime }={45}^{°}$, are considered in Figure 9, while H-polarization and several values of ${\phi }^{\prime }$, for ${\theta }^{\prime }={90}^{°}$, are assumed in Figure 10. On the one hand, as regards the patterns of the electric field intensity, Figure 9 suggests that the main lobe remains at $\mathsf{\phi }={225}^{°}$ regardless of the angle ${\theta }^{\prime }$. On the other hand, as far as the patterns of $|{\mathrm{H}}_{\mathrm{z}}^{\mathrm{s}\mathrm{c}}({\phi }_1)|$ are concerned (Figure 10), no trend is observed regarding the lobes; the formation of the latter depends strongly on the angle ${\phi }^{\prime }$.

5. Conclusions

The problem of electromagnetic scattering by a group of stratified lossy dielectric cylinders enclosed in a cylindrical core which is surrounded by a boundless dielectric space was treated herein in the uttermost general instance of an arbitrarily polarized and obliquely incident plane wave. A boundary-value approach was employed, and the Bessel/Hankel function’s translational addition theorem was applied, in order to form a group of linear equations for the unknown expansion coefficients of the scattered electromagnetic field intensity. The resulting solution may be considered as semi-analytical and exact since the only approximation used is the truncation of the multipole expansions. The validation of the developed computer codes was performed by checking the convergence of the solution and by carrying out extended comparisons with available published results, which were all successful. Plots of the total scattering cross section and the scattered far-field of various geometric configurations manifested how the structure and the material of the composite cylindrical model are imprinted on scattering.