Subspace Pseudointensity Vectors Approach for DoA Estimation Using Spherical Antenna Array in the Presence of Unknown Mutual Coupling

Featured Application

To obtain an antenna array with isotropic radiation, a spherical antenna array (SAA) is the correct array configuration. The knowledge of the direction-of-arrival (DoA) of an incoming signal by the receiving antenna is used to localize the locations of analogous sources. It improves the adaptive beamforming of the receiving radiation pattern to enhance system sensitivity towards the required signal directions and reduce unwanted interferences. Therefore, DoA estimation using SAA is an important task and basic challenge in signal processing, such as source identification and separation, spatial filtering etc. It has industrial applications in spacecraft, military surveillance, astronomy, radar, and vehicular technology.

Abstract

Spherical antenna array (SAA) exhibits the ability to receive electromagnetic (EM) waves with the same signal strength, regardless of the direction-of-arrival (DoA), angle-of-arrival, and polarization. Hence, estimating the DoA of EM signals that impinge on SAA in the presence of mutual coupling requires research consideration. In this paper, a subspace pseudointensity vectors technique is proposed for DoA estimation using SAA with unknown mutual coupling. DoA estimation using an intensity vector technique is appealing due to its computational efficiency, particularly for SAAs. Two intensity vector-based techniques that operate with spherical harmonic decomposition (SHD) of an EM wave obtained from SAA are presented. The first technique employed pseudointensity vectors (PV) and operates quite well under EM conditions when one source is in operation each time, while the second technique employed subspace pseudointensity vectors (SPV) and operates under EM conditions when multi-sources and multiple reflection cause more challenging problems. The degree of correctness in the estimation of the DoA via the PVs and SPVs is measured using baseline methods in the literature via simulations, adding noise to stationary, single-source and multi-source methods. In addition, incorporating mutual coupling effects, data from experiments, which are the generally acceptable ground truth when examining any procedure, are further used to illustrate the robustness and efficiency of the proposed techniques. The results are sufficiently inspiring for the practical deployment of the proposed techniques.

1. Introduction

Estimation of the direction-of-arrival (DoA) is an important and basic challenge in signal processing, such as source separation, spatial filtering, etc. It has applications in mobile communications systems, military surveillance, sonar, radar, and vehicular technology. The knowledge of the DoA of an incoming signal by the receiving antenna is employed to localize the locations of the analogous sources. It improves the adaptive beamforming of the receiving radiation pattern for system sensitivity enhancement in the required directions of signals and reduces unwanted interference. DoAs ensure that antennas provide the best beam in the direction of the required users, and null in the directions of interferences, consequently improving the fidelity of the base stations and mobile stations [1,2,3,4,5,6]. Hence, estimating the DoA of electromagnetic (EM) waves that impinge antenna arrays is important for effective mobile communication.

Spherical antenna array (SAA) (as shown in Figure 1) is an important configuration when obtaining an array with isotropic characteristics [1,3]. Estimating both the horizontal and vertical angle of arrivals requires a 3D antenna array configuration. An antenna array structure that samples EM waves in such a way that they can be described and defined in spherical harmonics (SH) domain is of interest, because this description makes it possible to analyze EM waves at the same resolution in all directions using approaches that are not dependent on the particular geometry of the array [1,7]. The SAA has applications in aerospace, spacecraft, and vehicular technology, which are critical in the military and other industrial areas.

Different DoA estimation approaches for use in the SH domain have been reported in the literature [3,4,5,6,8,9,10,11,12,13,14,15,16,17]. Some of the most popular approaches include the multiple signal classification (MUSIC) approach [3], estimation of signal parameters through rotational invariance technique (ESPRIT) technique [5,6,7,8,9], beamforming, and the maximum likelihood (ML) methods [4,15]. These methods have been considered and used for arrays of antenna with arbitrary structures and generate accurate DoA estimates [18,19]. Other methods include the MUSIC group delay [4], the steered response power with phase transform (SRP-PHAT) methods [20], generalized cross-correlation (GCC) method [21], adaptive eigenvalue decomposition method [22], 1-D MUSIC [23] approach, and order aware algorithm [24]. MUSIC has been considered for spherical structures in the near-field [19,22,23,24]; this is named MUSIC-SH. As a result of MUSIC-SH’s sensitivity to distortions in the multipath scenario, Nakamura [25] proposed an alternative method called direct path dominance (DPD). In the near-field, the mode strength is a function of source range, which is not known a priori. Therefore, DPD can only be measured in the time dimension, and for this reason, the MUSIC-SH-DPD uses higher frames [25]. When applying the near-field frequency smoothing, source normalization that depends on this range is required. Hence, the remaining DoA estimation technique, decomposed into the spherical domain, is the minimum variance distortionless response [26]. Other parameter estimate methods can be found in the literature, such as the SAGE algorithm [27] and Butler matrices [28].

Different DoA estimation approaches to planar and linear array configurations have been presented earlier. Due to the merits of SAA, various approaches that employed SAA are under consideration at present. For example, MUSIC and ESPRIT have been analyzed using spherical harmonics [22,23,24], and a comprehensive comparison is presented in [19]. These approaches have been applied to the localization of reflected signals, but not for DoAs sources.

There are other different methods for the estimation of DoA in the spherical realm that employed sources’ directional sparsity according to the literature [29,30,31,32]. For instance, Epain et al. [29] reported an independent component analysis of signals in the spherical realm and the DoAs were estimated via comparison between the unmixing matrix columns and signal steering vectors in each direction. Furthermore, the intensity-dependent methods of the DoA estimation [33,34,35,36] are different from the previously discussed methods, because with the direct computation of energy flow, the computation of spatial cost function is not needed. As such, there is a potential and significant saving in terms of computation. In specific directions, the intensity component was computed via two intensity probes [37]. The first probe operates using the velocity of particle approximation, using the differences that exist between the two firmly distanced omnidirectional pressure elements, and the second probe directly deals with the velocity of the particle [38]. The former technique is common but severely affected by noise and phase mismatch. The array with intensity probes generates an intensity vector in two or three dimensions in which the DoA is estimated [39,40].

Methods that can be used for the estimation of the DoA with SAA were developed in [33], where many elements were employed for the transformation of signals in the spherical domain in which the velocity of the particle was approximated. The resulting vectors were named pseudointensity vectors (PVs). The first set of results shows the efficiency of the DoA estimation technique with a single source under a high-SNR scenario. Furthermore, the DoA estimation with multiple sources was computed using PVs k-means clustering in [34]. The formulation review and function of PVs are presented in [33]. For an understanding of the basics and some mathematical formulations, readers are referred to References [33,41]. Compared to the previous works in the literature, the main innovation and contributions in this work are given as follows. We present the formulation of PV from an SH domain signal representation in Cartesian and propose an extended analysis of PVs in practical scenarios. Furthermore, a subspace pseudointensity vector (SPV) is proposed, which shows a higher level of robustness to noise and is more computationally efficient than PV. The main innovation of this work compared to [41] is that the PV methods are extended to a spherical antenna array, supported by measurements from experiments in EM vis-à-vis an SAA, which is a generally acceptable basis of testing and evaluating any procedure.

The remaining parts of this article are structured as follows. In Section 2, the pseudointensity vector is mathematically formulated; the signal intensity and pseudointensity are briefly reviewed, and the PV system model and the subspace PV are mathematically presented. Section 3 presents the numerical experiments, results, and discussion. An estimation of DoA from PVs and SPVs, comparison of the results with baseline approaches using simulation and experimental data, and computational complexity analysis are given in Section 3. Section 4 concludes the article and suggests some future research directions.

2. Mathematical Formulation of Pseudointensity Vector

The PV technique has been proposed to be an approximate of the active intensity vector [33]. In this section, a brief review of the PV is presented. We equally derived the equivalent vector from the SH of signal representation. Finally, the SPV is derived.

2.1. Overview of Signal Intensity and Pseudointensity

The intensity of active vector can be described as a magnitude of average direction and time of total energy flow, and can be expressed as [35]

$$\mathit{I}\left(k\right)=\frac{1}{2}\Re \left\{p{\left(k\right)}^{*}\mathit{u}\left(k\right)\right\},$$

(1)

where $p\left(k\right)$ represents omnidirectional pressure; $\mathit{u}\left(k\right)={\left[u_x\left(k\right) u_y\left(k\right) u_z\left(k\right)\right]}^T$ is the particle velocity vector in the Cartesian direction; $\Re \left\{·\right\}$ denotes the actual operator. $\mathit{u}\left(k\right)$ can be used to estimate the DoA because energy flows in the wave propagation direction. The particle velocity vector of plane wave associated with DoA $\left(\theta ,\varphi \right)$ is [33]

$$\mathit{u}\left(k\right)=-\frac{p\left(k\right)}{{\rho }_{0}c}\left[\begin{array}{c}sin\theta cos\varphi \\ sin\theta sin\varphi \\ cos\theta \end{array}\right]$$

(2)

where c and ${\rho }_0$ are speed of light and ambient density, respectively. The components of $\mathit{u}\left(k\right)$ exhibit dipole’s directivity patterns, which are in alignment with the Cartesian axes. The resultant vector faces the opposite direction from the estimation direction.

The beamformer that has a dipole directivity pattern is extracted from a first-order coefficient of spherical harmonic as

$$D\left(k,\phi ,{\mathit{a}}_{lm}\left(k\right)\right)={\displaystyle \sum }_{m=-1}^1{Y}_1^m\left(\phi \right)a_{1\left(m\right)}\left(k\right)$$

(3)

With $\phi$ representing the direction of steering. Hence, by approximating Equation (1) using the coefficients of the plane wave density function in the spherical domain, the PV is expressed as [35]

$$\mathit{I}\left(k\right)=\frac{1}{2}\Re \left\{{\mathit{a}}_{00}{\left(k\right)}^{*}\left[\begin{array}{c}D\left(k,{\phi }_{-x},{\mathit{a}}_{lm}\left(k\right)\right)\\ D\left(k,{\phi }_{-y},{\mathit{a}}_{lm}\left(k\right)\right)\\ D\left(k,{\phi }_{-z},a_{lm}\left(k\right)\right)\end{array}\right]\right\}$$

(4)

with ${\phi }_{-x}=\left(0.5\pi ,\pi \right), {\phi }_{-y}=\left(0.5\pi ,-0.5\pi \right)$ and ${\phi }_{-z}=\left(\pi ,0\right).$

2.2. PV System Model

The plane wave decomposition (PWD) of an n-th wave gives $a_{lm}^{\left(n\right)}\left(k\right)={\left[Y_l^m\left({\mathsf{\Psi }}_n\right)\right]}^{*}{s}_n\left(k\right)$ [41]. Describing or transforming the first-order coefficients in the Cartesian direction results in

$$\begin{gathered} a_{1\left(-1\right)}^{\left(n\right)}\left(k\right)=s_n\left(k\right)\sqrt{3/8\pi }\left(x_n+i{y}_n\right) \\ {a}_{10}^{\left(n\right)}\left(k\right)=s_n\left(k\right)\sqrt{3/4\pi }{z}_n \\ {a}_{11}^{\left(n\right)}\left(k\right)=s_n\left(k\right)\sqrt{3/8\pi }\left(-x_n+i{y}_n\right) \end{gathered}$$

(5)

with the SH of Equation (5) being computed on the unit sphere. Then, Equation (5) can be rearranged as

$$\begin{gathered} s_n\left(k\right)x_n=\sqrt{8\pi /3} \frac{1}{2}\left(a_{1\left(-1\right)}^{\left(n\right)}\left(k\right)-a_{11}^{\left(n\right)}\left(k\right)\right) \\ {s}_n\left(k\right)y_n=\sqrt{8\pi /3} \frac{1}{2i}\left(a_{1\left(-1\right)}^{\left(n\right)}\left(k\right)-a_{11}^{\left(n\right)}\left(k\right)\right) \\ {s}_n\left(k\right)z_n=\sqrt{8\pi /3} \frac{1}{\sqrt{2}}{a}_{10}^{\left(n\right)}\left(k\right), \end{gathered}$$

(6)

This could represent the weighted sum of the first-order coefficients of the PWD. The weight that corresponds to $a_{1\left(m\right)}^{\left(n\right)}\left(k\right)$ shares a proportional relationship with the first order, and the SH of degree m is calculated in the necessary axial direction as

$$\begin{gathered} s_n\left(k\right){\xi }_n=\frac{4\pi }{3}{\displaystyle \sum }_{m=-1}^1{Y}_1^m\left({\phi }_{\xi }\right)a_{1\left(m\right)}^{\left(n\right)}\left(k\right) \\ =\frac{4\pi }{3}D\left(k, {\phi }_{\xi },{\mathit{a}}_{lm}^{\left(n\right)}\left(k\right)\right) \end{gathered}$$

(7)

Note that Equation (3) was considered when obtaining Equation (7), $\xi \in \left\{x,y,z\right\},$ ${\phi }_x=\left(0.5\pi ,0\right), {\phi }_y=\left(0.5\pi ,0.5\pi \right)$ and ${\phi }_z=\left(0, 0\right)$. Obtaining a vector that points to the n-th DoA, $a_{00}^{\left(n\right)}\left(k\right)=\sqrt{\frac{1}{4\pi }}{s}_n\left(k\right)$, and computing Equation (2) for $\xi \in \left\{x,y,z\right\}$, gives

$$\tilde{\mathit{I}}\left(k\right)=\frac{4\pi \sqrt{4\pi }}{3}\Re \left\{a_{00}^{\left(n\right)}{\left(k\right)}^{*}\left[\begin{array}{c}D\left(k,{\phi }_x,{\mathit{a}}_{lm}\left(k\right)\right)\\ D\left(k,{\phi }_y,{\mathit{a}}_{lm}\left(k\right)\right)\\ D\left(k,{\phi }_z,{\mathit{a}}_{lm}\left(k\right)\right)\end{array}\right]\right\}$$

(8)

$$=\Re \left\{{\left|s_n\left(k\right)\right|}^2{x}_n\right\}$$

(9)

for a plane wave in ideal environments, the actual operator is intrinsically real, but the real operator is required for practical scenarios. The PV direction in the spherical domain is computed via Equation (10) and unit vector $\tilde{\mathit{I}}\left(k\right)/\Vert \tilde{\mathit{I}}\left(k\right)\Vert$, where ‖$·$‖ is $l_2-norm.$

$${\theta }_n=\arccos \left(z_n\right), {\varphi }_n=arctan2\left(y_n/x_n\right)$$

(10)

where $arctan2$ represents the arctangent function that is mapped to an acceptable quadrant based on the nature of $x_n$ and $y_n$.

The formulation of Equation (8) is similar to that of Equation (2), except that $\tilde{\mathit{I}}\left(k\right)$ and $\mathit{I}\left(k\right)$ face opposite directions because of the dipole steering. $\tilde{\mathit{I}}\left(k\right)$ is then considered as the PV with its orientation towards the DoA.

2.3. Subspace PV

The concept of PV is extended to the SPV to take the advantage of SHs a higher order, and provide a more reliable and accurate estimate of DoA with multiple sources. The covariance of ${\mathit{a}}_{lm}$ is [15]

$$\begin{gathered} {\mathit{R}}_{{\mathit{a}}_{lm}}=\mathrm{E}\left\{{\mathit{a}}_{lm}{\mathit{a}}_{lm}{}^H\right\} \\ ={\mathit{Y}}^H\left(\Psi \right){\mathit{R}}_s\mathit{Y}\left(\Psi \right) \end{gathered}$$

(11)

with ${\mathit{R}}_s=\left\{\mathit{s}{\mathit{s}}^H\right\}$. The singular value decomposition (SVD) gives

$${\mathit{R}}_{{\mathit{a}}_{lm}}=\mathit{U}\sum {\mathit{U}}^H=\left[{\mathit{U}}_s{\mathit{U}}_n\right][\begin{array}{cc}{\sum }_s& 0\\ 0& {\sum }_n\end{array}] [\begin{array}{c}{\mathit{U}}_s^H\\ {\mathit{U}}_n^H\end{array}]$$

(12)

U denotes unitary matrix, $\sum$ represents the diagonal matrix housing the singular values of ${\mathit{R}}_{{\mathit{a}}_{lm}}$, while ${\mathit{U}}_s$ and ${\mathit{U}}_n$ are the traditional partitioning of signal and noise subspace, respectively [42]. The plane wave ${\mathit{U}}_s={\left[{\widehat{a}}_{00}{\widehat{a}}_{1\left(-1\right)}{\widehat{a}}_{10}{\widehat{a}}_{11}\dots {\widehat{a}}_{LL}\right]}^T$ is a column vector, corresponding to the steering vector of plane wave DoA, $y\left({\mathsf{\Psi }}_n\right).$ Obtaining a vector pointing to the source, the SPV approach applies PV approach to a one-dimensional (1D) EM wave subspace, as follows:

$${\tilde{\mathit{I}}}_{\mathit{s}\mathit{s}}=\frac{4\pi \sqrt{4\pi }}{3}\Re \left\{{\widehat{a}}_{00}^{*}\left[\begin{array}{c}D\left(k,{\phi }_x,{\mathit{U}}_s\right)\\ D\left(k,{\phi }_y,{\mathit{U}}_s\right)\\ D\left(k,{\phi }_z,{\mathit{U}}_s\right)\end{array}\right]\right\}$$

(13)

Equation (13) is a function of 0 and first-order components of ${\mathit{U}}_s$, through Equations (11) and (12); their figure is a function of a higher-order SH of ${\mathit{a}}_{lm}$. As in the PV approach, the advantage of SPV is that the direction can be directly obtained for all TF-regions, i.e., there is no need to calculate the possible directions.

3. Numerical Experiment and Discussion

In this section, the proposed DoA methods are analyzed and compared with the PWD-SRP [8,41] and DPD-MUSIC [15,42] baseline approaches from the literature in a simulated environment. The methods were also compared using measured data from the experiment, which is a generally acceptable grounds to evaluate any method.

At first, an SAA of radius, $r=1.8 \mathrm{cm}$, and 32 elements working at 8.4 GHz (as shown in Figure 1) that was distributed uniformly on a rigid sphere was used for the simulations, as in [3,4,43,44]. The distance between two repeated samples in the uniform sampling scheme remained constant. The uniform sampling scheme led to a reduction in platonic solids. The phenomenon appeared for a particular number of sensors [44]. Four (4) was the highest order of the SAA. About 600 independent Monte Carlo simulations were performed using a 2019b version of matlab software. We employed a search step of 0.2⁰ for DPD-MUSIC, PWD-SRP, and the developed PV, and SPV methods. Two iterations were utilized during the simulations. To avoid aliasing problems, we ensured that kr was less than the order N. Furthermore, narrowband amplitude modulation (AM) signals in the far field were utilized in all the simulation scenarios.

The discrete time signals were transformed into the short-time Fourier transform (STFT) domain via a 77% overlapping Hamming window. A stacked vector of signals can be formulated as $\mathrm{x}\left(\varpi ,\mathcal{I}\right)$, where $\mathcal{I}$ and $\varpi$, respectively, denote the STFT frame index and frequency index. After a sample examination, we found that the frames from 6 to 10 ms provided the largest PVs concentration in the neighborhood of the actual DoA estimates compared to frames $\ge 18$ ms. This small frame provides a probability enhancement of the window disjoint orthogonality that is assumed [39] to be real. In addition, using additional TF-bins causes the directional distribution of the vectors to be highly regular.

The PVs, $\tilde{\mathit{I}}\left(\varpi ,\mathcal{I}\right)$ were computed using Equation (8), where k is substituted with the time–frequency index. The SPVs, ${\tilde{\mathit{I}}}_{\mathit{s}\mathit{s}}\left(\varpi ,\mathcal{I}\right)$ were computed by employing ${\widehat{\mathit{R}}}_{{\tilde{\mathrm{x}}}_{lm}}\left(\varpi ,\mathcal{I}\right)$ as a substitute for ${\mathit{R}}_{{\mathit{a}}_{lm}}$, which approximates in the surrounding frame index $\mathcal{I}$ and frequency index $\varpi$ by

$${\widehat{\mathit{R}}}_{{\tilde{\mathrm{x}}}_{lm}}\left(\varpi ,\mathcal{I}\right)=\frac{1}{J_{\varpi }{J}_{\mathcal{I}}}{\displaystyle \sum }_{j_{\varpi =0}}^{J_{\varpi }-1}{\displaystyle \sum }_{j_{\mathcal{I}}=0}^{J_{\mathcal{I}}-1}{\tilde{x}}_{lm}\left(\varpi +j_{\varpi }, \mathcal{I}+j_{\mathcal{I}}\right)\times x_{lm}^H\left(\varpi +j_{\varpi }, \mathcal{I}+j_{\mathcal{I}}\right)$$

(14)

where $J_{\mathcal{I}}$ and $J_{\varpi }$ represent timeframes and frequency bins, respectively, added in average form. Averaging over the frequency can be achieved, since the steering vector in the SH domain does not depend on frequency [10]. After a comprehensive study, calculating Equation (14) with a time of 35 ms and a 10 ms STFT frame length provided acceptable results, even though a frame length of 5–20 ms gave identical results. In each simulation, a source was positioned 1.5 m from SAA in one of the twenty-four directions provided by each combination of $\in \left\{{70}^0,{90}^0\right\},$ $\varphi \in \left\{0^0,{30}^0,\dots ,{330}^0\right\}$. For each test conditions, four EM signals were employed, providing 96 test samples per condition.

3.1. Estimating DoA from PVs and SPVs

Different DoA estimation methods have been developed in the literature that consider both single- [11,40] and multiple-source [34,36] scenarios. The direction of the computed PVs and SPVs concentrates around the DoAs of the dominating source. The methods estimate the maximums of the cost function that deals with the approximation of the vectors’ probability distribution over uniform directions of the 2D grid.

In practical applications, we initially calculated the dictionary as having a Gaussian kernel in the middle of each direction, spreading on a uniformly spaced $N_{K_{\theta }}\times N_{K_{\varphi }}$ grid. The element of both $j_{\theta }, j_{\varphi }$ can be expressed as

$${\mathit{K}}_{j_{\theta }, j_{\varphi }}\left(\phi \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{\angle {\left(\phi ,{\Psi }_{j_{\theta }, j_{\varphi }}\right)}^2}{2{\sigma }^2}\right)$$

(15)

where $\phi$ represents the look direction, $\sigma$ denotes Gaussian kernel’s standard deviation, $j_{\theta }\in \left\{0\dots N_{K_{\theta }}-1\right\}$ and $j_{\varphi }\in \left\{0\dots N_{K_{\varphi }}-1\right\}$ represents indices of elevation and azimuth of DoA ${\Psi }_{j_{\theta }, j_{\varphi }}=(j_{\theta }\pi /N_{K_{\theta }},j_{\varphi }2\pi /N_{K_{\varphi }}$, respectively. The dictionary (sparse) is computed using lesser entries than $\lambda$, and reaching down to zero, as

$${\widehat{\mathit{K}}}_{j_{\theta }, j_{\varphi }}\left(\phi \right)=\left\{\begin{array}{c}0 {\mathit{K}}_{j_{\theta }, j_{\varphi }}\left(\phi \right)<\lambda \\ {\mathit{K}}_{j_{\theta }, j_{\varphi }}\left(\phi \right) otherwise \end{array}\right.$$

(16)

Describing $\chi \left(\varpi ,\mathcal{I}\right)\triangleq \left({\theta }_{\chi },{\varphi }_{\chi }\right)$ as the direction associated with each region computed via PV or SPV, the dictionary indices are computed based on $J_{\theta }\left(\chi \left(\varpi ,\mathcal{I}\right)\right)=\lfloor {\theta }_{\chi }{N}_{K_{\varphi }}/\pi +0.5\rfloor$ and $J_{\varphi }\left(\chi \left(\varpi ,\mathcal{I}\right)\right)=\lfloor {\varphi }_{\chi }{N}_{K_{\varphi }}/0.5+2\pi \rfloor$, with $\lfloor ·\rfloor$, denoting the floor operator. Hence, the resulting function can be expressed as

$$\mathit{H}\left(\phi \right)={\displaystyle \sum }_{\left(\varpi ,\mathcal{I}\right)\in \mathcal{T}}{\widehat{\mathit{K}}}_{J_{\theta }(\chi \left(\varpi ,\mathcal{I}\right),J_{\varphi }(\chi \left(\varpi ,\mathcal{I}\right)}\left(\phi \right)$$

(17)

where $\mathcal{T}$ represents the TF-bins within the interval of observation. The directions-of-arrival were then computed from the corresponding directions towards the entire peaks in the H. The associated parameters of the developed techniques are $N_{K_{\varphi }}=175$ and $N_{K_{\theta }}=92$, $\sigma =5^0$, resolution is $2^0$ in both elevation and azimuth, and $\lambda =0.002/(\sigma \sqrt{2\pi )}$, which eliminates entries >15⁰ from the look direction.

For each approach under consideration (i.e., the PWD-SRP, SPV, DPD-MUSIC, and PV), the spatial form of cost function that corresponds to all the approaches was calculated over a 2D grid in elevation and azimuth. The number of sources was assumed to be known a priori. A single DoAs was obtained for each simulation, placing the observation interval at full length of the signal.

3.2. Results, Discussion, and Comparison with Baseline Approaches

In this subsection, the different simulation results of the two developed techniques are presented, discussed, and compared with two baseline techniques. In addition, we include the effects of the mutual coupling that exists between elements by using measured samples from experiment, which are the ultimate ground truth to test any method. Hence, the measured data from this experiment were further employed to evaluate the performance of the PV, SPV, PWD-SRP, and DPD-MUSIC.

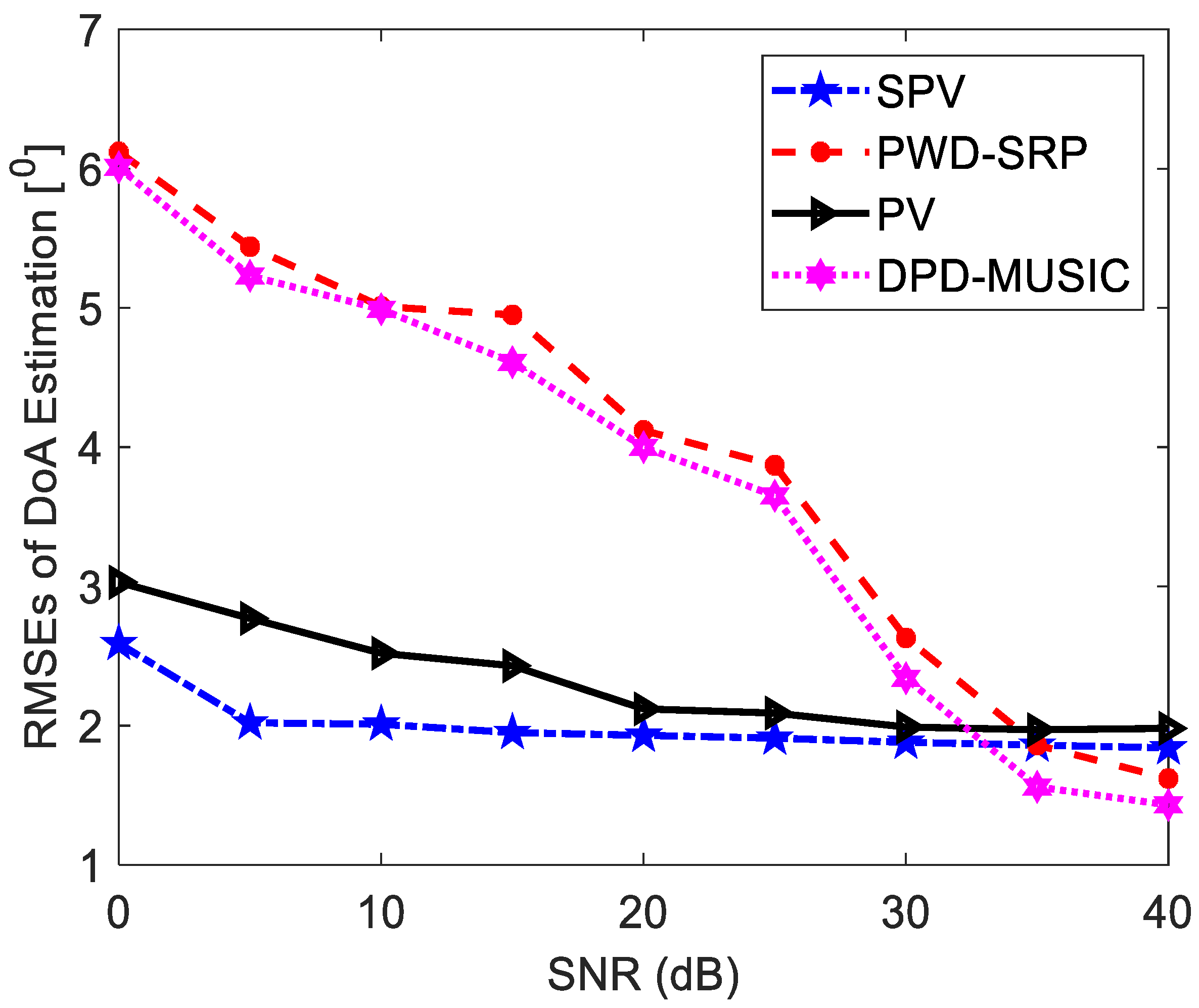
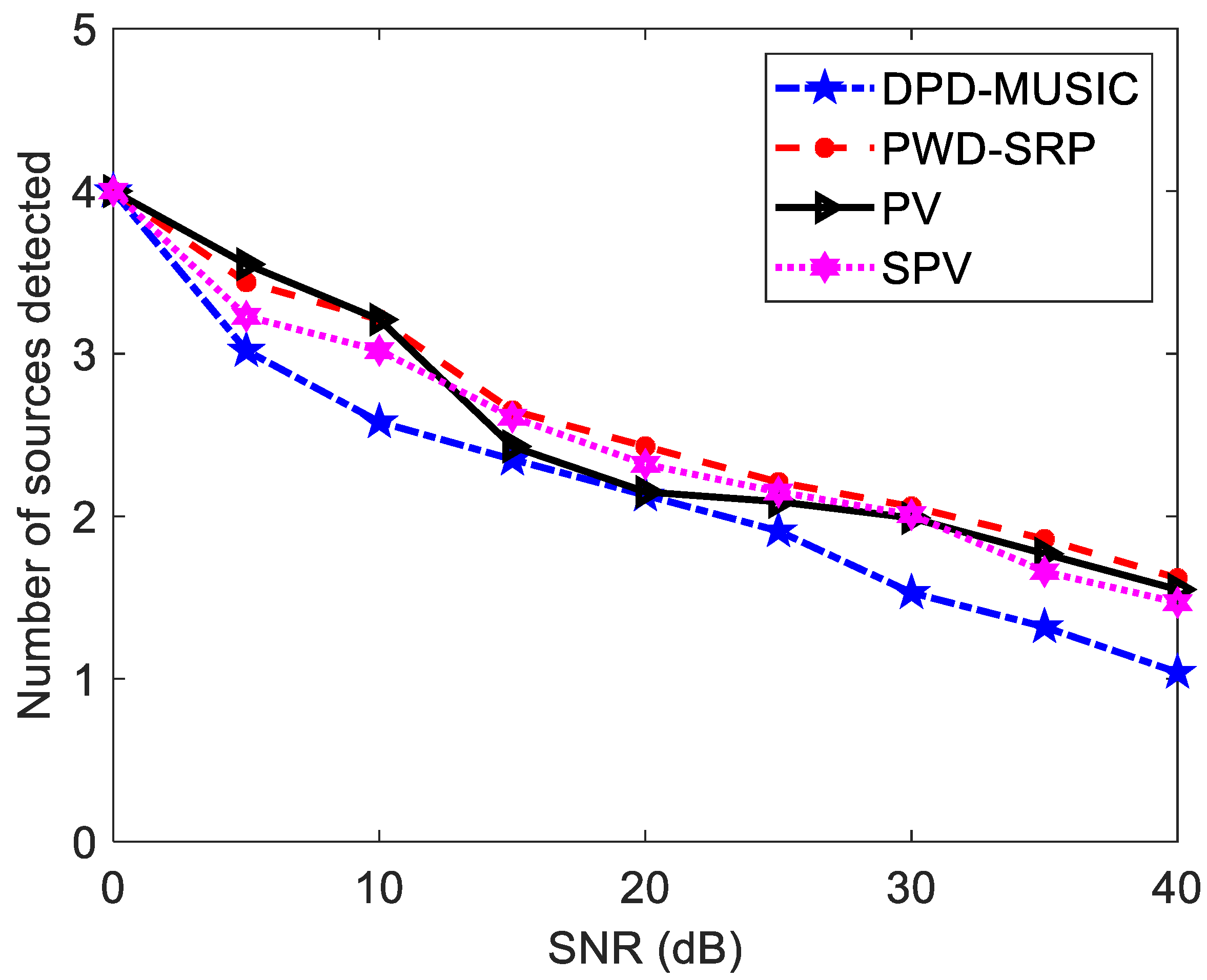
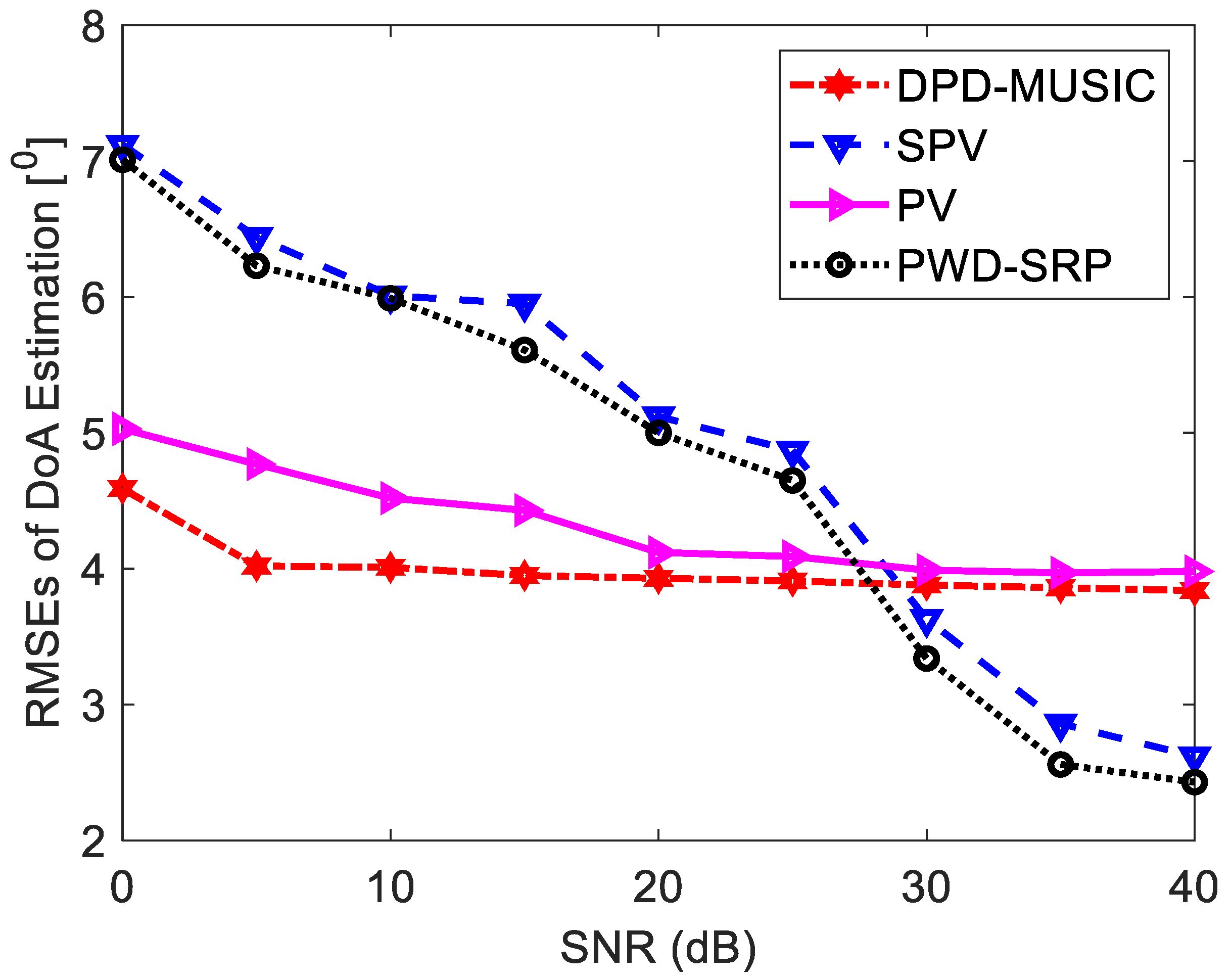
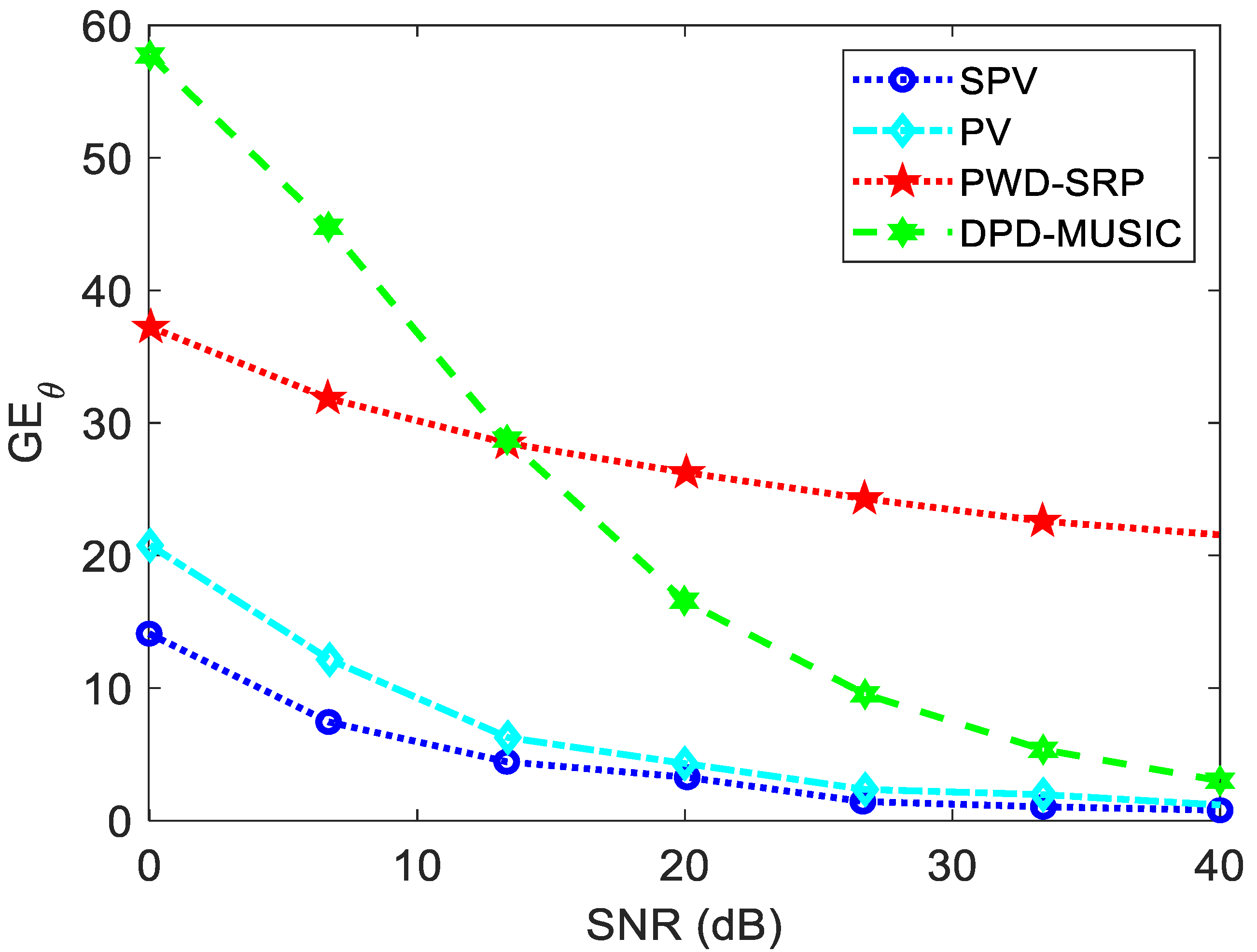
3.3. Simulation Results

For easy reading and comprehension, we considered two simulation cases. The first scenario is termed CASE ONE, where a single source is considered and positioned 1.5 m from the antenna array in one of the 24 different directions provided by possible combinations of $\in \left\{{70}^0,{90}^0\right\},$ $\varphi \in \left\{0^0,{30}^0,\dots ,{330}^0\right\}$. For all test conditions, four signals were employed, using 96 test samples for each condition. The second scenario is named CASE TWO, where 4 different sources were positioned 1.5 m away from the antenna array at a ${50}^0$ interval in the azimuth direction and switching between ${70}^0$ and ${90}^0$ elevation. Ensuring that the sources’ positions were not affecting the outputs, twelve possible orientations of sources were examined using the azimuths rotation of the four sources. For all orientations of the four sources, eight signal combinations were collected, i.e., 96 test samples in total for a condition.

We considered two uncorrelated EM signals impinging SAA from (40, 32) and (32, 64) degree sources, and at 10 dB SNR. The root mean square errors (RMSEs) decayed as snapshots increased, as depicted in Figure 2 using Cramer–Rao bound (CRB). This shows the accuracy level of the proposed PV and SPV methods as compared to the PWD-SRP and PWD-SRP baseline methods.

Using CASE ONE, the plots of angular RMSE in DoA estimation for all combinations of SNRs and algorithms are presented in Figure 3. Generally, the RMSE rises as the SNR increases, and the PWD-SRP exhibits a better performance than the DPD-MUSIC. The SPV performs better than the PV by about ${0.3}^0$, and this is more obvious in worse scenarios, where the SNR is 10 dB. This implies that, for DoA estimation with a single source, the PV approach is more efficient.

Figure 4 shows the number of detected sources versus SNR under CASE TWO. Both the PV and PWD-SRP methods are more affected by noise and interference, which impact the capacity of sources’ localization. The SPV method achieved a better performance than the PV, DPD-MUSIC and PWD-SRP methods, but the DPD-MUSIC is clearly not impacted by noise and other interferences.

Figure 5 shows the performance of each method using an RMSE plot versus SNR for trials where all four sources were found. The PV achieved a better performance than the SPV and PWD-SRP. Generally, the error in CASE TWO is significantly greater than that in CASE ONE (except for the scenario where the PWD-SRP is not perfect). The SPV method showed a reduced performance comapred to the PWD-SRP (heuristically viewed to be half of the error) and a more significant performance than PV. In the worse scenario, i.e., when the SNR was 10 dB, the RMSE was about ${3.7}^0$. When compared with the DPD-MUSIC, the rise in SPV error is between ${0.9}^0$ (at 25 dB SNR) and $2^0$ (40 dB).

In general, the results for CASE ONE and the computational benefits show, that for a single-source DoA estimation scenario, the PV method shows more robustness than the SPV, PWD-SRP and the DPD-MUSIC methods. Conversely, under CASE TWO, subspace method (i.e., the SPV) provides an improved performance when multiple sources are concurrently active. Considering TF-regions and noise subspace with one dominating source, the DPD-MUSIC exhibits a better degree of correctness than the SPV. At dense resolutions, since the SPV has a lower computational cost than the DPD-MUSIC, it is more appropriate for the DoA estimation under a scenario that involves multiple sources.

3.4. Experimental Results

Moreover, due to the current and future electronic systems demand, the distance between elements in an array becomes smaller, leading to a stronger mutual coupling effect causing unacceptable or bad impedance-matching and radiation behavior [45]. Adding the impact of mutual coupling in this study, measured experiment samples, which is the trusted way of testing all approaches, were further employed by subjecting the PV, SPV, PWD-SRP, and DPD-MUSIC to experimental tests. The SAA was situated in the middle of an anechoic chamber, and sources were positioned at 74 DoAs, obtained from various combinations of different 18 azimuths and elevations. The selected azimuths ranged from $5^0$ to ${365}^0$ using a ${20}^0$ step size. Readers are referred to [6], where the data were originally published, for more details about the experimental setup or architecture using the SAA. A gross error (GE) analysis of performance was used to judge all algorithms. Figure 6 shows a performance comparison between the PV, SPV, PWD-SRP, and DPD-MUSIC. The SPV and PV have an improved performance compared to the DPD-MUSIC and PWD-SRP, even with the mutual coupling (MC) effect. Antenna arrays generally have different advantages, such as beamforming capacity and a high gain, which are used for various mobile communications, including controlled radiation pattern antenna for EM immunity to interference and military radar applications. However, the current trend in technology means that recent systems are smaller, meaning that there is a smaller space between elements in the array. This leads to a higher MC, poor radiation features, and impedance mismatch. This has a severe effect on antenna array signal processing [4,6]. Therefore, when estimating the DoA of signals vis-à-vis antenna array, PV and SPV are recommended as they are more robust to MC. Therefore, the PV and SPV are good candidates for DoA estimation, particularly in practical situations.

3.5. Computational Complexity Analysis

Here, based on run-time, we conducted a complexity analysis of the PV, SPV, PWD-SRP, and DPD-MUSIC. The processing of the implementation of all the methods was not parallel. Matlab software installed on a personal computer (core i7, Intel processor, 8th Generation, 16 GB RAM, 64-bits and 1T hard-drive) was used for the implementation and execution of the algorithms. Measured data were used to estimate the elapse time for all the methods. Note that both the DPD-MUSIC and PWD-SRP methods employ pre-calculated steering vectors, but the PV and SPV algorithms employ pre-calculated elements of the dictionary. The average elapse time comparison for grid resolution {${10}^0,5^0,2^0,1^0$} for varying N and DoA search grids is depicted in

Table 1. Elapsed run-time for each signal for the DoA estimation of the DoA search grid resolution at various snapshot numbers.

N	PV (s)	SPV (s)	PWD-SRP (s)	DPD-MUSIC (s)
10	0.018	0.024	0.153	0.161
50	0.201	0.254	0.311	0.323
75	0.281	0.291	0.374	0.393
100	0.632	0.643	0.773	0.787

. An increment in the DoA search grid resolution affects the PWD-SRP, and DPD-MUSIC, more than the proposed PV and SPV methods. The developed methods lead to a significant reduction in computational complexity. Hence, the PV and SPV exhibit reduced computational complexity and better performance.

4. Conclusions and Future Direction

In this paper, DoA estimation methods were proposed for a spherical antenna array with unknown mutual coupling. These two intensity-based methods (PV and SPV) were compared with baseline methods in the literature. The PV method was demonstrated to be more computationally efficient, and accurate up to $1^0$ across SNR (20–40 dB), and within $3^0$ in the most severe of the considered scenarios (SNR of 10 dB). The second method, SPV, employed frequency smoothing along with a spatial covariance matrix subspace decomposition. It is more robust to noise and interference than the PV. The SPV runs faster than the PWD-SRP and DPD-MUSIC, but is marginally less accurate. The SPV’s good performance was demonstrated in the form of an interchange between measurement number and missed detections in a multiple-sources scenario. Hence, the SPV method is a good candidate for tracking applications. However, PVs and SPVs are adequate in practice for stationary single and multiple sources, and find applications in spacecraft, aerospace and other applications where SAA is found to be useful.

Despite the outcomes of this work, there are still issues that require further research. For example, the presented methods may further be extended to antenna array calibration and time-delay measurements in different applications, or their response to key characteristics that unavoidably cause alterations in the practical use of SAA could be examined, and a qualitative comparison could be provided with related works in the literature, based on their effectiveness, accuracy, and computational complexity.