Abstract
The article aims to describe stages of development of a mobile, anthropomorphic robot. The individual phases of the bio-inspired model-based design of a two-legged robot are described, from the analysis of human walking patterns, through the creation of a simulation model and a control system to the creation and testing the physical model of such a robot. The bio-inspired design is based on an analysis of the movements of the individual parts of a lower human body during walking locomotion. Based on this analysis, the chosen motion model is described as a combination of passive and dynamic walking with a controlled, linear inverted pendulum model. When creating the simulation model, an open kinematic chain consisting of a base (the frame) and two effectors (the legs) is used. The simulation of the virtual model is realized using the software tool Matlab with its toolboxes Simulink and Simscape, and the results confirm the correctness of the design. The feasibility of the design is confirmed by creation of a physical robot skeleton using 3D printing and by a commissioning of the control system based on Atmel ATmega2560 and Raspberry Pi Zero W microcontrollers.
1. Introduction
The trend of using robots in all spheres of life, especially in industry, is constantly growing. We are witnessing an increasingly massive scale of production processes robotization in order to relieve people from performing periodic operations or directly creating processes that are physically impossible for humans. In addition to industrial robotics, we can currently observe an increase in interest in experimental robotics. Humanoid robots such as Atlas [1], Digit [2] or many others [3,4] represent the current pinnacle of human effort and intelligence in this technical field.
More and more progress in the field of human walking emulation also brings the seeds of practical use in terrain inaccessible to other mobile robots. Apart from uneven natural surfaces, these are mainly urban and industrial environments designed for the movement of people, not wheeled, or flying robots.
The area of interest in our contribution is to provide an analytical view of human walking from a mechanical point of view and, based on it, to design robot models at different levels of abstraction. The different levels cover models from the most primitive model—a mathematical graph of the robot, which provides information about the degrees of freedom of individual joints and the links between them, and this model is a source of data for the creation of another—a kinematic model. The next one—three-dimensional model containing the physical and material properties of the future real model, such as the weight and density of the construction material, can be considered as another level of abstraction. This model serves as a source of information about specific dimensions for the kinematic model. Based on these dimensions, a movement model of the robot is created with utilization of the trajectories of individual joints in space during walking. A simulation model is a combination of motion and three-dimensional models. The diagram of the simulation model represents the physical relationships acting on individual parts of the robot, as well as the control interface. The final product after the simulation is finished is the physical model. The key design model is a motion model of the robot, and the model is designed based on the linear inverse pendulum method. An important part of the design is the control of the robot and the construction of its physical model, based on which the main idea—identification and transfer of the key features of human walking into the engineering design of technical equipment—can be verified.
2. Analysis of the Problem Area
2.1. Dynamic Side of the Problem—Human Walking
Human biomechanics deals with the analysis of gait as part of the movements of human beings. In order to analyze human gait, the human walking was divided into the unique atomic periodic movements called step phases (Figure 1). These phases are further divided into two primary step phases, which are made up of eight secondary step phases, referred to as BAC 1–8 (Basic Action Concept). A set of two primary or eight secondary phases constitutes a gait cycle. The cycle can be measured from the start of any phase back to the start of the same phase of the same leg. A cycle is defined by two basic parameters: the cycle time and the spatial measures of the step. Based on the parameters of the cycle, the symmetry, variability and quality of the step are further determined. It is obvious that the step quality parameters are variable for each individual [5,6].
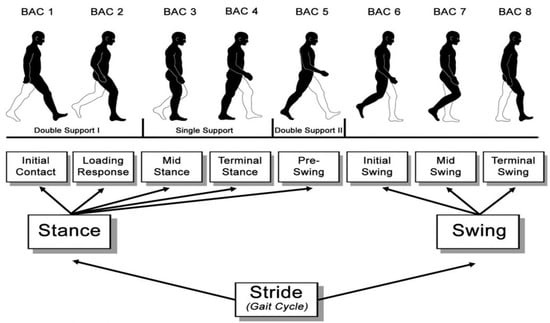
Figure 1.
Visual representation of the gait cycle [7].
Two primary phases of the step are identified as the stance and the swing. During the stance phase, the tracked leg is in contact with the ground at all times. In the swing phase, the tracked leg is in the air all the time. In secondary phases, it is possible to observe three basic events [5].
The weight transfer makes up 12% of the total gait cycle. This event can be observed in phases BAC 1 (3%) to BAC 2 (9%). During this event, the initial contact of the heel with the ground takes place and damping also occurs. Damping factors are in ascending order of total contribution: bending at the knee, rolling over the heel and elasticity of the skin, muscles and tendons in the leg. During weight transfer, there is an initial increase in the moment of force M acting on the person’s center of gravity [5,6].
The support of one leg makes up 38% of the total gait cycle. This event can be observed in phases BAC 3 (19%) to BAC 4 (19%). During this action, there is a movement of the upper part of the body and an overall increase in stability. At the end of the BAC 3 phase, the system (human body) acquires the greatest stability during the walking cycle. At the end of BAC 4, the person’s center of gravity is so deviated that it is not possible to finish the step stably. In general, single-limb stance as an event is best defined by ankle rotation [5].
The swing makes up 50% of the total gait cycle. This event can be observed at BAC 5 (12%), BAC 6 (13%), BAC 7 (12%) and BAC 8 (13%) phases. Three sub-events occur during this event.
- Lifting the heel off the ground while keeping the toe in contact with the ground. This action is included in the BAC 5 phase. It forms the transition between the one-limbed stance and the swing itself [5].
- The movement (swaying) of the leg in front of the person’s gravity center is described in the events of BAC 6 and BAC 7. The distance that the leg travels from the beginning of the BAC 6 phase to the end of BAC 7 is defined as the step length [5].
- Preparing for impact. During the BAC 8 phase, the center of gravity acquires the greatest moment of force (while reducing the acceleration) and the system (human being) prepares to absorb the impact [5,6].
Based on detailed standardized video footage of real human walking cycle considering previous movement analysis, data were experimentally collected from the figure’s walking cycle, which describes the movement of the hip, knee and ankle in space and time. A virtual measurement unit for distance j was involved in this video footage. During one phase, three measurements were taken, in which the position of the joint was monitored on the x and y axes (α-plane—side view of the figure) and in the z and y axes (β-plane—front view of the figure). The beginning of the measurement is in phase BAC 3, because the measurement also dealt with starting from the rest position, when the joints are located on one vertical axis.
From the graphical representation of the data in Figure 2 and Figure 3, the critical region and the damping region were identified. Relatively complicated events take place in these areas and cause significant deviations from the otherwise simply describable trajectory, especially in the ankle. The activity in this joint has a direct effect on the stability of the step. Furthermore, a deviation between the cycle lengths in different parts of the gait was observed from the data. Based on these deviations, the cycle stability function for the given figurant was visualized. The observed trajectory forms a set of desired values of joint positions in time. According to the deviations between the observed trajectory and the generated trajectory of the robot, it is possible to clearly indicate the complexity of the created model.
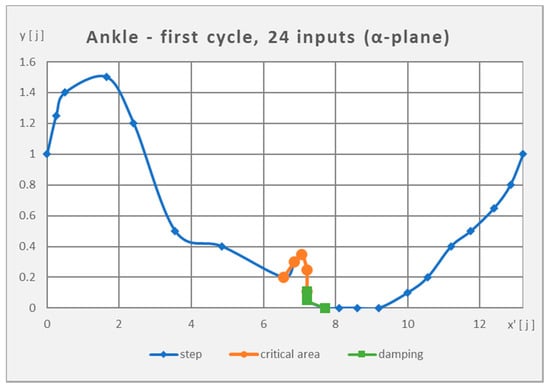
Figure 2.
Ankle trajectory (the first step).
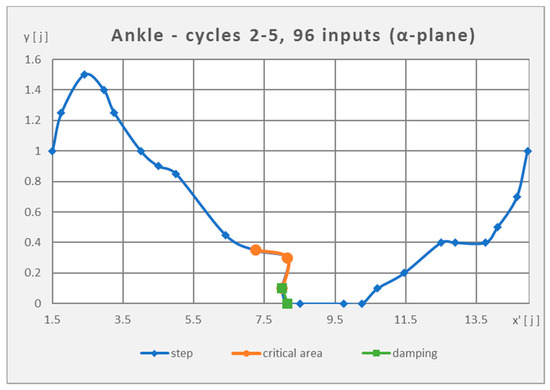
Figure 3.
Ankle trajectory (the second step).
In order to control the gait cycle of the robot, the zero-movement point (ZMP) concept is implemented in the linear inverse pendulum movement model (LIPM).
The place of operation of the pressure force is directly in the place of contact with the surface on which the robot walks. Therefore, it is a point on the robot foot that occurs during the physical interaction of the foot with the ground. The principle of the ZMP concept is that a new walking cycle is planned based on a reference trajectory. In the case of uncontrolled passive-walking robots, the ZMP forms the point of contact of the foot arch with the ground. The position of the ZMP during the stance phase is not stationary, but changes from heel to toe. This phenomenon causes complications in the simulation of flat-footed robots because the stability changes by leaps and bounds after the application of the pressure force moves beyond the tip of the flat edge. From the point of view of control, movement based on the ZMP concept forms one of several optimal trajectories. Walking appears visually fluid and energetically efficient [8].
By default, the robot step is modeled according to the inverted pendulum model (LIPM). Unlike an ordinary pendulum, an inverted pendulum does not make an oscillating motion, but tends to fall to a certain side. The moving base of the pendulum tries to compensate for the fall and keep it in a vertical position. The vertical position is the unstable equilibrium position of the pendulum [9,10,11]. The body of the robot represents the weight of the pendulum, which is supported by the leg, which represents the arm of the pendulum, and rotates around the ankle, which represents the base of the pendulum. The step cycle is thus formed by the controlled fall of the robot body in a certain range, after exceeding which the second arm of the pendulum—the other leg—hits. A system modeled in this way is considered passive, since the dynamics of the system depends on the force of gravity and the momentum of the system. To complete one walking cycle, the momentum of the system is required to produce forward motion. A system modeled by LIPM is inherently unstable, but for each input there are initial conditions from which the system will converge to a stable output. Likewise, there is a stabilization input for all initial conditions [9,10].
The LIPM model provides some variability in the robot design process, as it is independent of the dimensions and kinetic model of the structure, or the number of robot legs. However, it assumes that the weight of the robot’s body is much greater than the weight of the legs. In an ideal scenario, the weight of the legs is negligible, which is highly unlikely with a physical model. The LIPM model does not further limit the robot construction in the mutual position of the center of gravity and ZMP—the length of the pendulum arm. The implementation of the model is also possible with a higher weight of the legs, which, however, significantly reduces the stability of the gait cycle. LIPM limits the physical model only in the number of degrees of freedom in the leg, which must be at least six [12].
2.2. Static Side of the Problem—Construction Solution
The primary goal of the robot construction was to maintain an anthropomorphic shape and to copy the original as best as possible in terms of physical properties. For the proper functioning of the robot, it was necessary that:
- the ratio of the dimensions of the frame and individual arms, including the joints of the robot, was as similar as possible to the ratio of the dimensions of human limbs,
- the center of gravity of the robot was placed as close as possible to the position of the human body.
In order to fill the requirement that the construction design describes the shape of the human body as reliably as possible, one of the proportional models of the human body was chosen (Table 1). The selected model divides the distances between individual points on the human body into units of length. By observing the given proportions, it was possible to design a construction on a different scale while preserving the properties of the original. Since the shape of the body itself is not important in the LIPM model, but only the position of the center of gravity, the construction of the entire body of the robot was not absolutely necessary [13].

Table 1.
Proportions of the human body according to the R.B. Hale model [13].
Subsequently, based on published information [6,14,15], an analysis of individual joints in the lower part of the human body was carried out (Table 2). A rotational degree of freedom was granted to a joint if its angle range exceeded 10° [16].

Table 2.
Analysis of joints in the lower part of the human body.
The design of the robot also depends on the level of system control. According to this criterion, walking robots are divided into controlled and passive walking robots. Controlled walking robots are those in which the range of each robot movement is given by a controlled quantity. Passive walking robots are kinematic chains that move stably with a step without control and without an energy source. The passive step concept can be applied to both quadrupedal and bipedal robots. The movement is achieved by an initial impulse relative to the system and an inclined pad along which the robot moves downwards. A key feature of passive walking robots is the curved foot. As a rule, the bending radius is equal to the distance of the center of gravity from the ground when the robot is in a rest state. Some controlled robots are also based on this concept, where the bending of the foot—completely or in the position of the heel and toe—improves the energy efficiency of the step and eliminates a step change in stability. A combination of controlled and passive joints in walking robots is also frequent. A typical example is the reduction of the knee joint in the robot’s leg in exchange for a shock absorber. Another example is a robot leg composed of controlled joints in the hip and knee, or the other knee on the same leg, and a passive foot containing a spring in the toe. The stiffness of this spring ensures a flat foot shape in the secondary phases of the gait cycle, BAC 1 to 4 and later in BAC 7 to 8. In BAC phases 5 and 6, the foot bends under its own weight to such an extent that it directs part of the robot’s weight into the toe, similar to human walking. Of course, both mentioned methods can be replaced by a controlled process. Usually, a combination of controlled and passive elements of the robot is used to simplify complicated movements that are more difficult to control [17,18].
3. Modeling and Simulation of Biped Robot
The modeling process was based directly on the analysis results and involved designing the robot at different levels of abstraction and generating walking trajectories. The individual levels created a simulation model for which a control system was proposed in the next stages.
3.1. Design of a Simulation Model of a Bipedal Robot
The starting point for the design of the robot was the kinematic model of the robot, which can be obtained in different ways depending on the principles used [19,20]. In this case, the modeling process was dependent on the analyzed walking model LIPM and ZMP, which was adapted to the number of degrees of freedom of the robot. Since it is a mobile robot, no part of the robot is firmly attached to the ground, so we cannot talk about a mechanism, but about a kinematic chain. The kinematic chain was divided into three main parts.
- The frame is a mobile base on which two manipulators are attached. The center of gravity of the robot is also located in this part and forms the material part (the head) of the inverse pendulum. The frame represents the human pelvis.
- The left leg is the manipulator of the robot, one end of which is attached to the left side of the frame, and the other end is terminated by an effector. The manipulator consists of four arms and six joints. The manipulator represents the arm of the inverted pendulum and the human leg, where the effector fulfills the role of the foot.
- The right leg is a manipulator functionally identical to the left leg, but it is fixed on the right side of the frame.
Based on the movement analysis, it follows that there are two degrees of freedom in the ankle and up to three in the hip joint. The implementation of several degrees of freedom in one place—such as in a spherical kinetic pair—was realized by dividing the joint into three rotary kinematic pairs with the smallest possible arms. These rotation pairs rotate around different axes of the coordinate system. In this way, the three degrees of freedom of the spherical pair were preserved with a simpler implementation in practice. One manipulator has six degrees of freedom, just like the analyzed template. Five degrees of freedom are controlled and one degree of freedom at both ends of the chain is uncontrolled. The robot has two arms on a frame with six degrees of freedom. The additional six degrees of freedom were granted because it is a mobile robot which can freely move and rotate in space in all directions. The number of freedom degrees of the kinetic chain
where ni represents the number of degrees of freedom of the i-th kinematic pair and j is the total number of kinematic pairs, is greater than the minimum required number for the LIPM model.
The graph of the robot in Figure 4 shows the relationships between individual kinematic pairs. In the vertices of the graph, the number of degrees of freedom in each pair is indicated. The mobility of the robot is represented by the absence of a link between the ground and the kinematic chain. Furthermore, it can be observed that the graph of the robot is acyclic; therefore, we speak of an open kinematic chain.
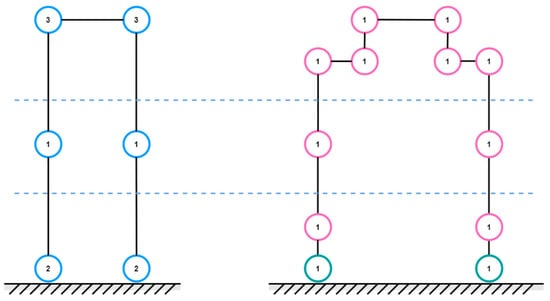
Figure 4.
Robot graph based on robot analysis (left), robot graph adapted for robot construction (right).
The kinematic model of the robot was derived from the robot graph (Figure 5). Kinematic pairs were defined in space and therefore in this model we are already talking about rotational joints with one degree of freedom. Relationships between joints are now represented by arms. This is a model with a combined type of walking (passive and controlled).
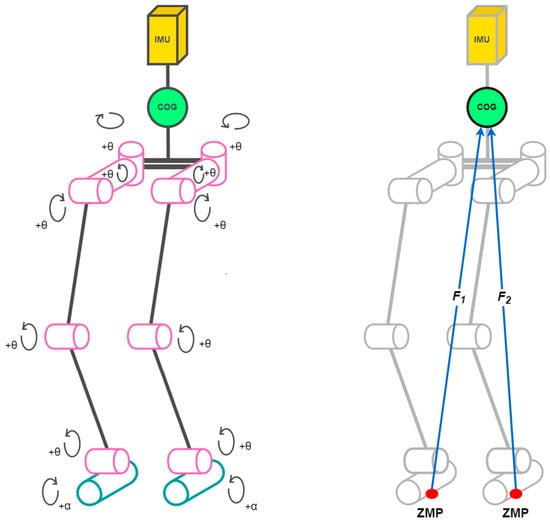
Figure 5.
Kinematic model of the robot (left), visualization of LIPM and ZMP principles on the kinematic model (right).
Denavit–Hartenberg (DH) parameters were determined in the kinematic model (Figure 6). Conventional DH parameterization uses a uniform method for marking the axes of coordinate systems in individual joints. It uses two rules:
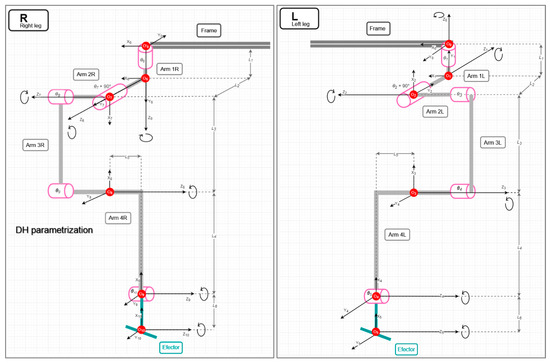
Figure 6.
DH parameterization of the right (R) and the left (L) legs.
Therefore, in DH, the representation of the homogeneous transformation contains two parameters less than the usual homogeneous transformation, which facilitates the analysis of the n-arm manipulator [21].
In the process of identifying the DH parameters, the axes of rotation were first marked depending on the types of joints. Convention states that the axis of rotation is the z-axis. Based on the positive direction of rotation, the direction of the axis was determined. For some opposing joints, the direction of the z-axis was chosen differently to preserve the natural direction of rotation. Subsequently, two different origins of zero coordinate systems were chosen, specifically for the right and left leg. In both cases, the origin was chosen at the joint that connects the leg to the frame. Unlike the rest of the centers of the coordinate systems, these were not numbered. The center of the coordinate system in the joint connecting the left leg and the frame was marked O0, and the center in the joint connecting the right leg and the frame was marked O0’. A different zero-system naming convention for walking robots led to this decision. After finding the remaining origins of the coordinate systems, the x and y axes were determined by convention according to relations (3) and (4).
In effector coordinate systems, the z-axis is generally oriented in the same way as the axis of the last arm. Thus, the two non-controlled joints at the ends of the kinematic chain will rotate along the y-axis, not along the z-axis like the controlled joints. In both cases, the origins of the effectors coordinate systems were chosen at the point created by the intersection of the axis perpendicular to the ground, passing through the center of gravity, and the straight line created when the given effector touches the ground when the robot is in the starting position. Under ideal conditions, this point is identical to the ZMP. The analysis of the DH parameters of the robot’s legs is shown in Figure 6. The specific values of the DH parameters of the kinematic model of the robot are listed in Table 3.

Table 3.
DH parameters of the robot kinematic model.
In the DH parameterization, the centers of the coordinate systems and their relative positions were found. Despite the fact that the effectors seem to fulfill the role of joints in the kinematic chain, this phenomenon is not included in the DH parameters, since they are uncontrolled “joints” between the ground and the robot. The parameterization of the effector was developed by creating a three-dimensional model of the entire kinetic chain based on the analyzed kinematic model.
When modeling the effector, knowledge from the materials for the construction of the foot of a passive walking robot was used. In the starting position, when in contact with the ground, the effectors create support in the form of two parallel lines. Since the position of the effector itself is controlled, the length of the foot was designed to be as small as possible in order to maintain relative stability in the controlled direction of rotation. The foot width was determined to be as large as possible for the longest arch of its lower part. The resulting shape of the foot design is shown in Figure 7.
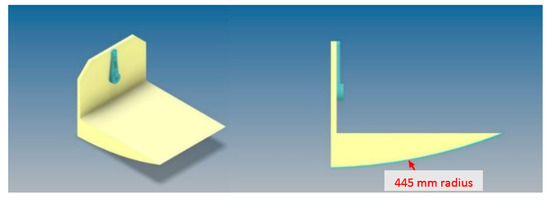
Figure 7.
Proposal of a robot effector.
Due to the chosen ratio of the weights of the legs together with the effectors, with respect to the weight of the robot frame, the requirement for the use of the LIPM walking model for the designed three-dimensional model is fulfilled. The basic parameters of the robot are listed in Table 4.

Table 4.
Parameters of the three-dimensional model.
The resulting dimensions from Table 4 were used in motion modeling using the inverse pendulum model. In the modeling process, the center of gravity of the robot represented the head of the pendulum in the form of a mass point p defined in space by default as p = (x, y, z) according to (5)–(7). This position is described in this model as a system of state variables q = (θr1, θp1, z) in which r represents the length of pendulum arm, or robot leg in this specific case [22].
τr, τp and f, as vectors acting on the center of gravity, arm and head of the pendulum in Formula (8), represent the inputs to the system of equations describing the movement of the inverse pendulum in space, in the Cartesian right-handed system [22] as
where m is the mass of the center of gravity. Since the arm of the pendulum is considered as a link, the variable m belongs to the mass point p. The Jacobian J is an antisymmetric matrix dependent on the current configuration q(t) and for motion analysis, according to [21,22], has the form
A similar Jacobian was later used in the recalculation of joint velocities of the robot in order to determine the inverse kinematics. In this case, it was used to create the dynamic equations of the pendulum, and therefore it is multiplied by the vector () from the left to create a mathematical model of the inverse pendulum in space [21,22] according to the relation
In order to use this model to generate step trajectories, restrictions on the movement of the pendulum along the z-axis were defined. These constraints ensure that the height of the pendulum head does not change under the influence of the inputs q(t). However, this height can be changed manually. This restriction is represented in a form of help vector (kx, ky, −1) of controlled inputs of height of the robot and the intersection zc of the z-axis. The step width was determined as the length of the arch of the foot; i.e., the maximum possible. The parameters for the design of the pendulum are listed in Table 5 [22].

Table 5.
Three-dimensional model parameters for the LIPM model.
Step generation took place in three stages. In the first stage, the movement of the center of gravity and the ZMP in space was identified (Figure 8). According to the limitations of the model, the height of the center of gravity was anchored. This phenomenon simulated the fact that the legs are not extended when walking as in a fully passive walking robot. A step with bent knees reduces the movement of the center of gravity along the z-axis. At this stage, the pendulum consisted of a head and one arm, which alternately played the role of the robot’s left and right legs. The weight of the pendulum head is preset to 1 and the weight of the arm is assumed to be zero.
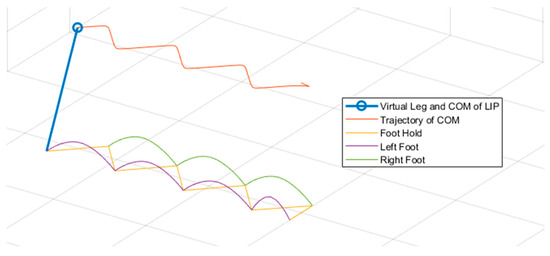
Figure 8.
Generated trajectories of the center of mass and the position of the ZMP.
In the second stage, the foot trajectory was generated based on the mutual position of the ZMP and the movement of the center of gravity. Trajectories were generated for eight cycle runs. The analysis showed that during the first two runs of the cycle, stride length and movement were less similar than during the rest of the runs. This phenomenon can also be observed in the first two steps of the model, when the feet in the initial position are located at a spacing of 91 mm from the robot axis, given by the construction. The model reaches the predetermined step width of 144 mm and length of 20 mm only during the third run of the cycle. The trajectories were stored in the data-structure footinfos 1 × 8 (Figure 9), where the column number determined the number of cycle run. One data element contained a 1 × 200 vector (timevec) with time values sampled for a one-second period. Furthermore, this element also contained the joint positions in space stored in two 6 × 200 matrices for the left leg (footleft) and the right leg (footright). The joints positions are represented by the amount of each joint rotation with respect to the defined direction using DH parameterization.
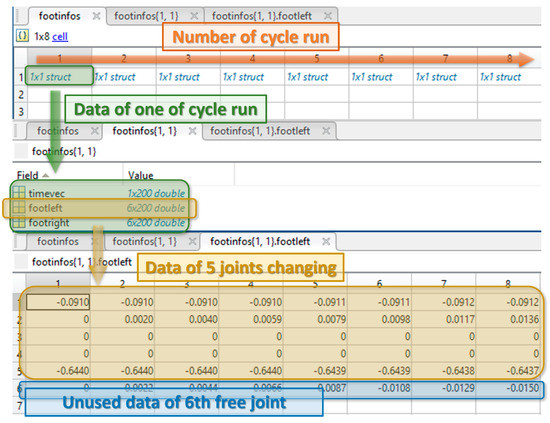
Figure 9.
Data-structure covering the changes of DH parametrization in kinematic, 3D and simulation models.
In the third stage, the trajectories were recalculated to the controlled variables of the DH parameters using the inverse kinematics task, and the result is the motion model of the robot made from a 3D material model, which was created with Autodesk Inventor software.
3.2. Simulation of a Bipedal Robot Walking
The simulation model of the biped robot was created by exporting the three-dimensional model to the Matlab-Simscape simulation environment. The three-dimensional model was divided into 27 parts, which created links corresponding to the three-dimensional model in the simulation environment. This process was automated using the Simscape Multibody Link toolbox. Six degrees of freedom were added to the model for kinematic chain simulation. Contact forces on the lower part of the effectors were also created. These forces ensure that the bottom of the foot behaves like an ideal rigid body when in contact with another object.
The axes of rotation in the joints were adjusted to the z-axis in order to follow the convention of the DH parameterization and the positive direction of rotation was chosen according to the kinematic model. The resulting block diagram of the simulation model is shown in Figure 10.
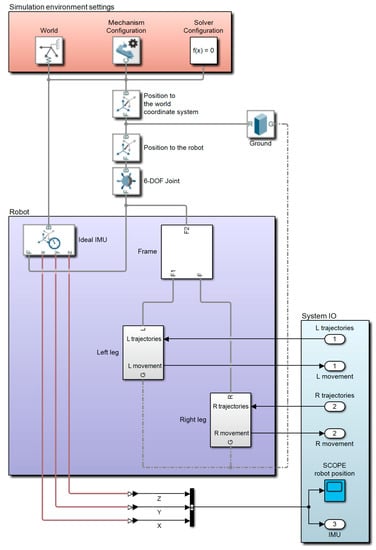
Figure 10.
Simulation model of bipedal robot walking.
The output of the inverse kinematic task is the required quantity in the unmodified form W’. The quantity W’ must be filtered before entering the controller, because the generated trajectory is in the form of a function that the simulation solver cannot process correctly. Sharp local extremes of the trajectories were evaluated as noise and removed with a low-pass filter. The filter was implemented using the Filter Design Toolbox as a part of Matlab R2022a software, which allows the user to design the required filter in a short time even without expert experience in the field of signal processing.
From the diagram of the simulation model shown in Figure 11, it follows that the control system is based on the principle of regulating the speeds and positions of the servomotors. To increase the level of robot autonomy, an ideal orientation sensor was included in the system. The sensor detects the acceleration and position of the frame in three axes. The value on the z-axis was monitored at the output of the system. If the deviation from the planned position is exceeded by 30 mm, the robot will be turned off in an emergency. The reason is to prevent damage to the robot due to redundant movements in an unwanted position on the ground.
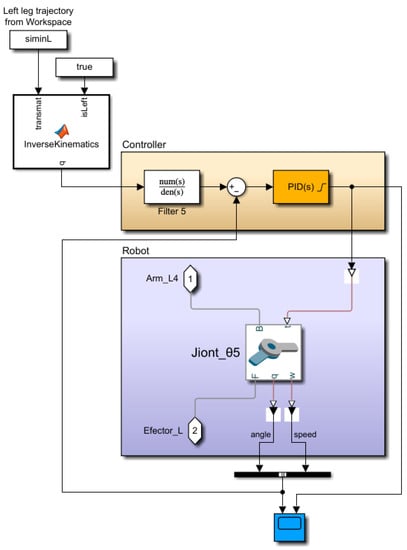
Figure 11.
Closed control loop for joint number 5.
The result of the simulation at this stage is the fact that the designed model of the robot can perform all eight planned steps from the starting position. The length and width of the first three steps contained negligible deviations from the movement model, which may be caused by using passive joints. The remaining seven steps were identical to the motion model. Figure 12 shows the simulation model in motion in different design phases from different perspectives.
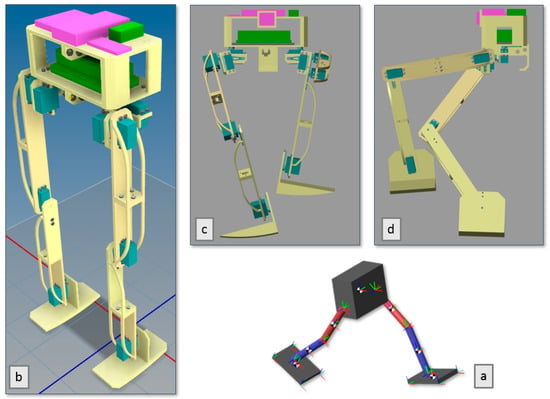
Figure 12.
Simulation of walking of the bipedal robot (a) basic kinematic model; (b) static 3D model; (c) walking 3D model—front view; (d) walking 3D model—side view.
4. Realization of a Physical Model of a Bipedal Robot
The supporting structure of the robot was made using 3D printing technology. This technology has proven itself as an effective method of manufacturing parts, mainly due to its sufficient accuracy and speed for prototyping purposes. The advantage of the material used in printing the parts is the low weight compared to other parts of the robot and the possibility to modify the parts even after printing. For most parts, the wall thickness was set to four layers and the material filling between the walls was 70%. The Micro-Electro-Mechanical Systems (MEMS) storage components and the component for stabilizing the robot in a seated position were printed with only three layers of wall thickness and 50% infill, as these components do not represent the load-bearing elements of the structure. On the contrary, the effectors were printed with a wall thickness of six layers and a filling of 80%.
4.1. Construction of a Bipedal Robot
The construction of the robot consists of three main parts.
The robot frame is made up of eleven parts and is divided into two floors. The first floor is intended for energy sources and is closed from above and below. The second floor is for the robot’s control interface and is open at the top. For this reason, simple handling of the interface is possible without the need to disassemble the frame. Each floor consists of two parts that are connected by a detachable joint. After connecting the two floors, two components were attached to the front and back of the upper floor to hold the two MEMS systems. In the space on the first floor, there is a part that allows the robot to sit without support.
The robot’s legs are made up of twelve parts, five of which are unique. The two parts are used to secure the servos together to create three degrees of freedom for the 3R and 4L arms. The connection of these three motors simultaneously creates arms 1L, 1R, 2L and 2R. The rest of the arms are structurally very similar. Each of them is composed of two parts connected by a detachable joint.
The effectors of the robot are made of one part, the same for the left and right effector. The decision, to model the effector as a single part instead of several detachable pieces, was justified by the fact that the entire effector fits within the scope of the printer and thus eliminates the possibility of the effector falling apart under pressure at the point of a potential joint (Figure 13).
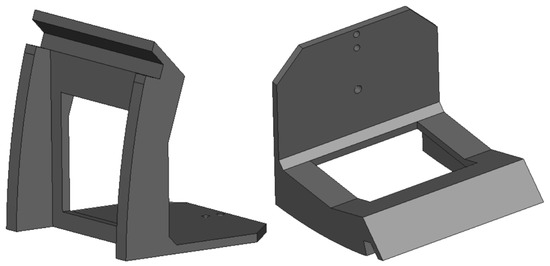
Figure 13.
Final shape of the effector.
4.2. Control Hardware
An Arduino Mega 2560 Rev3 device [23] was chosen to control the operation of the bipedal robot. This device has 14 PWM channels and thus can control all joints of the robot. The advantage of the Mega 2560 Rev3 model compared to other models is mainly a significantly larger number of I/O pins and PWM channels. In general, Arduino products are considered suitable for prototyping systems due to the low price, the large number of hardware accessories, and especially the open and freely distributable hardware architecture. To ensure simple remote control, the control interface was supplemented with Raspberry Pi Zero W [24]. The advantage of this device is the relatively large computing capacity and thus the extensive possibilities of expanding control from the current state to a robust system. Very small dimensions and low weight are also a big advantage of the device.
The communication linkage between the Raspberry Pi Zero W and the Arduino Mega 2560 Rev3 is possible using the I2C link, as both components contain the necessary bus. There are two positions in communication: master and slave, while I2C also supports multi-master mode. In this case, the Arduino microcontroller was chosen as the master.
The simulation model contains a measuring device for the orientation of a material object in space (Internal Measurement Unit—IMU), which in our case detects the translational movement of the robot in three axes. This sensory device is standard in stability control for biped and other mobile robots and forms the basis of the system’s feedback. In this case, it is used as a sensor to detect the fall of the robot, when the robot terminates the ongoing process prematurely. In the physical model, this block is represented by the MEMS system Bosch BNO055, which contains the three mentioned sensors and its own microcontroller. The device has the ability to send output data to the master device in the form of quaternions which are normally used in robotics when calculating direct and indirect kinematic tasks. The BNO55 was calibrated in the automatic NDoF FMC mode [14,25].
Due to the fact that the mobile robot carries the power source directly on its structure, a solution was proposed that is ensured by a source with the smallest possible weight for the longest possible operating time. Since the energy sources are structurally located on the first floor of the robot frame, it was necessary that they be rechargeable, and recharging was possible without the need to disassemble the frame. Because the selected servomotors have a different working voltage than the Arduino and Raspberry devices, the decision to divide the robot power supply into two parts was made. A possible solution is to connect a voltage stabilizer to 6 V, but in this case the servomotors overheat. Therefore, the first power source will power all the servo motors and the second power source will power the rest of the control hardware.
Based on the analysis of the available options, the BH Power 2S 6000 mAh Li-po battery was chosen to power the servomotors. In order to power the rest of the control interface, it was necessary to ensure the power supply of the Arduino Mega device, through which the remaining devices will also be powered. The use of an external battery for smartphones appeared to be the simplest solution from the point of view of recharging, dimensions, and weight, and for this reason the AVACOM PWRB-8001K external battery was chosen.
5. Solution Testing and Discussion
Testing of the proposed solution was divided into two parts. In the first stage, all parameters of the robot affecting walking were measured and their deviation from the simulation model was calculated. Each property was measured five times and then the average value was calculated. The results of the first part of the testing process are listed in Table 6.

Table 6.
Results of testing the dimensions of the biped robot structure.
From the measurement results of the first part, certain differences between the physical and simulation models can be observed. The weight difference is attributed to neglecting the weights of the cabling, different fillings of the plastic parts, material inhomogeneity of the printed parts and also inaccurate weight data of the used electronic parts.
The differences between the measured and the original values of the L1, L2 and L5 lengths were expected and are attributed to the replacement of the servo motor carriers. The original method designed in a three-dimensional model consisted of a detachable joint between a printed servo motor carrier and the wall which with the servo motor was supposed to rotate. In practice, the great flexibility of the carrier, which stood away from the given wall, was manifested, which was caused by the weight of the entire robot. This caused the bending of the shoulders, which led to deviations in the positions of the controlled joints. The chosen modification consisted of replacing the printed carrier with a standardized one, which was attached to the wall with self-tapping steel screws. These percentage deviations are large, but the reduction of the distances between the centers of the coordinate axes in these joints is desired. The deviations between the lengths of L4 and L5 are negligible and are attributed to either measurement error or plastic extensibility.
The reduction of the step width in the starting position can be attributed to the resulting deviations in the parameters L1, L2 and L5. The reason is the different starting point of the measurement of this distance, which was not possible to implement in the physical model. Therefore, a new frame height was derived from the simulation model and compared with the measured value. The resulting deviation is largely attributed to the resulting deviations between the lengths of L6, L3, L4 and L1.
All the differences identified in this phase of testing can be involved in the next phases of the spiral model of the engineering design of mechatronic systems in order to achieve an ideal overlap between the design, simulation and final implementation of the solution.
The second part of the testing was focused on monitoring of stability of the robot at different step lengths. The measurement in which the robot passed all eight steps from the generated trajectory was considered successful. Five measurements were taken at each step length. The robot walked on a horizontal concrete pad in a closed room. The robot walked independently without physical contact with another object. A successful step is considered the one after which the walking cycle is completed without falling. The beginning of the measurement of all cycles was in phase BAC 3. The results of the second part of the test experiments are shown in Table 7.

Table 7.
Functionality testing results of a bipedal robot.
From the test results it is clearly evident that the first three steps are critical, after which the gait is stabilized. The test experiments show that the robot is able to walk stably with steps up to 12.5 cm long. The number of all measurements during the second phase of testing was 90. The measurements took place without interference and external influences. It is necessary to emphasize that this testing stage served for verification of control system design proposal. The correctness of the intended idea in defined form was confirmed, but at the same time, it is necessary to declare that the designed solution is not ready for independent continuous infinite walking yet, except for some stable steps. The constructed and tested prototype of the two-legged robot is shown in Figure 14.

Figure 14.
A tested prototype of bipedal robot MaRoŠ (a) construction parts; (b) partial construction; (c) final version.
6. Conclusions
The topic of the development of humanoid robots is very extensive. Several possible approaches to the way of controlling bipedal robots in order to ensure movement as similar as possible to human walking have been published. This article is focused on one of the possible methods using the analysis of real human walking. The principle of model-based design is used, while the bio-inspired design is based on the analysis of the movements of individual parts of the human body while walking. The control system is designed based on a combination of passive and dynamic walking with a controlled, linear inverted pendulum model. Validation of the designed model using the Matlab simulation tool confirmed the feasibility of the design. The result of this article is the finding that the proposed concept can be developed further, after fine-tuning the details, as one of the real options for the design of walking humanoid robots. This statement is based on the course and results of the final experiments with the physically constructed prototype of the bipedal robot MaRoŠ. The development of the prototyping solution is constantly ongoing, inspired by the spiral model of software product development, and the goal is to completely reconcile the simulation and physical model of the robot, together with the optimization of energy use in the mechatronic subsystems of the robot.
Author Contributions
Conceptualization, D.P. and M.J.; methodology, D.P., M.J. and B.J.; software, D.P., M.J. and B.J.; validation, D.P., M.J. and Z.Č.; formal analysis, D.P. and Z.Č.; resources, M.J., B.J., D.P. and Z.Č.; data curation, D.P.; writing—original draft preparation, D.P. and M.J.; writing—review and editing, M.J., D.P. and B.J.; visualization, D.P. and M.J.; supervision, M.J.; funding acquisition, M.J., B.J. and Z.Č. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by VEGA agency, grant number 1/0176/22 “Proactive control of hybrid production systems using simulation-based digital twin”.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Boston Dynamics. ATLASTM. Available online: https://www.bostondynamics.com/atlas (accessed on 1 April 2022).
- IEEE. Robots—Your Guide to the World of Robotics. Available online: https://robots.ieee.org/robots/digit (accessed on 1 April 2022).
- Yang, X.; She, H.; Lu, H.; Fukuda, T.; Shen, Y. State of the Art: Bipedal Robots for Lower Limb Rehabilitation. Appl. Sci. 2017, 7, 1182. [Google Scholar] [CrossRef]
- Gulletta, G.; Erlhagen, W.; Bicho, E. Human-Like Arm Motion Generation: A Review. Robotics 2020, 9, 102. [Google Scholar] [CrossRef]
- Perry, J.; Burnfield, J.M. Gait Analysis: Normal and Pathological Function; Slack Incorporated: West Deptford, NJ, USA, 2010; p. 551. ISBN 978-1556427664. [Google Scholar]
- Čapek, L.; Hájek, P.; Henyš, P. Biomechanika Člověka; Grada Publishing: Prague, Czech Republic, 2018; ISBN 978-80-271-0367-6. [Google Scholar]
- Stöckel, T.; Jacksteit, R.; Behrens, M.; Skripitz, R.; Bader, R.; Mau-Moeller, A. The Mental Representation of the Human Gait in Young and Older Adults. Front. Psychol. 2015, 6, 943. [Google Scholar] [CrossRef]
- Mitobe, K.; Capi, G.; Takayama, H.; Yamano, M.; Nasu, Y. A ZMP Analysis of the Passive Walking Machines. In Proceedings of the SICE 2003 Annual Conference (IEEE Cat. No.03TH8734), Fukui, Japan, 4–6 August 2003; Volume 1, pp. 112–116. [Google Scholar]
- Omer, A.; Hashimoto, K.; Lim, H.-O.; Takanishi, A. Study of Bipedal Robot Walking Motion in Low Gravity: Investigation and Analysis. Int. J. Adv. Robot. Syst. 2014, 11, 139. [Google Scholar] [CrossRef]
- Lanari, L.; Hutchinson, S.; Marchionni, L. Boundedness Issues in Planning of Locomotion Trajectories for Biped Robots. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Atlanta, GA, USA, 18–20 November 2014; pp. 951–958. [Google Scholar]
- Bakaráč, P. Konštrukcia a Riadenie Inverzného Kyvadla. Master’s Thesis, Slovak University of Technology in Bratislava, Bratislava, Slovakia, 2017. [Google Scholar]
- Erbatur, K.; Kurt, O. Natural ZMP Trajectories for Biped Robot Reference Generation. IEEE Trans. Ind. Electron. 2009, 56, 835–845. [Google Scholar] [CrossRef]
- Prokopenko, S. Human Figure Proportions—Cranial Units—Robert Beverly Hale. Available online: https://www.proko.com/human-figure-proportions-cranium-unit-hale (accessed on 1 April 2022).
- Vachálek, J.; Takács, G. Robotika; STU Publishing: Bratislava, Slovakia, 2014; p. 166. ISBN 978-80-227-4163-7. [Google Scholar]
- Somisetti, K.; Tripathi, K.; Verma, J.K. Design, Implementation, and Controlling of a Humanoid Robot. In Proceedings of the 2020 International Conference on Computational Performance Evaluation (ComPE), Shillong, India, 2–4 July 2020; pp. 831–836. [Google Scholar]
- Hamilton, N.; Weimar, W.; Luttgens, K. Kinesiology: Scientific Basis of Human Motion, 12th ed.; McGraw Hill: New York, NY, USA, 2012; p. 640. ISBN 978-0078022548. [Google Scholar]
- McGeer, T. Passive Dynamic Walking. Int. J. Robot. Res. 1990, 9, 62–82. [Google Scholar] [CrossRef]
- Yamane, K.; Trutoiu, L. Effect of Foot Shape on Locomotion of Active Biped Robots. In Proceedings of the 2009 9th IEEE-RAS International Conference on Humanoid Robots, Paris, France, 7–10 December 2009; pp. 230–236. [Google Scholar]
- Virgala, I.; Miková, Ľ.; Kelemenová, T.; Varga, M.; Rákay, R.; Vagaš, M.; Semjon, J.; Jánoš, R.; Sukop, M.; Marcinko, P.; et al. A Non-Anthropomorphic Bipedal Walking Robot with a Vertically Stabilized Base. Appl. Sci. 2022, 12, 4108. [Google Scholar] [CrossRef]
- Che, J.; Pan, Y.; Yan, W.; Yu, J. Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model. Actuators 2022, 11, 75. [Google Scholar] [CrossRef]
- Babinec, A. Riadenie Robotických Manipulátorov. Lectures; Faculty of Electrical Engineering and Information Technology STU: Bratislava, Slovakia, 2019. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D Linear Inverted Pendulum Mode: A Simple Modeling for a Biped Walking Pattern Generation. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 1, pp. 239–246. [Google Scholar]
- Robotshop. Arduino Mega 2560 Datasheet. Available online: https://www.robotshop.com/media/files/pdf/arduinomega2560datasheet.pdf (accessed on 1 April 2022).
- Raspberry Pi Foundation. Raspberry Pi Hardware. Available online: https://www.raspberrypi.org/documentation/hardware/raspberrypi (accessed on 1 April 2022).
- Adafruit. Adafruit BNO055 Absolute Orientation Sensor. Available online: https://learn.adafruit.com/adafruit-bno055-absolute-orientation-sensor (accessed on 1 April 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).