Fluorimetry in the Strong-Coupling Regime: From a Fundamental Perspective to Engineering New Tools for Tracing and Marking Materials and Objects
Abstract
:1. Introduction
- -
- Frequency shifts make it possible to improve the signal-to-noise ratio;
- -
- Frequency splitting constitutes a signature of strong-coupling which is difficult to counterfeit.
2. Concept of “Quantum Filigran” Based on Strong-Coupling
2.1. Physically Unclonable Functions
2.2. Quantum Filigran
3. Fluorophore Coupled to a Resonant Cavity in the Strong-Coupling Regime
3.1. Strong-Coupling with a Perfect Lossless Cavity
3.2. Strong-Coupling with a Lossy Cavity
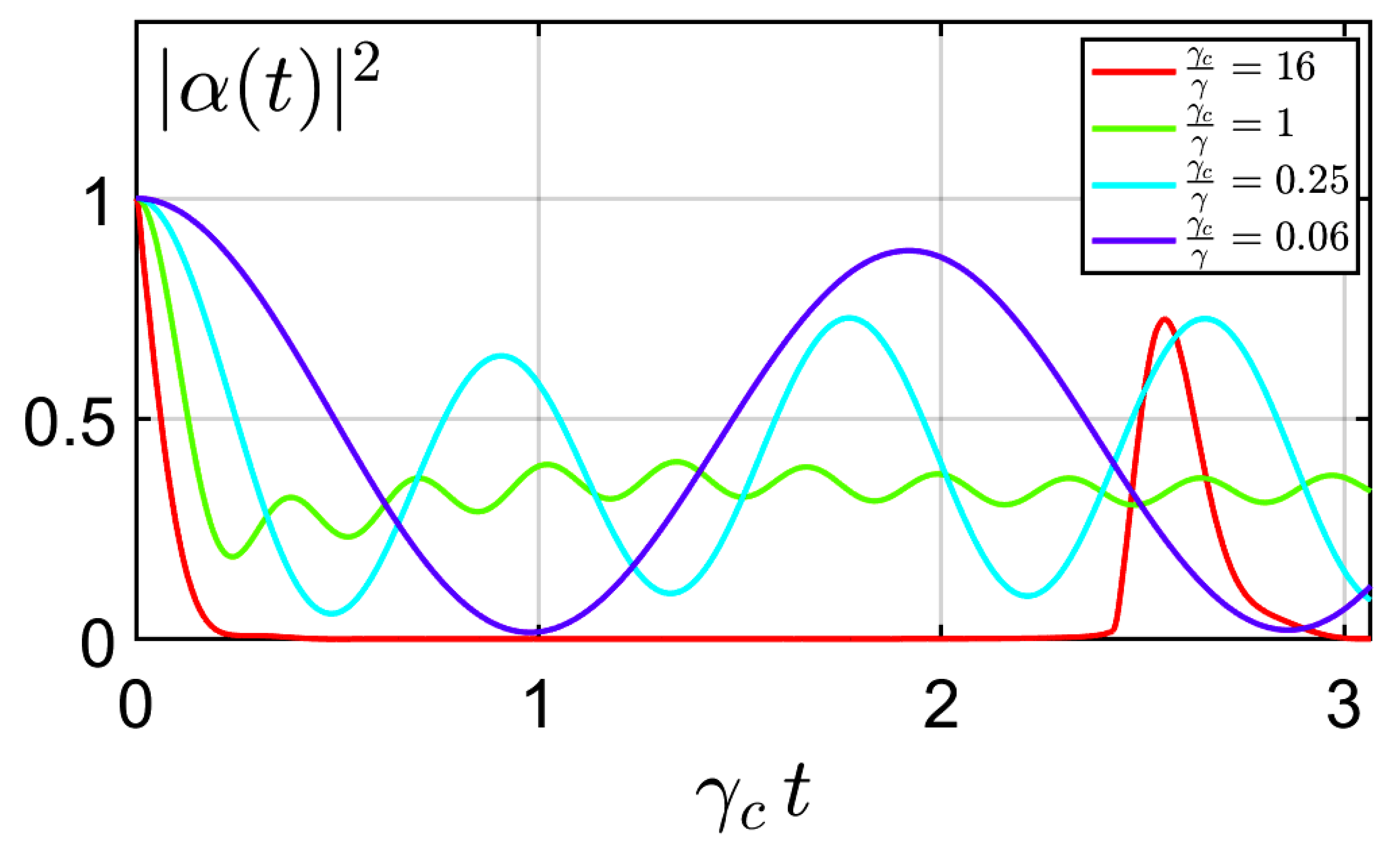
3.3. Weak and Strong-Coupling Regime in the Resonant Case
- (i)
- (ii)
- For a large coupling constant, , is real, and the eigen-frequencies (Equation (14)) show a different real part, leading to oscillations of the amplitude in the time-domain, known as the strong-coupling regime.
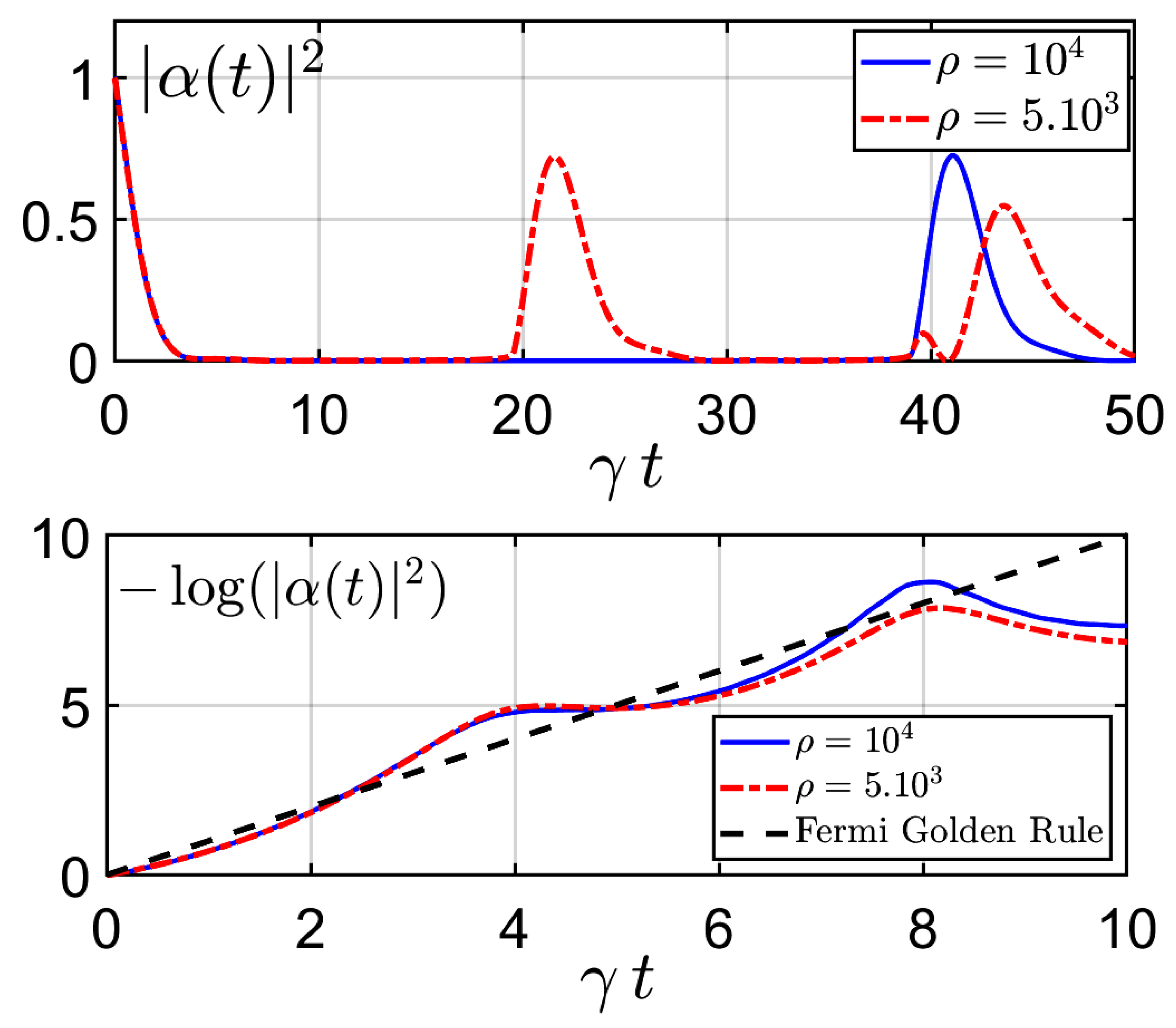
3.4. Emission Spectrum in the Strong-Coupling Regime
3.5. Studying Poincaré Recurrences with a Discrete Model of Evolution
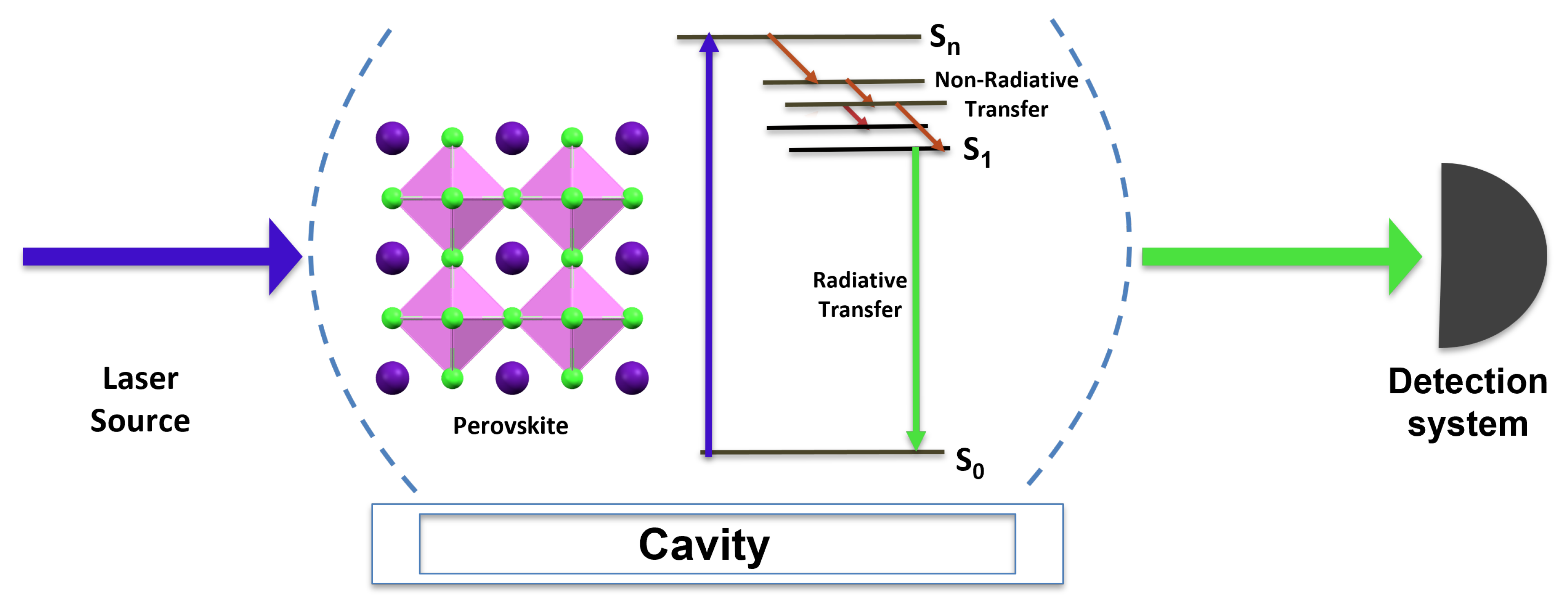
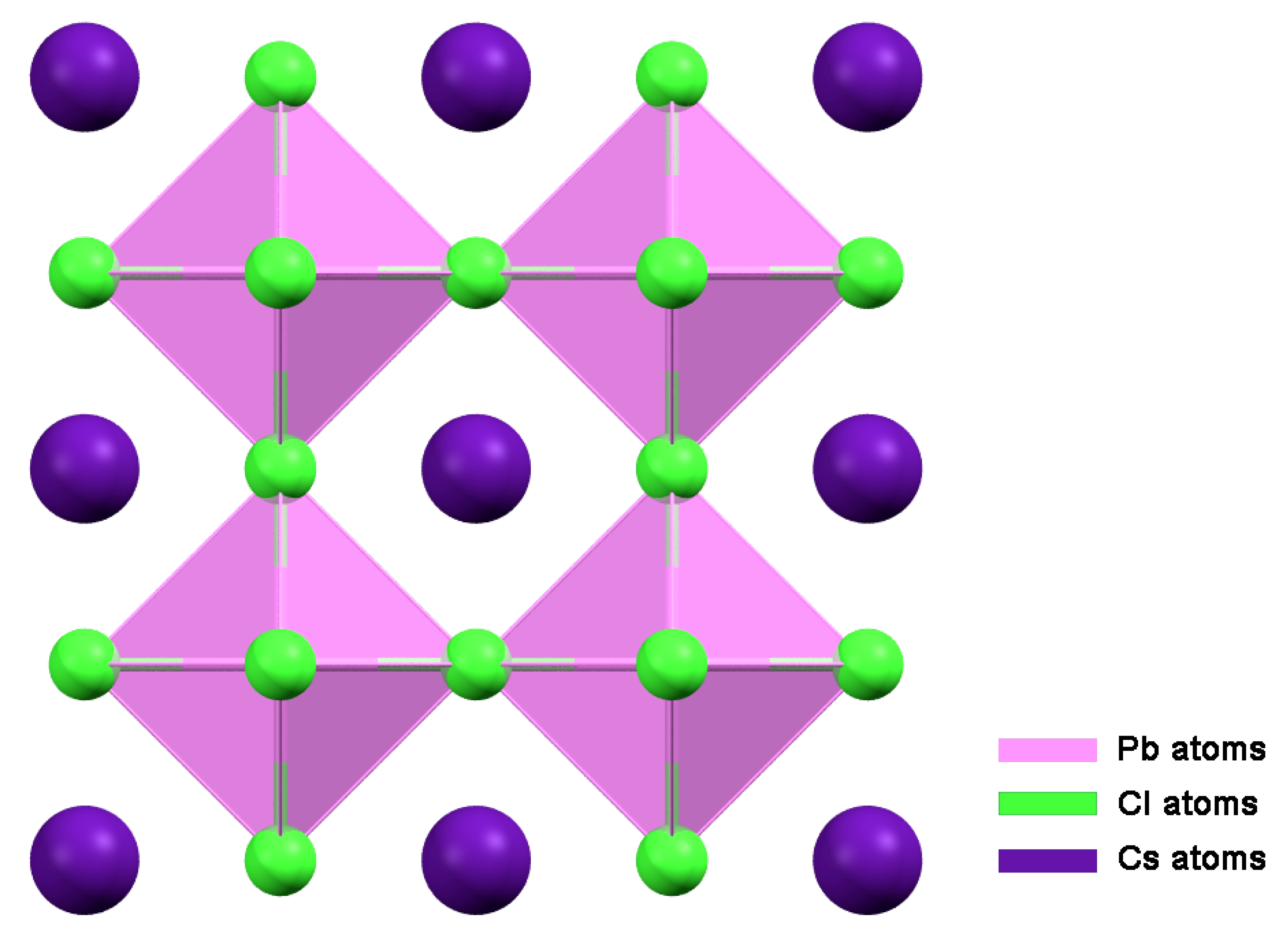
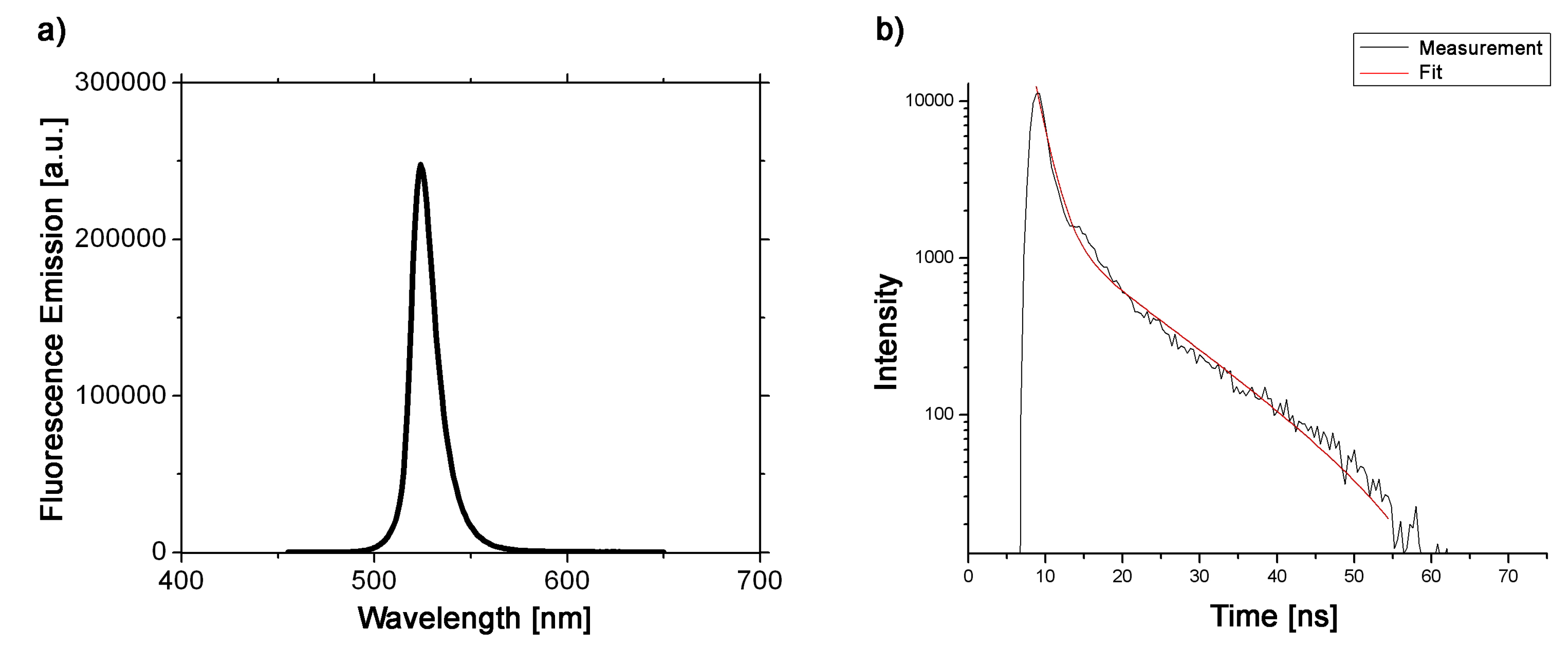
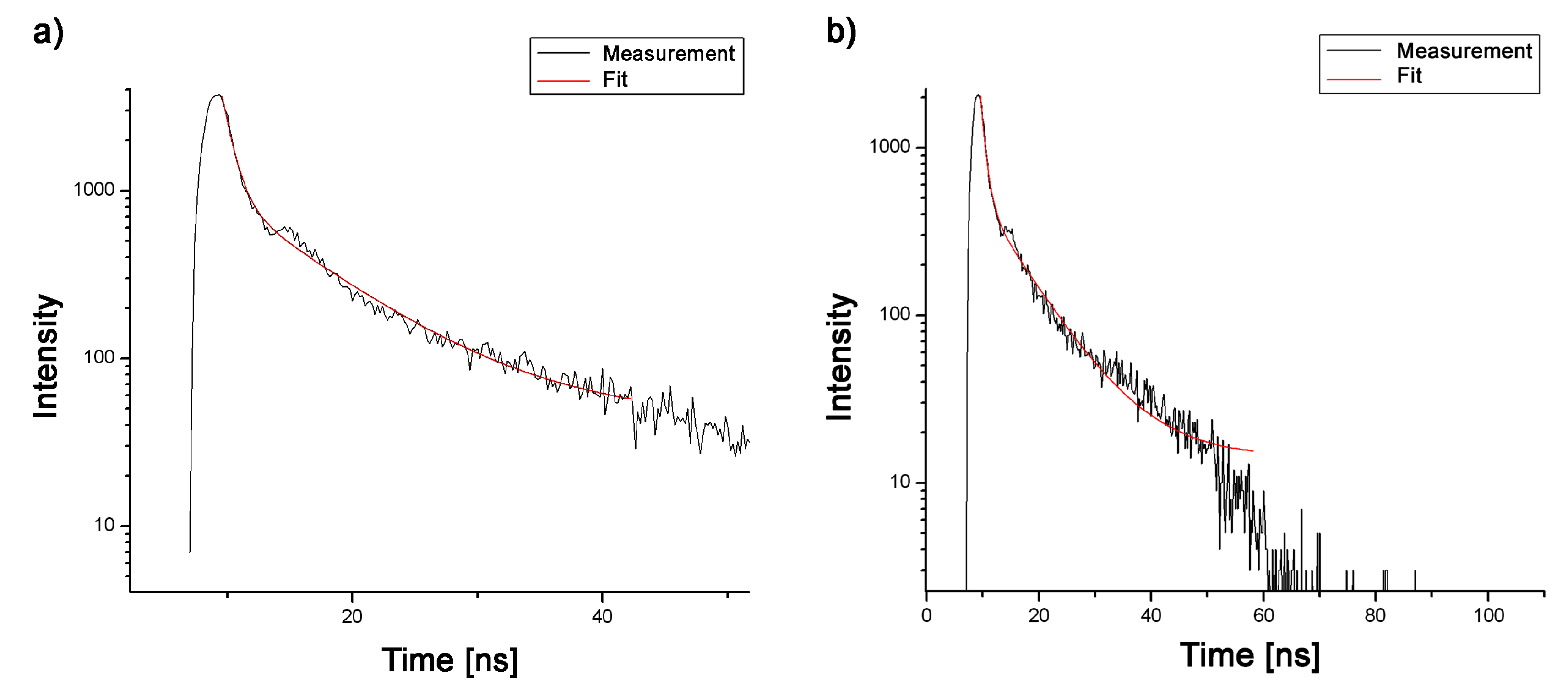
4. Experimental Study
4.1. Experimental Protocol
4.2. Results
5. Tracing and Marking in the Strong-Coupling Regime
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sengupta, P.; Khanra, K.; Chowdhury, A.R.; Datta, P. Lab-on-a-chip sensing devices for biomedical applications. In Bioelectronics and Medical Devices from Materials to Devices—Fabrication, Applications and Reliability, 1st ed.; Pal, K., Kraatz, H.-B., Khasnobish, A., Bag, S., Banerjee, I., Kuruganti, U., Eds.; Woodhead Publishing: Sawston, UK, 2019; pp. 47–95. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006; pp. 623–740. [Google Scholar]
- Kolaric, B.; Maes, B.; Clays, K.; Durt, T.; Caudano, Y. Strong Light-Matter Coupling as a New Tool for Molecular and Material Engineering: Quantum Approach. Adv. Quantum Technol. 2018, 1, 1800001. [Google Scholar] [CrossRef]
- Shalabney, A.; George, J.; Hiura, H.; Hutchison, J.A.; Genet, C.; Hellwig, P.; Ebbesen, T.W. Enhanced Raman Scattering from Vibro-Polariton Hybrid States. Angew. Chem. Int. Ed. 2015, 54, 7971–7975. [Google Scholar] [CrossRef]
- Orgiu, E.; George, J.; Hutchison, J.A.; Devaux, E.; Dayen, J.F.; Doudin, B.; Stellacci, F.; Genet, C.; Schachenmayer, J.; Genes, C.; et al. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 2015, 14, 1123–1129. [Google Scholar] [CrossRef] [PubMed]
- Vergauwe, R.M.A.; George, J.; Chervy, T.; Hutchison, J.A.; Shalabney, A.; Torbeev, V.Y.; Ebbesen, T.W. Quantum Strong Coupling with Protein Vibrational Modes. J. Phys. Chem. Lett. 2016, 7, 4159. [Google Scholar] [CrossRef]
- Ramezani, M.; Berghuis, M.; Gómez Rivas, J. Strong light–matter coupling and exciton-polariton condensation in lattices of plasmonic nanoparticles (Review). J. Opt. Soc. Am. B Opt. Phys. 2019, 36, E88–E103. [Google Scholar] [CrossRef]
- Pelton, M.; Storm, S.D.; Leng, H. Strong coupling of emitters to single plasmonic nanoparticles: Exciton-induced transparency and Rabi splitting. Nanoscale 2019, 11, 14540–14552. [Google Scholar] [CrossRef]
- Pappu, R.; Recht, B.; Taylor, R.; Gershenfeld, N. Physical One-Way Functions. Science 2002, 297, 2026–2030. [Google Scholar] [CrossRef] [PubMed]
- Pavlović, D.; Rabasović, M.D.; Krmpot, A.J.; Lazović, V.; Ćurčić, S.; Stojanović, D.V.; Jelenković, B.; Zhang, W.; Zhang, D.; Vukmirović, N.; et al. Naturally safe: Cellular noise for document security. J. Biophotonics 2019, 12, e201900218. [Google Scholar] [CrossRef]
- Wiesner Quantum Money. Available online: https://wiki.veriqloud.fr/index.php?title=WiesnerQuantumMoney (accessed on 1 September 2022).
- Jaynes, E.T.; Cummings, F.W. Comparison of Quantum and Semiclassical Radiation Theories with Application to the Beam Maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Bina, M. The coherent interaction between matter and radiation. Eur. Phys. J. Spec. Top. 2012, 203, 163–183. [Google Scholar] [CrossRef]
- Haroche, S.; Raimond, J.M. Exploring the Quantum—Atoms, Cavities and Photons; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Carminati, R.; Greffet, J.J.; Henkel, C.; Vigoureux, J. Radiative and non-radiative decay of a single molecule close to a metallic nanoparticle. Opt. Commun. 2006, 261, 368–375. [Google Scholar] [CrossRef]
- Lassalle, E. Environment Induced Modifications of Spontaneous Quantum Emissions. Ph.D. Thesis, University of Marseille, Marseille, France, 2019. [Google Scholar]
- Dutra, S.M. Cavity Quantum Electrodynamics: The Strange Theory of Light in a Box, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Grynberg, G.; Aspect, A.; Fabre, C. Introduction to Quantum Optics: From the Semi-Classical Approach to Quantized Light, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Debierre, V.; Goessens, I.; Brainis, E.; Durt, T. Fermi’s golden rule beyond the zeno regime. Phys. Rev. A 2015, 92, 023825. [Google Scholar] [CrossRef]
- Weisskopf, V.; Wigner, E. Berechnung der natürlichen linienbreite auf grund der diracschen lichttheorie. Z. Für Phys. 1930, 63, 54–73. [Google Scholar] [CrossRef]
- Hunton, J.; Nelmes, R.J.; Moyer, G.M.; Eriksson, V.R. High resolution study of cubic perovskites by elastic neutron diffraction: CsPbCl3. J. Phys. C Solid State Phys. 1979, 12, 5393. [Google Scholar]
- Cowen, E.A.; Ward, K.B. Chemical Plume Tracing. Environ. Fluid Mech. 2002, 2, 1–7. [Google Scholar] [CrossRef]
- Anti-Counterfeiting Technology Guide; European Union Intellectual Property Office: Alicante, Spain, 2021.
- Trace Chemical Sensing of Explosives, 1st ed.; Woodfin, R.L. (Ed.) Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Chan, W.P.; Chen, J.H.; Chou, W.L.; Chen, W.Y.; Liu, H.Y.; Hu, H.C.; Jeng, C.C.; Li, J.R.; Chen, C.; Chen, S.Y. Efficient DNA-Driven Nanocavities for Approaching Quasi-Deterministic Strong Coupling to a Few Fluorophores. ACS Nano 2021, 15, 13085–13093. [Google Scholar] [CrossRef] [PubMed]
- Punj, D.; Regmi, R.; Devilez, A.; Plauchu, R.; Moparthi, S.B.; Stout, B.; Bonod, N.; Rigneault, H.; Wenger, J. Self-Assembled Nanoparticle Dimer Antennas for Plasmonic-Enhanced Single-Molecule Fluorescence Detection at Micromolar Concentrations. ACS Photonics 2015, 2, 1099–1107. [Google Scholar] [CrossRef]
- Busson, M.; Rolly, B.; Stout, B.; Bonod, N.; Bidault, S. Accelerated single photon emission from dye molecule-driven nanoantennas assembled on DNA. Nat. Commun. 2012, 3, 962. [Google Scholar] [CrossRef] [PubMed]
- Busson, M.P.; Rolly, B.; Stout, B.; Bonod, N.; Wenger, J.; Bidault, S. Photonic Engineering of Hybrid Metal—Organic Chromophores. Angew. Chem. Int. Ed. 2012, 51, 11083–11087. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatifi, M.; Mara, D.; Bokic, B.; Van Deun, R.; Stout, B.; Lassalle, E.; Kolaric, B.; Durt, T. Fluorimetry in the Strong-Coupling Regime: From a Fundamental Perspective to Engineering New Tools for Tracing and Marking Materials and Objects. Appl. Sci. 2022, 12, 9238. https://doi.org/10.3390/app12189238
Hatifi M, Mara D, Bokic B, Van Deun R, Stout B, Lassalle E, Kolaric B, Durt T. Fluorimetry in the Strong-Coupling Regime: From a Fundamental Perspective to Engineering New Tools for Tracing and Marking Materials and Objects. Applied Sciences. 2022; 12(18):9238. https://doi.org/10.3390/app12189238
Chicago/Turabian StyleHatifi, Mohamed, Dimitrije Mara, Bojana Bokic, Rik Van Deun, Brian Stout, Emmanuel Lassalle, Branko Kolaric, and Thomas Durt. 2022. "Fluorimetry in the Strong-Coupling Regime: From a Fundamental Perspective to Engineering New Tools for Tracing and Marking Materials and Objects" Applied Sciences 12, no. 18: 9238. https://doi.org/10.3390/app12189238
APA StyleHatifi, M., Mara, D., Bokic, B., Van Deun, R., Stout, B., Lassalle, E., Kolaric, B., & Durt, T. (2022). Fluorimetry in the Strong-Coupling Regime: From a Fundamental Perspective to Engineering New Tools for Tracing and Marking Materials and Objects. Applied Sciences, 12(18), 9238. https://doi.org/10.3390/app12189238








