Abstract
This paper describes a simple, lossless and computationally efficient two-band single (s-) filter bank that creates an opposite band output by subtracting the primary filtered data from the original data. For computationally efficient and error-free s-filter bank achievement, a maximally flat (MAXFLAT) half-band filter with zero odd-order coefficients is characterized from a unique perfect reconstruction condition, and an explicit impulse–response formula (for non-zero integer coefficients of even order) is derived in a closed form of the filter. The examples are shown to provide a complete and accurate solution for the design of such s-filter banks. In addition, the effectiveness of the proposed s-filter banks is clearly verified by comparing the lossless 5/3 and lossy 9/7 filter banks (in the JPEG2000). The simulation results show that the s-filter banks lead to better performance than the JPEG2000 filter banks using two filters although allowing low computational complexity of less than 50%. This new approach is shown to provide significant advantages over existing lossless discrete wavelet transform (DWT) filter banks in both design flexibility and computational complexity.
1. Introduction
The discrete wavelet transform (DWT) filter bank using two-band quadrature mirror filter (QMF) structure provides the advantage of separating the input signal into several frequency subbands in both time and wavelet transform domains [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Recently, the DWT filter bank is vastly utilized in large-scale operational applications requiring a computationally demanding task such as remote-sensing (RS) image retrieval, classification in a DWT compressed image archive, analyzing quantization noise for medical imaging, image encryption and image deblurring with convolutional neural network [1,2,3,4,5,6,7,8,9]. Currently, Joint Photographic Experts Group (JPEG) 2000, available to lossy and lossless DWT, is most utilized for various image applications. To cite an example, M. A. Gungor et al. [1] dealt with the denoising effect of the JPEG2000 for the compression of noisy images. A. P. Byju et al. [2,3] reported RS image retrieval and classification in a JPEG2000 compressed image archive. Further, T. Brahimi et al. [4] presented a wavelet-based multimodal compression method that jointly compresses a medical image and an electrocardiogram (ECG) signal within a JPEG2000 single codec [1,2,3,4,28]. This research focus on minimizing the amount of computational complexity for image decompression, but there exists the disadvantage that should use two different wavelet filters (Cohen-Daubechies-Wavelet 9/7) causing a lot of computation in the lossy-mode JPEG2000 [1,2,3,4,7,8,9,10]. For the design of lossless DWT filter bank, a spectral factorization algorithm through energy partitioning in the z-plane was proposed by S. R. M. Penedo et al. [11]. However, since these lossless DWT filters have the real (irrational-number) coefficients, there exist problems of not only exponentially increasing computational complexity in the multiple-channel filter bank, but also causing large calculation errors [2,3,4]. For this reason, the DWT filter pair (wavelet 5/3) used in the lossless mode of well-known JPEG2000 has integer coefficients for computational-complexity minimization and computing-error free [5,10,28]. Nevertheless, existing two-channel lossless DWT filter banks using such filters provide the disadvantage of less flexibility (due to limited error-free conditions) in designing filters, resulting in lower performance due to relatively low image compression ratio and poor denoising efficiency (as compared to lossy DWT filter banks) [1,2,3,4,5,6,7,10].
A two-channel DWT filter bank consists of analysis and synthesis banks, as shown in Figure 1 where , are the transfer functions of analysis bank filters, and , are the synthesis filters. The reconstruction signal, in general, suffers from aliasing, amplitude and phase distortions, due to the fact that these filters are not ideal [15,16,17]. As is well known, aliasing frequencies are removed completely by substituting and . Then, the overall system function of the alias-free filter bank can be written as [18,19,20,21,22,23,24,25,26]

Figure 1.
Conventional two-band filter bank.
Apart from this regularity, the unit-amplitude and linear-phase properties are also very important in applications [17]. A system that is free from aliasing, amplitude and phase distortions is called a lossless DWT filter bank that yields a perfect reconstruction (PR) [18,19,20,21,22,23,24]. The reconstructed signal is therefore just a time-delayed version of the transmitted signal , i.e., if for some nonzero constant c and some positive integer . In [13,25], the PR conditions for two-band multi-rate DWT filter banks were given to be alias free and to have a unity frequency response. It was shown that the class of QMFs that satisfies these conditions is quite limited. One of the most common design methods for designing two-band lossless DWT filter banks is by starting from a half-band product filter and then factorizing it to obtain the filters in the lossless filter bank, i.e., , followed by its factorization to obtain and that satisfy . Regularity is imposed in the design of by forcing to have zeros at , i.e., terms of the form [26,27]. However, the number of possible spectral factors grows exponentially with respect to the order of the filters and the resulting filters are not guaranteed to be optimal. Moreover, the design of lossless DWT filters with integer coefficients for computational-complexity minimization and calculation-error free is more difficult. However, aside from the Le Gall 5/3 filters (of JPEG2000) among lossless DWT filters announced so far, integer coefficient filters are rare [11,24,28]. Hence, a new lossless filter bank structure is needed to obtain integer coefficient filters satisfying the perfect reconstruction conditions.
The objective of this paper is to present a novel two-band lossless single (s-) filter bank which allows more computationally efficient and flexible design strategies than existing lossless filter banks [11,24,28]. From PR conditions a generalized filter polynomial is derived which allows a unity frequency response and gives a computationally effective and efficient filter (half of coefficients are zeros). A single, arbitrary FIR filter (with integer coefficients) is demonstrated able to be easily obtained for the proposed s-filter bank. In that sense, the design of a computationally superior and error-free filter bank through this new approach gives an additional insight into the physical significance of the design flexibility. Design examples are shown which demonstrate the power of the new technique.
2. Design of Two-Band Lossless Single(s-) Filter Banks
Consider the two-channel biorthogonal filter bank of Figure 1, with the synthesis bank filters chosen as and . The elegant choices of (a pair of) analysis bank filters, and , cancel aliasing and yield a PR system.
Let be a FIR lowpass filter with the real impulse response of order, which can be written as
by using the transfer function
where represents a zero-phase FIR lowpass filter and has a linear-phase property if . For a complementary pair of analysis filters with strongly dependent responses (Figure 1), a highpass filter (or lowpass filter ) can be reconstructed by subtracting a lowpass filter (or highpass filter ) from allpass (or unity) as
or
where is a positive integer constant for system causality, and denotes an (allpass) -sample delay. Thus, in the case of Equation (4), the upper-band residual data is obtained by subtracting the lowpass filtered data from the unfiltered (-sample delay) original data, i.e., where and are the lower and upper band outputs before subsampling. Then, the value of has a significant effect on the subtracted (residual) quantities since determines the redundancy between the lower and upper band outputs. This is because the subtraction operation of the analysis filter bank has the same effect which uses the highpass filter (or lowpass filter) with its magnitude response dependent on . The overall system function of the alias-free s-filter bank can be obtained as
by substituting the results of Equations (2) and (4) into (1). For a given even , substituting into Equation (6) can yield
Figure 2 depicts the proposed single (s-) filter bank structure which consists of one single (analysis) filter and its mirrored subtraction loop. It can be seen that the analysis bank consists of a lowpass (or highpass) filter and a subtraction loop, which has more strongly dependent responses than the conventional QMF form. In addition to alias-free computations, so that of Equation (7) has a unity gain response in the whole frequency domain (i.e.,), a gain error-free s-filter bank can be achieved by designing. From Equation (7) it can be found that the even number indexed coefficient terms of completely cancel out those of if is
by introducing into Equation (2) [26,27,29]. Thus, substituting Equation (8) to (7) potentially leads to
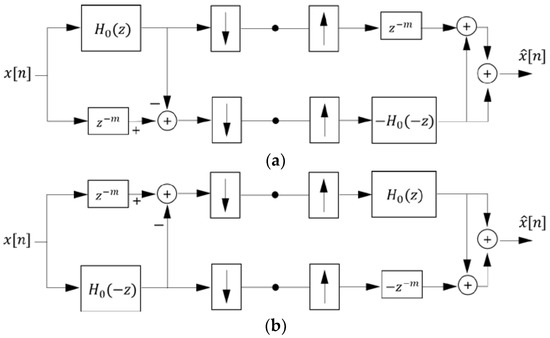
Figure 2.
Two-band PR s-filter bank structures with (a) lower-band subtraction loop (upper-band prediction) and (b) upper-band subtraction loop (lower-band prediction).
From Equation (9), it is shown that even though any is chosen, the s-filter bank produces zero distortion and also has a linear phase response. Consequently, the filter form of Equation (8) for the lossless s-filter bank can allow unusual flexibility in choosing a best filter for analysis and synthesis, i.e., the overall passband and stopband distortion (even if not flat) of the filter has no effect on producing the result of Equation (9). Further, these filters can lead to computationally efficient implementations due to the fact that all odd-order coefficients are zeros. The computational superiority of the proposed lossless s-filter bank can be confirmed even more by realizing a linear-phase half-band FIR filter, where has symmetric integer (even-order) coefficients of . Such linear-phase half-band FIR filter design will be discussed in next section.
Comments for additional designs: Using Equation (6), we can consider the other set of and (i.e., odd if is even) for the design of lossless s-filter banks. In this case, the PR condition is identical to the form of Equation (8) above, and only the system delay is different. Hence, similarly to the case of even and odd, the choice of in addition to the determination of has to be also seriously considered for the various applications of s-filter banks. This is because for a given has a significant effect on the residual band characteristics. Further Figure 2a,b have identical input/output behavior for analysis and synthesis, while providing different image compression and denoising effects if is not a half-band filter. For example, if is a lowpass filter with narrow passband, upper subband of Figure 2a has larger high-frequency bandwidth than that of Figure 2b, which results in relatively low image compression ratio and poor denoising efficiency. In other words, to achieve higher image compression ratio and denoising efficiency, the s-filter bank of Figure 2a is better to choose a large passband filter, while Figure 2b is better to use a narrow passband filter. For this reason, so that the lower and upper subbands have a symmetric bandwidth, the design of FIR half-band lowpass filter with linear phase is also significantly important. More importantly, the value of even defined as input sample delay of in Equation (4) for a given is decided from the relation of to minimize the redundancy between lower and upper subbands.
3. Design of Lossless s-Filter Banks
Design of the lossless s-filter bank reduces to the design of a FIR lowpass filter given by Equation (8) to yield the PR system satisfying Equation (9). For this reason, the unique lossless condition can characterize a FIR half-band lowpass filter with a linear-phase as below
by imposing and 1/2 on Equation (8). Then, the filter coefficients of Equation (10) can be easily designed by imposing zeros at (i.e., a term)—i.e., maximally flat (MAXFLAT) magnitude or relatively narrower transition band response [26,27,29]. In other words, the filter can be said to have a MAXFLAT frequency response at if has a maximum number of zeros at (i.e., ) as
Thus, this paper focuses on the design superiority of the lossless s-filter bank using MAXFLAT half-band lowpass filter with integer coefficients. Computation of half-band filter coefficients ’s, using Equation (10), had ever been reported in [29,30]. In a similar way, imposing the MAXFLAT condition of Equation (11) on (10), the filter can be expressed in terms of K (:flatness order) as a closed-form half-band solution:
From Equation (11), the frequency response of becomes
For the computation of the filter coefficients shown in Equation (10), transforming Equation (12) into interpolation-coefficient () form
and mapping Equation (14) to (10), the relationship between and is derived in terms of K as
and
where if A < B or B < 0. It can be seen from Equations (15) and (16) that both and directly produce integer values for a given value where the order of flatness is determined by the order of filter . This implies that the proposed lossless s-filter bank allows MAXFLAT half-band FIR filters with integer coefficients able to minimize computational complexity without calculation error (by using just only addition and shift operation).
3.1. Design Examples of MAXFLAT Half-Band FIR Filters
The design examples were demonstrated here using for the filter order of . In addition, the computations of MAXFLAT half-band filter coefficients ’s for the lossless s-filter bank were performed on the Equation (15) derived in closed form. This is due to the fact that two s-filter banks depicted in Figure 2 can produce equivalent results since the designed filter has a zero-phase half-band frequency response with respect to .
Table 1 shows the integer filter coefficients computed by solving Equation (15) for given . For example, in the case of (i.e., the order of filter is such that ), a closed form polynomial of order 10 can be given from Equation (14) as

Table 1.
Filter coefficients for given K = 1–5.
Then, ’s () are obtained from Equation (16) as
Substituting Equation (18) to (15) leads to ’s ():
Using Equation (19) yields the transfer function of the form shown in Equation (10), which is expressed as
Note that the odd number indexed coefficients of the half-band filter given by Equation (10) are zero—i.e., (). It is also shown that all the rest coefficients can be obtained as integer values. From Equation (13), the closed-form frequency response is given by
Figure 3 depicts the frequency responses of MAXFLAT half-band filters indicated in Table 1. The example shows that the impulse–response formula Equation (15), available for directly obtaining MAXFLAT half-band filters with integer coefficients, is effective and practically useful in designing highly accurate filters with a magnitude response passing exactly through the half-band cut-off frequency . Further, the MAXFLAT half-band filters can be found to have a trade-off between transition bandwidth and filter length. In another way, using a steepness parameter into Equation (10) can allow the design flexibility to obtain half-band FIR filters with a sharp transition band [29].

Figure 3.
The frequency responses of MAXFLAT half-band FIR filters for (the order of filter is
).
3.2. Special Design Examples of Two-Taps Symmetric Filters
The utilization of the proposed lossless s-filter bank structure shown in Figure 2 can produce another new filter satisfying PR conditions. On a condition that can permit and in Figure 1, imposing Equations (2) and (4) (for given even and yields a PR condition able to characterize :
This implies that and are odd symmetric with respect to. Substituting Equation (8) into (22), it follows that
From Equation (23), the equivalence of both sides can be found to be established by
Substituting Equation (24) to (8) with and using lead to a two-taps filter form
where . The filter of Equation (25) also satisfies the unity gain condition of Equation (7) (i.e.,) for a given even, and the realization of a gain error-free s-filter bank is possible. In particular, it can be seen that Equation (25) exhibits a linear phase comb filter having zeros equally spaced on the z-plane’s unit circle and leads to a completely symmetric comb filter of by replacing by . Conclusively, applying Equation (25) into the s-filter bank can be seen to produce a new two-channel orthogonal symmetric filter bank in which analysis and synthesis banks have a symmetric two-tap filter structure and each also consists of the perfect symmetric filters (of and with respect to . As an example, imposing on Equation (25) yields a simplest linear-phase half-band lowpass filter with two taps as
Then, Equation (7) becomes , and both the lower and upper bands have a half bandwidth of . Further, in the other case of allowing , the comb filter is obtained from Equation (25) as
Figure 4 shows the frequency responses of two filters with two coefficients described in Equations (26) and (27). The analysis s-filter bank using the two-tap lowpass filter of Equation (26) leads to a symmetric subband decomposition since both filtered and subtraction-loop bands have a half bandwidth of , while using the comb filter of Equation (27) displays the frequency response that shows regularly spaced peaks giving the appearance of a comb [31]. The two-tap filter examples show that the lower and upper bands performed by the analysis s-filter bank have centrally symmetric frequency responses.
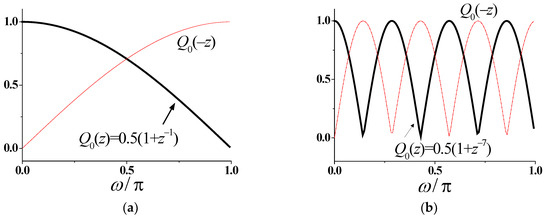
Figure 4.
The magnitude responses of two-taps filters: (a) half-band lowpass filter with order of 1 and (b) comb filter with order of 7.
4. Performance Evaluation
For performance evaluation, a reversible/irreversible JPEG 2000 (part 1) coding scheme [28,32] was used based on five grayscale images with resolution of 256 × 256 pixels. To demonstrate the effectiveness of the proposed s-filter bank, the 2, 3, 5 and 7-taps s-filter banks were compared with the (reversible) 5/3 and (irreversible) 9/7 filter banks [28,32]. Then, the s-filter bank structure of Figure 2b was chosen creating relatively narrower highpass bandwidth than Figure 2a. This is due to the fact that the narrow high-frequency bandwidth (by directly using a highpass filter) has lower entropy than the wide case (by lower-band subtraction loop). In the lossless (reversible) mode, each image was split into 4, 7 and 10 subbands and average entropy (bit-rate) was compared. Further, in the lossy (irreversible) mode, each image was split into the seven subband decompositions and coded at 0.6–0.4 bit per pixel (bpp) for Peak Signal to Noise Ratio (PSNR) comparison. Table 2 shows simulation results compared in the lossless compression mode of the JPEG2000 where integer operations by adding and shifting are performed. It can be seen that the proposed s-filter bank using a 3-tap filter (described in Table 1) provides lower bit rate(entropy) for test images than using the 5/3 filter bank, which is attributed to achieving a higher image compression ratio despite the use of only one 3-tap filter. Further, the PSNR comparison of lossy image compression is also indicated in Table 3. The proposed s-filter banks are experimentally verified to have PSNR performance that is better than or similar to the 9/7 filter banks, although providing a much more computationally efficient solution due to integer operations.

Table 2.
Lossless compression bit-rate comparison (bpp).

Table 3.
Coding performance comparison at 0.6–0.4 bpp.
Table 4 shows the comparison of computational complexity for two-channel analytic filter banks. It can be found that the proposed s-filter banks exhibit significantly low computational complexity of less than 50% of the (reversible) 5/3 and (irreversible) 9/7 filter banks. Consequently, the comparison results suggest that proposed lossless s-filter banks not only achieve relatively high image compression performance, but also provide low computational complexity without calculation error due to integer operation.

Table 4.
Computational complexity comparison of two-channel analysis filter banks.
5. Conclusions
The DWT filter bank is vastly utilized in large-scale operational applications requiring a computationally demanding task such as RS image retrieval, classification in a DWT compressed image archive, analyzing quantization noise for medical imaging, image encryption and image deblurring with convolutional neural network. However, existing two-channel filter banks provide the disadvantages of less flexibility (due to limited condition and structure) in designing lowpass and highpass analysis filters, causing undesired reconstruction errors and high computational complexity. In this paper, to address such issues, we proposed a novel two-band lossless s-filter bank with a computationally efficient and error-free structure, which consists of one single (analysis) filter and its mirrored subtraction loop. A unique lossless condition was shown to allow a closed-form half-band polynomial with zero odd-order coefficients, resulting in an explicit formula for directly obtaining integer-coefficient filters with maximally flat (MAXFLAT) half-band frequency response. The simulation results showed that the proposed s-filter banks have better performances than the lossless 5/3 and lossy 9/7 filter banks (of the JPEG2000), although providing low computational complexity of less than 50%. It can be concluded that this new approach allows more flexible and affordable PR DWT bank systems to be built, and it helps solve limited filter-design problems due to obtaining desired lossless filter banks.
Author Contributions
Conceptualization, D.C. and J.J.; methodology, J.J.; software, D.C.; validation, W.C. and Y.K.; formal analysis, D.C.; investigation, D.C.; resources, D.C and J.J.; data curation, D.C. and Y.K; writing—original draft preparation, D.C.; writing—review and editing, D.C. and J.J; visualization, W.C.; supervision, D.C.; project administration, D.C. and J.J.; funding acquisition, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (no. 20224000000020) and Korea Evaluation Institute of Industrial Technology (no. 20012884), which are funded by the Ministry of Trade, Industry and Energy of the Republic of Korea.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gungor, M.A.; Gencol, K.J.O. Developing a compression procedure based on the wavelet denoising and JPEG2000 compression. Optik 2020, 218, 164933. [Google Scholar] [CrossRef]
- Byju, A.P.; Sumbul, G.; Demir, B.; Bruzzone, L. Remote-sensing image scene classification with deep neural networks in JPEG 2000 compressed domain. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3458–3472. [Google Scholar] [CrossRef]
- Byju, A.P.; Demir, B.; Bruzzone, L. A progressive content-based image retrieval in JPEG 2000 compressed remote sensing archives. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5739–5751. [Google Scholar] [CrossRef]
- Brahimi, T.; Khelifi, F.; Kacha, A. An efficient JPEG-2000 based multimodal compression scheme. Multimed. Tools Appl. 2021, 80, 21241–21260. [Google Scholar] [CrossRef]
- Rahman, M.A.; Hamada, M.; Shin, J. The impact of state-of-the-art techniques for lossless still image compression. Electronics 2021, 10, 360. [Google Scholar] [CrossRef]
- Chervyakov, N.; Lyakhov, P.; Kaplun, D.; Butusov, D.; Nagornov, N. Analysis of the quantization noise in discrete wavelet transform filters for image processing. Electronics 2018, 7, 135. [Google Scholar] [CrossRef]
- Chervyakov, N.; Lyakhov, P.; Nagornov, N. Analysis of the quantization noise in discrete wavelet transform filters for 3D medical imaging. Appl. Sci. 2020, 10, 1223. [Google Scholar] [CrossRef]
- Shafique, A.; Hazzazi, M.M.; Alharbi, A.R.; Hussain, I. Integration of Spatial and Frequency Domain Encryption for Digital Images. IEEE Access 2021, 9, 149943–149954. [Google Scholar] [CrossRef]
- Wu, Y.; Qian, P.; Zhang, X. Two-level wavelet-based convolutional neural network for image deblurring. IEEE Access 2021, 9, 45853–45863. [Google Scholar] [CrossRef]
- Lone, M.R. A high speed and memory efficient algorithm for perceptually-lossless volumetric medical image compression. J. King Saud Univ.-Comput. Inf. Sci. 2020, 34, 2964–2974. [Google Scholar] [CrossRef]
- Penedo, S.R.M.; Netto, M.L.; Justo, J.F. Designing digital filter banks using wavelets. EURASIP J. Adv. Signal Process. 2019, 2019, 33. [Google Scholar] [CrossRef]
- Vetterli, M. A theory of multirate filter banks. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 356–372. [Google Scholar] [CrossRef]
- Vetterli, M.; Herley, C. Wavelets and filter banks: Theory and design. IEEE Trans. Signal Process. 1992, 40, 2207–2232. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P. Multirate Systems and Filter Banks; Prentice Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Vetterli, M.; Kovačević, J. Wavelets and Subband Coding; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Mintzer, F. Filters for distortion-free two-band multirate filter banks. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 626–630. [Google Scholar] [CrossRef]
- Balasingham, I.; Ramstad, T.A. On the relevance of the regularity constraint in subband image coding. In Proceedings of the IEEE Conference Record of the 31st Asilomar Conference Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 1997; Volume 1, pp. 234–238. [Google Scholar] [CrossRef]
- Patil, B.D.; Patwardhan, P.G.; Gadre, V.M. Eigenfilter approach to the design of one-dimensional and multidimensional two-channel linear-phase FIR perfect reconstruction filter banks. IEEE Trans. Circuits Syst. I Reg. Pap. 2008, 55, 3542–3551. [Google Scholar] [CrossRef][Green Version]
- Smith, M.; Barnwell, T. Exact reconstruction techniques for tree-structured subband coders. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 434–441. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Hoang, P.Q. Lattice structures for optimal design and robust implementation of two-channel perfect-reconstruction QMF banks. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 81–94. [Google Scholar] [CrossRef]
- Vetterli, M. Filter banks allowing perfect reconstruction. Signal Process. 1986, 10, 219–244. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Vaidyanathan, P.P. Two-channel perfect-reconstruction FIR QMF structures which yield linear-phase analysis and synthesis filters. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 676–690. [Google Scholar] [CrossRef]
- Patel, S.; Dhuli, R.; Lall, B. Analysis of Signals via Non-Maximally Decimated Non-Uniform Filter Banks. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 3882–3895. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, J.K. New linear phase QMF filter design for sub-band coding. Electron. Lett. 1991, 27, 319–320. [Google Scholar] [CrossRef]
- Tuncer, T.E.; Nguyen, T.Q. General analysis of two-band QMF banks. IEEE Trans. Signal Process. 1995, 43, 544–548. [Google Scholar] [CrossRef]
- Horng, B.R.; Wilson, A.N. Lagrange multiplier approaches to the design of two-channel perfect-reconstruction linear-phase FIR filter banks. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; pp. 1731–1734. [Google Scholar] [CrossRef]
- Patil, B.D.; Patwardhan, P.G.; Gadre, V.M. On the design of FIR wavelet filter banks using factorization of a halfband polynomial. IEEE Signal Process. Lett. 2008, 15, 485–488. [Google Scholar] [CrossRef]
- Christopoulos, C.; Skodras, A.; Ebrahimi, T. The JPEG 2000 still image coding system: An overview. IEEE Trans. Consum. Electron. 2000, 46, 1103–1127. [Google Scholar] [CrossRef]
- Cho, W.; Chung, D.; Kim, Y.; Kim, I.; Jeon, J. Design of FIR half-band filter with controllable transition-band steepness. IEEE Access 2021, 9, 52144–52154. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, D. Design of nonrecursive FIR filters with simultaneously MAXFLAT magnitude and prescribed cutoff frequency. Digit. Signal Process. 2012, 22, 1085–1094. [Google Scholar] [CrossRef]
- Moir, T.J. FIR Filter Design. In Rudiments of Signal Processing and Systems; Springer: Cham, Switzerland, 2022; pp. 205–243. [Google Scholar]
- Adams, M.D.; Ward, R.K. JasPer: A portable flexible open-source software tool kit for image coding/processing (ver.2.0.0). In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; Volume 5, p. 241. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).