Optimization of Aquifer Monitoring through Time-Lapse Electrical Resistivity Tomography Integrated with Machine-Learning and Predictive Algorithms
Abstract
:Featured Application
Abstract
1. Introduction
2. Background Theory
2.1. DC Electrical Method
2.2. Predictive Methods
2.2.1. Statistical Approaches
2.2.2. Recurrent Neural Networks
3. Datasets
3.1. Real Scale Field Dataset
3.2. Small-Scale Laboratory Dataset
4. Results
4.1. Application of VAR and RNN Methods to Field Dataset
4.2. Application of RNN to Laboratory Dataset
5. Discussion
5.1. Field Experiment: Prediction of Saline Tracer Displacement
5.2. Laboratory Experiment: Prediction of Contamination Evolution
6. Summary of Results
- -
- In the field experiment, based on multiple monitor geoelectrical surveys in cross-hole configuration, multiple resistivity models changing over a period of 28 days of the tracer test were defined;
- -
- A variational statistical method was applied for predicting electrical resistivity variations;
- -
- Transport characteristics of the studied aquifer were evaluated through both measured and predicted electrical resistivity data;
- -
- This predictive approach can be applied for defining optimal aquifer management policy;
- -
- In the lab experiment, Recurrent Neural Networks to retrieve a Multivariate LSTM Forecast Dynamic Model of the tracer displacements over time were applied;
- -
- The predictions obtained through RNN are fully consistent with the evolution of the experimental system effectively observed, confirming the effectiveness of such a type of approach applied to predictive analysis of hydrogeological time-series;
- -
- The predictions are based on the history path of electric potentials recorded through multiple surveys including thousands of measurement points.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater system and climate change: Present status and future considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]
- Lall, U.; Josset, L.; Russo, T. A Snapshot of the World’s Groundwater Challenges. Annu. Rev. Environ. Resour. 2020, 45, 171–194. [Google Scholar] [CrossRef]
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.-F.; Ducharne, A.; Yang, Z.-L. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef] [PubMed]
- Nordin, N.F.C.; Mohd, N.S.; Koting, S.; Ismail, Z.; Sherif, M.; El-Shafie, A. Groundwater quality forecasting modelling using artificial intelligence: A review. Groundw. Sustain. Dev. 2021, 14, 100643. [Google Scholar] [CrossRef]
- Zehe, E.; Loritz, R.; Edery, Y.; Berkowitz, B. Preferential pathways for fluid and solutes in heterogeneous groundwater systems: Self-organization, entropy, work. Hydrol. Earth Syst. Sci. 2021, 25, 5337–5353. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F.; Yin, S.; Wallace, C.D.; Soltanian, M.R.; Dai, Z.; Ritzi, R.W.; Ma, Z.; Zhan, C.; Lü, X. Application of upscaling methods for fluid flow and mass transport in multi-scale heterogeneous media: A critical review. Appl. Energy 2021, 303, 117603. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Hubbard, S.S.; Rubin, Y. Hydrogeological parameter estimation using geophysical data: A review of selected techniques. J. Contam. Hydrol. 2000, 45, 3–34. [Google Scholar] [CrossRef]
- Sandberg, S.K.; Slater, L.D.; Versteeg, R. An integrated geophysical investigation of the hydrogeology of an anisotropic unconfined aquifer. J. Hydrol. 2022, 267, 227–243. [Google Scholar] [CrossRef]
- Doetsch, J.; Linde, N.; Vogt, T.; Binley, A.; Green, A.G. Imaging and quantifying salt-tracer transport in a riparian groundwater system by means of 3D ERT monitoring. Geophysics 2012, 77, B207–B218. [Google Scholar] [CrossRef] [Green Version]
- Fernández de Vera, N.; Beaujean, J.; Jamin, P.; Hakoun, V.; Caterina, D.; Dahan, O.; Vanclooster, M.; Dassargues, A.; Nyugen, F.; Brouyère, S. Tracer experiment in a brownfield using geophysics and a vadose zone monitoring system. Vadose Zone J. 2017, 16, 1–15. [Google Scholar] [CrossRef]
- McLachlan, P.J.; Chambers, J.E.; Uhlemann, S.S.; Binley, A. Geophysical characterisation of the groundwater–surface water interface. Adv. Water Resour. 2017, 109, 302–319. [Google Scholar] [CrossRef]
- Bouzaglou, V.; Crestani, E.; Salandin, P.; Gloaguen, E.; Camporese, M. Ensemble Kalman Filter Assimilation of ERT Data for Numerical Modeling of Seawater Intrusion in a Laboratory Experiment. Water 2018, 10, 397. [Google Scholar] [CrossRef]
- Binley, A. 11.08-Tools and Techniques: Electrical Methods. In Treatise on Geophysics; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 233–259. [Google Scholar]
- Glover, P.W.J. 11.0-Geophysical Properties of the Near Surface Earth: Electrical Properties. In Treatise on Geophysics; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 89–137. [Google Scholar]
- Binley, A.; Cassiani, G.; Middleton, R.; Winship, P. Vadose zone flow model parameterisation using cross-borehole radar and resistivity imaging. J. Hydrol. 2002, 267, 147–159. [Google Scholar] [CrossRef]
- Perri, M.T.; Cassiani, G.; Gervasio, I.; Deiana, R.; Binley, A. A saline tracer test monitored via both surface and cross-borehole electrical resistivity tomography: Comparison of time-lapse results. J. Appl. Geophys. 2012, 79, 6–16. [Google Scholar] [CrossRef]
- Karaoulis, M.; Tsourlos, P.; Kim, J.H.; Revil, A. 4D time-lapse ERT inversion: Introducing combined time and space constraints. Near Surf. Geophys. 2014, 12, 25–34. [Google Scholar] [CrossRef]
- Watlet, A.; Kaufmann, O.; Triantafyllou, A.; Poulain, A.; Chambers, J.E.; Meldrum, P.I.; Wilkinson, P.B.; Hallet, V.; Quinif, Y.; Van Ruymbeke, M.; et al. Imaging groundwater infiltration dynamics in the karst vadose zone with long-term ert monitoring. Hydrol. Earth Syst. Sci. 2018, 22, 1563–1592. [Google Scholar] [CrossRef]
- Mary, B.; Peruzzo, L.; Boaga, J.; Cenni, N.; Schmutz, M.; Wu, Y.; Hubbard, S.S.; Cassiani, G. Time-lapse monitoring of root water uptake using electrical resistivity tomography and mise-à-la-masse: A vineyard infiltration experiment. Soil 2020, 6, 95–114. [Google Scholar] [CrossRef]
- Lapenna, V.; Perrone, A. Time-Lapse Electrical Resistivity Tomography (TL-ERT) for Landslide Monitoring: Recent Advances and Future Directions. Appl. Sci. 2022, 12, 1425. [Google Scholar] [CrossRef]
- Folch, A.; del Val, L.; Luquot, L.; Martínez-Pérez, L.; Bellmunt, F.; Le Lay, H.; Rodellas, V.; Ferrer, N.; Palacios, A.; Fernández, S.; et al. Combining fiber optic DTS, cross-hole ERT and time-lapse induction logging to characterize and monitor a coastal aquifer. J. Hydrol. 2020, 588, 125050. [Google Scholar] [CrossRef]
- Palacios, A.; Ledo, J.J.; Linde, N.; Luquot, L.; Bellmunt, F.; Folch, A.; Marcuello, A.; Queralt, P.; Pezard, P.A.; Martínez, L.; et al. Time-lapse cross-hole electrical resistivity tomography (CHERT) for monitoring seawater intrusion dynamics in a Mediterranean aquifer. Hydrol. Earth Syst. Sci. 2020, 24, 2121–2139. [Google Scholar] [CrossRef]
- Blazevic, L.A.; Bodet, L.; Pasquet, S.; Linde, N.; Jougnot, D.; Longuevergne, L. Time-Lapse Seismic and Electrical Monitoring of the Vadose Zone during a Controlled Infiltration Experiment at the Ploemeur Hydrological Observatory, France. Water 2020, 12, 1230. [Google Scholar] [CrossRef]
- Almpanis, A.; Gerhard, J.; Power, C. Mapping and monitoring of DNAPL source zones with combined direct current resistivity and induced polarization: A field-scale numerical investigation. Water Resour. Res. 2021, 57, e2021WR031366. [Google Scholar] [CrossRef]
- Nazifi, H.M.; Gülen, L.; Gürbüz, E.; Pekşen, E. Time-lapse electrical resistivity tomography (ERT) monitoring of used engine oil contamination in laboratory setting. J. Appl. Geophys. 2022, 197, 104531. [Google Scholar] [CrossRef]
- Cannavò, F.; Cannata, A.; Donner, R.V.; Kanevski, M. Editorial: Advanced Time Series Analysis in Geosciences. Front. Earth Sci. 2022, 9, 666148. [Google Scholar] [CrossRef]
- Hill, P.; Biggs, J.; Ponce-López, V.; Bull, D. Time-series prediction approaches to forecasting deformation in Sentinel-1 InSAR data. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020176. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. Int. J. Forecast. 2020, 37, 388–427. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M.; Mercer, A. Artificial neural networks and support vector machines: Contrast study for groundwater level prediction. In Proceedings of the ASABE Annual International Meeting, New Orleans, LA, USA, 26–29 July 2015; p. 1. [Google Scholar]
- Valadkhan, D.; Moghaddasi, R.; Mohammadinejad, A. Groundwater quality prediction based on LSTM RNN: An Iranian experience. Int. J. Environ. Sci. Technol. 2022, 12. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. One-step ahead forecasting of geophysical processes within a purely statistical framework. Geosci. Lett. 2018, 5, 12. [Google Scholar] [CrossRef]
- Bhardwaj, S.; Chandrasekhar, E.; Padiyar, P.; Gadre, V.M. A comparative study of wavelet-based ANN and classical techniques for geophysical time-series forecasting. Comput. Geosci. 2020, 138, 104461. [Google Scholar] [CrossRef]
- Dell’Aversana, P. Reinforcement Learning in Optimization Problems. Applications to Geophysical Data Inversion. AIMS Geosci. 2022, 8, 488–502. [Google Scholar] [CrossRef]
- Dell’Aversana, P. Reservoir prescriptive management combining electric resistivity tomography and machine learning. AIMS Geosci. 2021, 7, 138–161. [Google Scholar] [CrossRef]
- Lee, S.-J.; Yoon, H.-K. Discontinuity Predictions of Porosity and Hydraulic Conductivity Based on Electrical Resistivity in Slopes through Deep Learning Algorithms. Sensors 2021, 21, 1412. [Google Scholar] [CrossRef] [PubMed]
- Dell’Aversana, P. Combining Geophysical Inversion with Reinforcement Learning. In Proceedings of the 83rd EAGE Annual Conference & Exhibition, Madrid, Spain, 6–9 June 2022; Volume 2022, pp. 1–5. [Google Scholar] [CrossRef]
- Alali, A.; Kazei, V.; Sun, B.; Alkhalifah, T. Time-lapse data matching using a recurrent neural network approach. Geophysics 2022, 87, V405–V417. [Google Scholar] [CrossRef]
- Kunetz, G. Principles of Direct Current Resistivity Prospecting (Geoexploration Monographs, Series 1, Number 1); Schweizerbart Science Publishers: Stuttgart, Germany, 1966; 103p. [Google Scholar]
- Shima, H. 2D and 3D resistivity image reconstruction using crosshole data. Geophysics 1992, 57, 1270–1281. [Google Scholar] [CrossRef]
- Zhou, B.; Greenhalgh, S.A. A synthetic study on cross-hole resistivity imaging with different electrode arrays. Explor. Geophys. 1997, 28, 1–5. [Google Scholar]
- Exponential Smoothing for Predicting Demand; Arthur, D. (Ed.) Little Inc.: Cambridge, MA, USA, 1956; p. 15. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis; Wiley: New York, NY, USA, 1958; pp. 1–713. [Google Scholar]
- Feinstein, A.R. Multivariable Analysis: An Introduction; Yale University Press: New Haven, CT, USA, 1996; pp. 1–613. [Google Scholar]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Person New International Edition: London, UK, 2014; pp. 1–776. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin, Germany, 2005; pp. 1–553. [Google Scholar]
- Asteriou, D.; Hall, S.G. Vector Autoregressive (VAR) Models and Causality Tests. In Applied Econometrics; Palgrave MacMillan: London, UK, 2011; pp. 319–333. [Google Scholar]
- Barkan, O.; Benchimol, J.; Caspi, I.; Cohen, E.; Hammer, A.; Koenigstein, N. Forecasting CPI inflation components with Hierarchical Recurrent Neural Networks. Int. J. Forecast. 2022, in press. [Google Scholar] [CrossRef]
- Haşim, S.; Senior, A.; Beaufays, F. Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modelling. In Proceedings of the 15th Annual Conference of the International Speech Communication Association (INTERSPEECH 2014), Singapore, 14–18 September 2014. [Google Scholar]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2015), Bruges, Belgium, 22–24 April 2015. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Physica D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Saad, E.W.; Prokhorov, D.V.; Wunsch, D.C. Comparative study of stock trend prediction using time delay, recurrent and probabilistic neural networks. IEEE Trans. Neural Netw. 1998, 9, 1456–1470. [Google Scholar] [CrossRef]
- Tealab, A.; Hefny, H.; Badr, A. Forecasting of nonlinear time series using ANN. Future Comput. Inform. J. 2017, 2, 39–47. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2019, 323, 203–213. [Google Scholar] [CrossRef]
- Giampaolo, V.; Rizzo, E.; Straface, S.; Votta, M. Hydrogeophysics techniques for the characterization of a heterogeneous aquifer. Boll. Di Geofis. Teor. Ed Appl. 2011, 52, 595–606. [Google Scholar]
- Giampaolo, V.; Rizzo, E.; Straface, S.; Chidichimo, F.; Votta, M. Hydrogeophysical methods for saline tracer test. In Proceedings of the 1st International Workshop: Methods and Technologies for Environmental Monitoring and Modelling: Landslides and Groundwater Dynamics, Potenza, Italy, 29 September–3 October 2011; pp. 159–162. [Google Scholar]
- Giampaolo, V.; Rizzo, E.; Straface, S.; Chidichimo, F.; Votta, M. Transport processes in porous media by geophysical methods. In Proceedings of the XXX Convegno Nazionale del Gruppo Nazionale di Geofisica della Terra Solida (GNGTS), Trieste, Italy, 14–17 November 2011; pp. 568–571. [Google Scholar]
- Giampaolo, V. Hydrogeophysical Methods for Soils and Groundwater Contamination. Ph.D. Thesis, The Basilicata University, Potenza, Italy, 2013. [Google Scholar]
- Troisi, S.; Fallico, C.; Straface, S.; Migliari, E. Application of kriging with external drift to estimate hydraulic conductivity from electrical resistivity data in unconsolidated deposits near Montalto Uffugo, Italy. Hydrogeol. J. 2000, 8, 356–367. [Google Scholar] [CrossRef]
- Rizzo, E.; Suski, B.; Revil, A.; Straface, S.; Troisi, S. Self-potential signals associated with pumping-tests experiments. J. Geophys. Res. 2004, 109, B10203. [Google Scholar] [CrossRef]
- Straface, S.; Fallico, C.; Troisi, S.; Rizzo, E.; Revil, A. An inverse procedure to estimate transmissivity from heads and SP signals. Ground Water 2007, 45, 420–428. [Google Scholar] [CrossRef]
- Blanchy, G.; Saneiyan, S.; Boyd, J.; McLachlan, P.; Binley, A. ResIPy, an intuitive open source software for complex geoelectrical inversion/modelling. Comput. Geosci. 2020, 137, 104423. [Google Scholar] [CrossRef]
- Befus, K.M. Pyres: A Python Wrapper for Electrical Resistivity Modeling with R2. J. Geophys. Eng. 2018, 15, 338–346. [Google Scholar] [CrossRef]
- Capozzoli, L.; De Martino, G.; Giampaolo, V.; Parisi, S.; Rizzo, E. Integrated geophysical and hydraulic methodologies for the study of contaminant transport process in the subsoil: A sand box experiment. In Proceedings of the XXXIII Convegno Nazionale del Gruppo Nazionale di Geofisica della Terra Solida (GNGTS), Bologna, Italy, 25–27 November 2014; pp. 143–149. [Google Scholar]
- Capozzoli, L. Electric and Electromagnetic Geophysical Methods for the Characterization and Monitoring of Contamination Phenomena in the Subsoil. Ph.D. Thesis, The Basilicata University, Potenza, Italy, 2014. [Google Scholar]
- Straface, S.; Rizzo, E.; Chidichimo, F. Estimation of hydraulic conductivity and water table map in a large-scale laboratory model by means of the self-potential method. J. Geophys. Res. 2011, 115, B06105. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Christensen, N.K.; Christensen, S.; Ferre, T.P.A. Testing alternative uses of electromagnetic data to reduce the prediction error of groundwater models. Hydrol. Earth Syst. Sci. 2016, 20, 1925–1946. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Yang, X. Difference inversion of ERT data. A fast inversion method for 3-D in situ monitoring. J. Environ. Eng. Geophys. 2001, 6, 83–89. [Google Scholar] [CrossRef]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Schön, J.H. Physical Properties of Rocks: Fundamentals and Principles of Petrophysics; Elsevier: Amsterdam, The Netherlands, 2004; pp. 1–600. [Google Scholar]
- Riedel, M.; Collett, T.S.; Hyndman, R.D. Gas Hydrate Concentration Estimates from Chlorinity, Electrical Resistivity, and Seismic Velocity; Open-File Rep. 4934; Geological Survey of Canada: Ottawa, ON, Canada, 2005.
- Atekwanaa, E.A.; Atekwanaa, E.; Roweb, R.S.; Werkema, D.D.; Legalld, F.D. The relationship of total dissolved solids measurements to bulk electrical conductivity in an aquifer contaminated with hydrocarbon. J. Appl. Geophys. 2004, 56, 281–294. [Google Scholar] [CrossRef]
- Rusydi, A.F. Correlation between conductivity and total dissolved solid in various type of water: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 118, 012019. [Google Scholar] [CrossRef]
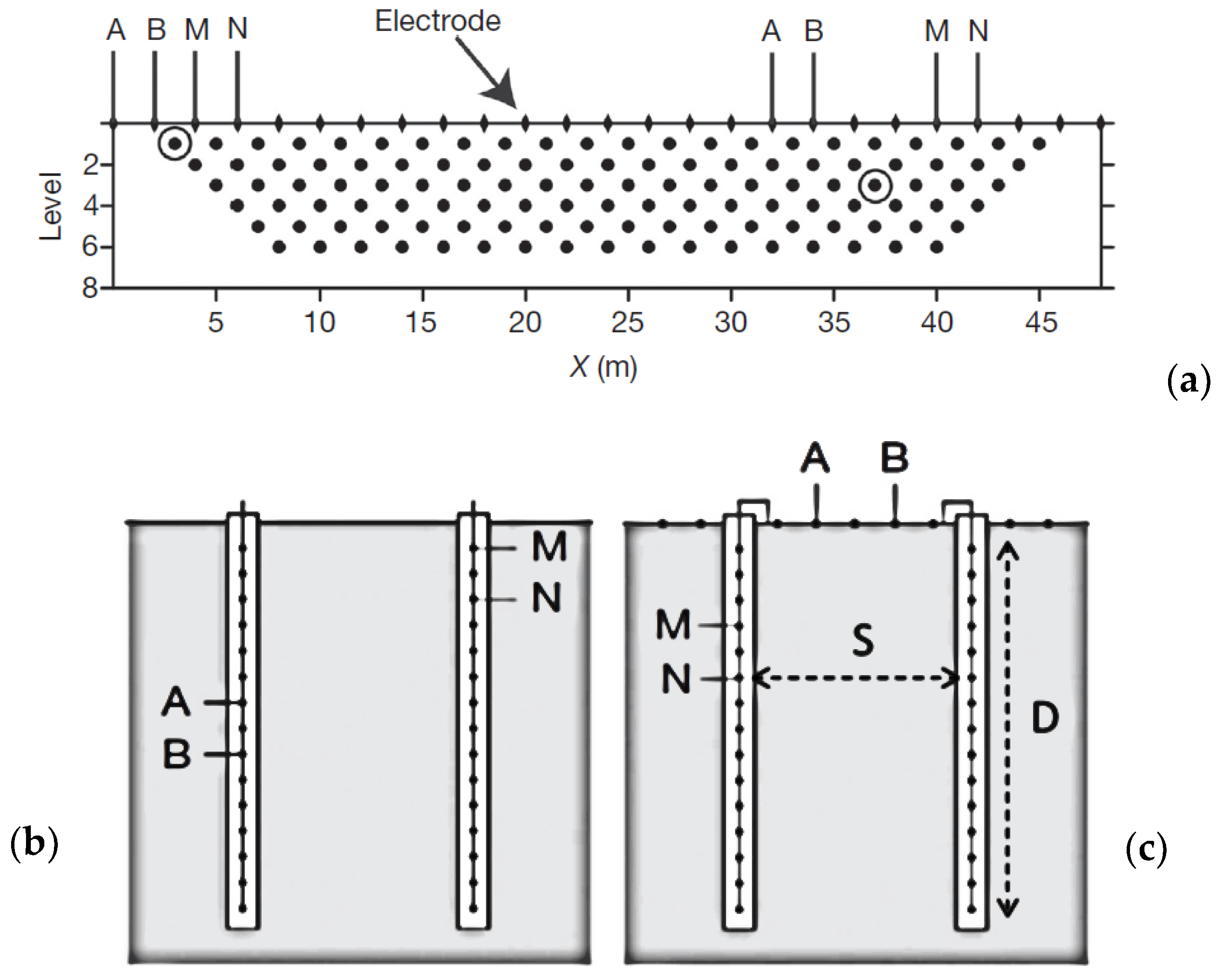


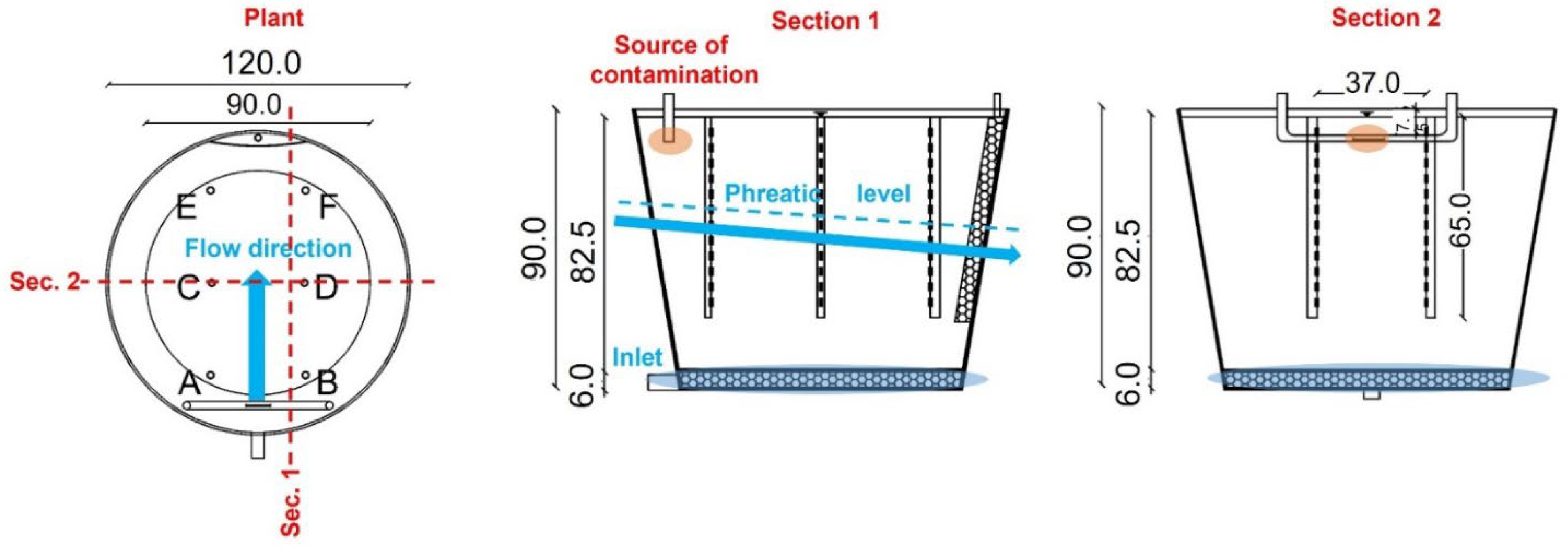
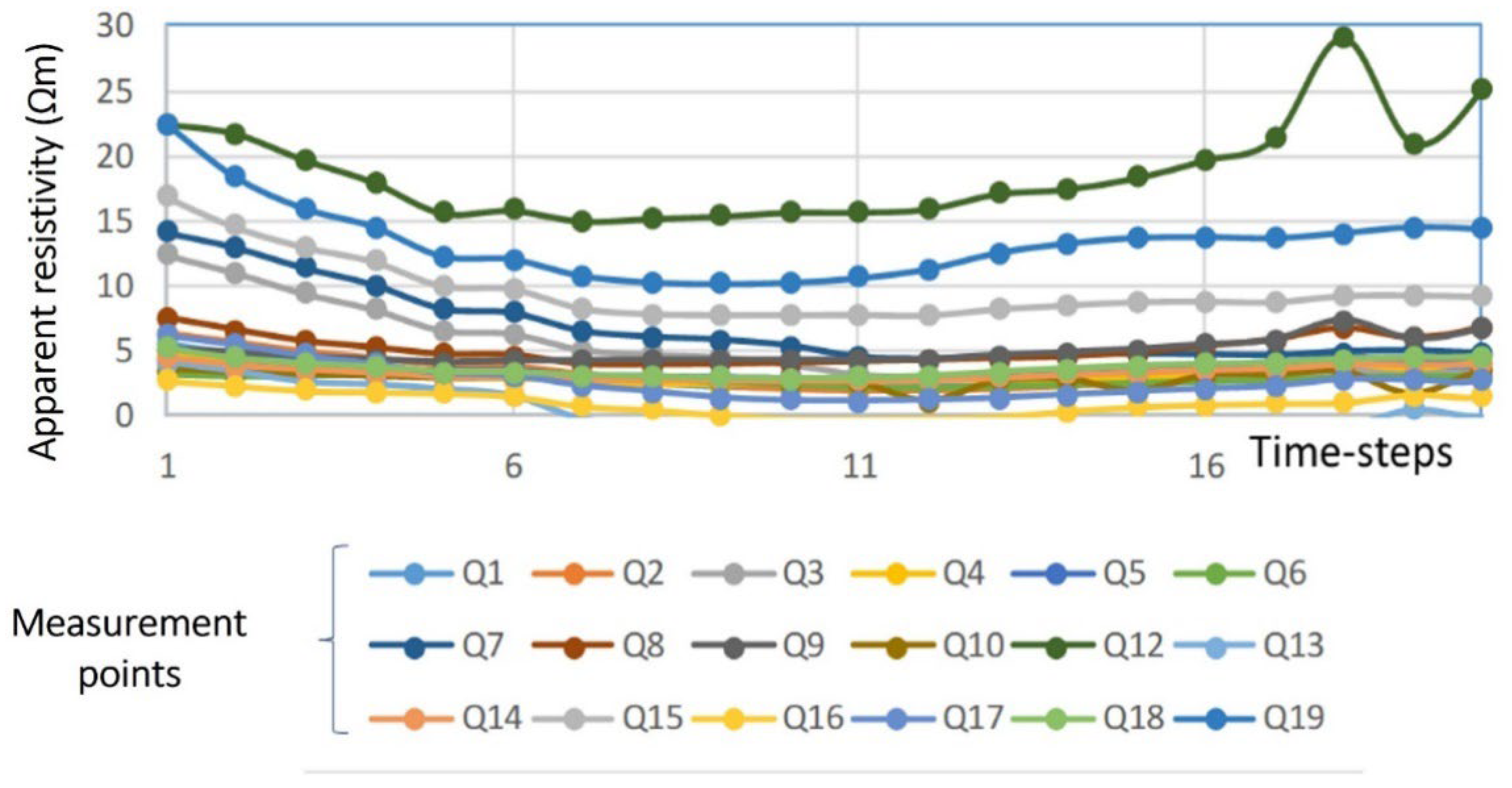
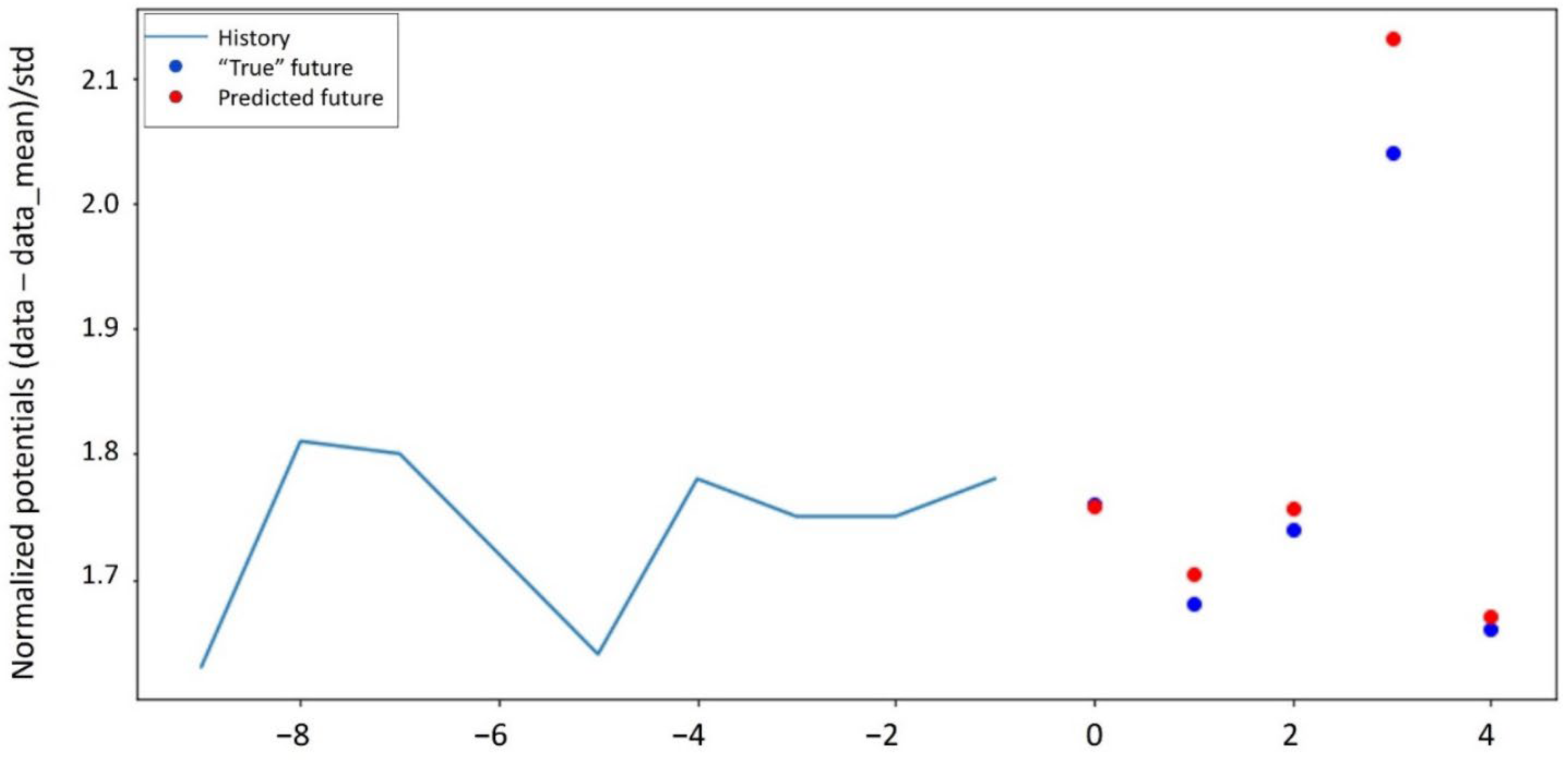
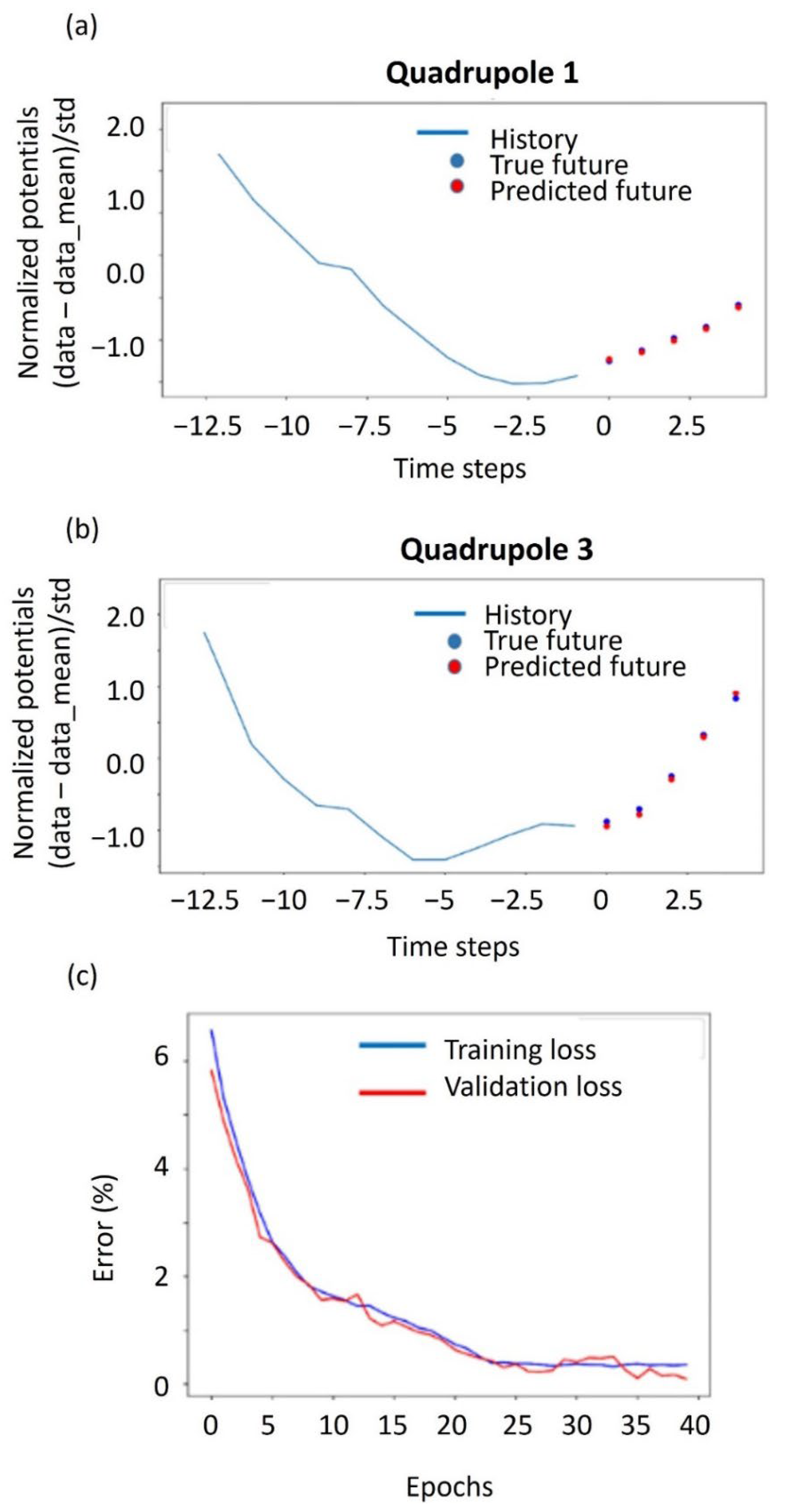

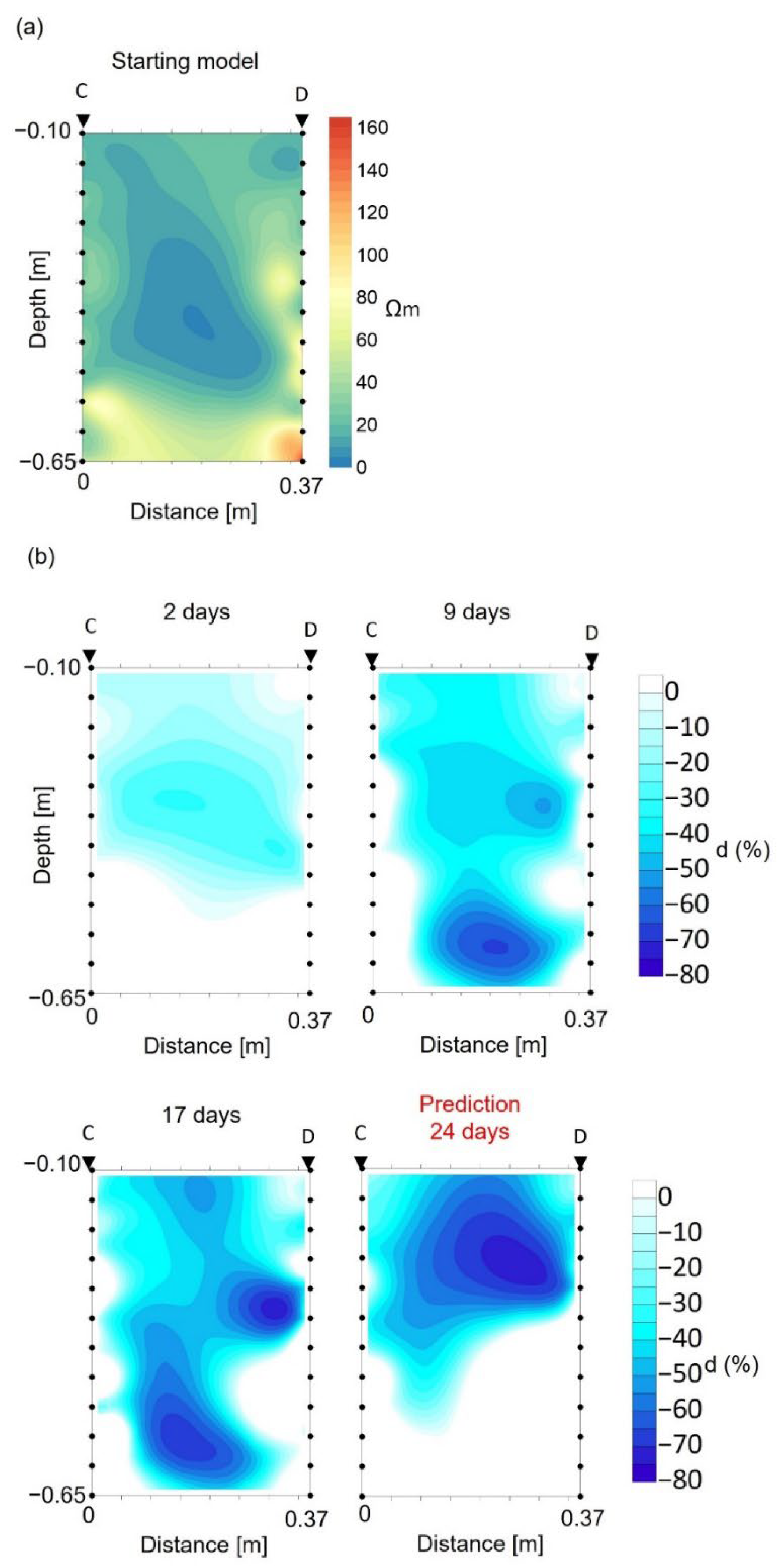
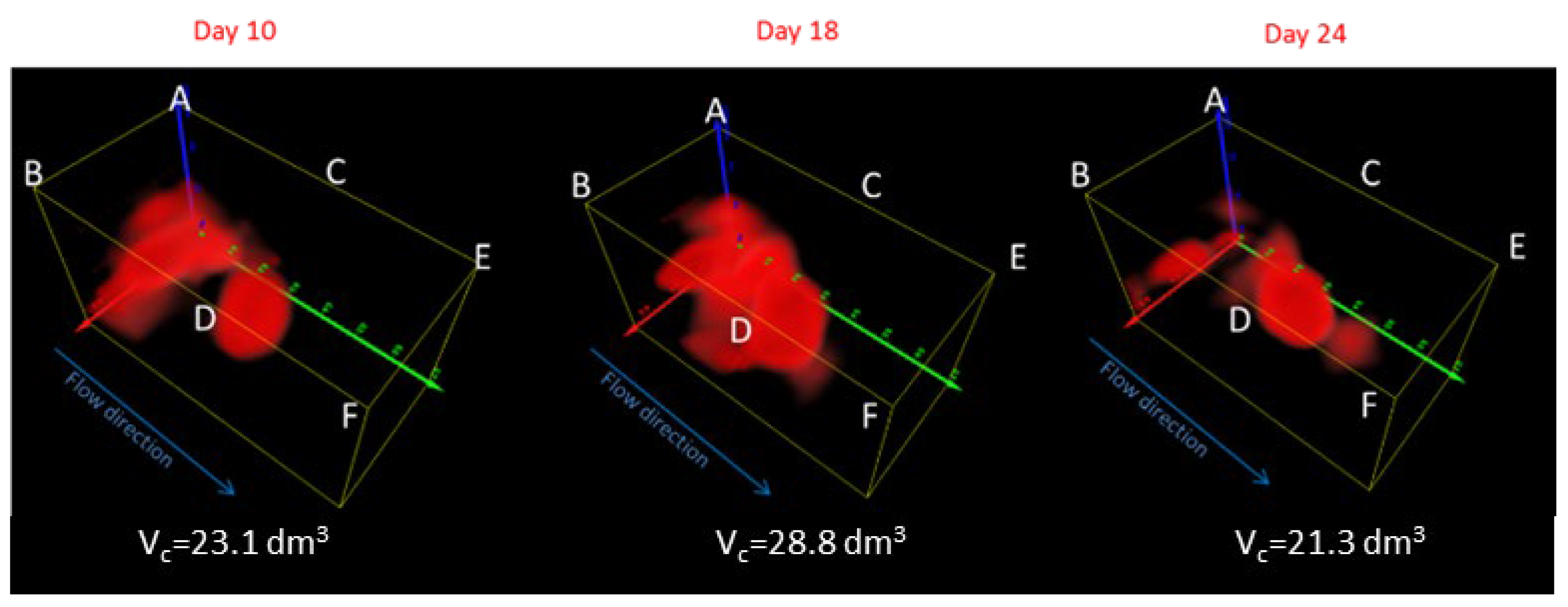
| Electrical Resistivity Dataset | Number of Surveys in Training Data | Number of Surveys in Test Data |
|---|---|---|
| Field data | 2–20 CH-ERT | 5 CH-ERT |
| (1836 data each) | (1836 data each) | |
| Laboratory data | 2–20 CH-ERT | 5 CH-ERT |
| (504 data each) | (504 data each) |
| Sequential ERT Surveys | Resistance at the Various Quadrupoles (Ω) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 | Q8 | Q9 | Q10 | |
| STEP 10 | 1.76 | 19.16 | 8.80 | 1.65 | 12.03 | 14.33 | 16.15 | 13.40 | 19.71 | 8.88 |
| STEP 11 | 1.68 | 19.21 | 8.46 | 3.59 | 9.63 | 13.15 | 15.29 | 12.93 | 19.13 | 9.16 |
| STEP 12 | 1.74 | 19.13 | 8.46 | 3.09 | 10.06 | 13.33 | 15.60 | 13.20 | 19.66 | 9.37 |
| STEP 13 | 2.04 | 18.87 | 9.33 | 1.08 | 9.64 | 12.81 | 15.66 | 13.37 | 20.80 | 10.33 |
| STEP 14 | 1.66 | 19.07 | 8.47 | 3.17 | 10.78 | 13.17 | 15.32 | 12.75 | 19.46 | 9.25 |
| STEP 15 | 1.77 | 19.02 | 8.50 | 3.24 | 10-08 | 12.94 | 15.18 | 12.81 | 19.65 | 9.11 |
| STEP 16 | 1.92 | 18.90 | 8.40 | 2.95 | 10.79 | 13.19 | 15.29 | 12.66 | 19.42 | 9.39 |
| STEP 17 | 1.83 | 19.12 | 9.69 | 1.15 | 9.24 | 12.72 | 16.72 | 14.35 | 21.21 | 11.87 |
| STEP 18 | 1.84 | 18.29 | 7.29 | 0.22 | 11.95 | 16.95 | 15.46 | 15.47 | 19.09 | 12.43 |
| Sequential Predictions | Predicted resistance at the Various Quadrupoles (Ω) | |||||||||
| PRED 1 | 1.85 | 18.80 | 8.47 | 1.38 | 10.95 | 14.07 | 15.80 | 14.12 | 20.05 | 11.10 |
| PRED 2 | 1.86 | 18.77 | 8.47 | 1.25 | 11.04 | 14.12 | 15.84 | 14.19 | 20.09 | 11.24 |
| PRED 3 | 1.87 | 18.75 | 8.47 | 1.12 | 11.12 | 14.18 | 15.88 | 14.27 | 20.13 | 11.37 |
| PRED 4 | 1.88 | 18.72 | 8.47 | 0.99 | 11.21 | 14.24 | 15.92 | 14.35 | 20.17 | 11.50 |
| PRED 5 | 1.89 | 18.69 | 8.47 | 0.88 | 11.29 | 14.30 | 15.96 | 14.43 | 20.22 | 11.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giampaolo, V.; Dell’Aversana, P.; Capozzoli, L.; De Martino, G.; Rizzo, E. Optimization of Aquifer Monitoring through Time-Lapse Electrical Resistivity Tomography Integrated with Machine-Learning and Predictive Algorithms. Appl. Sci. 2022, 12, 9121. https://doi.org/10.3390/app12189121
Giampaolo V, Dell’Aversana P, Capozzoli L, De Martino G, Rizzo E. Optimization of Aquifer Monitoring through Time-Lapse Electrical Resistivity Tomography Integrated with Machine-Learning and Predictive Algorithms. Applied Sciences. 2022; 12(18):9121. https://doi.org/10.3390/app12189121
Chicago/Turabian StyleGiampaolo, Valeria, Paolo Dell’Aversana, Luigi Capozzoli, Gregory De Martino, and Enzo Rizzo. 2022. "Optimization of Aquifer Monitoring through Time-Lapse Electrical Resistivity Tomography Integrated with Machine-Learning and Predictive Algorithms" Applied Sciences 12, no. 18: 9121. https://doi.org/10.3390/app12189121
APA StyleGiampaolo, V., Dell’Aversana, P., Capozzoli, L., De Martino, G., & Rizzo, E. (2022). Optimization of Aquifer Monitoring through Time-Lapse Electrical Resistivity Tomography Integrated with Machine-Learning and Predictive Algorithms. Applied Sciences, 12(18), 9121. https://doi.org/10.3390/app12189121









