A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model
Abstract
:1. Introduction
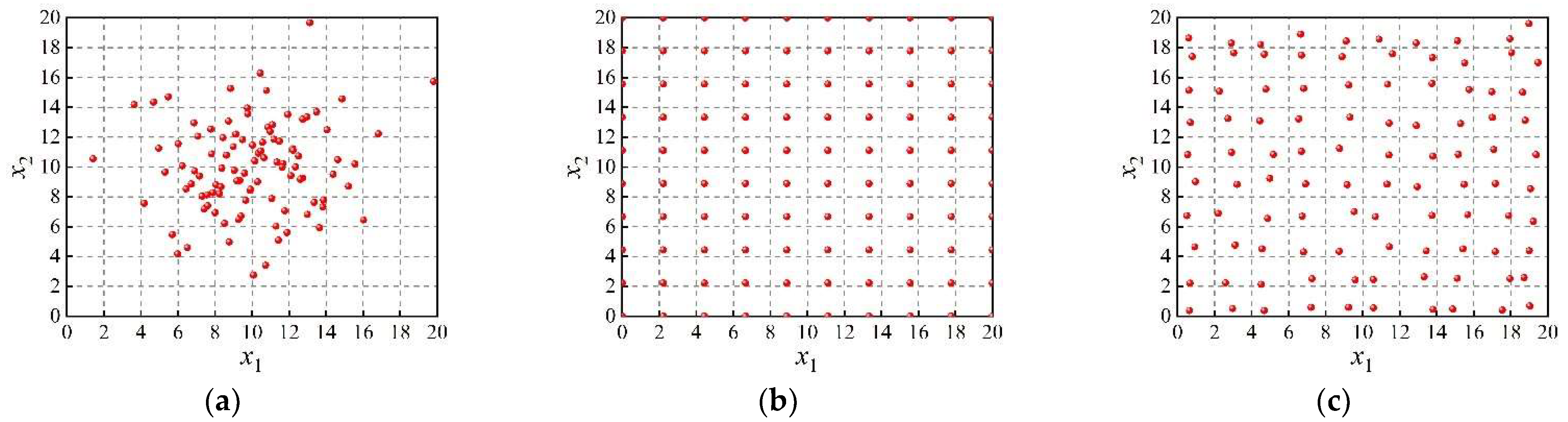
2. Random Moving Quadrilateral Grid Sampling Method
3. Reliability Analysis Approach under Multiple Failure Modes
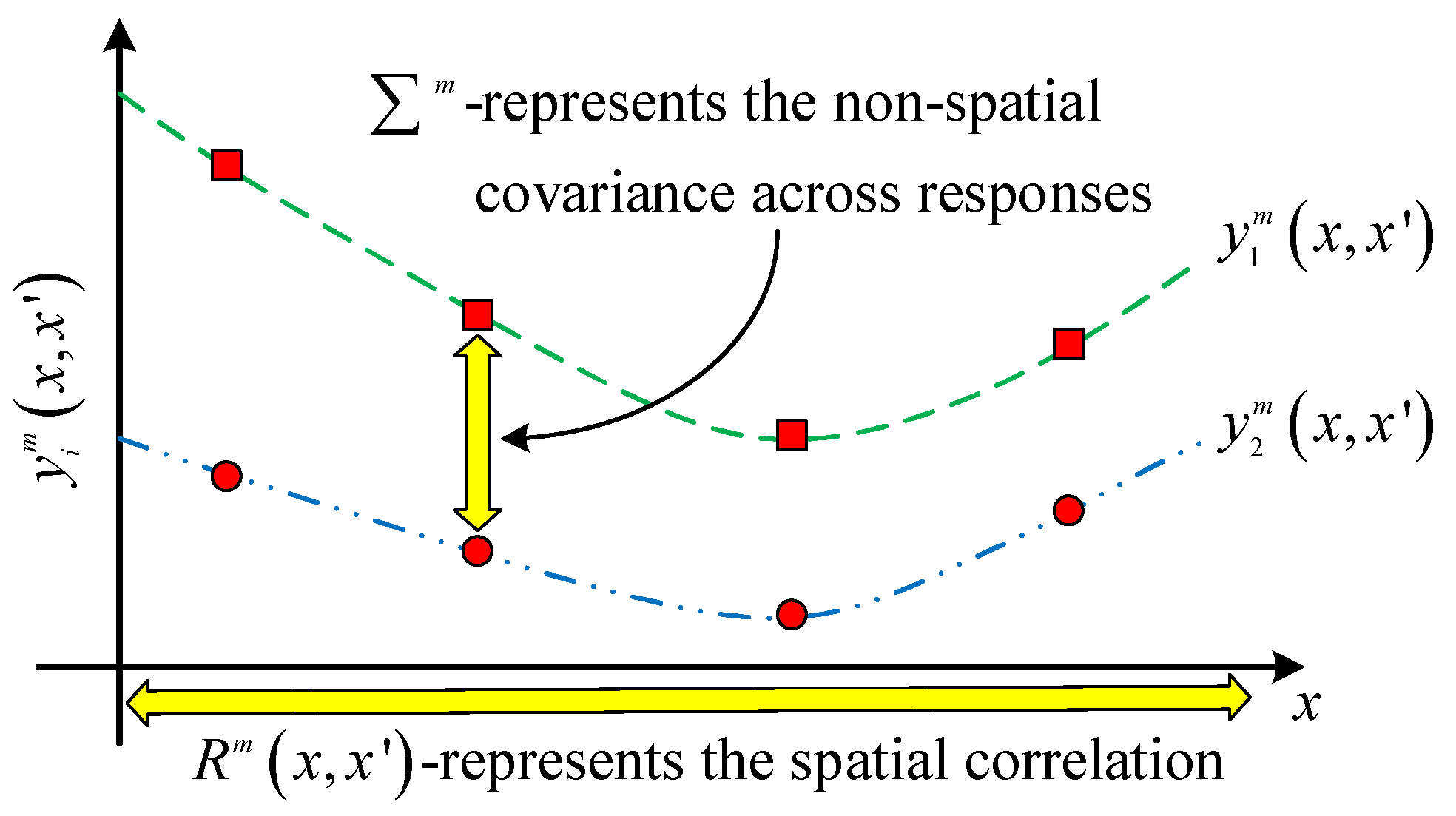
3.1. Adaptive Multiple Response Gaussian Process
3.2. MRGP-SS Based Structure Reliability Analysis
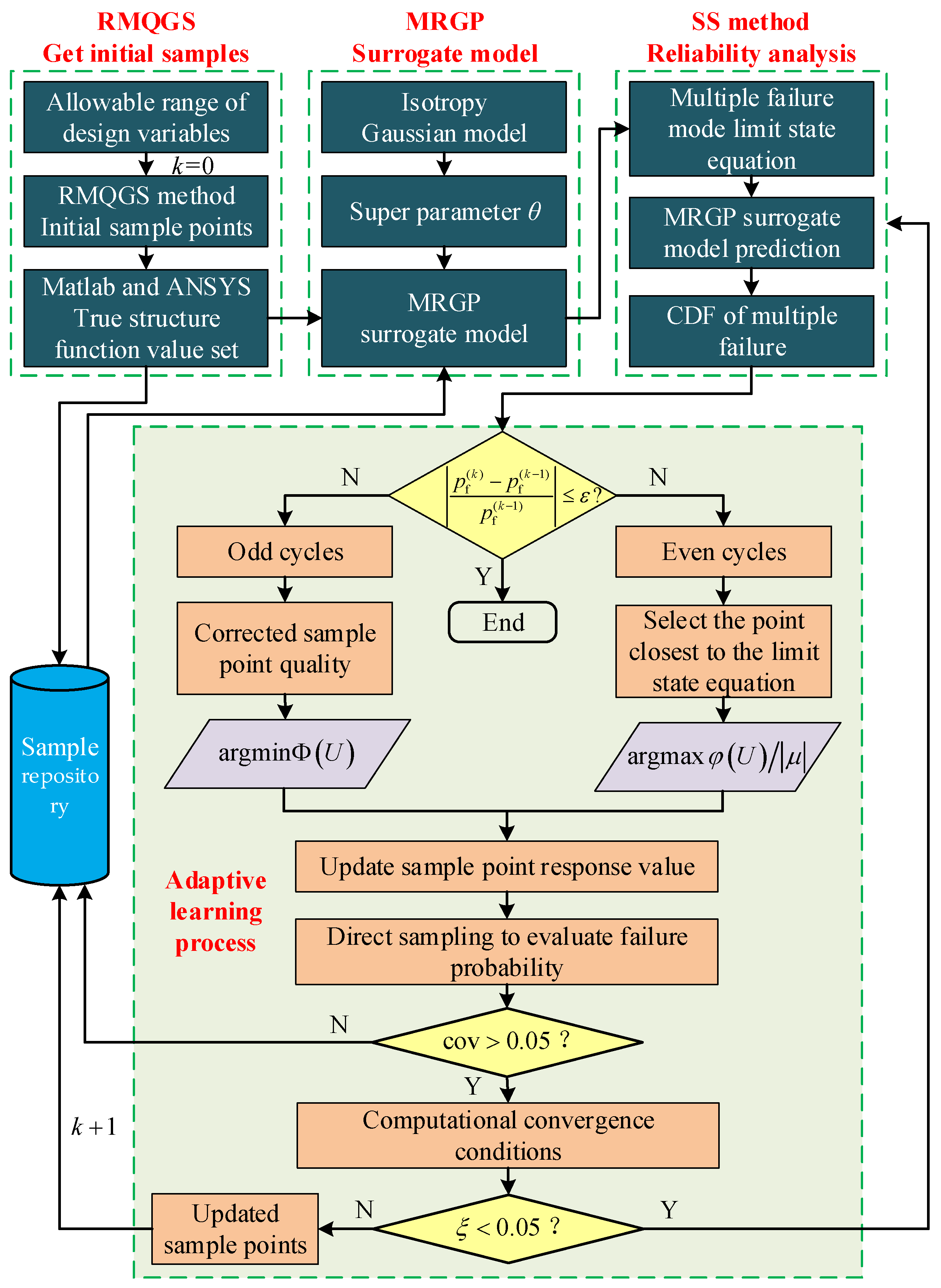
3.3. Summary of the Proposed Method
4. Case Studies
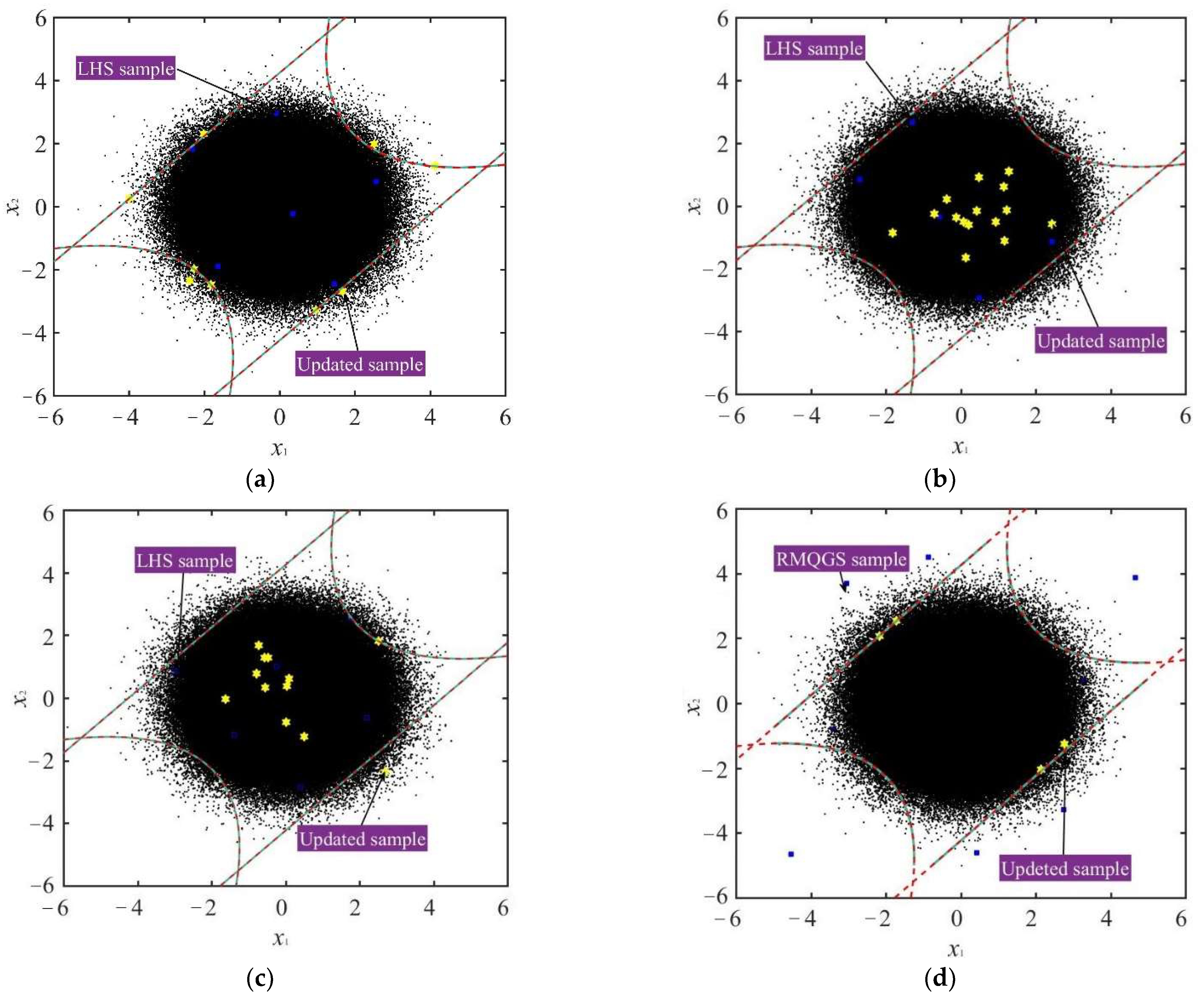
4.1. Validation of RMQGS Method
4.2. A Numerical Series System Analysis
4.3. A Numerical Parallel System Analysis
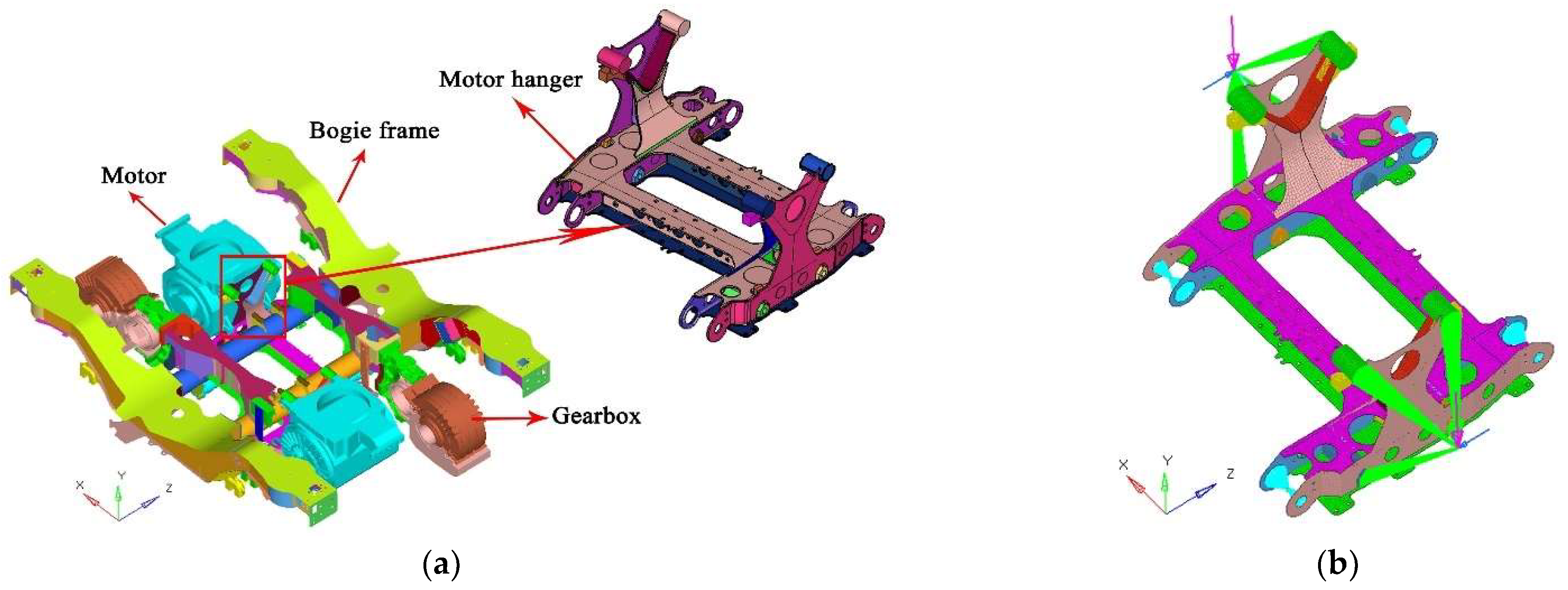
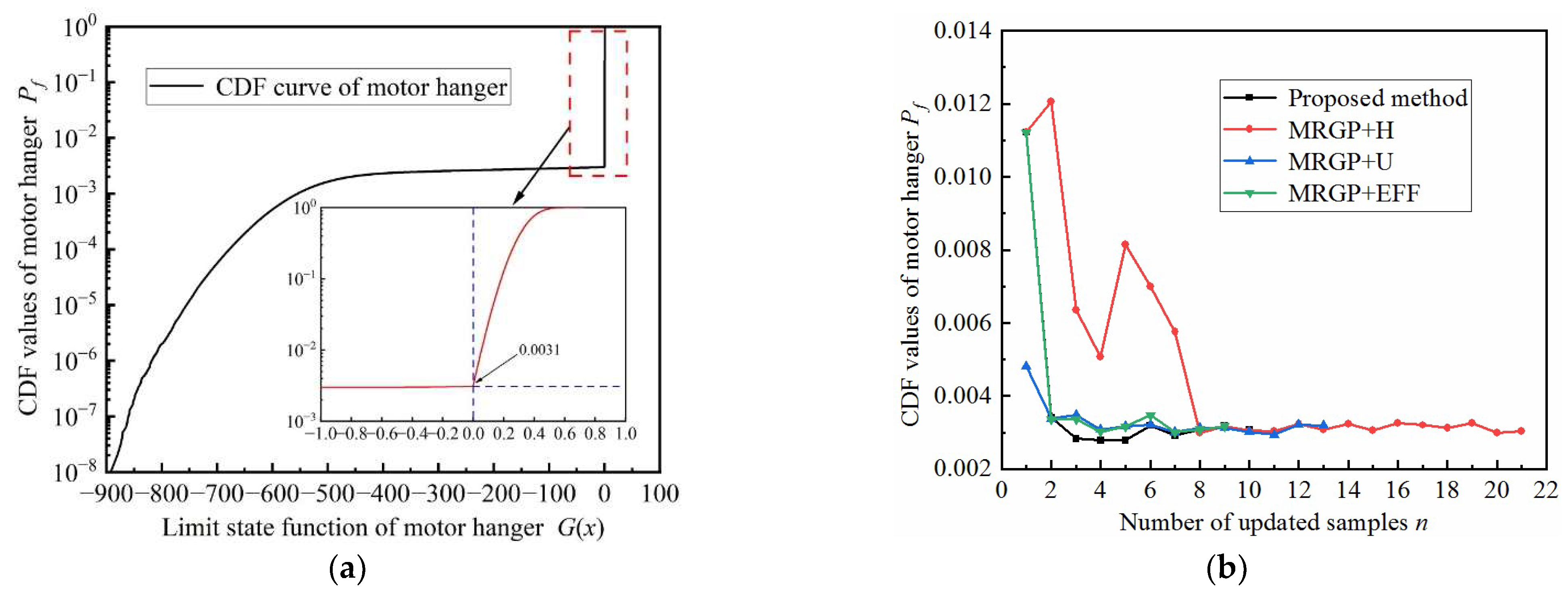
4.4. Motor Hanger Reliability Analysis under Multiple Failure Models
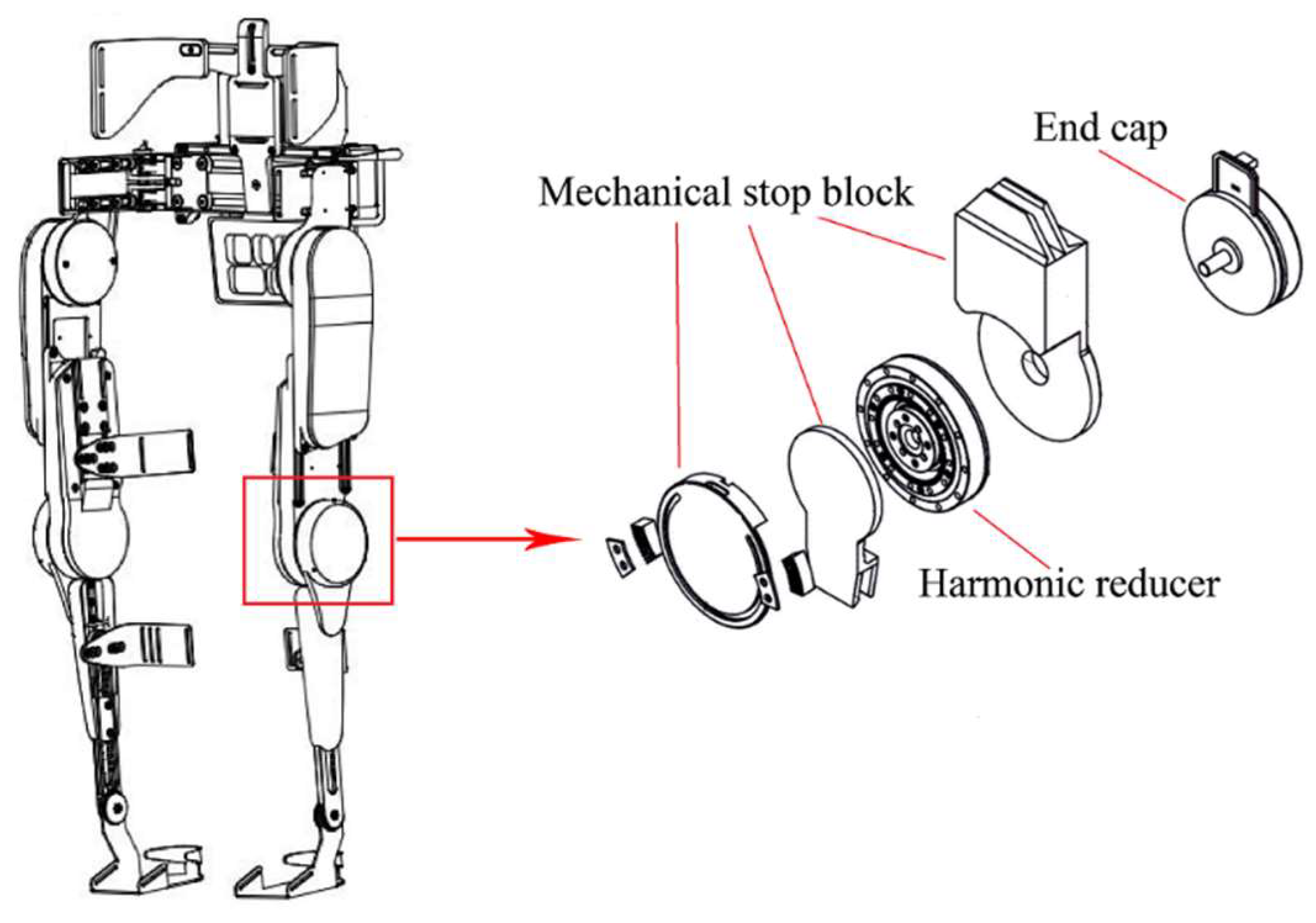
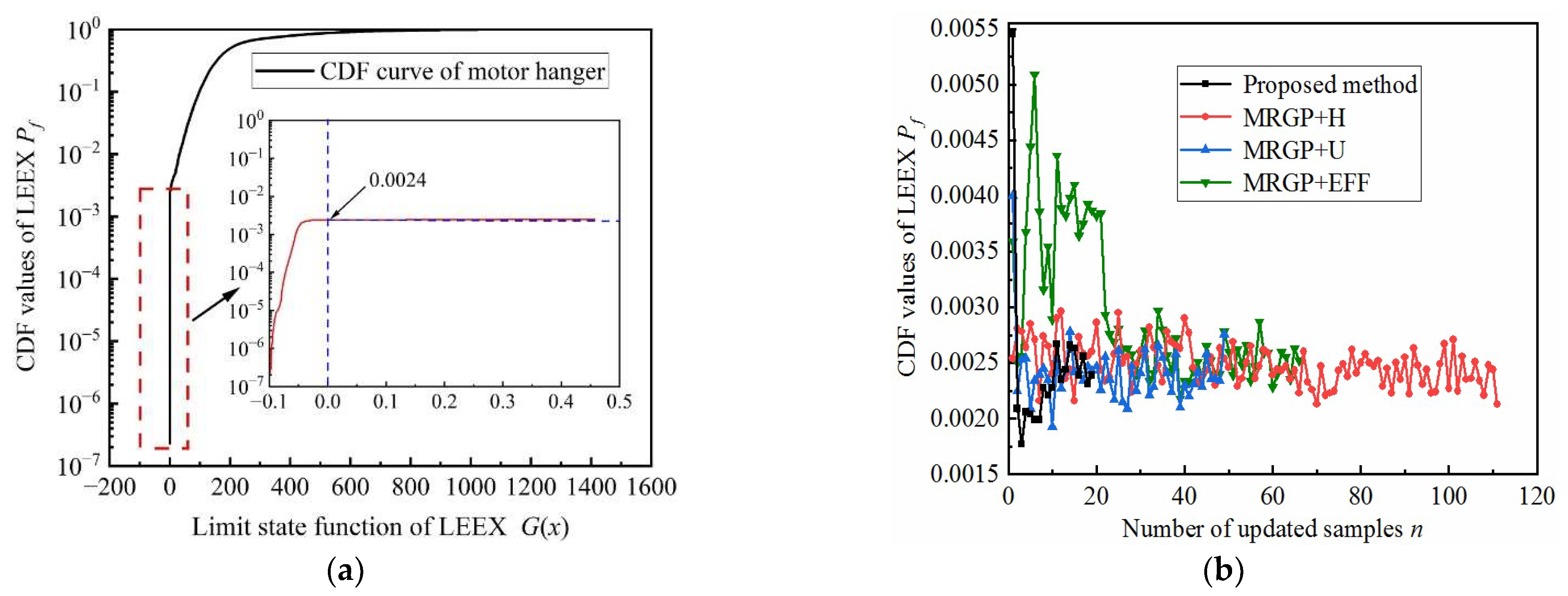
4.5. Reliability Analysis of A Bionic Robot Lower Extremity Exoskeleton (LEEX) under Multiple Failure Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bichon, B.J.; McFarland, J.M.; Mahadevan, S. Efficient surrogate models for reliability analysis of systems with multiple failure modes. Reliab. Eng. Syst. Saf. 2011, 96, 1386–1395. [Google Scholar] [CrossRef]
- Li, G.J.; Lu, Z.Z.; Zhang, X.B.; Zhang, F. A new reliability approach for the fuzzy and random structure based on the uniformly distributed membership level. Int. J. Fuzzy Syst. 2022, 24, 2753–2766. [Google Scholar] [CrossRef]
- Hasofer, A.; Lind, N. Exact and invariant second-moment code format. J. Eng. Mech. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Du, X.P.; Sudjianto, A. First order saddlepoint approximation for reliability analysis. AAIA J. 2004, 42, 1199–1207. [Google Scholar] [CrossRef]
- Huang, B.Q.; Du, X.P. Probabilistic uncertainty analysis by mean value first order saddlepoint approximation. Reliab. Eng. Syst. Saf. 2008, 93, 325–336. [Google Scholar] [CrossRef]
- Rosenblueth, E. Two-point estimates in probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]
- Gorman, M.R. Reliability of Structural Systems; Case Western Reserve University: Cleveland, OH, USA, 1980. [Google Scholar]
- Yu, S.; Wang, Z. A novel time-variant reliability analysis method based on failure processes decomposition for dynamic uncertain structures. J. Mech. Des. 2018, 140, 051401. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Murray, M.H.; Kaewunruen, S. Reliability-based conversion of a structural design code for railway prestressed concrete sleepers. Proc. Inst. Mech. Eng. Part F 2012, 226, 155–173. [Google Scholar] [CrossRef]
- Liu, Y.; Li, T.X.; Liu, K.; Zhang, Y.M. Chatter reliability of turning processing system based on fourth moment method. J. Mech. Eng. 2016, 52, 193–200. (In Chinese) [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Lim, C.H. Damage and failure modes of railway prestressed concrete sleepers with holes/web openings subject to impact loading conditions. Eng. Struct 2018, 176, 840–848. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.H.; Li, Y.H.; Wang, Y.D.; Wang, J. Structural optimization–based fatigue durability analysis of electric multiple units cowcatcher. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Zhi, P.P.; Li, Y.H.; Chen, B.Z.; Shi, S.S. Bounds-based structure reliability analysis of bogie frame under variable load cases. Eng. Fail. Anal. 2020, 114, 104541. [Google Scholar] [CrossRef]
- Villarrubia, G.; De Paz, J.; Chamoso, P.; Prieta, F. Artificial neural networks used in optimization problems. Neurocomputing 2018, 272, 10–16. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Corbetta, M.; Giglio, M.; Cadini, F. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks. J. Power Sources 2017, 344, 128–140. [Google Scholar] [CrossRef]
- Huang, H.Z.; Wang, H.K.; Li, Y.F.; Zhang, L.L.; Liu, Z.L. Support vector machine based estimation of remaining useful life: Current research status and future trends. J. Mech. Sci. Technol. 2015, 29, 151–163. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. An active-learning algorithm that combines sparse polynomial chaos expansions and bootstrap for structural reliability analysis. Struct. Saf. 2018, 75, 67–74. [Google Scholar] [CrossRef]
- Hu, Z.; Mahadevan, S. Global sensitivity analysis-enhanced surrogate (GSAS) modeling for reliability analysis. Struct. Multidiscip. Optim. 2016, 53, 501–521. [Google Scholar] [CrossRef]
- Gao, Y.H.; Wang, X.C. An effective warpage optimization method in injectionmolding based on the kriging model. Int. J. Adv. Manuf. Tech. 2008, 37, 953–960. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Li, H.S.; Yao, W.X. Reliability-based design optimization using a generalized subset simulation method and posterior approximation. Eng. Optim. 2018, 50, 733–748. [Google Scholar] [CrossRef]
- Huang, D.; Allen, T.T.; Notz, W.I.; Zeng, N. Global optimization of stochastic black-box systems via sequential kriging meta-models. J. Glob. Optim. 2012, 54, 431. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Ruan, S.; Gu, J.F.; Wang, X.Y.; Shen, C.Y. Investigation on parallel algorithms in efficient global optimization based on multiple points infill criterion and domain decomposition. Struct. Multidiscip. Optim. 2016, 54, 747–773. [Google Scholar] [CrossRef]
- Bichon, B.J.; Eldred, M.S.; Swiler, L.P.; Mahadevan, S.; Mcfarland, J.M. Efficient global reliability analysis for nonlinear implicit performance functions. AIAA J. 2008, 46, 2459–2468. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Zhao, D.Y.; Yu, S.; Wang, Z. A box moments approach for the time-variant hybrid reliability assessment. Struct. Multidiscip. Optim. 2021, 64, 4045–4063. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, J.; Li, R.; Tong, C. LIF: A new Kriging based learning function and its application to structural reliability analysis. Reliab. Eng. Syst. Saf. 2017, 157, 152–165. [Google Scholar] [CrossRef]
- Tee, K.F.; Ebenuwa, A.U. Combination of line sampling and important sampling for reliability assessment of buried pipelines. Proc. Inst. Mech. Eng. Part O 2018, 233, 1748006X1876498. [Google Scholar] [CrossRef]
- Yuan, X.K.; Zheng, Z.X.; Zhang, B.Q. Augmented line sampling for approximation of failure probability function in reliability-based analysis. Appl. Math. Model. 2020, 80, 895–910. [Google Scholar] [CrossRef]
- Jinsuo, N.; Ellingwood, B.R. Directional methods for structural reliability analysis. Struct. Saf. 2000, 22, 233–249. [Google Scholar] [CrossRef]
- Li, H.S.; Xia, S.; Luo, D.M. A probabilistic analysis for pin joint bearing strength in composite laminates using Subset Simulation. Compos. Part B-Eng. 2014, 56, 780–789. [Google Scholar] [CrossRef]
- Huang, X.X.; Chen, J.Q.; Zhu, H.P. Assessing small failure probabilities by AK-SS: An active learning method combining kriging and subset simulation. Struct. Saf. 2016, 59, 86–95. [Google Scholar] [CrossRef]
- Ditlevsen, O. Narrow reliability bounds for structural system. J. Struct. Mech. 1979, 7, 453–472. [Google Scholar] [CrossRef]
- Zhi, P.P.; Wang, Y.D.; Wang, Z.L.; Li, Y.H.; Zhang, M. IDEPSO-SS based reliability analysis of bogie frame under multiple load cases. China Railw. Sci. 2021, 42, 134–143. (In Chinese) [Google Scholar]
- Zhang, Y.C. High-order reliability bounds for series systems and application to structural systems. Comput. Struct. 1993, 46, 381–386. [Google Scholar] [CrossRef]
- Song, J.H.; Der Kiureghian, A. Bounds on system reliability by linear programming. J. Eng. Mech. 2003, 129, 627–636. [Google Scholar] [CrossRef]
- Fauriat, W.; Gayton, N. AK-SYS: An adaptation of the AK-MCS method for system reliability. Reliab. Eng. Syst. Saf. 2014, 123, 137–144. [Google Scholar] [CrossRef]
- Yang, X.F.; Mi, C.Y.; Deng, D.Y.; Liu, Y.S. A system reliability analysis method combining active learning Kriging model with adaptive size of candidate points. Struct. Multidiscip. Optim. 2019, 60, 137–150. [Google Scholar] [CrossRef]
- Yun, W.Y.; Lu, Z.Z.; Zhou, Y.C.; Jiang, X. AK-SYSi: An improved adaptive Kriging model for system reliability analysis with multiple failure modes by a refined U learning function. Struct. Multidiscip. Optim. 2019, 59, 263–278. [Google Scholar] [CrossRef]
- Arendt, P.D.; Apley, D.W.; Chen, W. Improving identifiability in model calibration using multiple responses. J. Mech. Des. 2012, 134, 100909. [Google Scholar] [CrossRef]
- Wei, P.; Liu, F.; Tang, C. Reliability and reliability-based importance analysis of structural systems using multiple response Gaussian process model. Reliab. Eng. Syst. Saf. 2018, 175, 183–195. [Google Scholar] [CrossRef]
- Shu, Z.; Jirutitijaroen, P. Latin hypercube sampling techniques for power systems reliability analysis with renewable energy sources. IEEE Trans. Power Syst. 2011, 26, 2066–2073. [Google Scholar] [CrossRef]
- Xiao, N.C.; Yuan, K.; Zhan, H.Y. System reliability analysis based on dependent Kriging predictions and parallel learning strategy. Reliab. Eng. Syst. Saf. 2022, 218, 108083. [Google Scholar] [CrossRef]

| Method | Ncalls | |||
|---|---|---|---|---|
| MC simulation | 106 | 4.52 | 2.6105 | _ |
| Proposed method | 10 | 4.50 | 2.6121 | 0.0613 |
| MRGP + U | 15 | 4.45 | 2.6159 | 0.2069 |
| MRGP + H | 21 | 4.40 | 2.6197 | 0.3524 |
| MRGP + EFF | 18 | 4.35 | 2.6236 | 0.5018 |
| Method | Ncalls | |||
|---|---|---|---|---|
| MC simulation | 106 | 0.19242 | 0.8690 | _ |
| Proposed method | 27 | 0.19260 | 0.8684 | 0.0690 |
| MRGP + U | 123 | 0.19340 | 0.8654 | 0.4143 |
| MRGP + H | 51 | 0.19230 | 0.8695 | 0.0575 |
| MRGP + EFF | 52 | 0.19180 | 0.8713 | 0.2647 |
| Method | Ncalls | |||
|---|---|---|---|---|
| MC simulation | 106 | 3.2 | 2.7266 | — |
| Proposed method | 18 | 3.1 | 2.7370 | 0.3814 |
| MRGP + U | 22 | 3.1 | 2.7370 | 0.3814 |
| MRGP + H | 30 | 2.9 | 2.7589 | 1.1846 |
| MRGP + EFF | 19 | 3.0 | 2.7478 | 0.7775 |
| Symbol | Unit | Distribution | Mean | Mean Square Deviation |
|---|---|---|---|---|
| — | Gaussian | 1 | 0.02 | |
| K | — | Gaussian | 1 | 0.13 |
| — | Gaussian | 2 | 0.06 | |
| d | mm | Gaussian | 24 | 0.24 |
| mm | Gaussian | 4 | 0.40 |
| Method | Ncalls | |||
|---|---|---|---|---|
| MC simulation | 106 | 2.5 | 2.8070 | — |
| Proposed method | 78 | 2.4 | 2.8202 | 0.4681 |
| MRGP + U | 99 | 2.3 | 2.8338 | 0.9548 |
| MRGP + H | 161 | 2.4 | 2.8202 | 0.4681 |
| MRGP + EFF | 116 | 2.4 | 2.8202 | 0.4681 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, P.; Yun, G.; Wang, Z.; Shi, P.; Guo, X.; Wu, J.; Ma, Z. A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model. Appl. Sci. 2022, 12, 8961. https://doi.org/10.3390/app12188961
Zhi P, Yun G, Wang Z, Shi P, Guo X, Wu J, Ma Z. A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model. Applied Sciences. 2022; 12(18):8961. https://doi.org/10.3390/app12188961
Chicago/Turabian StyleZhi, Pengpeng, Guoli Yun, Zhonglai Wang, Peijing Shi, Xinkai Guo, Jiang Wu, and Zhao Ma. 2022. "A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model" Applied Sciences 12, no. 18: 8961. https://doi.org/10.3390/app12188961
APA StyleZhi, P., Yun, G., Wang, Z., Shi, P., Guo, X., Wu, J., & Ma, Z. (2022). A Novel Reliability Analysis Approach under Multiple Failure Modes Using an Adaptive MGRP Model. Applied Sciences, 12(18), 8961. https://doi.org/10.3390/app12188961









