Abstract
Background: The infinite shear viscosity model of Carreau fluid characterizes the attitude of fluid flow at a very high/very low shear rate. This model has the capacity for interpretation of fluid at both extreme levels, and an inclined magnetic dipole in fluid mechanics has its valuable applications such as magnetic drug engineering, cold treatments to destroy tumors, drug targeting, bio preservation, cryosurgery, astrophysics, reaction kinetics, geophysics, machinery efficiency, sensors, material selection and cosmology. Novelty: This study investigates and interprets the infinite shear rate of Carreau nanofluid over the geometry of a cylindrical channel. The velocity is assumed to be investigated through imposing an inclined magnetic field onto cylindrical geometry. Activation energy is utilized because it helps with chemical reactions and mass transport. Furthermore, the effects of thermophoresis, the binary chemical process and the Brownian movement of nanoparticles are included in this attempt. Formulation: The mathematics of the assumed Carreau model is derived from Cauchy stress tensor, and partial differential equations (PDEs) are obtained. Similarity transformation variables converted these PDEs into a system of ordinary differential equations (ODEs). Passing this system under the bvp4c scheme, we reached at numerical results of this research attempt. Findings: Graphical debate and statistical analysis are launched on the basis of the obtained computed numerical results. The infinite shear rate aspect of Carreau nanofluid gives a lower velocity. The inclined magnetic dipole effect shows a lower velocity but high energy. A positive variation in activation energy amplifies the concentration field.
1. Introduction
Imposing a magnetic field during the flow of fluid at an acute angle is called an inclined magnetic field. Discussing the magnetic effect related to fluid mechanisms is called as magnetohydrodynamics (MHD). MHD covers the key aspects of fluid flow during motion and has valuable applications such as magnetic drug engineering, MHD generators, cryosurgery, cooling of metallic sheets, cold treatments to destroy tumors, astrophysics, geothermal energy differentiation, reaction kinetics geophysics, mensuration flow in blood vessels, machinery efficiency, paper production, sensors, drug targeting, fiberglass manufacturing, bio preservation, material selection and cosmology. By placing a magnetic field over a flowing fluid, the Lorentz force is generated by the interaction of inter-mutual particles. Such important key and vital applications have induced researchers to put their focus into MHD. MHD flow with different fluidics models [1,2,3,4,5,6,7] has been encountered along with multiple features such as Carreau diffusion, activation energy, thermophoresis, inclined magnetic field, convection transportation of energy, etc., by different scholars. Khan et al. [1] studied the impact of convective boundary conditions on Carreau nanofluid moving while subjected to a stretching/shrinking cylinder and noticed that the velocity profile diminishes owing to a magnification in the magnetic parameter. Ayub et al. [2] employed a Keller box scheme to achieve the numerical solution of a magneto- Cross nanofluid accompanied by blood as a base fluid and found that electrically conducting fluid generates a force termed the Lorentz force, which is responsible for a decrement in the fluid’s velocity. Chen et al. [3] achieved the analytical solution of MHD fluid flow between two coaxial cylinders and came up with the conclusion that the velocity of fluid diminishes owing to a magnification in Grashoff number. Alsaedi et al. [4] employed MATLAB built in a bvp4c scheme to achieve the numerical solution of a magneto hybrid nanofluid flow between two coaxial cylinders and noticed that a positive change in magnetic field strength diminishes the performance of hybrid nanofluids. Wahab et al. [5] scrutinized the influence of an inclined magnetic field on a Cross nanofluid moving over a slippery surface and observed that magnification in the magnetic field parameters depreciates the velocity of the fluid flow. The impact of investigating the influence of higher-order chemical reactions and magnetic field effects on Cross nanofluid movement subjected to a stretching wedge was scrutinized in detail by Shah et al. [6]. They noticed that a positive change in Lorentz force generates a resistive force, which is responsible for a decrement in velocity phenomenon. Lim et al. [7] scrutinized the effect of thermal radiation and chemical reaction on magnetically driven Carreau fluid movement subjected to an expanding cylinder and found that a positive variation in thermal radiation parameters enhances the heat transfer rate of the fluid. Shaw et al. [8] recently discussed how the hydromagnetic flow of Cross-hybrid nanofluid influenced quadratic thermal radiation. It was found that hybrid nanofluid is more effective than other nanofluid models. Cross nanomaterials and MHD entropy, along with cubic autocatalytic chemical reaction, analysis has been made by Nayak et al. [9]. Soret and Dufour numbers and their physical impacts on MHD nanofluid over the geometry of a finned cavity including a rotating circular cylinder are discussed by Aly et al. [10]. Nanoparticles of Fe3O4/Cu/Ag-CH3OH in MHD stagnation point flow have been utilized over a heated surface and partial slip, activation energy facts which the study of Nandi et al. [11] has also engaged with. Recent studies [12,13] related to the hydromagnetic transport of Casson nanofluid and thermo-solutal convection of a nanofluid have been published with superb results.
Carreau nanofluid has the capability to judge the attitude of nanofluid at extreme levels. When external force is imposed on a fluid, shear stress is generated in it and deformation takes place. If the magnitude of the applied force is very high, a very high shear rate results, and it is the same when a very low force is exerted on a fluid; a very low shear rate is produced. There was no such mathematical model for depicting the characteristics of a fluid when a very low and very high shear rate is produced in the fluid. Carreau fluid is a competent, authorized mathematical model that describes the characteristics of fluid mechanics at extreme levels. This unique quality of Carreau fluid distinguishes it from other fluid models. Khan et al. [14] conducted a numerical analysis of steady Carreau fluid flowing over a wedge. In this attempt, they incorporated infinite shear rate as a factor along the Carreau fluid and obtained its effect on several physical variables. Further, they [15] obtained multiple solutions of the Carreau fluid model. The heat transportation aspect of Carreau fluid, containing an infinite shear-rate viscosity term, has been investigated by Ayub et al. [16]. Sardar et al. [17] conducted work on heat transportation with a mixed convection mechanism, taking Carreau nanofluids under the effect of infinite shear-rate viscosity. Ali et al. [18] published valuable work related to the concentration and thermal aspects in the Carreau viscosity model via a wedge, and the latest study related to melting and the entropy generation of infinite shear-rate viscosity of the Carreau model over a Riga plate with erratic thickness was performed by Wang et al. [19]. Mosaferi et al. [20] presented their study related to an aligned magnetic field on the 2DOF VIV suppression of heat transportation and its comprehensive characteristics. Many other scholars [21,22,23] conducted their investigations over cylindrical geometry with different effects, such as turbulent cylinder-stirred flow, tunable filtering and demultiplexing with a hollow cylinder and heat-transfer augmentation in a tube mixture of ethylene glycol as a base fluid.
Rapid heat transportation was a wish of many scholars because there is energy consumption at the industrial and engineering sides. To solve this issue, investigators have looked for a rapid heat-transfer fluid, and they have presented that, for that purpose, we have to increase the thermal conductivity of fluid. Later on, a judgment was passed that conductivity is increased by using nanoparticles in the base fluid. Nano-sized particles are very small in size, approximately less than 100 nm, and are referred to as nanoparticles. These particles boost the heat transportation in a base fluid. Many scholars have presented their work about nanofluid. The latest article published by Waqas et al. [24] is related to activation energy, magnetic fields and mixed radiative-convective couple-stress, with a mathematical model of stratified nanofluid flows along with utilizing the important feature of motile microorganisms. Muhammad et al. [25] worked recently on doubly stratified bioconvective transport augmentation with the factors of gyrotactic motile microorganisms with a mathematical model of nanofluid. Furthermore, he [26] made another study which relates to the thermodynamics performance of hybrid nanofluids and a thermohydraulic system. Song et al. [27] expressed his valuable study of the unsteady flow of magneto-Williamson nanofluid with several factors about cylinder geometry.
The process by two or more substances are engaged with each other and as a result they are transformed into two or more different substances is called a chemical process. A process of conversion of two or more substances into two or more different substances that takes two steps to complete is called a binary chemical process. They play vital roles in our daily life. Without chemical processes, there is no concept of life, and without them, we cannot investigate any changes in the physical world. Through chemical processes, we can come to understand properties of matter, how the natural world works, solve crimes and explain mysteries and determine which planets and moons are likely to be able to sustain life. Considering its importance in daily life, it also helpful in fluid mechanics to judge mass transportation. Kumar et al. [28] gave a numerical review of recent advancements in nanofluids considering thermal systems. Dina et al. [29] also worked on nanofluids and depicted the enhancement of the transportation of heat, and limit cycle analysis, consistency preserving discretization and cubic autocatalytic chemical reactions were utilized. Other investigators [30,31] have revealed their research on models of membranes containing nanofluids and performance evaluations of nanofluids in solar and thermal photovoltaic systems.
The minimum energy required to produce a reaction is called activation energy. Swante Arrhenius presented the idea of activation energy in 1889. The proper amount of adequate energy supplied by the reactants for the manifestation of a chemical reaction is known as activation energy. It can be thought of as the highest potential issue or energy that divides both the least number of materials and the highest potential energy devices. Exothermic and endothermic-type reactions are examples of activation energy. Activation energy has various engineering and industrial applications such as enzymes and the fermentation of sugar with the utilization of yeast. Research across the world has tried to investigate the effect of activation energy on fluid flow subjected to various media such as cones, wedges, stretching sheets, etc. Madhukesh et al. [32] investigated the impact of activation energy on a hybrid nanomaterial past a circular cylinder in order to observe the effects, such as the saddle and nodal points, and found that the heat transfer rate amplifies by the virtue of a magnification in the fractional volume of nanoparticles. Zhang et al. [33] studied the influence of motile microorganisms and activation energy on Williamson nanofluid movement subjected to an extendable cylinder and noted that the positive variation in the activation energy parameter amplifies the concentration field. Mahdy et al. [34] scrutinized the effect of heat-source sink, thermal conductivity and activation energy on dusty Carreau fluid flow along a cylinder and came to the conclusion that a positive variation in the thermal conductivity and reaction rate constant amplifies the temperature field. The impact of Soret/Dufour effects and activation energy on Casson nanofluid movement subjected to a deformable cylinder was investigated in detail by Shaheen et al. [35]. They noted that that an amplification in Soret number and activation energy provides an eminent effect on the concentration field. Colak [36] employed an artificial intelligence approach to investigate the impact of activation energy and temperature-dependent viscosity on Maxwell fluid flow along a cylinder and noticed that the concentration field is amplified owing to a magnification in the activation energy phenomenon. For more information on non-Newtonianism fluids, please see the studies [37,38,39,40,41,42,43,44,45,46].
The literature review is listed to form the basis of the current study. There are several studies related to Carreau fluid, but a study on an infinite shear Carreau fluid model on cylindrical geometry has not been discussed yet. This investigation was launched to investigate the binary chemical process and inclined magnetic effect with infinite shear rate model of Carreau nanofluid with cylindrical geometry. Nanofluid heat transportation is also investigated with the help of variable thermal conductivity. The article is novel in the sense that the effect of activation energy and MHD in the case of Cross nanofluid flowing towards an expandable cylinder has not been investigated yet in the available literature. This paper is an extension of the work reported by Khan et al. [1], with the inclusion of additional effects such as activation energy, a Cross nanofluid model in the place of a Carreau nanofluid model and magnetohydrodynamics (MHD).
The paper is further organized into several sections. Section 2 discusses the novelty of the physical model, Section 3 discusses the validity of the study in pictorial form, Section 4 elaborates on the comprehensive analysis of the outcomes of attached parameters and Section 5 presents the final and concluding remarks. Chart 1 defines the fluid problem and the mathematical modeling of the current problem.
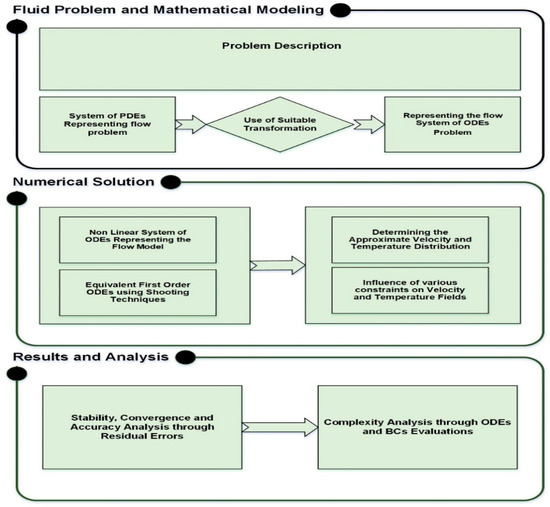
Chart 1.
Mathematical modeling of present model.
2. Novelty of Physical Model
In this segment, the geometry of the problem is presented by facts and Figure 1. It is assumed that the fluid is flowing through a horizontal cylinder, which has the capability of stretching and contracting. is the radius of the considered cylinder with which are the positive constant and the parameters of stretchiness and contraction under certain conditions on . It is further assumed that the fluid is flowing in a permeable horizontal cylinder with a velocity of . Flow is two-dimensional laminar boundary layer flow of Carreau fluid, and it is unsteady as well. Inclined magnetic effect is placed with inclination angle . Equations are launched in cylindrical coordinates from Navier–Stokes equations. Convective conditions are being enrolled for convection transport. Variable and temperature-dependent thermal conductivity is also engaged for rapid heat transportation, which is mathematically shown as , with the parameter of conductivity and thermal conductivity away from cylinder . The geometry is depicted in Figure 1.
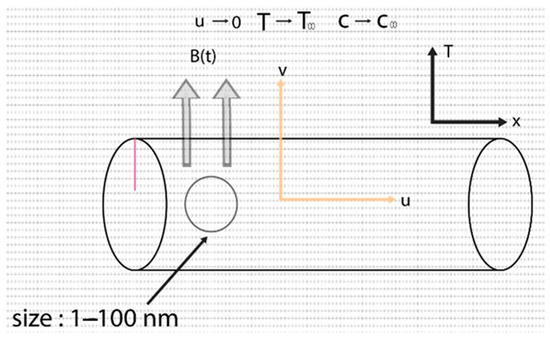
Figure 1.
Physical behavior of fluid moving over cylindrical geometry.
Cauchy stress tensor for the mathematical model of Carreau fluid and its related mathematical expressions.
Carrying further calculations on the Cauchy stress tensor and given all requirements with finally applying the boundary layer assumptions, we obtained this system of PDEs:
Boundary conditions for PDEs:
Mentioned parameters appearing in (5)–(11) are
Using the above transformations, the governing Equations (5)–(7) are transmuted into a set of nonlinear ODEs, given as:
The corresponding boundary conditions are written as:
Physical quantities, i.e., Nusselt number and skin friction coefficients, are, respectively, expressed as and and are derived in dimensionless form as:
3. Methodology
The modeled equations are highly nonlinear in nature, and their analytical solutions are not feasible. The above system of Equations (14)–(16) along with boundary conditions (17)–(19) can be handled numerically with the utilization of MATLAB built in bvp4c scheme. Finite difference scheme package is utilized by bvp4c scheme. During this procedure, the modeled PDEs are converted into first-order ODEs by considering what is suitable along with boundary conditions and are furthermore solved numerically with bvp4c package in MATLAB. The maximum residual error and step size are and .
The methodology of current numerical technique is explained step by step in Chart 2.
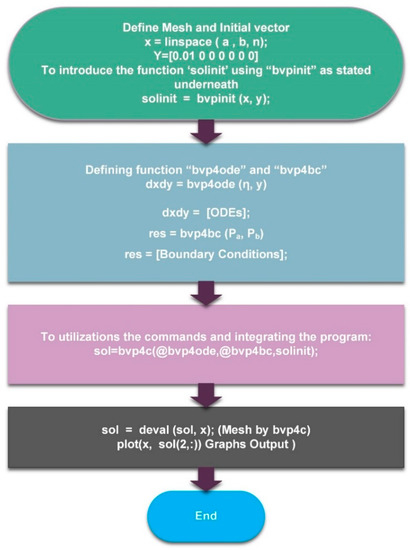
Chart 2.
Methodology of bvp4c scheme.
4. Validity of the Study in Pictorial Form
The graph in Figure 2 is brought into this section to compare the old literature [1] with the new computed values for the case of a positive variation in unsteadiness parameter A by keeping other parameters such as Re = 1 and A = 0 when n = 1 and We = 0 in the case of . This seems to be in agreement with existing literature. Blue lines represent the results obtained by Khan et al. [1], and green lines represent the results after current numerical simulation of the problem. From comparison analysis, it is quite evident that the obtained results are quite satisfactory and reliable.
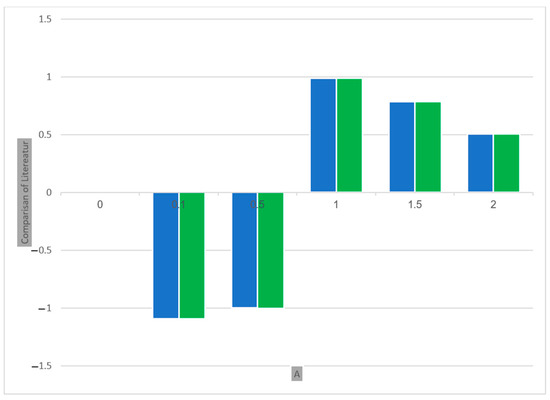
Figure 2.
Comparison of this outcome vs. previous literature [1].
5. Comprehensive Analysis of Outcomes of Attached Parameters
This segment of the study was conducted for the comprehensive analysis of the outcomes of the attached parameters. All physical interpretations regarding associated parameters are explored in this section. Physical quantities are represented through a statistical approach. The velocity judgment is made with help of an inclined magnetic field, and for initiation of the chemical process, the activation energy is assumed. The variable thermal conductivity responsible for the rapid transportation of heat and mass is being considered with the aid of Brownian and thermophoresis. Furthermore, infinite shear-rate viscosity depicts the key characteristics of these assumptions. All the figures are plotted in both cases through shear thinning/thickening with different values of n, and the value of n lies in . It is a case of shear thinning when , and it is a case of shear thickening when . Figure 3, Figure 4, Figure 5 and Figure 6 reveal the consequences of the attached parameters with the velocity field. Mathematical expression of “We” contains a time relaxation constant due to velocity field growth, with numerical increment in We both in the cases of thinning and thickening. The viscosity of a fluid diminishes by the virtue of a magnification in We. Shear thickening behavior is reported in the case of a positive change in We, which depreciates the fluid velocity. This fact is shown in Figure 3. Figure 4 displays the effect of inclined angle on the velocity field. Note that a positive change in . depreciates the velocity. The fluid velocity diminishes as a result of a magnification in , which lessens the fluid velocity. Figure 5 depicts the influence of inclination and magnetic effect on velocity distribution. Electrically conducting fluid in the presence of an electric and magnetic field generates a force referred to as Lorentz force. This Lorentz force is basically a resistive force. This Lorentz force acts like a barrier against fluid velocity. When an inclined magnetic field is imposed on fluid flow, Lorentz force is then automatically generated, and this Lorentz force is interrelated with speed of fluid. The velocity decreases when both the magnetic and inclination parameters are numerically augmented. The infinite shear-rate viscosity parameter causes a decrease in the velocity, and this fact is revealed by Figure 6. It is noted that shear-rate viscosity diminishes in the case of an incremental change in , which brings about a decrement in velocity. Figure 7, Figure 8, Figure 9 and Figure 10 are revealing the consequences of the parameters being attached with an energy field. The inclination angle reduces the magnitude of velocity distribution. Figure 7 is the expression of this fact. Brownian parameter increments cause an exchange of tiny particles, and due to this reason, the temperature increases. The molecules of the fluid collide more randomly, shift kinetic energy to each other and enhance the thermal conductivity phenomenon much better in the presence of the Brownian diffusion phenomenon. That is why a positive variation in Nb improves the thermal conductivity and amplifies the temperature field. The Brownian parameter and its connection with temperature are shown in Figure 8. Figure 9 is included for showing the impact of the magnetic parameter effects on the distribution of temperature. The magnetic field causes Lorentz force, and this causes lower temperature. Viscosity is inversely related to the temperature. A positive variation in M depreciates the viscosity phenomenon, which reduces the velocity and amplifies the temperature, on the other hand. As a result, the temperature field escalates. Thermal conductivity is in direct relation with temperature, and its consequences on the energy field are exhibited in Figure 10. The ability of any material to conduct heat is called thermal conductivity. A material’s ability to transfer heat increases with the consideration of nanoparticles in the base fluid. Molecules collide more frequently due to a change in thermal conductivity, which increases the kinetic energy of the fluid’s molecules and the temperature field. Figure 11, Figure 12 and Figure 13 reveal the consequences of the attached parameters with the mass transportation field. Mass diffusivity is related to the Schmidt number, and due to this fact, the mass transportation becomes lower. The Schmidt number’s role is the same for mass transportation as the Prandtl number is for heat transportation. The Schmidt number is the ratio of momentum diffusivity to mass diffusivity. A positive variation in Sc magnifies the concentration of nanofluid, which provides a resistance-free motion to the mass transport and depreciates the concentration field. The Brownian motion parameter also results in a reduction of mass transportation. The temperature of the fluid is magnified by virtue of an amplification in Nb, which otherwise diminishes the concentration of fluid molecules and depreciates the concentration field. Note that a positive change in A encourages the fluid viscosity phenomenon, which amplifies the temperature and diminishes the concentration field phenomenon. Similarly, the unsteadiness parameter gives the same result as Sc and Nb.
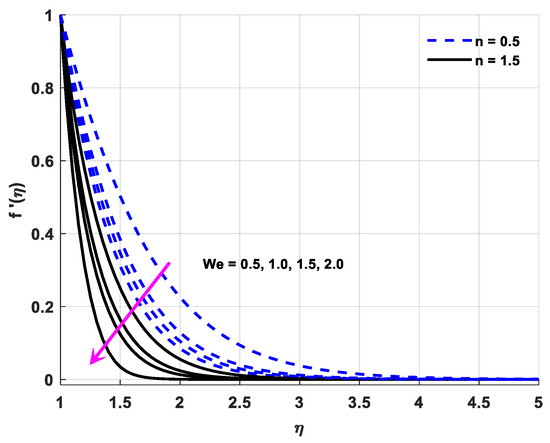
Figure 3.
Fluid velocity profile variations owing to changes in We.
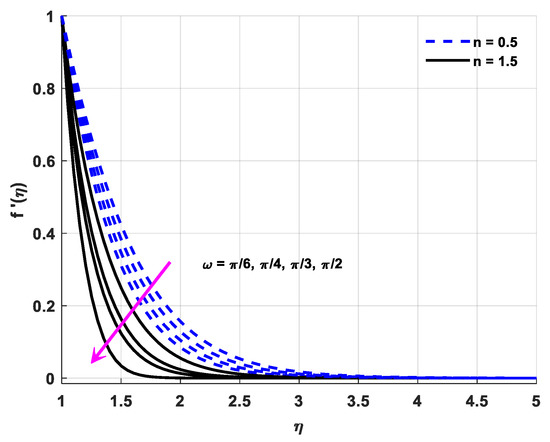
Figure 4.
Fluid velocity profile variations owing to changes in .

Figure 5.
Fluid velocity profile variations owing to changes in M.
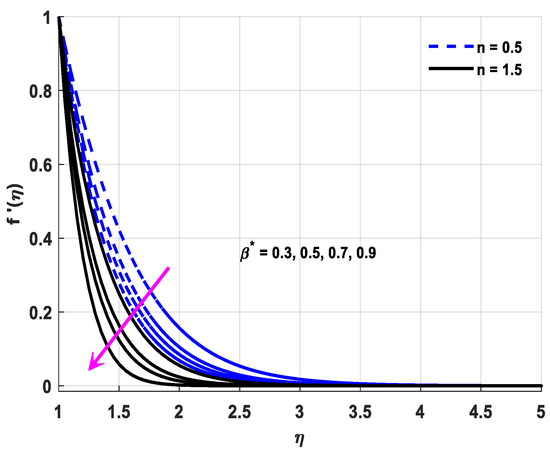
Figure 6.
Fluid velocity profile variations owing to changes in .
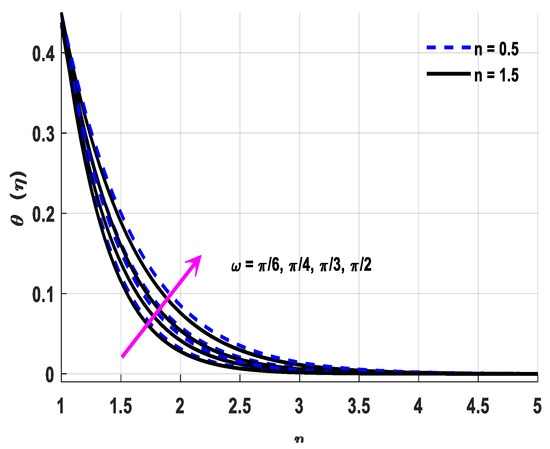
Figure 7.
Variations in temperature profiles owing to changes in .
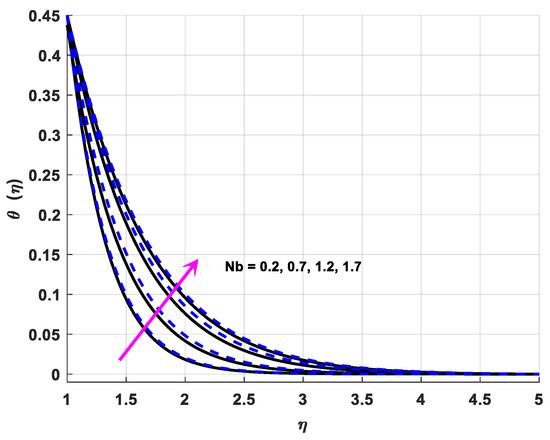
Figure 8.
Variations in temperature profiles owing to changes in Nb.
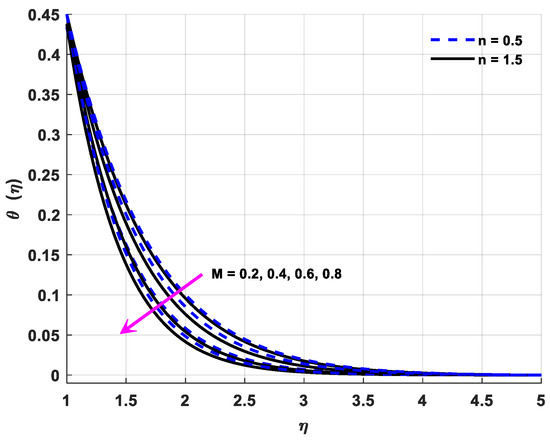
Figure 9.
Variations in temperature profiles owing to change in M.
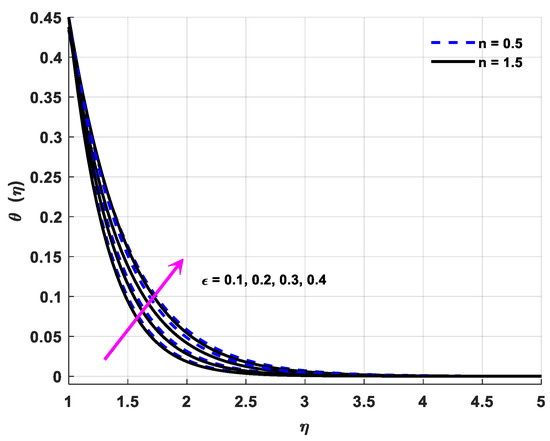
Figure 10.
Variations in temperature profiles owing to changes in .
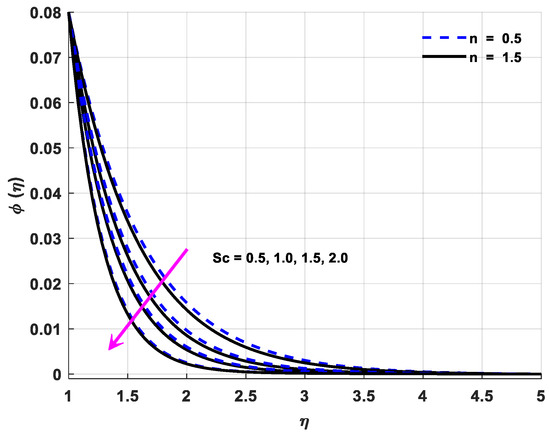
Figure 11.
Variations in species concentration profiles owing to changes in Sc.
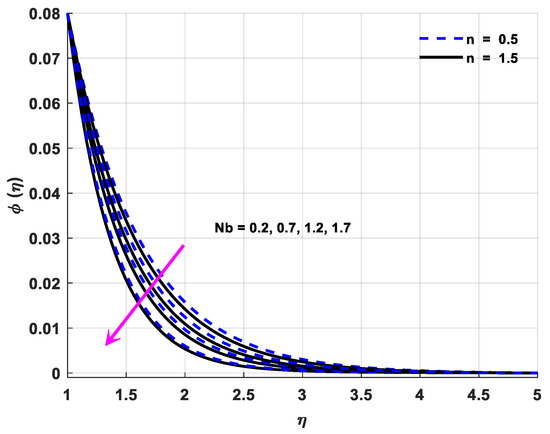
Figure 12.
Variations in species concentration profiles owing to changes in .
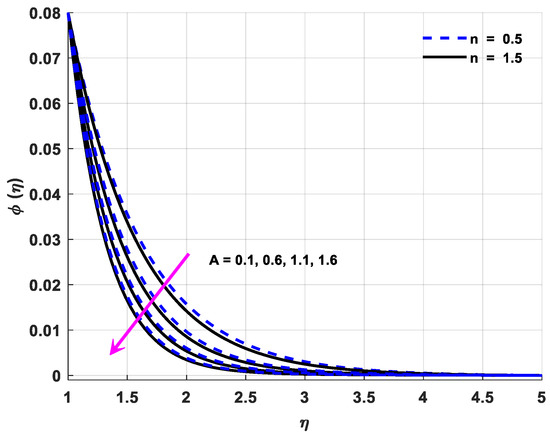
Figure 13.
Variations in species concentration profiles owing to changes in A.
Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 discuss the impact of various dimensionless parameters on the surface drag coefficient. From the figures, it is crystal clear that a positive change in We, Pr diminishes the surface drag coefficient, but surface drag phenomenon escalates as a result of magnifications in Sc, A, M and . From Figure 14, it is quite evident that a positive variation in the Weissenberg number We depreciates the skin friction phenomenon. The Weissenberg number is directly related with the relaxation time. Relaxation time is the time needed by the fluid in order to regain its original shape. During this time, the fluid is allowed to relax, and its viscosity increases. Paint is an example of the Weissenberg phenomenon. The skin friction coefficient, also called drag friction, is the drag created by the friction of the fluid opposite to the object surface over which the fluid is moving. It is quite established that a positive variation in We amplifies the fluid viscosity, which is responsible for a decrement in the fluid velocity and skin friction phenomenon. Figure 15 provides the statistical analysis of the power law index against the surface drag coefficient. The viscosity of the fluid solely depends on power law index n. The fluid behavior is shear thinning in the case of n < 1, Newtonian for n = 1 and shear thickening for n > 1. It is well established that the viscosity of fluid decreases by virtue of magnification in n. Velocity is directly related with viscosity. The velocity of fluid topples the sheet velocity in the case of amplification n, which magnifies the skin friction phenomenon.
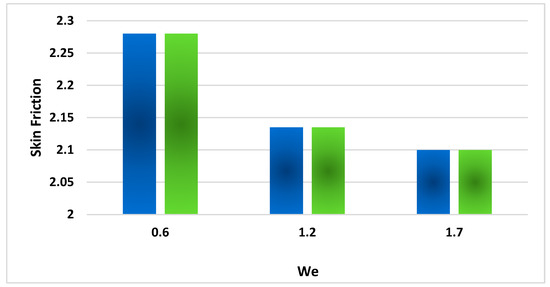
Figure 14.
Revealing the consequences of with the related skin friction coefficient.
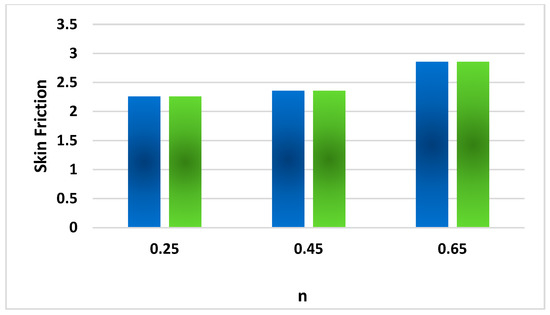
Figure 15.
Revealing the consequences of n with the related skin friction coefficient.
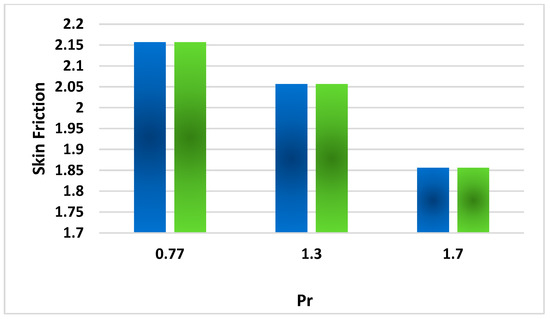
Figure 16.
Revealing the consequences of Pr with the related skin friction coefficient.
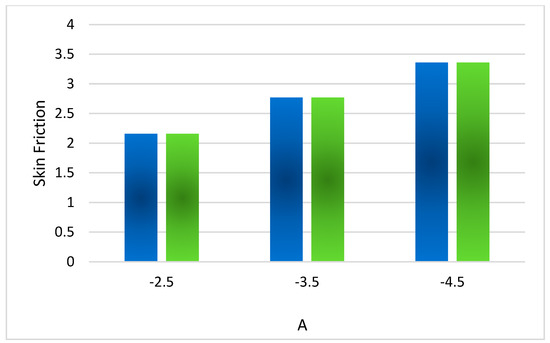
Figure 17.
Revealing the consequences of A with the related skin friction coefficient.
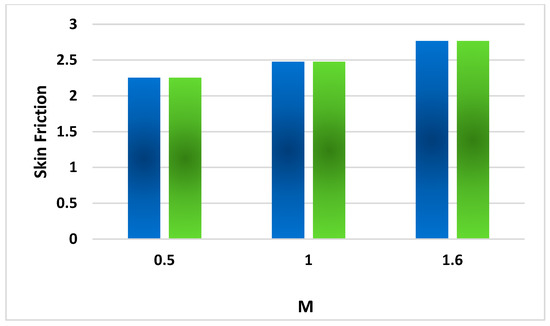
Figure 18.
Revealing the consequences of M with the related skin friction coefficient.
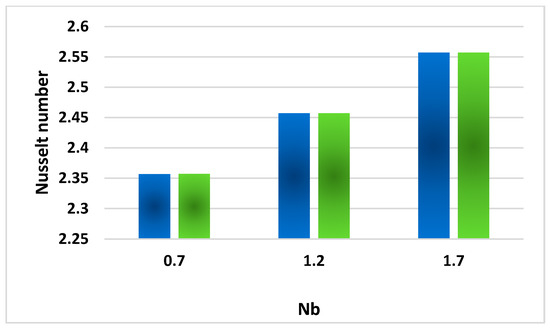
Figure 19.
Revealing the consequences of Nb related to the Nusselt number.
Figure 16 displays the impact of the Prandtl number Pr on the drag coefficient. The Prandtl number is the dimensionless quantity expressing the ratio of momentum diffusivity to the thermal diffusivity. Momentum diffusivity is the dynamic viscosity to fluid density ratio, and thermal diffusivity expresses the ratio of thermal conduction to density and specific heat. Viscosity is inversely related to temperature. A decrement in temperature depreciates thermal diffusivity and moreover strengthens the fluid viscosity and momentum diffusion phenomenon. That is why a positive variation in Pr magnifies the fluid velocity and surface drag phenomenon. The effect of unsteady parameter A on the surface drag coefficient is highlighted in Figure 17. Velocity is inversely related to the surface drag phenomenon. Note that the fluid velocity decreases as a result of a magnification in A. The fluid is almost impossible to move due to an increment in A, which depreciates the fluid velocity and amplifies the surface drag phenomenon because the velocity of the fluid flow is inversely linked with the drag phenomenon. Figure 18 is designed to explore the effect of magnetic parameter M on the surface drag coefficient. Electrical conducting fluid when passing through electric and magnetic fields produces a force called Lorentz force. Lorentz force is basically a resistive force. Lorentz force acts like a barrier in the case of fluid flow across the medium. This Lorentz force slows the fluid motion. This is called the MHD phenomenon, which has distinguished applications such as in MHD generators, metal batteries, cooling of nuclear reactors, etc. It is observed that the flow velocity diminishes in the presence of Lorentz forces, which brings about a reduction in fluid velocity and moreover amplifies the drag friction phenomenon. Figure 19 is designed to study the effect of Nb on the heat transfer Nusselt number. The parameter Nb indicates the Brownian motion of the molecules. Molecules collide more randomly as a result of an amplification in Nb. The molecules shift kinetic energy to each other and amplify the temperature inside the fluid. It is well established that the thermal conduction of the fluid also increases due to a positive change in Nb, which escalates the fluid temperature and heat transfer Nusselt number.
6. Conclusions of Debate
This study dealt with the infinite shear rate of Carreau nanofluid over the geometry of a cylindrical channel. Velocity analysis was conducted through imposing an inclined magnetic field on cylindrical geometry. The key results are listed as:
- Infinite shear rate aspect of Carreau nanofluid gives lower velocity.
- Inclined magnetic dipole effect shows lower velocity but high energy.
- Unsteadiness parameter is related to time factor due to this magnitude of velocity decreasing.
- Relaxation time of fluid increasing by the virtue of magnification in We, which diminishes the velocity field.
- A positive variation in magnetic parameters diminishes the surface drag phenomenon.
- Amplification in thermal conductivity magnifies Nb and the temperature field.
Author Contributions
Conceptualization, A.A. and T.S.; methodology, W.J.; software, W.R.M.Z.; validation, L.A.V.M. and L.M.G.T.; formal analysis, N.I.R.O.d.P.; investigation, S.M.H.; resources, M.B.H.; data curation, M.K.; writing—original draft preparation, A.A.; writing—review and editing, T.S.; visualization, W.J.; supervision, W.J.; project administration, M.K.; funding acquisition, S.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Authors are grateful to the Deanship of Scientific Research, Islamic University of Madinah, Ministry of Education, KSA for supporting this research work through research project grant under Research Group Program/1/804.
Conflicts of Interest
There is no conflict of interest, all authors contributed equally.
Ethical Statement
This material is the authors’ own original work, which has not been previously published elsewhere.
Nomenclature
| Wall heat transfer coefficient | Schmidt number | ||
| Wall mass transfer coefficient | Density of fluid | ||
| Specific heat | |||
| Ambient concentration | Operative heat capability | ||
| Surface temperature | u, v | Velocity components | |
| Density of fluid | Reaction rate parameter | ||
| Thermophoresis diffusion coefficient | Thermophoresis parameter | ||
| U | Stretching velocity | Rex | Local Reynolds number |
| Thermal diffusivity | I | Identity tensor | |
| Kinematic viscosity | Power law index | ||
| Unsteadiness parameter | A1 | First Rivlin–Ericksen tensor | |
| Brownian diffusion coefficient | Magnetic parameter | ||
| Schmidt number | Magnetic parameter | ||
| Local Weissenberg number | Temperature constant | ||
| Reaction rate parameter | Pr = | Prandtl number | |
| Brownian motion parameter | Activation energy | ||
| Distance along the axial direction | Expansion or contraction strength | ||
| Distance along the radial direction | Dimensionless velocity | ||
| Dimensionless temperature | Radius of cylinder | ||
| Dimensionless concentration | Thermal Biot number | ||
| Concentration Biot number | Time | ||
| We | Local Weissenberg number | V | Velocity field |
| Thermal conductivity parameter | C | Concentration field | |
| Skin friction coefficient | Cauchy stress tensor | ||
| Wall heat transfer coefficient | Pressure | ||
| Wall mass flux | Apparent viscosity | ||
| Wall heat flux | Zero shear rate viscosity | ||
| Wall shear stress | Infinite shear rate viscosity | ||
| Surface temperature | Shear rate | ||
| Brownian motion parameter | Time material constant | ||
| Thermophoresis parameter | Local similarity variable | ||
| Variable thermal conductivity |
References
- Khan, M.; Azam, M.; Alshomrani, A.S. On unsteady heat and mass transfer in Carreau nanofluid flow over expanding or contracting cylinder with convective surface conditions. J. Mol. Liq. 2017, 231, 474–484. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Altamirano, G.C.; Sadat, R.; Ali, M.R. Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller–Box and BVP4C method. Eng. Comput. 2022, 38, 3705–3719. [Google Scholar] [CrossRef]
- Chen, L.; Abbas, M.A.; Khudair, W.S.; Sun, B. Analytical Solution for the MHD Flow of Non-Newtonian Fluids between Two Coaxial Cylinders. Symmetry 2022, 14, 953. [Google Scholar] [CrossRef]
- Alsaedi, A.; Muhammad, K.; Hayat, T. Numerical study of MHD hybrid nanofluid flow between two coaxial cylinders. Alex. Eng. J. 2022, 61, 8355–8362. [Google Scholar] [CrossRef]
- Wahab, H.A.; Hussain Shah, S.Z.; Ayub, A.; Sabir, Z.; Bilal, M.; Altamirano, G.C. Multiple characteristics of three-dimensional radiative Cross fluid with velocity slip and inclined magnetic field over a stretching sheet. Heat Transf. 2021, 50, 3325–3341. [Google Scholar] [CrossRef]
- Shah, S.Z.; Wahab, H.A.; Ayub, A.; Sabir, Z.; haider, A.; Shah, S.L. Higher order chemical process with heat transport of magnetized cross nanofluid over wedge geometry. Heat Transf. 2021, 50, 3196–3219. [Google Scholar] [CrossRef]
- Lim, Y.J.; Shafie, S.; Mohamad Isa, S.M.; Rawi, N.A.; Mohamad, A.Q. Impact of chemical reaction, thermal radiation and porosity on free convection Carreau fluid flow towards a stretching cylinder. Alex. Eng. J. 2022, 61, 4701–4717. [Google Scholar] [CrossRef]
- Shaw, S.; Samantaray, S.S.; Misra, A.; Nayak, M.K.; Makinde, O.D. Hydromagnetic flow and thermal interpretations of Cross hybrid nanofluid influenced by linear, nonlinear and quadratic thermal radiations for any Prandtl number. Int. Commun. Heat Mass Transf. 2022, 130, 105816. [Google Scholar] [CrossRef]
- Nayak, M.K.; Agbaje, T.M.; Mondal, S.; Sibanda, P.; Makanda, G. Entropy minimized MHD microrotations of Cross nanomaterials with cubic autocatalytic chemical reaction. Heat Transf. 2022, 51, 490–533. [Google Scholar] [CrossRef]
- Aly, A.M.; El-Sapa, S. Effects of Soret and Dufour numbers on MHD thermosolutal convection of a nanofluid in a finned cavity including rotating circular cylinder and cross shapes. Int. Commun. Heat Mass Transf. 2022, 130, 105819. [Google Scholar] [CrossRef]
- Nandi, S.; Kumbhakar, B.; Sarkar, S. MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int. Commun. Heat Mass Transf. 2022, 130, 105791. [Google Scholar] [CrossRef]
- Zeeshan, A.; Mehmood, O.U.; Mabood, F.; Alzahrani, F. Numerical analysis of hydromagnetic transport of Casson nanofluid over permeable linearly stretched cylinder with Arrhenius activation energy. Int. Commun. Heat Mass Transf. 2022, 130, 105736. [Google Scholar] [CrossRef]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K. Numerical treatment of MHD flow of Casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Contin. 2020, 66, 229–245. [Google Scholar] [CrossRef]
- Khan, M.; Sardar, H. On steady two-dimensional Carreau fluid flow over a wedge in the presence of infinite shear rate viscosity. Results Phys. 2018, 8, 516–523. [Google Scholar] [CrossRef]
- Khan, M.; Sardar, H.; Gulzar, M.M.; Alshomrani, A.S. On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Results Phys. 2018, 8, 926–932. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Shah, S.Z.H.; Mahmoud, S.R.; Algarni, A.; Sadat, R.; Ali, M.R. Aspects of infinite shear rate viscosity and heat transport of magnetized Carreau nanofluid. Eur. Phys. J. Plus 2022, 137, 247. [Google Scholar] [CrossRef]
- Sardar, H.; Khan, M. Mixed convection flow and heat transfer mechanism for non-Newtonian Carreau nanofluids under the effect of infinite shear rate viscosity. Phys. Scr. 2020, 95, 035225. [Google Scholar]
- Ali, U.; Rehman, K.U.; Alshomrani, A.S.; Malik, M.Y. Thermal and concentration aspects in Carreau viscosity model via wedge. Case Stud. Therm. Eng. 2018, 12, 126–133. [Google Scholar] [CrossRef]
- Wang, F.; Sajid, T.; Ayub, A.; Sabir, Z.; Bhatti, S.; Shah, N.A.; Sadat, R.; Ali, M.R. Melting and entropy generation of infinite shear rate viscosity Carreau model over Riga plate with erratic thickness: A numerical Keller Box approach. Waves Random Complex Media 2022, 1–25. [Google Scholar] [CrossRef]
- Mosaferi, A.A.; Esmaeili, M.; Rabiee, A.H. Effect of aligned magnetic field on the 2DOF VIV suppression and convective heat transfer characteristics of a circular cylinder. Int. Commun. Heat Mass Transf. 2022, 130, 105807. [Google Scholar] [CrossRef]
- Sierra-Espinosa, F.Z.; Amjad, S.; Carrillo, F.; Soria, J.; Atkinson, C. Turbulent cylinder-stirred flow heat and momentum transfer research in batch operated single-phase square reactor. Int. J. Therm. Sci. 2022, 172, 107325. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.O.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 2004, 69, 046608. [Google Scholar] [CrossRef]
- Keklikcioglu, O.; Ozceyhan, V. Heat transfer augmentation in a tube with conical wire coils using a mixture of ethylene glycol/water as a fluid. Int. J. Therm. Sci. 2022, 171, 107204. [Google Scholar] [CrossRef]
- Waqas, H.; Wakif, A.; Al-Mdallal, Q.; Zaydan, M.; Farooq, U.; Hussain, M. Significance of magnetic field and activation energy on the features of stratified mixed radiative-convective couple-stress nanofluid flows with motile microorganisms. Alex. Eng. J. 2022, 61, 1425–1436. [Google Scholar] [CrossRef]
- Muhammad, T.; Waqas, H.; Manzoor, U.; Farooq, U.; Rizvi, Z.F. On doubly stratified bioconvective transport of Jeffrey nanofluid with gyrotactic motile microorganisms. Alex. Eng. J. 2022, 61, 1571–1583. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Vuthaluru, H.B.; Liu, S. Thermohydraulic and thermodynamics performance of hybrid nanofluids based parabolic trough solar collector equipped with wavy promoters. Renew. Energy 2022, 182, 401–426. [Google Scholar] [CrossRef]
- Song, Y.Q.; Hamid, A.; Sun, T.C.; Khan, M.I.; Qayyum, S.; Kumar, R.N.; Prasannakumarae, B.C.; Khanf, S.U.; Chinram, R. Unsteady mixed convection flow of magneto-Williamson nanofluid due to stretched cylinder with significant non-uniform heat source/sink features. Alex. Eng. J. 2022, 61, 195–206. [Google Scholar] [CrossRef]
- Kumar, L.H.; Kazi, S.N.; Masjuki, H.H.; Zubir, M.N.M. A review of recent advances in green nanofluids and their application in thermal systems. Chem. Eng. J. 2022, 429, 132321. [Google Scholar] [CrossRef]
- Dina, Q.; Shabira, M.S.; Asif, M. A Cubic Autocatalator Chemical Reaction Model with Limit Cycle Analysis and Consistency Preserving Discretization. Match-Commun. Math. Comput. Chem. 2022, 87, 441–462. [Google Scholar] [CrossRef]
- Scholes, C.A. Mass transfer basics and models of membranes containing nanofluids. In Nanofluids and Mass Transfer; Elsevier: Amsterdam, The Netherlands, 2022; pp. 369–384. [Google Scholar]
- Tembhare, S.P.; Barai, D.P.; Bhanvase, B.A. Performance evaluation of nanofluids in solar thermal and solar photovoltaic systems: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 153, 111738. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Roopa, G.S.; Prasannakumara, B.C.; Shah, N.A.; Yook, S.J. 3D Flow of Hybrid Nanomaterial through a Circular Cylinder: Saddle and Nodal Point Aspects. Mathematics 2022, 10, 1185. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, D.; Israr Ur Rehman, M.; Mousa, A.A.; Hamid, A. Numerical simulation of bioconvection radiative flow of Williamson nanofluid past a vertical stretching cylinder with activation energy and swimming microorganisms. Case Stud. Therm. Eng. 2022, 33, 101977. [Google Scholar] [CrossRef]
- Mahdy, A.; Hady, F.M.; Mohamed, R.A.; Abo-zaid, O.A. Activation energy effectiveness in dusty Carreau fluid flow along a stretched cylinder due to non-uniform thermal conductivity property and temperature-dependent heat source/sink. Heat Transf. 2021, 50, 5760–5778. [Google Scholar] [CrossRef]
- Shaheen, N.; Alshehri, H.M.; Ramzan, M.; Shah, Z.; Kumam, P. Soret and Dufour effects on a Casson nanofluid flow past a deformable cylinder with variable characteristics and Arrhenius activation energy. Sci. Rep. 2021, 11, 19282. [Google Scholar] [CrossRef]
- Colak, A.B. Analysis of the effect of arrhenius activation energy and temperature dependent viscosity on non-newtonian maxwell nanofluid bio-convective flow with partial slip by artificial intelligence approach. Chem. Thermodyn. Therm. Anal. 2022, 6, 100039. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Entropy Analysis of TiO2-Cu/EG Casson Hybrid Nanofluid via Cattaneo-Christov Heat Flux Model. Appl. Nanosci. 2018, 08, 1–14. [Google Scholar]
- Jamshed, W. Numerical Investigation of MHD Impact on Maxwell Nanofluid. Int. Commun. Heat Mass Transf. 2021, 120, 104973. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S. Computational single phase comparative study of Williamson nanofluid in parabolic trough solar collector via Keller box method. Int. J. Energy Res. 2021, 45, 10696–10718. [Google Scholar] [CrossRef]
- Jamshed, W.; Devi, S.U.; Nisar, K.S. Single phase-based study of Ag-Cu/EO Williamson hybrid nanofluid flow over a stretching surface with shape factor. Phys. Scr. 2021, 96, 065202. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S.; Ibrahim, R.W.; Shahzad, F.; Eid, M.R. Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. J. Mater. Res. Technol. 2021, 14, 985–1006. [Google Scholar] [CrossRef]
- Jamshed, W.; Nisar, K.S.; Ibrahim, R.W.; Mukhtar, T.; Vijayakumar, V.; Ahmad, F. Computational frame work of Cattaneo-Christov heat flux effects on Engine Oil based Williamson hybrid nanofluids: A thermal case study. Case Stud. Therm. Eng. 2021, 26, 101179. [Google Scholar] [CrossRef]
- Jamshed, W.; Mishra, S.R.; Pattnaik, P.K.; Nisar, K.S.; Devi, S.S.U.; Prakash, M.; Shahzad, F.; Hussain, M.; Vijayakumar, V. Features of entropy optimization on viscous second grade nanofluid streamed with thermal radiation: A Tiwari and Das model. Case Stud. Therm. Eng. 2021, 27, 101291. [Google Scholar] [CrossRef]
- Jamshed, W.; Nasir, N.A.A.M.; Mohamed Isa, S.S.P.; Safdar, R.; Shahzad, F.; Nisar, K.S.; Eid, M.R.; Abdel-Aty, A.H.; Yahia, I.S. Thermal growth in solar water pump using Prandtl–Eyring hybrid nanofluid: A solar energy application. Sci. Rep. 2021, 11, 18704. [Google Scholar] [CrossRef]
- Jamshed, W. Finite element method in thermal characterization and streamline flow analysis of electromagnetic silver-magnesium oxide nanofluid inside grooved enclosure. Int. Commun. Heat Mass Transf. 2021, 130, 105795. [Google Scholar] [CrossRef]
- Jamshed, W.; Eid, M.R.; Hussain, S.M.; Abderrahmane, A.; Safdar, R.; Younis, O.; Pasha, A.A. Physical specifications of MHD mixed convective of Ostwald-de Waele nanofluids in a vented-cavity with inner elliptic cylinder. Int. Commun. Heat Mass Transf. 2022, 134, 106038. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).